Small-Area Estimation of Health Insurance Coverage for California Legislative Districts

Abstract

Objectives. To aid state and local policymakers, program planners, and community advocates, we created estimates of the percentage of the population lacking health insurance in small geographic areas of California.

Methods.Finally, calibration ensured the consistency and stability of the estimates when they were aggregated.

Results. Health insurance coverage among nonelderly persons varied widely across assembly districts, from 10% to 44%. The utility of local-level estimates was most apparent when the variations in subcounty uninsured rates in Los Angeles County (19%–44%) were examined.

Conclusions. Stable and useful estimates of health insurance rates for small areas such as legislative districts can be created through use of multiple sources of publicly available data.

Lack of health insurance is a chronic public health problem for over 45 million children and nonelderly adults in the United States.1 California, the most populous state,2^,3 has the third highest uninsured rate nationally.4^–6 An estimated 19% of California’s population, 6.3 million adults and children, went without health insurance coverage in 2001.7 Although California is a large and diverse state, its uninsured population is unevenly distributed. Having no health insurance has been associated with socioeconomic status, race/ ethnicity, age, and area of residence.8^–12

Expanding health insurance coverage has been a priority in many state legislatures. Federal funds for the State Children’s Health Insurance Program have been used to create many new state initiatives. In the past decade, there have been other state health policy initiatives to further expand health insurance to children, as well as to reduce the number of uninsured adults.13

Legislators want to know how their districts will be affected by these initiatives; however, current sources of data on health insurance do not provide information at the legislative district level. Nationally, the primary source of health insurance information is the March Current Population Survey (CPS) of the US Census Bureau, which provides annual estimates of the uninsured population. Its ability to generate substate estimates is limited, however, especially for metropolitan areas with populations under 500 000.14 In addition, California legislative districts do not follow administrative boundaries, such as counties or metropolitan statistical areas (MSAs), that public data sources identify. Estimates are therefore needed for California Assembly districts, which have approximately 400 000 residents each, and geographic areas with meandering census tract boundaries. (In 2000, legislative districts were redrawn with census blocks used as boundaries.)

In response to the demand for local-level data on health insurance, we developed a small-area estimation procedure to calculate the numbers and percentages of the population without health insurance in California’s legislative districts in 2000, including all 80 assembly districts. Rao15 has reviewed the methodology and application of small-area estimation in health-related research. Small-area estimation has been used to produce estimates for the prevalence of overweight adults,16 substance abuse,17^,18 and physician visits.19 The US Census Bureau’s Small Area Income and Poverty Estimates program provides intercensual data of selected income and poverty statistics for states, counties, and school districts.20^,21 However, small-area methodology has only recently been applied to health insurance coverage. The US Census Bureau’s Small-Area Health Insurance Estimates project developed model-based estimates for the numbers of the uninsured population for states and counties.22 However, the Small-Area Health Insurance Estimates project is limited in its ability to derive estimates for areas smaller than the county level.

Using regression models and data from multiple sources, we developed a small-area methodology to derive synthetic estimates of uninsured rates at subcounty levels. Our method, which is similar to another approach independently developed by Twigg et al.,23 is flexible and can be replicated to develop similar estimates at any geographic level of interest that is compatible with public data sources.

METHODS

The estimates we produced are “synthetic estimates” because we begin with a survey designed for estimating rates for a larger area and use the pattern of associations for that area to derive estimates for a smaller area.24 The CPS was a rolling sample design in which a portion of sampled subjects are included in the sample of the following year and questioned again. The survey we used was the CPS, which was designed to make unbiased estimates of states and larger metropolitan areas. To apply the findings from this survey to create estimates of legislative districts, we also used 1990 decennial census data, legislative district boundary files, and updated small-area population projections available from Claritas (San Diego, Calif), a private marketing research firm that produces annual demographic updates. The methodology we developed involved 3 major steps: modeling, merging, and calibrating.

Modeling

In the first step, we modeled the probabilities of being uninsured using the March CPS. The CPS conducts interviews with approximately 60000 households nationwide annually and obtains information on more than 150 000 individuals, including more than 14000 in California. The March supplemental survey includes comprehensive questions on health insurance coverage and other demographic characteristics. Questions about insurance coverage at any time during the preceding calendar year provide approximate rates of uninsurance for that entire year. We linked data from 1998–2000 California samples from the March CPS to ensure sufficient sample sizes for this study. Previous studies have found strong associations between insurance status and demographic and socioeconomic characteristics.12 We therefore included age, gender, race/ethnicity, and income-to-poverty ratio as predictors in logistic regression models. These variables are available in both the CPS and the 1990 census, allowing us to apply the results from the CPS-based models to the census-based population data at the census tract level. We used cross-classifications of age, gender, race/ethnicity, and poverty (see Table 1 ▶ for detailed categories).

TABLE 1—

Distribution of Age, Race/Ethnicity, and Income-to-Poverty Ratios in Selected Metropolitan Statistical Areas: California, 2000

	Los Angeles	Oakland	Anaheim–Santa Ana	Riverside–San Bernardino	Sacramento	San Diego	San Francisco	San Jose
Age, y, %
0–4	8.47	6.96	8.18	8.50	7.11	6.90	4.36	9.12
5–17	20.62	16.32	17.59	24.69	19.23	19.92	12.69	17.78
18–24	10.30	8.54	8.50	8.98	10.28	11.77	10.18	7.22
25–44	32.64	34.15	33.91	31.09	27.71	30.94	39.44	35.93
45–64	18.78	22.74	20.72	17.15	21.68	19.09	23.92	20.63
≥65	9.19	11.30	11.11	9.59	14.00	11.38	9.41	9.32
	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00
Race/ethnicity, %
Latino	44.51	10.38	24.30	31.49	11.37	22.54	15.90	22.89
Non-Latino White	34.83	62.23	59.40	50.33	67.07	56.18	57.40	46.47
African American	8.20	12.32	1.76	10.44	5.98	5.19	3.51	4.04
Asian	11.66	14.78	13.80	6.27	15.21	15.80	21.39	24.95
Native American	0.80	0.29	0.74	1.47	0.37	0.29	1.79	1.65
	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00
Income-to-poverty ratio,a %
< 100	19.60	7.45	8.63	16.30	17.35	14.48	6.84	8.00
100–133	8.08	2.91	6.43	6.79	7.74	6.18	4.92	5.22
134–200	14.74	7.40	12.53	14.20	7.69	13.22	9.14	8.00
201–250	9.11	6.55	7.20	11.21	8.42	7.08	6.05	6.09
251–300	7.14	6.82	6.91	8.44	5.57	10.55	5.63	5.91
≥ 301	41.33	68.87	58.30	43.06	53.24	48.50	67.42	66.78
	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00

Source. Current Population Survey, 1998–2000.

^aIncome as a percentage of the federal poverty line.

In creating the outcome variable for the logistic regression models, we classified individuals as insured in the previous calendar year if they had employment-based coverage, privately purchased coverage, or public assistance coverage; individuals who did not have any identifiable coverage were classified as uninsured.

We expected that racial/ethnic populations, especially immigrants, would cluster in defined geographic areas. We therefore divided California into 12 smaller regions based on individual MSAs or groups of adjacent MSAs: San Jose, Sacramento, Oakland, Riverside–San Bernardino, San Francisco, San Diego, Anaheim–Santa Ana, Los Angeles, the remainder of Southern California, the Greater Bay Area, the remainder of Northern and Central California, and all other areas. The last group included all areas not identifiable in the CPS (Table 1 ▶ shows data for the 8 largest regions). We then fit separate logistic regressions for each region (stratified models). This approach is a departure from that by Twigg et al.,23 which used multilevel models. By fitting separate regressions, we simplified models that preserved geographic variation of the effects of predictors on uninsured rates across California.

Merging

Next we merged the predicted probabilities derived from the CPS models into population data at the census tract level within the geographic regions noted in the previous paragraph. By 2000, the 1990 census data at the tract level were outdated, and the 2000 census data were not yet available. We therefore had to update the 1990 census data.

For updated data at the census tract level, we purchased population estimates from Claritas. Their total population and household estimates at national, state, county, and place levels start with estimates produced by the Census Bureau and, in some cases, by state agencies. The intercensual populations at the census tract and block group levels incorporate counts of addresses to which the US Postal Service delivers mail and household counts from the Total Source consumer database of Equifax (Atlanta, Ga), a major credit report agency. When Claritas recently compared their 2000 population household estimates with the 2000 census population and household counts, it found an average of 11.6% census tract–level errors and 15.3% block group–level errors in the Claritas estimates. However, the error rate drops substantially after a small aggregation of 6 block groups (Claritas, unpublished data, 2004). We therefore anticipated that potential errors in the Claritas population projections would not have a significant effect on our results because we were aggregating our estimates to larger assembly and senate districts.

The Claritas population projections were based on noninstitutionalized populations, consistent with the CPS sampling universe. The population projections thus included the total US resident population regardless of citizenship status, minus persons living in group quarters, such as nursing homes, college dormitories, and prisons. Although the Claritas 2000 population projections contained basic demographic variables—such as age, gender, and race/ethnicity—at the census tract level, they did not include information on poverty. Adding poverty estimates to the Claritas data required additional steps. The base information was the 1990 census tract–level poverty ratios. Because the 1990 census did not contain sufficient details on incomes above 100% of the federal poverty line, the income data was insufficient for application of model of insurance coverage (developed in CPS). Therefore, we modeled the distributions of 6 income-to-poverty ratios in concatenated 3-year CPS data (1989–1991). The estimated income distributions were then merged into and adjusted by the same income categories in the 1990 census Summary File 4 (SF4) data. This step created estimates that aggregated to the published rates for the less detailed poverty ranges at the tract level by age and race/ ethnicity. The derived poverty ratio distributions were then adjusted by the data from concatenated 3-year CPS data (1998–2000) to account for changes in income distributions during the decade. This step provided the data on poverty ratios, which the Claritas data previously lacked. (Detailed procedures are available upon request from the first author.)

Goodness-of-fit is important when the predicted probabilities from a logistic regression model are applied to new data.25 A commonly used measure is the Hosmer–Lemeshow goodness-of-fit test, which compares observed to predicted outcomes across several strata. In our modeling, most of the models in both steps (imputing poverty and predicting uninsurance) fit well (χ² test with P >.05), although some models had P values less than .05, which happened mainly in large metropolitan areas with diverse populations. Given the limited predictors available, we tried to improve the fit by including interactions in the models. For the logistic model predicting uninsurance in Los Angeles County, which used only the main factors of age, gender, poverty, and race/ethnicity, the P value for χ² was less than .0001, indicating inadequate fit. To improve this, we included second-order interactions. A stepwise procedure was then used to select interaction terms in the model while forcing the main factors to stay in the model. The P value of the resulting model was .323, indicating a satisfactory fit.

The final step in the merging process was to calculate the numbers of uninsured in each legislative district. We first applied the parameter estimates from the CPS uninsurance models to the created 2000 population projections to derive the predicted probabilities of being uninsured; this procedure was conducted for each of the 12 regions. We then multiplied the predicted probabilities by the population projections to estimate the numbers of uninsured. Finally, we calculated the numbers of uninsured for each legislative district by aggregating the numbers of uninsured for all the census tracts within each legislative district.

Calibrating

Because the CPS is widely used for estimates of the uninsured population and our predictive model was created with the CPS, our estimates needed to be consistent with direct estimates from the CPS. We therefore “calibrated” our synthetic estimates with direct estimates from the 2000 March CPS, using 3 steps. First, we obtained direct estimates of the uninsured rate (E₁) from the CPS for a given geographic area A, such as Los Angeles. Second, we derived the uninsured rates (E ₂) from the merged Claritas data in area A by aggregating the numbers of uninsured in each census tract in the area calculated in the merging step and then dividing it by the total population in that area. An adjustment factor r was derived as r = E₁/E ₂. The third step was to apply this r to all the census tracts in the defined area to calculate the adjusted numbers of uninsured. The uninsured rates in legislative districts were calculated by aggregating the final adjusted number of uninsured in the census tracts in each district and dividing it by the total population in that district.

This calibration step also reduced potential errors in the estimates that would have resulted from the models lacking an ideal fit. Calibration kept our estimates at local levels consistent with the latest CPS estimates and, in essence, reduced the function of the models to distributing the number of the “known” uninsured among the census tracts within each region. That is to say, our final goal was not to estimate the number of uninsured persons but rather to estimate the distribution of a fixed number of uninsured persons into geographic subareas (legislative districts) that had specific population characteristics.

Our final step in the calibration process was to calculate the variances of the uninsured estimates for legislative districts and their corresponding coefficients of variation. We designated 30% as the cutoff for acceptable coefficients of variation, consistent with the standard practice of the National Center for Health Statistics.26 When coefficients of variation were larger than 30%, we enlarged the area A and repeated the calibration until the coefficient of the estimate became less than 30%.

In these calculations, we assumed that the population data were fixed and that all the variances came from the components related to the CPS survey. The calculation of variances consisted of 2 steps. First, we applied the formula by Taylor expansion in which the variance–covariance matrix for estimated regression coefficients in the model was “sandwiched” by the partial derivatives of the probability estimator with respect to the regression coefficients in the model. The matrix was derived from the CPS model. Second, another Taylor approximation was applied to take into account the ratio adjustment of the calibration. (Further details can be found in the methodological appendix, available upon request from the first author.)

RESULTS

Table 1 ▶ shows demographic characteristics of California’s population for 8 of the 12 regions. These 8 regions are the largest in the state and illustrate the variations in population characteristics. Overall, Riverside–San Bernardino had the youngest population and San Francisco the oldest. The highest proportions of Latinos were located in Los Angeles and Riverside–San Bernardino. The highest proportions of non-Latino Whites, Asians, and Native Americans were found in Northern California, whereas the largest proportions of African Americans were found in both Northern (Oakland) and Southern California (Riverside–San Bernardino). Los Angeles and Riverside–San Bernardino also had the highest proportions of poor and near-poor residents, whereas the greater San Francisco area had the highest proportions of residents with income-to-poverty ratios of 300% and higher. This regional variation supports the importance of modeling insurance coverage through use of samples stratified by region.

Figure 1 ▶ shows the point estimates and corresponding confidence intervals for the uninsurance rate in California’s 80 assembly districts, which are the smallest geographic areas in our study. The estimates show that health insurance coverage among nonelderly persons varied widely across assembly districts, from 10% to 44%.

FIGURE 1—

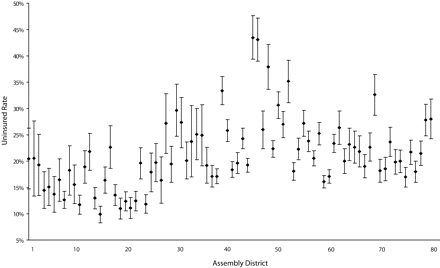
Uninsured rates, with corresponding 95% confidence intervals, among population aged 0 to 64 years by assembly district: California, 2000.

Note. California assembly districts are numbered north to south, from Assembly District 1 (AD1) along the Oregon border to AD80 along the Mexican border.

The utility of local-level estimates was most apparent when the variations in subcounty uninsured rates in Los Angeles County were examined (Table 2 ▶). The CPS direct estimate of the uninsured rate for Los Angeles County was 32%. This rate, though alarmingly high, provided insufficient specificity for a diverse and populous area like Los Angeles County. The county comprised 25 assembly districts with varying incomes and racial/ethnic distributions. On the basis of known correlates of insurance status, we expected that districts with higher average incomes and lower proportions of Latino residents were likely to have lower uninsured rates than were districts with lower average incomes and higher proportions of Latino residents. For example, Assembly District 38 in northwestern Los Angeles County had a population that was predominantly non-Latino White with incomes above 300% of the federal poverty level in 2000. In contrast, Assembly District 46, located in and around downtown Los Angeles, had the most ethnically diverse population and the highest concentrations of low-income residents of all California assembly districts. As expected, the uninsured rate in Assembly District 38 (19%) was the lowest in Los Angeles County, and the rate in Assembly District 46 (44%) was the highest.

TABLE 2—

Estimated Uninsured Rates of Selected California Assembly Districts (ADs) in the Greater Los Angeles Area: California, 2000

		Population by Race/ Ethnicity (All Ages), %					Population by Income-to-Poverty Ratioa (All Ages), %
Assembly District	Rate of Uninsured (Ages 0–64 y), %	White	Latino	API	African American	Native American	< 100	100–200	201–300	≥301
AD38 (San Fernando Valley)	19	64	22	12	2	0	7	16	18	59
AD47 (Culver City and Crenshaw)	28	24	31	9	36	0	20	23	15	42
AD51 (Inglewood)	31	15	44	9	32	0	22	25	16	37
AD46 (Downtown Los Angeles)	44	3	75	15	7	0	37	35	10	18

Note. API = Asian/Pacific Islander. Tables of the uninsured rates and corresponding demographic data for all assembly and senate districts in California can be found in Brown et al.27

^aIncome as a percentage of the federal poverty line.

Figure 2 ▶ is a map of estimated uninsured rates across Los Angeles County, as well as all of California. Such maps are popular with policymakers and advocates because the maps allow policymakers to determine quickly and intuitively how their districts are faring compared with others.

FIGURE 2—

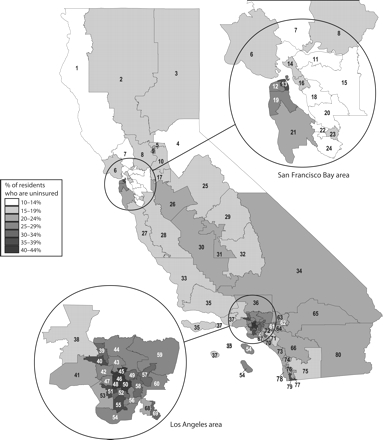
Map showing uninsured rates among population aged 0 through 64 years by assembly district: California, 2000.

DISCUSSION

Small-area estimation methods have 2 aspects, generality and specificity. The former reflects the fact that to derive relatively stable estimates for small areas, a method has to “borrow strength.” This occurs by making use of the shared characteristics in a larger area that contains the smaller area of interest. Specificity reflects the fact that a desirable estimate should preserve some “locality” that makes the area distinct from others. Therefore, most methods for small-area estimation have fixed effects for characteristics that are shared by the large domain and also random effects that accommodate the variations among the small areas of interest.

Twigg and Moon28 compared their synthetic estimations with direct estimates from 3 local surveys on smoking and unsafe drinking. They found a clear disparity between the 2 sets of estimates, a finding that could be attributed to differences in the design of the surveys and how they were conducted but also to the very nature of small-area estimation. In their study, the estimates for small areas that used global models based on national (United Kingdom) data tended to be closer to the mean for the entire data set than the direct estimates for the same areas. The extent of this phenomenon is called “shrinkage.” “Borrowing strength” therefore has the effect of forcing the estimates into a narrower range than that provided by the direct measurements.

Our method departs in several aspects from that of Twigg et al.23 Most notably, we fit separate models for individual MSAs or groups of MSAs so that we could retain regional variations in the state, thereby reducing the problem of shrinkage to the global mean (i.e., statewide average). The second major difference was that we also calibrated our small-area estimates to “reliable” direct estimates. The CPS data is widely used to estimate uninsured rates; therefore, we used the data as a gold standard and made our estimates consistent with other published estimates. However, because the calibration process was applied uniformly across the MSA level, it may have overadjusted or underadjusted the uninsured rates in some subareas within an MSA.

Limitations

There are several limitations to our study. First, our small-area estimations are not the actual rates of the uninsured, even though studies have indicated that income, race/ ethnicity, age, and gender are good predictors of having no health insurance.29 In particular, we were not able to account for the effects of local initiatives on the true uninsured rate. For instance, if a community had a successful outreach effort to enroll those who were uninsured but eligible for public programs, the success of that effort might not be reflected in the estimates that were derived from the patterns of a much larger area. Small-area estimations are therefore not appropriate for evaluating the success of local coverage initiatives. Second, the accuracy of our results heavily relied on the quality of the CPS and Claritas data. The CPS data underestimates the participation rate in public insurance, such as Medicaid, which may result in an overestimation of uninsured rates.30 Consequently, our uninsured rates may have been overestimated for some areas, especially areas with high concentrations of Medicaid enrollees.

Finally, the CPS’s “rolling sample” design means that some of the same respondents are surveyed in consecutive years, making the samples not fully independent across years. However, we lacked the precise information to measure, and therefore to account for, its effect in the models and variance calculations. In addition, by assuming that the population data from Claritas were fixed, we omitted a potential measurement error associated with the projection process. These factors would potentially make the true confidence intervals wider than those presented in Figure 1 ▶.

Conclusions

These findings show that small-area estimation is a powerful tool for revealing variations in uninsured rates in local areas. Our statewide estimates of uninsured rates by legislative districts, which were the first of their kind, were well received by policymakers. The data became an essential reference for state politicians and advocates to gauge their constituencies’ needs. Even in districts with comparatively low rates of uninsured persons, advocates made influential arguments that the numbers of uninsured persons were unacceptably high.

Using a small-area estimate methodology provides 1 route to producing stable estimates of the uninsured population at local levels. By applying models derived from regional data to more localized population projection data, this method allows the creation of small-area estimates for many different geographic units, including legislative districts, cities, and small counties, that can be created from census and other data. The resulting data are informative for decisionmaking and planning efforts to expand health insurance coverage across the country.