Phosphatidic Acid Domains in Membranes: Effect of Divalent Counterions

Abstract

Phosphatidic acid (PA) is emerging as a key phospholipid in a wide range of biological processes such as signal transduction, secretion, or membrane fusion. In most cases, the biological functionality of PA is associated with the presence of micromolar to millimolar calcium concentrations. It has been argued that PA can create defects in the packing of lipids in membranes due to lateral phase separation by divalent ions, which in turn aggregate proteins with high affinity for PA. In this article, we present a detailed investigation of the properties of PA domains in the presence of divalent ions by a combination of molecular dynamics simulations and theoretical methods. Our results show that PA is extremely effective in binding divalent ions through its oxygen atoms, with a broad distribution of binding constants and exhibiting the phenomenon of charge inversion (a total number of bound counterion charges that exceeds the negative PA charge). We predict that a PA-rich domain undergoes a drastic reorganization when divalent cations reach micromolar concentrations (i.e., typical physiological conditions), as PA lipids become doubly charged by releasing their protons. We also present a detailed investigation of the properties of interfacial water, which determine the binding of proteins or other molecules. We conclude with a discussion of the implications of our results in the context of recent experimental studies in model systems and in real cells.

INTRODUCTION

Phosphatidic acid (PA) is not particularly abundant in any living organism membrane, yet is emerging, together with Lyso-PA (LPA) (which differs from PA in that it has only one hydrocarbon chain), as key phospholipids in both animals and plants, with an astonishing implication in a wide variety of processes such as signal transduction, secretion, membrane trafficking, or cytoskeleton rearrangement among others (1–4). In plants, for example, PA is involved in aggregating signaling proteins in domains (rafts), which, at least in some cases, have been identified (4). LPA is also extremely important biologically; it is produced by many different cell types and most mammalian cells express receptors for LPA. Interest for LPA has been also stimulated by a correlation between an increase on its concentration and the first stage of human ovarian cancer (3). Furthermore, it is well established that both PA and LPA are involved in the mechanism of fission in cell membranes (2,5–7), although its precise role is still unclear (8).

The different biological roles of both PA and LPA are strongly related to changes in concentration of Ca²⁺ ions (1), itself an ubiquitous intracellular messenger (9). This strong Ca²⁺ sensitivity is not unique to PA or LPA, but it is shared by the phosphatidylinositides (PI,PIP₂,PIP₃, etc..), whose roles often overlap or complement with those of PA (4). There is experimental evidence, for example, that the presence of small divalent ion concentrations induces the formation of PA-rich domains that in turn activate PLA₁ (phospholipase A1) (10). Other phospholipases (PLD or PLC) are also activated by Ca²⁺ ions in the micromolar regime, although millimolar concentrations have also been reported (11).

What is specific about PA or LPA that enables these relatively simple lipids to perform such diverse biological roles? Investigations on the physicochemical properties of PA in model systems provide some interesting clues. At physiological conditions (0.1 M NaCl) and in the absence of Ca²⁺, fluorescence microscopy studies on Langmuir monolayers of dimiristoyl PA (DMPA) reveal highly ordered gel domains, in some cases forming a hexagonal superlattice, coexisting with liquid domains for a wide range of surface pressures (12). In the presence of Ca²⁺ ions, it is found that the surface pressure decreases drastically and the domains disorder (13). Very recently, surface sensitive anomalous x-ray studies have allowed precise quantitative studies on the binding of both divalent (Ba²⁺) and trivalent (La³⁺) ions to DMPA (14,15), and show a strong binding already at the micromolar range, with a total number of bound counterion charges that exceeds the negative DMPA charge, that is, the system exhibits charge inversion. These experiments show that divalent ions bind very strongly to PA domains, even at very low concentrations (10⁻⁶ M), drastically changing their lateral organization. Furthermore, the vanishing surface pressure almost up to close packing observed in the pressure-area isotherms provides evidence that divalent ions may induce PA aggregation.

While the strong affinity of PA and LPA for Ca²⁺ ions and its ability to induce drastic lipid reorganizations is well established experimentally and it is believed to be of fundamental biological importance, very little is known about PA. It is not known, for example, what is the lateral organization of bound Ca²⁺ and PA in lipid domains. Furthermore, with two dissociable protons, the electric charge of a single PA molecule may range from q = 0 to q = −2e, depending on environmental conditions such as pH or divalent ion concentrations. This ability of PA to regulate its charge may be of critical importance in, for example, its role as a second messenger (4). Other properties, such as the role of interfacial water near PA domains are also of interest, as it is directly related to the dielectric response, which in turn determines the binding constants of Ca²⁺ ions and the precise way in which PA functions as an effector. The charge inversion observed in Langmuir monolayers of PA is quite striking, as it takes place already in very dilute regimes (micromolar or less) (14,15). Although other charged phospholipids, such as phosphatidylserine, also exhibit charge inversion, it is necessary to reach salt concentrations that are five orders of magnitude larger (∼0.1 M)(16).

In this article, we present a detailed study combining all united atom molecular dynamics (MD) simulations of PA with theoretical arguments to investigate the different structures formed by bound ions and PA, the restructuring of water near a PA interface, charge inversion, phospholipid charge regulation, and their biological implications. The main tool used in our investigation is MD simulations, which although limited to systems with a few hundred lipids and timescales of the order of a nanosecond, is becoming a powerful tool to investigate model membranes (17,18). MD has provided valuable insight into electrostatic properties such as dipole moment, electric potentials, or effects associated with ionic strength, in systems such as phosphatidylcholine (PC) and phosphatidylserine (PS) bilayers (18,19), PC/PS mixtures (20), or PS/cationic lipids mixtures (21).

Our study presents, to our knowledge, the first MD simulation of a PA system and differs from previous MD simulations on membranes in several significant aspects, which we now describe. PA distribution in biological membranes is very asymmetric, with PA basically confined to the leaflet in contact with the cytosol (1). We therefore conducted our studies on a single DMPA leaflet in contact with an aqueous solution. Although appropriate for the goals of our study, our simplification precludes the analysis of parameters, often reported in other MD simulations, such as hydrocarbon tilt or molecular area (18). All our simulations were conducted with DMPA (1,2-dimyristoyl-sn-glycero-3-phosphatidic acid) in contact with a BaCl₂ solution. We perform our study with the divalent ion Ba²⁺ because this ion is particularly well suited for experimental studies because of its resonance in the x-ray region (14). This will allow us to compare and validate our results with ongoing x-ray experiments that make use of the Ba²⁺ ion. In the absence of ion channels or proteins with specific Ca²⁺ binding sites, the results obtained with Ba²⁺ should not result in significant quantitative differences from Ca²⁺, since Ba²⁺ only differs from Ca²⁺ in that it has a slightly larger radius (by 0.35 Å) (22).

MODEL AND METHODS

Formulation of the model

Our model for a PA membrane domain consists, as explained in the introduction, in a single phospholipid leaflet in contact with aqueous solution. The phospholipid leaflet containing PA is modeled as a monolayer of DMPA phospholipid with the same area per phospholipid (41 Ų) used in x-ray experiments (14).

An important point in the modeling of the DMPA molecule is the dependence of its charge with environmental conditions such as the concentration of divalent ions. Let us remark that this dependence of the dissociation of DMPA protons on ion concentration cannot be simulated within present molecular dynamics techniques, so one needs to rely on theoretical arguments and/or experimental data to assume a priori a fixed protonation state of the phospholipids in the simulations. Isolated PA molecules should be found as both PA⁻ and PA²⁻ in equal concentrations since phosphoric acid has a first 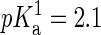and second 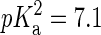(23). However, the situation is different in a membrane in contact with aqueous solution containing counterions. Counterions compete with the protons for the oxygen binding sites, modifying the protonation state of the phospholipids. This effect is already observed for monovalent ions (24–26), but becomes more drastic for divalent or trivalent ions. In the case of divalent ions, there is a critical ion concentration (n_c) where DMPA releases its two protons in favor of the divalent ions. This concentration is obtained by equating the free energy of binding for divalent ions and protons, 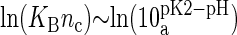, where K_B is the equilibrium constant describing the binding of divalent ions. At neutral pH, this gives n_c ∼ 1/K_B. All the simulations reported assume that DMPA is doubly deprotonated, so DMPA has an electric charge of q = −2e. Later in the article we will obtain self-consistent predictions for K_B, thus showing the validity of this assumption within the regimes where our simulations are performed.

Methods employed in the analysis of ion binding

To study the binding of Ba²⁺ counterions to DMPA using MD simulations, we need to introduce a definition allowing us to distinguish between a bound counterion belonging to the Stern layer and a bulk counterion, belonging to the diffuse layer. We employ a structural definition, assuming that a Ba²⁺ counterion is bound to a DMPA molecule if there is at least one DMPA oxygen in its first coordination shell. Consequently, a bulk Ba²⁺ ion (or equivalently, one belonging to the diffuse layer) contains only oxygens from water molecules in its first coordination shell. As usual in MD simulations (34), the identification of the first coordination shell is based on the radial distribution function (rdf). The rdf functions g(r) describing the correlations between Ba²⁺ and the different types of oxygen atoms are defined by:

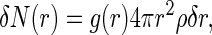(1)

where δN(r) is the number of oxygen atoms of a given type (from water molecules or from DMPA molecules, named according to Fig. 1) in a small shell between r and r + δr around a given Ba²⁺ ions and ρ is the number density of the oxygen atoms. An oxygen atom (from a water molecule or from DMPA) is assigned to the first coordination shell of a Ba²⁺ ion if their separation is smaller than the distance r corresponding to the first minimum of the g(r) function between these two types of atoms.

FIGURE 1.

Scheme of the DMPA molecule, indicating the name and partial charge of each united atoms.

In the study of ion binding we are also interested in the determination of the equilibrium constants for ion binding to phospholipids. These constants can be estimated by a combination of theoretical methods and simulation results. Assuming an electrostatic binding of counterions, K_B can be computed using a generalization of the Bjerrum pairing theory in electrolytes (38), which gives the formula:

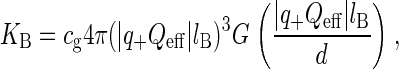(2)

where 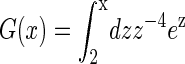and 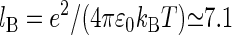Å is the Bjerrum length. Here d is the sum of the crystallographic radius of Ba²⁺ and the electronegative atoms bound to Ba²⁺ (in this case oxygen atoms, so d ≈ 3 Å) and q₊ = 2 is the valence of Ba²⁺ and Q_eff is the effective charge of the interface interacting with the bound counterion. An accurate evaluation of Q_eff requires a complex analysis, discussed for example in Faraudo and Travesset (41). In this article, we will estimate Q_eff by the sum of the valences of all DMPA oxygens bound to the counterion, an approximation that is sufficiently accurate for the purpose of this article (41). The factor c_g < 1 is a geometric correction that takes into account steric constraints (38). For example, for counterions binding at a planar surface in contact with water, c_g ≈ 1/2 because half of the space (the one that is not in contact with water) is not accessible to the counterions.

Evaluation of K_B from Eq. 2 requires the knowledge of the number of DMPA atoms bound to the counterion (to obtain Q_eff) and its spatial organization (to compute c_g). We will estimate these quantities from the simulation results, thus providing an estimate for K_B, and obtain the critical concentration n_c where DMPA becomes doubly deprotonated by the formula 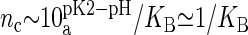, with 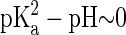as discussed previously.

Simulation algorithms and force field

MD simulations were carried out using the DLPOLY2.15 package (33) running in parallel mode with 64 dual processors PowerPC 970FX. All simulations correspond to ambient temperature (T = 298 K), which was simulated using the Nose-Hoover thermostat, with a relaxation constant of 0.5 ps. The equations of motion were solved using the Verlet leapfrog algorithm (34) with a time step of 0.002 ps.

The force field employed in our MD simulations is based on the AMBER 94 force field (27), taking into account the modifications proposed in Smondyrev and Berkowitz (28) for simulations of phospholipids and the results in Kim (31) and Dang (32) for the simulations of Ba²⁺ and Cl⁻ ions. Intermolecular interactions are described by electrostatic and Lennard-Jones 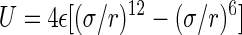potentials. The Lennard-Jones interactions were cut off at 14 Å. The partial charges and Lennard-Jones parameters for all united atom are summarized in Table 1.

TABLE 1.

Nonbonding interactions

United atom	ε (kJ/mol)	σ (Å)	q/e
Ba	1.8815	3.8166	2.0
Cl	0.4179	4.4010	−1.0
O (water)	0.6502	3.1660	−0.8476
H (water)	0	0	0.4238
CH3	0.7322	3.9050	0
CH2	0.4937	3.9050	0
CH2A	0.4937	3.9050	0.400
CH2B	0.4937	3.9050	0.500
CH	0.3347	3.8500	0.300
CA	0.4393	3.7500	0.700
CB	0.4393	3.7500	0.800
OA	0.8786	2.9600	−0.600
OB	0.8786	2.9600	−0.700
OS	0.7133	3.0000	−0.700
O2	0.8786	2.9600	−0.800
P	0.8368	3.7400	1.100

Parameters for Lennard Jones interactions and partial charges (in units of the elementary charge). The cross Lennard-Jones interactions between atoms of different species were obtained from the data given in this table using the combining rules σ_ij = (σ_i + σ_j)/2 and .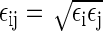

Water was modeled using the SPC/E model (29), which has been shown to provide an accurate representation of water properties at ambient temperature at a relatively low computational cost (30). The DMPA²⁻ molecule was modeled using the united atoms shown in Fig. 1. The bonds between united atoms of each DMPA molecule were described by harmonic potentials U = k_b(r − r_eq)²/2 with parameters from Smondyrev and Berkowitz (28). Bending and torsional intramolecular forces use the potentials and parameters described in detail in Smondyrev and Berkowitz (28).

The Coulombic interactions were computed using the Ewald summation method (34) with a precision of 10⁻⁵ with periodic conditions along the three directions. We avoided Ewald summation methods periodic only in the x- and y-directions because simulation times become prohibitive (see, for instance, Yeh and Berkowitz (35) and Spohr (36)). This three-dimensional Ewald summation technique introduces in the simulation a spurious electrostatic interaction of the system with its own images in the z-direction, which needs to be minimized. This undesired effect can be effectively eliminated (35,36) by using sufficient empty space in the z-direction and adding a correction force F_z ≈ Kq_iP_z/V acting on each charge q_i of the system (where P_z and V are, respectively, the total dipolar moment and the volume of the simulation cell). Hence, we use a large value of L_z (L_z = 200 Å) in our simulations and we also monitor the total dipolar moment per unit volume P_z/V during the production runs. We consider two different system setups to identify and minimize possible effects due to the total dipolar moment. The first simulation (designed as MS simulation from now on) corresponds to a phospholipid/water/vacuum system. During the production runs (described in detail in the next subsection), we observe a very small total dipolar moment per unit volume P_z/V ≈ 1.1 × 10⁻³ C/m². This dipolar moment causes a force F_z ≈ 1.6 pN over a charged particle (with charge e) which is negligible in our simulations since the typical instantaneous vertical forces observed over ions are of the order F_z ≈ 10²–10³ pN. Also, we consider a second simulation with a phospholipid/water/phospholipid bilayer (designed as BS simulation from now on) where the average dipolar moment is zero by construction. In this case, the thickness of the water film has to be large enough to minimize possible interactions between both phospholipid layers. As we will see in the analysis of simulation results, we found that the results for both simulations are consistent, as expected from our previous arguments.

The value of the cutoff employed in the calculation of electrostatic interactions is crucial since it determines both the accuracy and the computational cost of the simulations. It has been shown that the errors in the Ewald calculation of the electrostatic interaction decrease exponentially with the cut-off value (34) and the magnitude of the errors depend strongly on the system considered. Simulations of PC or PS⁻ bilayers typically require cutoffs ∼1 nm (19–21). In the case of ionic Newton black films, which are highly charged systems (charge density −e/33 Ų) cutoffs of 2.2 nm are required (42,37). To guarantee the correctness of our results we employed the same cutoff as in Newton Black Films simulations. As a result, our tests indicate that simulations are slowed down by a factor of 3 (with respect to a 1-nm cutoff).

Equilibration and production runs

We have performed one simulation for a monolayer system (MS) and a simulation for a system containing two monolayers (BS) separated by a water film. The MS simulation contains N_w = 9132 water molecules, a layer of N_DMPA = 100 phospholipid molecules, 100 Cl⁻ ions, and 150 Ba²⁺ neutralizing counterions. The simulation BS contains two layers of N_DMPA = 100 phospholipid molecules coating a water film containing N_w = 9372 water molecules, 40 Cl⁻ ions, and 220 Ba²⁺ counterions. The size of the simulation box is L_x = L_y = 64 Å and L_z = 200 Å, and periodic boundary conditions were applied in all three directions. With these values, we obtain a molecular area per phospholipid ∼41 Ų (the same employed in the experimental system of Vaknin et al. (14)).

The initial configuration for the simulations was obtained by adding the phospholipids with an equal number of Ba²⁺ counterions on the top or the bottom of a previously equilibrated water slab. Then, several runs were performed in which some water molecules were transformed in ions until we obtained the desired number of ions. Using the configuration generated in this way, we performed (for both MS and BS simulations) an equilibration run of duration t_eq followed by a production run of t_prod. The values t_eq = 1.5 ns and t_prod = 2.3 ns were selected after a careful analysis of the equilibration process and the time decay of correlations present in the binding process, which we will discuss now in detail. At this point, we would like to remark that these values for equilibration and production times are of the same order of magnitude than those previously employed by other authors in the study of similar systems. For example, according to Pandit et al. (20), the study of the binding of Na⁺ to DPPS⁻ bilayers required production runs of 2 ns. Furthermore, putative PA domains are expected to be in a gel-like phase, where the diffusion constants of the phospholipids are extremely small. Therefore, we can ignore diffusion of DMPA molecules within the domain and focus our analysis in the thermalization of both ions and water molecules.

The duration of the equilibration runs (t_eq) was identified by ensuring the stability of relevant physical quantities (such as number of bound counterions, center of mass of ions,…). For example, we observed that the number of bound counterions increased systematically during the first 400 ps of the equilibration run at a net rate of ∼1 counterion per each 80 ps. After this initial behavior, the flux of incoming counterions binding to the interface decreased to match the rate of counterions leaving the interface and the observed evolution of the number of bound counterions is consistent with a zero net flux.

The duration of the production runs was identified by ensuring that the selected t_prod is much larger than the characteristic time of decay of the correlations between binding of counterions, t_c. To determine t_c, we have employed a block analysis (34) of the number of bound counterions during the production runs. First, we have computed the number of bound counterions at intervals of 1 ps obtaining a first data set. Then, we have averaged this data set into blocks of fixed duration t_A, and the operation is repeated for different values of t_A. Also, we have computed the variance σ²(t_A) from the “block averaged” data sets. From these results, we compute the quantity 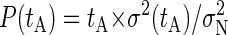, where 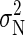is the equilibrium ensemble average of the variance in the number of bound ions (which in principle is different from σ²(t_A) due to correlations). In the calculation of P, we need an estimate for 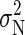, which is obtained using the method of Flyvbjerg and Petersen (34). We obtain 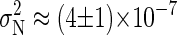for the BS simulation. If the simulation run is long enough, the evolution of P for large t_A shows a well-defined tendency, approaching the correlation time t_C for 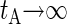. In our BS simulations the behavior of P for the largest available values of t_A can be fitted by P ≈ 1.15 × 10⁻² + 0.82/t_A (in picoseconds). This gives an estimation for the correlation time 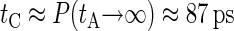, which is much smaller than the duration of our equilibration and production runs.

We have to emphasize that our use of large values for the cutoffs implies that our simulations, even lasting only a few nanoseconds, require a substantial use of computational power. Each nanosecond of simulation requires ∼100 h running in 64 dual processors PowerPC 970FX.

SIMULATION RESULTS

Representative snapshots

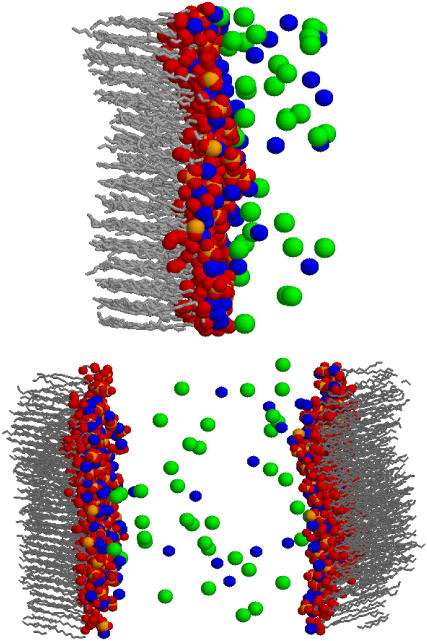
In Fig. 2, we show representative snapshots of our simulations. Several remarkable features can be observed in these snapshots. First of all, we observe a large number of Ba²⁺ counterions in close proximity of oxygen atoms from DMPA molecules. It is also found that counterions often penetrate inside the layer defined by the DMPA²⁻ headgroups. Also apparent is the presence of a diffuse layer next to the interface, which contains a surprisingly large number of Cl⁻ ions only explained by the large amount of Ba²⁺ ions bound to the DMPA interface.

FIGURE 2.

Representative snapshots of simulations. Oxygen atoms are shown in red, P in orange, Ba²⁺ in blue, and Cl⁻ in green. Water molecules are not shown for the sake of clarity. (Top) Simulation MS. (Bottom) Simulation BS.

Binding of divalent counterions

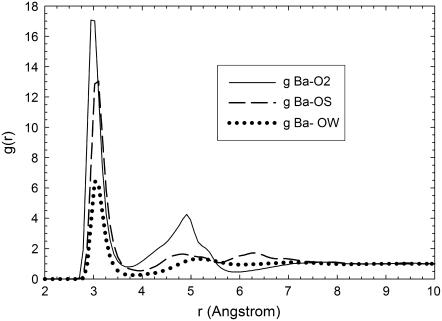
As a first step in the identification of bound and bulk counterions we have computed the g(r) between Ba²⁺ counterions and the different types of oxygen atoms present in the simulations (representative results for rdfs are shown in Fig. 3). As explained in the Model and Methods section, an oxygen atom (from a water molecule or from DMPA) is assigned to the first coordination shell of a Ba²⁺ ion if their separation is smaller than the distance r corresponding to the first minimum of the g(r) function between these two types of atoms. Using this definition, we have computed the number N_b of bound Ba²⁺ ions for the different simulations (see Table 2). N_b is larger than the number of DMPA²⁻ molecules, thus the Stern layer has reversed its bare negative charge, becoming positively charged. Hence, we observe the phenomenon of charge inversion in our simulations. The observed charge inversion is larger in the MS simulation due to the fact that in this simulation we have a larger bulk concentration of ions (the concentration profiles of the different species are discussed in the next subsection).

FIGURE 3.

Radial distribution functions g(r) between Ba²⁺ ions and oxygen atoms. (Solid line) g(r) between Ba²⁺ and O2 oxygens from DMPA. (Dashed line) g(r) between Ba²⁺ and OS oxygens from DMPA. (Dotted line) g(r) between Ba²⁺ and OW (oxygens from water molecules).

TABLE 2.

Bulk concentration of ions (in ions/nm³) and number of bound Ba²⁺ ions per DMPA²⁻ molecule, N_bound/N_DMPA (error estimates correspond to mean ± SD 2)

	MS	BS
[BaCl2]	0.2 nm−3	0.06 nm−3
Nbound/NDMPA	1.0788 ± 0.0004	1.0219 ± 0.0001

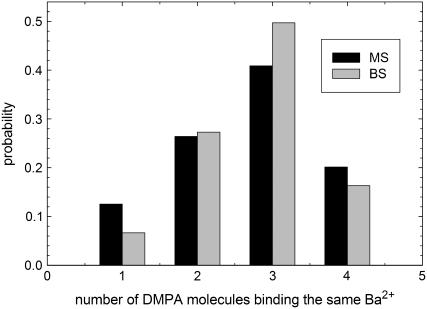
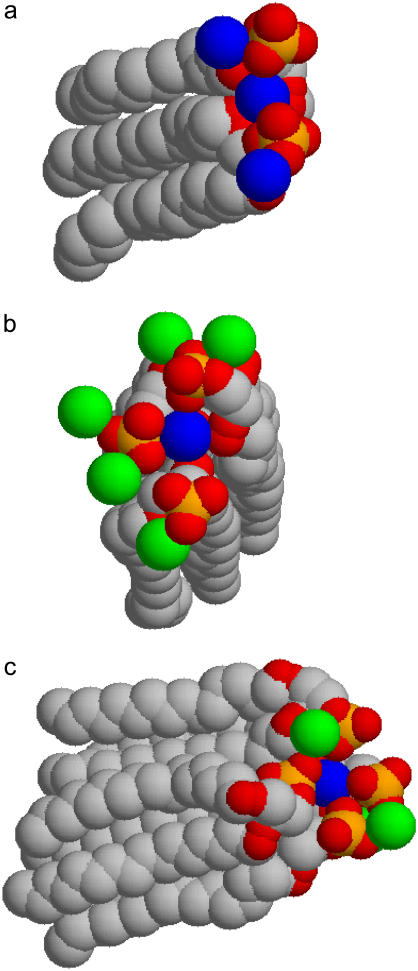
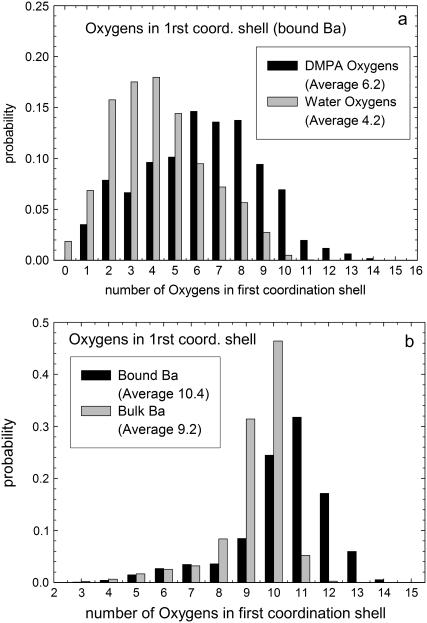
The lateral organization of bound counterions is investigated from the analysis of different quantities. A first insight is provided by the probability of finding a Ba²⁺ ion bound to n DMPA molecules, shown in Fig. 4. We obtain that the maximum number of DMPA²⁻ molecules bound to a single Ba²⁺ is four, with three being the most likely situation. The results show a small trend toward higher number of bound DMPA molecules for increasing salt concentration. In Fig. 5 we show several snapshots, corresponding to Ba²⁺ ions binding to one, two, three, and four DMPA molecules illustrating the different cases. These snapshots show that ions tend to be bound to several DMPA molecules to be surrounded by a large number of oxygen atoms, which contain all the partial negative charges of DMPA. To quantify this effect, we have computed the number of oxygen atoms from DMPA molecules and from water molecules in the first coordination shell of bound ions. The results for simulation M are shown in Fig. 6 a (similar results are obtained for the other simulations). The most likely number of DMPA oxygens is six, seven, or eight, all with similar probabilities. It is also remarkable how broad this distribution is, with Ba²⁺ atoms in contact with as few as one or as many as 13 DMPA oxygens.

FIGURE 4.

Histogram showing the number of DMPA molecules in contact with a bound counterion.

FIGURE 5.

Typical configurations of a bound counterion attached to DMPA molecules. Yellow spheres are P atoms, red spheres are oxygen atoms from DMPA, blue spheres are the bound Ba²⁺ counterions under study, and green spheres are other neighboring Ba²⁺ ions. (A) A detail of a protrusion in the interface, formed by two DMPA and three Ba²⁺ (note that one Ba²⁺ is bound to two DMPA and the others are bound to only one DMPA). (B) Detail of the interface showing one Ba²⁺ bound to three DMPA. (C) Detail of the interface showing one Ba²⁺ bound to four DMPA.

FIGURE 6.

(a) Histograms showing the number of oxygens from DMPA and oxygens from water molecules in the first coordination shell of bound Ba²⁺ ions. (b) Histograms showing the number of oxygens in the first coordination shell of bulk and bound Ba²⁺ ions.

Bound Ba²⁺ ions still retain a partial hydration sheath, which contains an average of 4.2 water molecules (the most probable value is three or four water molecules). Overall, bound counterions have an average of 10.4 oxygen atoms in the first coordination shell, where 6.2 are from DMPA and 4.2 from solvating water molecules. As a comparison, bulk Ba²⁺ ions have a first hydration sheath with an average of 9.2 water molecules, so the DMPA/water interface provides a larger average number of oxygens in the vicinity of ions than bulk water. Also, the details of the distribution of coordination numbers are very different, as can be seen in Fig. 6 b. Bound counterions have a much broader distribution, whereas bulk counterions have a sharp distribution, where only coordination numbers between nine or 10 oxygens have a significant probability.

These results show that the affinity of PA for divalent cations is a consequence of having many electronegative atoms (eight oxygens) that are located within groups with conformational degrees of freedom that maximize the number of oxygens in contact with divalent cations, as it is clear from Fig. 5.

Atomic distributions

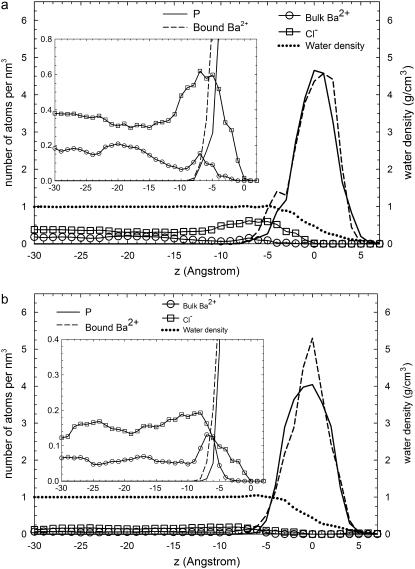
To describe the structure of the Stern and diffuse layers, we have computed the number density of the P atoms from DMPA molecules, the number density of ions (Ba²⁺ and Cl⁻), and the mass density of water (Fig. 7). These quantities are averaged over the x- and y-coordinates and over all configurations corresponding to production runs. In Fig. 7, the z = 0 point is arbitrarily defined as the maximum of the P atoms number density distribution.

FIGURE 7.

Density profiles for P atoms (solid line), bound Ba²⁺ ions (dashed line), bulk Ba²⁺ (circles), Cl⁻ ions (squares), and water (dotted line) for simulation S3. The insets show the results with a different scale to facilitate the visualization of bulk concentrations of ions. The units are atoms per nm³ except in the case of water density, which is given in g/cm³. Panel a corresponds to simulation MS and panel b to simulation BS.

Concerning the diffuse layer, there is a clear excess of Cl⁻ ions and a depletion of Ba²⁺, corresponding to a diffuse layer in contact with a positively charged Stern layer. Hence, the distribution of ions in the diffuse layer clearly shows that this interface presents charge reversal. At large distances from the interface, the concentrations of ions approach a constant bulk concentration.

It is clear from Fig. 7 that the number density profile for bound Ba²⁺ ions (i.e., Ba²⁺ ions belonging to the Stern layer) is strongly correlated with the P distribution. This indicates that Ba²⁺ ions are strongly bound and located well within the layer defined by the DMPA headgroup, as it is also apparent from the snapshots (Fig. 2).

Another interesting result is that the density of water remains the same as the bulk value up to the immediate vicinity of the interface, and it is half of its bulk value near the peak of the P distribution (z = 0). This shows that the interface retains a significant amount of water.

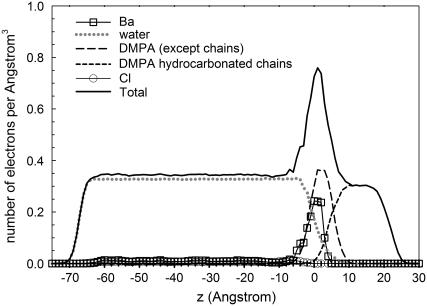
We compute the electron density (ED) in Fig. 8, where the plot includes the contribution of the different chemical structures. We find a constant ED corresponding to the aqueous solution, a peak corresponding to the headgroup with a width of the order of 11 Å subsequently followed by a plateau, of size ∼10 Å corresponding to the hydrocarbon chains, which decays to zero over a distance of ∼6 Å. All these results are in good agreement with the experimental results reported in Vaknin et al. (14). The actual values of the ED are virtually the same as the ones reported in Vaknin et al. (14), except for the main peak, corresponding to the headgroup region, where our simulations show a significantly larger ED. We point out that the experimental results correspond to a 1-mM concentration of BaCl₂, that is, a concentration two orders of magnitude smaller than the concentration in MS simulations, so this difference may point out that at this smaller concentration there is less barium and chlorine than the one reported in our simulations.

FIGURE 8.

Electron density computed from simulation MS.

Water structure

Water close to interfaces and surfaces is usually more ordered as a result of optimizing their hydrogen bonds according to the geometrical constraints imposed by these boundaries. If the interface or surface is charged, there is also a tendency of water molecules to orient creating an electric field opposite to the interface. These mechanisms influence the structure of the hydrogen bond network of water near interfaces in a very complex way. Furthermore, perturbations of the hydrogen bonding water network are usually related to both hydration and hydrophobic forces (22) and may determine the binding constants of proteins and other molecules.

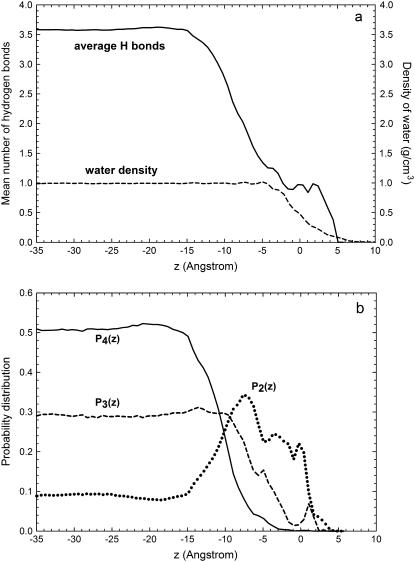
In our MD simulations, we study hydrogen bonding by assuming that two water molecules are hydrogen bonded only if their interoxygen distance is <3.5 Å, and simultaneously the OH…O angle is <30°. This definition is consistent with known results for both static and dynamic properties of hydrogen bonding in liquid water at ambient conditions (39). The results in the case of simulation MS are shown in Fig. 9 (the results for simulation BS are almost identical). The mean number of hydrogen bonds strongly decreases near the phospholipids, and the perturbation is appreciable even at distances of 15 Å away from the peak of the P atom distribution (for comparison, the size of the SPC/E water molecule is 3.16 Å). The disruption in the hydrogen bonding network is significantly long ranged, which should be contrasted with the density of water, which remains basically at its bulk value up to distances very close to the interface, as shown in Fig. 9 and discussed previously. That implies that there is a region near the interface where water shows bulk density values but has a hydrogen bond structure manifestly different from bulk water.

FIGURE 9.

Structure of water hydrogen bonding in simulation MS. (a) Mean number of hydrogen bonds per water molecule. The density of water is also shown for reference. (b) Probability distributions of finding a water molecule with two hydrogen bonds (dotted line), three hydrogen bonds (dashed line), and four hydrogen bonds (solid line).

A more quantitative assessment of the disruption of the hydrogen bond network is provided by the probability P_n of finding a water molecule with exactly n hydrogen bonds with other water molecules (P_n is a probability so 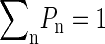). In terms of the standard picture of liquid water as a distorted random tetrahedral network of hydrogen bonds, each water molecule has an optimum of four hydrogen bonds with other water molecules (but many molecules use only three of these possible bonds). In the bulk region, we find that ∼50% of water molecules have four hydrogen bonds with other water molecules and around 30% of water molecules have three hydrogen bonds. This high probability of four hydrogen bonds for a water molecule requires a substantial structure of the surrounding water, which extends beyond the nearest neighbor molecules to a distance of the order of the nanometer. In the vicinity of an interface, these bulk water correlations cannot be maintained, and this is reflected in the probabilities P_n, which acquire a dependence on the distance z from the interface, as shown in Fig. 9, where the cases n = 2, 3, 4 are shown. The probability P₄(z) of finding a water molecule with four hydrogen bonds has a small increase in the region between z ≈ −20 Å and z ≈ −15 Å and then follows a sharp decrease becoming vanishingly small at z ≈ 0 Å. Water molecules at distances of the order of 1 nm from the interface have significant difficulties in obtaining four hydrogen bonds, as compared with water molecules in bulk water. This difficulty in forming the hydrogen bond network is also evidenced by an increase in the probability P₂(z) of finding a water molecule with only two hydrogen bonds with other water molecules (see Fig. 9). This significant increase in P₂(z) (from P₂ ∼ 9% at z ≈ −15 Å to P₂ ∼ 34% at z ≈ −7 Å) occurs in the same region in which P₄ decays from P₄ ≈ 50–4%. A similar, but less pronounced effect can be observed in the probability P₃ of finding a water molecule having exactly three hydrogen bonds.

Electrostatic potential

The electrostatic potential (averaged over x,y and production runs) is computed from:

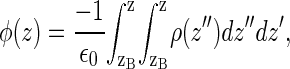(3)

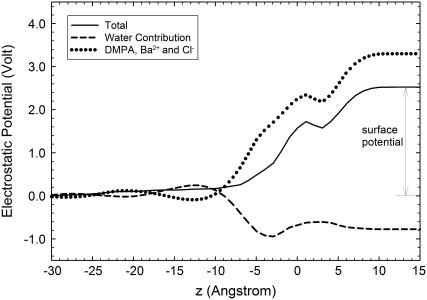
where ρ(z) is the charge density and z_B is a reference point in the electrolyte solution, far from the interface, in which the potential is defined to be zero. Both charged species (DMPA and ions) and water molecules contribute to the electrostatic potential given by Eq. 3, as shown in Fig. 10. The main contribution to φ(z) is due to the charged species and is positive (we recall that there is charge inversion in the MS simulations). On the other hand, the contribution of water molecules is negative and is significantly smaller than the contribution from ions and phospholipids (see Fig. 10). Hence, the total electrostatic potential φ(z) is positive and increases monotonically from a reference value of zero in the electrolyte solution toward a constant potential at the hydrocarbon region of ∼2.5 V. This increase in the electrostatic potential is generated within a very thin region of a few angstroms near the phospholipid headgroups. It is also interesting to note that the surface potential (∼2.5 V) is only slightly smaller than the bare potential generated by the DMPA and the ions (∼3.3 V), which is essentially generated at the Stern layer. The contribution of water to the surface electrostatic potential is modest, only about −0.8 V.

FIGURE 10.

Electrostatic potential φ across the interface (solid line). We also show the contribution due to DMPA and ions (dashed line) and the contribution from water molecules (dotted line).

DISCUSSION

Summary of simulation results

The main results of our MD simulations are:

• The number of oxygen atoms from DMPA required to bound a given Ba²⁺ ion show a broad distribution being the most likely values six, seven, and eight (all with similar probabilities) and the average value being 6.2 oxygens per Ba²⁺.

• Bulk Ba²⁺ ions have a hydration shell of from approximately nine to 10 water molecules, but, roughly five to six of them are lost on binding to six to eight oxygens in interfacial groups. Hence, Ba²⁺ increase the number of oxygen atoms (including O from water and DMPA) in binding to the interface.

• The hydrogen bonding structure is perturbed by the interface up to distances of ∼15 Å but the density of water remains almost the same as in bulk.

• Simulations show charge inversion, that is, the charge of bound counterions reverses the bare charge of the phospholipid layer.

• The electrostatic potential of the membrane is essentially generated at the Stern layer. The dominant contribution to the electrostatic potential is due to phospholipids and bound counterions. The contribution of water to the electrostatic potential is significantly smaller.

Implications for divalent ion binding to phospholipids

In our simulations we observe that divalent ions can bind to as many as four DMPA molecules. In fits to experimental data, it is assumed that divalent ions bind as 1:1 (one counterion/one phospholipid) (16) or 1:2 (40) to phospholipids. Our results show that this binding is, in fact, a broad distribution, where 1:3 or 1:4 are quite common, but also 2:1 or 3:1 (several counterions bound to a single phospholipid) are observed. We conclude that fits assuming a fixed stoichiometry provide average values for binding constants, but, in general, a distribution of binding constants representing different stoichiometric ratios should be expected.

The broad distribution of the number of oxygens needed to bound a divalent ion, which ranges from one to 13 (see Fig. 6), gives raise to a broad distribution of binding constants, according to Eq. 2. The negative charge (Q_eff) in contact with a bound divalent ion ranges from −1.4 to −10 according to the valences of the oxygens in DMPA (see Fig. 1). As a simplifying approximation, similarly as it is done in analyzing experimental data, we take the average value Q_eff ≈ −4, which leads to an average binding constant K_B ≈ c_g10⁷ M⁻¹. Assuming a geometric steric factor c_g in the range 0.1–1, K_B is in the range 10⁶–10⁷ M⁻¹. This result gives a quantitative evaluation of the exceptional ability of DMPA to capture divalent ions. These large values of the binding constant are due to the fact that divalent ions bind to many oxygen atoms from DMPA and K_B grows exponentially with the total number of bound oxygens (see Eq. 2). From a similar calculation, the binding constant of Ca²⁺ to phosphatidyl serine lipids is estimated to be K_B ≈ 10 M⁻¹ (38), in good agreement with experimental results (16).

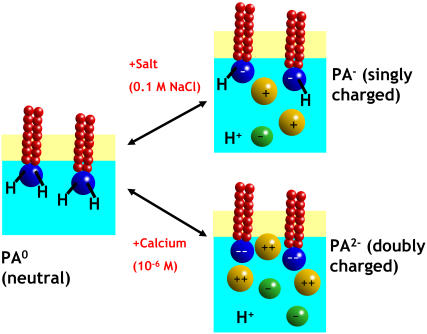
The binding constant calculated from Eq. 2 can now be used to discuss the electrical charge of DMPA in different conditions. As explained previously, the presence of divalent ions is able to doubly deprotonate DMPA (thus leading to DMPA²⁻) at concentrations of order 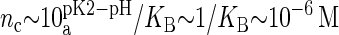. Therefore, we predict that competition between divalent ions and protons for binding with oxygens will lead to double deprotonation already at micromolar concentrations. Hence, we predict that the charge inversion observed in the experiments of a DMPA monolayer in contact with mM concentrations of BaCl₂ (14) could be better interpreted by assuming a doubly deprotonated DMPA²⁻ instead of the single deprotonated DMPA⁻ originally assumed by the authors. The regulation of the charge of a DMPA domain by counterion valency and concentration is summarized in Fig. 11. In pure water, the DMPA molecule is basically neutral, as the protons are bound due to the electrostatic attraction from the interface. If the solution contains monovalent ions, DMPA releases its first proton and becomes singly charged at concentrations in the 0.1-M range (24,25). In the presence of divalent ions in concentrations in the micromolar range, DMPA becomes doubly charged.

FIGURE 11.

A PA domain in pure water is neutral. In the presence of monovalent ion concentrations gradually become charged as one of the protons is released, reaching a single charge per PA at around 0.1 M. With divalent ions, micromolar concentrations are enough to release both protons leaving PA doubly charged.

Our simulations show charge inversion. The origin of this charge inversion is the electrostatic attraction and the resulting correlations between divalent ions and DMPA oxygens, which is due to its large electronegativity, retaining a significant negative charge (as shown in Table 1) even when part of neutral groups. The oxygens are within groups that are not rigid, so conformational degrees of freedom are used to optimize their positions to facilitate bending at a presumably low entropic cost. A detailed presentation of the physical mechanism leading to charge inversion is presented elsewhere (41). Here it suffices to mention that this charge inversion is an electrostatic effect due to transverse correlations (correlations between the interfacial O and Ba²⁺ ions) (38) and that it is expected to take place at n_inv ∼ 1/K_B ∼ 10⁻⁶ M (26). This value for the concentration at which charge inversion appears is smaller than the concentrations employed in the experiments of Vaknin et al. (14) in which a DMPA monolayer was in contact with a BaCl₂ electrolyte. Hence, our calculations predict that charge inversion must take place in these experiments, as it is indeed observed (14).

Implications for the electrostatic potential of lipid layers and membranes

The results showing a small contribution of water in the electrostatic potential are surprising in view of previously published results concerning electrostatics of membranes and monolayers. MD simulations of PC membranes (18) show a negative potential drop across the membrane, whereas the contribution of PC lipids to the potential is positive. This implies that the sign of the electrostatic potential of the membrane is determined by the interfacial water, which overcompensates the electric field from dipalmitoyl phosphatidylcholine; that is, there is overscreening. In ionic amphiphilic systems these effects are even more pronounced as recently shown in computer simulations of a thin water film coated with anionic sodium dodecyl sulphate (SDS) surfactant (42,43). Also, electrostatic theories accounting for water restructuring near interfaces predict this phenomenon of dielectric overscreening (44).

Our results provide a different perspective on these previous results since no evidence for overscreening is found. Also, recent surface sensitive x-ray scattering experiments with dihexadecyl phosphate (DHDP) phospholipids do not show any evidence of overscreening (24,25). In these experiments, the counterion distribution (Cs⁺) near the charged DHDP⁻ interface was obtained with high accuracy and complete agreement with the Poisson-Boltzmann theory (which does not include water overscreening) was found. A comparison between systems exhibiting dielectric overscreening and systems in which this effect is absent indicates a correlation of this effect with the amount of hydration water in the interface. For example, in the case of the SDS thin films, simulations show that dielectric overscreening is essentially due to water molecules belonging to the hydration sheath of bound Na⁺ ions (37,42). On the other hand, our results in this article indicate that PA does not show dielectric overscreening because bound divalent ions retain only a small part of the hydration sheath. It is clear that the electrostatic effects of interfacial water are highly specific, and strongly depend on the chemical structure of the phospholipids.

In view of these results, it is also clear that effective distance dependence dielectric constants (45), which are invoked in theoretical descriptions of lipids and protein interfaces, do not seem justified in describing PA membranes.

Implications for PA domains in biological membranes

We first discuss the consequences of the different simplifications in extrapolating our results for real biological systems. The simulation of one leaflet of the bilayer, as opposed to a bilayer introduces tension into the system and modifies membrane fluctuations. This is a long wavelength effect, which given the relative small size of our system (100 DMPA molecules) should not significantly modify the conclusions of the problems addressed in this article. Furthermore, the realistic biological situation would involve an asymmetric membrane, whose outer leaflet composition is not precisely known. All our simulations have been performed with DMPA molecules with saturated hydrocarbon chains, whereas most of the biologically relevant PA molecules present different degrees of unsaturation. The consequence of this is a slight increase in molecular area. For LPA, which contains only one hydrocarbon chain, this effect is unimportant, but for PA lipids this may slightly reduce the number of oxygens bound to a single Ca²⁺ ion or other divalent ion. In any case, to assess this point will require further work, as it is possible that the binding of divalent ions may reduce the molecular area.

Domains of PA act through three modes of action in cells: i), alter membrane structure; ii), act as a messengers by specific interactions with proteins; iii), tether a protein to a membrane and/or modulate its catalytic activity (1). These three effects are far from universal, as they differ in many fundamental aspects for different cells. There are, however, a number of general considerations that follow from the results in this article. The most important result is the versatility of PA to bind divalent ions, with a broad distribution of binding constants. These broad distributions suggest the possibility of PA to respond to Ca²⁺ signaling in different degrees, depending on Ca²⁺ concentration. Divalent ions bind many DMPA lipids, three and four with highest probability, which in turn suggests that Ca²⁺ ions may act as tethers that favor the formation of small size PA-rich domains. This result is further supported by experiments with Langmuir monolayers, which show a drastic drop in surface pressure whenever Ca²⁺ counterions are present. This PA-rich domains are quite compact, as they are held together by the Ca²⁺ ions, so it should be expected that results in significant alterations of the membrane structure. As already noted, PA-rich domains should be very sensitive to changes in Ca²⁺ concentration on the cytosol. In unexcited membranes Ca²⁺ concentrations are of the order of 10² nM (46), and biological responses are usually triggered by Ca²⁺ concentrations in the micromolar range or higher. These biological thresholds are the same as n_c and n_inv, the critical Ca²⁺ concentrations at which both double deprotonation and charge inversion occur. Our results clearly support a situation where at micromolar concentrations PA domains do change membrane structure. Therefore, we expect that a PA-rich domain will undergo a drastic lipid reorganization when Ca²⁺ concentrations change according to the physiological conditions observed in real cells.

Proteins are critical for the biological function of PA. Clear evidence of activation of proteins in PA-rich domains by physiological changes in Ca²⁺ concentration have been reported (10). This situation is similar as it is found in the inositides, although the detailed mechanism is quite complex involving several proteins such as MARCKS that are electrostatically bound and the system becomes sensitive to divalent Ca²⁺ ions through calmoludin or kinase C phosphorylation (47). Clearly, more detailed theoretical work including the specific proteins explicitly will be required to clarify these subjects.

The problem of the lateral organization of Ca²⁺ in charged membranes has been discussed in the context of retinal rod outer segment membranes. Early studies reported a gel phase of charged lipids (PS) with Ca²⁺ segregated from the zwitterionic lipids (48,49). Recent experiments (40), however, have found no evidence for such gel phase, at least for polyunsaturated lipids. Our study suggests that the strongest affinity of PA for divalent ions (as compared with PS) should lead to the formation of such gel phase.

CONCLUSIONS

Our results have allowed us to identify the different structures of divalent ions bound to PA domains in membranes, quantify its binding constants, charge inversion, the role of interfacial water, and the dielectric response. Our results show that the biological functionality of PA is strongly related to its molecular structure, which allows charge regulation with a broad distribution of binding constants (schematically shown in Fig. 11) and is such that facilitates binding of a large number of phospholipids through oxygen binding sites with Ca²⁺ ions (see Fig. 5). Furthermore, our results strongly support that PA should undergo lipid reorganizations in response to physiological changes of divalent ionic concentration. The comparison of our simulations and theoretical considerations with precise x-ray surface sensitive data (14) has allowed a more robust assessment of the validity of our results. Although restricted to PA, our results should be qualitatively similar for other phospholipids, particularly the inositides, which play somewhat similar roles as PA, but have richer charge regulation possibilities and additional oxygens available for binding. We hope to explore these possibilities in the near future.