Internal Structure and Dynamics of Isolated Escherichia coli Nucleoids Assessed by Fluorescence Correlation Spectroscopy

Abstract

The morphology and dynamics of DNA in a bacterial nucleoid affects the kinetics of such major processes as DNA replication, gene expression. and chromosome segregation. In this work, we have applied fluorescence correlation spectroscopy to assess the structure and internal dynamics of isolated Escherichia coli nucleoids. We show that structural information can be extracted from the amplitude of fluorescence correlation spectroscopy correlation functions of randomly labeled nucleoids. Based on the developed formalism we estimate the characteristic size of nucleoid structural units for native, relaxed, and positively supercoiled nucleoids. The degree of supercoiling was varied using the intercalating agent chloroquine and evaluated from fluorescence microscopy images. The relaxation of superhelicity was accompanied by 15-fold decrease in the length of nucleoid units (from ∼50 kbp to ∼3 kbp).

INTRODUCTION

In bacteria, the genetic material is located in the cytoplasm and is organized in a body called the nucleoid, which has no specialized membrane around it. The Escherichia coli nucleoid contains one or more circular DNAs of 4,600,000 basepairs with overall length of ∼1.6 mm (for a general review see (1)). A free DNA coil of that length would occupy a volume of ∼1000 μm³. Thus, DNA in an E. coli nucleoid undergoes an ∼1000-fold compaction (2). Remarkably, despite this highly compacted state (or perhaps due to it), the bacterial DNA is highly active in gene expression, replication, and segregation.

Although bacteria are much simpler organisms than eukaryotic cells and are better studied in general, our knowledge of the structure of the bacterial nucleoid is much poorer than that of eukaryotic chromatin. The main reason for this is that unlike chromatin, which has a well-defined microscopic structure (known as 10 nm and 30 nm fibers (3)) prone to investigations with high-resolution x-ray techniques, the bacterial nucleoid appears to be rather unstructured.

Thus, the experimental approaches to study nucleoid morphology assess mostly the largest scale structural units of isolated nucleoids. In solution, several important parameters of nucleoid structure (local packing density and molecular weight of DNA, specific linking number deficit, and domains of supercoiling) are preserved during isolation. Thus, at a minimum, isolated nucleoids provide a useful model system for studying the organization of bacterial DNA (1,4). Isolated nucleoids, as seen in the electron microscope (5,6), are organized in a series of supercoiled loops of ∼10 kbp in size. Atomic force microscopy (AFM) (7) reveals the existence of 40 nm and 80 nm fibers as a basic structural motif. Both electron microscopy (8) and AFM (7) point to a large-scale organization of the nucleoid into a “coral reef” structure with several supercoiled “coral arms.” Nicking enzyme assays reveal the presence of topologically independent domains (9) of ∼100 kbp. Furthermore, fluorescence microscopy studies show that there are apparently yet larger macrodomain units of 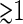Mbp in size (10,11).

Although the fundamental mechanism of chromosome packing in the nucleoid is unknown, three major factors are conjectured to cause nucleoid compaction in a cell (1,2,7,12,13): macromolecular crowding of proteins in the bacterial cytoplasm, negative supercoiling of DNA in the chromosome, and binding of histonelike proteins. The relatively small quantity of DNA binding proteins in bacteria implies that the last factor is too weak to explain the compact state of the DNA. On the other hand, the enormously high protein concentration in bacterial cytoplasm (300–400 mg/ml) causes phase separation between nucleoid and cytoplasm in the cell (14); this factor is relieved during the nucleoid isolation from lysed cells and may be simulated by addition of synthetic polymers (15). A number of activities lead to accumulation of DNA supercoils, which, in view of their importance for both nucleoid structure and function, will be considered in more detail below. In general, the relative importance of each of three proposed mechanisms is not known.

Here we propose a new approach to study nucleoid morphology, which is based on extracting structural information from the measurement of the internal dynamics of the nucleoid. Although this method is less direct than electron or atomic force microscopy, it still yields important information on the size and density of structural units at the scale of ≳200 nm. So far, we have used it to study isolated nucleoids; however, our method could, in principle, be applied to studying the nucleoid in the intact cell. Finally, perhaps the most important feature of our approach is that it allows structural studies under varying external conditions, so that the effects of each of the proposed mechanisms of nucleoid compaction (macromolecular crowding, binding of histonelike proteins, and DNA supercoiling) can each be studied concurrently.

In this work, we focus on the effect of DNA supercoiling on nucleoid structure. The overall average degree of DNA supercoiling in the E. coli nucleoid is characterized by an estimated specific linking deficit of ∼σ ≈ −0.05 (16). This negative supercoiling is built up in the course of openings of the double helix by DNA and RNA polymerases in the interplay with the activities of gyrases and topoisomerases. Furthermore, anchoring/tethering of mRNA to both the DNA template by means of RNA polymerase and to the membrane via nascent proteins results in an additional negative supercoiling: since mRNA is not free to rotate around DNA during transcription, it creates a twisting force on DNA (17–19). In this mechanism, DNA supercoiling is determined mainly by the balance between transcription intensity of genes coding for membrane proteins and topoisomerase I activity (20).

Although DNA superhelicity is an interesting problem in itself, even when considered outside of the context of nucleoid morphology, there are very few methods to measure it. The superhelicity of short plasmids can be measured rather straightforwardly by electron microscopy (21,22) or gel electrophoresis (23,24). However, the superhelical density of isolated nucleoid DNA has been assessed solely by DNA sedimentation (25). The sedimentation of supercoiled DNA in increasing concentrations of intercalating agent allows calculation of the writhe in the DNA from the known affinity of the agent. This method provides information on the average degree of supercoiling, reflected in the change of its compactness. In living cells of E. coli, torsional tension within the DNA double-helix can be detected from measurements of the rate of trimethylpsoralen photobinding to the intracellular DNA (9,16).

As described in the next section, our method of assessing the nucleoid structure is based on the measurements of the internal dynamics of the nucleoid by means of fluorescence correlation spectroscopy (FCS) (26–29) (reviewed in e.g., (30–33)). We measure the dynamics of single isolated nucleoids with varying densities of fluorescent labels and we make use of fact that the amplitude of the FCS correlation function is sensitive to the number of independently moving objects. At low densities of labels, their motion is independent of each other and the amplitude of the correlation function reflects the number of labels in the field of view. As the label density increases and the structural units of a nucleoid become multipally labeled, the amplitude of the correlation function start to depend on the number of structural units. The analysis of this dependence allows determination of the characteristic size of the structural units.

Furthermore, we perform these measurements while treating the nucleoid with an intercalating agent (chloroquine) which changes DNA superhelicity. Fluorescence microscopy as well as FCS demonstrate changes typical for titration by an intercalating agent: compensation of the existing negative supercoiling and accumulation of positive supercoiling with increasing concentrations of the agent, allowing us to evaluate the superhelical density of the nucleoid DNA. The superhelicity obtained is consistent with values in the literature obtained using different techniques (16). Finally, the comparison of the structural information for negatively supercoiled, fully relaxed, and positively supercoiled nucleoids allows us to estimate the effect of superhelicity on nucleoid compaction.

In the next section, we describe briefly the principles of FCS and adapt the FCS formalism for structural studies. Then we present the details of sample preparation and experimental procedures and follow by describing the results of fluoresence microscopy observations and of FCS measurements on natively supercoiled, fully relaxed, and positively supercoiled nucleoids. In the final sections, we discuss our experimental approach and results.

THEORY

In this section, we show that quantitative information on nucleoid structure can be gained by FCS measurements performed on nucleoids with varying densities of fluorescent labels.

Preliminaries

The FCS technique is based on monitoring fluctuations δI_em(t) = I_em − 〈I_em〉 in fluorescence emission I_em(t) as fluorescence species diffuse in a spatially restricted excitation field, formed typically with the help of confocal optical scheme (29). The autocorrelation function G(t) = 〈δI_em(0)δI_em(t)〉 of emission fluctuations reflects the kinetics of motion of fluorescent sources.

The FCS autocorrelation function is typically normalized by the square of the average emission intensity:

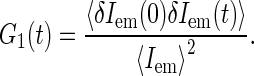For independently moving sources of fluorescence, the value of the correlation function at short timescales is related to the average number 〈N〉 of the sources in the effective confocal volume v,

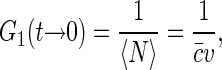where 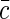is the average concentration of fluorescent species. Indeed, in a qualitative way one can view the fluctuations in emission as arising from the fluctuations δN in the number of fluorescence sources in the confocal volume: δI_em = EδN, where E is the average emission of a single source in the confocal volume. Then taking into account that 〈I_em〉 = E〈N〉 and for Poisson statistics that 〈(δN)²〉 = 〈N〉, we have

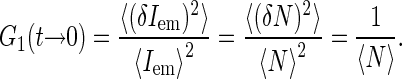We find another normalization of the correlation function

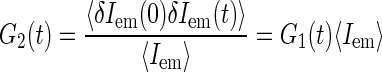convenient as well, since its short time value gives the average emission of a single source and thus is independent of the concentration of the fluorescence species (again in the case of independently moving sources):

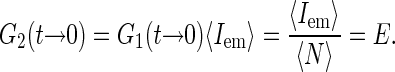With this background in mind, we first present the general idea of our method to assess nucleoid structure, and then follow with the formal description of our approach.

General idea

Nucleoids are labeled with fluorophores that bind tightly to DNA (such as TOTO dye, which intercalates into the DNA double-helix) and an FCS measurement is performed on these nucleoids at varying fluorophore-per-basepair ratios. Over the timescale of measurement the nucleoid overall is assumed to be immobile, thus the fluctuations in fluorescence are caused solely by the internal dynamics of the nucleoid, e.g., by the motion and conformational changes of its structural units. At low fluorophore densities, the distances between bound dye molecules are large, their positions are uncorrelated, and their motions are independent of each other. At such densities, the apparent number of independent fluorescence sources given by 1/G₁(t → 0) is just equal to the number of fluorophores in the confocal volume and is proportional to fluorophore density. Respectively, in these conditions the average emission rate per source of fluorescence given by G₂(t → 0) is just equivalent to that of a single fluorophore and is independent of the fluorophore density.

However, as fluorophore density increases, fluorophore positions and motions become increasingly correlated since numerous dye molecules label each structural element of a nucleoid. Therefore, 1/G₁(t → 0) dependence on fluorophore concentration will deviate from simple proportionality, and at the limit of high fluorophore densities will asymptotically approach the number of structural units in the confocal volume (which serve as independent sources of fluorescence in these conditions). Likewise, G₂(t → 0) is no longer constant at high fluorophore densities, but rather increases in proportion to the number of labels tagging a single structural unit and to the length of DNA involved in the unit. Thus study of the dependence of the amplitude of the FCS correlation function on fluorophore density gleans some (admittedly coarse-grained) information on the structural units of the bacterial nucleoid.

Formalism

In the following subsection we give a formal analysis of the method, which supports and refines the qualitative description above.

The instantaneous detected emission, average emission, and the correlation function of fluorescence fluctuations are found through the spatial distribution 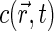of fluorescent dyes and excitation-detection profile 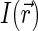(27),

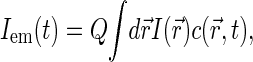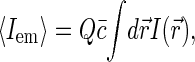(1)

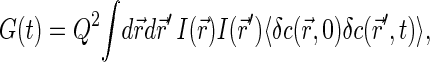(2)

where Q is specific brightness of a fluorescent molecule dependent on fluorophore properties and the efficiency of detection optics, 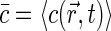is the average concentration of fluorophores, and .

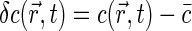We will be mostly interested in the amplitudes of the correlation functions G₁(t) and G₂(t), i.e., their asymptotic values at short timescales. Thus we will start by considering correlation functions for t → 0. Using Eqs. 1 and 2, we have

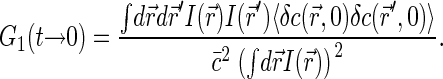(3)

If the positions of fluorophore molecules are completely uncorrelated, then 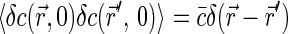and, as discussed above, 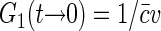, where v is the effective sampling volume defined by the excitation-detection profile:

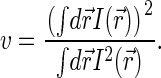In confocal setups, 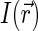is usually approximated by three-dimensional Gaussian profile, axisymmetric with respect to optical axis Z,

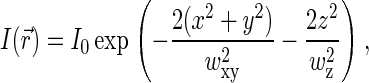(4)

where w_xy and w_z define the width of the profile in the XY plane and in the Z direction, respectively. Such a profile yields 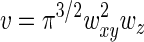for the confocal sampling volume.

However, the positions of fluorophores intercalating into nucleoid DNA are not totally random since they are determined by the underlying nucleoid structure. Fluorophores bind to DNA basepairs and DNA basepair positions are correlated in space such that the probability of finding a basepair in the vicinity of another basepair is higher than the probability of finding a basepair in some random location within the nucleoid. The most trivial reason for such correlations is the polymer nature of DNA: DNA basepairs are necessarily connected to one another. However, a more significant and interesting source of correlation is the DNA packing/packaging into structural units within the nucleoid.

Denoting the average density of basepairs within the nucleoid by 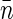and borrowing the definitions from physics of disordered media (such as liquids and polymers) we can describe the density of basepairs at the distance r from another basepair by the product of 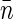and pair distribution function g(r). For small separations r the function g(r) is larger than unity. As the separation increases and exceeds some characteristic correlation distance ξ (which is associated with the typical size of the structural units of the nucleoid), g(r) approaches 1. More relevant to us is pair correlation function h(r) = g(r) − 1. The product 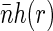describes the excess of basepairs over 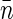at the distance r from another basepair. Obviously, h(r) > 0 at short separations and 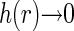for r ≫ ξ (yet r should not exceed the size of the nucleoid in our description). Assuming that all of the fluorophores are bound to the nucleoid and that the average label density 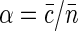defines the probability that any given basepair is labeled with an intercalating dye, we can write

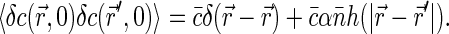(5)

The first term in the Eq. 5 is the same as in the absence of correlations and just describes the fact that the position of any fluorophore is always correlated to itself. The second term relates the correlations in the positions of two different dye molecules to the correlations in the positions of DNA basepairs.

Substitution of Eq. 5 into Eq. 3 leads to

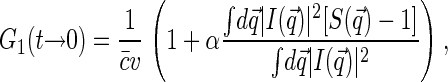(6)

where 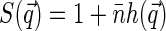is the static structure factor of the nucleoid 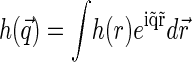and and 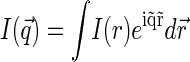are the spatial Fourier transforms of 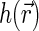and 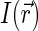, respectively. We note that Eq. 6 is just a counterpart of a similar relation derived in the context of the dynamic light scattering approach to DNA dynamics (34).

At this point, one could consider some specific models of nucleoid structure to evaluate 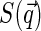dependence, or, alternatively, take the expression for 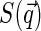from some phenomenological model of the structure of dense polymer solutions, e.g., 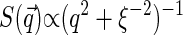for exponentially decaying spatial correlations or 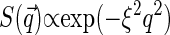for Gaussian decay. However, we use a different approach, assuming for simplicity that the typical correlation length ξ is smaller than the size of the sampling volume w_xy. This means that at large 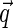, 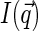decays faster than 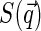(the former decays over 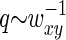and the latter over q ∼ ξ⁻¹). Then over the range of the decay of 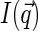, we can assume the structure factor to be constant and close to its zero-vector value 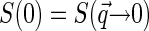. Then Eq. 6 simplifies to

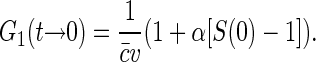(7)

Thus the dependence of G₁(t → 0) of fluorophore concentration is directly related to the zero-vector structure factor. Admittedly, the knowledge of S(0) is far from being enough to reconstruct the structural features of the nucleoid. Nevertheless, the value of S(0) characterizes at least two important features of the nucleoid. First, it determines the osmotic compressibility χ of the nucleoid through fluctuation-dissipation theorem relation 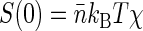. Second, through its definition, S(0) gives the total excess Δ of basepairs in neighborhood of another basepair 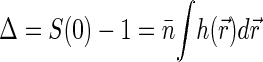. The value Δ roughly defines the number of basepairs in a structural unit of the nucleoid whose motion is independent of the motion of other units.

We define the apparent number of moving objects as N_app = 1/G₁(t → 0). Then making use of Eq. 7 and of the definitions of Δ and α, we have

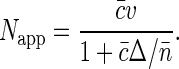(8)

At small fluorophore concentrations 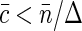, N_app is just equal to the number of fluorescent molecules in the sampling volume: 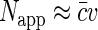. At high fluorophore concentrations 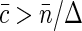, N_app becomes independent of dye density, and approaches the amount of independent structural units in the sampling volume, 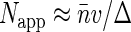. Thus the calculation supports the qualitative arguments at the beginning of this section.

The relation for G₂(t → 0) = G₁(t → 0) 〈I_em〉 follows from the equations above and can be written as

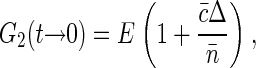(9)

where 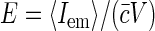is molecular brightness defined as average fluorescence of single fluorophore in the sampling volume. The value E is independent of fluorophore concentration (unless there are some photodynamic processes between dyes, e.g., quenching), and depends on the excitation power. Again, as described in the introduction to this section, G₂(t → 0) is equal to fluorophore brightness at low dye concentrations and increases linearly with dye concentration as two and more dyes label the same structural unit.

Since in experiment it is hard to control the actual amount of fluorophore bound to nucleoid, we determine the concentration of fluorophores through their average emission 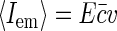. Thus we rewrite Eq. 9 as

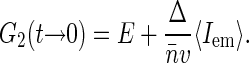(10)

Equation 10 suggests the way to experimentally evaluate Δ (and thereby S(0)) by performing FCS measurements on nucleoids with varying label densities and noting G₂(t → 0) and 〈I_em〉 at different dye concentrations. According to Eq. 10, the plot of G₂(t → 0) versus 〈I_em〉 should give a linear line that intercepts the ordinate axis at E and has a slope equal to 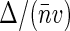. The sampling volume v can be measured and average basepair concentration 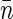can be estimated in separate experiments, thereby allowing us to evaluate Δ. We note that Eq. 10 holds also for 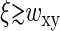: in this case, Δ is defined more generally as a ratio of integrals in Eq. 6 and has a meaning of excess basepairs within a distance ∼w_xy from another basepair.

Finally, we stress that our discussion in this article is almost entirely limited to the amplitudes G₁(t → 0) and G₂(t → 0) of FCS correlation functions and their relation to nucleoid structure. There clearly is a wealth of information about nucleoid dynamics in the temporal behavior of the correlation function G_1,2(t). However, the modeling of nucleoid dynamics is a still more complicated matter than the modeling of nucleoid structure, and the interpretation of complete FCS correlation functions is inherently difficult. Nevertheless, we attempt a very crude analysis of nucleoid dynamics in Discussion.

To summarize, based on the above formalism we present here two types of measurements of isolated nucleoids:

1. Fluorescence imaging of nucleoids titrated with various concentrations of chloroquine. These measurements allow us to evaluate nucleoid volume and, hence, the average density of basepairs (parameter 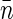in Eq. 10). Furthermore, the dependence of nucleoid volume on chloroquine concentration gives us a measure of the degree of nucleoid supercoiling.

2. FCS measurements of nucleoids labeled with varying amounts of intercalating dye TOTO-1. The changes in dye density lead to changes in average emission rate 〈I_em〉 and in the amplitude of the correlation function G₂(t → 0). The slope on the dependence of G₂(t → 0) versus 〈I_em〉 gives us the characteristic size of the structural unit Δ by means of Eq. 10. We performed these measurements in three situations: for native, fully relaxed, and positively supercoiled states of nucleoids. This allows us to evaluate the size of the nucleoid structural units and the effect of supercoiling on nucleoid structure.

MATERIALS AND METHODS

Preparation of isolated nucleoids

The basic E. coli strains employed in this study were B/r H266 (36) since its growth physiology is well studied, a variety of mutants are available, and most of the previous studies in this laboratory were performed on this strain. Strain E. coli B/r H266 was grown at 37°C in M9 minimal salt medium supplemented with 0.4% glucose and 1% casein hydrolysate (GC medium). Strains were cultivated with vigorous shaking (gyratory water bath shaker, model G76; New Brunswick Scientific, Edison, NJ). Fresh overnight cultures were diluted between 1:50 and 1:1000 and grown to an optical density of 0.15 at 450 nm (OD450) measured with a spectrophotometer (Novaspec II, Pharmacia LKB, Uppsala, Sweden). Nucleoid isolation was performed by a modified method of Woldringh laboratory (4). Samples of 3 ml cells from steady-state growing cultures were centrifuged (1.5 min, 16,000 × g, room temperature). The pelleted cells were resuspended at room temperature in 0.8 ml buffer A (0.01 M Tris, pH 8, 0.1 M NaCl, 20% sucrose) and 0.2 ml buffer B (0.12 M Tris, pH 7.7, 0.05 M EDTA, 40 μg/ml lysozyme). In general within 20–30 min of incubation on ice ∼90% of the cells became spheroplasts. Nucleoids were released from these spheroplasts disrupted by osmotic shock in low concentration NaCl solution. A sample 10 μl of spheroplasts suspension was added to 50 μl of 10mM NaCl solution with addition of 0.025% formaldehyde. Formaldehyde fixation was used for sample preparation to avoid changes caused by enzymatic activities during labeling and measurement. Lysis was achieved by carefully mixing this suspension in a round-bottomed tube and confirmed by phase-contrast and fluorescence microscopy.

Fluorescence imaging of nucleoids

For imaging, nucleoids were labeled with 1 μM of TOTO-1 (Molecular Probes, Eugene, OR) and treated with chloroquine in 0–35 μg/ml range, diluted ∼10-fold in 10 mM NaCl buffer and gently deposited onto glass coverslips. Within a few minutes the nucleoids sedimented in the vicinity of the glass surface at the density of ∼1 nucleoid per 1000 μm². Microscopy was performed using a Nikon Digital Sight DS-U1 cooled CCD camera mounted on an Nikon inverted fluorescence microscope (Nikon Eclipse TE2000-S, Badhoevedorp, The Netherlands) equipped with a Plan Fluor 100× oil NA1.3 objective (Nikon). The fluorescence was excited and detected with a 100 W mercury lamp in combination with an Endow GFP BP filter set (Chroma Technology, Rockingham, VT; exciter HQ470/40 nm, dichroic mirror Q495lp, emitter HQ525/50). Images were obtained and processed using the microscope domain program NIS-Elements Basic Research (Nikon Instruments, Melville, NY).

In the images nucleoids have a rounded shape (see Fig. 1). The area S occupied by each nucleoid was measured from images using an automated routine built-in to the NIS program. To calculate nucleoid volume, its shape was assumed to be spherical with a cross-section equal to S (15). For each chloroquine concentration ∼70 nucleoid images were analyzed and averaged.

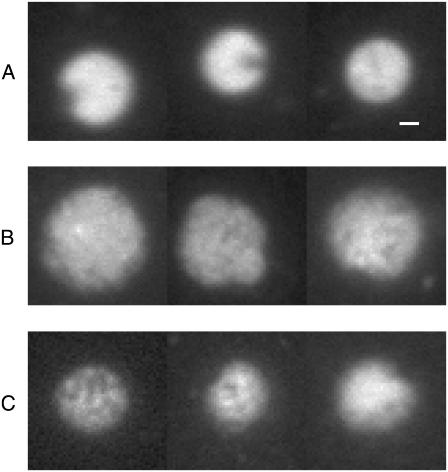
FIGURE 1.

Typical images of isolated nucleoids as seen in fluorescent microscope: (A) natively supercoiled, volume 18 ± 4 μm³ (mean ± SD over 74 nucleoids), (B) relaxed, volume 52 ± 18 μm³ (85 nucleoids), and (C) positively supercoiled, volume 19 ± 4 μm³ (67 nucleoids). Bar = 1 μm.

Sample preparation for FCS measurements of structural units

To have good linear dependences of G₂(t → 0) on 〈I_em〉 as predicted by Eq. 10, we found it absolutely essential to have measurements carried out on the same nucleoid with varying amounts of dye. Thus in these experiments nucleoids were prelabeled with low density of TOTO-1 (0.05 μM), diluted 100-fold and deposited onto the bottom coverslip of the home-made flow chamber. A single nucleoid was chosen for FCS measurements. After a set of measurements was carried out, dye solution was gently introduced into the chamber and another set of measurements was carried on the same nucleoid with respectively higher label density (up to 1 μM). Typically, we were able to make measurements with four different label densities on the same nucleoid.

When deposited onto a coverslip, nucleoids sedimented down toward the coverslip surface arriving at a stationary position at ∼5–7 μm distance above the surface. We believe that the stabilization in nucleoid position is caused by a steric effect of several far extending loops. The outstretched loops must be few in number since the visible nucleoid radius is only ∼2 μm (Fig. 1.) The loops apparently attach to the coverslip surface so that there is no observable motion of the whole nucleoid. Nevertheless, there is a substantial internal motion as observed by FCS. The dynamics of this motion does not change significantly over the course of approximately an hour. After that the internal motion appears to slow down significantly. We attribute this effect to the eventual increase in the number of contacts between the nucleoid and the surface and firm attachment of the nucleoid to the coverslip. The transition from the “dynamic” to “immobilized” internal state is rather abrupt. This transition puts an essential limit on the duration of measurement and the number of different TOTO-1 concentrations tried on the same nucleoid. In the course of FCS measurement the confocal beam is focused in the center of the nucleoid ∼5–7 μm above the coverslip surface. As long as the nucleoid shape is not significantly perturbed by the interactions with the surface and there are only a few loops attached to the surface, the contribution of these loops to the overall fluorescence signal can be neglected due to the relatively low level of their emission and due to the high efficiency of the confocal optics in rejecting out-of-focus light. And, in fact, as long as the nucleoid stays in the “dynamic” state, scanning the sampling volume along the optical axis toward coverslip surface does not reveal any appreciable background.

The flow chamber has a rounded shape of 12 mm in diameter and 7 mm spacing between the bottom and upper coverslips. Inlets and outlets are syringe needles placed at equal distances from the coverslips and at ∼7 mm overall distance from the observation area. The wide separation between the coverslips and the remote position of the needles allows for a gentle flow when changing fluorophore density. To ensure this, the nucleoids were observed with white light illumination at all times during injection.

In experiments on relaxed and positively supercoiled nucleoids, chloroquine was added to all the buffers at 25 μg/ml and 35 μg/ml concentrations, respectively.

FCS setup

The optical setup is home-built based on the Nikon Eclipse TE300 inverted microscope (Nikon, Tokyo, Japan). The confocal excitation is provided by 514 nm line (∼2 μW power before microscope objective) of an Ar-ion laser (Advantage 163D, Spectra-Physics, Mountain View, CA) deflected by Q525 dichroic beamsplitter (Chroma Technology) into a high-power objective lens (UPLAPO 60 × 1.2 W, Olympus Europe, Hamburg, Germany). The collected emission passes through the beamsplitter, then a bandpass filter HQ565/80 (Chroma Technology) and a pinhole of 25 μm in diameter. The emission is detected by a photon counting avalanche photodiode (SPCM-AQR-14 PerkinElmer Optoelectronics, Vaudreuil, Quebec, Canada) whose output is fed into digital correlator Flex2k-12D×2 (Correlator.com, Bridgewater, NJ).

The parameters w_xy ≈ 0.21 μm, w_z ≈ 1.1 μm, and v ≈ 0.28 μm³ of the confocal volume are calibrated before and after each experiment by measuring the diffusion of free Rh6G fluorophores (29).

Correlation functions were accumulated typically over the course of 5 min by short runs of 10–20 s. To determine amplitudes, correlation functions were fit in 10⁻⁴ to 10 s range by a general FCS expression for rectified motion (30)

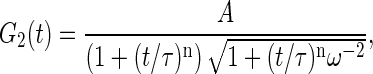(11)

where A, τ, and n are free parameters, respectively, corresponding to correlation function amplitude, characteristic decay time, and dynamic exponent characterizing the restricted motion. The parameter ω = w_xy/w_z defines the sampling volume aspect ratio and is determined independently as described above. Thus the values of the correlation function amplitudes resulted for this fitting procedure G₂(t → 0) = A.

Control measurements

TOTO-1 has a substantial rate of triplet state formation. We calibrated its dependence on excitation intensity in a separate set of experiments on different DNA fragments. To be on the safe side, the excitation intensity for nucleoid experiments was chosen to be low enough (∼2 μW) to minimize triplet state formation.

The effect of fluorophore photobleaching and triplet state formation on measured nucleoid properties was found to be negligible in several control experiments at high excitation intensities (∼10 μW).

For FCS measurements of DNA supercoiling we were concerned by the possible effect of interaction of chloroquine with TOTO-1, e.g., chloroquine displacing TOTO-1 from DNA. To ensure this is not the case, we performed FCS and steady-state fluorescence measurements of different λ-DNA restriction fragments labeled with TOTO-1 under different concentrations of chloroquine. No effect of chloroquine (in the concentration range of interest) on TOTO-1 binding to DNA was found.

RESULTS

Fluorescence imaging of nucleoids

In Fig. 1 typical images of nucleoids are presented for their native, fully relaxed, and positively supercoiled states, respectively. Nucleoids in their native state (Fig. 1 A) have a well-rounded shape with a small cap, which corresponds apparently to the remains of the bounded membrane (15). Their volume estimated from images is V = 18 ± 4 μm³.

As nucleoids are titrated with chloroquine their shape appears to be less defined and their volume increases. We associate these changes with the relaxation of DNA supercoiling. At chloroquine concentration C_ch ≈ 25 μg/ml, nucleoid volume reaches maximum (52 ± 18 μm³) and further increase in C_ch leads to nucleoid compaction (Fig. 1, B and C, and Fig. 2). Thus C_ch ≈ 25 μg/ml apparently corresponds to full relaxation of nucleoid, and further addition of chloroquine leads to the accumulation of positive supercoiling. At C_ch ≈ 35 μg/ml, nucleoid volume roughly returns to its native value. The overall changes in nucleoid volume are in a reasonable agreement with the results of sedimentation studies (37).

FIGURE 2.

Dependence of nucleoid volume on chloroquine concentration: as negative supercoiling relaxes, the nucleoids expand, reaching maximum volume at full relaxation. Further increase in chloroquine concentration leads to the accumulation of positive supercoiling and associated contraction of nucleoids.

With known dissociation constants of chloroquine (38) and the twist angle it introduces into the DNA double-helix (39), the nucleoid superhelicity can be evaluated from C_ch leading to full relaxation of nucleoid. The superhelicity σ is defined as a ratio of the number of superhelical turns to the number of turns of DNA double-helix. Using the binding parameters from Cohen and Yielding (38) and C_ch ≈ 25 μg/ml, we evaluate that at full relaxation, the bound chloroquine per basepair ratio is 1:10. With the twist angle of 28° per chloroquine molecule, this means superhelicity of σ = −0.08 ± 0.01. This value is roughly consistent with known literature data (16).

FCS measurements of structural units

Equation 10 predicts that in FCS measurements performed for different label densities, the amplitude of the correlation function G₂(t → 0) should depend linearly on the average emission rate 〈I_em〉. The slope of this dependence should reflect the size of the structural units of a nucleoid.

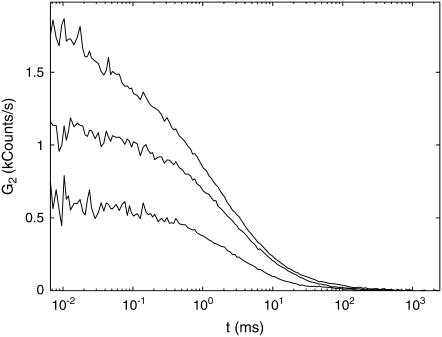
We collected such measurements on isolated nucleoids stained with TOTO-1 for several label densities on the same nucleoid. Overall, we measured 10 natively supercoiled nucleoids for 3–4 different TOTO-1 concentrations each. The typical correlation functions G₂(t) collected from the same nucleoid for different label densities are presented in Fig. 3. The amplitudes of the correlation functions grow progressively with increasing label densities. The characteristic timescales of ∼1 ms are similar to those measured by FCS on DNA fragments (40–42).

FIGURE 3.

Examples of correlation functions G₂ measured on the same isolated nucleoid at different label densities. Nucleoid is in its native state. G₂ has units of photon count rate and is given in the units of kilocounts per second. Bulk concentrations of TOTO-1: (bottom to top) 0.1 μM, 0.25 μM, and 0.75 μM, respectively.

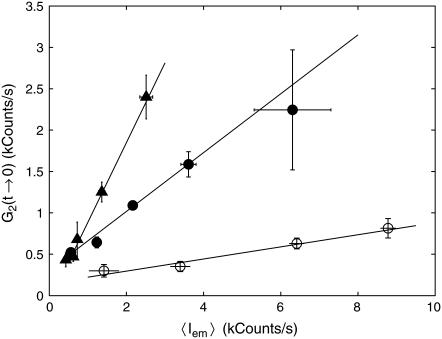
The reproducibility of G₂(t → 0) versus 〈I_em〉 data collected on different nucleoids is reasonably good. All of the data points were split into several ranges of average emission rate, and both G₂(t → 0) and 〈I_em〉 were averaged over each range. Solid circles in Fig. 4 show the resulting G₂(t → 0) versus 〈I_em〉 dependence for native nucleoids. The slope of the linear fit gives 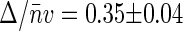and the intercept gives E = 310 ± 60 counts/s. We can estimate average basepair density 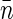by assuming that roughly two genome equivalents of L = 2 × 4.6 × 10⁶ basepairs spreads over the natively supercoiled nucleoid volume V = 18 μm³ (see Figs. 1 A and 2). (Note that E. coli B/r H266 grown on GC medium has a generation time of 30 min. This growth rate corresponds to average DNA content of three genome equivalents per cell on average (44). Assuming that half of population has single nucleoid and the other half has two already segregated nucleoids per cell, we estimate average DNA content of ∼2 genome equivalents per nucleoid.) Then using the calibrated value of v = 0.28 μm³ for sampling volume, we evaluate the size of the structural unit of Δ ≈ 50 kbp. This value is in the range of other estimates of characteristic size of nucleoid units (5,6,9).

FIGURE 4.

Dependence of the amplitude of FCS correlation function G₂(t → 0) on the average emission rate 〈I_em〉 for native (solid circles), relaxed (open circles), and positively supercoiled (triangles) nucleoids. Lines are linear fits to the data.

We performed similar measurements on nucleoids intercalated with chloroquine at 25 μg/ml concentration, which corresponds to the fully relaxed state of a nucleoid (see Fig. 2). For similar concentrations of TOTO-1, both the amplitude G₂(t → 0) and average emission rate 〈I_em〉 are smaller than those for native nucleoids. The dependence of G₂(t → 0) on 〈I_em〉 is shown in open circles in Fig. 4. The slope of the linear fit to these data 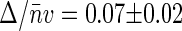is smaller than that for native nucleoids, reflecting a weaker structure. Similarly to native nucleoids, we can evaluate the size of the structural elements for relaxed nucleoids from their volume V = 52 μm³ to be Δ ≈ 3.4 kbp. Thus the relaxation of nucleoid supercoiling is accompanied by an ∼15-fold decrease in the size of the structural units.

Finally, we measured positively supercoiled nucleoids at 35 μg/ml chloroquine concentration. At this concentration of chloroquine the nucleoids bring their volume back to that of their native, negatively supercoiled, state (Fig. 2). The dependence of G₂(t → 0) on 〈I_em〉 is rather strong with 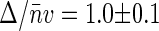corresponding to Δ ≈ 130 kbp (triangles in Fig. 4).

DISCUSSION

Three types of new experimental approaches were proposed in this work: 1), the measurement of nucleoid superhelicity through analysis of the fluorescent images of nucleoids titrated with chloroquine; 2), FCS measurements of the structural features of isolated nucleoids; and 3), as a consequence, the evaluation of the effect of superhelicity on nucleoid structure through FCS measurements at different degrees of supercoiling.

To the best of our knowledge, superhelicity of isolated nucleoids has only been measured by DNA sedimentation in sucrose gradients at different concentrations of intercalating agent, such as chloroquine or ethidium bromide (25). As an intercalating agent unwinds the DNA, nucleoid density decreases and, accordingly, the nucleoid sedimentation coefficient decreases as well.

Our visualization approach builds upon the same principle: the increase in nucleoid volume as DNA is relaxed by the intercalating agent. We believe that the main advantage of the imaging approach over sedimentation is that the imaging allows us to see the effect of changing superhelicity on individual nucleoids. In addition, the feature directly measured by visualization, the nucleoid dimensions, is easier to interpret and to understand than the sedimentation coefficient.

The chloroquine concentration leading to maximal nucleoid volume allows us to estimate the superhelicity σ of native nucleoids. The obtained values of σ = −0.08 ± 0.01 are consistent with literature values (16).

In a number of experimental approaches (5–8) a large-scale organization of the nucleoid was found and analyzed. Different studies (6,9) point to the supercoiled loops or domains of ∼10–100 kbp in size as the main structural motif of the nucleoid.

Our method leads to a similar value ∼50 kbp for the structural unit of native nucleoids. The FCS approach to nucleoid structure is admittedly less direct than electron microscopy and AFM. However, it causes smaller perturbations to the structure of isolated nucleoids, as the nucleoids do not undergo any special treatment and remain in their dynamic state. Moreover, in principle, this approach can be used to study nucleoids in vivo.

FCS approach allows us also to perform measurements in different external conditions with relative ease. Here, we use this feature to study the effect of supercoiling on nucleoid structure. The effect appears to be rather strong with ∼15-fold reduction in the structural unit size Δ associated with relaxation of nucleoid superhelicity. Notably, both negative and positive supercoiling lead to a similar effect: strengthening of nucleoid structure. The effect, however, appears to be somewhat asymmetric: the addition of chloroquine above the concentration of complete relaxation leads to larger changes in both nucleoid volume and Δ than the respective changes in the negatively supercoiled state (Figs. 2 and 4).

An interesting comparison can be made between our results and Cunha et al. (15) data on the free energy F of isolated nucleoids. Based on their measurements of nucleoid volume versus osmotic pressure, Cunha et al. arrive at the semiempirical expression F = gk_BT(V/V₀)^d, where V is the nucleoid volume under osmotic pressure, V₀ is the volume of an unperturbed isolated nucleoid, and d and g are the parameters dependent on the details of interaction between nucleoid segments. Then the osmotic compressibility χ = V(∂²F/∂V²)⁻¹ of a nucleoid can be evaluated and the zero-vector structure factor can be determined from the fluctuation-dissipation theorem: 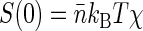. The parameters given by Cunha et al.: V₀ = 27 μm³, d ≈ 1.34, g ≈ 362, total DNA L = 1.64 × 4.6 × 10⁶ bp in a nucleoid equivalent to 1.64 of a genome (the difference with our estimation of L stems from the differences in growth medium (44)) lead to Δ ≈ S(0) = L(gd(d + 1))⁻¹ ≈ 6.5 kbp for an unperturbed nucleoid (V = V₀). This estimation should be compared with our measurement of Δ ≈ 50 kbp. The discrepancy in the estimated size of the structural unit can be attributed to the large difference in nucleoid superhelicities resulting from the difference in growth conditions between our experiments and those of Cunha et al. Indeed, for E. coli grown on glucose minimal medium as in Cunha et al. (15) we measured σ ≈ −0.021, which is close to σ = −0.025 cited in (15) and is nearly four times smaller in absolute value than the superhelicity of native nucleoids used in the current study (from E. coli grown on GC medium). Intuition supported by our results on relaxed nucleoids suggests that lower superhelicity leads to weaker structure and smaller Δ. A larger volume of unperturbed nucleoids and their more diffuse shape in Cunha et al. as compared to our experiments are also indications of a weaker structure. Finally, we note that the systematic studies of the dependence of nucleoid structure on E. coli growth conditions are underway in our laboratory and the preliminary results suggest that, indeed, E. coli grown on glucose minimal medium are characterized by significantly smaller values of Δ than E. coli grown on GC medium.

Up to now, we restricted our analysis to the amplitudes G₂(t → 0) of the correlation functions, which reflect essentially the structural properties of a nucleoid. As we mentioned above, the interpretation of the decaying part of G₂(t), which reflects the internal dynamics of a nucleoid, is inherently more complicated and speculative than the analysis of the static part. With this concern in mind, we perform below the simplest treatment of the correlation function decay kinetics.

The analysis is helped by the fact that for both native and positively supercoiled nucleoids, the fit parameter n in Eq. 11 is close to 1: n = 0.9 ± 0.1. We note that n = 1 corresponds to simple diffusion kinetics such as that of noninteracting molecules (see, e.g., (26,27,29)). Thus the fact that n is close to 1 may mean that the structural units are rather compact and interact with one another only weakly. (Although this is the simplest assumption, it is by no means the only one possible. It is worth remembering that the FCS correlation functions reflect essentially collective dynamics of the nucleoid, which can be either accelerated or slowed down by the interactions between nucleoid segments (48).) Fits to the correlation functions for native nucleoids with Eq. 11 having fixed n = 1 are reasonably good and lead to the characteristic diffusion time τ = 1.7 ± 0.6 ms (average ± SD over all measurements). From the diffusion times and confocal volume dimensions, the characteristic diffusion coefficient can be determined 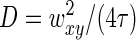(26,27,29), leading to D = 6.5 ± 2.3 μm²/s.

Assuming for simplicity that the structural units have a spherical shape, their effective diameter d can be evaluated from the corresponding diffusion coefficient via the Einstein relation D = k_BT/(3πηd) giving d = 70 ± 20 nm, where for calculation we used the room temperature T = 293 K and aqueous solution viscosity η = 1 mPa s. Having the size of the structural motif Δ ≈ 50 kbp in terms of DNA length and its spatial dimensions defined by d, we can estimate the basepair volume density in the structural unit to be ∼0.3 bp/nm³. This value points to a rather dense structure with the density somewhat higher than that of 30-nm chromatin fiber in eukaryotes (∼0.14 bp/nm³) (46). Interestingly, AFM experiments (7) reveal 40-nm and 80-nm fibers as the basic units of nucleoid structure. Given the similarity of fiber dimensions measured with AFM and structural unit dimensions d evaluated from FCS, it is tempting to speculate that the structural units measured in our experiments correspond to the fibers observed with AFM. In this case the AFM results taken together with our data would indicate that the organization of bacterial nucleoid is rather similar to that of eukaryotic chromatin, at least in terms of basepair density.

Positively supercoiled nucleoids exhibit larger Δ ≈ 130 kbp than that of native nucleoids. However, the characteristic diffusion time in this case is also larger τ = 2.0 ± 0.4 ms, giving an estimate for the spatial dimensions of the structural unit d = 80 ± 16 nm and the basepair density of ∼0.5 bp/nm³ comparable with that of native nucleoids.

We note that the internal dynamics of isolated nucleoids was measured previously by tracking single labeled DNA segments (47). The characteristic diffusion coefficient estimated from these studies D ∼ 0.12 μm²/s is significantly lower than that extracted from our data. Nevertheless, there is no necessary contradiction between these results because of the difference in the timescales assessed in the two sets of measurements: most of the decay of the correlation function in FCS measurements happens below 10 ms, while the tracking measurement starts only at ∼50 ms (47). It is likely that at these large timescales the motion of the structural units is restricted by their mutual interaction and thus slows down. Indeed, Cunha et al. (47) find that the motion of labeled DNA segment is characteristic of confined diffusion. The dynamic light scattering measurements of nucleoid dynamics by the same group (15) give an internal diffusion coefficient D = 1.3 μm²/s, which agrees much better with our result.

To conclude, we present here a novel approach to extract structural information on isolated nucleoids from dynamic data obtained by fluorescence correlation spectroscopy. This approach allows us to evaluate the characteristic size of the structural units in terms of the DNA length involved and to estimate their spatial dimensions. We apply this method to assess the effect of supercoiling on nucleoid structure: the effect appears to be large with ∼15-fold difference in the characteristic sizes of structural units between nucleoids in their native and relaxed states. In addition, we propose and apply here a visualization method to measure nucleoid superhelicity.