The Cellulose Synthase Complex: A Polymerization Driven Supramolecular Motor

Abstract

We present a biophysical model for the propulsion of the cellulose synthase complex, the motile transmembrane protein complex responsible for the biosynthesis of cellulose microfibrils, the dominant architectural component of the cell walls of higher plants. Our model identifies the polymerization and the crystallization of the cellulose chains as the combined driving forces and elucidates the role of polymer flexibility and membrane elasticity as force transducers. The model is elaborated using both stochastic simulations and a simplified analytical treatment. On the basis of the model and approximate values for the relevant physical constants, we estimate the speed of the cellulose synthase complex to be in the range v_p ≈ 10⁻⁹–10⁻⁸ m/s, consistent with the recently reported experimental value of 5.8 × 10⁻⁹ m/s.

INTRODUCTION

A distinctive feature of the cells of higher plants is the cell wall, an extracellular assembly that acts like an external skeleton. Among other things, it allows the cell to support a sizeable internal osmotic pressure, a prerequisite for withstanding the pull of gravity. The cell wall derives its robust mechanical properties from its ingenious construction: it consists of stacks of thin lamellae (1), all deposited parallel to the plasma membrane, that are formed by long parallel almost purely crystalline cellulose microfibrils (CMFs) embedded in a matrix of polysaccharide “packing” material (2,3). Its ubiquitous presence within plant cell walls makes cellulose the most abundant polymeric material in the biosphere. Despite its vital importance both in plant cell function and as a raw material, the primary event of the biosynthesis of cellulose is still only partially understood.

In vascular plants the CMFs are synthesized by a transmembrane protein complex, which we will call the cellulose synthase complex (CSC)1. Although already identified through electron micrograph microscopy for several decades, the definite biochemical proof that these structures indeed are the location of the cellulose synthases, was only provided in 1999 (4). Current estimates of the diameter of the CSC on the endoplasmatic of the plasma membrane are in the range of 40–60 nm (5), making the CSC one of the largest protein complexes so far observed. Electron micrograph images of freeze fracture preparations of the plasmatic face of plant plasma membranes reveal a characteristic structure of six hexagonally arranged particles with a diameter of ∼8 nm forming a ring, or “rosette” (6,7), which has a diameter of ∼25 nm (Fig. 1). The current view is that each of the six lobes of the rosette in turn consists of six cellulose synthases that each polymerizes a single glucan chain using UDP-glucose as a substrate (8). These individual chains are then assembled into the CMF, which by implication consists of 6 × 6 = 36 chains, consistent with the known crystal structure and the measured cross section of ∼3.5 nm (8,9).

FIGURE 1.

Electron micrographs from freeze-fracture preparations of plant cell walls showing a so called terminal-complex, the imprint of a CSC, with an attached CMF in the exoplasmatic face of the plasma membrane (left panel), a so-called particle rosette, the outward facing side of the CSC, within a characteristic depression of the plasma membrane (middle panel, scale bars are 100 nm, both images courtesy A. M. C. Emons) and a close-up of the particle rosette with its typical six-sided symmetry (right panel, scale bar is 10 nm, image courtesy C. Haigler).

The cell wall is deposited from the inside out, with all the relevant materials delivered through exocytosis of Golgi vesicles. As the CSC is bound to the membrane, the deposition of new CMFs thus takes place in the limited space between the outer surface of the fluid plasma membrane and the earlier deposited rigid cell wall. For this process to work, it had to be assumed that the CSC would have to move in the plane of the membrane (10) leaving behind a CMF in its track. The latter hypothesis has now finally been confirmed by the direct real-time in-vivo observation of fluorescently labeled CSCs (11).

Although the idea that the CSC moves was widely accepted, the question of the origin of this movement has so far received less attention. Obvious candidates for the required force production are motor proteins, molecular chemical energy transducers that are involved in many different biological tasks (12,13). Examples are processive molecular motors such as kinesin, which can transport organelles and vesicles using cytoskeletal elements as tracks, or nonprocessive motors such as myosins that deliver the power strokes for muscle contraction, both using ATP as fuel. Indeed, one of the early theories (14) assumed the CSC to be linked by a motor protein to a cortical microtubule, which then acted as a rail to guide the motion. Another proposal (15) had the cortical microtubules act as force producers themselves, which by setting up a shear flow in the membrane, provide a motive force to the CSC. Later, it was realized that in principle the energy released by the glucose polymerization process could by itself be sufficient to propel the CSC (16). In addition, it was shown that preventing the proper crystallization of the CMF by treatment of cells with the drug Calcofluor led to a thickening of the cell wall, suggesting a dysfunctional dispersion of the CSC along the membrane (17). This observation clearly correlates the movement of the CSC with the polymerization and crystallization processes of the CMFs. To date, however, a detailed mechanistic explanation of how the motion of the CSC is achieved was lacking.

Here we develop an explicit biophysical model of CSC motility. We show that the concept of a Brownian polymerization ratchet, originally proposed by Peskin et al. to explain force production by growing polymeric filaments such as microtubules (13,18), can serve as a basis for describing CSC propulsion. However, we argue that to obtain a full understanding also requires taking into account the geometry of the deposition process, the additional driving force provided by the crystallization of the cellulose and the role of the elastic energy stored in the nascent microfibril as well as in the deformable plasma membrane. To achieve our aim, we develop our approach in three steps: First, we formulate a model that integrates the relevant physical components to obtain a heuristic explanation for the propulsion process. In the next step, we implement this model in a stochastic simulation, providing a proof of principle of the proposed mechanism. In the final step, we simplify the model into a form that allows analytical predictions to be made and show that we can reproduce the experimentally measured value for the CSC speed.

MATERIALS AND METHODS

Stochastic simulation

The Monte Carlo scheme used in the stochastic simulation consists of a series of stochastic transitions between different system configurations, all satisfying the imposed constraints. The probability of a given transition depends on the energy difference between the two successive configurations and satisfies the detailed balance condition that ensures the correct sampling of the equilibrium phase space. In the following, even though the simulated systems are discretized for numerical purposes, we will express their Hamiltonians in the continuum limit.

In the simulation, aggregates of six glucan chains are represented by a single effective filament that is modeled as a discrete linear chain of N_f spherical beads of diameter σ that are rigidly connected by bonds of fixed length δ = σ. The length of each chain is thus , where the subscript i = (1..6) refers to the ith filament. The angular bending potential between two subsequent bonds in the chain is given by U(θ) = J_f[1 − cos(θ)], where θ is the angle and J_f is the bending constant that determines the stiffness of the filament. The first monomer-monomer bond (tip) of each filament is constrained to be oriented along the vertical axis of the laboratory frame and the last monomer-monomer bond (tail) is parallel to the horizontal axis. The tips of the filaments are moreover constrained to be located at the vertices of a regular hexagon, with edge-length R_hex = 6σ. No part of any of the filaments is allowed to occupy the space above the rigid wall located at z = 0. The individual filaments can be described by inextensible space curves r(s), where s is the arc-length parameter. Because of the inextensibility, , so that the local curvature of a filament is given by 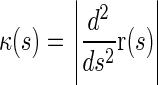. In the absence of the constraints, the Hamiltonian for the full bundle of 6 filaments is then given by

(1)

where the binding energy ɛ is attributed to each pair of monomers on different filaments that are closer than the attraction radius 2^1/2σ.

The liquid bilayer forming the plasma membrane is modeled as a l × l grid of 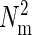point particles of size σ that are capable of moving only in the vertical direction. The edges of the membrane are kept fixed at z = 0. The Hamiltonian for the membrane is described by the Helfrich functional (19)

(2)

where h is the local vertical distance with respect to the equilibrium position, J_m the bending modulus, γ the surface tension contribution, and the integration runs over the area of the membrane. This Hamiltonian is the base model to describe lipid bilayers, since such membranes are fluid in their lateral direction but resistant to stretching forces due to the hydrophobic effect. In this model, we neglect the internal pressure P of the cell, since it has been shown that it makes only a trivial contribution (20).

Analytical treatment

In the analytical version of our model, we consider the whole CMF as a single chain whose configurations are constrained to lie in a vertical plane. The chain is modeled as a semiflexible filament with a persistence length ξ_f significantly larger than the typical dimensions of the region where the filament is bent. Again we have the constraint that the tail of the filament is horizontal and the tip vertical, and that no part of the filament can penetrate the wall at z = 0. To minimize its elastic energy under the given constraints, the equilibrium shape of the filament will be given by a quarter arc of circle of length 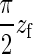, with energy E_f(z) = πJ_f/4z_f, where z_f is the distance from the filament tip to the wall. (The geometry of this situation is schematically depicted in Fig. 4.) The force the tip of the filament exerts on the supporting membrane thus is

(3)

FIGURE 4.

(a) Schematic cross-sectional drawing of the geometry used in the analytical model. (b) The effective model of two coupled springs the analytical model maps onto.

The membrane in turn also tries to minimize its energy by flattening out as much as possible. To obtain this opposing force F_m(z_m), we follow the method of Daniels et al. (21), first calculating the partition function for the fluctuations of a membrane described by the energy functional (2), that is constrained such that its midpoint cannot come closer than a distance z from its unconstrained equilibrium location. Assuming that we are in a regime where the fluctuations of the membrane around its equilibrium position, which scale as , are small compared to the amplitude z of the induced deformation, we can neglect the presence of the rigid wall in z = 0 and extend the relevant integrations over all the possible membrane conformations.

The partition function is then given by

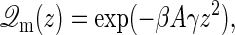(4)

where β = (k_BT)⁻¹ and , with Ω = l² the area of the membrane frame, γ the surface tension, and J_m the bending modulus. We assume throughout that the size of the frame is large enough such that all physical results obtained are insensitive to the shape of the frame. When the membrane is constrained such that the midpoint cannot be above the location z_m, as is the case when an impinging filament is present, it can only explore those configurations where its midpoint is located at positions z ≥ z_m. The force the membrane exerts on the filament is thus given by

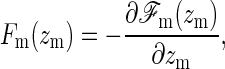(5)

where the free energy is given by

(6)

with Λ an irrelevant constant added for dimensional purposes. In case 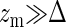, the force is approximately linear in the displacement and given by

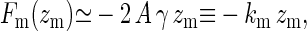(7)

which defines the spring constant k_m. Balancing the two opposing forces F_f and F_m yields the equilibrium position for the filament tip and the membrane midpoint

(8)

To study the fluctuations around this equilibrium position, and assuming that these are small with respect to z_f itself, we linearize the force F_f around z_eq yielding

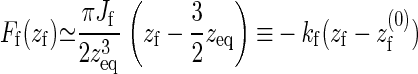(9)

with the effective spring constant given by k_f = −4 Aγ and the effective rest length of the spring by .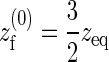

To determine the velocity of polymerization (see Eq. 14), we need to evaluate the probability that a gap is opened between the filament tip and the membrane midpoint larger than the monomer size δ. Note that, after linearization of the filament force, both the filament tip and the membrane midpoint can be considered as harmonic oscillators, which are coupled by the requirement that the filament tip is always above the membrane since the two cannot interpenetrate, i.e., that z_m − z_f ≥ 0. Recalling that the probability distribution for a one-dimensional harmonic oscillator in a thermal bath is given by

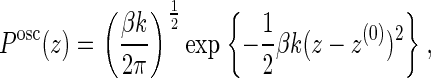(10)

we can determine the probability for a gap of given size Z > 0 from

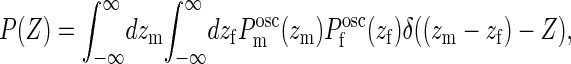(11)

where, as before, we have freely extended the upper limit of the integrations boundaries to + ∞ since the product (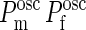) is significantly different from zero only in a small region around Z = 0. Performing these integrations yields

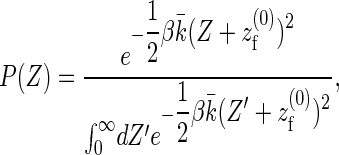(12)

where the effective spring constant of the coupled system is given by 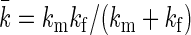. To assess the validity of the approximations made in deriving the analytical model, we compare the prediction of the gap distribution in Eq. 12 with the results we obtain from sampling of a one-filament version of the full stochastic model we will present in the section “Stochastic simulation”. The results are presented in Fig. S1 in the Supplementary Material and show a perfect agreement. Finally, Eq. 15 follows from the definition

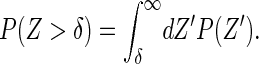(13)

The model

The mechanical cycle that we propose is responsible for CSC propulsion is illustrated in a schematic fashion in Fig. 2. We model the CSC as a planar, membrane-bound object. On the side of the object facing away from the cell a regular array of cellulose polymers is extruded. We model these polymers as inextensible semiflexible chains of beads. The configuration of these polymers is constrained by three factors. The first is their attachment to the CSC itself. Here we assume that this attachment not only fixes the location of the polymer tips, but also specifies the orientation of their first bonds to be perpendicular to the plane of the CSC. The latter assumption is consistent with the hypothesis that the chains emerge from narrow channels in the complex. The second constraining factor is the confining influence of the already deposited cell wall, which we model as an impenetrable barrier. The final constraint arises from the fact that the polymers are at their other ends all linked up into a nascent CMF, which on this scale is an effectively rigid linear structure constrained to lie in the plane of the membrane. Because the polymers have a finite resistance to bending, the combination of geometrical constraints imposed on them implies that they are in a nonrelaxed conformation, resulting in forces acting on their attachment points. At the loci where the polymers emerge from the CSC, these forces will typically have both a perpendicular component and an in-plane component. The perpendicular component has two effects: i), it acts as a barrier for the polymerization process, thus influencing the rate of addition of new monomers, and ii), it contributes to a net force that pushes the CSC downward, counteracted by an elastic response of the membrane. The latter effect is consistent with the membrane-indentations that are seen in some freeze-fracture images of the CSC (22) (see also Fig. 1). Note that we disregard the possibility that the CSC “tilts” with respect to the global membrane orientation, as the energetic cost of such short length-scale deformations of the membrane is probably appreciable.

FIGURE 2.

Snapshots at four different time points in a stochastic simulation of the motion of a six filament CSC. Note the rotation of the complex, induced by the helical nature of the crystalline arrangement in the CMF.

The result of all the in-plane force components due to the individual polymers is the net force that drives the linear motion of the CSC. Energy is injected into this system by the polymerization as well as the crystallization process, as both will tend to increase the stress in the polymers. The energy is dissipated by the work the CSC as a whole performs against the frictional forces it experiences. We stress the fact that thermal fluctuations, which are a dominant effect at the relevant molecular scale, play a crucial role in the whole process. It is these fluctuations that allow the system to cross (and also to recross) the energetic barriers associated with the mechanical constraints imposed on the polymerization process. In fact, it is the rectification of these fluctuations that allow the system to convert chemical energy into directed motion.

Stochastic simulation

We now implement the conceptual model presented above in terms of a stochastic simulation. For simplicity, we consider a CSC producing six effective filaments (EFs), each representing six cellulose chains. This simplification is consistent with the mechanism proposed by Cousins et al. (23) in which the ∼36 cellulose strands that emerge from the CSC are first assembled into six glucan chain aggregates, which subsequently coalesce crystallizing into a CMF. The EFs are modeled as bead chains with a bending potential governing the relative orientation of pairs of neighboring bonds. The beads on different chains have a short-range attractive interaction allowing them to crystallize into a compact arrangement. The already extant cell wall is taken to be a rigid wall, into which the beads are not allowed to enter. The EFs emerge from six hexagonally arranged channels representing the CSC, with their first bond constrained to be perpendicular to the plane of the CSC. This whole construct interacts with a fluid membrane modeled as a dynamically reconfigurable squared network of beads and springs. The tips of the EFs cannot penetrate the membrane, thus coupling the EFs energetically to the membrane. Starting from an initial condition in which the end of one of the chains is clamped, the simulation now proceeds as follows. An attempt is made to move one of the particles in the system (either a chain or a membrane bead). The proposed movement is accepted with a probability proportional to the Boltzmann weight of the associated change in energy of the whole system (including the energies associated with various constraints). This procedure is then repeated for several sweeps over all the particles in the system. This standard Metropolis Monte Carlo scheme allows the system to equilibrate its state to the current lengths of the individuals EFs. After this equilibration step, the gap between the tips of the EFs and the membrane is monitored for all the EFs. If this gap is larger than the size of a chain bead, a new bead is added at the tip, preserving the perpendicular orientation of the first bond. The system is then allowed to equilibrate again, and the whole cycle is repeated. The justification for this procedure is found in the large separation in timescale between the molecular relaxation mechanisms and the rate at which the polymerization process progresses, which allows one to treat the system in a quasi-stationary manner. Note that this algorithm is therefore a microscopic implementation of a Brownian ratchet (18), in the case that the fluctuations are fast compared to the polymerization rate. The full details of the simulation were discussed in the Materials and Methods section.

The results of our simulation show that after initial effects have died down, a stationary regime is reached in which the CSC moves with a statistically stationary velocity in a direction dictated by the essentially straight CMF produced. This shows that indeed, the polymerization and crystallization processes, both exothermic, are coupled by thermal fluctuations to the membrane and the partially flexible chains as energy transducers, are sufficient to obtain the directed motion of the synthase.

Fig. 3 shows four snapshots of our simulation at successive times (a short movie is available in the Supplementary Material). We note that although the trajectory of the CSC is approximately linear, the complex itself undergoes a rotation during its motion. This is caused by the helical nature of the crystalline structure of our pseudo-CMF, which is a natural consequence of the maximization of the binding energy between the spherical monomers. Intriguingly, cellulose microfibrils have also been observed experimentally to “twist” (24,25), an effect generally attributed to the chirality of the planar glucan chains, which spontaneously “twist” to relieve the strain built around the oxygen bridge that connects the successive glucan units together. Clear evidence of this phenomenon is provided by the twisted cellulose ribbon produced by Acetobacter, the so-called vinegar bacterium that lives at water-air interfaces and propels itself by forces derived from cellulose polymerization. Interestingly, moving Acetobacter cells undergo a continuous rotation about their longitudinal axis: again, this is believed to be caused by the relaxation of the torques generated by the crystallization during the biogenesis of the CMFs (26). Also clearly visible in the side views of Fig. 3 is the marked indentation of the membrane at the locus of CSC, over an area several times the area of the complex itself. This indentation is a consequence of the forces generated by the bent EFs, and has been observed experimentally (see Fig. 1 and Emons (22)), and as such provides direct evidence in favor of our model.

FIGURE 3.

Schematic representation of the mechanical cycle in our model of CSC propulsion, illustrated for the case of a single CMF. (From top to bottom) Step 1: the filament and the membrane are in thermal equilibrium. Step 2: due to fluctuations of the filament and/or the membrane, a gap of sufficient size is opened allowing a new monomer to be added to the filament. Step 3: the increase in length of the filament causes an accumulation of elastic energy in the system, which generates a force on the tip of the filament. Step 4: the accumulated energy is released in a unidirectional motion of the tip of the filament, which is attached to the CSC. Step 5: the filament has effectively advanced by one monomer unit δ and equilibrium is restored, allowing the cycle to repeat itself.

Analytical treatment

Although the simulation presented above is able to illustrate the mechanism we propose, its inherent complexity nevertheless impedes a fully quantitative analysis of how the different factors work together to produce the outcome: directed motion of the synthase at a given average speed. We therefore undertake to strip the model to its bare essentials, focusing on a single growing polymer constrained to a two-dimensional planar geometry interacting with a three-dimensional elastic membrane. In this simplified setting, whose projection on a vertical plane is already illustrated in Fig. 2, the model can be solved exactly, allowing the polymerization velocity to be determined. The details of the full calculation were presented in the Materials and Methods section.

In the following, we neglect the thickness of the polymer and the membrane. The membrane is fixed at its edges to a rigid frame of size Ω = l². The equilibrium position of the membrane is taken to coincide with the hard top wall that represents the already extant cell wall. We neglect the spatial extent of the CSC, which is now simply represented by the constraint on the verticality of the first bond of the polymer. We first investigate the equilibrium configuration of the polymer. The active part of the filament can be considered as an elastic rod clamped at one end horizontally to a rigid part, representing the crystallized CMF, and vertically at the tip by the CSC. Such a rod adopts a quarter arc of circle configuration, whose length is πz_f/2, where z_f is the vertical distance of the filament tip to the wall. In the following, we will consider the polymer so stiff as to always maintain the definite shape of an arc of circle: thermal fluctuations have the only effect to modify its radius of curvature z_f. The force the filament exerts on the membrane at its tip is given by 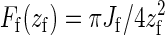, where J_f is the bending modulus of the filament. In response to this force, the membrane will deform, generating a counterforce on the tip of the polymer. This counterforce is given by F_m(z_m) = −2A γ z_m, where A = 2π/[ log(1 + γΩ/J_mπ²)], γ the membrane surface tension, J_i the membrane bending modulus, and z_m the vertical displacement from the equilibrium configuration of the membrane. Balancing these two opposing forces yields the equilibrium position 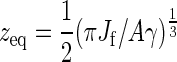. Note that the force exerted by the membrane is already linear in the displacement z_m. We now also linearize the force exerted by the polymer around the equilibrium position, anticipating the fact that we will be concerned only with small fluctuations around it. This procedure maps our model conceptually onto a system of two linear springs acting in opposite directions, the polymer downward and the membrane upward, with the constraint that the tip of neither spring may pass the other, reflecting the fact that the polymer and the membrane cannot interpenetrate (Fig. 4). The dynamics of the growing polymer is governed by the balance between the rate of addition of new monomers and the rate of removal of monomers (assuming a reversible polymerization reaction). In the case that the timescale of the thermal fluctuations is fast compared to the polymerization kinetics, and under the common assumption that the effect of the applied force only influences the on-rate and not the off-rate, the polymerization speed is given by (18)

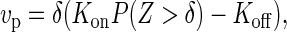(14)

where δ is the size of the monomer, K_on and K_off the bare rates of monomer addition and removal, respectively, Z = z_m − z_f the size of the gap between the filament tip and the membrane, and P(Z > δ) the probability that this gap is larger than the monomer size. For the effective two-spring system we derived above, the probability distribution for the tip-membrane gap can be evaluated exactly. This in turns allows the explicit evaluation of the probability that the gap is larger than the monomer size

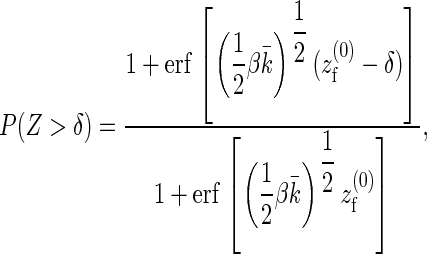(15)

where erf(x) is the error function, 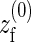the equilibrium position of the linearized polymer-spring, 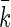an effective spring constant, and β = 1/k_BT the standard inverse temperature (see the Materials and Methods section for details). Taken together, Eqs. 14 and 15 allow the polymerization velocity, which equals the velocity of motion of the CSC, to be determined as a function of all the relevant parameters. Deferring the numerical estimate of this velocity to the next section, we remark that we can readily deduce that the polymerization velocities increases with increasing temperature and decreases with increasing stiffness of the system, caused either by increased stiffness of the filaments or the membrane.

DISCUSSION

The model proposed for the mechanism of the CSC propulsion in this article achieves three goals. First of all, on a conceptual level it provides an explicit and physically consistent heuristic for understanding CSC motion. Secondly, our stochastic simulations, albeit simplified with respect to reality, provide a proof of principle of this mechanism. Finally, the analytical approach, which abstracts the model to its bare essentials, allows the observable result of the mechanism, i.e., the velocity of motion of the CSC, to be quantified in terms of the underlying physico-chemical parameters. Our fundamental assumption that the microscopic fluctuations occur on a timescale fast compared to that of the motion of the CSC justifies the use of the coarse graining that underlies the analytical approach, which replaces the many individual microscopic degrees of freedom, with a small number of effective ones. We can therefore use the results of the analytical approach in an attempt to estimate the velocity of the CSC. In this attempt we are of course limited by the availability of quantitative estimates of the relevant parameters.

We first consider the bending modulus of the effective filament, arguably the least well-determined parameter. Using crystallographic data, we can provide an upper and a lower bound to the value of J_f, as the Young's modulus Y of cellulose is known to vary between 5 GPa for the amorphous state and 150 GPa for the crystalline state (27). We can, however, extract a more appropriative estimate from the depth of the observed indentation of the plasma membrane at the locus of the CSC, which provides an estimate for the equilibrium value of the filament tip to wall distance z_eq. Through the use of relation Eq. 8, we can then determine . For typical values of the membrane surface tension γ = 5 × 10⁻⁵ N/m, the membrane bending modulus J_m = 2 × 10⁻²⁰ Nm, an indentation depth of z_eq = 100 nm, and size of the relevant membrane patch l ≈ 300 nm, we find J_f = 2.5 × 10⁻²⁵ Pa m⁴. Taking the radius of the effective filament to be r = 1/2 diameter of the CMF = 2 nm, we obtain an estimate of Y = 4J_f/(πr⁴) = 20 Gpa, which falls squarely between the bounds mentioned above. We have to keep in mind that, even if the structure of the CMF is almost perfectly crystalline, at the moment of the extrusion from the CSC, the glucan chain aggregates are in a noncrystallized state. Thus the effective Young's modulus of the aggregate is much lower that the one of a cellulose crystal.

For the polymerization rate, we use the value of free polymerization of cellulose achieved by the bacterium Acetobacter, (26,28). Strictly speaking, these experiments determine the net rate K_on − K_off, but we assume that the off rate for these almost irreversible chemical bonding processes is negligible. The final parameter necessary is the size of the monomer, which is equal to the size of a glucose subunit, making 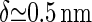. With these ingredients, we can now estimate the speed of the CSC to be 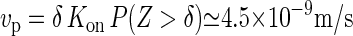. This number compares favorably to the measured average speed 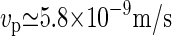observed by the Somerville group (11). We can also compare our results to the estimate of Hirai et al. (29), who observed calcofluor-stained CMFs growing from membrane fragments isolated from tobacco BY-2 protoplasts. Their estimated elongation rate of is higher than that observed in vivo, presumably due to the absence of the spatial constraint of an existing cell wall, which lowers the counterforce experienced by the polymerization process. Nevertheless, given the inevitable effects of friction with surrounding aqueous medium, this value is still lower than that which we would estimate for totally unobstructed deposition, in which case P(Z > δ) = 1 and we obtain .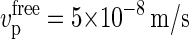

We contend that the biophysical model presented here provides a solid basis for understanding the propulsion of an individual CSC. Moreover, it gives an estimate for the polymerization velocity of the CMF that is consistent with the observed speed of the CSC within the uncertainty imposed by the approximations used. This opens the way for considering the much more challenging problem of understanding the full dynamics of cell wall deposition, which involves the simultaneous and apparently highly coordinated deposition of many CMFs. Indeed, the question of the origin of the highly regular CMF textures found in secondary cell walls is still actively debated. Although the textbook explanation involves the guidance of CSCs by ordered arrays of cortical microtubules (30), there is also a body of evidence against this idea, and a few models have been suggested that rely more strongly on the physical interactions between the CSCs and the CMFs they produce (see, e.g., Emons and Mulder (31) and Baskin (32)). Clearly, all these approaches will benefit from a fuller understanding of the motive processes of the CSC in interaction with its direct environment.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.