Dwell-Time Distribution Analysis of Polyprotein Unfolding Using Force-Clamp Spectroscopy

Abstract

Using the recently developed single molecule force-clamp technique we quantitatively measure the kinetics of conformational changes of polyprotein molecules at a constant force. In response to an applied force of 110 pN, we measure the dwell times of 1647 unfolding events of individual ubiquitin modules within each protein chain. We then establish a rigorous method for analyzing force-clamp data using order statistics. This allows us to test the success of a history-independent, two-state model in describing the kinetics of the unfolding process. We find that the average unfolding trajectory is independent of the number of protein modules N in each trajectory, which varies between 3 and 12 (the engineered protein length), suggesting that the unfolding events in each chain are uncorrelated. We then derive a binomial distribution of dwell times to describe the stochastic dynamics of protein unfolding. This distribution successfully describes 81% of the data with a single rate constant of α = 0.6 s⁻¹ for all N. The remainder of the data that cannot be accounted for suggests alternative unfolding barriers in the energy landscape of the protein. This method investigates the statistical features of unfolding beyond the average measurement of a single rate constant, thus providing an attractive alternative for measuring kinetics by force-clamp spectroscopy.

INTRODUCTION

Statistical analysis of single molecule kinetics of biological reactions has revealed the mechanisms of several important processes (1), including the function of ion channels in cell membranes (2,3) and the evoked synaptic transmission in neurons (4). With the advent of new single molecule techniques that can probe folding and unfolding of biomolecules over time (5–9), appropriate histogram fits and maximum-likelihood methods (10,11) to overcome problems of noise and artifacts are becoming increasingly important in the field. In these experiments, a single module protein fluctuates over time between different conformational states that can be observed and their lifetimes measured. If the reaction is modeled by the simplest two-state Markov process, as is often the case in protein (un)folding (12,13), the distribution of unfolding times can be fitted by a single exponential curve, yielding the rate constant of the reaction.

On the other hand, many modular proteins perform their function in tandem, such as the immunoglobulin modules in the muscle protein titin (14) or multiple ubiquitin modules in protein degradation (15). The influence of the proximity of multiple protein modules in a chain on the unfolding process is a biologically relevant question, since it may introduce correlations via domain swapping (16), module-module interactions (17), aggregation (18) or energy storage through the molecular spring (19). A wealth of information about the underlying kinetics of the process can be inferred from the distribution of unfolding times of the individual protein modules. However, the number of modules in the chain, N, and the order number of each unfolding event in the chain, k, must first be taken into account in the statistical analysis. Such an analysis can then test the system's dynamics, as purely stochastic (random) or including memory (correlations), as well as the presence of alternative unfolding energy barriers.

Force-clamp spectroscopy using atomic force microscopy (AFM) unambiguously follows single polyprotein unfolding and refolding trajectories under a stretching force as a function of protein end-to-end length (13,20). Identical protein modules in the chain serve as a firm signature of the single molecule in the experiment. These measurements then yield the precise dwell time, t, defined as the time it takes for each module in the chain to unfold from the moment the force is applied, which is marked by a step increase in length in the force-clamp trajectories. Measuring the dwell times to a large number of individual unfolding events allows for a statistical analysis of the system's kinetics. Previously, we have shown that the average of just a few such unfolding trajectories, analogous to bulk measurements (12), can be fitted with a single exponential curve, suggesting that the process at a given force appears stochastic (Markovian) (13). Moreover, the average rate of unfolding, α, was shown to be exponentially dependent on the stretching force (21).

Here, with a large statistical pool of 1647 unfolding events of ubiquitin, we are able to perform thorough tests of Markovian behavior, the effects of the chain length N on the kinetics of unfolding, as well as the validity of the two-state model for unfolding. In the AFM, the cantilever picks up single molecule chains at random points on the surface, implying that any number of protein modules within a chain, N ≤ 12, may be picked up in a pulling experiment. In single polyprotein chains, if the unfolding events are truly independent of one another, the number of modules in the chain N should not influence the time course of the average unfolding trajectory. On the other hand, histograms of dwell times can be fitted with a probability density function that is dependent on N. In this study we demonstrate that ubiquitin modules unfold independent of one another in each protein chain, refuting arguments of module-module correlations. Finally, the assumption of two-state unfolding is explored, by testing how successful a unique unfolding rate constant is in fitting all the dwell times using the derived stochastic model. We conclude that a single rate constant is unable fit to all the obtained dwell-time distributions, which is indicative of other pathways in the free energy landscape. We thus provide a statistical analysis for data obtained by the force-clamp technique, while probing important questions as to the microscopic mechanism of unfolding of ubiquitin.

MATERIALS AND METHODS

We used the polyprotein of human ubiquitin, engineered by consecutive cloning of the monomer ubiquitin using the “sticky” ends of the BamHI and BglII restriction sites (22) to form 12 identical domains in the polyprotein chain. The 12-mer ubiquitin is cloned into the pQE30 (Qiagen, Valencia, CA) expression vector and transformed into the BLR(DE3) Escherichia coli expression strain. This construct has a C-terminus His-tag and has two additional residues (arginine and serine) between each module in the chain. The proteins were purified by histidine metal-affinity chromatography with Talon resin (Clontech, Palo Alto, CA) and by gel-filtration using a Superdex 200 HR column (GE Biosciences). The length of the individual folded protein is 3.8 nm from the PDB and the step length at 110 pN is measured to be 20.4 ± 0.7 nm, totaling 24.2 ± 0.7 nm for the fully extended length of the unfolded protein. This corresponds to the unraveling of all the 78 amino acid residues in the protein structure.

The homemade AFM is constructed as described elsewhere (20). Using analog electronics based on a proportional-integral-derivative amplifier whose output is fed to the piezoelectric positioner, the AFM can be operated under force-clamp conditions, in which the cantilever is kept at a constant deflection (force) for a few seconds. The drift of the cantilever introduces an error in the force calibration and is important to address. There are mainly two sources of drift: mechanical relaxation of the whole experimental setup, and the bending of the cantilever because of temperature changes in the room, changes in adsorption on the surface, and the presence of air bubbles. The drift manifests itself in the length trajectories as a nonstationary value of the length over time at constant force, and can therefore be quantified. We have a procedure that rejects any trajectory with an error in the cantilever position of ±5 pN over the course of the experiment (several seconds), thus avoiding any influence of drift on the theoretical model and its results. This corresponds to a change in cantilever position of ≈0.33 nm. Also, to avoid drift, we only start taking data when the experiment is equilibrated at room temperature to ensure constant force conditions.

The typical feedback response is set to 4–6 ms. The used cantilevers (Veeco, MLCT-AUHW, Woodbury, NY) are individually calibrated using the equipartition theorem (23) yielding spring constant values in the range of 12–18 pN/nm. As a result, the force-clamp technique maintains the calibrated cantilever in a constant position, such that the molecule is under a fixed stretching force for the time of the experiment. Typical measurements of protein length yield peak-to-peak noise of ±0.5 nm. The polyprotein is suspended in phosphate buffer solution on a gold cover slide.

RESULTS

A single ubiquitin molecule is held under a constant stretching force between the cantilever and the surface, as shown in Fig. 1 a, tilting the protein energy landscape such that the unfolded state becomes energetically favored. Consequently, the individual modules unfold stochastically in a two-state manner on the millisecond timescale of the experiment. This is evidenced by the stepwise increases of 20 nm in the protein end-to-end length, corresponding to the unraveling of all the amino acids within each module in the chain, as illustrated by the staircases in Fig. 1, b and c. We only include those trajectories that have a minimum of three consecutive 20-nm steps in the staircase, corresponding to the unfolding of at least three protein modules as the signature of the polyubiquitin molecule. On very rare occasions, <0.1%, multiple molecules can attach to the cantilever, but the likelihood of those giving a staircase fingerprint of single molecule unfolding is negligible. Instead, they give rise to a variety of unfolding step sizes, corresponding to the parallel unfolding of individual modules in different chains, and are therefore not included in the analysis. The cantilever picks up molecules of any chain length, N, as shown in Fig. 1 b. Inherent to the technique, there is an uncertainty in N since the detachment of the molecule from the cantilever takes place at random times, irrespective of whether all the protein modules have unfolded. As the rate of detachment is comparable to the average unfolding rate of the protein, many molecules detach before the unfolding of all the modules. For this reason, we only include those traces that lasted longer than 4 s.

FIGURE 1.

Single molecule force-clamp experiments. (a) Schematic showing a polyprotein stretched under a constant force of 110 pN between the cantilever tip and the gold surface. The unfolding of a single domain is associated with a 20-nm release in the protein end-to-end length for ubiquitin. (b) Unfolding kinetics data for ubiquitin chains of varying number of protein modules, N. Length versus time traces show the 20-nm stepwise increase in length each time a single protein domain unfolds. Zero displacement is set at the point where the molecule is taught. The dwell times to the multiple unfolding events k are measured, as indicated in the trace with N = 3. Statistically, the larger the N, the shorter the time it takes to observe an unfolding event. (c) For a given N, the modules unfold within a range of times since the process is probabilistic. This gives rise to dwell-time distributions.

Owing to the large data set (272 trajectories = 1647 events), we can segregate the trajectories according to the number of modules in the chain, N. The normalized sum of all the trajectories for each N is shown in Fig. 2. The single exponential fitting rate constants do fluctuate within the range of N (α = 0.90–1.57 s⁻¹). This narrow range and the absence of a trend as a function of N demonstrates that the average unfolding rate is independent of N. Because the length of the chain does not influence the average rate of unfolding, it would seem that the events are independent of one another. The average over all the data (i.e., chain lengths of N = 3–12, black curve) naturally passes in between the rest of the curves and is fit with a single exponential (dashed gray curve) with α = 1.03 s⁻¹. This result is in remarkable agreement with the previous estimation of the unfolding rate at 110 pN, α = 1.0 ± 0.1 s⁻¹, obtained from a fit of a much reduced unfolding data set as a function of force (13). Nevertheless, this large statistical pool of data reveals significant deviations from the single exponential fit, indicating the presence of other unfolding pathways, which are discussed in detail elsewhere (22).

FIGURE 2.

Comparison of the average unfolding trajectories obtained by summing over traces containing the same number of unfolding events N. The unfolding trajectories are independent of N, as obtained from the two-state fits of Eq. 1 to the data. The variation in the single exponential fits with a rate constant range 〈 α 〉 = 0.90–1.57 s⁻¹ arises from additional pathways in the landscape, also evidenced by the deviations of the single exponential fits with χ² = 40. The average trace over all the data is also shown with α = 1.03 s⁻¹.

The N independence of the average unfolding trajectories can be rationalized assuming a stochastic process in which the modules unfold independent of each other. If the average rate of unfolding is α, the average time course of the normalized protein length, , as in Fig. 1, would then predict

(1)

where P(t) is the probability of unfolding over time, independent of N, as shown in Fig. 2. Our result of N independence of 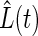therefore agrees with the assumption of probabilistic Markovian unfolding, yet the deviations from the single exponential fits are indicative of violations of the two-state model for unfolding.

Next, we probe the stochastic dynamics of the forced unfolding trajectories. We directly measure the dwell times to the unfolding events of individual protein modules in each polyubiquitin chain under a stretching force. The time it takes to observe multiple unfolding events as a function of chain length is then statistically investigated. If each module unfolds probabilistically with the same rate constant, it should take longer (on average) to observe three events out of three than out of a pool of 12 modules, given that there are more choices. Several such trends become apparent from the length versus time trajectories shown in Fig. 1, b and c. In agreement with the previous remark, the longer the chain length N, the shorter the dwell times to the same number of consecutive events, k, as observed in Fig. 1 b. Second, multiple events k in chains of the same length, e.g., N = 5, are shown to unfold at progressively longer times in Fig. 1 c. Because the unfolding process is stochastic and not deterministic, these observations are only true on average, and can be quantitatively shown in the dwell-time histograms of all the unfolding data. The dwell times of all the events that occur first in the sequence, k = 1, for different chain length ranges N in Fig. 3 a confirm faster unfolding times for longer chains. Also, dwell times to multiple events (k = 1, 4, 7) occurring in sequences of the same N range in Fig. 3 b show not only longer dwell times for more events, but also a change in the shape of the distributions from exponential for a single event to broad distributions for large k. These distributions indicate that the unfolding is probabilistic and that the dwell-time distributions depend on both N and k, which we next investigate theoretically.

FIGURE 3.

Histograms of unfolding dwell times. (a) Distribution of dwell times to the first unfolding event, k = 1, as a function of N reveals that the waiting time is longer for chains with fewer ubiquitin modules. The curves are fitted with Eq. 3, which is the binomial distribution. (b) Distribution of dwell times for k number of unfolding events, for a fixed N range. The distributions range from exponential for k = 1 to normal for large k, characteristic of the binomial distribution.

If we assume that each individual unfolding event is a two-state process and that the events are independent of one another we first calculate the probability of unfolding multiple protein modules within a certain period of time. More specifically, let us construct the probability as a function of time of observing k unfolding events from N folded modules, that is, P(t, N, k). The probability that exactly (k − 1) modules out of N unfold until time t, given that the probability to unfold until time t is denoted p(t), is binomial

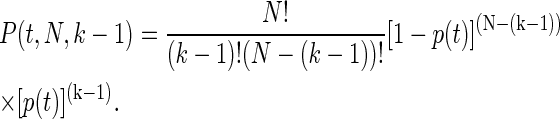(2)

Because the probability of a module to unfold in the time range [t, t + dt] is αdt, it follows that p(t) = 1 − e^−αt. Thus the probability of the k^th module to unfold in the time range [t, t + dt], is then just (N − (k − 1))α dt, since there are N − (k − 1) modules that remain folded. Summing over all the unfolding events, the probability P(t, N, k), that exactly k − 1 modules out of N unfold until time t and then the k^th module unfolds in the time range [t, t + dt], is then

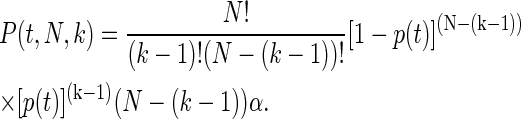(3)

This equation is normalized from zero to infinity over t.

We then used Monte Carlo simulations to test the probability theory. The simulations were based on a Markovian (stochastic) process, with a single unfolding rate constant of α = 1.0 s⁻¹, obtained for the average trajectory over all the data shown in Fig. 2. Each simulation generated 1000 length trajectories over time for each chain length N, while marking the unfolding events by an increase in length of 20 nm, mimicking the experiments. The resulting distribution of dwell times for multiple unfolding events k = 1, 3, 5, 7 for N = 7 is shown in Fig. 4. The success of the fits of Eq. 3 with α = 1.0 s⁻¹ confirms that the probability theory we derived captures the stochastic two-state dynamics.

FIGURE 4.

Dwell-time distributions obtained using Monte Carlo simulations for 1000 traces with chain length N = 7. The success of the fits shows that a Markovian, two-state process with a single rate constant of unfolding gives rise to a binomial distribution derived in Eq. 3.

Next, we examine the success of the theory on the experimental data. Fits of Eq. 3 to the experimental distributions in Fig. 3 indicate that the functional form of the equation is correct. However, in Fig. 3, the data is grouped into N ranges to give better statistics, but this introduces errors in the breadth of the distributions and a large variation in the rate constants used to fit the histograms. We therefore measure the average dwell-time values, rather than the actual distributions, for the best fits of the rate constant for each chain length N. The average dwell times are fitted with the expectation values of 〈 t 〉 for each event k and chain length N that are obtained from Eq. 3, according to

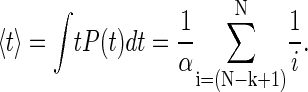(4)

For each N, the average dwell times are successfully fitted with Eq. 4, as shown in Fig. 5, with a relatively narrow distribution of rate constants, α = 0.87 ± 0.13 s⁻¹, shown in the inset. These variations in the average rates indicate discrepancies from the two-state model, but are also affected by the following experimental artifacts.

FIGURE 5.

Fits of the experimental average dwell times as a function of k and N. Average dwell times to the first, second, k^th event in the sequence of each trace, segregated by the total number of steps in the staircase, N, show that the data is successfully fitted with Eq. 4, with a rate constant of α = 0.87 ± 0.13 s⁻¹. The error bars represent the mean ± SE. The variation in α shown in the inset is independent of N, confirming that the process is Markovian.

In this figure the total number of modules N is assumed to be the number of observed unfolding steps, since all the experiments have lasted a minimum of 4 s. Although all the average dwell times shown in Fig. 5 take place before this threshold time, there is a finite but small probability of events occurring at even longer times, as seen in the tails of the distributions in Fig. 6 a. Their probability of occurrence is low, however, trajectories that have detached from the cantilever before the unfolding of all the events have an underestimated N, which could contribute to the observed variation in the unfolding rate constants. Also, there is noise in the stretching force arising from the thermal noise of the cantilever, on which the unfolding rates are exponentially dependent. Given these experimental errors, on average the binomial model fits the experimental data reasonably well. Note, however, that our analysis method is not capable of capturing the diversity in the unfolding pathways of each individual module, rather, it tests which single pathway (α) fits the majority of the data for each chain length N.

FIGURE 6.

(a) Dwell-time distributions of experimental data that is best fitted with a single rate constant of α = 0.7 s⁻¹, consisting of 81% of all data. They are fitted with Eq. 3 as a function of both N and k, clearly indicating the success of the model. (b) Comparison of the average unfolding trajectories obtained by summing over: traces accepted by the iteration procedure (green line), and the outliers (red line). They reveal a clear separation in the rate constants (indicated in the legend) between the selected data and the outliers, suggesting a heterogeneity in the unfolding pathways. The single exponential fits still deviate from the two separated populations.

Finally, we test the two-state model of unfolding by searching for the most successful single rate constant in fitting all the dwell-time data using the binomial distribution. It is known that the length of each polyprotein chain N must lie between the number of observed steps, k_max, and 12, the engineered protein length. For each trajectory, we take the time of the last unfolding event, i.e., of k_max, as well as an input α-value and we solve Eq. 3 to obtain N as the maximum in the probability P. We therefore find the most likely N for each single molecule trajectory. We then determine the average rate constant α that best fits all the dwell-time data, segregated by both k and the allocated N, as in the inset of Fig. 5. This average rate output from the data is then input into the binomial distribution in Eq. 3 in the next step of the iteration procedure. When the input and the output rates converge, we consider this to be the best possible rate constant that fits the data. Using this iteration procedure, we find the data to converge to α = 0.6 s⁻¹ from values far above and below it, but only 81% of the data is allocated an N that is within the possible experimental range. These data are shown in Fig. 6 a, beautifully fitting the binomial distribution across the available range of N and k with the predetermined single rate constant. The remainder of the data is allocated an unrealistic N value in this procedure. Comparing the normalized average trajectories of the data selected by the iteration procedure and the outliers, shown in Fig. 6 b, we observe a fourfold faster average rate constant for the outliers. Previous analysis presented in Fig. 5 included all the data, as it did not assume a single best-fitting rate constant for all N, such that the 19% representing the outliers are accounted for in the variations of the fitting rate constants.

These results suggest that there is a subpopulation of modules unfolding much faster than the most probable pathway (the most likely rate constant). Our statistical analysis reveals this heterogeneity at the chain level when the faster outlier modules are a majority. It is a coarse grained approach, which implies an even larger population of outliers at the single module level. One explanation for the outlier population is that there is at least one alternative pathway in the protein free energy landscape. However, even the populations separated by our iteration method significantly deviate from the single exponential fits in Fig. 6 b, which is suggestive of an even more complex unfolding landscape. Although we cannot rule out a small contribution from misfolded proteins on the surface with our technique, we have previously found that they occur in <2% of the cases and are accompanied by extensions that do not correspond to the signature in length of the protein (24). The outliers are therefore highly unlikely to arise from misfolding. We next investigate whether the noise in the stretching force arising from the thermal noise of the cantilever could be the source of the outlier population.

Fig. 7 a shows a typical length trajectory of a polyprotein unfolding and the corresponding constant force trace in Fig. 7 b. A histogram of forces experienced by the protein due to thermal noise of the cantilever is shown in Fig. 7 c, with an average force pN and a standard deviation of σ_f = 6.82 pN. We investigate the influence of this force noise on the rate of unfolding and show that it is negligible compared to the deviations we measure with the outliers.

FIGURE 7.

Thermal noise of the cantilever. (a) A typical unfolding length trajectory of ubiquitin, under a constant stretching force of 110 pN, shown in panel b. (c) The distribution of forces in the trajectory in panel b represents the thermal noise of the cantilever and gives an average force 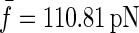and a mean ± SD of σ_f = 6.82 pN. It broadens the distribution of measured rates of unfolding by 10% (see text) and cannot account for the outliers in the distribution.

The barrier crossing to unfold a protein is a thermally driven process, where the barrier height is modulated by the external force, F, as:

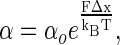(5)

where α is the rate of unfolding, α₀ is the rate of unfolding in the absence of force, Δx is the distance to the transition state, and k_BT is the thermal energy. Because of Brownian motion the applied force is not constant, and has a probability distribution given by:

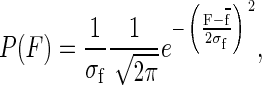(6)

shown in Fig. 7 c. A simple change of variables in Eq. 5 leads to an exponential distribution of rates instead of a single value of α,

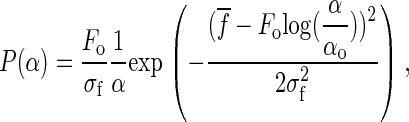(7)

where 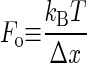. This probability distribution has an expected value of

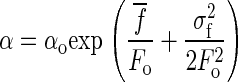(8)

Using the experimental values of σ_f and 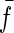in Fig. 7 we obtain an expected value of the narrow distribution of rates to be within 10% of the rate measured without taking the force noise into account. On the other hand, we find a four times higher average value of the rate of unfolding of the “outlier” population, which shows that this effect is negligible compared to the experimentally observed discrepancy.

DISCUSSION

Using a large pool of single module unfolding data obtained by force-clamp spectroscopy, we were able to test the validity of a stochastic model on the mechanism of unfolding in polyprotein chains. We found that the average unfolding trajectory over time is independent of the number of modules in the chain, N, thus supporting the Markov hypothesis of history-independent unfolding. We have demonstrated that the proximity of multiple protein modules in a given chain does not accelerate ubiquitin unfolding, as the events are independent of one another. Therefore, our results show that the dynamics of a single ubiquitin module is independent of the length of the chain despite the recent evidence that aggregation or stabilization due to interactions between the individual modules may occur (18,17).

Another signature of Markovian behavior was shown to be the binomial distribution of unfolding dwell times, in which the average fitting rate constants in Fig. 5 were also independent of N. The experimental data also proved that the dwell times to the unfolding events are dependent on N since N is small. For example, the longer the chain, the shorter one has to wait for the same number of events to occur. On the other hand, the last event in each chain takes place at later times for longer chains.

While the Markovian assumption was shown to hold well, we also discovered significant deviations from the two-state model, which implies a single rate constant for unfolding. First, the single exponential fits to the average trajectories in Figs. 2 and 6 b clearly strayed from the experimental data. Also, there were significant variations in the rate constant fits of the average dwell times as a function of N in the inset of Fig. 5. Furthermore, the single best fitting rate constant for the data according to the binomial model did not account for all the dwell times in Fig. 6 a. Instead, the two separated populations in Fig. 6 b had vastly different average rate constants and still could not be fitted with single exponentials. All these discrepancies suggest that multiple unfolding barriers do exist in the energy landscape of ubiquitin. Indeed, a theoretical analysis at the single molecule level facilitated the discovery of a distribution of unfolding pathways in the glassy landscape of ubiquitin (22). Our results are consistent with that finding, since the “selected” data in Fig. 6 b corresponds to the most probable pathway at the peak of the distribution in Fig. 4 of Oberhauser et al. (24), while the “outliers” account for the tail of the observed broad distribution.

In our experiments we are probing the lifetimes of different conformational states of the single protein molecules explored under a constant stretching force. Arguably, this is a much reduced phase space as compared to the molecules that are free in solution, which is determined by the pulling direction and the magnitude of the pulling force. We are perturbing the system away from its native state in solution to deduce the mechanical stability of the molecules. These states are relevant in nature as the cell is an environment that is often under stress (25). A protein's mechanical stability and conformational diversity under force are therefore relevant parameters in nature.

Bulk kinetic measurements of ubiquitin show both single pathway mechanisms and intermediates that appear as a function of unfolding conditions (26–32). However, they are unable to distinguish between the pathways of individual molecules that are blurred in the ensemble. Single molecule data has the important advantage of distinguishing between the individual molecules, which reveals a wealth of new information. We have demonstrated how measuring dwell-time distributions can produce kinetic signatures of the conformations of ubiquitin at any given pulling force. Such a capability is useful, particularly for future studies of how the unfolding path depends on thermodynamic variables, such as the temperature. With the advent of new statistical energy landscape theories of protein folding and insight into the complexity of the dynamics of folded protein structures, there is an increasing need for more sophisticated statistical analysis of protein unfolding/folding measurements.