Studying Molecular Motor-Based Cargo Transport: What Is Real and What Is Noise?

Abstract

Noise is a major problem in analyzing tracking data of cargos moved by molecular motors. We use Bayesian statistics to incorporate what is known about the noise in parsing the trajectory of a cargo into a series of constant velocity segments. Tracks with just noise and no underlying motion are fit with constant velocity segments to produce a calibration curve of fit quality versus average segment duration. Fits to tracks of moving cargos are compared to the calibration curves with similar noise. The fit with the optimum number of constant velocity states has the least number of segments needed to match the fit quality of the calibration curve. We have tested this approach using tracks with known underlying motion generated by computer simulations and with a specially designed in vitro experiment. We present the results of using this parsing approach to analyze transport of lipid droplets in Drosophila embryos.

INTRODUCTION

The internal organization of eukaryotic cells depends upon intracellular trafficking of cargos along microtubules (MT) and actin filaments. Kinesin, dynein, and myosin-V are motor proteins that are responsible for hauling a diverse array of vesicles and organelles. These include mitochondria, endosomes, and even viruses that have entered the cell (1,2). Cytoplasmic kinesin goes toward the plus end of a microtubule (MT) whereas cytoplasmic dynein moves toward the minus end of an MT. Although individual motors have been studied extensively (3,4), the way in which multiple motors work together to transport a single cargo is not well understood. For example, even though individual motors usually move in only one direction along a filament, cargos in vivo are observed to move bidirectionally. These reversals in direction are likely the result of coordinated switching between different types of motors, though the mechanism controlling this is not understood (1,2,5).

Because it is difficult to visualize individual motors in vivo, one can study the trajectories or tracks of cargos to help shed light on how multiple motors move a cargo. Video recordings can be made of the positions of a cargo in vivo with a spatial resolution of a few nanometers and a temporal resolution of a few hundred Hertz (6–8).

One can fit these tracks with a series of line segments where each segment represents a state of constant velocity motor motion (9–12). However, it is difficult to do this reliably due to the uncertainty in inferring the position of the motor from the position of the cargo. This uncertainty is caused by the thermal fluctuations of the cargo that is connected to each motor by a long (∼100 nm) floppy linkage. Throughout this article we will refer to these thermal fluctuations as noise. Other contributions to the overall uncertainty, such as noise in the imaging system, can affect the accuracy of the detection of the position of the cargo itself. In our approach these sources of uncertainty are handled separately from the thermal fluctuations by choosing an appropriate likelihood function.

So, it is important to separate the underlying motion of the motor complex from the thermal fluctuations. We have developed a way to do this that incorporates information or assumptions about the noise. The result is an algorithm that reliably parses cargo tracks into constant velocity segments given what is known about the noise. The major advantage of our method is that it provides an objective criterion to determine the number of segments.

Previous approaches to parsing

Several approaches to interpreting the tracking data have been developed previously. One approach, introduced in Gross et al. (10), treats the tracks as a sequence of runs and pauses. Here a run is defined as uninterrupted motion of a cargo in one direction. A pause is a state with no net motion. The ambiguity introduced by the thermal fluctuations (noise) is resolved by requiring the durations of all states to be greater than some minimum threshold. The value of this threshold represents the additional information that is required to determine the number of states.

A second approach, called multiscale trend analysis (MTA), was used to analyze the tracks in Zaliapin et al. (13). MTA uses a “best least squares linear approximation” to fit the tracks by a set of linear segments of constant velocity and constructs a hierarchy of increasingly accurate approximations in which the number of segments increases. The MTA error spectrum is constructed by plotting the fit error versus the number of segments. The optimal fit is determined by finding a corner point of this spectrum.

Both of these approaches are based upon untested assumptions. The first approach guesses at a reasonable level for the relevant thresholds, but in principle this guess could be inaccurate. Moreover, the value of the threshold can change depending on the system studied and on the conditions of the experiment. The MTA approach assumes that there is only one underlying timescale (other than noise), so that a change in slope can be interpreted as the transition from signal to noise, as opposed to from one type of signal to another. It also assumes that the noise has sufficiently different properties from the signal to provide a recognizable change in slope of the MTA error spectrum.

More sophisticated approaches to parsing complex biological trajectories were recently presented in (14,15). These approaches use statistical properties of the trajectories to detect regions of direct motion as well as pauses and regions of diffusive motion. They work by independently analyzing and classifying either a small portion of a track (15) or frame-to-frame displacements (14). In contrast, the approach that we are presenting here works by repeatedly analyzing a track as a whole and rejecting or accepting the results of that analysis based on the properties of the noise present in the track.

Independent noise information is used in parsing

In this article we develop a method of parsing tracks as a series of constant velocity segments based on the Bayesian formalism. We define a quantitative measure of the quality of the fit, which can be interpreted as the probability that a set of states represents a particular tracking series. The number of segments that is necessary to represent the underlying motion (as opposed to the thermal fluctuations) of the track is determined by using independent noise measurements, namely direct observations of the fluctuations of the position of a cargo that is not being moved. Using this data we construct a calibration curve that represents the best fit quality for a given number of segments. The optimal number of segments for a track with unknown underlying motion is then determined by comparing the fit quality of various parsing iterations with the value given by the calibration curve.

When it is impossible to directly observe the fluctuations of a cargo with no underlying motion, additional assumptions about the fluctuations are necessary to determine the number of states. This kind of information can also be incorporated into our method by adding a special term to the distributions used to compute the fit quality.

Overview of the rest of the article

The rest of the article provides more details to clarify these ideas, with technical details in the supplement. We first outline the parsing procedure. Then we evaluate the accuracy of the parsing procedure using tracking data with “known underlying motion”. These tests demonstrate how thermal fluctuations present in the data affect our ability to detect small changes in the velocity or the direction of the underlying motion. To the best of our knowledge, this is the first systematic investigation of the reliability and accuracy of a parsing procedure where the properties of the underlying motion are cleanly known. We further proceed to discuss the parsing of in vivo data and apply the technique to an established experimental system. We describe approaches that can be used to obtain calibration data appropriate for use with tracking data from an in vivo experiment. After obtaining suitable calibration data, we use the parsing program to analyze the tracking data of lipid droplets in a Drosophila embryo. First, we check a previous result (10) that the motion of lipid droplets can be modeled by a five-state system. The five states are pauses and long-fast or short-slow runs in both plus and minus end directions. We conclude by investigating the possibility that there is a discrete set of preferred velocities of in vivo cargo motion. Such a possibility was recently suggested in Levi et al. (16) and Kural et al. (17).

PARSING PROCEDURE

Constant velocity states

Data representation

We are analyzing tracking data, i.e., a time series with each point giving the location (X and Y coordinates) of the cargo at some time T. Tracks are chosen that are believed to represent the cargo moving along a single straight filament (microtubule, actin filament). However, the precise location of the filament is in most cases not known. So, first a straight line that best fits all the data points in the X-Y plane is found. This line serves as an approximate representation of the filament. This is, indeed, a reasonable approximation to the actual location of the filament as was demonstrated in Gross et al. (11). The positions of the cargo with respect to the filament are then computed by determining the coordinates along and perpendicular to the line.

The position of the cargo on the filament is specified by the distance (L) along the filament from the initial position of the cargo. The time series of these positions is referred to as the distance versus time (L-T) data. Thus, the purpose of our algorithm is to approximate L-T data as a segmented line with the slope of each segment being the velocity of a state. Put differently, we aim to parse the L-T data into segments reflecting the underlying series of constant velocity states.

Fitting tracking data by line segments

This task is complicated by the fact that the trajectories are distorted by the thermal fluctuations of the position of the cargo around the position of the motors. The thermal fluctuations may make the cargo appear to have more constant velocity states than actually present or, conversely, several short constant velocity states may appear as a single segment. The task of parsing such a trajectory is a two-stage process. First, the number of segments (the optimal configuration given the level and character of noise) has to be determined. Second, the properties of each segment are found (such as start time, end time, and slope or velocity). We have developed a procedure, based on the Bayesian approach, that accomplishes both of these goals.

Bayesian approach

Consider the general problem of fitting a set of data points D by some mathematical model M such as a straight line or a polynomial. In the Bayesian approach, the measure of the quality of a fit is defined as the probability that the model represents a given set of data and is referred to as the posterior probability P(M|D).

The posterior probability is proportional to the product of two terms:

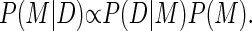(1)

The relationship described above is known as Bayes theorem. The first term P(D|M) is called the likelihood function and is a measure of how close the data points are to the model (in our case a particular segmented line). This function reflects the uncertainty in determining the position of the cargo. It accounts for the effects of the noise present in the imaging system (such as interlace or shot noise) on the cargo tracking algorithm. The second term P(M) is called the prior probability and represents any preexisting knowledge of the system. An optimal fit maximizes P(M|D). Examples of applications of this approach, as well as a more detailed introduction, can be found in Gelman et al. (18) and Werman et al. (19).

In our case the model is a piecewise linear approximation. The unknown parameters of this model are the locations of the end points of the segments. The likelihood function, which takes into account the measurement error associated with each L-T data point, is analytically derived in Supplement A of the Supplementary Material. We use the prior probability to ensure causality, i.e., that there are no segments of negative duration.

Fitting procedure

The fitting procedure works by constructing a family of approximations of a track. This is done by first fitting a track by many short segments and then gradually reducing the number of segments by merging pairs of adjacent segments. This process continues until there is only one segment left. Each iteration consists of selecting the pair of segments that is the best candidate for merging, merging the two segments by eliminating the vertex connecting the segments, and optimizing the locations of the remaining vertices (see Supplement C in Supplementary Material for a detailed outline).

At every iteration the optimal fit of the track by the current number of segments is determined by maximizing the posterior probability of the model. We do not simultaneously optimize the positions of all end points (a prohibitively complex task). Instead we optimize the positions of the segments one at a time, in random order, while keeping all the other segment end points fixed. The optimization loop continues until the required accuracy has been achieved. A more detailed description of the optimization algorithm can be found in the supplement.

Although this optimization algorithm does not guarantee the globally optimal solution in the general case, it works well when the initial positions of the end points are close to their optimal positions. We ensure that this condition is fulfilled by using the result found in the previous iteration to initialize the current iteration. This is done by eliminating one vertex connecting two segments in the optimized segmented line found in the previous iteration and replacing these segments by a single segment connecting the remaining end points. The vertex that is eliminated is chosen so that its removal produces the smallest geometric distortion of the optimized segmented line. This ensures that the configuration of the new segmented line is close to optimal (for the system with the number of segments reduced by one).

Model selection

Up to this point we have established an algorithm that allows us to fit the distance versus time data by any number of constant velocity segments. Now we need a method for determining the appropriate number of segments.

Using tracks with no motion to estimate noise

Models with a larger number of segments will generally fit the data better. Thus, it is impossible to determine the optimal number of segments without using additional information or making assumptions. To address this problem, we use tracking data with no underlying motion as the source of the information about the noise present in the tracking data with unknown underlying motion.

We refer to the tracking data with no underlying motion as the calibration data. Such data can be obtained in an in vitro experiment by coating a bead with molecular motors and allowing it to attach to a filament with no adenosine triphosphate (ATP) present. Under these conditions, the bead is tethered to the filament through molecular motors, which are immotile. The fluctuations of this tethered bead can be recorded, and are expected to reproduce the noise of a bead/cargo being moved by the motors when ATP is present.

After obtaining a few calibration tracks, we fit each of them by segmented lines consisting of different numbers of segments. Then we construct a calibration curve that shows how well the data that has only noise can be fit by a specific number of segments.

For a track with unknown underlying motion, the quality (posterior probability of the model) of the fit for a given number of segments cannot be higher than the calibration value. In the case when it is comparable to the calibration value, the underlying motion can be faithfully represented by the number of segments that are currently used. On the other hand, if the quality of the fit is significantly worse, then more segments are needed to represent the motion. Therefore, the best estimate of the optimal number of segments is equal to the minimum number of segments of the model that gives a posterior probability comparable to the calibration value.

An example of using the calibration procedure

We have developed a computer simulation that allows us to generate artificial tracks with known underlying motion and different amounts of noise to be able to evaluate the performance of our method. A detailed description of this simulation can be found in the Supplementary Material. Here we shall use this simulation to give an example of using the calibration procedure described above.

We start by generating several tracks with no underlying motion that will serve as calibration data. The calibration curve is obtained by fitting these tracks by segmented lines with different numbers of segments. Each track produces its own unique calibration curve. The final calibration curve is constructed by averaging the calibration data from all tracks. Lastly, to mimic experimental data, we produce simulated tracking data with some known underlying motion.

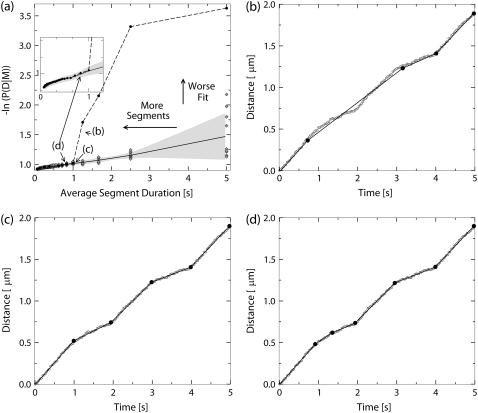
The fit quality of this simulated track is compared with the calibration curve in Fig. 1 a. Here we can see that the fit quality starts to match the calibration curve (falls in the gray area around the calibration curve) at the fifth point from the right. This observation implies that fitting the track in question by less than five segments produces a fit quality that is significantly worse than the calibration value. This is confirmed by the plot (Fig. 1 b), which shows that fitting the tracking data by four segments leads to significant deviations of the segmented line from the tracking data. Fitting the tracking data by five (Fig. 1 c) or more (Fig. 1 d) segments results in quality comparable to the calibration value. So, the simulated underlying motion can be described by five or more constant velocity states. However, given the noise, we can only reliably distinguish five states of motion. There is no way to determine whether the extra vertex in Fig. 1 d (as compared to Fig. 1 c) corresponds to a change in the motion or is merely an artifact of the noise in the track. We therefore conclude that the optimal number of segments for this track is five. This is indeed the number of segments specified when the track was generated.

FIGURE 1.

An example of using the calibration procedure to determine the most likely number of segments in a track. (a) The calibration curve is derived from a set of computer simulated tracks with no underlying motion. The horizontal axis is the average duration of a line segment that is used to fit the tracking data. The vertical axis gives the value of the negative logarithm of the posterior probability scaled by the number of data points, so lower values correspond to better quality of the fit. The original calibration data derived from individual tracks is represented by the hollow diamonds. The lower solid line represents the calibration curve that is obtained by averaging the calibration data. The gray area represents the estimate of the error in determining the calibration value. It was computed as the mean ± SE and interpolated along the x axis. The dashed line and solid black circles represent the dependence of the quality of the fit on the average duration of a segment in a fit to a computer-generated track that corresponds to the underlying motion with five distinct constant velocity states. The duration of each state is 1 s, the velocity alternates between 200 nm/s and 500 nm/s. The track and the segmented lines corresponding to the points labeled b, c, and d are shown on corresponding figures. The tracking data of the motion combined with the noise is represented by circles. The solid lines represent the constant velocity states that were determined by the parsing procedure. Panel b shows the track fitted by a segmented line consisting of four segments; panel c shows the same track fitted by a segmented line consisting of five segments (the correct number); and panel d shows the track fitted by six segments.

Calibration procedure is an objective representation of the noise

The major advantage of using the calibration procedure described here is that one does not have to rely on any assumptions about the noise in the system. It serves as an objective criterion that enables us to determine the number of distinguishable segments in the presence of the noise.

In a situation where it is impossible to obtain suitable calibration data one has to make some assumptions about the noise. Such assumptions can be incorporated in our method by introducing additional terms into the prior probability distribution (this case is addressed in more detail in Supplement F, Supplementary Material).

Testing

To test our parsing procedure we used it to parse sets of tracking data corresponding to known underlying motion. Three different approaches (described below) were used to obtain such sets of tracking data. In all three cases, the underlying motion is modeled by a set of discrete velocity states.

Three approaches to generating testing data

In the first approach the tracking data is obtained by superimposing uncorrelated Gaussian noise on top of deterministic underlying motion. The second approach is similar, however, the noise profile derives from a more complex model of the thermal motion of the cargo that accounts for time correlations of the positions of the cargo (see Supplement B in Supplementary Material for more details). The third approach requires a special in vitro experiment to be performed. We use an optical microscope to observe a slide that contains a polystyrene bead attached to a microtubule by a molecular motor (dynein). With no ATP present in the environment, the motor does not move, so thermal fluctuations of the bead bound by a molecular motor are observed directly (20). The underlying motion is then simulated by using a piezoelectric stage to move the whole slide in the field of view of a microscope. This setup allows us to obtain tracking data with known underlying motion and the noise characteristics of a real cargo attached to a microtubule by a molecular motor.

Calibration curves

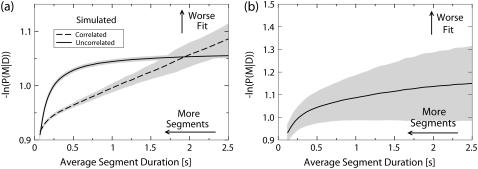
We start the testing by constructing a separate calibration curve for each of the three sets of testing data described above (shown in Fig. 2). The parameters of the computer simulations were adjusted so that the average displacement of a cargo between two consecutive video frames (30 frames per second) caused by thermal fluctuations would match that of a flopping bead bound by a dynein motor. Because of this, the calibration curves coincide at very short average segment durations Fig. 2. However, they diverge as the average duration of the segments used to fit the data increases.

FIGURE 2.

Calibration plots for (a) the simulated data with no underlying motion and (b) flopping beads attached by dynein are shown. The horizontal axis is the average duration of a line segment used to fit the tracking data. The vertical axis is the value of the negative logarithm of the posterior probability scaled by the number of data points. In panel a the dashed line represents the calibration curve for the data simulated using the computer model of a flopping cargo; the solid line represents the calibration curve for data simulated using uncorrelated Gaussian noise as the model of thermal fluctuations. In panel b the solid line represents the calibration curve obtained from the tracks of flopping beads attached by dynein. The calibration curves were obtained by (a) averaging the raw calibration data (not shown) obtained by processing 20 simulated tracks each lasting 20 s, and (b) four tracks with a combined duration of ∼250 s for the flopping beads attached by dynein. The gray areas around the curves represent the uncertainty in the calibration values computed as the standard deviation of the mean of the raw calibration data.

The probability that the positions of several consecutive data points can be approximated by a straight line is very low for the case of uncorrelated noise. Hence, the calibration curve for the uncorrelated Gaussian noise simulation grows rapidly in the region of very short segments but saturates quickly as average segment duration increases. This stands in contrast to the calibration curve corresponding to the data simulated with a tethered cargo. In this case the data is correlated because the cargo has a continuous trajectory. The corresponding calibration curve at first falls below the uncorrelated noise calibration curve. This reflects the fact that the tethered cargo's trajectory can be well approximated by short line segments. However, due to the larger range of motion (250 nm for the tethered cargo versus ∼30 nm for the uncorrelated Gaussian noise), at large segment durations the quality of the fit is much worse for the correlated data than for the uncorrelated noise.

The calibration curve derived from the in vitro tracking data of a bead attached by a dynein motor (Fig. 2 b) has a shape similar to the curve for uncorrelated simulated data, however, it grows more slowly at short timescales and continues to grow at large timescales implying the presence of some correlation.

Reversals and velocity changes

We want to test the ability of the parsing program to identify segments (changes in velocity) in the presence of the noise. We identify two extreme types of motion that present a challenge for a parsing program: small velocity changes and short reversals. Noise can mask small velocity changes or even large velocity changes if they occur for a very short time.

Biologically, short reversals correspond to a situation when a motor complex that is pulling a cargo, changes direction, moves in the opposite direction for a short distance, and then reverses again and continues in the original direction. This type of behavior is commonly observed in bidirectional transport (4,11). Such behavior of the motor complex is simulated using a two-state model with the first state corresponding to a long segment in one direction and the second state corresponding to a short segment in the opposite direction. The motor complex alternates between these two states. Examples of the motion produced by this model are shown in inserts (see Fig. 5).

FIGURE 5.

The dependence of the ability of the parsing program to recover the correct sequence of states on the length of the reverse state (in the testing data corresponding to the underlying motion with short reversals) is presented. The vertical axis gives the probability that any three consecutive segments detected by the parsing program will be in the right sequence (see text for more details). The horizontal axis is the length of the reverse state. The length of the forward state of underlying motion was fixed at 500 nm. The velocity of the forward state was set at 500 nm/s; the velocity of the reverse state was −500 nm/s. The tracks were either (a) simulated on a computer or (b) produced by moving a microscope stage with in vitro preparation of a flopping bead attached to a microtubule by a dynein motor. Sample tracks are shown in inserts. The tracking data are represented by open circles, and the segments detected by the parsing program are represented by the solid lines. For these tracks the length of the short reverse state of the motor complex is 40 nm.

Small velocity changes occur when a motor complex changes velocity without changing the direction of motion, e.g., when load per motor changes (21). Recent studies attempted to investigate the velocity changes of motor driven cargos and relate them to the number of active motors present on a cargo (12,16). It is thus important to have an objective measure of the accuracy of detecting velocity changes. Here again we use a two-state system to model the behavior of the motor complex.

Testing procedure

For each of these two types of motion we generate three sets of tracking data using procedures described earlier. We then parse each track in these data sets into constant velocity segments using the corresponding calibration curve.

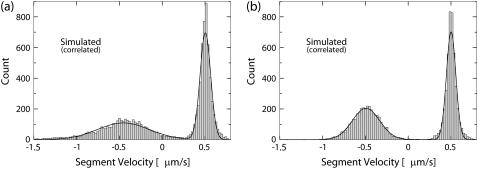
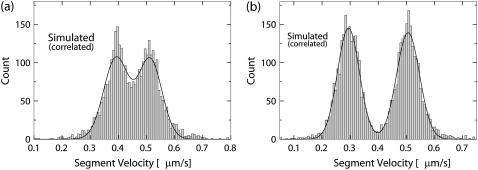
Due to the noise present in the data, the motion described by the segments identified by the parsing program is not identical to the underlying motion. We have developed a procedure that enables us to gauge the ability of the parsing program to recover the properties of the underlying motion. First, we construct a distribution of segment velocities for each set of testing tracks. Figs. 3 and 4 show examples of such distributions for the cases of short reversals and small velocity changes, respectively. There are clearly identifiable peaks in the distributions that represent the different states of underlying motion, confirming that the number of states of underlying motion can be recovered by analyzing the segments detected by the parsing program. The velocities of these states are recovered by fitting the velocity distributions by a sum of two Gaussian distributions. As expected, the uncertainty in determining these velocities (standard deviation) decreases as the lengths of segments increase.

FIGURE 3.

Velocity distributions of the segments detected by parsing simulated data corresponding to the underlying motion with short reversals. The horizontal axis is the velocity of segments detected by the parsing program. The vertical axis is the number of segments with that velocity. The velocity of the underlying motion is 500 nm/s for the forward state and −500 nm/s for the reverse state. The length of the forward state of the underlying motion is 500 nm. The length of the reverse state is (a) 40 nm, or (b) 60 nm. The distributions were fitted by a sum of two Gaussian distributions (solid line). (a) Mean velocities are: −453 nm/s, 503 nm/s. Mean ± SD are: 304 nm/s, 62 nm/s. (b) Mean velocities: −492 nm/s, 502 nm/s. Mean ± SD are: 160 nm/s, 55 nm/s.

FIGURE 4.

Velocity distributions of the segments detected by parsing simulated data corresponding to the underlying motion with small velocity changes. The horizontal axis is the velocity of segments detected by the parsing program. The vertical axis is the number of segments with that velocity. The durations of both the fast and the slow state of the underlying motion are equal to 1 s. The velocity of the fast state is 500 nm/s. The velocity of the slow state is (a) 400 nm/s, (b) 300 nm/s. The distributions were fitted by a sum of two Gaussian distributions (solid line). (a) Mean velocities are: 392 nm/s, 512 nm/s. Mean ± SD are: 43 nm/s, 43 nm/s. (b) Mean velocities are: 294 nm/s, 506 nm/s. Mean ± SD are: 39 nm/s, 41 nm/s.

In the second step of the testing procedure we check whether the transition probabilities between the two states of the underlying motion can be recovered by analyzing the sequence of the segments detected by the parsing program. The underlying motion of the testing tracks was generated using a model of two alternating states. So, if all segments were correctly identified by the parsing program, a segment corresponding to the first state would be between two segments corresponding to the second state and vice versa. Using this observation, we define a numerical measure of the accuracy of parsing as the probability that a randomly selected sequence of three consecutive segments corresponds to a valid sequence of states of underlying motion (state 1/state 2/state 1 or state 2/state 1/state 2). This probability is computed using the velocity distributions constructed earlier. See Supplement G in the Supplementary Material for details.

Detecting short reversals

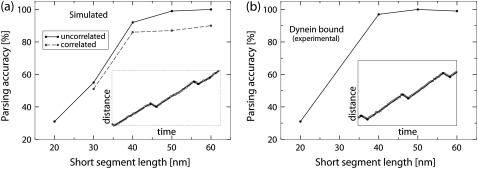
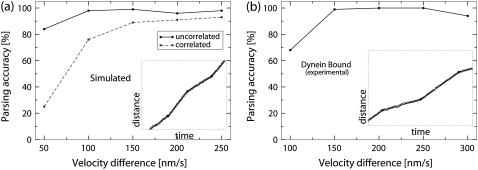
The procedure outlined above enables us to make a consistent estimate of the effect that the properties of the underlying motion and noise have on the parsing accuracy. Fig. 5 shows the dependence of the parsing accuracy on the length of the short reverse state.

The ability of the parsing program to detect segments deteriorates as the length of the short state decreases because it becomes harder and harder to distinguish the motion produced by the motor complex from the thermal fluctuations of the position of the cargo. From Fig. 5 it is evident that the chances of correctly parsing a track with a 20-nm reverse state are close to 30% for the data simulated with uncorrelated noise and for the experimental data. At the frame rate that we are using (30 frames per second), 80% of segments corresponding to the 20-nm state are represented by a single data point. The remaining 20% are represented by two data points.

For the tracks simulated with identical underlying motion and correlated noise, the distribution of segment velocities cannot be accurately represented by a sum of two Gaussian distributions. So, the velocity states cannot be identified and the parsing accuracy cannot be determined.

The probability of correctly parsing the test tracks grows rapidly as the length of the short state increases. The curves depicting the dependence of the parsing accuracy on the length of the short reversed state are very similar for the testing data generated using the computer simulation with uncorrelated noise and for the data obtained in vitro. They both reach 90% when the length of the reversed state approaches 40 nm. Typically such a state is represented by two or three data points. The curve corresponding to the data simulated using correlated noise grows slower than the other two curves.

Detecting small velocity changes

We now turn our attention to the test tracks that correspond to motion in the same direction with changing velocity. A plot of the dependence of the parsing accuracy on the difference in velocities between consecutive segments is shown in Fig. 6.

FIGURE 6.

The dependence of the ability of the parsing program to recover the correct sequence of states on the velocity difference between the states (in the testing data corresponding to the underlying motion with small velocity changes) is presented. The vertical axis gives the probability that any three consecutive segments detected by the parsing program will be in the right sequence (see text for more details). The horizontal axis is the velocity difference between the first and the second states. The velocity of the first state was fixed at 500 nm/s, the duration of each state was fixed at 1 s. The tracks were either (a) simulated on a computer or (b) produced by moving a stage with in vitro preparation of a flopping bead attached to a microtubule by a dynein motor. Sample tracks are shown in insets. The tracking data is represented by open circles, and the segments detected by the parsing program are represented by the solid lines. For these tracks the velocity difference between the two states of motor complex is 200 nm/s.

As expected, the ability of the program to correctly identify states of motion decreases as the difference in velocity between the two states decreases. The curves depicting the dependence of the probability of correctly parsing a set of three segments on the velocity difference between the slow and the fast state have similar trends to the curves from the previous test. The curve corresponding to the in vitro experimental data (Fig. 6 b) matches closely the curve for the simulated data with uncorrelated noise (Fig. 6 a, solid line). The accuracy of parsing the simulated data with correlated noise (Fig. 6 a, dashed line) is considerably lower.

Noise limits parsing accuracy

We attribute the difference in the ability of the program to correctly parse segments in different types of testing data to the difference in the properties of the noise present in the data, which is reflected by the shapes of the calibration curves (see Fig. 2).

If the calibration curve is flat for some range of the average segment duration, there is very little chance that a cargo trajectory with such an average segment duration could be caused by thermal fluctuations. So, underlying motion with that average segment duration can be reliably distinguished from the thermal fluctuations. On the other hand, cargo trajectories that correspond to nonflat regions of the calibration curve could be caused by the thermal fluctuations. In such a case it is not always possible to distinguish the underlying motion from thermal noise.

For our simulated testing data, the average duration of states with different velocities is 1 s. In that region the calibration curve derived from the simulated data with uncorrelated noise is absolutely flat. So, we expect to be able to identify segments with very high accuracy. For the same segment duration, the calibration curve for the data with correlated noise is growing. In this situation we can only expect to recover the underlying motion if it moves the cargo a significantly larger distance than the amplitude of the thermal fluctuations. Both of these expectations are confirmed by the results in Fig. 6 a.

For the testing data with reversals the average segment duration of underlying motion is between 0.5 and 0.6 s. In that region both calibration curves are not flat, so the ability of the program to correctly parse tracking data strongly depends on the length of the short-reversed segment. This explains the results in Fig. 5.

Application to experimental data with unknown underlying motion

In this section we described our tests of the parsing program on data with known underlying motion. We obtained accurate estimates of the performance of the parsing program, and we find that our algorithm works well. We believe the algorithm should work well on real experimental data. As shown above, in the simulated data a pair of states with different velocities can be identified by two peaks in the distribution of the segment velocities. The same approach can be applied to the experimental data. If the motion of the motor complex can be described by a set of states with distinct properties, then it should be possible to identify these states by using distributions of lengths and velocities, or by using length-velocity and duration-velocity plots of segments detected by the parsing program.

Parsing in vivo data

We now use the parsing procedure to analyze in vivo experimental data that was produced by tracking the motion of lipid droplets along microtubules in wild-type Drosophila embryos (phase 2 of development) (9).

Embryos were hand dechorionated and flattened in halocarbon oil between the glass slide and a coverslip as previously described (9). Differential interference contrast images of the moving lipid droplets were collected by a charge-coupled device camera (Dage-MTI CCD 100, Michigan City, IN) and recorded on video cassettes (30 frames per second). Lipid droplets were then tracked after digitization as previously described (9).

Obtaining the calibration data

Before proceeding with parsing the tracking data, we need to calibrate the parsing program by using suitable noise samples. One way to obtain such calibration data would be to hand pick cargos in a living cell that do not show any persistent motion and use their random motion for calibration. This approach is problematic since some cargos are known to move bidirectionally for very small distances by repeatedly switching the direction of motion. This undermines our ability to determine if the cargo is being moved by a molecular motor just by looking at the recording of the cargo position. In an attempt to get rid of any motor-driven motion we microinjected the Drosophila embryos with a mixture of adenylylimidodiphosphate (AMP-PNP) and apyrase. The former is an ATP analog that works as a motor inhibitor and the latter is an enzyme that catalyzes the hydrolysis of ATP to yield AMP and orthophosphate. Both should act together to inhibit motor-driven motion (22). The apyrase concentration used was 0.5 unit/ml (Sigma Aldrich No. A6410-100UN, St. Louis, MO) and that was mixed 1:1 with either 100 mM or 1 M of AMP-PNP (EMD Biosciences 120002, San Diego, CA). The total volume injected was ∼1/50th that of the embryo. For both AMP-PNP concentrations lipid droplet motion was significantly inhibited, but residual motion was still observable. This, again, made it problematic to use apparently stationary cargos for noise calibration.

Because of this we have chosen to calibrate the program using tracking data from video recordings of a flopping bead in an in vitro environment. To make such recordings, 500-nm diameter polystyrene beads were covered by molecular motors that were allowed to attach to a microtubule. With no ATP present, the motors do not step, and the motion of the beads caused by thermal fluctuations was observed directly. Two calibration curves were obtained (see Fig. 7)—one for dynein motors (this curve is the same as the one discussed in the previous section) and one for kinesin motors. Notice that the calibration curves corresponding to the two types of motors are similar. Therefore we do not expect strong changes in the thermal fluctuations when a cargo inside a cell reverses direction (switches from one type of motor to another).

FIGURE 7.

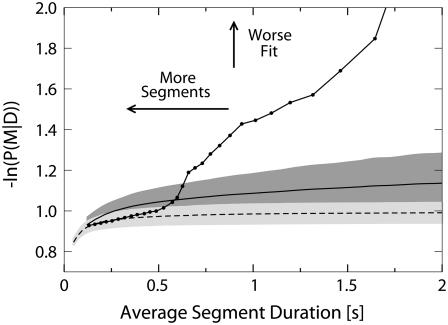
Shown are two calibration curves derived from in vitro tracking of flopping beads attached to a microtubule by multiple dynein motors (solid curve on dark gray background) or by multiple kinesin motors (dashed line on light gray background) as well as a curve depicting the dependence of the fitting quality on the average duration of segments for an in vivo track of a lipid droplet in a Drosophila embryo (solid line and black dots). The horizontal axis is the average duration of a segment in a segmented line used to fit the data. The vertical axis is the negative logarithm of the posterior probability scaled by the number of data points in a tracking series (lower values correspond to better fit quality).

The calibration curves obtained using the data from an in vitro experiment could be different from what one would obtain using an ideal set of in vivo calibration data. However, we believe that the in vitro data provides an overestimate of the noise. There are two reasons that lead us to this conclusion. First, the viscosity of the buffer used in the in vitro experiment is much lower than viscosity of the cytoplasm. Increased viscosity suppresses particle diffusion, so over the same time period thermal fluctuations of the position of the cargo in buffer will be larger than in cytoplasm. Second, there are often additional tethers in vivo stabilizing the cargos (e.g., the dynactin complex). The increased rigidity of the linkage between the cargo and the microtubule is expected to further reduce the random motion of the cargo (compared with the conditions of our in vitro assays).

We will not be able to detect all constant velocity segments present in the data because some segments will be merged together. This is the price we pay for overestimating the noise by using the in vitro calibration data. It is important to note that our approach will not detect more segments than there are distinct states of motion. This is because noisier calibration data produces a higher calibration curve. So when the fit quality for a track intersects this calibration curve, the corresponding segment duration will be larger than for a calibration curve corresponding to less noise. An example illustrating this argument is shown in Fig. 7.

Parsing tracking data into runs and pauses

Having constructed the calibration curves we can now proceed to parsing the tracking data of the lipid droplets in Drosophila embryos. There are a number of studies that have looked at this system (9,10) and used other methods to analyze the tracks. In particular, the tracking data was interpreted in Gross et al. (10) in terms of runs—states of uninterrupted motion in one direction. The difference between runs and segments is that a segment corresponds to a state of constant velocity motion whereas a run corresponds to a state of motion in one direction (possibly with changing velocity).

The model proposed in Gross et al. (10) features two states of motion in each direction: a short slow run and a long fast run, as well as a state that corresponds to a pause in motion. We have decided to check this conclusion by using our parsing procedure. This was done by first parsing the tracking data into constant velocity segments, then converting the segments into runs. To accomplish this, all consecutive sets of segments of motion in the same direction with velocity higher than 100 nm/s were merged into runs. Segments of motion with velocity lower than 100 nm/s were interpreted as pauses. Consecutive segments with such low velocities were merged into a single pause.

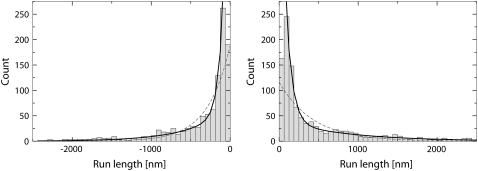
After parsing the tracking data in terms of runs and pauses, we constructed the distribution of run lengths shown in Fig. 8. The left part of the figure corresponds to motion toward the minus end of the microtubule and the right part corresponds to motion in the plus end direction. Fitting the run length distributions by a single decaying exponential does not give an acceptable fit. Fitting the distributions by a sum of two exponentials improves the fit dramatically. This suggests that to adequately describe the motion, two types of runs (long and short) in each direction are necessary. This confirms the result previously reported in Gross et al. (10).

FIGURE 8.

Distributions of run lengths for minus (left) and plus (right) end transport in a wild-type Drosophila embryo are shown. The runs were determined by first parsing the tracking data into segments of constant velocity motion using the parsing program with a multiple kinesin calibration curve (shown in Fig. 7). Then consecutive segments of motion in the same direction were combined to produce runs. A velocity threshold of 100 nm/s was used to determine pauses in motion. The run length distributions were fitted by single (gray dashed line) and double (black solid line) exponential curves. The value of reduced χ² produced by fitting the plus-end distribution by a single exponential curve is 5.89 and the optimal value of the fitting parameter (average run length) is 427 nm. For the double exponential fit, the value of the reduced χ² is 0.86 and the values of the fitting parameters are 78 nm and 852 nm. Fitting the distribution of minus-end run lengths by a single exponent produced average run length of 282 nm with 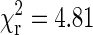. For the double exponential fit, the values are 62 and 503 nm with .

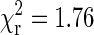Parsing the tracking data into constant velocity segments

Recent studies of melanosome transport in Xenopus melanophores (16) and of peroxisome transport in S2 Drosophila cells (17) raised the interesting possibility that there is a discrete set of preferred velocities of cargo motion. These preferred velocities manifested themselves as peaks in the distribution of segment velocities. In both of these studies, the velocity distributions were constructed by hand by approximating regions of motion by segments and using the velocities of these segments.

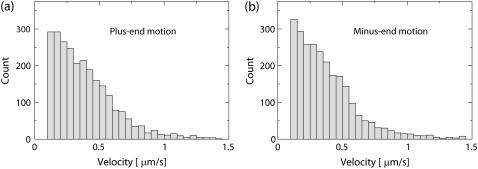
To test these conclusions in the lipid droplet system, we used our parsing procedure on tracking data of the lipid droplet motion in Drosophila embryos. The distributions of segment velocities obtained from this data do not show any significant peaks (Fig. 9). These distributions were constructed using the procedure described in this manuscript, by first fitting tracks by connected constant velocity segments. However, for comparison with Levi et al. (16), we only used the velocities of the segments that closely match the tracking data (root mean square (RMS) deviation from the fit line of <20 nm) and have duration exceeding 0.4 s. Unlike Levi et al. (16), no upper limit on segment duration was imposed, since our approach independently establishes the number of segments in a track. Another difference between our approach and the approach used in Levi et al. (16) and Kural et al. (17) is that we analyze whole tracks whereas only select portions of the tracks were considered in Levi et al. (16) and Kural et al. (17).

FIGURE 9.

Distributions of segment velocities of (a) plus-end and (b) minus-end directed motion of lipid droplets in Drosophila (phase 2) embryos are shown. The segments were obtained by parsing the tracking data using multiple kinesin calibration curve. For each segment a RMS value of the deviation of the data points from the segmented line was computed. Only segments with the RMS value of deviation <20 nm, velocities >100 nm/s, and duration >0.4 s were used to construct the histograms.

SUMMARY

We have presented a method of parsing the motion of actively transported cargos into a series of constant velocity states. This is a probabilistic method based on the Bayesian approach. The main advantage of this method is that it determines the appropriate number of segments present in a given track. This is done in an objective way by comparing the fit quality produced by fitting a track with unknown underlying motion by some number of segments to the fit quality produced by fitting a track with no underlying motion by the same number of segments. The number of segments that adequately represent the underlying motion in the track is equal to the minimum number of segments that are necessary to get comparable fit qualities for the track with unknown underlying motion and for the track with no underlying motion.

Another advantage of our method is flexibility. The Bayesian approach is more flexible than conventional fitting methods based on the least squares distance approach. In our method the function that describes the uncertainty associated with the position of the data points is not fixed (as is the case in the least squares distance approach) and can be specified explicitly. This potentially allows us to analyze data with different types of noise using the same method.

We have extensively tested the parsing method by using it on tracking data with known underlying motion. Three sets of tracks with different noise characteristics were used in testing. Two of them were generated on a computer and the third was obtained in a special in vitro experiment. In each set there were tracks corresponding to two types of underlying motion. Tracks that correspond to persistent motion of the motor complex in one direction that would periodically get reversed for a short time were used to test the ability of the program to detect reversals in motion. The ability of the program to detect changes in velocity that are not accompanied by a change in the direction of motion was investigated using data that corresponded to continuous motion of the motor complex in one direction with periodic changes in velocity.

The results of the testing indicate that the parsing program can successfully recover the number of states of underlying motion and the properties of these states (velocity, duration, and length). The accuracy of the program is defined as the shortest duration of the reversed segment or the minimum velocity difference that can be detected reliably. By using testing data with different models of thermal fluctuations we have established that the accuracy of the method is only limited by the characteristics of the thermal fluctuations.

Finally, we have applied our method to parse in vivo tracking data. We used recordings of lipid droplets being transported along microtubules in wild-type Drosophila embryos. In an earlier study (10) it was established that motion of lipid droplets in a Drosophila embryo can be described as a five-state system. Every state represents a run of uninterrupted motion in some direction or a pause. The model consists of short and long runs in both directions on the microtubule and a pause. A run ends in a pause or in a run in the opposite direction. By definition a run cannot immediately follow a run in the same direction. We were able to verify the previous result using our Bayesian parsing technique. This was done by first parsing the tracking data in terms of constant velocity segments and then converting the segments into runs by merging consecutive segments of motion in the same direction and using a fixed velocity threshold to determine pauses. Finally the distributions of lengths of runs were analyzed to show that for each direction, there were two distinct populations of runs.

Finally, we have checked the possibility that in vivo cargoes have a discrete set of well-defined preferred velocities. Using our parsing technique and the tracking data of lipid droplets in wild-type Drosophila we find no evidence for any preferred velocities.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.