Further Evidence for the Absence of Polyproline II Stretch in the XAO Peptide

Abstract

It has been suggested that the alanine-based peptide with sequence Ac-XX-[A]₇-OO-NH₂, termed XAO where X denotes diaminobutyric acid and O denotes ornithine, exists in a predominantly polyproline-helix (P_II) conformation in aqueous solution. In our recent work, we demonstrated that this “polyproline conformation” should be regarded as a set of local conformational states rather than as the overall conformation of the molecule. In this work, we present further evidence to support this statement. Differential scanning calorimetry measurements showed only a very small peak in the heat capacity of an aqueous solution of XAO at 57°C, whereas the suggested transition to the P_II structure should occur at ∼30°C. We also demonstrate that the temperature dependence of the ³J_HNHα coupling constants of the alanine residues can be explained qualitatively in terms of Boltzmann averaging over all local conformational states; therefore, this temperature dependence proves that a conformational transition does not occur. Canonical MD simulations with the solvent represented by the generalized Born model, and with time-averaged NMR-derived restraints, demonstrate the presence of an ensemble of structures with a substantial amount of local P_II conformational states but not with an overall P_II conformation.

INTRODUCTION

The question of the nature of chemically denatured proteins was first raised some 40 years ago. In 1966 Tanford et al. (1) claimed that, under highly denaturing conditions, proteins “are true random coils retaining no element of their original native conformation”. Based on this statement, the random-coil (or rather statistical-coil) model became the standard reference state for interpretation of experimental data regarding unfolded proteins and the starting point for most theoretical considerations of the folding process. However, in 1973 Tiffany and Krimm (2) suggested that the shapes of the ultraviolet (UV)-CD spectra of denaturated proteins are best explained by the presence of a significant population of locally ordered polyproline II (P_II) conformation, even for sequences with low proline content. This observation was supported by recent experimental studies: NMR (3–5) and CD spectroscopy (3,4,6) and Raman optical activity reviewed by Barron et al. (7).

In 2004, Kohn and co-workers (8) supported the proposal of Tanford et al. (1) that chemically denatured proteins obey random-coil statistics. The extent or type of local backbone structure present in denatured states remains unknown. Thus, it is commonly believed that the coil state of peptides and proteins is structurally random in that the molecules sample the entire allowed region of the Ramachandran map. This view is also based on Flory's (9) classic independent site approach. However, as mentioned above, during the last 15 years, numerous works have reported experimental and theoretical evidence for the existence of regular structural motifs in the coil state. In this context the left-handed P_II helix has become particularly relevant. In recent years, the poly-L-proline type II conformation has gained more and more importance. This structure is very common in elastomeric proteins like elastin and abductin (10,11), where it is often found in equilibrium with other structures, as well as in lamprin (10) (a matrix protein of laprey annular cartilage). Although elastin and abductin are both elastomeric proteins, the first showing elastic behavior during the extension state and the second during the compression state, lamprin is not classified as an elastomer (10–12). The common characteristic of all three proteins is both their presence in the extracellular matrix and their propensity to form fibrils (10). The P_II structure has been shown to occur in a number of proteins and seems to be a critical structural element for protein-protein interaction with SH3 domains (13). This structural element is also present in collagen, serine proteinases, aspartic proteinases, and immunoglobulin constant domains (14). P_II helices may be involved in DNA major groove recognition (15). The P_II conformation exists in plant cell wall glycoproteins and in antifreeze glycoproteins (16). In summary, the P_II structure has been suggested to be essential for biological activities such as signal transduction, transcription, cell motility, and immune response (17). However, it must be emphasized that the stability of the P_II structure depends very much on the presence of proline and glycine residues along the polypeptide chain. Martino et al. (18) showed that, in the solid state, the presence of PG or GGG sequences in polypeptide chains and even in a short peptide such as Boc-PG-OH induces the acquisition of the P_II structural motif. However, this conformation appears to be much more unstable in solution (water), even in the case of long polypeptide chains (18).

As mentioned above, experimental evidence, mainly from CD spectra, supports the statement that P_II is quite a common conformational state in the conformations of peptides and unfolded proteins. However, many investigators, including Chen et al. (19), Shi et al. (3,20), Asher et al. (21), and Schweitzer-Stenner et al. (22), have extended their interpretation of the available experimental data and concluded that not only local P_II conformational states but also P_II structure persisting through a sequence of consecutive residues are common conformations of peptides and unfolded proteins. The seminal work has been carried out by Shi and co-workers (3). Based on CD and NMR measurements, these researchers (3) proposed that an alanine-based peptide with sequence Ac-XX-A₇-OO-NHMe, where X denotes diaminobutryic acid and O ornithine, adopts the P_II conformation at low temperatures and, upon melting, this conformation is converted into a mixture of β-extended and statistical coil at ∼30°C. The support for this was i), the presence of characteristic P_II-like features in the CD spectra, ii), the value of the ³J_HNHα coupling constants that suggested φ-angles of the alanine-core residues characteristic of P_II, together with iii), lack of nuclear Overhauser enhancement (NOE) signals, which is indicative of extended values of the ψ-angles. Together, this evidence suggested the presence of the P_II conformation in the XAO peptide in water. Moreover, later, Asher et al. (21) determined the mean ψ-angle value from UV Raman data to be 147°, which is in good agreement with the value for the P_II conformation. The evidence for a conformational transition was the temperature dependence of ³J_HNHα and of the ellipticity at the 217-nm maximum in the CD spectrum of XAO. Altogether, the results by Shi et al. (3) and Asher et al. (21) presented a consistent picture of a stable P_II conformation of XAO, which melts at ∼30°C.

Shi and co-workers subsequently extended the conclusion about the predominance of the P_II conformation to all peptides and unfolded proteins (see Shi et al. (20) for a review). They also implied that the P_II conformation plays a fundamental role in protein folding, because it is a common initial state of this process (20). In their view, this solves the Levinthal paradox (23) because the existence of a highly restricted initial state greatly reduces the number of states that a protein has to visit on its way to the native conformation.

As nice as the idea of well-defined conformations of peptides might appear, one must be cautious about assuming that a linear peptide has a stable conformation even at low temperatures. A wealth of experimental data (e.g., fluorescence quenching (24–26)) suggests that the distances between residues are broadly distributed rather than being focused. It should, therefore, at least be considered that the observables measured for XAO and other alanine-based peptides are conformational averages rather than being indicative of specific conformation(s). Therefore, we carried out two studies: i), to understand whether a P_II helix propagates through adjacent nonproline residues (27), and ii), to shed light on the conformational preferences of the alanines and ionizable residues in the XAO peptide (28). Results from both studies were consistent with each other and with the existing experimental evidence. In particular, these studies show that i), in presence of water, there is no propagation of the P_II conformation for several PXP sequences in which X is not Pro (27), namely for X = Ala, Gln, Gly, and Val (27); and ii), the XAO peptide seems to populate an ensemble of conformations with only a few residues in the P_II region of the Ramachandran map (28).

Recently (29), we reexamined the conformation of this peptide by carrying out NMR and CD measurements and determining the conformational ensemble from NMR data by using simulated annealing molecular dynamics (MD). The conformational ensemble determined in that work (29) consisted of conformations with mainly a bent shape, which contained alanine residues in local P_II conformational states but no structure with the whole alanine core in the P_II conformation. The ensemble-averaged radius of gyration of XAO was in excellent agreement with the value determined by Zagrovic et al. (30) from small angle x-ray scattering (SAXS) measurements; this value should be much greater even if a few residues of the alanine core in a row had the P_II structure. We also demonstrated that the CD spectra of XAO depend not only on temperature, pH, or denaturant concentration but also on the kind of buffer; this suggests that the P_II conformation is very diffuse, and it is more reasonable to consider it in terms of local conformational states than as a persistent structure. Our study was severely criticized by Shi and co-workers in their recent review (20). They claimed that it is hard to counter the wealth of experimental evidence for the presence of the P_II conformation of XAO and other alanine-based peptides and that in particular, the observed temperature dependence of the coupling constants and CD spectra are a clear indicator of a conformational transition.

In this study, we present more experimental and theoretical results pertaining to the conformation of XAO, including differential scanning calorimetry (DSC), temperature and solvent dependence of CD spectra, and a reevaluation of the conformational ensemble of the peptide by using canonical NMR-restrained MD simulations taking water into account rather than carrying out simulated annealing MD in vacuo. We also demonstrate that the temperature dependence of the coupling constants is consistent with Boltzmann averaging over all conformational states of the alanine residues. We conclude that the available experimental data can easily be interpreted in terms of the existence of XAO as an ensemble of interconverting conformations, if the observables are interpreted only as conformational averages and not as values characteristic of particular conformation(s).

MATERIALS AND METHODS

Peptide synthesis

The XAO peptide was synthesized on a 0.19-mmol scale by the solid-phase method using the Fmoc strategy with an automated 9050 Plus PepSynthesizer (Millipore, Milford, MA). N^α-Fmoc amino acids, with natural abundance isotopic content, were in a fourfold excess of the required amount of peptide, and DIPCI (diisopropylcarbodiimide) was used as the coupling agent. Purification was carried out on a Kromasil-5-C8 (EKA Chemicals, Bohus, Sweden) preparative high-performance liquid chromatography (HPLC) column using a linear gradient of an aqueous solution of acetonitrile and 10% trifluoroacetic acid. The yield was 46.8% (fast atom bombardment mass spectroscopy: [M+H]⁺ = 985.5; the calculated mass of an observed singly protonated XAO is 985.2 g/mol). The purity of the peptide was also checked by HPLC chromatography on a TentaGel R RAM resin (Rapp Polymere GmbH, Tuebingen, Germany), resulting in a chromatogram with a single peak.

CD spectroscopy

Circular dichroism (CD) spectra were recorded on a Jasco J-20 (water, methanol, D₂O, TFE) and Jasco-715 (urea, GnHCl) automatic recording spectropolarimeter with 1-mm quartz cuvettes (Jasco, Tokyo, Japan). CD measurements were made at 0.05, 0.1, and 0.2 mM peptide concentration in water (pH = 4.6) from 1° to 80°C. CD measurements were also made in trifluoroethanol (TFE) and methanol from 20°C to 70°C at a peptide concentration of 0.05 mM and in 10% D₂O, at 5°C, at a peptide concentration of 0.2 mM. The spectra were recorded from 193 to 260 nm, using a sensitivity of 5 mdeg/cm and a scan speed of 2 cm/min. The CD spectra were measured three times and were plotted as mean ellipticity Θ (degree × cm² × dmol⁻¹) versus wavelength λ (nm).

Differential scanning calorimetry

Calorimetric measurements were performed with a VP-DSC microcalorimeter (MicroCal, Studio City, CA) at a scanning rate of 65°C/1 h. Scans were obtained at a protein concentration of 0.5 mM. The cell volume was 0.5 ml. All scans were run at pH = 4.6 in water in the range of temperature 5°C–80°C. The reversibility of the transition was checked by cooling and reheating the same sample. These measurements were recorded three times. Results from DSC measurements were analyzed with the Origin 7.0 software from MicroCal using the routines of the software provided with the instrument (31).

Calculation of NMR-related observables and conformational averages

Theoretical NOE intensities were calculated by using the MORASS (multiple Overhauser relaxation analysis and simulation) program (32,33). This program solves the system of Solomon differential equations (34) for the cross relaxation of a system of interacting proton spins. The theoretical NOE intensities were calculated for the XAO peptide in the extended-strand, P_II, and α-helical conformations. The NOEs were computed using a mixing time of 400 ms (this being the value used in our NMR experiments (29)) and a correlation time of 200 ns (a consensus value for flexible peptides (35)). The theoretical NOE intensities were calculated for all pairs of protons separated by a distance of <5 Å.

The values of the ³J_HNHα coupling constant were computed from the Karplus equation (36,37) with the parameters, namely A, B, and C, from Pardi et al. (37). It is worth noting that different existing parameterization of the Karplus equation led to similar results (28):

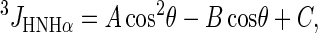(1)

where 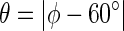, A = 6.4 Hz, B = 1.4 Hz, C = 1.9 Hz.

The Boltzmann-averaged values of the ³J_HNHα coupling constants were computed from Eq. 1, and the energy map calculated in Arnautova et al. (38) by the quantum-mechanical ab initio method at the MP2/6-31G** level by using Eq. 2:

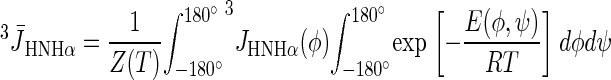(2)

with

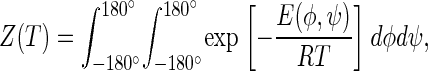(3)

where T is the absolute temperature, E(φ,ψ) is the energy at point (φ,ψ) of the conformational energy map, and Z(T) is the partition function. In Arnautova et al. (38), E(φ,ψ) was computed as a nonadiabatic energy surface (i.e., the energy was minimized over all but the values of φ and ψ).

The potential of mean force, W(φ), was computed from Eq. 4:

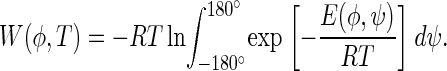(4)

The integrals in Eqs. 2–4 were evaluated by summation over a grid of the energy map of terminally blocked L-alanine as calculated in Arnautova et al. (38).

Molecular dynamics calculations with time-averaged NMR-derived restraints

MD calculations were carried out using the AMBER 8 program (39) with the AMBER 99 force field in the NTP ensemble at temperature T = 298 K. The integration time step was 2 fs. The total time of simulation was 6 ns. The charges of the nonstandard residues—diaminobutyric acid and ornithine—were calculated using the restrained electrostatic potential method (40) based on HF/6-31G* calculations carried out with Gaussian98 (41). The charges of the atoms of the nonstandard residues (diaminobutyric acid and ornithine) were determined in an earlier work (42). The time-averaged restraint method (39,43,44) was used to include interproton distance (a total of 40) and dihedral-angle restraints (a total of 23, pertaining to the φ-and ψ-angles for Ala residues, the φ- and χ-angles for the ornithine residues, and the φ-, ψ-, and χ-angles for the diaminobutyric acid residues) determined from the rotating frame Overhauser effect (ROE) intensities, Raman spectroscopy (21), and coupling constants, respectively. The interproton distances were restrained with the force constant k = 20 kcal/(mol × Å²), and the dihedral angles with k = 3.64 kcal/(mol × rad²) for the ψ-angles of the alanine residues and k = 2 kcal/(mol × rad²) for the φ-, ψ-, and χ-angles for the alanine, ornithine, and diaminobutyric acid residues, respectively. The dihedral angles ω were restrained to 180° with k = 10 kcal/(mol × rad²). The improper dihedral angles centered at the C^α atoms (defining the chirality of amino acid residues) were restrained with k = 50 kcal/(mol × rad²). We obtained 13 ensembles of conformations starting from the extended, P_II, and α-helical structure and 10 randomly generated structures. Conformations were saved every 10 MD steps (a total of 12,000 conformations per run). The 200 last conformations from each trajectory (corresponding to the 2,000 last MD steps) were used to calculate ensemble-averaged quantities and to determine the families of conformations by clustering. The set of the final conformations was clustered with the MOLMOL program (45). A root mean-square deviation (RMSD) cutoff of 2.0 Å over the A-3–A-9 residues was used for the clustering.

RESULTS

CD spectra

The CD spectra of the P_II conformation of nonproline peptides are characterized by a strongly negative band around 200 nm and by a weaker positive band at ∼217 nm (10,46,47). For peptides rich in proline or hydroxyl-proline, the positive band is shifted to ∼225 nm because of the presence of tertiary amide chromophores (48,49). The spectral features of P_II structure are quite characteristic and, therefore, are easily distinguished from structures such as α-helix, β-sheets, β-turns, or statistical coil. The CD spectra of the XAO peptide in water and in phosphate buffer under different conditions were presented in our earlier work (29), where we have shown that, in water and in acetate buffer, the shape of the CD plots possesses the features characteristic of well-defined P_II structure such as in collagen. In phosphate buffers, the XAO peptide exhibits a CD spectrum partially characteristic of a statistical-coil structure (50). The shape of the CD curves depends on the pH, peptide concentration, and the composition of the buffer. These results are much easier to interpret in terms of local (uncorrelated) P_II conformational states of the individual Ala residues of XAO than in terms of an overall P_II fold of the heptaalanine segment (or, at least, a 2–3 residue part of this segment) of this peptide. As Shi and co-workers pointed out in their recent review (20), the amount of polyproline structure might be reduced in phosphate buffers; however, such a behavior is in agreement with the existence of a conformational equilibrium rather than a unique structure that undergoes an all-or-none folding-unfolding transition.

To gain more insight into the structure of XAO in solution, in this work we carried out CD experiments in methanol and TFE as well as in D₂O and in aqueous solutions containing 1 M urea or 1 M GdnHCl, respectively; the last two compounds serve as denaturants. We present CD studies of the XAO peptide in water, methanol, and aqueous solution with denaturants. Replacing water with an organic solvent is usually considered a structure-inducing process in peptides because it favors intramolecular hydrogen bonding, thus promoting elements of secondary structure such as α-helices and β-turns (51–53).

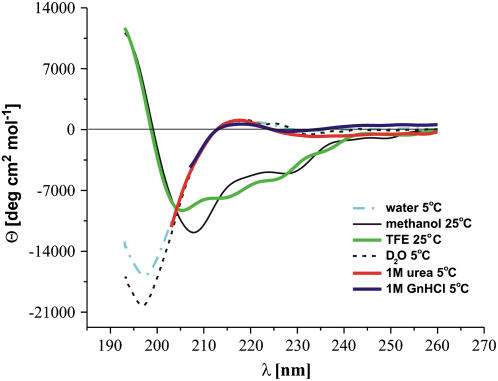
The spectra of XAO in water, D₂O, TFE, and methanol are shown in Fig. 1. The spectra in aqueous solutions of urea and GdnHCl are qualitatively similar to that in water and differ only in the height of the maximum at ∼217 nm. The spectra in both nonaqueous solvents are different from those in water or D₂O. Their characteristic feature is the presence of a deep and broad minimum at ∼208 nm for methanol and ∼206 nm for TFE. A second minimum at ∼230 nm is also present in methanol solution, and a shoulder at ∼226 nm is present in TFE solution. This suggests the existence of a mixture of statistical-coil structure with α-helix and/or β-turn structure elements rather than the P_II conformation in any detectable amount. A quantitative analysis (54) of the CD spectra revealed 37.4% statistical coil, 23.8% α-helix, 16.5% β-structure, 13.2% β-turns, and 7.8% P_II in methanol, and 41.9% statistical coil, 19.5% β-structure, 16.2% α-helix, 11.7% β-turns, and 8.1% P_II in TFE. These findings demonstrate that XAO does not possess well-ordered structure even in such an α-helix-promoting solvent as TFE. A similar CD spectrum of a related peptide (Ac-OO-A₇-OO-NHMe) in TFE was reported by Chen et al. (19), who claimed that the heptaalanine core of that peptide forms an α-helix in TFE.

FIGURE 1.

Sample CD spectra of XAO in water (dashed-dotted blue line), D₂O (short-dashed black line), methanol (thin gray line), TFE (red), 1 M urea (green), and 1 M GdnHCl (navy blue).

The CD spectra of XAO in water and in D₂O possess a maximum at ∼217 nm and a minimum at ∼198 nm, these features being characteristic of local P_II structure. The CD spectrum of the XAO peptide measured in D₂O has a stronger negative band at 198 nm than the CD spectrum in water and a positive band around 218 nm, which means that D₂O promotes the formation of P_II structure, as also found in an earlier study (55).

The temperature dependence (from 1°C to 85°C) of the molar ellipticity of XAO at λ = 217 nm (the maximum characteristic of the P_II structure; Fig. 1) in pure water, D₂O, acetate buffer, 6 M solution of urea, 6 M solution of GdnHCl, 1 M solution of urea, and 1 M solution of GdnHCl is shown in Fig. 2. It can be seen from Fig. 2 that the intensity of the P_II band and, consequently, the amount of local P_II structure decreases with increasing temperature in all of these solvents. The plots of molar ellipticity versus temperature do not possess a sigmoidal shape but are, within experimental error, linear in temperature. Consequently, these plots by themselves do not indicate an “all-or-none” transition to an overall P_II structure but may be characteristic of the shift of a conformational equilibrium with temperature. This conclusion is also supported by the fact that the CD spectra depend not only on temperature but also on the environment (pH, kind of salt, and denaturant).

FIGURE 2.

Temperature dependence of the ellipticity of XAO solutions. Blue squares, water; black circles, D₂O; light gray triangles, acetate buffer; orange inverted triangles, 6 M urea; red left-pointing triangles, 6 M GdnHCl; green right-pointing triangles, 1 M urea; and navy blue diamonds, 1 M GdnHCl.

It can also be seen from Fig. 2 that the ellipticity at 217 nm is significantly larger in 6 M urea than in water, i.e., strong denaturants seem to promote the formation of P_II structure.

A similar increase of P_II structure content upon addition of denaturants was observed for polyglutamic acid and polylysine peptides (2).

DSC measurements

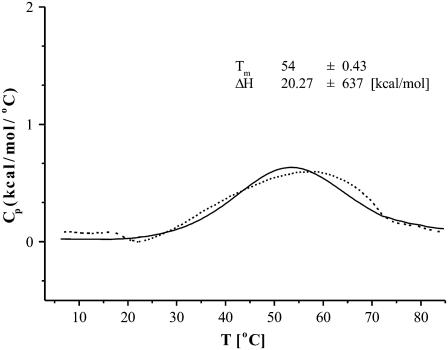
To determine if a conformational transition occurs in XAO, we carried out DSC measurements in pure water. The measured heat-capacity curve and the curve fitted by using a two-state model (56) are shown in Fig. 3. The experiment was repeated three times, and the computed standard deviation of the measurements was 0.06 kcal/(mol × °K). It can be seen that the experimental heat-capacity curve has a very broad maximum at T ≈ 57°C. The height of the maximum is only ∼0.6 kcal/(mol × °K) and is not accompanied by any major change in molar ellipticity at this temperature (Fig. 2) or in the ³J_αN coupling constants (Fig. 2 in Shi et al. (3)). This behavior is very different from collagen-peptide models (57) in which the height of the heat-capacity peak is ∼6 kcal/(mol × °K) and the position of the peak coincides with the change in molar ellipticity. It can, therefore, be concluded that any change of the secondary-structure pattern, e.g., from β to P_II, deduced from CD or NMR data, is not coupled with an energy change. This result corroborates our conclusion from the preceding section that the structure of XAO should be regarded as a mixture of conformations in a dynamic equilibrium with populations of conformations varying steadily with temperature.

FIGURE 3.

Temperature dependence of the partial molar heat capacity of the XAO peptide in water at pH = 4.6. The dashed curve is the experimental curve, and the solid curve was obtained by fitting the experimental curve with a two-state model leading to a T_m = 54°C.

Comparison of the measured and calculated NMR observables

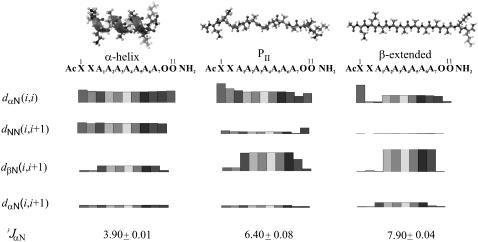
The NMR-spectroscopy measurements carried out for the XAO peptide have been published in our previous work (29). In this work, we used the NMR restraints determined from the ROE intensities and from the ³J_HNHα coupling constants in MD simulations. In addition, we also calculated theoretical NOE integral intensities of all protons in the XAO peptide for the canonical α-helical, P_II, and β-extended structures using the MORASS program (32,33), which is based on solving a system of coupled Solomon equations (34) for the magnetization of the protons in the molecule. All the characteristic NOE effects calculated for the canonical β-extended, α-helical, and P_II conformation of the XAO peptide are shown in Fig. 4 (d_xN, where x = N, α, β). The calculated d_αN(i,i) NOEs are equal in α-helical and P_II structure, whereas these NOEs are ∼30% lower for the β-strand conformation, as shown in Fig. 4. The calculated d_NN(i,i + 1) NOEs are the strongest for the α-helical conformation of XAO. The calculated d_NN(i,i + 1) NOEs for the extended structure are more than 10 times smaller than those for the α-helical conformation, i.e., too small to observe experimentally. For the P_II conformation, the d_NN(i,i + 1) values of the NOEs are four times lower than for the α-helix but much higher than in β-strand structure and, therefore, they could be observed in experimental NOESY spectrum. The d_NN(i,i + 1) NOEs were not observed for any pair of successive amide protons for proline-rich peptides (58) but were observed for peptides derived from tropoelastin (59), which probably possess a significant amount of P_II structure. The calculated d_βN(i,i + 1) NOEs are the lowest for the α-helix and comparable in value for the P_II and extended conformations, respectively. The d_αN(i,i + 1) NOEs are comparable in value for all investigated structures. In addition, the theoretical d_αN(i,i + 3) and d_αβ(i,i + 3) NOEs, characteristic of α-helical structure were found but are not shown in Fig. 4. The calculated NOE patterns of well-defined α-helical and β-extended structures (60) are in very good agreement with the experiment.

FIGURE 4.

Calculated ROE pattern (d_XN, where X = N, α, and β) and the vicinal coupling constants (³J_HNHα). The heights of the bars correspond to the strength of the NOEs, and the different degree of shading is used to separate amino acid residues.

For our model canonical conformations (α-helical, P_II, and β-extended structures), we also calculated theoretical values of coupling constants ³J_HNHα for every amino acid residue separately, and the average values are shown in Fig. 4. These coupling constants were calculated by using the Karplus relationship (36) (Eq. 1), as described in the Materials and Methods section. The calculated mean values over the whole sequence for the ³J_HNHα of XAO are 3.90 (±0.01) Hz for the α-helical structure, 6.40 (±0.08) Hz for the P_II structure, and 7.90 (±0.04) Hz for the β-extended structure. The values calculated for the α-helical and β-extended conformations are in very good agreement with the experimental values measured for other peptides (61). The ³J_HNHα values for P_II structure (6.4 Hz) are much higher than for α-helical structure and much lower than for the extended structure but are in a range of ³J_HNHα vicinal coupling constants characteristic of statistical-coil conformations or for β-turns. The values observed by Shi et al. for XAO vary from 5.2 Hz to 6.2 Hz (3), depending on temperature and residue. Such values of coupling constants can correspond to φ-angle values close to those of the P_II conformation and, consequently, could indicate a significant content of P_II. However, this is not the only possible solution of the Karplus equation for φ, as shown in Fig. 5 in which a plot of Eq. 1 is presented together with horizontal lines corresponding to the lower and upper boundary of the ³J_HNHα coupling constants of the alanine residues measured at room temperature in our (29) work and in the work of Shi et al. (3). It can be seen that each of the horizontal lines intersects the curve corresponding to Eq. 1 at four points. The points with positive φ values can be dismissed because the corresponding conformations have high energies for L-Ala. However, the solutions with φ about −160° are possible and could correspond to extended structures. It should be noted that Fig. 4 A in Shi et al. (3) omits the leftmost part of the plot of Eq. 1 and, consequently, the solution with φ ≈ −160° cannot be seen. Shi et al. (3) have not provided any justification as to why they dismissed this solution.

FIGURE 5.

Solid curve, variation of the ³J_HNHα with φ calculated from Eq. 1. Dashed horizontal lines, boundaries of the experimental ³J_HNHα values.

For potentially flexible peptides, the coupling constants should be regarded as conformational averages. Using Eq. 1 and the energy map of terminally blocked L-alanine calculated in Arnautova et al. (38) with a quantum-mechanical ab initio method at the MP2/6-31G** level, we calculated the Boltzmann-averaged value of the ³J_HNHα coupling constant (Eq. 2) at T = 298 K. With the parameters of Eq. 1 used in this work, we obtained a value of 7.04 Hz. This value is considerably higher than the ³J_HNHα values of XAO (3,29) and higher by ∼1 Hz than ³J_HNHα measured for terminally blocked alanine (62), which means that the quantum mechanical calculations in vacuo underestimate the amount of states with φ ≈ 180° or small φ values. Nevertheless, using Eqs. 1 and 2 we also calculated the dependence of the average ³J_HNHα on temperature. The results are presented in Fig. 6 a. It can be seen from Fig. 6 a that the average coupling constant increases with temperature as observed by Shi et al. for the alanine residues in XAO (3) and for shorter alanine-based sequences (63) and that the slope of the calculated ³J_HNHα(T) curve decreases at higher temperatures as observed experimentally for alanine-based peptides (Fig. 2 in Shi et al. (3)). The range of the variation of ³J_HNHα (7.02–7.11 Hz) is much smaller in our calculations than that observed experimentally, but we have considered only an isolated alanine residue in vacuo. Nevertheless, it can clearly be seen that the temperature dependence of ³J_HNHα of XAO (3) and other alanine-based peptides (63) can qualitatively be explained in terms of Boltzmann averaging of local conformational states of alanine. In summary, the measured values of ³J_HNHα cannot be considered as evidence for the value of the φ-angle characteristic of the P_II conformation, and the dependence of ³J_HNHα on temperature does not prove that a conformational transition occurs in the alanine-based peptides (including XAO) considered as models of P_II structure.

FIGURE 6.

(a) A plot of Boltzmann-averaged ³J_HNHα coupling constant (Eq. 2) versus temperature. Points are calculated values. (b) Plots of the potential of mean force, W(φ), (Eq. 4) for T = 5°C (solid line), 20°C (long-dashed line), 50°C (dot-dashed lines), and 80°C (dotted line).

To investigate the origin of the increase of ³J_HNHα for terminally blocked L-alanine with temperature, we examined the potential of mean force of this system as a function of φ, W(φ), (see Eq. 4 for definition) at different temperatures. The plots of W(φ) at −180° ≤ φ ≤ −40° for temperatures from 5°C to 80°C are shown in Fig. 6 b (for φ > −60°, W(φ) is more than 2.5 kcal/mol above the global minimum at φ = −80° and, consequently, these points have negligible statistical weights). It can be seen that the height of the maximum of W(φ) at φ = −120° diminishes gradually with increasing temperature. This maximum lies only 1.2–1.5 kcal/mol above the global minimum of W(φ) at φ = −80° and, consequently, the conformational states from the region of the maximum do contribute to the conformational averages. It can be seen from Fig. 5 that the maximum of ³J_HNHα occurs at φ ≈ −120°, i.e., close to the thermally accessible maximum of W(φ). Therefore, as temperature increases, more conformational states with φ corresponding to the highest values of ³J_HNHα enter the conformational averages and, consequently, the average coupling constant increases (Fig. 6 a).

Based on our theoretical NOE pattern and calculated coupling constants in comparison with the experimental data (29) of the XAO peptide, as well as the computed results of the Boltzmann-averaged coupling constants, we propose that the alanine residues do not have a particularly pronounced preference for the P_II region and, hence, the XAO peptide seems to populate an ensemble of conformations with only a few residues (X-1, X-2, Ala-6, Ala-7, O-10, and O-11) in the P_II region. We suggest that the diaminobutyric acid and ornithine residues have a large propensity to populate the P_II region of the Ramachandran map and make a more significantly increased contribution to the polyproline-like CD spectrum because their values of the ³J_HNHα coupling constants are 6.8 Hz, which suggests an increased contribution from the regions characteristic of local P_II states. The conformational preference of both diaminobutyric acid and ornithine residues for the P_II region is not surprising because the lysine residues, which are similar in chemical composition, also have large propensities to form a P_II structure in lysine-rich or lysine- and arginine-rich oligopeptides (27,46,64,65).

Molecular dynamics simulations of the conformational ensemble of XAO with the use of experimental information from NMR measurements

As mentioned in the Materials and Methods section, we used the AMBER 99 force field (39) for MD simulations. Initially, we tried to perform unrestrained simulations. However, the resulting ensembles contained only α-helical conformations, which is in clear contradiction with NMR results (29). These computed results did not improve when we used explicit water and included phosphate ions in the buffer or even included explicit urea molecules, which act as a denaturant. Therefore, since the AMBER force field is known to be heavily biased toward α-helical conformations (30), we subsequently included the interproton distances and dihedral angles computed from the NMR data acquired in our earlier work (2) in the form of time-averaged restraints. We also included the ψ-angle restraints for Ala residues determined from the UV Raman spectra by Asher et al. (21); we used their determined distribution of the ψ-angle to calculate the corresponding potential of mean force, to which we fitted a parabola to determine the position of the minimum and the force constant of the harmonic restraining potential. These parameters were ψ = 147° and k = 3.4 kcal/(mol × rad²).

In our earlier work, we used simulated annealing as a conformational search technique, which restricted the simulation to an in vacuo mode; here, we performed canonical MD simulations, which enabled us to include the solvent in the calculations. We performed runs with explicit water and with implicit water considered at the generalized Born surface area level.

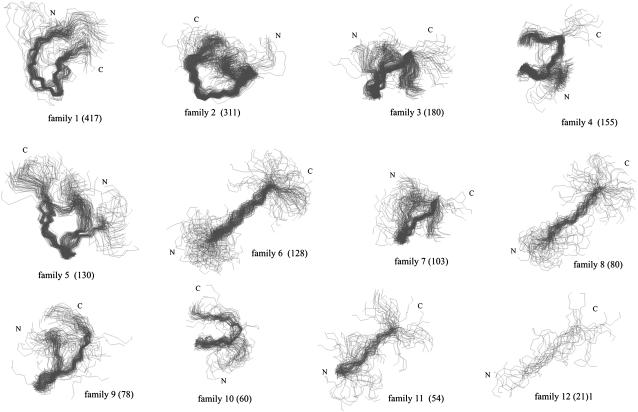
We carried out 13 runs (total) starting from the extended, α-helical, P_II, and 10 random conformations, respectively. In all runs, the system diverged quickly from the initial conformation, as judged by examining plots of the RMSD from the initial conformation versus time (data not shown). The conformations from the last 2,000,000 MD steps of all runs (a total of 2,000 conformations) were clustered together into families by using the algorithm included in the MOLMOL program (45); the families together with the numbers of conformations in each are shown in Fig. 7. It can be seen that the families can be grouped into those which have a bent shape; these families are more populated, and the less populated families have a straighter shape. The same results were obtained qualitatively in our earlier work (29) in which simulated annealing was used as a search technique.

FIGURE 7.

Families clustered by using the MOLMOL program together with the numbers of conformations (in parentheses). The families are shown in descending order according to the numbers of conformations in a family.

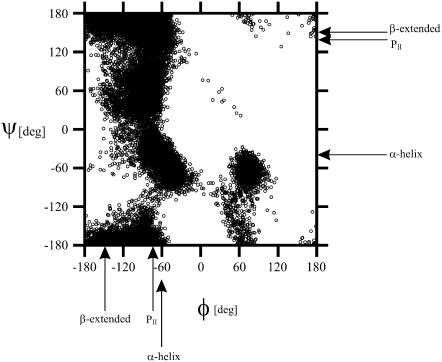
The scattered plots of the φ- and ψ-angles for all conformations and selected families are shown in Fig. 8. It can be seen that, although P_II (φ = −75°, ψ = 145°) is a populated local conformational region, it is not dominant. It should also be noted that the local conformational states corresponding to an α-helix (φ = −60°, ψ = −40°), the α_R states, seem to be populated, although even one turn of an α-helix does not form in any of the families (Fig. 7). The α_R states pertain only to isolated residues as do the P_II states in most of the conformations. The ensemble-averaged value of the ³J_HNHα coupling constant for the alanine residues is 5.08 Hz, which is in good agreement with the measured values, which range from 5.1 to 5.7 Hz (29).

FIGURE 8.

Scattered plot of the φ- and ψ-angles for all conformations.

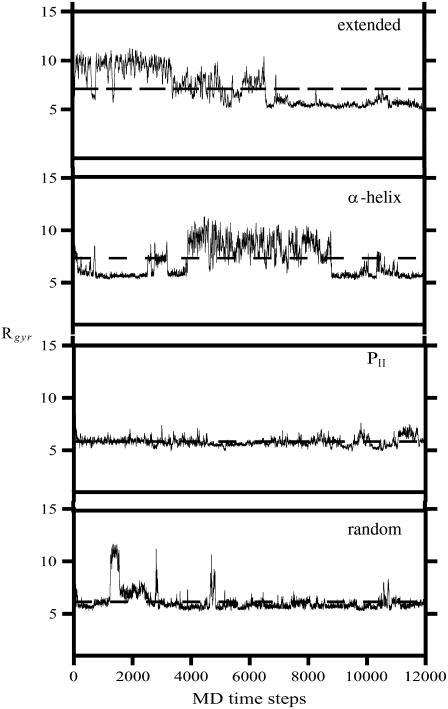
We also calculated the radius of gyration (R_gyr) which was determined for XAO by Zagrovic and co-workers (30) from independent SAXS measurements; this information was not used as a restraint in our simulations. We must stress at this point that no information of the experimental radius of gyration was included in the calculations and, consequently, comparison of the radius of the calculated average value of the radius of gyration with the experimental value is a good test of the quality of the conformational ensemble determined based on MD simulations with experimental restraints. The variation of the radius of gyration, R_gyr, with time for sample runs started from the extended, α-helical, P_II, and random conformations is shown in Fig. 9, and the mean values of R_gyr calculated for each of the runs taking the conformations from the last 2,000,000 MD steps are summarized in Table 1. For simulations started from the extended and P_II structures, R_gyr decreases rapidly at the beginning and then reaches the value of ∼5.5–7 Å, whereas for simulations started from the α-helical structure, R_gyr reaches the equilibrium value more slowly because the system needs more time to leave the low-energy α-helical basin and reach conformations consistent with NMR data. The mean values of R_gyr averaged over all ensembles is 7.06 ±0.96 Å (Table 1), which is in agreement with the value of 7.4 Å determined from SAXS experiments (30). It should be noted that excellent agreement with the experimental R_gyr value was also obtained in our previous calculations (29) in which we used simulated annealing and not canonical MD simulations, and water was not included because of the limitations of the conformational search technique. This suggests that, in all series of calculations, the conformational ensemble was determined mainly by the NMR-derived restraints imposed and the force field served mainly to exclude conformations with steric overlaps. Consequently, the calculated conformational ensembles appear reliable.

FIGURE 9.

Variation of radius of gyration (R_gyr) with time for sample runs started from the extended, α-helical, P_II, and random conformations.

TABLE 1.

Ensemble-averaged values (over 2,000,000 last MD steps) of radius of gyration of XAO calculated for consecutive MD runs

Run number	Starting conformation	Rgyr [Å]	Standard deviation [Å]
1	α-helix	7.35	1.53
2	Extended	7.11	1.75
3	PII	5.83	0.44
4	Random_1	7.52	1.00
5	Random_2	7.45	1.41
6	Random_3	8.03	1.30
7	Random_4	6.13	0.90
8	Random_5	5.81	0.57
9	Random_6	6.36	0.63
10	Random_7	6.29	0.91
11	Random_8	7.72	1.40
12	Random_9	7.08	1.60
13	Random_10	9.12	1.71
14	Averaged	7.06	0.96

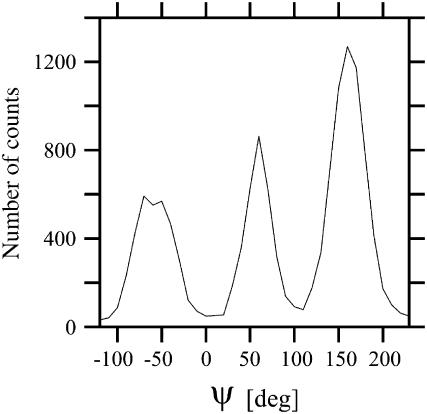
Another conformational-dependent observable available for XAO is the average ψ-angle determined by Asher et al. (21) from UV Raman spectroscopy measurements. These authors determined not only the average value of ψ but also the distribution of this observable and we, therefore, compare this distribution with the distribution calculated from our MD-determined conformational ensemble. Our calculated distribution averaged over all alanine residues is shown in Fig. 10. It can be seen that the major peak occurs at ψ = 155°, which is in good agreement with the most probable value of ψ = 147° determined by Asher et al. (21). The distribution agrees with that determined from the experiment except for the presence of secondary peaks at ψ = 60° and −80°. These secondary peaks might be the result of a bias in the AMBER force field but are not inconsistent with the UV Raman data because the distribution of ψ-angles was estimated in Asher et al. (21) based on the assumption that the amide III frequency does not depend on φ. In their infrared Raman study (22), Schweizer-Stenner and co-workers determined the value of (φ, ψ) for trialanine as (−95°, 150°); they, however, dismissed the second possible solutions with (φ, ψ) = (−100°, 55°); the latter is in agreement with the results of our calculations (see Fig. 8). Moreover, it is clear that a multi-modal distribution of ψ can lead to a unimodal distribution of frequency (Fig. 8 in Asher et al. (21)) if averaging over conformational states is fast enough, which is the case of flexible peptides. The fact that the major peak in our calculated distribution of ψ (Fig. 10) is shifted forward by 10° with respect to that determined by Asher et al. (Fig. 9 in Asher et al. (21)) and that it is accompanied by secondary peaks centered at lower values of ψ (Fig. 10) supports this conclusion.

FIGURE 10.

Distribution of ψ-angles calculated from the results of the MD simulations.

Finally, we analyzed the families of conformations determined in this work in terms of the values of φ- and ψ-angles consistent with a persistent P_II conformation, i.e., which possess the φ- and ψ-values within the range φ ≥ −120° and φ ≤ −60° ψ ≤ −120°, and ψ ≥ 100°. We found that only the conformations of families 4 and 10 (Fig. 7) possess three or four consecutive alanine residues (from Ala-5 to Ala-7 or Ala-8 or from Ala-6 to Ala-8) within the ranges of the φ- and ψ-angles specified above. This corresponds to a region with an irregular bend at Ala-6-Ala-7 and, consequently, the conformation of XAO cannot be considered as P_II in this fragment of the molecule although the φ- and ψ-angles are in the allowed range but should rather be regarded as a mixture of isolated extended and P_II states. Moreover, families 4 and 10 are not particularly numerous (Fig. 7).

DISCUSSION

On the basis of CD and NMR evidence as well of the experimental evidence from the UV Raman Fourier transform infrared spectroscopy (21) and polarized visible Raman spectroscopy (22), as well as other measurements (66–68), Shi et al. (3) and Chen et al. (19) concluded that the alanine core of XAO and other alanine-based peptides adopt the P_II shape at low temperature. Recently (29), we demonstrated that although the P_II conformation seems to be abundant in XAO at room temperature, it should be regarded as a local conformational state and not an overall conformation of that peptide. This conclusion, as well as the results of our earlier theoretical (27,28) and experimental studies (29) were criticized by Shi et al. (20), whose primary argument was that it is difficult, if not impossible, to counter their hard experimental evidence that supports the presence of the overall P_II conformation of XAO and that our results do not provide convincing evidence to support our conclusion. However, in our earlier work (1), as well as in this work, we demonstrated that all of the “hard evidence of Shi et al.” (20) pertains to conformationally averaged observables and can easily be reconciled with a picture of XAO as a mixture of interconverting conformations.

First, the results of our DSC measurements presented here indicate only a low and very broad peak in heat capacity, which occurs at ∼60°C. This peak does not correspond to any major change of the ³J_NHNα coupling constants or the ellipticity with temperature which, according to Shi et al. (3), would take place at ∼30°C. Consequently, no clear conformational transition seems to occur in XAO and the only plausible conclusion from the DSC measurements could be that it exists in an ensemble of interconverting conformations.

According to Shi et al. (3,20), strong evidence for the presence of a unique P_II conformation is provided by the value of the φ-angle determined from ³J_HNHα coupling constants measured for the Ala residue and that a remarkable dependence of the coupling constant on temperature is a clear indicator of the transition from the P_II conformation to extended/statistical-coil ensemble. However, as we demonstrated in the Results section, such values of ³J_HNHα simply correspond to Boltzmann averages over the conformational states of the terminally blocked L-alanine. Consequently, the NMR measurements provide no information as to the preferred value of φ. As mentioned in the Results section, the values of the coupling constants could suggest that the ornithine and diaminobutyric acid residues rather than the alanine residue in XAO possess a pronounced tendency to exist in local P_II states, in line with previous theoretical calculations (28). This is reflected in the fact that the φ-angles of the conformations obtained in our MD calculations with time-averaged NMR-derived restraints carried out in this work have virtually all possible values (Fig. 8). In our earlier work (29), in which simulated annealing was used and, consequently, the averaging of restraints was less extensive, the φ-angle was more restricted, although its distribution was still centered at three values (Fig. 5 in Makowska et al. (29)). We also demonstrated that the experimentally observed monotonic increase of ³J_HNHα with increasing temperature is fully reproduced by Boltzmann averaging over local conformational states of terminally blocked L-alanine. Consequently, the observed dependence of ³J_HNHα on temperature cannot be considered as proof for a strong conformational transition. Presumably, the same argument can be applied to the temperature dependence of the CD spectra, which is considered by Shi et al. (3,20) as additional evidence for a conformational transition (however, our DSC measurements counter this evidence).

The next evidence for the presence of persistent P_II conformation in XAO is, according to Shi et al. (3,20), the shift of the short wavelength minimum and the presence of a longer wavelength maximum in the CD spectra of this peptide, these features making them resemble the CD spectra of collagen and proline-based peptides in general. It must be noted, though, that the features of the CD spectra are determined by the immediate environment of the peptide chromophore and, consequently, can demonstrate that only local P_II states occur in remarkable quantity but say nothing about the presence of a persistent P_II fold. We demonstrated (29) that the CD spectra of XAO not only depend on temperature or on the presence of denaturants or pH but equally strongly depend on the kind of buffer, which further suggests that the P_II states of XAO are local and not a global fold.

In our opinion, the other evidence for the “P_II conformation” of XAO and other alanine-based peptides also comes from overinterpretation of conformation-dependent observables. These quantities are ensemble averages by definition but are often interpreted as values characteristic of a single structure. For example, based on the results of their UV Raman study, Asher et al. (21) concluded that the value of the ψ-angle must be around 147°, this being characteristic of P_II. Together with φ = −75°, as calculated from the ³J_HNHα coupling constant (20,29), this would make an ideal P_II conformation; however, even if the value of ³J_HNHα is not considered as a conformational average, it can very well correspond to φ ≈ −160° (Fig. 5). That the value of ³J_HNHα should be regarded as an ensemble average is proved by the results of our MD simulations from which we obtained the average value of 5.08 Hz, which is in good agreement with the values measured for the alanine residues in XAO (from 5.1 to 5.7 Hz), although, based on the value of ³J_HNHα, the φ-angle spans a very wide range (Fig. 8). The value of ψ determined by Asher et al. (21) should also be regarded as a conformational average. These authors claim that the UV Raman spectra of XAO are “essentially invariant” with temperature, but Figs. 1 and 5 in Asher et al. (21) demonstrate that the temperature dependence of the amide II and amide III is of the same character as those of the coupling constants or CD spectra.

We note that the overall P_II conformation of XAO is not compatible with the full experimental evidence available at present. The radius of gyration of XAO measured by Zagrovic et al. (30) is 7.4 Å, a value too small to be reconciled with P_II conformation persisting even for a few residues. In their review (20), Shi et al. suggest that the P_II helix of XAO could be bent to conform to the measured R_gyr value. However, because the length of the alanine core of XAO is only seven residues, the presence of such a bend would kill the overall picture of P_II structure (see, e.g., families 12 and 13 in Fig. 7, which contain the largest P_II-like segments among the conformations determined in our MD study). We also note that the ensemble-averaged values of R_gyr calculated in this (7.06 ± 0.96 Å) and in our earlier study (29) (7.4 ± 1.0 Å), in which we used simulated annealing as a conformational search technique, are in good agreement with the experimental value.

Using the MORASS software (32,33), we calculated the interproton distances, and hence NOE patterns, for the XAO peptide in the α-helix, P_II, and extended structures (Fig. 4). Those NOE patterns are useful for determining whether the P_II conformation is present in the XAO peptide. The experimental NMR signals of the α and β protons in the Ala residues of the XAO peptide (29) are overlapped, and the signals from only the H^N and H^α atoms have good dispersion; therefore, only d_NN (i,i + 1) NOEs are useful for describing the peptide structure. By using MORASS, our calculated theoretical NOEs show that the ratio of the 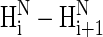NOE intensity for the P_II conformation to that computed for the α-helical conformation is 1:4 (29), which suggests that weak NOEs would be observed if the whole chain adopted the P_II conformation. In our experimental rotating frame Overhauser effect spectroscopy (ROESY) spectrum, we have observed (29) three weak ROE effects between amide protons of X-1-X-2, Ala-6-Ala-7, and Ala-9-O-10 residues, which could suggest the existence of a P_II local conformational state for these residues but also could be characteristic for turns without hydrogen bonds. In light of our theoretical NOE calculations, the absence of 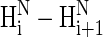NOEs for the remaining amino acid residues (X-2-Ala-6, Ala-7-Ala-8, and O-10-O-11) of the XAO peptide in the experimental ROESY spectrum implies the existence of other than a P_II conformation for these residues. In other words, if a longer alanine segment adopted the P_II conformation, weaker 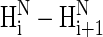NOE (or ROE) signals should be observed for such an alanine segment. (We note that in their review article (20), Shi et al. wrote that we were inconsistent in first writing that the presence of some 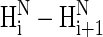signals precludes the presence of P_II and, second, that weak 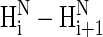signals should be observed for an all-P_II conformation; we hope that the text above clarifies this issue).

We conclude that, although it cannot be said whether or not XAO possesses a persistent P_II conformation at low temperatures, the statement of Shi et al. (3) that XAO possesses a persistent P_II conformation at low temperature is not supported by the available experimental evidence. On the contrary, the conformation-dependent observables are fully consistent with the picture of XAO existing in a mixture of sterically allowed conformations. On the other hand, even if at low temperatures this peptide does have a P_II structure that extends to a number of consecutive residues, this conformation is only part of a mixture of possibilities favored in free energy by a stepwise shift of a conformational equilibrium with temperature and certainly not by even a slight conformational transition. It is necessary to carry out more detailed NMR and other experiments to determine the extent and range (conformational state of isolated residues or of several residues in a row) of P_II structure in short, nonproline peptides.

Finally, let us consider the implications of the formation of P_II structure in the early stages of protein folding. Shi and co-workers (20) suggest that the fact that unfolded proteins are in P_II conformation solves the Levinthal paradox by reducing the entropy of the unfolded state. However, this conclusion remains valid even if P_II is considered a local state which coexists mainly with the extended state which is also favored both by the local conformational propensities and by hydration (20). It should be noted that recent simulations of denaturated structures of polypeptides using a simplified five-state model, steric restrictions, and a simplified solvation-free energy function (69) also suggest that, although the conformational space of amino acid residues is severely restricted even in a denaturated state, the “P_II conformation should be considered as one of sterically feasible and favorable conformational states”. Such restrictions of local conformational states still largely reduce the available conformational space although no specific overall conformation is assigned to an unfolded polypeptide chain. On the other hand, the fact that folding might start from a given conformation rather than from an ensemble of conformations does not seem to solve the Levinthal paradox. Each segment of the polypeptide chain still has an enormous number of possibilities from which to choose, no matter what its starting conformation is. The major driving force of folding seems to be the relationship between free energy and native-likeness which enables the system to narrow down the range of possible conformations of chain segments very quickly; this is consistent with the “folding funnel” picture (70). It must be noted, however, that the funnel is rugged and the conformational states corresponding to different stages of folding can be separated by significant barriers, which leads to complex folding kinetics.