Magnetic Field Effects in Arabidopsis thaliana Cryptochrome-1

Abstract

The ability of some animals, most notably migratory birds, to sense magnetic fields is still poorly understood. It has been suggested that this “magnetic sense” may be mediated by the blue light receptor protein cryptochrome, which is known to be localized in the retinas of migratory birds. Cryptochromes are a class of photoreceptor signaling proteins that are found in a wide variety of organisms and that primarily perform regulatory functions, such as the entrainment of circadian rhythm in mammals and the inhibition of hypocotyl growth in plants. Recent experiments have shown that the activity of cryptochrome-1 in Arabidopsis thaliana is enhanced by the presence of a weak external magnetic field, confirming the ability of cryptochrome to mediate magnetic field responses. Cryptochrome's signaling is tied to the photoreduction of an internally bound chromophore, flavin adenine dinucleotide. The spin chemistry of this photoreduction process, which involves electron transfer from a chain of three tryptophans, can be modulated by the presence of a magnetic field in an effect known as the radical-pair mechanism. Here we present and analyze a model of the flavin-adenine-dinucleotide-tryptophan chain system that incorporates realistic hyperfine coupling constants and reaction rate constants. Our calculations show that the radical-pair mechanism in cryptochrome can produce an increase in the protein's signaling activity of ∼10% for magnetic fields on the order of 5 G, which is consistent with experimental results. These calculations, in view of the similarity between bird and plant cryptochromes, provide further support for a cryptochrome-based model of avian magnetoreception.

INTRODUCTION

The ability of some animals to perceive the Earth's magnetic field has been known since the 19th century (1,2) and has been studied scientifically since the 1960s (3). The best-studied example is the use of the geomagnetic field by migratory birds for orientation and navigation. Reviews of these studies can be found in Wiltschko and Wiltschko (4,5,8), Beason (6), and Mouritsen and Ritz (7). Despite decades of research, the mechanism of avian magnetoreception remains elusive. The two candidates discussed most often are a magnetite-based mechanism (9–18) and a chemical reaction mechanism called the radical-pair model (19–22). Evidence suggests that birds use both types of magnetoreception simultaneously, using small magnetite particles to form a magnetic “map” while using a radical-pair mechanism as the basis of the orientational compass (11).

There are several reasons to prefer a radical-pair-based compass over one based on magnetite. The avian compass is an inclination compass, sensitive only to the inclination of the Earth's magnetic field lines and not to their polarity (4,5). The avian compass is also known to be highly sensitive to the strength of the ambient magnetic field, requiring a period of acclimation before orientation can occur at intensities differing from that of the natural geomagnetic field (23). Further evidence favoring a radical-pair-based compass is offered by recent experiments probing the effects of low-intensity radiofrequency radiation on bird orientational behavior (24–27). Furthermore, the avian compass is light-dependent, as first suggested by theory (19,21), normally requiring light in the blue-green range to function properly (28,29) and is known to be localized in the right eye of migratory birds (30). A radical-pair model in which a light-driven, magnetic-field-dependent chemical reaction in the eye of the bird modulates the visual sense indeed predicts these properties (19–22,31–34). Finally, a protein harboring blue-light-dependent radical-pair formation, cryptochrome, is found localized in the retinas of migratory birds (35,36), where its effects could intercept the visual pathway.

The radical-pair mechanism, in general, involves a process by which a pair of spin-1/2 radicals leads to distinct reaction products for the spins in either an overall singlet or triplet state. The mechanism has been explored for a variety of model systems (19,20,22,32,37–39). In such instances, hyperfine coupling, exchange, dipole-dipole, and Zeeman interactions acting on the electron spins can induce magnetic field effects in the reaction yields.

The radical-pair mechanism supposedly linked to the avian compass arises in the protein cryptochrome (22). Cryptochrome is a signaling protein found in a wide variety of plants and animals (40–42), and is highly homologous to DNA photolyase (43,44). The role of cryptochrome varies widely among organisms, from the entrainment of circadian rhythms in vertebrates to the regulation of hypocotyl elongation and anthocyanin production in plants (45–47). The role of cryptochrome as a magnetic compass, as suggested in Ritz et al. (22) and Ahmad et al. (48), is still hypothetical.

Photolyase and cryptochrome both internally bind the chromophore flavin adenine dinucleotide (FAD). In photolyase, the presence of FAD in its fully reduced FADH⁻ state is necessary for its DNA repair activity. The FAD cofactor, which typically exists in photolyase in its semireduced FADH form, is brought to the FADH⁻ state by a series of light-induced electron transfers involving a chain of three tryptophans that bridge the space between FAD and the protein surface (49–53).

Although little is presently known about the activity of cryptochromes, it has been suggested (54,55) that a light-induced autophosphorylation reaction is involved in the early stage of cryptochrome's signaling activity. Recent experiments (56) have shown that light-induced electron transfer from a tryptophan chain conserved from photolyase is the dominant FAD reduction pathway in Arabidopsis thaliana (mouse-eared cress) cryptochrome, and that disruption of this photoreduction pathway impedes the protein's autophosphorylation activity. However, although photolyase seems to be activated when the semireduced FADH form is converted to the fully reduced FADH⁻ form, cryptochrome seems to be activated when the fully oxidized FAD form is converted to the semireduced FADH form (57).

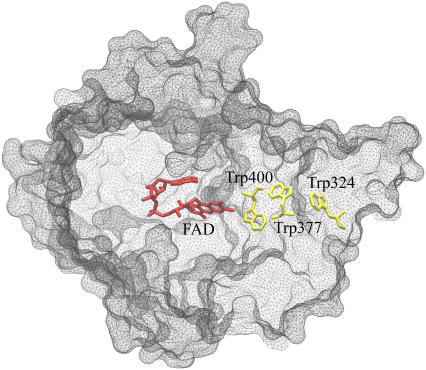
The tryptophan chain in Arabidopsis cryptochrome consists of Trp-324, Trp-377, and Trp-400, as shown in Fig. 1. Trp-324 is located near the periphery of the protein body, and Trp-400 is proximal to the flavin cofactor, with Trp-377 located in between. Before light activation of cryptochrome, the flavin cofactor is present in its fully oxidized FAD state. FAD absorbs blue light photons, being promoted thereby to an excited state, FAD*. FAD* is then protonated, likely from a nearby aspartic acid (58), producing FADH⁺. Once the electronically excited flavin is in the FADH⁺ state, light-induced electron transfer is initiated. An electron first jumps from the nearby Trp-400 into the hole left by the excited electron in FADH⁺, forming FADH + Trp-400⁺. An electron then jumps from Trp-377 to Trp-400, forming FADH + Trp-377⁺, and subsequently from Trp-324 to Trp-377, forming FADH + Trp-324⁺. Finally, Trp-324⁺ becomes deprotonated to Trp-324_dep, i.e., forming FADH + Trp-324_dep (50), fixing the electron on the FADH cofactor. This scenario is summarized in Fig. 2.

FIGURE 1.

FAD cofactor and tryptophan chain in Arabidopsis thaliana cryptochrome-1. Cryptochrome is in its signaling state when the FAD cofactor is in the semireduced FADH state. The signaling state is achieved through photoreduction via a chain of three tryptophans (Trp-400, Trp-377, and Trp-324) that bridge the space between FADH and the surface of the protein, followed by deprotonation of Trp-324 to Trp-324_dep.

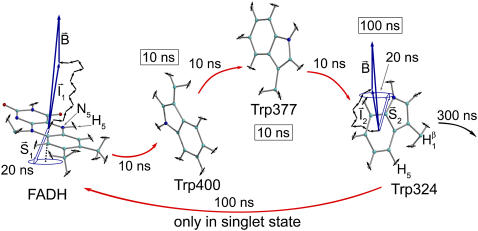
FIGURE 2.

Schematic presentation of the radical-pair reaction pathway in cryptochrome. After the flavin cofactor in its fully oxidized form, FAD, is excited by a blue photon (FAD → FAD*) and subsequently protonated (FAD* → (FADH⁺)*), an electron jumps from the nearby Trp-400 to FADH⁺, creating a radical-pair (FADH + Trp-400⁺) state. Electron transfer from Trp-377 to Trp-400 and from Trp-324 to Trp-377 follows, creating the radical-pair state FADH + Trp-377⁺ and then FADH + Trp-324⁺. For each radical-pair state, the spins of the unpaired electrons are in either the singlet or triplet state, as denoted by ¹[⋯] or ³[⋯], respectively. Electron back-transfer, the effect of which is to quench the cryptochrome signaling state, is possible only when the two unpaired electron spins of one of the three possible radical-pair states form a singlet state ¹[⋯]. If Trp-324⁺ becomes deprotonated (Trp-324⁺ → Trp-324_dep), electron back-transfer FADH → Trp-324_dep is impeded, and cryptochrome is stabilized in its signaling state, FADH + Trp-324_dep. Transitions between the three radical-pair states, i.e., ^1,3[FADH + Trp-400⁺], ^{1, 3}[FADH + Trp-377⁺], and ^{1, 3}[FADH + Trp-324⁺], are governed by the rate constant k_et and correspond to an electron jumping between tryptophans in the direction opposite to that of the arrows shown (arrows show electron hole transfer). Electron back-transfer from FADH to one of the tryptophans is governed by the rate constant k_b and deprotonation of the third tryptophan by the rate constant k_d. The steps denoted by rate constants (k₁)′ and (k₂)′ correspond to reverse electron transfer in the tryptophan chain and are neglected in our description.

However, before the final deprotonation takes place, it is possible for the electron on FADH to back-transfer to one of the tryptophans, which quenches the signaling state. This back-transfer, leading to the formation of FADH⁺, as shown in Fig. 2, can only occur if the spins of the two unpaired electrons are in an overall singlet state. An external magnetic field can influence the overall electron spin state through the Zeeman interaction acting jointly with hyperfine coupling to the nuclear spins associated with the hydrogen and nitrogen atoms (37). If the overall spin state is triplet, electron back-transfer and formation of FADH⁺ cannot occur, extending the time cryptochrome stays in its signaling state. This, in turn, could affect the visual perception of a bird, as described in Ritz et al. (22), permitting the bird to visually discern the magnetic field.

In this article, we seek to investigate computationally the electron transfer and spin dynamics in cryptochrome as depicted in Fig. 2. This requires an atomic-level structure of the protein. Unfortunately, no structures of avian cryptochromes are available yet. The only available structure at this time is that of Arabidopsis thaliana cryptochrome-1 (43). However, the cryptochromes of birds and plants are very similar. A BLAST (59) comparison of Erithacus rubecula (European robin) cryptochrome-1a and cryptochrome-1b with Arabidopsis thaliana cryptochrome-1 gives expect values of 3 × 10⁻³⁸ and 2 × 10⁻³⁷, respectively, with 28% sequence identity for each (see Fig. 3). Therefore, we will base our computational analysis on the electron transfer and spin dynamics of Arabidopsis cryptochrome-1.

FIGURE 3.

BLAST sequence alignment between Erithacus rubecula (European robin) and Arabidopsis thaliana (mouse-ear cress) cryptochromes. The alignment shows a high similarity between the bird and plant cryptochromes. Erithacus rubecula cryptochrome-1a gives an expect value of 3 × 10⁻³⁸ and cryptochrome-1b gives an expect value of 2 × 10⁻³⁷ when compared to Arabidopsis thaliana cryptochrome-1. Residues conserved between the three cryptochromes are marked with the ∧ character.

In regard to the similarity of avian and plant cryptochromes, a recent experiment on the effect of an external magnetic field on Arabidopsis thaliana seedlings (48) is encouraging. It was found that signaling from cryptochrome-1, measured through a hypocotyl inhibition and anthocyanin production assay, is enhanced when seedlings are placed in a magnetic field of 5 G, compared with an assay at an Earth-strength (0.5 G) magnetic field. Mutant seedlings lacking cryptochromes showed no change under different magnetic-field strengths. This observation suggests that the plant cryptochrome spends a longer time in its signaling state when placed in an external magnetic field of 5 G than it spends under Earth-strength magnetic field conditions.

In this article, a model of the FADH-tryptophan chain system is developed and analyzed. The model incorporates realistic electron-transfer rate constants and magnetic interactions for electron spins. Our goal is to show that a weak magnetic field can have a measurable effect on cryptochrome signaling.

THEORY

In this section a calculation of cryptochrome activation and its magnetic-field dependence is outlined. This calculation expands upon previous work (22) by creating a relatively realistic model of the radical-pair system in cryptochrome-1. This is achieved by incorporating realistic hyperfine coupling tensors for FADH and tryptophan, by including multiple tryptophans in the photoreduction pathway, and by using realistic reaction rate constants for electron forward transfer, electron back-transfer, and tryptophan deprotonation.

Radical-pair Hamiltonian

The Hamiltonian for the intermediate radical-pair systems, FADH + Trp-400⁺, FADH + Trp-377⁺, or FADH + Trp-324⁺, as shown in Figs. 2 and 4, is the sum of two Hamiltonians for each radical pair, e.g., a Hamiltonian for FADH and a Hamiltonian for Trp-400⁺. In addition, a Hamiltonian 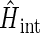arises that accounts for the exchange and dipolar interactions within the radical pair.

FIGURE 4.

Schematic illustration of electron hole transfer and electron spin dynamics in the FADH cofactor and tryptophan chain. After photoexcitation of the FADH cofactor, an electron hole propagates outward through the three-tryptophan chain (transfer time, 10 ns), forming in sequence the radical-pair states FADH + Trp-400⁺ → FADH + Trp-377⁺ → FADH + Trp-324⁺. The latter radical-pair state is terminated through either electron back-transfer or deprotonation with transition times 100 ns and 300 ns, respectively. The system spends ∼100 ns in the FADH + Trp-324⁺ state but only 10 ns in the FADH + Trp-400⁺ or FADH + Trp-377⁺ states (radical-pair state lifetimes are shown in square boxes), making the FADH + Trp-324⁺ radical-pair state the major contributor to the magnetic field effect. Electron hole migration (10 ns), spin precession (20 ns), electron back-transfer (100 ns), and deprotonation of Trp-324 (300 ns) are shown with arrows. Also shown are the electronic and nuclear spins in the FADH + Trp-324⁺ radical pair; in Trp-400 and Trp-377, only the nuclear spins are shown. The nuclear spins are shown with typical random orientations; the electron spins are shown in the initial antiparallel, i.e., singlet, alignment. The picture corresponds to the so-called semi-classical description of electron-nuclear spin dynamics (32,20). 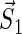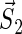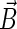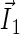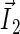In this description, the electron spins ( and ) precess about a local magnetic field produced by the addition of the external magnetic field and contributions and from the nuclear spins on the two radicals. The spin precession continuously alters the relative spin orientation, causing the singlet (antiparallel) ↔ triplet (parallel) interconversion underlying the magnetic field effect. The nuclei which are actually included in our calculations (radical-pair model 2, see text) are labeled.

The Hamiltonian for one specific pair is denoted generically

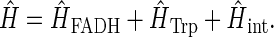(1)

The Hamiltonians 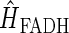and 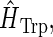as explained in (20), are composed of a Zeeman interaction term and a hyperfine coupling interaction term and are written

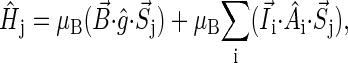(2)

where 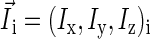is the spin operator of nucleus i, 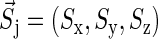is the electron spin operator, 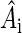is the hyperfine coupling tensor for nucleus i, μ_B = 5.78843 × 10⁻⁹ eV/G is the Bohr magneton, and 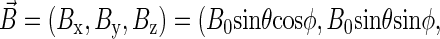B₀ cos θ) is the external magnetic field. The nuclear spins, electron spins, and external magnetic field are depicted in a so-called semiclassical manner in Fig. 4. As explained in detail by Schulten and co-workers (20,32), in the semiclassical picture, the electrons precess in the local magnetic field corresponding to the term 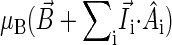in Eq. 2, with contributions from the external field 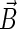and from the nuclear spins 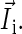The sum over i in Eq. 2 is performed over all nuclei of one radical; j denotes the FADH or tryptophan radical. The operator 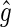is the so-called g-tensor, which can be brought to the following diagonal form in an appropriate coordinate system

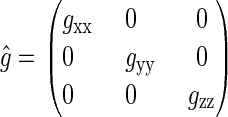(3)

The diagonal values are called g-factors. In this article, an isotropic g-tensor is assumed, with g_xx = g_yy = g_zz = g = 2.

The dimension of the Hamiltonian in Eq. 2 is determined by the dimensions of the spin spaces of the nuclei. The spin operator in Eq. 2 can be written

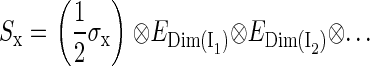(4)

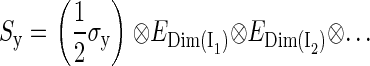(5)

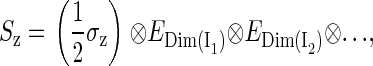(6)

where (σ_x, σ_y, σ_z) are the Pauli spin matrices (60) and E_n is the identity matrix of dimension n. The dimension of the identity matrices is determined by the dimension of the spin spaces of the corresponding nuclei, shown in Eqs. 4–6 as a subscript. Each nuclear spin is coupled to the electron spin by a hyperfine coupling tensor This hyperfine coupling tensor is split into an isotropic part and an anisotropic part:

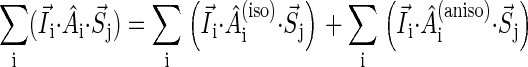(7)

The isotropic part can be written (for the sake of simplicity, the index j is left out)

(8)

where 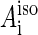are hyperfine coupling constants.

The isotropic part of the hyperfine tensor is diagonal in the same basis as the g-tensor, but the anisotropic part, in general, is not. The hyperfine axes define the orthonormal basis in which the anisotropic part of the hyperfine tensor is diagonal. To compute the inner product 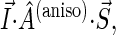the electron and nuclear spins must be rotated into the same basis. If the coordinate frames of the g-tensor and of the anisotropic hyperfine tensor are denoted as (x, y, z) and (x′, y′, z′), corresponding to the unit vectors 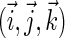and 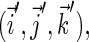respectively, then the anisotropic part of the tensor can be written

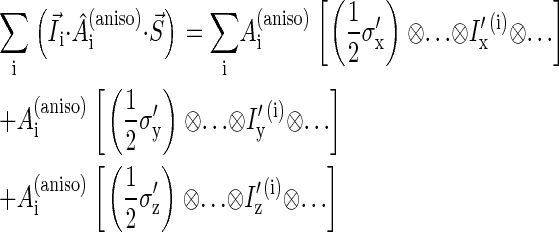(9)

Here the rotated spin matrices are

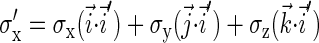(10)

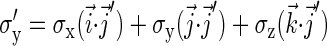(11)

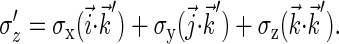(12)

In our model, we consider each of the three tryptophans to be identical, and we neglect orientational differences between them, so each will have an identical Hamiltonian.

In addition to the Zeeman and hyperfine coupling interaction terms one needs to account, in general, also for the electron-electron exchange and dipolar interactions in the radical pair. This is done through the term 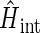in Eq. 1. These interactions play an important role when the distances between the radicals are small. The part of the Hamiltonian describing the electron-electron exchange and dipolar interactions is

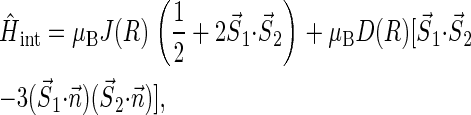(13)

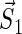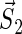where and are the unpaired electron spins on the FADH and Trp- radicals, respectively. The functions J(R) and D(R) describe the strength of the exchange and dipolar couplings and are assumed, as is often done, to take the simple functional form

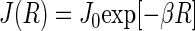(14)

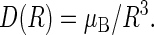(15)

In Eqs. 13–15, R is the edge-to-edge distance between the radicals, J₀ is the exchange coupling constant, is the unit vector in the direction of and β is a range parameter. The exchange and dipolar coupling parameters rapidly decrease with the distance between the radicals and can be neglected if the distance between the radicals is sufficiently large. It is possible to estimate the values of the coupling parameters for given distances between FADH and Trp- radicals using Eqs. 13–15. The characteristic distances R_{FADH–Trp-400}, R_{FADH–Trp-377}, and R_{FADH–Trp-324} are 6.0, 8.9, and 13.3 Å, respectively. The values for J₀ and β are taken, from a study of acyl-ketyl biradicals (61,62), to be J₀ = 7 × 10⁹ G and β = 2.14 Å⁻¹; these values are typical for radical pairs in solution. With these values for J₀, β, and R, one makes the following estimates for the exchange coupling parameters: J(R_{FADH–Trp-400}) = 18,568 G, J(R_{FADH–Trp-377}) = 37 G, and J(R_{FADH–Trp-324}) = 0.006 G. The estimated values for the dipolar coupling parameters are D(R_{FADH–Trp-400}) = 43 G, D(R_{FADH–Trp-377}) = 13 G, and D(R_{FADH–Trp-324}) = 4 G.

The estimated exchange interaction in the FADH + Trp-400⁺ radical pair is significantly larger than the hyperfine interaction, which is characterized by a coupling constant (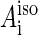 in Eq. 8) of ∼10 G per nucleus (see below). In the FADH + Trp-377⁺ radical pair, the exchange interaction is significantly smaller than for the FADH + Trp-400⁺ pair, but is comparable with the typical hyperfine interaction. In the FADH + Trp-324⁺ radical pair, the exchange interaction is much smaller than both the typical hyperfine interaction and the external magnetic field. It must be stressed that the given estimates are qualitative and the real exchange interaction in cryptochrome may be significantly different from the values given above. An accurate calculation of the exchange interaction depends on knowledge of the constants J₀ and β, and the coupling parameter is especially sensitive to the constant β. For example, a value of β = 4.28 Å⁻¹ (61) produces J(R_{FADH–Trp-400}) = 0.05 G, J(R_{FADH–Trp-377}) = 2 × 10⁻⁷ G, and J(R_{FADH–Trp-324}) = 4.8 × 10⁻¹⁵ G, all of which are negligible in comparison with the hyperfine interaction. The estimated dipole-dipole interaction appears to be of the same order of magnitude as the hyperfine interaction term for the FADH + Trp-400⁺ and FADH + Trp-377⁺ radical pairs, but is notably smaller than the typical hyperfine interaction for the FADH + Trp-324⁺ radical pair.

Large values of the exchange or dipolar coupling parameters in the Hamiltonian of a radical pair mean that the singlet-triplet interconversion process in the radical pair will be suppressed (61). The large estimates for the exchange and dipolar couplings for the FADH + Trp-400⁺ and FADH + Trp-377⁺ pairs would then seem problematic for the production of a magnetic field effect. However, because the characteristic rate for electron transfer from Trp-377 to Trp-400 and from Trp-324 to Trp-377 is of the same order of magnitude as the singlet-triplet interconversion rate (see rate constants below), neglecting the exchange and dipolar interaction terms for these pairs will not significantly affect the spin dynamics. As is further illustrated in Fig. 4, the main contribution to the spin dynamics of the system comes from the FADH + Trp-324⁺ radical pair due to the disparity in the lifetimes, τ(FADH + Trp-400⁺) ≈ τ(FADH + Trp-377⁺) ≈ 10 ns and τ(FADH + Trp-324⁺) ≈ 100 ns, so that the neglect of the exchange and dipolar interaction in the FADH + Trp-400⁺ and FADH + Trp-377⁺ pairs is acceptable. For the FADH + Trp-324⁺ radical pair, the estimates for both the exchange and dipolar couplings are smaller than the typical hyperfine interaction, so the exchange and dipolar interactions may be neglected for this pair as well. For these reasons, we have chosen to neglect the term H_int in Eq. 1 and consider only the effects of the Zeeman and hyperfine interaction terms.

Stochastic Liouville equation

To describe FAD photoreduction and a radical-pair-based magnetic-field effect in cryptochrome, we extend the description in Ritz et al. (22) and include three intermediate radical pairs, i.e., FADH + Trp-400⁺, FADH + Trp-377⁺, and FADH + Trp-324⁺, as shown in Figs. 2 and 4. The time evolution of the corresponding spin system is described through a modified stochastic Liouville equation (63). For this purpose, three density matrices ρ_i are defined for the states 1 ≤ i ≤ 3, corresponding to FADH + Trp-400⁺, FADH + Trp-377⁺, and FADH + Trp-324⁺. Each density matrix follows a stochastic Liouville equation that describes the spin motion and also takes into account the transitions into and out of a particular state from or into other states, as illustrated in Fig. 2. The equations that govern the evolution of the density matrices ρ_i are generalizations of Eq. 3 in Ritz et al. (22) and read

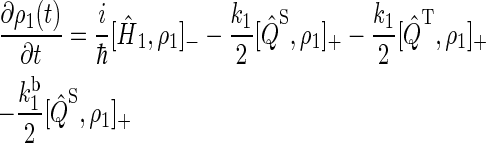(16)

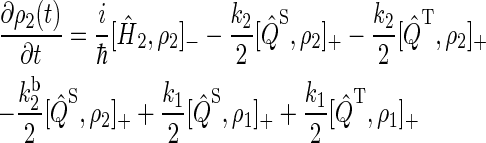(17)

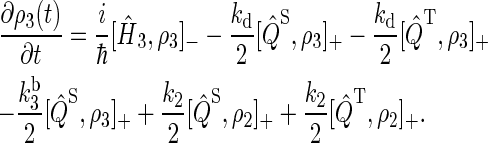(18)

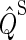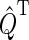Here, and are the projection operators onto the singlet and triplet states of the electron spin pair, which are defined as

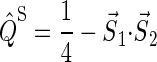(19)

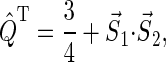(20)

where 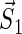and 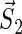denote the unpaired electrons on FADH and Trp, respectively. 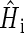in Eqs. 16–18 is the Hamiltonian associated with the radical pair that consists of FADH and the ith tryptophan. Since all tryptophans are assumed to be identical, we set 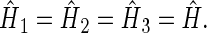The rate constants associated with the process of electron jumping from one tryptophan to the next are denoted by k₁ and k₂. The rate constants for electron back-transfer from each of the three tryptophans are denote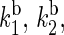d and 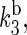and k_d is the rate constant associated with tryptophan deprotonation (50). [A, B]_± = AB ± BA denotes the commutator and anticommutator, respectively. We will adopt the following assumptions and notational conventions about the rate constants:

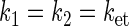(21)

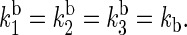(22)

These assumptions will be rationalized below in the “Rate constants” section.

To illustrate the derivation of Eqs. 16–18, we explain the right-hand side of Eq. 17. The first term describes the electron spin motion; the second and third terms describe the loss of density due to the electron hole transition FADH + Trp-377⁺ → FADH + Trp-324⁺; the fourth term describes the electron back-transfer FADH + Trp-377⁺ → FADH⁺ + Trp-377; the last two terms account for the electron hole transition FADH + Trp-400⁺ → FADH + Trp-377⁺. The second, third, fifth, and sixth terms correspond to spin-independent reactions, but the fourth term describes a manifestly spin-dependent reaction, as electron back-transfer is only permitted when the FADH + Trp-377⁺ radical pair is in an overall singlet electron spin pair state.

By using the relationship 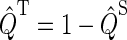and collecting terms, Eqs. 16–18 can be rewritten

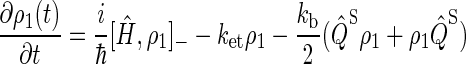(23)

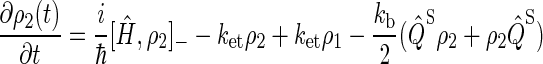(24)

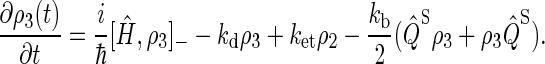(25)

Simplifying once more, the final set of coupled differential equations for our model is obtained:

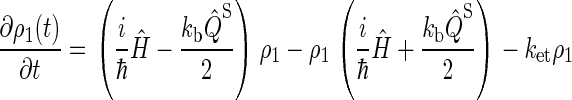(26)

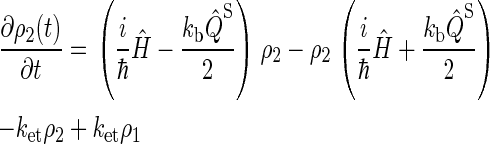(27)

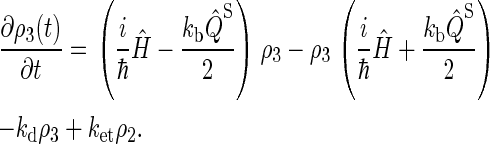(28)

We assume that the system begins with the hole (left from electron transfer) on the first tryptophan and with the electron spin pair in the singlet (rather than triplet) state, so that the initial conditions are

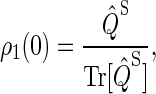(29)

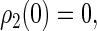(30)

(31)

This assumption is inspired by experimental data from photolyase (53). The actual initial state of cryptochrome is not known and might be a triplet state; however, the results of our calculation would be qualitatively similar had we chosen a triplet state for the initial condition. The system of differential equations (Eqs. 26–31) was solved numerically.

We do not include in our model the possibility of electrons transferring backward in the tryptophan chain, i.e., electrons undergo the transfers Trp-377 → Trp-400 or Trp-324 → Trp-377, but never the transfers Trp-400 → Trp-377, or Trp-377→ Trp-324. Although the latter transfers are feasible, calculations in the literature (52) and our own estimates presented below suggest that the rate constants for electrons transferring backward in the chain are 2–3 orders of magnitude smaller than the rate constants for forward transfer. This implies that the probability for such behavior is small and, therefore, we neglect this reverse electron transfer in our model.

Hyperfine coupling

The cryptochrome activation yield is very sensitive to the hyperfine coupling tensors chosen for the FADH and tryptophan radicals. For the yield to acquire a dependence on the angle between the magnetic field vector and the radical-pair axis, the hyperfine tensor of at least one radical must have significant anisotropy. One of the improvements made in our model of the FADH-tryptophan radical pair is to use realistic hyperfine coupling tensors for the two radicals, rather than relying on an order-of-magnitude guess as was done in Ritz et al. (22). Information regarding the hyperfine tensors of nuclei in FADH and tryptophan in photolyase and other molecules has been published (64–66). We assume that the hyperfine tensors for FADH and tryptophan in cryptochrome are similar to those exhibited by related systems. Indeed, the possibility for magnetic field effects in photolyase has previously been examined using similar hyperfine tensors (67). Our model differs from those previously considered in that it allows for a more complex reaction mechanism in which electron transfer and back-transfer rate constants are considered.

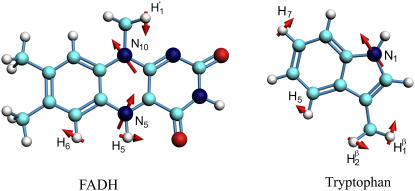
The hyperfine coupling constants and principal hyperfine axes used in the calculation are presented below (see Table 2). Because of the computational cost of calculating the activation yield for systems with a high-dimensional Hamiltonian, we include only up to four nuclei in each of our models of the FADH-tryptophan radical pair. Several combinations of nuclei in each radical were considered, and the activation yield for each configuration was calculated. However, the dependence of the activation yield on the magnetic field is sensitive to the choice of nuclei and associated hyperfine coupling constants. Fig. 5 shows the labeling used for the nuclei in FADH and tryptophan.

TABLE 2.

Hyperfine tensors of nuclei in FADH and tryptophan

Hyperfine constants and axes chosen for FADH
Nucleus	aiso (G)	Tii (G)	Hyperfine axes
N5	3.93	−4.98	0.4380	0.8655	−0.2432
		−4.92	0.8981	−0.4097	0.1595
		0, 9.89*	−0.0384	0.2883	0.9568
H5	−7.69	−6.16	0.9819	0.1883	−0.0203
		−1.68	−0.0348	0.2850	0.9579
		7.84	−0.1861	0.9398	−0.2864
Hyperfine constants and axes chosen for tryptophan
Nucleus	aiso (G)	Tii (G)	Hyperfine axes
Hβ1	16	0.00	1.000	0.000	0.000
		0.00	0.000	1.000	0.000
		0.00	0.000	0.000	1.000
H5	5	0.00	1.000	0.000	0.000
		0.00	0.000	1.000	0.000
		0.00	0.000	0.000	1.000

Information on the hyperfine tensors in photolyase and other molecules has been published previously (64–66). The chosen values listed are similar or identical to those published earlier. The hyperfine coupling constants incorporate the g-value of the electron and are in units of Gauss.

^*The value of 9.89 G was used for radical-pair model 1 and 0.00 G for radical-pair model 2.

FIGURE 5.

FADH and tryptophan shown with those of their nuclei involved in the strongest hyperfine coupling. The numbering of the nuclei in each radical is chosen to be consistent with that of other studies (64,65,67).

In this article, we take into consideration two representative choices of nuclei. The first choice includes the nuclei N₅ in FADH and H₅ and H^β₁ in tryptophan; the second choice includes N₅ and H₅ in FADH and H₅ and H^β₁ in tryptophan. The two radical-pair models are listed in Table 1, and the corresponding hyperfine coupling constants are given in Table 2. We included in our choices the nuclei with the strongest hyperfine coupling, according to the literature, as the calculated magnetic field dependence of cryptochrome activation proved to be most sensitive to the influence of these nuclei. We then modified the coupling constants from the values reported in the literature and chose values that gave the largest change in activation upon increase of the magnetic field to 5 G (Table 2). Our goal was to demonstrate the possibility of obtaining a large (on the order of 10%) variation (either an increase or decrease) in activation yield when the magnetic field is varied according to the experiments reported in Ahmad et al. (48).

TABLE 1.

Choices of nuclei for two radical-pair models

Radical-pair model	Nuclei in FADH	Nuclei in tryptophan
1	N5	H5, Hβ1
2	N5, H5	H5, Hβ1

To determine the magnetic field effect on cryptochrome activation more precisely, one needs to obtain more accurate values for the hyperfine coupling constants for the relevant nuclei in FADH and tryptophan. The results presented below can only show the feasibility of obtaining a significant magnetic field effect in cryptochrome based on estimates for the hyperfine coupling within the radical pair.

Rate constants

For realistic estimates of the reaction rate constants for electron forward transfer, electron back-transfer, and tryptophan deprotonation, we used a combination of experimental values from the literature (50,53) and our own theoretical estimates.

As indicated in Fig. 2, we denote the rate constants for forward electron transfer Trp-377 → Trp-400 and Trp-324 → Trp-377 by k₁ and k₂. These transfers correspond to an electron jumping between tryptophans in the direction opposite to that of the arrows shown in Fig. 2, as the arrows actually indicate hole transfer. We denote the rate constants for reverse electron transfer by (k₁)′ and (k₂)′. The electron forward transfer rate constants were experimentally determined for DNA photolyase and estimated to be ∼10⁸ s⁻¹ (50,53).

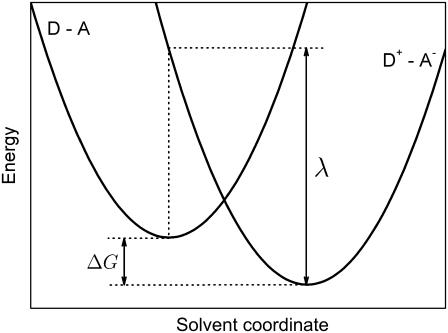
The rate constant for electron transfer can be estimated if one considers the tunneling process of an electron through protein. The rate constant is commonly expressed as the product of two factors (68). The first factor is an electronic term arising from the strength of the coupling of the electron donor/acceptor wavefunctions, leading to a roughly exponential fall-off in the electron tunneling rate with distance through the insulating barrier and, accordingly, is proportional to exp(−βR), where R is the edge-to-edge distance and β is proportional to the square root of the barrier height; the second factor depends on the energy, λ, required to repolarize the protein matrix upon electron transfer, and the driving force, ΔG, for the electron transfer. These quantities are depicted in the Marcus diagram (68,69) shown in Fig. 6. Both classical (69) and quantum mechanical (70–72) versions of the Marcus theory of electron transfer suggest a roughly parabolic dependence of log rate on ΔG.

FIGURE 6.

Schematic representation of the energetics assumed in electron transfer theory from a donor D to an acceptor A. The energy, λ, required to reorganize nuclear coordinates upon electron transfer, and the driving force, ΔG, for the electron transfer are indicated. The solvent coordinate describes schematically the effect of the protein degrees of freedom on the energy needed to transfer the electron in the process D − A → D⁺ − A⁻.

Electron tunneling between covalently bridged redox centers in synthetic systems (β ≈ 0.9 Å⁻¹) (73) is clearly much faster than tunneling through vacuum (β ≈ 2.8–3.5 Å⁻¹) (74,75). Earlier experimental examination of tunneling in proteins suggested an intermediate value (β ≈ 1.4 Å⁻¹) corresponding to a weighted average of the two extreme β values (74,76). A simple empirical expression that incorporates an exponential decay of the tunneling rate constant k (in s⁻¹) with edge-to-edge distance R (in Å) and a parabolic dependence of the rate on ΔG and λ (in eV) is (77)

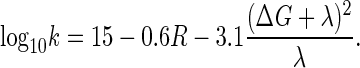(32)

The coefficient 0.6 corresponds to β = 1.4 Å⁻¹ on a common log scale, whereas the coefficient 3.1 collects the room-temperature constants for the quantized nuclear term (71), as suggested by extensive studies of photosynthetic reaction centers (74,78,79). Equation 32 has proven to be a useful approximation for electron-transfer rate constants in the absence of a detailed protein structure; however, it does not explicitly address the variations in polypeptide structure or whether those variations have been naturally selected to influence tunneling rate constants to physiological advantage.

The use of the edge-to-edge distance R in Eq. 32 provides only a rough estimate of the electron tunneling rate constant. The edge-to-edge distance is suitable in the case when the molecules are static, but in a protein at thermal equilibrium, the tryptophans move and rotate, and the average distance between donor and acceptor groups offers a better variable for the spatial dependence of the electron transfer rate. Accordingly, we substitute in Eq. 32 the average distance between tryptophans,

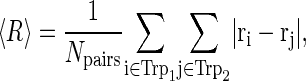(33)

for R, where i and j denote the atoms in the first and second tryptophan, respectively, and N_pairs is the total number of atomic pairs. The average distance between Trp-377 and Trp-400 calculated from Eq. 33 is 7.21 Å, whereas the average distance between Trp-324 and Trp-377 is 8.37 Å. With ΔG = −0.2 eV (see Figs. 2 and 6) and the generic value λ = 1.0 eV for the reorganization energy of electron-tunneling processes in proteins (76), we estimate that k₁ = 4.9 × 10⁸ s⁻¹ and k₂ = 9.9 × 10⁷ s⁻¹ for electron transfer from Trp-377 to Trp-400 and from Trp-324 to Trp-377, respectively.

The value ΔG is estimated to be negative (see Figs. 2 and 6), despite differences in the polarities of the tryptophan environments (50). From inspection of the crystal structure, it was suggested (50) that the polarities increase and, hence, the potentials decrease in the order Trp-400, Trp-377, Trp-324. The value for ΔG in DNA photolyase is calculated and discussed in Popovic et al. (52).

The estimates above for k₁ and k₂ are in good agreement with experimentally determined values and correctly reproduce the order of magnitude of the electron-transfer rate constants. For a more accurate evaluation of the rate constants, it is necessary to employ a more detailed model that accounts explicitly for the structure and vibrations of the protein; such a model (80) is far beyond the scope of this study. Since the estimated rate constants are of the same order of magnitude as the experimentally measured values, we will use the experimentally measured rate constants in our calculations. The estimated rate constants k₁ and k₂ are of about the same order of magnitude, which supports our assumption, k₁ = k₂, used in the system of coupled stochastic Liouville equations, Eqs. 16–18.

The rate constants for electron transfers Trp-400 → Trp-377 and Trp-377 → Trp-324 can also be estimated through Eq. 32. In this case, we employ ΔG = 0.2 eV for both processes. Thus, one estimates 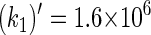s⁻¹ and 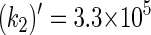s⁻¹ for Trp-400 → Trp-377 and Trp-377 → Trp-324 transitions, respectively. These rate constants are significantly smaller than k₁ and k₂ and, accordingly, electron transfer in the reverse direction of the Trp-400, Trp-377, Trp-324 chain can be neglected.

The rate constants for electron back-transfer from FADH to a tryptophan, 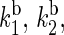and 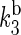(see Fig. 2) can also be estimated through Eq. 32. For this purpose, one needs to know the distances between the fragments, the reorganization energies, and the driving forces. The characteristic distances R_{FADH–Trp-400}, R_{FADH–Trp-377}, and R_{FADH–Trp-324} are 6.0, 8.9, and 13.3 Å, respectively. The reorganization energies are expected to increase with increased distance between the two fragments and, thus, we choose them as 0.85, 1.0, and 1.4 eV for the pairs FADH + Trp-400, FADH + Trp-377, and FADH + Trp-324, respectively. The driving forces for these processes can be estimated from the energy diagram in Fig. 2. Since cryptochrome is excited by a blue light photon, the energy difference between the ground and excited states should be ∼2.6 eV. The initial electron transfer step, from Trp-400 to FADH, proceeds downhill with a driving force of ∼0.5 eV (50). The next two electron-transfer steps proceed with a decrease in energy of 0.2 V (50,52). Accordingly, the driving energies are ΔG_{FADH–Trp-400} = −2.1 eV, ΔG_{FADH–Trp-377} = −1.9 eV, and 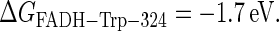With these driving energies, one obtains 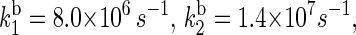and 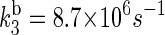for the electron back-transfers FADH → Trp-400, FADH → Trp-377, and FADH → Trp-324, respectively. The rate constants compare well with each other. For the sake of simplicity, we will consider the three rate constants to be equal, assuming a value of 10⁷ s⁻¹ (see Table 3).

TABLE 3.

Rate constants of various processes in cryptochrome-1

Process	Rate constant	Estimate (s−1)	Measured value (s−1)
Electron forward transfer	k1 = k2 = ket	1 × 108	1 × 108, (50,53)
Electron reverse transfer	(k1)′	1.6 × 106	—
Electron reverse transfer	(k2)′	3.3 × 105	—
Electron back-transfer		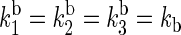1 × 107	—
Tryptophan deprotonation	kd	—	3.3 × 106, (50,53)
Singlet-triplet interconversion	Ω	8.3 × 107	—

The measured deprotonation rate of Trp-324 at pH 7.4 is k_d = 3.3 × 10⁶ s⁻¹ (50,53). This rate constant can also be estimated, but it depends on the temperature and on the concentration of the external agent, which induces deprotonation.

To test the feasibility of singlet-triplet interconversion to facilitate magnetic-field-dependent cryptochrome activation, it is necessary to estimate the characteristic time for the process, which should be of the same order of magnitude as (or shorter than) the time needed for forward electron transfer. In this subsection, an estimate for the singlet-triplet interconversion time is derived for a model radical pair with one nucleus and two electrons. In this case, the spin Hamiltonian, given by Eq. 1 with H_int neglected, is

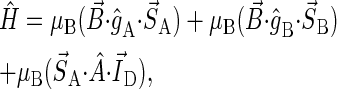(34)

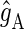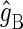where and are the g-tensors of the electrons in radicals A and B, which comprise the radical pair; D denotes the spin-1/2 nuclei involved in hyperfine coupling to one of the electron spins.

To describe the spin motion, one needs to choose the basis states of the wavefunction. For three spin-1/2 particles, eight basis states are required, which will be denoted as ψ_i, where i = 1, 2, …, 8. The determination of the basis states is an exercise in basic quantum mechanics, and the reader is referred to an introductory textbook (60). If the two electrons of the radical pair are found in the singlet state, then the corresponding basis states are

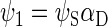(35)

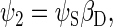(36)

where

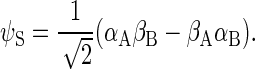(37)

α_i and β_i are the eigenfunctions of the operator S_iz with eigenvalues 1/2 and −1/2, respectively; α_D and β_D denote the analogous states for the nuclear spin.

Another six states are connected with the triplet states of the radical pair, which will be denoted as 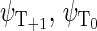and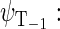

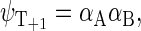(38)

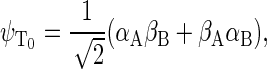(39)

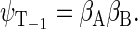(40)

If the radical pair is found in the triplet state, the total spin of the system can be 1/2 or 3/2. The basis states that describe the state of the system with total spin 1/2 are

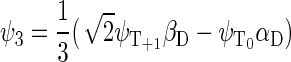(41)

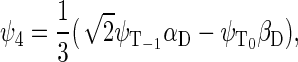(42)

whereas the basis states that describe the four states of the system with total spin 3/2 are

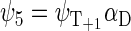(43)

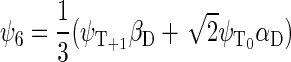(44)

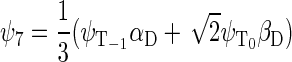(45)

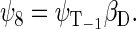(46)

One can now calculate, for example, the transition probability from a singlet state, e.g., the one described by wavefunction ψ₁, to a triplet state, e.g., the one described by wavefunction ψ₃. This transition is possible if the conditions

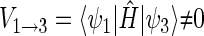(47)

(48)

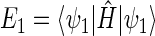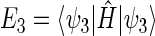are met, where and are the energy expectation values of the system in states corresponding to ψ₁ and ψ₃, respectively. The matrix element for the 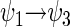transition can be evaluated in terms of the parameters specifying the Hamiltonian (34). One obtains

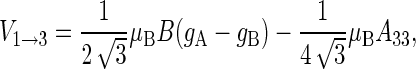(49)

and the energies of states ψ₁ and ψ₃ calculated likewise are

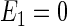(50)

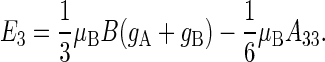(51)

With g_A = g_B = 2, A₃₃ = 16 G, B = 0.5 G, μ_B = 5.78843 × 10⁻⁹ eV/G, one obtains 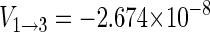eV and E₃ = − 1.158 × 10⁻⁸ eV, and conditions defined in Eqs. 47 and 48 are satisfied.

If the system is initially in state ψ₁, the probability to find it in state ψ₃ at a later time t is

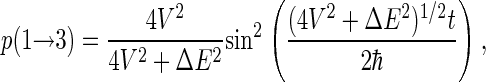(52)

as long as the other six states (ψ₂ and ψ₄–ψ₈) are neglected. Thus, the radical pair oscillates from singlet to triplet state with characteristic frequency

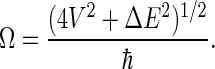(53)

With the values above, one obtains Ω ≈ 8.3 × 10⁷ s⁻¹, which is indeed of the same order of magnitude as the electron forward transfer rate constant, k_et = 1 × 10⁸ s⁻¹, discussed above.

The estimated values of the rate constants for various processes considered in the calculation are compiled in Table 3. It should be noted that the measured rate constants referenced in this article refer to photolyase, not cryptochrome, and could easily be off by an order of magnitude for cryptochrome. However, since accurate data for the rate constants in cryptochrome are not available, we used our estimated values in conjunction with the measured rate constants from photolyase. Although the values presented here must be considered approximate, the fact that magnetic field effects are observed in Arabidopsis (which would not be possible for unsuitable cryptochrome rate constants, as explained below in the Discussion) suggests that our values are likely accurate to within an order of magnitude.

Cryptochrome activation yield

Once the density matrix has been obtained as a solution of the coupled stochastic Liouville equations (Eqs. 26–31), observables of interest can be evaluated. The main quantity of interest is the activation yield of cryptochrome. This yield corresponds to the formation of the product FADH + Trp-324_dep. The yield depends on the strength and orientation of the magnetic field, described through (B₀, θ, φ) and is given by the expression

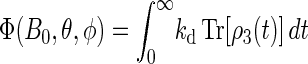(54)

In case the cryptochrome is oriented randomly relative to the external field, the total yield is averaged over θ and φ,

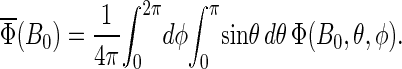(55)

The magnetic-field dependence of Φ(B₀, θ, φ) and 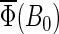develops due to the electron back-transfer reaction FADH + Trp⁺ → FADH⁺ + Trp (see Fig. 2) and, in particular, due to the reaction FADH + Trp-324⁺ → FADH⁺ + Trp-324. This reaction is possible only in the singlet state of the FADH + Trp-324⁺ radical pair, and its yield is given by

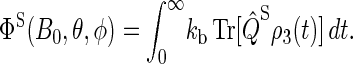(56)

One can recognize that the activation yield is determined by the function Tr[]. Consequently, we refer to Tr[] and its complement Tr[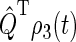] as the singlet and triplet state populations, respectively.

RESULTS AND DISCUSSION

The theory and methods described above have been used to study spin dynamics in cryptochrome. In the following sections, the magnetic field dependence of the formation of FADH stabilized by deprotonation of Trp-324⁺ to Trp-324_dep, averaged over the orientation of the magnetic field, is analyzed by means of the observable 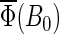defined in Eq. 55. We found that the suggested radical-pair mechanism is consistent with a cryptochrome-mediated magnetic-field response in Arabidopsis thaliana. The dependence of the activation yield Φ(B₀, θ, φ), defined in Eq. 54, on the orientation (θ, φ) of an external magnetic field is also discussed and it is shown that cryptochrome activation might serve as an inclination compass. Results are presented on the time evolution of the singlet population Tr[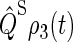] and discussed in detail.

Magnetic-field dependence of activation yield

The dynamics of electron spins is governed by the hyperfine interaction with the nuclei of the radical pairs. Due to computational costs it is impossible to account for all nuclei in the system explicitly. Thus, two radical-pair models have been considered, each of which includes only selected nuclei from each of the radicals (see Theory).

The choice of radical-pair model 1 was inspired by the work of Ahmad et al. (48) on magnetic field effects in Arabidopsis thaliana, in which it was shown that an external magnetic field can inhibit hypocotyl elongation, a process regulated by cryptochrome. The results of this work suggest that cryptochrome is responsible for the magnetic-field dependence of hypocotyl elongation in Arabidopsis thaliana, although it is not clear which of several possible radical pair processes is affected. Radical-pair model 1 was used to justify this suggestion and to show that the external magnetic field can lead to an increase of the activation yield in cryptochrome. For this model, nuclei that have the highest hyperfine coupling constants according to the literature were used. Radical-pair model 2 was chosen to show that the activation yield in cryptochrome depends strongly on the hyperfine coupling constants of the nuclei, and that changes in their values can lead to rather different behavior of the activation yield. For the purpose of demonstration, some of the experimentally measured hyperfine coupling constants were altered (see Table 2).

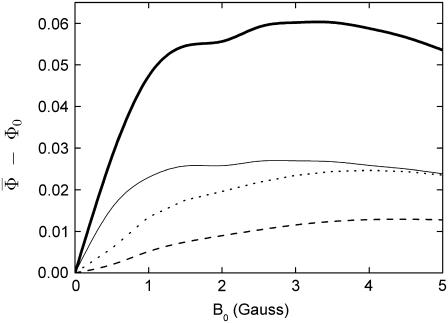
Figs. 7 and 8 present the magnetic field dependence of the total activation yield 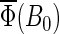calculated for two chosen radical-pair models. The total activation yields for 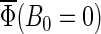are given in Table 4. The results in Fig.7 are consistent with the hypothesis that cryptochrome harbors a measurable radical-pair effect. The experimental results of Ahmad et al. (48) on magnetic field effects in Arabidopsis thaliana suggest that cryptochrome spends more time in its signaling state when in a field of 5 G than it does in an earth-strength magnetic field. The activation yield 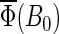presented in Fig. 7 is proportional to the time that the protein spends in its signaling state. Fig. 7 shows that the activation yield is increasing with increase of the external magnetic field. For an electron back-transfer rate constant of 10⁷ s⁻¹ (Fig. 7, solid line), the relative increase of 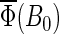at 5 G is ∼10%, which is of the same order of magnitude as the plant-growth-inhibition effect reported in Ahmad et al. (48). This supports the suggestion that cryptochrome is responsible for the magnetic-field-dependent stem growth in plants.

FIGURE 7.

Cryptochrome activation yield 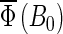for radical-pair model 1. The probability for the formation of FADH + Trp-324_dep, averaged over angles θ and φ, for radical-pair model 1, which contains nuclear spins N₅ on FADH and H₅ and 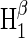on the tryptophans, was calculated for different electron back-transfer rate constants: thin solid line, k_b = 10⁶ s⁻¹; thick solid line, k_b = 10⁷ s⁻¹; dotted line, k_b = 5 × 10⁷ s⁻¹; dashed line, k_b = 10⁸ s⁻¹. Φ₀ represents the value of the yield at B₀ = 0. The values of the activation yield at B₀ = 0 are given in Table 4. The difference in yield over the range from 0 to 5 G is approximately +10% for this model.

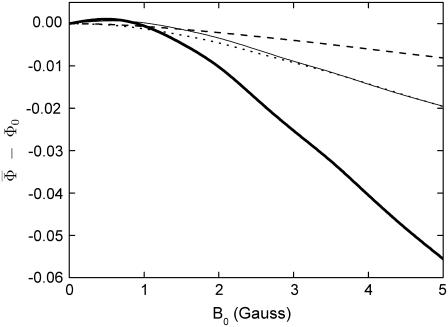
FIGURE 8.

Cryptochrome activation yield 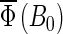for radical-pair model 2. The probability for the formation of FADH + Trp-324_dep, averaged over angles θ and φ, for radical-pair model 2, which contains nuclear spins N₅ and H₅ on FADH and H₅ and 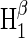on the tryptophans, was calculated for different electron back-transfer rate constants: thin solid line, k_b = 10⁶ s⁻¹; thick solid line, k_b = 10⁷ s⁻¹; dotted line, k_b = 5 × 10⁷ s⁻¹; dashed line, k_b = 10⁸ s⁻¹. Φ₀ represents the value of the yield at B₀ = 0. The values of the activation yield at B₀ = 0 are given in Table 4. The difference in yield over the range from 0 to 5 G is approximately −11% for this model.

TABLE 4.

Values of the total activation yield 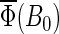for B₀ = 0 G calculated for two radical-pair models with different electron back-transfer rate constants

Rate constant kb (s−1)	Radical-pair model 1	Radical-pair model 2
106	0.873	0.892
107	0.425	0.524
5 × 107	0.121	0.163
108	0.058	0.080

The magnetic field dependence of the activation yield 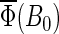for radical-pair model 2 is shown in Fig. 8. This example shows that the activation yield can decrease with an increase of the external magnetic field. Of the considered electron back-transfer rate constants, the maximal relative decrease occurs for a constant of 10⁷ s⁻¹ and is ∼11%. The comparison of model 2 with model 1 above, which showed an increase of total FADH + Trp-324_dep yield with field strength, demonstrates dramatically that the hyperfine coupling constants influence the activation yield behavior in a complex way. Unfortunately, the hyperfine coupling constants are not well known for the nuclei of the FADH and tryptophan in cryptochrome. To determine the exact magnetic-field response, it will be necessary to obtain experimental information regarding the hyperfine coupling constants of FADH and of each of the three tryptophans in their native environment within cryptochrome. It will also be necessary to greatly extend the present numerical calculation to include a large number of nuclear spins hyperfine-coupled to the unpaired electronic spins.

Figs. 7 and 8 also show the magnetic field dependence of the activation yield 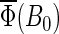calculated for different electron back-transfer rate constants. From the estimates performed above, one expects the rate for electron back-transfer to be on the order of 10⁷ s⁻¹. From Figs. 7 and 8, it is clear that for this particular value of the electron back-transfer rate constant the magnetic-field effect is maximal (Figs. 7 and 8, solid lines).

The fact that lower and higher values of the electron back-transfer rate constants lead to less pronounced magnetic field effects on cryptochrome activation has a simple explanation. If the electron back-transfer rate constants (k_b) are 10⁶ s⁻¹ or less, then most of the hole density will reach Trp-324 and the protein will reach its signaling state with only minor loss of the hole density. This happens because the rate constants of the electron forward transfer process and of the tryptophan deprotonation process are larger than the rate constant of electron back-transfer (10⁶ s⁻¹). The external magnetic field modulates the probability for the radical pair to be in the singlet state of FADH + Trp-324⁺, the only state in which the electron back-transfer process is possible. If electron back-transfer is slower than the deprotonation Trp-324⁺ → Trp-324_dep (k_d ≈ 3 × 10⁶ s⁻¹), the external field can only slightly influence the signaling state of the protein (Figs. 7 and 8, thin solid lines).

If the electron back-transfer rate constant, on the other hand, is larger than 10⁷ s⁻¹, e.g., 5 × 10⁷ s⁻¹ or 10⁸ s⁻¹ (Figs. 7 and 8, dotted and dashed lines), it becomes comparable to the rate constants of forward electron transfer (10⁸ s⁻¹) and with the rate of singlet-triplet interconversion (∼10⁸ s⁻¹, see Eq. 53). In this case, formation of the FADH + Trp-324⁺ radical pair is impeded and magnetic-field-dependent spin conversion processes will arise to a lesser degree so that the activation yield 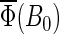becomes reduced.

Angular dependence of activation yield

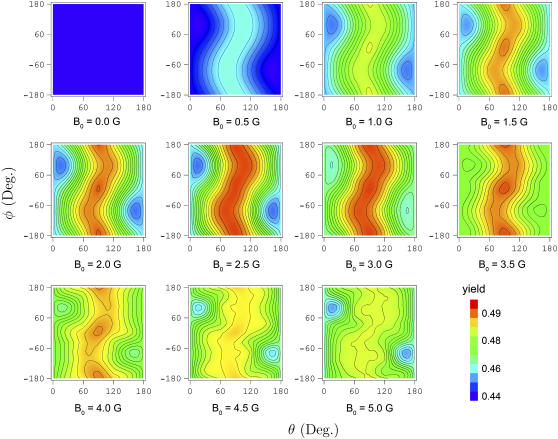
For a radical-pair-based activation in cryptochrome to function as an inclination compass, the FADH + Trp-324_dep yield must exhibit variation with respect to the orientation of cryptochrome relative to an external magnetic field. This orientational dependence could modulate the visual sense of a bird to produce the avian magnetic compass, as described in (22). The variation of the total activation yield for the case of radical-pair model 1 is shown in Fig. 9. The angular dependence of the activation yield depends strongly on the hyperfine coupling constants of the nuclei and, therefore, should be different for radical-pair model 2. In this article, we do not discuss this difference and show only a single example as an illustration of the possible outcome, namely, for radical-pair model 1.

FIGURE 9.

Contour plots of the angular dependence of the cryptochrome activation yield. The plots show the FADH + Trp-324_dep yield for radical-pair model 1. The yield exhibits a maximal ridge at about θ = 90°, which is most prominent around B₀ = 2.5 G and fades away at higher and lower magnetic field strengths.

Fig. 9 shows that at (θ = 15°,φ = 90°) and (θ = 165°,φ = −90°) the activation yield has profound minima at all magnetic field strengths. Fig. 9 shows also that the activation yield, Φ(B₀, θ, φ), in the θ, φ-plane has a maximal ridge near θ = 90°, which is most prominent around B₀ = 2.5 G and is less pronounced at higher and lower magnetic field strengths. These minima and the maximal ridge at θ = 90° can be explained if one examines the principal axes of the hyperfine coupling tensors and considers the fact that each nuclear spin contributes an effective local field (see Fig. 4) 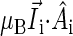to the electron spin precession. The nuclei that contribute ansiotropic hyperfine coupling are N₅ and H₅ on FADH (see Fig. 4), the hyperfine tensors being listed in Table 2. The dominant contribution to the hyperfine coupling stems from the principle axes of N₅ and H₅ that happen to both be oriented closely along the z axis, deviating from it by θ = 15°, φ = 90°. N₅ contributes a local field of ± 14 G (combining isotropic and anisotropic contributions), whereas H₅ contributes ± 5 G. These fields are larger than the external field, so that the effect of the external field is minimized in the direction θ = 15°, φ = 90° (as well as in the opposite direction θ = 165°, φ = −90°). This behavior indeed is revealed in Fig. 9.

The effective field contributed by N₅ and H₅ in the xy-plane, on the other hand, is small enough that an external field of ∼2.5 G can effectively modulate the electron spin precession around the combined (nuclear and external) local field. The reader is advised to view the semiclassical picture of the radical-pair electron spin dynamics in Fig. 4. N₅ contributes only ±1 G in each component of the xy-plane whereas H₅ contributes ± 7 G along the x axis and a negligible field along the y axis. Therefore, the external field can contribute significantly to the effective local field on FADH in the xy-plane, leading to the maximal ridge in the orientation dependence in Fig. 9.

The projection of the local magnetic field in the FADH radical on the xy-plane is described by an ellipsoid that has principal radii b_x = 8 + B₀ G and b_y = 1 + B₀ G. The contributions of the N₅ and H₅ nuclei are 8 G and 1 G, respectively, and B₀ is the contribution of the external magnetic field. The average field created by the N₅ and H₅ nuclei in the xy-plane is given by the geometrical mean of b_x and b_y

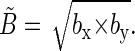(57)

At B₀ = 0 G, 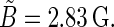This value corresponds to the upper left contour plot in Fig. 9, which is constant and without angular dependence. The ridge in the orientation dependence at θ = 90° in Fig. 9 has its maximal value at B₀ = 2.5 G, which is also close to the field value where has its maximum (see Fig. 7).

It is important to note that the activation yield is dependent only on the inclination of the external magnetic field and not on its polarity, a feature explained by Schulten and co-workers (19,20). This can be seen from the contour plots in Fig. 9, which obey the symmetry property Φ(θ, φ) = Φ(180° − θ, − φ − 180°), small deviations from this condition arising due to the interpolation error of the contour plots. The fact that the activation yield depends only on the inclination of the magnetic field, but not its direction, supports the hypothesis that the radical-pair mechanism is involved in avian magnetoreception, as migratory birds possess an inclination-only compass.

Time dependence of singlet and triplet populations

The probability arising in Eq. 56 and its complement 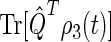represent the populations for the FADH + Trp-324⁺ radical pair in the singlet and triplet state, respectively. The time dependence of these quantities provides information on the characteristic time scales of the spin dynamics underlying the radical-pair mechanism. From the time evolution of the singlet and triplet populations, it is possible to establish the time needed for the electron hole to reach Trp-324, for FADH + Trp-324⁺ to assume a maximal singlet or triplet state character, and the characteristic time of the entire process, i.e., the time when the population of FADH + Trp-324⁺ has decayed to zero.

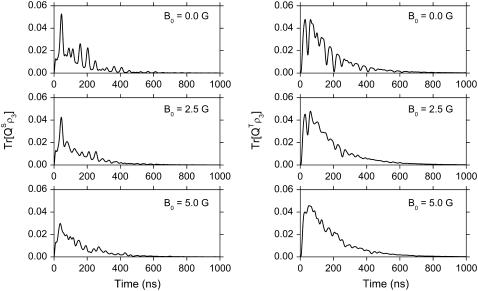
The time dependence of the singlet and triplet populations (Tr[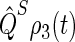] and Tr[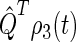]) for radical-pair model 1 are plotted in Fig. 10. The populations oscillate about an initial rise and subsequent exponential decay. The oscillations arise due to the singlet-triplet interconversion, whereas the decay stems from electron back-transfer and Trp-324⁺ deprotonation.

FIGURE 10.

Time dependence of singlet and triplet populations. The results shown are those for radical-pair model 1, calculated for rate constants k_et = 1 × 10⁸ s⁻¹, k_b = 1 × 10⁷ s⁻¹, and evaluated at θ = 0°, φ = 0°.

From the maxima and minima of the singlet/triplet population one can establish the characteristic time of singlet-triplet interconversion. The first five maxima and minima that arise in the time dependence of the triplet population at an external field of 0 G are compiled in Table 5. The time difference between two neighboring maxima and minima corresponds to the time of the interconversion process governed by the hyperfine coupling only. From the data presented in Table 5, one finds τ_T–S ∼ τ_S–T ∼ 15–25 ns (k_S–T = 5–6.7 × 10⁷ s⁻¹). This estimate is in agreement with the estimate performed earlier (see Eq. 53). The results for the time evolution of the spin populations might be used for the experimental verification of the suggested mechanism. For example, time-resolved ESR techniques could be applied that probe the spin correlation of photoinduced radical pairs in cryptochrome in the same manner as these techniques have been applied to photosynthetic reaction centers (81,82).

TABLE 5.

The first five maxima and minima in the time evolution of the triplet population at 0 G

Maxima (ns)	Minima (ns)	Δτ (ns)
29	45.5	16.5
62 (74)	91	29 (23.5)
100.5	114.5	14
128.5 (139)	158	29.5 (24.3)
177.5	204	26.5

Δτ gives the time difference between two neighboring maxima and minima. The values in parentheses correspond to cases where there are two close-lying maxima.

At 0 G, the singlet and triplet populations reach their first maxima at 45 ns and 29 ns, respectively. Note that a maximum in the singlet population corresponds to a minimum in the triplet population and vice versa. Thus, at 45 ns the triplet population has a profound minimum (see Fig. 10). The positions of maxima and minima depend on the magnetic field strength; the first maximum for the singlet population is shifted to shorter times with increasing magnetic field strength, whereas the first triplet population maximum is shifted to longer times. At 5 G, the first maximum occurs at 37.5 ns for the singlet population and at 52.5 ns for the triplet population. The triplet population also exhibits a strong second maximum which occurs at 61 ns and 62.5 ns for 0 and 5 G, respectively.

The value of the singlet and triplet populations at these maxima (especially in the singlet population) decreases with increasing magnetic field strength. This fact has a simple explanation. The two maxima in the triplet population come closer to each other with increasing magnetic field, and nearly merge at 5 G. Thus, the value of the population at the minimum between the maxima rises and the magnitude of the maximum in the singlet population decreases.

From Fig. 10 it is also possible to estimate the time of the overall radical-pair reaction. From this figure it is clear that at t ∼ 700 ns both singlet and triplet populations have decayed to zero.

CONCLUSION

That magnetic sensing in plants and animals may be mediated by magnetic field effects on the activation of the signaling protein cryptochrome is a hypothesis worthy of investigation. Such a magnetic-field-sensing mechanism can explain many long-observed properties of avian magnetoreception (4–8,22) and of a recently observed magnetic field effect in plants (48). In this article, we investigated the possibility that a weak external magnetic field alters the photoreduction of the FAD cofactor in cryptochrome via a radical-pair mechanism involving the FADH cofactor of cryptochrome and three of the protein's tryptophans involved in a dominant electron transfer pathway. Changes in cryptochrome's FAD reduction activity alter the protein's ability to autophosphorylate (56), which in turn alters the protein's signaling behavior. The results of our calculations on cryptochrome's photoreduction pathway demonstrate the possibility of cryptochrome's activation to exhibit a dependence on magnetic field strength and orientation. The results also support the hypothesis that a radical-pair mechanism in cryptochrome is responsible for the magnetic field effects observed in Arabidopsis thaliana (48). Although the extension of our findings to a cryptochrome-based magnetic sensor in animals involves several factors beyond the scope of this article (see Mouritsen and Ritz (7) for a review), our results suggest that such a mechanism is clearly possible.

Unfortunately, lack of sufficient information regarding isotropic and anisotropic hyperfine coupling in cryptochrome hinders one to draw conclusions about the precise magnetic field effects in cryptochrome, limiting our investigation to be a study of feasibility. It is also not certain if the radical pair reaction involving FADH is responsible for the observed magnetic field effect in (48) or if another radical pair reaction takes this role. When more experimental data regarding hyperfine coupling constants and reaction rate constants in cryptochrome become available, this investigation can be extended to a quantitative description.