Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2007 Jan 26;92(8):2975–2981. doi: 10.1529/biophysj.106.097097

Boolean Dynamics of Biological Networks with Multiple Coupled Feedback Loops

Yung-Keun Kwon 1, Kwang-Hyun Cho 1
PMCID: PMC1831709  PMID: 17259267

Abstract

Boolean networks have been frequently used to study the dynamics of biological networks. In particular, there have been various studies showing that the network connectivity and the update rule of logical functions affect the dynamics of Boolean networks. There has been, however, relatively little attention paid to the dynamical role of a feedback loop, which is a circular chain of interactions between Boolean variables. We note that such feedback loops are ubiquitously found in various biological systems as multiple coupled structures and they are often the primary cause of complex dynamics. In this article, we investigate the relationship between the multiple coupled feedback loops and the dynamics of Boolean networks. We show that networks have a larger proportion of basins corresponding to fixed-point attractors as they have more coupled positive feedback loops, and a larger proportion of basins for limit-cycle attractors as they have more coupled negative feedback loops.

INTRODUCTION

Since the inception by Kauffman, random Boolean networks (RBNs) (1,2) consisting of a set of Boolean variables and regulatory relationships between the variables have been used as useful tools for understanding the complex dynamics of various biological networks. Despite their structural simplicity, RBNs can represent a variety of complex behaviors and share many features with other continuous models (3,4). An RBN consists of N Boolean variables, x1, x2, … , xN, having either 1 or 0, which represent the possible states of corresponding elements (e.g., in gene networks, the value 1 represents the “turn-on” status in which a gene is expressed). The value of each variable xi at time t + 1 is determined by the values of ki randomly selected other variables Inline graphic at time t by a Boolean function Inline graphic. Hence, we can write the update rule as Inline graphic and all the variables are synchronously updated.

In RBNs, a state trajectory starts from an initial state and eventually converges to either a fixed-point or a limit-cycle attractor. So, these attractors can describe the various behaviors of biological systems such as multistability, homeostasis, and oscillation. The structural properties of RBNs influence the characteristics of the attractors. In fact, there have been many studies investigating the structural properties in relation to the operating mode of networks (1,5,6). The most frequently studied properties are the connectivity K and the function bias p where Inline graphic is the mean number of input variables in the update rules and p is the maximum probability for the Boolean function to take either 1 or 0. If we vary these parameters, the network shows different dynamics: ordered, critical, or chaotic phases. However, the connectivity and the function bias are not enough to describe the converging dynamics to the attractors. There is another important structural parameter—a feedback loop, which is a circular chain of relationships. There are two major motivations for us to consider a feedback loop. The first motivation is from the need of developing an update rule that can better describe real biological networks. In RBNs, the number of possible Boolean functions grows very rapidly as the number of input variables increases. It is, however, desirable to constrain the plausible Boolean functions such that the resulting model can reasonably well describe the behaviors of real biological systems. Several classes of Boolean functions have been studied in this direction. Some studies suggested that canalyzing functions can more accurately describe the real biological systems (2,7). (Note that a function is canalyzing if at least one input value determines the output value irrelevantly to the other inputs. That is, Inline graphic is a canalyzing function if and only if there is a canalyzing variable xi such that if xi has a value s ∈ {0, 1}, then f always outputs the same value v ∈ {0, 1} for all 2K–1 combinations of the other input variables. For instance, Inline graphic is a canalyzing function because if x1 is one, then f outputs one irrelevantly to the values of x2 and x3.) However, they often include nonrealistic relationships. For instance, Inline graphic is a canalyzing function on x1; however, it is nonrealistic since the function in terms of x2 and x3 expresses an exclusive-OR relationship. (In the formula, · and + mean the “AND” and “OR” logical functions, respectively.) To resolve this problem, other classes of functions were developed such as nested canalyzing functions (8,9) and hierarchically canalyzing functions (10). Both nested and hierarchically canalyzing functions are natural subsets of canalyzing functions since 1), the function itself is canalyzing; and 2), when the canalyzing input takes a noncanalyzing value, the function is still canalyzing with respect to one of the remaining inputs. We note that the relationship between one variable and another in these functions is fixed as either positive or negative, whereas a relationship in random Boolean networks based on canalyzing functions is not fixed. Hence, we can assign a specific sign, plus (+) or minus (−), representing a positive or negative effect respectively, to each relationship. Then, a circular chain of relationships (a feedback loop) appears in the network. The sign of a feedback loop is easily determined by the parity of the number of negative relationships involved. If the parity number is even or zero, the feedback loop is positive; otherwise, it is negative. The second motivation is from the observation that such feedback loops are ubiquitously found in various biological systems. The dynamical roles of such feedback loops have been well known (11). From the view of dynamics, a positive feedback loop induces bi-stationarity whereas a negative feedback loop generates a damped or sustained oscillatory behavior. Biologically, the positive feedback loops seem developed to accomplish multistationary tasks such as differentiation through alternative patterns of gene expression whereas negative feedback loops have been developed primarily for homeostasis. These conjectures formulated by Thomas (11) have recently been demonstrated in a more general context (12–14). The functional roles of feedback loops were exemplified through a genetic control of flower morphogenesis (15) and infectious disease behavior (16). The dynamical properties and the role of feedback loops in biological networks have, however, not been fully addressed.

Let us consider other examples on the different roles of positive and negative feedback loops. In the regulatory network of inducing phenotype variations in bacteria, some epigenetic traits depend on the presence of a positive feedback loop (17). This feedback-based multistability is a common feature of adaptive processes in the bacteria realm. In addition, mitogen-activated protein kinase cascades in animal cells (18,19) and cell cycle regulatory circuits in Xenopus and Saccharomyces cerevisiae (20,21) show the role of positive feedback loops in producing multistability. On the other hand, in the transcription of mRNAs for Notch signaling molecules, the oscillation with a 2-h cycle depends on a negative feedback by hes1 transcription (22). This Hes1 oscillation is found in various cell types. The negative feedback was also found in the embryonic cell cycle (23) where Cyclin-Cdk activates APC-Cdc20, which causes the degradation of cyclin, and then APC-Cdc20 gets inactivated. Moreover, it has been revealed that a system with multiple feedback loops is more robust than those with a single feedback loop (24,25). It is intriguing that the feedback loops exist in the form of multiple coupled feedback loops in many biological systems such as budding yeast polarization (26), eukaryotic chemotaxis (27), and Ca2+ spikes (28). In particular, many biological networks have both positive and negative feedback loops and this makes the underlying dynamics more difficult to understand. Hence, in this article, we consider RBNs with multiple coupled positive and negative feedback loops and investigate the dynamical roles of such feedback loops with a particular attention to the characteristics of attractors. Specifically, we examine the effect of multiple coupled positive (negative) feedback loops on the fixed-point or limit-cycle attractors. Throughout mathematical simulations, we have discovered that the ratio of fixed-point basins increases along with the proportion of positive feedback loops, and the ratio of limit-cycle basins increases along with the proportion of negative feedback loops.

FEEDBACK LOOPS AND ATTRACTORS

Let us define some notions required for analyzing the dynamics of Boolean networks. Given a network with N Boolean variables, we define a state as a vector consisting of N Boolean variables, x1, x2, … , xN; there are 2N states in total. Each state makes a transition to another state through a set of N Boolean update functions, f1, f2, … , fN. We can construct a state transition network that represents the transition of each state. Fig. 1 illustrates an example of a Boolean network with three Boolean variables, x1, x2, and x3, and their update functions, f1, f2, and f3, respectively. The state transition table of a size eight is then specified according to the update functions. Based on this table, we can construct a state transition network in which there are eight trajectories starting from each state (the three Boolean values in each node denote the values of x1, x2, and x3 in sequence). A trajectory is classified into two kinds: fixed-point-converging or limit-cycle-converging trajectories. If a trajectory converges to a state that can only transit to itself in the state transition network, it is called a fixed-point-converging trajectory. Otherwise, it is a limit-cycle-converging trajectory. In Fig. 1, the number of fixed-point-converging and limit-cycle-converging trajectories is four, in both cases. The state transitive to only itself is called a fixed-point attractor (e.g., 000 and 111 in Fig. 1) and the state returning to itself through one or more other states is called a limit-cycle attractor (e.g., 011 and 100 in Fig. 1).

FIGURE 1.

FIGURE 1

Open in a new tab

An example of a Boolean network and a state transition network.

There have been various studies investigating the dynamics of biological networks based on the notion of attractors. We note that the dynamical attractors can represent the different cell types or cell fates in an organism (2). In Li et al. (29), the biological stationary state, G1 state, of the cell-cycle regulatory network in the budding yeast is encoded into the global attractor of the RBN. In this modeling, it was shown that the biological pathway of the cell-cycle sequence is well-attracting and also robust. In the study of flower morphogenesis, attractors were considered as different mutant phenotypes (15). Through simulations, a possible pathway of inducing gene expressions during flower morphogenesis was identified. In addition, there have been many other studies that support the close linkage between the dynamical attractors and cellular phenomena (30–33). In this article, we focus on the relationship between feedback loops and the characteristics of attractors. Fig. 2 shows a simple example illustrating that the feedback loop is highly related with the attractors. In Fig. 2 A, we consider a Boolean network with a single feedback loop. In this network, for i = 1, 2, … , N, each variable xi+1 at time t + 1 is determined only by the value of xi at time t (we assume that x1 = xN+1). Thus, xi+1(t + 1) = xi(t) or Inline graphic holds, depending on whether the relationship from xi to xi+1 is positive or negative, respectively. A state vector x = [x1x2…xN] is a fixed-point attractor if and only if xi(t + 1) = xi(t) holds for all xi-values. Hence, in the network with a single feedback loop, xi+1(t) = xi(t) or Inline graphic must be satisfied according to the sign of the relationship so that the state x becomes a fixed-point attractor. However, this is not possible if the number of negative relationships is odd. We consider another circuit with two feedback loops coupled in one node (Fig. 2 B). In this circuit, both xb and xc are affected by xa through different paths. Here, xa is determined by the two variables xb and xc through (xb or Inline graphic or Inline graphic) or (xb or Inline graphic or Inline graphic) (see Appendix A for details). For any case, if all the feedback loops are negative, the necessary conditions for x to be a fixed-point lead to the contradiction, Inline graphic. Hence, x cannot be a fixed-point in the circuit with coupled dual negative feedback loops. We also note that there is no fixed-point in a circuit with four negative feedback loops as illustrated in Fig. 2 C (see Appendix B for details). From these examples, we presume that the characteristics of attractors might be highly related with the coupled positive or negative feedback loops.

FIGURE 2.

FIGURE 2

Open in a new tab

An example illustrating the relationship between feedback loops and Boolean dynamics.

METHODS AND RESULTS

The structure of models

In this section, we detail the structure of two types of RBNs under consideration. Given N Boolean variables, the number of input variables is fixed to K for each variable in one model (NK model) and the total number of relationships is fixed to E in the other model (NE model). We note that the expected number of input variables per each Boolean variable is E/N in NE model. As mentioned before, a positive or a negative sign is assigned to each relationship. Then, the networks of both NK and NE models can be represented by a directed graph G = (V, A) where V is a set of Boolean variables (|V| = N) and A is a set of ordered pairs of the variables, called directed links. Each vi ∈ V has the value of 1 or 0. A link (vi, vj) is denoted by vi → vj or vi⊣vj depending on a positive or a negative relationship from vi to vj, respectively. In this article, we consider only a connected Boolean network. This is because an RBN consisting of disconnected multiple subnetworks can be considered as a composition of subnetworks. We note that such connected networks have multiple coupled feedback loops in many cases. The behavior of RBNs can be affected by update functions. Although we cannot compare all kinds of update functions, previous studies showed that canalyzing functions can most properly describe the real biological systems (2,7). In addition, the bias of update functions is known to affect the dynamical behavior of RBNs. In these regards, we consider three types of update functions which are canalyzing ones with different biases as follows: AND(x1, x2, … , xM) = x1 · x2 · … · xM, OR(x1, x2, … , xM) = x1 + x2 + … + xM, and UNBIAS(x1, x2, … , xM) = xi + x1 · … · xi–1 · xi+1 · … · xM for M input variables, x1, x2, … , xM. (The simulation results using the OR function are provided in Supplementary Material since it shows almost the same dynamical behavior as the AND function.) The bias of AND and OR3 is 1 − 1/2M so the functions are heavily biased. On the other hand, UNBIAS is almost unbiased since its bias is 1/2 + 1/2M. (In fact, the UNBIAS function is not exactly unbiased but almost unbiased. Among those functions that are dependent on all the variables, x1, x2, … , xM, and satisfy the fixed relationship constraint, there is no general formula that can represent an exactly unbiased function.)

Feedback effects in Derrida plots

In traditional RBN models, the connectivity and the bias are most frequently used as characterizing parameters. However, as we mentioned before, we note that a feedback loop effect is also essential in understanding the dynamics of Boolean networks. To investigate the effect of feedback loops, we drew a Derrida plot, one of the typical approaches in analyzing the dynamics of RBNs (34). For this plot, all pairs of states having the same initial Hamming distance, H(0), are chosen, and the average Hamming distance in the next time step, H(1), is computed. (Hamming distance between two states is defined as the number of Boolean variables having different values.) If H(1) is larger than H(0), the network shows a chaotic behavior and if H(1) is smaller than H(0), the network shows an ordered behavior. Fig. 3 shows the result where 2000 networks were randomly created with K = 2 from NK model and the AND update function was used. We examined two cases where H(0) = 1 (Fig. 3 A) and H(0) = 2 (Fig. 3 B). In the figure, H(1) was plotted against the number of feedback loops in the networks. We note that all the generated networks are identical in terms of the connectivity and the bias. Although the networks are always ordered owing to the low sensitivity (S = 2Kp(1 − p) = 0.75 < 1, where p is the function bias), the perturbation effects in the networks are different according to the number of feedback loops. As shown in this example, the two parameters, the connectivity and the bias, are not enough to fully explain the dynamics of Boolean networks.

FIGURE 3.

FIGURE 3

Open in a new tab

The relationship between the number of feedback loops and the Derrida value where the number of networks is 2000.

Proportion of attractor basins

To investigate the relationship between the feedback loops and the attractors, we have generated a number of random Boolean networks by NK and NE models and examined the ratio of fixed-point basins according to the variation of feedback loops (Fig. 4). In particular, 2N×K … (number of trials) and 2E × (number of trials) number of networks from NK and NE models were created, respectively. (In this experiment, “number of trials” was set to 30.) In Fig. 4, A–C, are the results of networks generated from NK models, and Fig. 4, D and E, are the results from NE models. In addition, the networks in Fig. 4, A, B, and D, use the AND function, and those in Fig. 4, C and E, use the UNBIAS function for their update rules. The mean value of the proportion of the fixed-point basins (y axis) is plotted against the ratio of the number of negative feedback loops to the total number of feedback loops (x axis). (The proportion of the fixed-point basins is the ratio of the number of fixed-point-converging trajectories to the total number of trajectories.) In the Boolean networks generated from NK model (K = 2) with the AND function, the ratio of fixed-point basins decreases almost linearly along with the ratio of negative feedback loops (Fig. 4 A). Note that the size of a network (N) is not a relevant parameter in this case. For the networks with a higher connectivity (K = 3), the decreasing rate of fixed-point basins was smaller (Fig. 4 B). To take a closer look at the effect of the connectivity, we have examined the networks obtained from NE model where N is fixed to 6 and E varies over 12, 14, 16, and 18 (Fig. 4 D). It turns out that all the classes of the networks showed similar patterns and the networks with higher connectivity induced a relatively higher expectation of fixed-point-converging trajectories. In the next, we have investigated the effect of update functions. The networks in Fig. 4 C are identical to those in Fig. 4 B except that the UNBIAS function is used instead of the AND function. In the case of Fig. 4 C, the ratio of fixed-point basins decreases more rapidly along with the ratio of negative feedback loops. We have also examined the effect of connectivity in the networks using the UNBIAS function (Fig. 4 E). In contrast with the result of the networks using the AND function, the networks with a higher connectivity have induced a lower expectation of fixed-point-converging trajectories. In addition, the networks using the OR function showed almost the same result as those using the AND function (see Fig. S1 in Supplementary Material). In summary, we found that the higher the ratio of negative feedback loops (or, the lower the ratio of positive feedback loops), the lower the ratio of fixed-point basins (or, the higher the ratio of limit-cycle basins).

FIGURE 4.

FIGURE 4

Open in a new tab

The effects of negative feedbacks on the fixed-point basins.

The number of attractors

We have examined the number of fixed-point states instead of the proportion of fixed-point basins in the same networks. The results are shown in Fig. 5 (the AND and the UNBIAS functions) and Fig. S2 (the OR function; see Supplementary Material) where y axis denotes the average number of fixed-point states and the x axis indicates the ratio of negative feedback loops to the total number of feedback loops in the network. These results are consistent with those of Fig. 4 and Fig. S1 (see Supplementary Material) in that the expected number of fixed-point attractors decrease as the ratio of negative feedback loops gets higher. Note that the network size N was not influential to the number of fixed-point attractors. Intriguingly, when the ratio of negative feedback loops is ∼0.5, the expected number of fixed-point attractors is almost one in all the networks.

FIGURE 5.

FIGURE 5

Open in a new tab

The effects of negative feedback loops on the number of fixed-points.

Circuits with positive or negative feedback loops

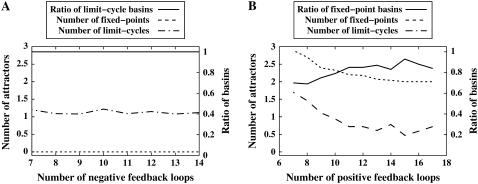
From the foregoing experimental results, we hypothesize that the higher ratio of positive (negative) feedback loops increases the ratio of fixed-point (limit-cycle, respectively) basins. In addition, we have compared the networks consisting of only positive feedback loops with those consisting of only negative feedback loops. Fig. 6 shows the results of the networks from NK models (N = 7 and K = 2) with the AND update function. We have randomly created 568 networks consisting of only negative feedback loops (Fig. 6, left) and 3100 networks consisting of only positive feedback loops (Fig. 6, right). In Fig. 6, the x axis denotes the number of negative or positive feedback loops. The right y axis indicates the average ratio of limit-cycle basins or fixed-point basins, and the left y axis denotes the number of fixed-point attractors or limit-cycle attractors. In the networks with multiple negative feedback loops, all the states were included in the limit-cycle basins and there was no fixed-point attractor (see Appendix C for details). In addition, the number of limit-cycle attractors was independent of the number of negative feedback loops. On the other hand, in the networks consisting of only positive feedback loops, the percentage of fixed-point basins was larger than that of limit-cycle basins although it was not always 100%. The ratio of fixed-point basins has been slightly increased as the number of positive feedback loops has increased. In addition, the numbers of both fixed-point and limit-cycle attractors have decreased as the number of positive feedback loops increased. This implies that the average size of each basin has become larger.

FIGURE 6.

FIGURE 6

Open in a new tab

The dynamics of networks with multiple-positive-feedback and multiple-negative-feedback loops.

Converging dynamics of biological networks

The simulation results have shown that converging dynamics of RBNs is highly dependent on the coupled positive and negative feedback loops in the networks. The proportion of the fixed-point basins was positively correlated to the ratio of multiple coupled positive feedback loops in the networks. On the other hand, the proportion of the limit-cycle basins was positively correlated to the ratio of multiple coupled negative feedback loops. Some previous experimental results partially support our hypothesis. For instance, the network regulating flower morphogenesis in Arabidopsis has coupled six positive and two negative feedback loops and the essential states converge to either five fixed-point attractors corresponding to well-known flower types or one fixed-point attractor representing an unknown type (15). In the regulatory network on cell differentiation, seven positive and two negative feedback loops were found coupled where only a small number of states representing cell division converge to limit cycles while many other states converge to fixed-point states representing quiescence, terminal differentiation, or apoptosis (32). The core circadian regulatory network of animals consists of two negative feedback loops coupled with one positive feedback loop and produces cyclic dynamics despite state changes caused by external stimulus (35). We note, however, that these examples only partially support the proposed relationship between converging dynamics and the coupled feedback loops since it is very difficult to check the whole converging dynamics in real biological networks.

CONCLUSIONS

In this article, we have investigated the relationship between positive/negative feedback loops and fixed-point/limit-cycle attractors in RBNs through computational simulations. We found that the presented results are consistent with the various phenomena observed in biological systems—cellular circuits with positive feedback loops induce multistationary behavior and those with negative feedback loops induce oscillations. In particular, we have elucidated the general trend of the relationship in the networks with multiple coupled feedback loops. We have discovered that the higher the ratio of multiple coupled positive (negative) feedback loops, the higher the proportion of the fixed-point (limit-cycle, respectively) basins. It turns out that such relationships hold regardless of the connectivity and update rules. This implies that we may predict the converging dynamics of biological systems to a certain extent by examining the coupled feedback loops in the underlying biochemical networks. This study can also be useful for synthetic biological applications when we design or engineer regulatory circuits with particular converging dynamics.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Acknowledgments

This work was supported from the Korea Ministry of Science and Technology through the Korean Systems Biology Research grant (No. M10503010001-05N030100111) and the 21C Frontier Microbial Genomics and Application Center Program (grant No. MG05-0204-3-0), and in part from the Korea Ministry of Commerce, Industry & Energy through the Korea Bio-Hub Program (grant No. 2005-B0000002). K.-H. Cho was supported by the second stage Brain Korea 21 Project in 2006.

APPENDIX A: A CIRCUIT WITH TWO NEGATIVE FEEDBACK LOOPS

When the number of input variables is two, we can consider the following 24 Boolean functions: Inline graphic and Inline graphic. Among these, let us exclude 0, 1, xb, Inline graphic, xc, and Inline graphic as they do not depend on both variables. In addition, we exclude Inline graphic and Inline graphic, since they are not realistic; the relationship of input variables to a target is neither positive nor negative. Thus, the remaining eight formulae are Inline graphic or Inline graphic. Let us consider one of the formulae, Inline graphic. In case there are two negative feedback loops, Inline graphic and xc(t + 1) = xc(t) = xa(t) must be satisfied. So, we get the following condition: Inline graphic. It turns out that there is no specification for a state vector x to be a fixed-point attractor in this case. For the other formulae, we also arrive at the same conclusion. In summary, there cannot be any fixed-point attractor if the circuit in Fig. 2 B consists of two negative feedback loops.

APPENDIX B: A CIRCUIT WITH FOUR NEGATIVE FEEDBACK LOOPS

In this case, there are two paths from xa to xb, xa −→ xd −→ xb and xa −→ xf −→ xb and also two paths from xb to xa, xb −→ xc −→ xa and xb −→ xe −→ xa. There are four feedback loops from these combinations. When all the feedback loops are negative, the intermediate variables in the same directional paths should have the same information but those in the different directional paths should have different information. In other words, xc(t) = xe(t) ≠ xd(t) = xf(t) should be satisfied. This implies that the circuit is equivalent to the single negative feedback circuit in Fig. 2 A, and thereby there is no fixed-point state in the circuit.

APPENDIX C: A CIRCUIT WITH ONLY NEGATIVE FEEDBACK LOOPS

As shown in the simulation result, there is no fixed-point attractor in the network with only negative feedback loops and based on the AND function. Let us prove this. Given a network with N variables, x1, x2, … , xN, we assume that every variable in the network is involved in one or more feedback loops. For any xi, let us consider a feedback loop including xi. As it is a negative feedback loop, Inline graphic where Li is the number of variables consisting of the feedback loop along with xi and yj(t)(j = 1, 2, … , Li) is xk(t) or Inline graphic for some k ≠ i. If the specification of a state vector x is a fixed-point attractor, a state vector x = [0 0 … 0] should be the only candidate for the fixed-point attractor. Thus, for every xi, there is yj such that yj(t) = xi′(t) from Inline graphic. We note that there is a path from xi′ to xi with a positive relationship. So, beginning from x1, we can find x1′ that satisfies the above positive relationship. Then, we repeat this process. By tracing the path, we can always find a cycle due to the finite number of variables. Each relationship is positive and therefore the cycle forms a positive feedback loop, which contradicts the assumption. Hence, if a network based on the AND function has only negative feedback loops, there is no fixed-point state.

References

  • 1.Kauffman, S. A. 1969. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 22:437–467. [DOI] [PubMed] [Google Scholar]
  • 2.Kauffman, S. A. 1993. The Origins of Order: Self-Organization and Selection in Evolution. Oxford University Press, New York.
  • 3.Stern, M. D. 1999. Emergence of homeostasis and “noise imprinting” in an evolution model. Proc. Natl. Acad. Sci. USA. 96:10746–10751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Bhattacharjya, A., and S. Liang. 1996. Power-law distributions in some random Boolean networks. Phys. Rev. Lett. 77:1644–1647. [DOI] [PubMed] [Google Scholar]
  • 5.Derrida, B., and Y. Pomeau. 1986. Random networks of automata: a simple annealed approximation. Europhys. Lett. 1:45–49. [Google Scholar]
  • 6.Aldana, M., S. Coppersmith, and L. P. Kadanoff. 2003. Boolean dynamics with random couplings. In Perspectives and Problems in Nonlinear Science, E. Kaplan, J. E. Marsden, and K. R. Sreenivasan, editors. Springer Applied Mathematical Sciences Series, Springer, New York.
  • 7.Harris, S. E., B. K. Sawhill, A. Wuensche, and S. Kauffman. 2002. A model of transcriptional regulatory networks based on biases in the observed regulation rules. Complexity. 7:23–40. [Google Scholar]
  • 8.Kauffman, S., C. Peterson, B. Samuelsson, and C. Troein. 2003. Random Boolean network models and the yeast transcriptional network. Proc. Natl. Acad. Sci. USA. 100:14796–14799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Kauffman, S., C. Peterson, B. Samuelsson, and C. Troein. 2004. Genetic networks with canalyzing Boolean rules are always stable. Proc. Natl. Acad. Sci. USA. 101:17102–17107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Szallasi, Z., and S. Liang. 1998. Modeling the normal and neoplastic cell cycle with “realistic Boolean genetic networks”: their application for understanding carcinogenesis and assessing therapeutic strategies. Proc. Pacif. Symp. Biocomput. 3:66–76. [PubMed] [Google Scholar]
  • 11.Thomas, R., D. Thieffry, and M. Kaufman. 1995. Dynamical behavior of biological regulatory networks. I. Biological role of feedback loops and practical use of the concept of the loop-characteristic state. Bull. Math. Biol. 57:247–276. [DOI] [PubMed] [Google Scholar]
  • 12.Plahte, E., T. Mestl, and S. W. Omholt. 1995. Feedback loops, stability and multi-stationarity in dynamical systems. J. Biol. Sys. 3:409–413. [Google Scholar]
  • 13.Gouzé, J. L. 1998. Positive and negative circuits in dynamical systems. J. Biol. Sys. 6:11–15. [Google Scholar]
  • 14.Snoussi, E. H. 1998. Necessary conditions for multistationarity and stable periodicity. J. Biol. Sys. 6:3–9. [Google Scholar]
  • 15.Mendoza, L., D. Thieffry, and E. R. Alvarez-Buylla. 1999. Genetic control of flower morphogenesis in Arabidopsis thaliana: a logical analysis. Bioinformatics. 15:593–606. [DOI] [PubMed] [Google Scholar]
  • 16.Martinet-Edelist, C. 2004. Kinetic logic: a tool for describing the dynamics of infectious disease behavior. J. Cell. Mol. Med. 8:269–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Smits, W. K., O. P. Kuipers, and J. W. Veening. 2006. Phenotypic variation in bacteria: the role of feedback regulation. Nat. Rev. Microbiol. 4:259–271. [DOI] [PubMed] [Google Scholar]
  • 18.Ferrell, J. E., Jr., and E. M. Machleder. 1998. The biochemical basis of an all-or-none cell fate switch in Xenopus oocytes. Science. 280:895–898. [DOI] [PubMed] [Google Scholar]
  • 19.Bhalla, U. S., P. T. Ram, and R. Iyengar. 2002. Map kinase phosphatase as a locus of flexibility in a mitogen-activated protein kinase signaling network. Science. 297:1018–1023. [DOI] [PubMed] [Google Scholar]
  • 20.Sha, W., J. Moore, K. Chen, A. D. Lassaletta, C. S. Yi, J. J. Tyson, and J. C. Sible. 2003. Hysteresis drives cell-cycle transitions in Xenopus laevis egg extracts. Proc. Natl. Acad. Sci. USA. 100:975–980. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Pomerening, J. R., E. D. Sontag, and J. E. Ferrell, Jr. 2003. Building a cell cycle oscillator: hysteresis and bistability in the activation of cdc2. Nat. Cell Biol. 5:346–351. [DOI] [PubMed] [Google Scholar]
  • 22.Hirata, H., S. Yoshiura, T. Ohtsuka, Y. Bessho, T. Harada, K. Yoshikawa, and R. Kageyama. 2002. Oscillatory expression of the Bhlh factor hes1 regulated by a negative feedback loop. Science. 298:840–843. [DOI] [PubMed] [Google Scholar]
  • 23.King, R. W., R. J. Deshaies, J. M. Peters, and M. W. Kirschner. 1996. How proteolysis drives the cell cycle. Science. 274:1652–1659. [DOI] [PubMed] [Google Scholar]
  • 24.Venkatesh, K. V., S. Bhartiya, and A. Ruhela. 2004. Multiple feedback loops are key to a robust dynamic performance of tryptophan regulation in Escherichia coli. FEBS Lett. 563:234–240. [DOI] [PubMed] [Google Scholar]
  • 25.Brandman, O., J. E. Ferrell, Jr., R. Li, and T. Meyer. 2005. Interlinked fast and slow positive feedback loops drive reliable cell decisions. Science. 310:496–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Ozbudak, E. M., A. Becskei, and A. van Oudenaarden. 2005. A system of counteracting feedback loops regulates cdc42p activity during spontaneous cell polarization. Dev. Cell. 9:565–571. [DOI] [PubMed] [Google Scholar]
  • 27.Weiner, O. D., P. O. Neilsen, G. D. Prestwich, M. W. Kirschner, L. C. Cantley, and H. R. Bourne. 2002. A Ptdinsp(3)- and Rho GTPase-mediated positive feedback loop regulates neutrophil polarity. Nat. Cell Biol. 4:509–513. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Keizer, J., Y. X. Li, S. Stojilkovic, and J. Rinzel. 1995. Insp3-induced Ca2+ excitability of the endoplasmic reticulum. Mol. Biol. Cell. 6:945–951. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Li, F., T. Long, Y. Lu, Q. Ouyang, and C. Tang. 2004. The yeast cell-cycle network is robustly designed. Proc. Natl. Acad. Sci. USA. 101:4781–4786. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Espinosa-Soto, C., P. Padilla-Longoria, and E. R. Alvarez-Buylla. 2004. A gene regulatory network model for cell-fate determination during Arabidopsis thaliana flower development that is robust and recovers experimental gene expression profiles. Plant Cell. 16:2923–2939. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Albert, R., and H. G. Othmer. 2003. The topology of the regulatory interactions predicts the expression pattern of the segment polarity genes in Drosophila melanogaster. J. Theor. Biol. 223:1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Huang, S., and D. E. Ingber. 2000. Shape-dependent control of cell growth, differentiation, and apoptosis: switching between attractors in cell regulatory networks. Exp. Cell Res. 261:91–103. [DOI] [PubMed] [Google Scholar]
  • 33.Huang, S., G. Eichler, Y. Bar-Yam, and D. E. Ingber. 2005. Cell fates as high-dimensional attractor states of a complex gene regulatory network. Phys. Rev. Lett. 94:128701. [DOI] [PubMed] [Google Scholar]
  • 34.Derrida, B., and G. Weisbuch. 1986. Evolution of overlaps between configurations in random Boolean networks. J. Phys. (Fr.). 47:1297–1303. [Google Scholar]
  • 35.Bell-Pedersen, D., V. M. Cassone, D. J. Earnest, S. S. Golden, P. E. Hardin, T. L. Thomas, and M. J. Zoran. 2005. Circadian rhythms from multiple oscillators: lessons from diverse organisms. Nature Rev. Genet. 6:544–556. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES