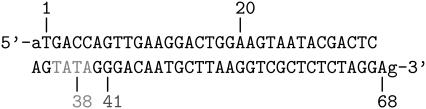Breathing Dynamics in Heteropolymer DNA

Abstract

While the statistical mechanical description of DNA has a long tradition, renewed interest in DNA melting from a physics perspective is nourished by measurements of the fluctuation dynamics of local denaturation bubbles by single molecule spectroscopy. The dynamical opening of DNA bubbles (DNA breathing) is supposedly crucial for biological functioning during, for instance, transcription initiation and DNA's interaction with selectively single-stranded DNA binding proteins. Motivated by this, we consider the bubble breathing dynamics in a heteropolymer DNA based on a (2+1)-variable master equation and complementary stochastic Gillespie simulations, providing the bubble size and the position of the bubble along the sequence as a function of time. We utilize new experimental data that independently obtain stacking and hydrogen bonding contributions to DNA stability. We calculate the spectrum of relaxation times and the experimentally measurable autocorrelation function of a fluorophore-quencher tagged basepair, and demonstrate good agreement with fluorescence correlation experiments. A significant dependence of opening probability and waiting time between bubble events on the local DNA sequence is revealed and quantified for a promoter sequence of the T7 phage. The strong dependence on sequence, temperature and salt concentration for the breathing dynamics of DNA found here points at a good potential for nanosensing applications by utilizing short fluorophore-quencher dressed DNA constructs.

INTRODUCTION

Textbook pictures of double-stranded DNA molecules may lead one to believe that the Watson-Crick double-helix represents a static geometry. As a matter of fact, even at room temperature DNA opens up intermittent flexible single-stranded domains, so-called DNA-bubbles. Their size typically ranges from a few broken basepairs (bps), increasing to some 200 broken bps closer to the melting temperature T_m (1–4). The stability of DNA is characterized by the two free energies ε_hb for breaking the Watson-Crick hydrogen bonds between complementary AT and GC bps, and the 10 independent stacking free energies ε_st for disrupting the interactions between neighboring bps; at 100 mM NaCl concentration and temperature 37°C, it was found that ε_hb = 1.0 k_BT for a single AT and 0.2 k_BT for a single GC-bond (at T = 37°C, k_BT = 0.62 kcal/mol). Under the same conditions the weakest (strongest) stacking interaction was found to be the TA/AT (GC/CG) with free energies ε_st = −0.9 k_BT (–4.1 k_BT) (5). In addition, the initiation of a bubble in an unperturbed DNA molecule, creating two interfaces between single-stranded bubble and vicinal double-helix at the zipper forks, is associated with an activation factor 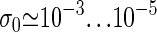(2,3,6,7) related to the ring-factor ξ used in Protozanova et al. (5) and Krueger et al. (8) and below. That is, despite the rather low free energy for breaking the bps, the high bubble nucleation barrier guarantees that below T_m bubbles are rare and well separated, particularly under physiological conditions. However, once a bubble opens, since typical free energies are of the order k_BT localized denaturation zones can open up, predominantly in AT-rich regions (1–3). These DNA-bubbles fluctuate in size (i.e., DNA-breathing). It has been demonstrated recently by fluorescence correlation methods that DNA-breathing can be probed on the single molecule level, revealing a multistate kinetics of stepwise (un)zipping of bps with a bubble lifetime ranging up to a few milliseconds (9).

Theoretically, based on the statistical mechanical Poland-Scheraga model (2), DNA-breathing has been described in homopolymer DNA in terms of a continuous Fokker-Planck equation (10), and through a stochastic Gillespie scheme (11). A discrete master equation (ME) approach was developed in Ambjörnsson and Metzler (12,13), including the coupled (un)binding dynamics of selectively single-stranded DNA binding proteins. Continuous and discrete approaches are compared and studied in Bicout and Kats (14). Heteropolymer DNA-breathing was considered in a reduced one-variable approach using a random energy model (15).

Here, we develop a full (2+1)-variable approach to breathing in heteropolymer DNA that allows us to study the sequence dependence of the dynamics, through the initiation and the stochastic motion of the two forks of an open DNA bubble. Two approaches are used: the stochastic motion is obtained by generating stochastic (Gillespie) time series from which equilibrium distribution as well as autocorrelation functions are obtained. We also use the corresponding master equation to calculate the complementary ensemble-averages; excellent agreement is found between time-averages and ensemble-averages. Novelties in our study include: 1), we study the full dynamics (2+1 variable problem) of a heteropolymer region of arbitrary (not just random) sequence; 2), we compare our results to the fluorescence correlation spectroscopy (FCS) experiments in Altan-Bonnet et al. (9) using the directly measured DNA parameters in Krueger et al. (8) (see below); and 3), recently, for the first time, the (two) hydrogen bond energies, and (ten) stacking interactions characterizing DNA stability within the Poland-Scheraga model were separately determined (5,8); these stability parameters are utilized in our study. Among the consequences of these new results compared to previously used parameters (6) are the more pronounced sequence dependence and the fact that Watson-Crick and stacking interactions can be completely separated as required when studying internal bubble dynamics (a bubble involving m broken Watson-Crick bonds and m+1 broken stacking interactions).

Based on this new approach, we study the question of transcription initiation at the TATA motif of the biological sequence in the bacteriophage T7 promoter sequence. Using the newly obtained stacking parameters from Krueger et al. (8), we demonstrate the delicate dependence of both the equilibrium opening probability as well as the breathing dynamics on the sequence dependence of the stacking. While in our model the opening times of bubbles only marginally depend on their position along the sequence, the recurrence frequency of bubble events is much more sensitive to the position. The latter might therefore be a clue toward the understanding of transcription initiation.

This article is organized as follows: In General Model and Transfer Rates, we describe the DNA bubble dynamics in terms of the relevant transfer coefficients. In Dynamic Approaches to DNA Breathing, Gillespie Approach, a stochastic scheme based on these transfer coefficients in terms of the Gillespie algorithm is introduced. In Dynamic Approaches to DNA Breathing, Tagged BP Survival and Waiting Time Densities, a complementary master equation scheme is described. In Results, we apply our two complementary formalisms to 1), the experimental constructs in Altan-Bonnet et al. (9); 2), The T7 phage promoter sequence; and 3), we show a strong dependence on sequence, temperature, and salt concentration and demonstrate the good potential for nanosensing applications.

Technical details necessary for the introduction of our model appear in a separate publication (16).

GENERAL MODEL AND TRANSFER RATES

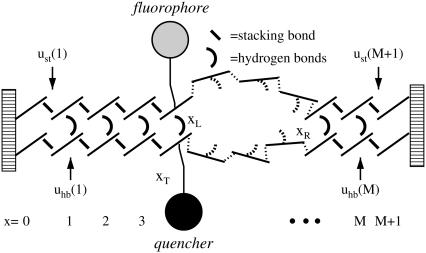
With typical experimental setups (9) in mind, we consider a segment of double-stranded DNA with M internal bps that are clamped at both ends, i.e., the bps x = 0 and x = M + 1 are always closed (Fig. 1). The heteropolymer character of the problem enters via the position-dependence of the statistical weights u_hb(x) = exp {ε_hb(x)/(k_BT)} for breaking the hydrogen bonds of the bp at position x, and u_st(x) = exp {ε_st(x)/(k_BT)} for disrupting the stacking interactions between bps x − 1 and x; ε_st(x) and ε_hb(x) are the corresponding free energies, which in general have energetic as well as entropic contributions. Due to the high free energy barrier for bubble initiation (ξ ≪ 1, see below), opening and merging of multiple bubbles are rare events, such that a one-bubble description is appropriate (13). The positions x_L and x_R of the zipper forks correspond, respectively, to the right- and leftmost closed bp of the bubble; these are stochastic variables whose time evolution characterizes the bubble dynamics. Note that writing the Boltzmann factors for the free energies as exp {ΔG/(k_BT)}, a positive ΔG denotes an unstable bond.

FIGURE 1.

Clamped DNA domain with internal bps x = 1 to M, and tag position x_T. The DNA sequence enters through the statistical weights u_st(x) and u_hb(x) for disrupting stacking and hydrogen bonds respectively. The bubble breathing process consists of the initiation of a bubble and the subsequent motion of the forks at positions x_L and x_R.

In terms of x_L and bubble size m = x_R − x_L − 1, the bubble partition factor is (m ≥ 1)

(1)

completed by Here, ξ′ = 2^cξ, where ξ ≈ 10⁻³ is the ring factor for bubble initiation from Krueger et al. (8). For a homopolymer ξ is related to the cooperativity parameter σ₀ ≈ 10⁻⁵ (2,6) by σ₀ = ξ exp {ε_st/(k_BT)} (8). For the entropy loss on forming a closed polymer loop we assign the factor (1 + m)^−c (6,17) and take c = 1.76 for the critical exponent (18). Note that a bubble with m open bps needs breaking of m hydrogen bonds and m+1 stacking interactions (see Eq. 1). The equilibrium probability for finding a bubble with a given x_L and m is

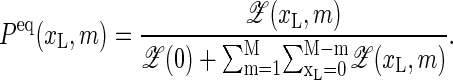(2)

Below we impose the detailed balance condition when introducing the rates to guarantee that P_eq(x_L, m) is indeed reached for long times.

Let us proceed by introducing the transfer (rate) coefficients for the bubble dynamics. For the left zipper fork we define 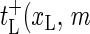) as the transfer coefficient for the process x_L → x_L + 1, corresponding to bubble size decrease, and 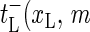) as the transfer coefficient for x_L → x_L − 1 (bubble size increase). For the right zipper fork we similarly introduce 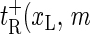) for x_R → x_R + 1 (bubble size increase) and 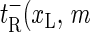) for x_R → x_R − 1 (bubble size decrease). In addition for the transition m = 0 → m = 1, i.e., for the initial bubble opening process occurring at position x_L, we introduce 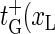), and for the bubble closing process m = 1 → m = 0 we employ 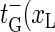). Note that 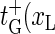) and 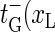) correspond to closing or opening of the bubble at position x = x_L + 1. Due to the clamping we require that x_L ≥ 0 and x_R ≤ M + 1, and we therefore introduce reflecting conditions

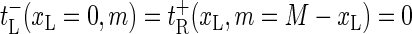(3)

(also, 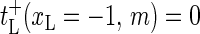and 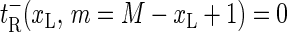for m = 2, …, M + 1 for completeness).

Let us consider explicit forms for the transfer coefficients. For bubble size decrease we take

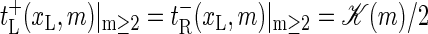(4)

for the left fork and right forks, respectively. We above defined the m-dependent rate coefficient

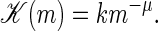(5)

As in previous studies, this expression imposes the hook exponent μ, related to the fact that during the zipping process not only the bp at the zipper fork is moved, but also part of the vicinal single-strand is dragged or pushed along (13,19,20). One would expect that the hook exponent is only relevant for larger bubbles, and we put μ = 0 in the remainder of this work, mainly focusing on T well below T_m, where the bubbles sizes are small. The rate k characterizes a single bp zipping. Its independence of x corresponds to the view that bp closure requires the diffusional encounter of the two bases and subsequent bond formation; as sterically AT and GC bps are very similar, k should not significantly vary with bp stacking. The value k is the only adjustable parameter of our model, and has to be determined from experiment or future MD simulations. The factor 1/2 is introduced for consistency with previous approaches (12,13). We note that, in principle, an x-dependence of k can easily be introduced in our approach by choosing different powers of the statistical weights entering the rate coefficients such that they still fulfill detailed balance.

Bubble size increase is controlled by

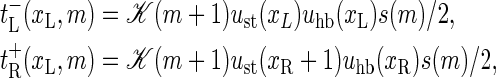(6)

for m ≥ 1, where

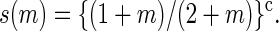(7)

For m ≥ 1 we thus take the rate coefficients for bubble increase proportional to the Arrhenius factor u_stu_hb = exp {(ε_hb + ε_st)/(k_BT)} multiplied by the loop correction s(m). Note that an unzipping event on average involves the motion of one more open basepair compared to a zipping event, and the transfer coefficients above are therefore proportional to 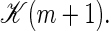Finally, bubble initiation and annihilation from and to the zero-bubble ground state, m = 0 ↔ 1, occur with rates

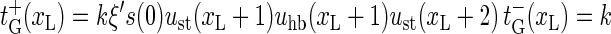(8)

with the bubble initiation factor ξ′ included in the expression for 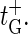Note that 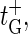in contrast to the opening rates for m ≥ 1, is proportional to an Arrhenius-factor involving two units of stacking free energy. The annihilation rate 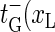) is twice the zipping rate of a single fork, since the last open bp can close from either the left or right. The t-rates, together with the boundary conditions, fully determine the bubble dynamics.

We see that the rates 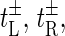and 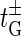are chosen such that they fulfill the detailed balance conditions:

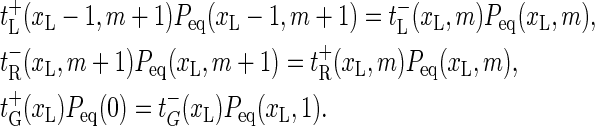(9)

These conditions guarantee relaxation toward the equilibrium distribution P^eq(x_L, m) (see Eq. 2). In the next two sections we use the above explicit expressions for the transfer coefficients and describe the DNA breathing dynamics pursuing two complementary approaches: the stochastic Gillespie scheme (Dynamic Approaches to DNA Breathing, Gillespie Approach) and the master equation (Dynamic Approaches to DNA Breathing, Tagged BP Survival and Waiting Time Densities).

DYNAMIC APPROACHES TO DNA-BREATHING

Gillespie approach

In this section we use the Gillespie algorithm together with the explicit expressions for the transfer coefficients introduced in the previous section to generate a sequence-specific stochastic time series of breathing bubbles. In particular, we show how the motion of a tagged bp is obtained.

To denote a bubble state of m broken bps at position x_L we define the occupation number b(x_L, m) with the properties b(x_L, m) = 1 if the particular state {x_L, m} is occupied and b(x_L, m) = 0 for unoccupied states. For the completely zipped state m = 0 there is no dependence on x_L, and we introduce the occupation number b(0). The stochastic DNA breathing then corresponds to the nearest-neighbor jump processes in the lattice of permitted states (16). In the Gillespie scheme, each jump away from the state {x_L, m} (i.e., from the state with b(x_L, m) = 1) occurs at a random time τ, and in a random direction to one of the nearest-neighbor states. This stochastic process is governed by the reaction probability density function (11,21,22)

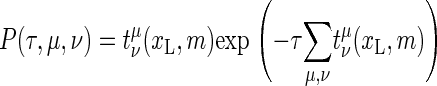(10)

More explicitly, for a given state (x_L, m) the joint probability density (10) defines after what waiting time τ after the previous random step the next step occurs, and in which reaction pathway, ν ∈ {G, L, R}, μ ∈ {±}. In the present case, ν and μ denote x-dependent zipping or unzipping of a bp at the left or right zipper fork. A simulation run produces a time series of occupied states {x_L, m} and how long a time τ = τ_j (j = 1, …, N, where N is the number of steps in the simulation) this particular state is occupied. This waiting time τ, in particular, according to Eq. 10 follows a Poisson distribution (23). Note that the waiting times governed by Eq. 10 vary widely, as the reaction rates occur in the exponential (in particular, the bubble initiation with the ξ-factor has a long characteristic timescale). The fact that the Gillespie scheme uses the weighted reaction timescale instead of fixed simulation time steps makes this algorithm very efficient.

Tagged bp survival and waiting time densities

Motivated by the experimental setup in Altan-Bonnet et al. (9) we study the motion of a tagged bp at x = x_T (see Fig. 1). In the fluorescence correlation experiment, fluorescence occurs if the bps in a Δ-neighborhood of the fluorophore position x_T are open (9). Measured fluorescence time series thus correspond to the stochastic variable I(t), with the properties I(t) = 1 if at least all bps in (x_T − Δ, x_T + Δ) are open, and I(t) = 0 otherwise. Thus, if I = 1, we are in the phase space region defined by

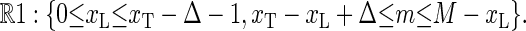(11)

Conversely, I = 0 corresponds to the complement R0 of R1. The stochastic variable I(t) is then obtained by summing the Gillespie occupation number b(x_L, m) (b(x_L, m) takes only values 0 or 1) over region R1, i.e.,

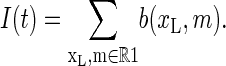(12)

From the time series for I(t) one can, for instance, calculate the waiting time distribution ψ(τ) of times spent in the I = 0 state, as well as the survival time distribution φ(τ) of times in the I = 1 state. Explicit examples for ψ(τ) and φ(τ) are shown in Results.

The probability that the tagged bp is open becomes

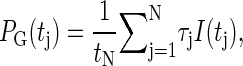(13)

where 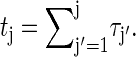For long times the explicit construction of the Gillespie scheme together with the detailed balance conditions guarantee that P_G(t_j) tends to the equilibrium probability, i.e., that 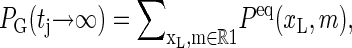where P^eq(x_L, m) is given in Eq. 2.

Tagged basepair autocorrelation function

The autocorrelation function for a tagged bp is obtained through

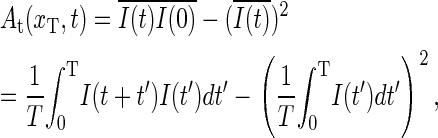(14)

which for long sampling times T converges to the ensemble average, Eq. 18, from the master equation (introduced in the next section). The function A_t(x_T, t) corresponds to the quantity obtained in the fluorescence correlation experiment of Altan-Bonnet et al. (9).

Master equation formulation

Complementary to the stochastic simulations of DNA-breathing detailed in the preceding section we here introduce a master equation (ME) for the joint probability distribution P(t) = P(x_L, m, t;x′_L, m′, 0) that at time t the system is in state {x_L, m} and that it was in state {x′_L, m′} at t = 0. The ME, which is equivalent (in the sense that it produces the same averaged quantities) to the Gillespie scheme, can be formally written as

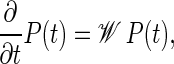(15)

where the explicit form of the matrix 𝒲 is given in terms of the rate coefficients from the previous section in Ambjörnsson et al. (16). A standard approach to the master equation is the spectral decomposition (24,25)

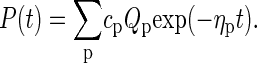(16)

The coefficients c_p are obtained from the initial condition. Inserting Eq. 16 into Eq. 15 produces the eigenvalue equation

(17)

From the eigenvalues η_p and eigenvectors Q_p of Eq. 17, any quantity of interest can be constructed.

Dynamic quantities for a tagged bp

The waiting time density ψ(t) and the survival time density φ(t), as obtained in a Gillespie scheme, correspond to the first passage problem to start from an initial state with I = 1 (I = 0) and passing to I = 0 (I = 1). It is discussed in detail in Ambjörnsson et al. (16) how these quantities can be obtained from the ME, Eq. 15.

The equilibrium autocorrelation function

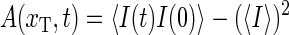(18)

is a measure for the relaxation dynamics of the tagged bp. This can be seen from the identity

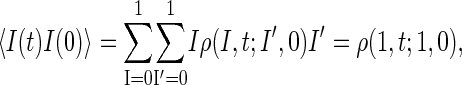(19)

where ρ(1, t;1, 0) is the survival probability density that I(t) = 1 and that I(0) = 1 initially. Using the fact that ρ(1, t;1, 0) is obtained by summing P(x_L, m, t;x′_L, m′, 0) exclusively over region R1, we obtain

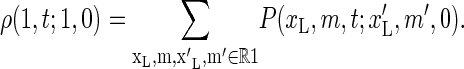(20)

Combining this result with Eq. 19, the spectral decomposition (16), and assuming that we initially are at equilibrium, 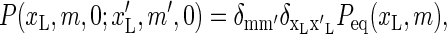the autocorrelation function (Eq. 18) can be rewritten as

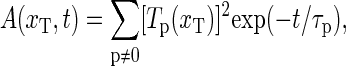(21)

with relaxation times τ_p = 1/η_p, and where

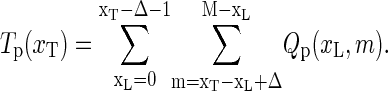(22)

For long times, i.e., when the time average is long enough, A(x_T, t) agrees with A_t(x_T, t) given in Eq. 14 as will be illustrated in the next section. We can rewrite the correlation function according to the spectral decomposition

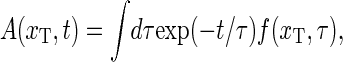(23)

where we introduced the weighted spectral density

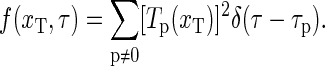(24)

This relaxation time spectrum directly provides the spectral content of the relaxation behavior of the DNA-bubble, and sometimes a better (but equivalent) visualization of the system than the autocorrelation function.

RESULTS

In this section we apply our two complementary formalisms to study the behavior of 1), the designed DNA constructs used in the experiments of Altan-Bonnet et al. (9); and 2), the T7 phage promoter sequence.

Comparison to experimental results

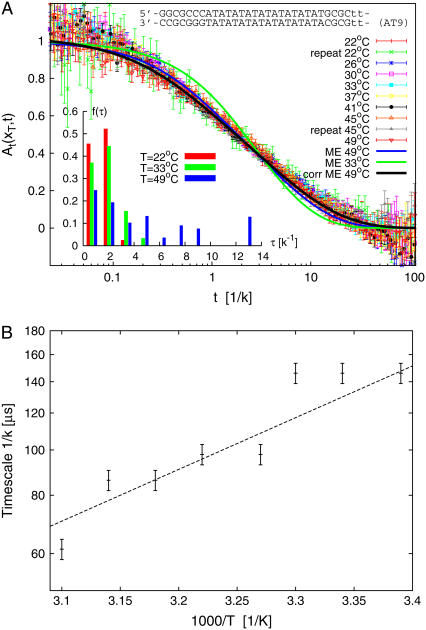
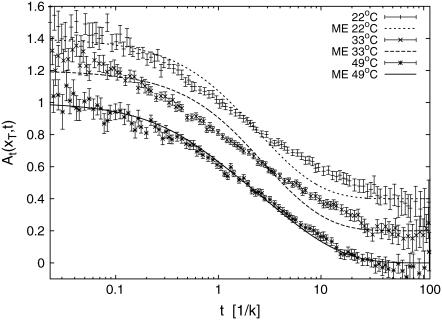
In Fig. 2 the autocorrelation functions A_t(x_T, t) for the sequence AT9 from Altan-Bonnet et al. (9) are shown for various temperatures T. The data were scaled by k such that the curves coincide where A(t) = 1/2. The strong scatter at short times is mainly ascribed to quantum transitions in the fluorophore (9,26). The lower graph shows the temperature dependence of the characteristic zipping time, 1/k. Individual autocorrelations for three temperatures are compared in Fig. 3.

FIGURE 2.

(Top) Autocorrelation function A_t(x_T, t) at various temperatures T measured for the sequence AT9 from Altan-Bonnet et al. (9) at 100 mM NaCl. The sequence is indicated in the figure, where the four lower-case t characters symbolize a small bulge loop. The full lines show the results from the master equation based on the DNA parameters from Krueger et al. (8). (Inset) Relaxation time spectrum f(τ) = f(x_T, τ), showing broadening with increasing temperature. (Bottom) Characteristic zipping time 1/k as a function of temperature in an Arrhenius plot. The line shows a least-squares fit to an Arrhenius law τ ∝ exp(A/T) with A = 2.6 × 10³ K.

FIGURE 3.

Individual autocorrelation functions A_t(x_T, t) for three different temperatures (22°C, 33°C, 49°C) spanning the T-range probed in the fluorescence experiment. While for the highest temperature, the match between data and theory is very good, deviations occur at lower temperatures. Reasons for these deviations are discussed in the text. Note that the data for 33°C are shifted vertically by 0.2, and those for 22°C by 0.4.

In the combined autocorrelation plot, Fig. 2, the black line shows the predicted behavior of A(x_T, t), calculated by numerical solution of the eigenvalue Eq. 17 by help of Eq. 21. Stability parameters from Krueger et al. (8) for T = 49°C and 100 mM NaCl concentration were used. As in the experiment we assumed that fluorophore and quencher attach to bps x_T = 17 and x_T + 1, and that both are required open to produce a fluorescence signal (the outermost GC-pairs in the sequence given in Fig. 2 were taken as clamped, i.e., labeled as x = 0 and x = M + 1). From the scaling plot, we calibrate the zipping rate as k = 7.1 × 10⁴/s for T = 49° in good agreement with the findings from Altan-Bonnet et al. (9). The calculated behavior reproduces the data within the error bars. The green curve corresponds to the ME result for T = 33°C, showing more pronounced deviations from experimental data. Notice that for lower temperatures the relaxation time distribution f(x_T, τ) becomes narrower (Fig. 2 inset). Thus, our model predicts that the dynamics for smaller temperatures involve fewer modes, which is in contrast to the experimental data that have also a broad, multimodal behavior for low temperatures.

The individual behavior of the autocorrelation is dissected in Fig. 3 for three temperatures spanning the full T-range probed in the fluorescence experiments. Note the good quality of the match between experimental data and model prediction for the highest temperature (49°C). This temperature is already close to the denaturation temperature of the bubble domain of the AT9 construct (the contribution of the longest relaxation time in the rather broad spectrum of relaxation times is considerably larger than the three previous ones). The tendency of overestimation of the slope in the autocorrelation function by our model at lower temperatures is obvious for curves at 22°C and 33°C, while the experimental slope remains almost constant over this T-range.

We expect three effects to contribute to the deviations by broadening the relaxation time spectrum, i.e., lowering the free energy of the system:

1. In the present fluorescence correlation spectroscopy experiments, two contributions superimpose to produce the fluorescence signal (26): The diffusional motion of the molecule carrying the fluorophore in and out of the confocal volume, and the actual breathing dynamics. Without the breathing, the autocorrelation function takes the form A(t) ∼ 1/(1 + t/τ_D) (for a narrow beam waist), where τ_D = w²/(4D) ≈ 150 ms, with w being the linear size of the beam waist and D is the diffusion constant of the construct. In Altan-Bonnet et al. (9) the pure diffusive contribution was eliminated by performing a separate experiments with the quencher being removed (measuring the solely diffusive contribution), and dividing out this result from the signal. However, as the quencher is removed the diffusion constant of the construct is slightly changed. To roughly account for this fact, the blue curve shown in Fig. 2 was obtained by a 3% reduction of the diffusion time τ_D. Note that the agreement of the blue line with the data is excellent. This underlines the sensitivity of the DNA-breathing single molecule data, pointing toward potential dynamic methods to calibrate both k and ΔG.

2. It is very likely that the presence of the fluorophore and quencher molecules destabilizes the DNA—despite the short stalk through which fluorophore and quencher are attached—by altering the Watson-Crick and stacking interactions. The resulting decrease of the stacking free energy therefore is expected to effect a lower free stacking energy in comparison to the undressed DNA, for which the stability data are measured and which are used in our model.

3. Finally, our present model does not take into account the entropic contributions due to the degrees of freedom of the fluorophore/quencher pair, i.e., the fact that for bigger bubbles the fluorophore/quencher pair has more freedom to diffuse around and rotate. To approximately account for this we would change the partition from 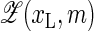to 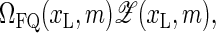where Ω_FQ(x_L, m) is the number of configurations for the fluorophore/quencher pair for a given bubble size and position. To demonstrate this effect, assume for simplicity that each bps that opens up provides one unit of entropy, ΔS_FQ, so that 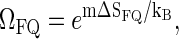i.e., effectively we increase the statistical weight u according to 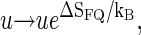leading to a shift in the melting curve toward lower temperatures (as seen in experiments, compare also Fig. 4). In reality, however, we would expect a more intricate m-dependence of the complexions Ω_FQ; for instance, it may be so that as the first bps close the tag-position opens up, a relatively large amount of fluorophore/quencher entropy is released, while further opening of bps contributes less.

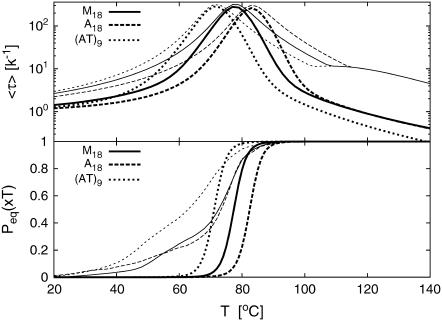
FIGURE 4.

(Top) Mean correlation time versus temperature for the three constructs in Altan-Bonnet et al. (9). The thick curves are for the mean correlation time τ_corr, whereas the thin curves are the longest relaxation time τ₁. (Bottom) Melting curves. The thin curves are experimental results. For the theoretical curves, we used parameters from Krueger et al. (8) for 100 mM NaCl concentration.

We stress once more that all three effects will broaden the relaxation time spectrum. Further control experiments will be needed to obtain more precise information on the effects caused by the presence of the fluorophore and quencher molecules.

The activation plot in Fig. 2 was obtained from the construction of the scaling plot for the blinking autocorrelation function by the relative shift of the individual curves along the logarithmic time axis. The corresponding error bars were estimated from the width of the collapsed data at the midpoint (A_t(x_T, t) = 1/2) as 20% of the absolute value. The real experimental error is likely to be higher. However, it is difficult to estimate. The activation plot indicates an Arrhenius-type behavior, which is probably due to an energetic barrier crossing when the bp-bond establishes.

We point out that we here only considered the AT9 sequence from Altan-Bonnet et al. (9), and not the other to constructs A18 and M18. The latter two constructs have four or more consecutive AT-bps, and it is known that such sequences assume the B′-conformation rather than the usual B-structure (27) for which the parameters of Krueger et al. (8) apply. In B′ DNA, the breathing dynamics is significantly altered (27). Fitting our model to the A18 and M18 constructs, we found indeed that these sequences showed more pronounced deviations from our model.

In Fig. 4, the top panel shows the mean correlation time 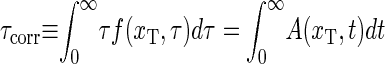(see Eqs. 21 and 24), for the three constructs of Altan-Bonnet et al. (9); these constructs all consist of 18 consecutive AT-bps with end-clamps consisting of GC-pairs. The bottom panel depicts the probability P_eq(x_T) that the bps at x_T and x_T + 1 are open, i.e., the probability to get a fluorescence signal. We notice that τ_corr has pronounced maxima at the melting transition (the point where P_eq = 1/2 in the bottom panel). This critical slowing down at the melting is indeed a characteristic signature of a phase transition (compare (14)). Notice that the experimental results (dashed lines) for P_eq(x_T) deviate from the one predicted here, indicating that the fluorophore-quencher pair indeed has a destabilizing effect on the DNA helix. Also note the different melting behaviors of the three constructs despite identical AT and GC contents predicted here as well as by experiments; this illustrates the importance of stacking interactions. Also notice that there is nice agreement between our theoretical results and experiments concerning the relative ordering of the melting temperatures: AT9 melts first, and A18 last. The horizontal line (τ_max 1D) in the top panel represents the longest relaxation time (2M + 1)²/π²k⁻¹ obtained from the homopolymer model of Ambjörnsson and Metzler (12,13) in the limit u → 1, σ₀ → 0 and c = 0 (for M = 27, length of the three constructs), thus giving a scaling consistent with the first exit of unbiased diffusion; see Ambjörnsson et al. (16).

Bacteriophage T7

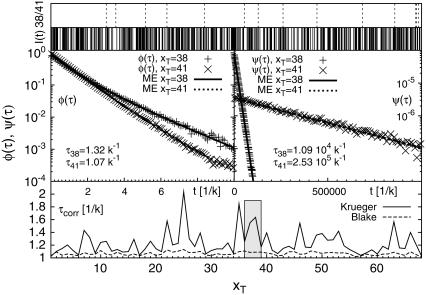
By master equation and stochastic simulation we investigate the promoter sequence of the T7 phage (a bacteriovirus). A promoter is a sequence (often containing the 4-bp-long TATA motif) marking the start of a gene, to which RNA polymerase is recruited and where transcription then initiates. Previous studies (28,29) based on the Dauxois-Peyrard-Bishop model found that the TATA motif is characterized by a particularly low stability and therefore proneness to bubble formation, although the statistical relevance of those data were under discussion (30–34). We here revisit the problem of the stability and dynamics of the TATA motif using the necessary full set of stacking interactions. The T7 promoter sequence we investigate is shown in Scheme 1; its TATA motif is marked gray (28,29). Fig. 5 shows the time series of I(t) at 37°C for the tag positions x_T = 38 in the core of TATA, and x_T = 41 at the second GC bp after TATA. Bubble events occur much more frequently in TATA (the TA/AT stacking interaction is particularly weak (8)). This is quantified by the density of waiting times ψ(τ) spent in the I(t) = 0 state, whose characteristic timescale 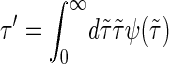is more than an order-of-magnitude longer than at x_T = 41. In contrast, we observe similar behavior for the density of opening times φ(τ) for x_T = 38 and 41, where the characteristic time is 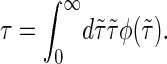The solid lines are the results from the ME (see Eq. 15) showing excellent agreement with the Gillespie results. Notice that whereas ψ(t) is characterized by a single exponential, φ(t) shows a crossover between different regimes. For long times both ψ(τ) and φ(τ) decay exponentially as they should for a finite DNA stretch. As shown in the bottom for the parameters from Krueger et al. (8), the variation of the mean correlation time 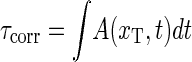obtained from the ME is small for the entire sequence, consistent with the low sensitivity to the sequence of φ(τ). However, note the even smaller variation predicted for the parameters of Blake et al. (6), indicating that the stability parameters of Krueger et al. (8) are more sequence-sensitive compared to previously used values (6). We speculate that the recurrence frequency of bubble events may be a clue in the understanding of transcription initiation: If the protein, which is supposed to bind to the specific site, senses a time-averaged energy landscape, the significantly more frequent bubble events at TATA may trigger its binding and thus trigger transcription initiation.

SCHEME 1.

FIGURE 5.

(Top) Fluorescence time series I(t) for the T7 promoter sequence, with tag position x_T = 38 (solid lines) and x_T = 41 (dashed lines). (Middle) Waiting time (ψ(τ)) and fluorescence survival time (φ(τ)) densities, in units of k. The data points (solid lines) are results from the Gillespie algorithm (master equation). (Bottom) Mean correlation time for Δ = 0. All results are for T = 37°C and 100 mM NaCl with DNA parameters from Krueger et al. (8).

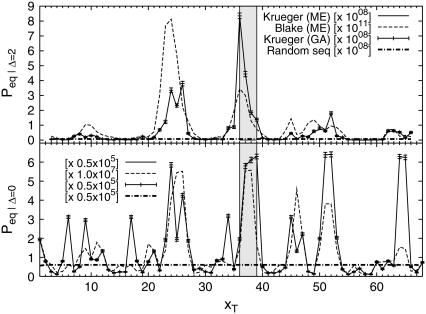
Fig. 6 shows the equilibrium probability that the bps (x_T − Δ, x_T + Δ) are open, as necessary for fluorescence to occur. We plot data obtained from the 0^th mode (an ME eigenvalue problem always has one zero eigenvalue, the corresponding eigenvalue is the equilibrium probability (24)) of the ME together with the time average from the stochastic simulation (GA), finding excellent agreement. Whereas for Δ = 0 several segments show increased tendency to denaturation, for the case Δ = 2, one major peak is observed; the data from Krueger et al. (8) coincide precisely with TATA. For comparison, the equilibrium probability obtained using DNA stability data from Blake et al. (6) have their maximum peak upstream. Analysis for various Δ-values indicate best discrimination of the TATA sequence being open for Δ = 2. Biologically, this finding is significant, as it corresponds to the probability for simultaneous opening of the whole TATA motif. For future FCS or energy transfer experiments investigating the relevance of denaturation-induced facilitation of transcription initiation, it therefore appears important to optimize the Δ-dependence for best resolution, e.g., by adjusting the linker lengths of fluorophore and quencher. In principle, this could be experimentally achieved as (assuming a circular bubble of five open bps with bp-bp distance 3.4 Å) the distance between fluorophore and quencher on bubble opening increases by 6–7 Å, the same magnitude as the Förster transfer radius.

FIGURE 6.

Probability to have at least the bps (x_T − Δ, x_T + Δ) open (as assumed to be necessary for fluorescence to occur) for different tag positions x_T, and for Δ = 0 and 2. The results from master equation and Gillespie algorithm show excellent agreement. Same parameters as in Fig. 5.

In Fig. 6 we compare the opening probabilities to the values for a random sequence, for which we chose the free energies such that the content of AT and GC bps is 50:50. Then, we define

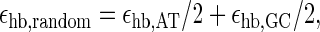(25)

for the hydrogen bonding, and

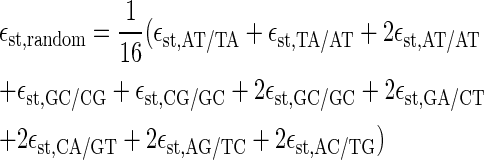(26)

for the stacking free energies. The numerical values are ε_{hb, random} = 0.4 kcal/mol and ε_{st, random} = −1.6 kcal/mol at T = 37°C and 100 mM NaCl. Inserting both into the expressions for the partition factor (1) and the rates t, the dashed lines in Fig. 6 are obtained. Thus, the peaks in the opening probabilities are distinctly significant.

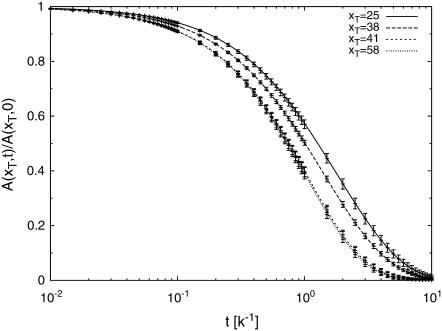
To illustrate the breathing dynamics of the T7 sequence using experimentally measurable quantities, Fig. 7 shows the autocorrelation functions for four different tag positions x_T (same parameters as above) within the promoter region. Both the Gillespie approach as well as the ME were used and compared; excellent agreement between them are found. The autocorrelation function for the tagged bp decays faster if positioned in a GC-rich region than in an AT-rich region. Comparing with Fig. 2 it should be possible to resolve the different decay times of the autocorrelation function experimentally.

FIGURE 7.

Autocorrelation function A(x_T, t) for a tagged bp for the T7 sequence. The lines are master equation results whereas the data points represent results from the Gillespie scheme. Note that the autocorrelation function is sensitive to the DNA sequence as well as the tagging position. Same parameters as in Fig. 5.

Nanosensing applications

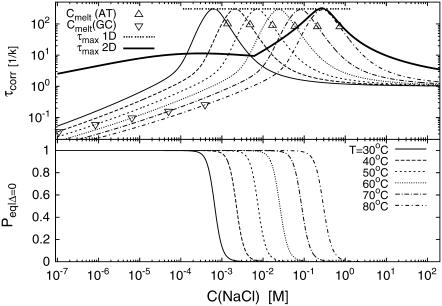
In Krueger et al. (8), the DNA Watson-Crick and stacking parameters were obtained for different NaCl concentrations, allowing us to study the effect of salt concentration on the breathing dynamics and equilibrium properties of DNA. Fig. 8 shows the dependence of the mean correlation time τ_corr and the equilibrium opening probability P_eq(x_T) for the AT9 sequence on salt concentration C and temperature T, using the same tagging position as in Comparison to Experimental Results. We point out that the mean correlation time is directly accessible in experiments. Note the logarithmic axis. The triangles denote the melting concentration of infinitely long random AT and GC stretches, respectively (from (8)). The maxima of the τ_corr curves signify the critical slowing down of the autocorrelation at the phase transition as before; note that the maxima coincide with the melting concentrations in the bottom panel. The thick line (τ_max 2D) corresponds to the longest relaxation time obtained numerically from the ME; it agrees well with τ_corr close to the maximum (equivalently for the other T), indicating that at melting there is a single (slow) relevant relaxation mode. The horizontal line (τ_max 1D) represents the analytically obtained longest relaxation time (2M + 1)²/π²k⁻¹ for a homopolymer model, compare Ambjörnsson et al. (16).

FIGURE 8.

(Top) Mean correlation time versus NaCl concentration for various temperatures T for the AT9 construct, showing a critical slowing-down at the melting concentration (compare lower panel). The triangles denote the melting concentration for infinitely long random AT and GC stretches. (Bottom) Opening probability for Δ = 0.

The predicted variation with C and T shown in Fig. 8 is significant. Thus, different solvent conditions such as temperature or salt alter the opening probability of the DNA construct, and therefore the blinking activity. For a fixed salt concentration, for instance, a higher temperature would therefore lead to more frequent, and longer blinking events, such that one could measure the effect by both recording individual blinking events and integrating the blinking signals. As shown in our analysis, the stability parameters are sufficiently sensitive to externally detect changes of these parameters. Note that a DNA construct of 30 bps roughly corresponds to a length of 10 nm. Such nanoprobes would easily fit into nanochannels, small lipid vesicles, or microdishes in gene arrays. We therefore propose to investigate in more detail the suitability of DNA-breathing constructs as nanosensors (35,36).

CONCLUSIONS

In this study we considered the bubble breathing dynamics in a heteropolymer DNA-region characterized by statistical weights u_st(x) for disrupting a stacking interaction between neighboring bps, and the weight u_hb(x) for breaking a Watson-Crick hydrogen bond (x labels different bps), as well the bubble initiation parameter (the ring-factor) ξ. For that purpose, we introduced a (2+1)-variable ME governing the time evolution of the probability distribution to find a bubble of size m with left fork position x_L at time t, as well as a complementary Gillespie scheme. The time averages from the stochastic simulation agree well with the ensemble properties derived from the master equation. We calculate the spectrum of relaxation times, and in particular the experimentally measurable autocorrelation function of a tagged bp is obtained. All parameters in our model are known from recent equilibrium measurements available for arbitrary temperature and NaCl concentration, except for the rate constant k for (un)zipping that is the only free fit parameter. We note that the value for the zipping rate obtained from the fluorescence correlation studies is significantly lower than from NMR experiments (37). The difference may stem from the higher temperatures and longer AT sequences probed in the fluorescence experiments. However, a perturbing effect of the fluorophore-quencher pair in the FCS approach cannot be excluded. For a better understanding of k, a more detailed microscopic modeling and additional experimental study are needed.

We applied recent DNA stability data from Protozanova et al. (5) and Krueger et al. (8) based on separation of hydrogen bond and stacking energies. A distinct feature of these parameters is the low stacking in a TA/AT pair of bps, translating into a pronounced instability of the TATA motif, as shown for the T7 promoter sequence. We demonstrated that the probability of simultaneous opening of a stretch of the size of 4–5 bps well discriminates the TATA motif from the other positions along the promoter sequence, reflecting its biological relevance. This demonstrates that single DNA fluorescence spectroscopy experiments can likely be used to investigate in more detail the role of the interplay between TATA-breathing, TATA-box binding proteins, and transcription initiation. Regarding the mechanism how TATA may guide this initiation we speculate that it is not primarily the bubble lifetime (much shorter than the timescale of typical conformational changes of proteins) but the recurrence frequency of bubble events that triggers the protein binding.

We note that there exists also a Langevin equation approach to DNA-breathing, the Dauxois-Peyrard-Bishop model (38,39), with seven free parameters. Values of these parameters were assigned by comparison to experimental melting curves for three different short DNA sequences obtained for rather specific solvent conditions in Campa and Giansanti (40). In particular, stacking interactions were taken to be independent of bp sequence (40). In view of the direct measurement of the stacking free energy in Krueger et al. (8) under various conditions, it would be desirable to modify the DPB model to accommodate for the full set of new stability parameters.

We expect this study to encourage further-going investigations on the theoretical understanding of DNA-breathing and the experimental possibilities to obtain detailed sequence and stability information of DNA and its interactions with binding proteins from DNA-breathing dynamics. We furthermore point out the possibility to use the results of this study for designing a small fluorophore/quencher-dressed DNA construct for nanosensing applications in nanochannels, vesicles, or microdishes.