Abstract
Polymerization volume change (PVC) was measured systematically using mercury dilatometry for 41 epoxide and methacrylate monomers with quartz filler. Quantitative structure property relationship (QSPR) models were developed based on this previously unreported data to gain insight in the data collection method for future models. Successful models included only data from those samples which polymerized to hardness. The most significant descriptors in these models related to monomer reactivity. In contrast, PVC data collected under experimental conditions which maximized monomer conversion resulted in descriptors describing size and branching, indicating conversion must be considered for future PVC measurements. A Rule of Mixtures (ROM) correction term improved correlations of the dilatometer data with varying quartz content, and an adjustment for conversion may similarly enable inclusion of data which had not polymerize to hardness.
Keywords: Dilatometry, QSPR, Dental Composite
1. Introduction
One of the inherent problems found with current dental composite restorative materials is polymerization volume change (PVC), which can lead to marginal discontinuity. Polymerization shrinkage is due to the formation of covalent bonds between monomers that were previously separated by van der Waals distances [1]. In addition to seal disruption between the restorative and tooth, internal stresses accumulate as the reaction continues beyond the gelation stage. These stresses contribute a variety of forces leading toward premature failure of the restorative.
Addition of an inert filler results in reduced volume change and stress [2,3] due to the decreased number of bonds formed and results in improved material properties. Although the relationship between added filler and decreased volume change is complex and not always strictly predictable [4–6], this relationship has been found to continue until some threshold value is attained [7]. Ring-opening reactions, with compounds such as epoxides or bicyclic monomers, are generally assumed to limit volume change as each newly formed bond is counteracted by the breaking of another bond(s) [8]. Due to the lower ratio of bonds formed by the reaction to the total number of bonds in the monomer, larger monomers reduce volume change as compared to smaller monomers. Effects such as molecular mobility, intramolecular/intermolecular attractive forces, and steric hindrance to the reactive site complicate the connection between larger structure size and PVC.
The relationship between PVC and conversion is well established and volume change has been used to estimate the degree of methacrylate conversion [9–11] based on the consistent molar volume change for each methacrylate group [9]. Further work has shown that this relationship is likely not simple, as FT-NIR analysis measuring methacrylate conversion may result in substantial deviation when compared with the estimated conversion from PVC [12]. Also, there is a point in monomer conversion at which the sample becomes incapable of volume change, consequently building up internal stresses while conversion continues [13].
There are a variety of methods to measure PVC, such as dilatometry (usually Hg), bonded disk, strain gage, and linometer [4,14]. Unfortunately, published values from the different methods are not directly comparable with one another [14]. As the use of a systematic experimental method is a necessary requirement for development of a predictive model, the purpose of this work was to measure PVC in a single laboratory under identical experimental conditions using mercury dilatometry. Single monomer experiments were performed to reduce the number of variables for this study. This data was then used to develop a quantitative structure property relationship (QSPR). Attempts to correlate volume change with structure also included data with a correction factor adjusting for the amount of filler added to the system. In addition, a model is described for volume change measurements using monomer and polymer densities which included a peroxide initiator system ensuring maximum monomer conversion. The contributing components from each model were then compared to elucidate a means to improve the collection of PVC data.
2. Materials and Methods
2.1 Experimental
All compounds were purchased and used without further purification. Phenyl[p-(hydroxytetradecyloxy)phenyl] iodium hexafluorantimonate (PI) was purchased from GELEST, Inc. CYGEP and PHEPSI were obtained from 3M ESPE (Seefeld, Germany). Camphorquinone (CQ), ethyl 4-dimethylaminobenzoate (EDMAB), and the remaining test monomers were purchased from Aldrich Chemical Company. The monomer structures and designations are shown in Fig. 1 and 2 below. Test monomers were chosen based on structure similarity for a series of commercially available monomers.
Fig. 1.
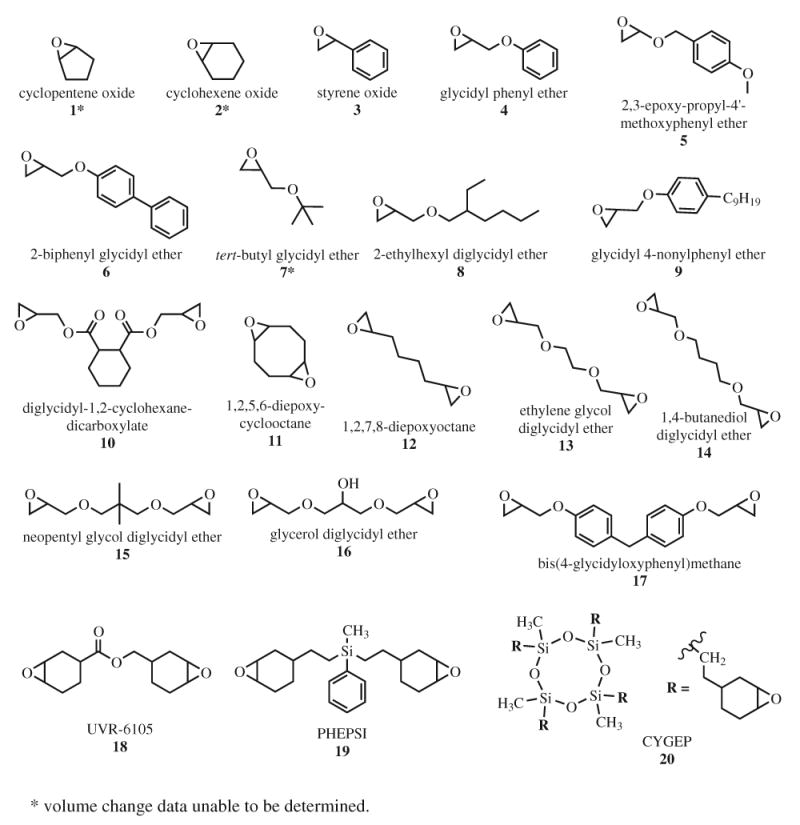
Epoxide compounds tested using mercury dilatometry.
Fig. 2.
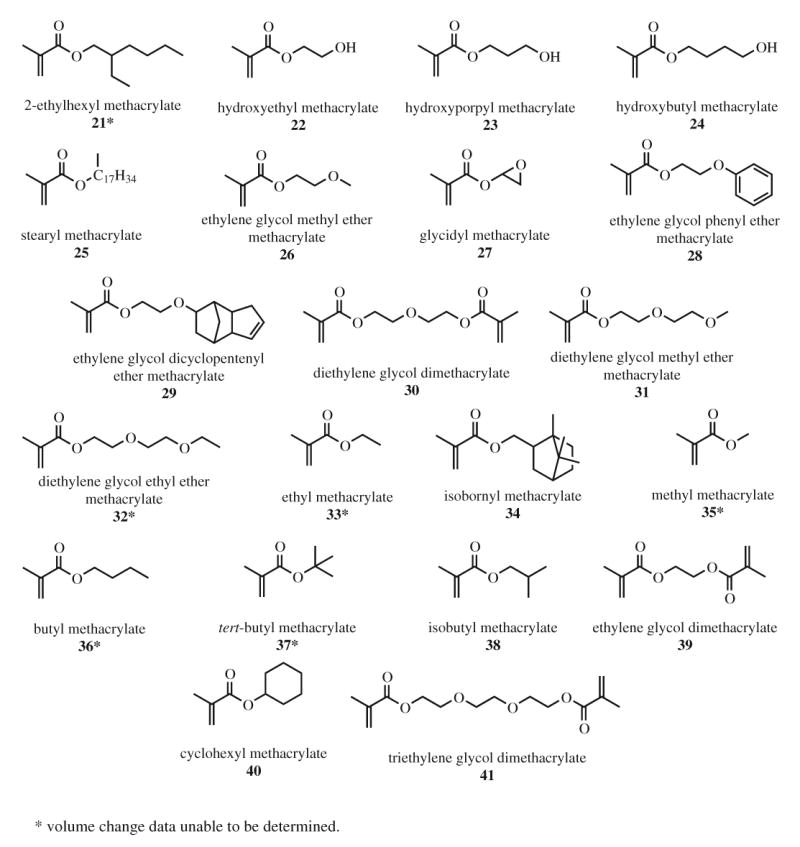
Methacrylate compounds tested using mercury dilatometry.
The experimental procedure was performed at room temperature (22–24° C) under yellow light to avoid photoinitiation by ambient light. The photoinitiator and monomer were mixed in the following mass percents: PI (3.0%), CQ (1.0%), EDMAB (0.1%), and test monomer (95.9%). When the monomer was solid or highly viscous, or if there were solubility issues between the photoinitiator system and monomer, the material was placed in a warm water bath on a hot plate and heated to a temperature to ensure mixing. In such cases, consideration was taken for each compound’s boiling point as to not facilitate monomer evaporation. The monomer was mixed continuously with the photoinitiator system using a magnetic stirrer in a glass scintillation vial until no solid particles remained.
Approximately 0.5 g of the photoinitiator/monomer mixture sample was weighed and placed in a Crescent® mixing capsule [15]. Passivated quartz filler [16] was added in small increments and blended in a Silmat® Dental Amalgamator, Model A, for 8 seconds. The quartz filler has been passivated with respect to acidic functionalities to reduce potential interactions between the filler and monomer during curing. The addition of quartz was repeated until the composite reached a consistency similar to that of commercial toothpaste, ensuring samples would be usable in the instrument despite substantial variation in monomer viscosities [17]. The final composite mixture was then weighed to determine the amount of filler added.
Following composite preparation, a 0.080–0.100 g sample was weighed and deposited on a glass microscope slide and placed in a NIST dilatometer [18]. Special care was taken to ensure there were no air pockets in the sample as it was evenly distributed on the slide. The slide was then clamped into the apparatus and inverted. Mercury was added to the dilatometer chamber until the linear variable differential transformer (LVDT) reading was ±1000.00 bits. Once the instrument stabilized (< 4 standard deviations) as determined by the computer software, the sample was photoinitiated for 60 seconds with a Spectrum© dental lamp (415 mW/cm2). The instrument automatically corrected for temperature variation due to light initiation. Volume change data was collected for 60 minutes, and the sample was then re-irradiated for 30 seconds to ensure thorough curing. Each compound was tested two to ten times depending on the initial precision of the measurements.
Based on Archimedes’ principle, the density of each cured product was determined by measuring the mass of the dry product followed by its measurement in degassed water using a Mettler-Toledo density determination apparatus [19]. To reduce water uptake, attempts were made to minimize sample exposure to water, usually no more than 30 seconds. The cured sample density was entered into the dilatometer software [20] and the polymerization volume change (%PVC) was calculated [21]. This was determined from the measured mass of the uncured polymer, Muncured, (also equivalent to mass of the cured polymer, Mcured), the determined density of the polymer, ρcured, and the volume change measured by the dilatometer, ΔV. The software calculates the volume of the cured polymer, Vcured, from input of ρcured and Mcured using Eq. 1. Utilizing Eqs. 2 and 3 provided %PVC based on Vuncured. While this deviates from the method to calculate shrinkage based on volume change relative to the Vcured as reported by Stansbury and Ge [22], the difference is minor and the method consistent throughout the study.
| (1) |
| (2) |
| (3) |
The Rule of Mixtures (ROM) adjustment was used to determine the volume change of only the monomer fraction. This normalized %PVC experimental values, enabling direct comparison of monomer shrinkage despite the variation in quartz filler content which was necessary to test the different monomers. The procedure includes calculation of the volume fraction of monomer (Eq. 4). The volumes used in this equation were obtained from densities and measured masses of the monomer and filler using Eq. 1. The measured change in volume of the composite, ΔV, is actually the change in volume of the monomer and filler (Eq. 5). Assuming the change in volume of the filler is negligible and acts primarily as a diluent (ΔVfiller = 0) [23], all change in volume is attributed to the monomer, ΔVmonomer. Obviously, the quantity of filler is important, as even tests for the same monomer would be affected by variation in the filler/monomer ratio. Equation 6 adjusts ΔVcomposite to estimate the change in volume attributable to the monomer
| (4) |
| (5) |
| (6) |
Polymer hardness tests were performed using a modified Gilmore needle test (GNT) with a mass of 453 g similar to a reported procedure [24]. The 1 mm needle was placed on the sample surface for 30 seconds. To pass the GNT, the sample was required to support the needle with no visible indentations, cracking, or breaking resulting from the test.
2.2 Model Development
Data used in the models contained negative values for volume change, as all measurements resulted in shrinkage. Calculations were performed on monomers using the AM1 [25] and SAM1 [26] semiempirical methods implemented in AMPAC 8.0 with Graphical User Interface [27]. Conformational analysis was performed by systematic dihedral angle rotation to identify the lowest energy conformation for each monomer. All geometries were identified as stationary points by frequency calculations which had no imaginary frequencies following unconstrained optimization. Properties were computed from these geometries for use in the development of the QSPR models. The program CODESSA [28] was then used to calculate descriptors from the output files. A heuristic algorithm [29] was used to derive several correlations from these descriptors resulting in a final set of multilinear regression equations. Several hundred possible descriptors were created which may be categorized as follows: constitutional (# atoms, bonds, and rings); topological (atomic connectivity indices); geometric (molecular volume and surface area); electrostatic (charge distribution); quantum chemical (orbital energies, charge distribution based on quantum chemical calculations); and thermodynamic (enthalpies and entropies). Acceptable models were determined based on R2, adjusted R2, cross-validated R2CV (leave one out method), F-test, and t-test. Statistical analyses were performed using SPSS 11.5 (SPSS Inc.) to eliminate the possibility of high intercorrelation between descriptors and chance correlations. The quantities used for this purpose include the variance inflation factor (VIF < 5) and significance (p < 0.01). In our approach, correlations are developed using a standard forward stepwise method [30] beginning with a single descriptor. A second descriptor was included in each model following the requirement that criteria for significance and orthogonality were satisfied.
For ab initio calculations, closed shell restricted Hartree Fock (RHF) optimizations were performed with the 6–31G** basis set [31,32] using Gaussian03 [33] beginning with AM1 geometries. All optimizations were continued to default convergence criteria and were confirmed as stationary points by frequency calculations [34,35]. Open shell radical structures were optimized using the unrestricted Hartree Fock (UHF) method and the same basis set. To enable formation of the radical species, a proton was added to the terminal alkene carbon at the reactive site and the charge remained 0 for a doublet electronic state.
3. Results and Discussion
In our study, dilatometry experiments were performed on 41 compounds. Not all of the tested compounds produced results usable for a QSPR correlation. Difficulties arose when the monomer or cured product was too volatile for density measurement. Therefore no volume change was able to be determined.
3.1. Epoxides
Several trends are seen in the polymerization volume change measurements for the epoxides, give in Table 1. In general, the samples with greater volume change following the ROM correction passed the GNT, although exceptions do exist. Polymerization of glycidyl phenyl ether (4) exhibited an 8% shrinkage, a large value relative to the other epoxides measured, but the product failed the GNT. All epoxide monomers which passed the GNT contained more than one epoxide group and the single epoxide group in compound 4 resulted in a linear polymer with a less rigid polymer matrix. A similar explanation may be applicable for 8 which also failed the GNT, yet exhibited more shrinkage than the other “hard” polymerizates.
Table 1.
Epoxide compounds tested using mercury dilatometry listed in decreasing volume change by %ROM.
| Compound | %TVC | %ROM | % Filler | Hard | Tests |
|---|---|---|---|---|---|
| 1,4-butanediol diglycidyl ether (14) | −4.3 | −8.3 ± 2.0 % | 64 | YES | 6 |
| glycidyl phenyl ether (4) | −4.2 | −8.0 ± 0.7 % | 68 | NO | 4 |
| 1,2,7,8-diepoxyoctane (12) | −3.8 | −8.0 ± 5.1 % | 75 | YES | 3 |
| glycerol diglycidyl ether (16) | −4.0 | −7.3 ± 1.6 % | 64 | YES | 4 |
| neopentyl glycol diglycidyl ether (15) | −3.0 | −5.2 ± 0.8 % | 63 | YES | 3 |
| CYGEP (20) | −3.0 | −5.2 ± 1.0 % | 62 | YES | 7 |
| ethylene glycol diglycidyl ether (13) | −2.5 | −5.0 ± 0.9 % | 71 | YES | 5 |
| 2-ethylhexyl glycidyl ether (8) | −2.1 | −4.2 ± 0.8 % | 74 | NO | 8 |
| UVR-6105 (18) | −2.2 | −4.0 ± 0.6 % | 66 | NO | 7 |
| bis(4-glycidyloxyphenyl) methane (17) | −2.5 | −3.9 ± 1.7 % | 68 | YES | 3 |
| PHEPSI (19) | −1.5 | −2.7 ± 0.9 % | 64 | YES | 5 |
| 2-biphenyl glycidyl ether (6) | −1.7 | −2.5 ± 0.3 % | 56 | NO | 5 |
| 2,3-epoxy-propyl-4′-methoxyphenyl ether (5) | −1.4 | −2.2 ± 1.5 % | 60 | NO | 2 |
| glycidyl 4-nonylphenyl ether (9) | −1.2 | −2.1 ± 0.2 % | 68 | NO | 4 |
| diglycidyl-1,2-cyclohexanedicarboxylate (10) | −0.81 | −1.5 ± 0.4 % | 64 | NO | 3 |
| 1,2,5,6-diepoxycyclooctane (11) | −0.31 | −0.56 ± 0.52 % | 66 | NO | 5 |
| styrene oxide (3) | −0.12 | −0.21 ± 0.42 % | 66 | NO | 3 |
Note: Standard deviations are at a confidence level of 95%.
The presence of a single epoxide does not explain the GNT failure of 18, which is a diepoxide known to homopolymerize to hardness by cationic initiation [36]. However, past research showed that for 18, complications arise from inter- or intramolecular interactions via the ester group, resulting in potential backside attack [37]. The nucleophilic character of the ester carbonyl is generally considered to be greater than an epoxide [38], and formation of a crosslinked product may take substantially longer than the 60 minute period of our current systematic procedure. This is further substantiated by the observation that 18 polymerized to hardness and passed the GNT following a 24 hour dark cure period. The volume change following a longer cure time for 18 was not considered for QSPR correlations. Modifications to light intensity and photoinitiator concentration were not studied due to our standardized procedure. This is a different study.
Similar to 18, a reduction in crosslinking due to ester interactions is likely responsible for failure of the GNT by the diepoxide 10. Diepoxide 11 is an anomaly because it did not contain an ester nor did it polymerize to hardness. However, the small volume change may indicate low reactivity for this monomer under these conditions.
As noted above, the size of the monomer is, at least conceptually, related to the relative amount of volume change for the monomer to polymer conversion. Such a relationship was not evident from this data. Just considering those compounds that were “hard”, the smallest monomer certainly did not demonstrate the largest shrinkage. This result suggests that electronic or steric effects play a significant role in producing polymerization volume change.
3.2 Methacrylates
All of the methacrylates which passed the GNT exhibited greater shrinkage than the samples which failed (Table 2). This again points to a strong relationship between conversion and volume change. However, unlike the epoxides, a number of hard polymer products were formed from monofunctional methacrylates. Similar to the epoxides, no general size trend of monomer vs. volume change could be discerned for all of the measured methacrylates. When considering only the monomethacrylates, the greatest shrinkage was measured for the smallest monomer, methacrylate 22. The slightly larger hydroxymethacrylate compounds 23 and 24 exhibited approximately equivalent shrinkage, which was significantly less than compound 22. The fused rings on the monomethacrylates 29 and 34 resulted in less shrinkage than the hydroxymethacrylates. This effect is likely a consequence of a combination of size and steric hindrance. The dimethacrylates which passed the GNT were separated by one (39), two (30), or three (41) ethylene glycol (EG) units. Each additional EG unit produces greater shrinkage, which is contrary to the expected size effect. This information further supports the importance of electronic effects and complexity of the phenomenon of polymerization volume change.
Table 2.
Methacrylate compounds tested using mercury dilatometry listed in decreasing volume change by %ROM.
| Compound | %TVC | %ROM | % Filler | Hard | Tests |
|---|---|---|---|---|---|
| HEMA (22) | −6.9 | −13.0 ± 0.7 % | 69 | YES | 4 |
| TEGDMA (41) | −6.2 | −11.5 ± 0.6 % | 71 | YES | 7 |
| DEGDMA (30) | −4.8 | −10.4 ± 0.8 % | 72 | YES | 8 |
| HBMA (24) | −5.4 | −9.8 ± 1.3 % | 69 | YES | 3 |
| HPMA (23) | −5.7 | −9.6 ± 1.2 % | 74 | YES | 7 |
| EGDMA (39) | −4.4 | −8.5 ± 1.1 % | 69 | YES | 4 |
| EG dicyclopentenyl ether MA (29) | −3.7 | −6.8 ± 0.4 % | 72 | YES | 5 |
| isobornyl MA (34) | −2.7 | −4.7 ± 0.5 % | 68 | YES | 4 |
| glycidyl MA (27) | −2.0 | −3.7 ± 0.8 % | 68 | NO | 4 |
| EG phenyl ether MA (28) | −2.0 | −3.7 ± 0.4 % | 69 | NO | 10 |
| DEG methyl ether MA (31) | −1.5 | −3.6 ± 1.1 % | 80 | NO | 5 |
| stearyl MA (25) | −1.8 | −3.3 ± 0.4 % | 71 | NO | 10 |
| cyclohexyl MA (40) | −1.3 | −3.2 ± 0.7 % | 74 | NO | 7 |
| EG methyl ether MA (26) | −1.2 | −2.4 ± 1.0 % | 71 | NO | 4 |
Note: Standard deviations are at a confidence level of 95%.
Even though there is evidence from the data reported in this study advocating a relationship between electronic effects and volume change, it is troubling in light of past evidence associating the size of a molecule with PVC [9]. It clearly emphasizes that the degree of conversion must be a significant contributing factor in this connection. In consideration of this conclusion, future dilatometry experiments in this series of studies must be performed in tandem with degree of conversion measurements. Such results may allow for a proportional correction factor, and therefore enable the adjustment of the observed volume change to the actual amount of material that reacted.
3.3 Initial QSPR Models
Initial correlations were developed using %PVC and ROM data for all of the compounds, an admittedly small set for QSPR analysis. However, we seek insight by this process rather than a strictly predictive model. Regardless of the number of descriptors allowed, no correlation passed our standard statistical analysis criteria. It must be noted here that the polymerization mechanisms are very different for the two classes of monomers. Epoxides react via a cationic process, whereas methacrylates follow a radical mechanism. Given this major difference, it is not surprising that the QSPR models describing them would not be compatible. The full set of tested molecules was, therefore, subdivided into two categories based on the reaction mechanism: seventeen epoxides and fourteen methacrylates.
Correlations for %PVC using all 17 epoxide compounds as a training set resulted in unacceptable results (3 descriptors, R2 = 0.61, t-test < 2). ROM correlations using these molecules were likewise far below statistical requirements. As noted above, monomer conversion is often directly correlated with PVC, and it may not be reasonable to use all of the measured volume change data. One study investigating degree of conversion indicated that a threshold value for the crosslink density exists, beyond which increased conversion has little or no impact on the mechanical properties [39]. Based on this, it seems reasonable that PVC may have a threshold beyond which the monomer conversion has only minor influence on volume change. This would occur after matrix vitrification, and further reaction would manifest itself as internal stresses. To test this hypothesis, we developed a correlation using only those epoxides which polymerized to hardness (passed the GNT). The AM1-QSPR model passed statistical tests for the overall correlation and individual descriptors (Fig. 3).
Fig. 3.
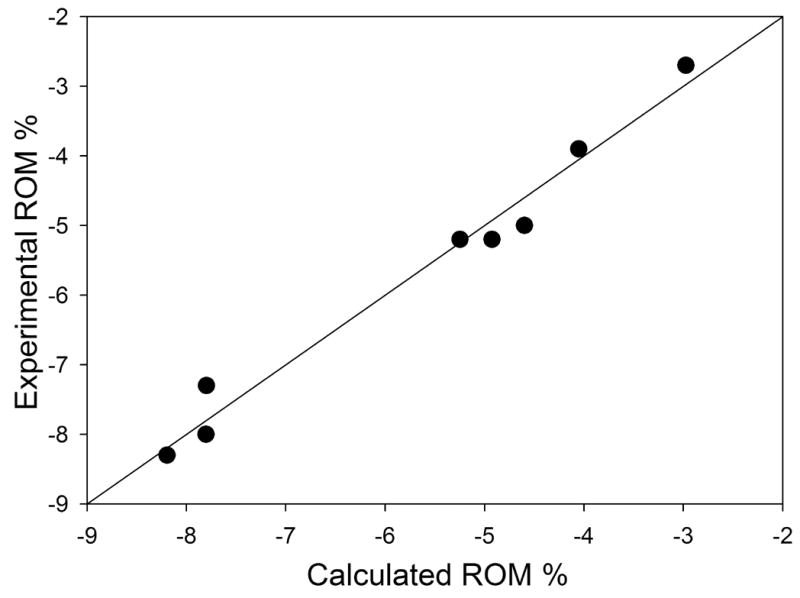
Epoxide model for samples polymerizing to hardness. Statistics include N=8, R2=0.977, R2adj=0.968, R2CV=0.928, F=107, RMSE=0.3, s2=0.1, t-test >4, VIF=1.0, p significance ≤ 0.006.
3.3.1 Epoxide Correlation
The descriptors for this epoxide correlation included YZ Shadow/YZ Rectangle and Maximum Atomic State Energy on an oxygen atom (Eq. 7). The geometric descriptor likely has a relationship with the ability of a polymer to pack after the monomers react. The negative coefficient indicates a larger value (more complete shadow of the rectangle) would have greater (more negative) volume change, which may be due to better packing ability. The descriptor for the Max. At. St. EO atom is localized on the oxygen contained in the epoxide ring. The descriptor can be interpreted as the quantum chemical potential energy of the electrons on the oxygen atom and is calculated by summing the electron/electron repulsion energies and the electron/nuclear attraction energies. As the attraction is of much greater magnitude, the value is negative, and a more negative atomic state energy describes a more stable oxygen atom. The negative coefficient in Eq. 7 is consistent with a more stable epoxide oxygen atom (i.e. less reactive) having reduced change in volume relative to a less stable epoxide oxygen.
| (7) |
3.3.2 Methacrylate Correlation
Similar to the epoxides, no statistically significant correlation was possible for the entire set of methacrylates using data measured with the dilatometer (Table 2). However, a model (Eq. 8) was developed for the hardened methacrylates using the SAM1 semiempirical method (Fig. 4). The first descriptor, PNSA-3 [40], is the partial negatively charged solvent accessible surface area of the monomer. The positive coefficient and negative value of each descriptor indicates that a larger PNSA-3 would lead to greater volume change. This descriptor is calculated by summing the products of each calculated negative quantum chemical charged atom with its solvent accessible surface area. The structure of each methacrylate contains not only a terminal alkene (Fig. 5), but carbonyl and ether oxygens with partial negative charges. The charge on the atoms of the terminal alkene is substantially greater than the charge of each oxygen atom. This means that the contribution of each terminal alkene is much greater than the contribution of each oxygen, despite the larger solvent accessibility of the carbonyl oxygens. This describes reactivity, as an electron deficient radical species has greater affinity toward an electron rich, highly charged terminal alkene. The second descriptor has a negative coefficient and a positive value. In every case, the atom with the minimal electron–electron repulsion was located on the carbonyl adjacent to the reactive site (the radical of the activated species). Greater electron/electron repulsion near the reaction site suggests greater instability of the radical. The electron/electron repulsion is a complex quantity comprised of a number of contributions. Thus, it is preliminary to deduce its involvement in the radical form of each monomer, although the location in the molecule is certainly worth noting.
Fig. 4.
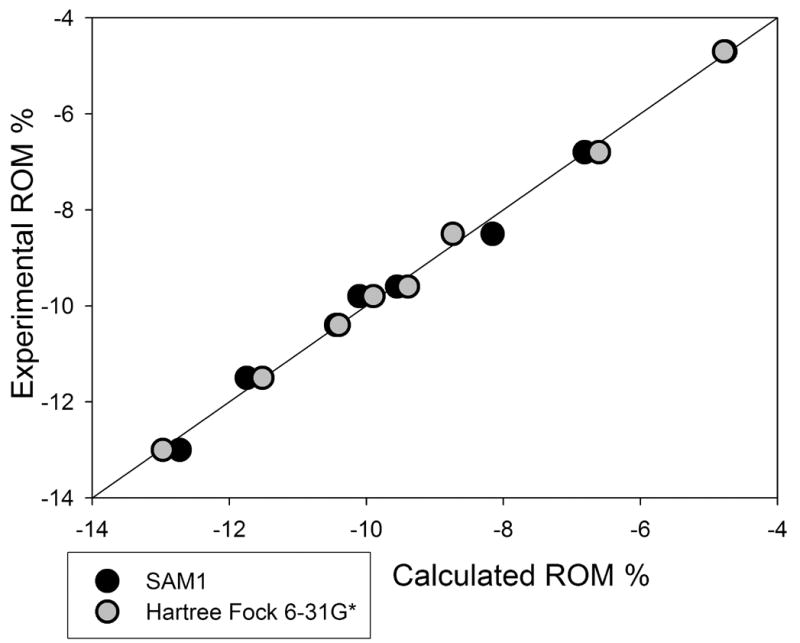
Methacrylate model for samples polymerizing to hardness. SAM1 statistics include: N=8, R2=0.993, R2adj=0.995, R2CV=0.972, F=339, RMSE=0.2, s2=0.1, t-test >4, VIF=1.0, p significance ≤ 0.005. Hartree Fock statistics include: R2=0.997, R2adj=0.932, R2CV=0.988, F=773, RMSE=0.1, s2=0.03, t-test >4, VIF=1.0, p significance ≤ 0.005.
Fig. 5.
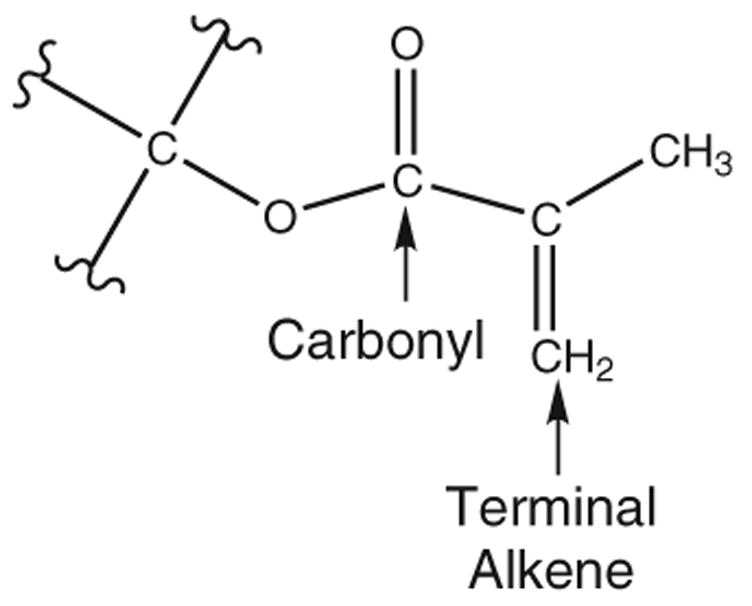
Reactive site of a methacrylate group. All labeled atoms were used in ab initio fragment calculations.
| (8) |
3.3.3 QSPR Treatment of Reactive Species
To further investigate the interpretation for calculated reactivity of the methacrylates relative to PVC, descriptors were also calculated for the radical methacrylate species. While it is common to develop QSPR models for polymer products based on ground state structures, the reaction actually involves both the ground state and radical forms of each compound and it was thought inclusion of descriptors from both species for each property value better represents the polymerization process. From this expanded pool of descriptors, no better correlation was found based on a semiempirical model. The modest size of the methacrylate monomers also enabled Hartree-Fock ab initio calculations for both the ground state and radical forms of each compound for a model. (The size of the epoxide structures did not allow a similar study).
Additionally, CODESSA can calculate descriptors from selected portions of the molecules (fragments) as well as the entire molecule. The decision to include only the reactive portion (Fig. 5) of each molecule was based on the likelihood that a correlation involving this fragment may lead to additional insight in support of the relationship between the reactivity of these species and volume change. In addition, this fragment procedure essentially normalizes descriptors such as the solvent accessible surface area. No prior reference to such a technique, where the descriptor pool for a QSPR included the ground state and activated monomer forms, both in fragments and entirety, appears to exist in the literature.
A successful correlation was found for the ab initio method with two descriptors (Eq. 9). The first descriptor is DPSA-3 [40] similar to the SAM1 methacrylate descriptor. However, this descriptor uses the difference between the positively and negatively charged solvent accessible surface areas. The negative coefficient and positive value of the descriptor indicates a greater difference in the charged surface area leads to greater PVC. This descriptor also suggests that charge interactions of the monomers may be more important than the charge of the terminal alkene as in the SAM1 model. One reasonable interpretation is that the charge interactions draw the molecules closer and react due to increased statistical probability rather than reactivity as described above.
| (9) |
The second descriptor is the maximum 1-electron reactivity index for a C atom. In all cases, the locale of this descriptor was limited to the reactive site of the radical species, as shown in Fig. 5. As the name suggests, it is based on the potential reactivity of a C atom, and the restriction of this descriptor to the reactive site supports its relevance to methacrylate polymerization. The negative value of the coefficient and positive value of the descriptor indicate increased reactivity leads to increased volume change.
3.3.4 QSPR for Fully-Converted Polymers
Descriptors for the reported models were consistent with reactivity (degree of conversion) of the monomer. It seems counterintuitive that such a PVC model does not contain size descriptors as well. To test our interpretation of these effects, a QSPR was developed using the work by Patel et al. [9] for total volume change of a polymerization reaction for a series of methacrylates. Experimental conditions held the temperature of the reaction vessel > 80° C for three hours. Further, chemical initiation was carried out using a peroxide initiator. These procedures are intended to ensure high monomer conversion. In contrast, dilatometry experiments performed in this study were at room temperature for just one hour, with a different initiatior system, and contained quartz filler.
The resulting model for the 17 molecule training set contains two descriptors (Eq. 10). The first descriptor was first order bonding information content (BIC-1). This parameter was previously found to correlate with solvent effects for decarboxylation rates [41] and van der Waals’ constants [42]. It indexes branching and size effects for a particular geometry. The second descriptor (maximum nuclear/nuclear repulsion for a C-C bond) is quantum mechanical and also indirectly describes branching. For molecules in the training set, longer alkyl chains exhibited the least amount of volume change and had substantially larger descriptor values.
| (10) |
A number of statistically significant correlations were also developed using only the nine linear alkane methacrylates reported by Patel [9]. It is not surprising that many single descriptor correlations were successful for these structures, as the reported PVC decreased regularly with the size of the alkyl chain. As expected, systematic increase of methylene groups [43] and molecular weight [44] have been found to correspond to decreased volume change in the past. That is consistent with this correlation. Successful models included the Balaban index (Eq. 11) as well as quantum mechanical descriptors with a normalization factor for effect of size of the monomer (total number of atoms in the denominator, Eqs. 12–14).
| (11) |
| (12) |
| (13) |
| (14) |
The success of predictions based on density data indicates that more intuitive descriptors will likely be found for additional volume change measurements using a consistent experimental protocol coupled with the effect of monomer conversion.
4. Conclusions
In this study, we have successfully correlated molecular structure to volume change of quartz filled samples systematically measured with a mercury dilatometer. Statistically valid models included only compounds which polymerized to hardness as determined by the Gilmore needle test, a qualitative test which required substantial monomer conversion. These compounds generally showed greater shrinkage than those that did not, in keeping with greater monomer conversion for increased volume change. Additionally, separation of data by reaction mechanism (cationic/radical) based on reactive substituent type was also necessary. Application of a Rule of Mixtures (ROM) correction to normalize variation in quartz/monomer ratio resulted in superior models to correlations without this adjustment (not reported), supporting incorporation of this term in future studies.
Descriptors for each dilatometry model reported in this study were based on reactivity, indicating monomer conversion must be considered for future experiments to develop a second correction term for this effect. Elimination of interference from reactivity in this connection would likely result in descriptors based on size and branching of the molecule rather than on reactivity. This correction term may lead to correlations that will predict polymerization volume change for samples which react by different mechanisms or incompletely (do not polymerize to hardness). Support for this conclusion is evidenced by topological descriptors in models that were derived using experimental data in which monomer conversion was maximized.
Table 3.
Unfilled methacrylate prediction for %TVC.
| Structure | Exp. | Calc.a | Calc.b | Calc.c | Calc.d | Calc.e |
|---|---|---|---|---|---|---|
| Methyl | −21.0 | −21.8 | −20.8 | −21.1 | −21.0 | −20.9 |
| Ethyl | −18.8 | −20.1 | −18.7 | −18.5 | −18.4 | −18.4 |
| Propyl | −14.9 | −15.2 | −16.4 | −16.1 | −16.1 | −16.2 |
| Butyl | −15.7 | −14.2 | −14.4 | −14.4 | −14.5 | −14.6 |
| Hexyl | −12.9 | −12.4 | −11.7 | −12.1 | −12.2 | −12.2 |
| Octyl | −9.1 | −11.2 | −10.1 | −10.6 | −10.7 | −10.7 |
| C12 | −8.4 | −9.1 | −8.7 | −8.8 | −8.8 | −8.7 |
| C13 | −8.9 | −8.5 | −8.5 | −8.5 | −8.4 | −8.4 |
| C16 | −8.1 | −7.1 | −8.2 | −7.7 | −7.6 | −7.5 |
| Isopropyl | −19.7 | −19.1 | – | – | – | – |
| Isobutyl | −19.3 | −17.5 | – | – | – | – |
| Tert-butyl | −16.3 | −18.0 | – | – | – | – |
| 2-epoxypropyl | −20.2 | −18.1 | – | – | – | – |
| Tetrahydropyranylmethyl | −12.8 | −13.6 | – | – | – | – |
| Tetrahydropyranyl | −16.4 | −15.3 | – | – | – | – |
| Isobornyl | −10.1 | −10.8 | – | – | – | – |
| Tetrahydrofurfuryl | −14.7 | −15.3 | – | – | – | – |
Eq. 10 statistics include R2=0.919, R2adj=0.907, R2CV=0.887, F=79.3, RMSE=1.2, s2=1.8, t-test >4, VIF=1.3, p significance ≤ 0.005.
Eq. 11 statistics include R2=0.964, R2adj=0. 959, R2CV=0.950, F=186.6, RMSE=0.9, s2=1.0, t-test >4, p significance ≤ 0.005.
Eq. 12 statistics include R2=0.963, R2adj=0.958, R2CV=0.949, F=183.1, RMSE=0.9, s2=1.0, t-test >4, p significance ≤ 0.005.
Eq. 13 statistics include R2=0.963, R2adj=0.958, R2CV=0.948, F=181.5, RMSE=0.9, s2=1.0, t-test >4, p significance ≤ 0.005.
Eq. 14 statistics include R2=0.962, R2adj=0.957, R2CV=0.947, F=179.1, RMSE=1.0, s2=1.0, t-test >4, p significance ≤ 0.005.
Acknowledgments
This work was supported by DE09696 (to A.J.H.), R15BM61314 (to K.V.K.), and T32DE07294 (to J.D.E.) from the National Institutes of Health and by internal grants from the University of Missouri–Kansas City (FRG, SEARCH, and UMRB), all of which are gratefully acknowledged. Jamie Fleckenstein, Kathleen Marzluf, Patrycja, Wilczyska, Jacyln Butler, Heather Vastlik, Matt St. George, and Robert Clevenger are acknowledged for assistance in data collection.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Tobolsky AV, Leonard F, Roeser GP. J Polym Sci. 1948;3(4):604–606. [Google Scholar]
- 2.Razak AA, Harrison A. J Prosthet Dent. 1997;77(4):353–358. doi: 10.1016/s0022-3913(97)70158-6. [DOI] [PubMed] [Google Scholar]
- 3.Miyazaki M, Hinoura K, Onose H, Moore BK. J Dent. 1991;19(5):301–303. doi: 10.1016/0300-5712(91)90078-d. [DOI] [PubMed] [Google Scholar]
- 4.de Gee AF, Feilzer AJ, Davidson CL. Dent Mater. 1993;9(1):11–14. doi: 10.1016/0109-5641(93)90097-a. [DOI] [PubMed] [Google Scholar]
- 5.Bang HC, Lim BS, Yoon TH, Lee YK, Kim CW. J Oral Rehabil. 2004;31(8):803–810. doi: 10.1111/j.1365-2842.2004.01301.x. [DOI] [PubMed] [Google Scholar]
- 6.Kwon YH, Jeon GH, Jang CM, Seol HJ, Kim HI. J Biomed Mater Res B: Appl Biomater. 2006;76B:106–113. doi: 10.1002/jbm.b.30333. [DOI] [PubMed] [Google Scholar]
- 7.Walls AW, McCabe JF, Murray JJ. J Dent. 1988;16(4):177–181. doi: 10.1016/0300-5712(88)90032-2. [DOI] [PubMed] [Google Scholar]
- 8.Eick JD, Byerley TJ, Chappell RP, Chen GR, Bowles CQ, Chappelow CC. Dent Mater. 1993;9(2):123–127. doi: 10.1016/0109-5641(93)90088-8. [DOI] [PubMed] [Google Scholar]
- 9.Patel MP, Braden M, Davy KW. Biomat. 1987;8(1):53–56. doi: 10.1016/0142-9612(87)90030-5. [DOI] [PubMed] [Google Scholar]
- 10.Loshaek S, Fox TG. J Am Chem Soc . 1953;75:3544–3550. [Google Scholar]
- 11.Venhoven BA, de Gee AJ, Davidson CL. Biomat. 1993;14(11):871–875. doi: 10.1016/0142-9612(93)90010-y. [DOI] [PubMed] [Google Scholar]
- 12.Ge J, Trujillo M, Stansbury J. Dent Mater. 2005;21(12):1163–1169. doi: 10.1016/j.dental.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 13.Braga RR, Ferracane JL. J Dent Res. 2002;81(2):114–118. [PubMed] [Google Scholar]
- 14.Sakaguchi RL, Wiltbank BD, Shah NC. Dent Mater. 2004;20(4):388–396. doi: 10.1016/j.dental.2003.11.002. [DOI] [PubMed] [Google Scholar]
- 15.Cresent®, C14005. DENTSPLY Ltd.; Weybridge, Surrey: KT14015 14002SE, UK. [Google Scholar]
- 16.3M Experimental Material. :130573–130540. [Google Scholar]
- 17.Skrtic D, Stansbury JW, Antonucci JM. Biomat. 2003;24(14):2443–2449. doi: 10.1016/s0142-9612(02)00574-4. [DOI] [PubMed] [Google Scholar]
- 18.ADA Health Foundation Computer-Controlled Mercury Dilatometer Folder, Section 3, Standard Operating Procedures.
- 19.Density determination kit used with Mettler-Toledo PG603S balance. Mettler-Toledo; CH-8606 Geifensee, Switzerland: [Google Scholar]
- 20.Dental Association Health Foundation Mercury Dilatometry Program version RS232.
- 21.Operating Instructions for Mettler-Toledo density determination kit. pp. 6–8.pp. 14 [Google Scholar]
- 22.Stansbury J, Ge J. RadTech Report. 2003;17(3):56–62. [Google Scholar]
- 23.Holder AJ, Kilway KV, Code JE, Giese GJ, Travis DM, Fleckenstein JE, Marzluf KR, Clevenger RC, Vastlik HL, Eick JD, Chappelow CC. Macromol Theo Sim. 2005;14(2):117–124. [Google Scholar]
- 24.Cherng A, Takagi S, Chow LC. J Biomed Mater Res. 1997;35(3):273–277. doi: 10.1002/(sici)1097-4636(19970605)35:3<273::aid-jbm1>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- 25.Dewar M, Zoebisch E, Healy E, Stewart J. J Am Chem Soc. 1985;107:3902–3909. [Google Scholar]
- 26.Dewar M, Coaxian J, Yu J. Tetrahedron. 1993;49(23):5003–5038. [Google Scholar]
- 27.Ampac 8.16 with Graphical User Interface. Semichem, Inc., P.O. Box 1649; Shawnee Mission, KS: pp. 66222–60649. [Google Scholar]
- 28.COmprehensive DEscriptors for Structural and Statistical Analysis. Semichem, Inc., P.O. Box 1649; Shawnee Mission, KS: pp. 66222–60649. [Google Scholar]
- 29.Karelson M. Molecular descriptors in QSAR/QSPR. New York: John Wiley & Sons, Inc.; 2000. pp. 396–400. [Google Scholar]
- 30.Xu Y, Zhang WJ. Anal Chim Acta. 2001;446:477–483. [Google Scholar]
- 31.Hehre WJ, Ditchfield R, Pople JA. J Chem Phys. 1972;56(5):2257–2261. [Google Scholar]
- 32.Hariharan PC, Pople JA. Chem Phys Lett. 1972;16(2):217–219. [Google Scholar]
- 33.Gaussian RA, 03, Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Jr, Vreven T, Kudin KN, Burant JC, Millam JM, Lyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian Inc; Pittsburgh PA: 2003. [Google Scholar]
- 34.McIver JW, Komornicki A. Chem Phys Lett. 1971;10(3):303–306. [Google Scholar]
- 35.McIver JW, Komornicki A. J Am Chem Soc. 1972;94(8):2625–2631. [Google Scholar]
- 36.Decker C, Moussa K. J Polym Sci, Part A: Polym Chem. 1990;28(12):3429–3443. [Google Scholar]
- 37.Crivello JV, Varlemann U. Photopolymerization: Fundamentals and Applications. 1997. Structure and reactivity relationships in the photoinitiated cationic polymerization of 3,4-epoxycyclohexylmethyl-3′,4′-epoxycyclohexane carboxylate; pp. 82–94. [Google Scholar]
- 38.Crivello JV, Varlemann U. J Polym Sci Part A: Polym Chem. 1995;33(14):2473–2486. [Google Scholar]
- 39.Ferracane JL, Greener EH. J Biomed Mater Res. 1986;20(1):121–131. doi: 10.1002/jbm.820200111. [DOI] [PubMed] [Google Scholar]
- 40.Stanton DT, Jurs PC. Anal Chem. 1990;62:2323–2329. [Google Scholar]
- 41.Katritzky AR, Perumal S, Petrukhin R. J Org Chem. 2001;66:4036–4040. doi: 10.1021/jo0011843. [DOI] [PubMed] [Google Scholar]
- 42.Luan F, Zhang R, Yao X, Liu M, Hu Z, Fan B. QSAR Comb Sci. 2005;24:227–239. [Google Scholar]
- 43.Bogdal D, Pielichowski J. Boron A J Appl Polym Sci. 1997;66:2333–2337. [Google Scholar]
- 44.Chung C, Kim J, Choi J. J Appl Polym Sci. 2000;77:1802–1808. [Google Scholar]


