Abstract
Experimentally naive mice matched the proportions of their temporal investments (visit durations) in two feeding hoppers to the proportions of the food income (pellets per unit session time) derived from them in three experiments that varied the coupling between the behavioral investment and food income, from no coupling to strict coupling. Matching was observed from the outset; it did not improve with training. When the numbers of pellets received were proportional to time invested, investment was unstable, swinging abruptly from sustained, almost complete investment in one hopper, to sustained, almost complete investment in the other—in the absence of appropriate local fluctuations in returns (pellets obtained per time invested). The abruptness of the swings strongly constrains possible models. We suggest that matching reflects an innate (unconditioned) program that matches the ratio of expected visit durations to the ratio between the current estimates of expected incomes. A model that processes the income stream looking for changes in the income and generates discontinuous income estimates when a change is detected is shown to account for salient features of the data.
Keywords: law of effect, matching, reinforcement learning, behavioral dynamics, income, investment, economic rationality, hopper entry, mice
Matching is a widely observed behavioral phenomenon in which the proportion of a subject's foraging time or effort invested in an option approximately matches the income (rewards per unit time) from that option relative to the total income (Herrnstein, 1961). In symbols: 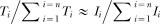 , where Ti is the time invested in the ith option and Ii is the income from the ith option (e.g., number of food pellets obtained per session). In the typical matching experiment, where the number of options is 2, the formula reduces to the familiar T1/(T1 + T2) ≈ I1/(I1 + I2). This formula is observed to apply in free-operant paradigms, where subjects can move back and forth between locations where food is found infrequently and unpredictably. We call the proportions in this approximate equation Herrnstein fractions. The proportion on the left, T1/(T1 + T2), is the investment fraction—the relative amount of time devoted to a behavioral option. The proportion on the right, I1/(I1 + I2), is the income fraction. The differences between complementary fractions—I1/(I1 + I2) − I2/(I1 + I2) = (I1 − I2)/(I1 + I2) and T1/(T1 + T2) − T2/(T1 + T2) = (T1 − T2)/(T1 + T2)—are the income imbalance and the investment imbalance. They range from +1 (all income from, or all investment in the first option) to −1 (all income from, or all investment in the second option). Matching also may be thought of as matching the investment imbalance to the income imbalance.
, where Ti is the time invested in the ith option and Ii is the income from the ith option (e.g., number of food pellets obtained per session). In the typical matching experiment, where the number of options is 2, the formula reduces to the familiar T1/(T1 + T2) ≈ I1/(I1 + I2). This formula is observed to apply in free-operant paradigms, where subjects can move back and forth between locations where food is found infrequently and unpredictably. We call the proportions in this approximate equation Herrnstein fractions. The proportion on the left, T1/(T1 + T2), is the investment fraction—the relative amount of time devoted to a behavioral option. The proportion on the right, I1/(I1 + I2), is the income fraction. The differences between complementary fractions—I1/(I1 + I2) − I2/(I1 + I2) = (I1 − I2)/(I1 + I2) and T1/(T1 + T2) − T2/(T1 + T2) = (T1 − T2)/(T1 + T2)—are the income imbalance and the investment imbalance. They range from +1 (all income from, or all investment in the first option) to −1 (all income from, or all investment in the second option). Matching also may be thought of as matching the investment imbalance to the income imbalance.
In our experimental arrangement for studying matching, mice move back and forth between two feeding hoppers, interrupting infrared beams when they poke their heads into the hoppers. At unpredictable intervals, the interruption of a beam triggers the release of a small food pellet into that hopper. The most commonly used reward-scheduling algorithm in matching studies is concurrent variable intervals. In our version of this paradigm, the intervals are programmed according to a random interval (RI) schedule: The arming of the pellet-release trigger for a hopper is scheduled by a random rate (Poisson) process. The process at a given location stops when it sets up a pay-off (arms the infrared beam trigger) and resumes when the subject harvests it (interrupts the beam, triggering the release of a pellet). Thus, pellet delivery, once it is set up (once the trigger is armed), blocks the setting up of further deliveries at that location until the pellet already set up there has been harvested.
A visit cycle consists of a visit to one hopper followed by a visit to the other, with an arrival back at the first hopper completing the cycle. We measure the durations of the two visits within each cycle. When, as generally happens, the period (average duration) of a visit cycle is less than the expected interval between pellet set-ups, the proportions of the subject's time allotted to visits at the two locations have little effect on the proportions of total income it derives from them. Return on investment is defined as income divided by investment, Ri = Ii/Ti, that is, the number of pellets obtained from a feeding hopper divided by the amount of time spent visiting it. On typical concurrent schedules such as ours, there is negative feedback between the subject's behavioral investments (the relative durations of the two visits) and the returns realized from them. This occurs because increased investment in an alternative does not result in proportional gains in income from that alternative: the contingencies maintain a more-or-less constant relative payoff in the face of different allocations.
The distinction between income and return is critical. Both quantities are rates—amount of food obtained per unit time—but the time base for income is the time on a clock that runs whenever the subject is in the foraging environment (the experimental chamber), whereas the time base for the return from a hopper is the time on a clock that runs only while the subject is visiting that hopper. The distinction between the income from a hopper and the return from a hopper corresponds roughly to the distinction often made between overall, or global, reinforcement rate (income) and local reinforcement rate (return). The correspondence is imperfect, however, because the overall reinforcement rate is usually computed only from session totals. In our data analysis, we compute and plot income reinforcement-by-reinforcement, without regard to how much time the animal has invested to obtain the reinforcement. Therefore, income is just as temporally localized as return.
Matching equates returns, not incomes. The matching formula given above is algebraically equivalent to I1/T1 ≈ I2/T2. Thus, matching yields equal returns by proportioning investments to incomes. When a mouse in our experimental arrangement matches, the numbers of pellets obtained per unit of time that it spends at each of two feeding hoppers are approximately equal. When it is not matching, the amount of reward it gets per unit time invested in one side is greater than the amount of reward it gets per unit time invested in the other. It is reasonable to suppose, therefore, that matching results from learned adjustments in relative behavioral strengths, made in reaction to the unbalanced returns from earlier nonmatching behavior. This is the assumption from which modeling efforts have typically proceeded (Davis, Staddon, Machado, & Palmer, 1993; Herrnstein & Prelec, 1991; Hinson & Staddon, 1983; Lea & Dow, 1984). The alternative, first suggested by Heyman (1982), is that matching is unconditioned behavior—an innate behavioral program based on the income records alone, with no account taken of the behavior that produced those incomes. In this work, we attempt to decide between these alternatives.
The distinction between an income-based model and a return-based model may be understood in associative terms as follows: Consider two hopper locations, L1 and L2, and the behaviors of going to and/or poking into each of them, which we denote by B1 and B2. These behaviors produce outcomes (pellet deliveries), O1 and O2. The subjects' experiences in this environment may be thought to produce an associative structure containing stimulus–response associations (L1–B1 and L2–B2), response–outcome associations (B1–O1 and B2–O2), and stimulus-outcome associations (L1–O1 and L2–O2). Return-based models of matching behavior attribute the behavior to the relative strengths of either the stimulus–response associations or the response–outcome associations.
The law of effect has traditionally been taken to imply that the effect of the outcomes produced is to alter the strengths of the stimulus–response associations or relations. Neo-behaviorists (that is, Hullians) interpret the law of effect as a manifestation of the stamping in of S–R associations by reinforcing outcomes in instrumental conditioning, whereas in Skinnerian terms, where Sd*R−>SR is the unit of analysis, the law of effect refers to the strengthening effect of the R−> SR contingency on the Sd*R tendency. The term ‘reinforcement’ as a synonym for reward or punishment connotes the presumed strengthening of a tendency to perform the response in the presence of the stimulus situation. Because we question that interpretation, we prefer the term ‘reward,’ although we will use ‘reinforcement’ when avoiding it would be awkward. In the reinforcement-learning tradition in contemporary computer science, it is more natural to interpret the law of effect as the modification of response–outcome associations, because the behavior observed is taken to be a consequence of the values assigned to the behavioral options by some algorithm (e.g., the temporal-difference algorithm; see Sutton & Barto, 1998) applied to the outcomes they have produced. By contrast, an income-based model asserts that the observed behavior depends only on the stimulus–outcome (L–O) associations. In both the neo-behaviorist and operant conditioning frameworks, this association would be said to determine the secondary reinforcing power of a location. From a computer science reinforcement-learning perspective, the subject's model of the world contains experience-derived estimates of the incomes associated with different locations. On the hypothesis that matching is driven by income rather than return, the subject would be said to have an innate and immutable policy of prorating the expected durations of its visits to those locations in accord with its current estimates of the expected incomes.
Hill-Climbing
Return-based models take matching to be a consequence of the law of effect: when one investment (behavior) produces more of a desirable effect (reward) per unit invested than another, the subject adjusts its investment ratio (the relative amounts of time spent at each hopper) so as to invest more in the more profitable alternative and less in the less profitable. With random-interval schedules, shifting the investment proportions in favor of the more profitable alternative reduces the difference in the returns, because, provided it cycles often enough between the locations, increasing the proportion of each visit cycle spent at one location does not increase (by much) the number of pellets obtained there, nor decrease by much the number of pellets obtained at the other location. Thus, relative income (the ratio of the pellets obtained) is little affected by the relative investment (the ratio of the average visit durations). The return is income (pellets obtained) divided by investment (time spent). Therefore, as the relative investment in the richer location increases while the relative income stays roughly constant, the relative return from the richer location goes down and the relative return from the poorer location goes up. In other words, there is negative feedback from the investment ratio (a behavioral variable) to the return ratio (an input variable). Matching is assumed to be the equilibrium state of this negative-feedback process: the shifting of investment toward the more profitable location continues until the returns are equal. At that point, the relative return (R1/R2) is 1/1.
The discovery by trial and error of the investment-ratio that equates returns is a hill-climbing process (Hinson & Staddon, 1983). Hill-climbing processes, like negative feedback processes in general, are slow. To reach the equilibrium (the top of the hill), the subject must try an apportionment of its investments, compare the returns obtained, adjust the apportionment in favor of the behavior producing the greater return, and so on, repeatedly until it hits on the apportionment that equates the returns. Return (the food obtained divided by the time spent obtaining it) is an extremely noisy variable when computed visit by visit (small investment by small investment). It requires a considerable number of visits even to determine the sign of a difference in two average returns with any reliability, let alone to estimate the magnitude of the difference in the average returns. Thus, the comparison of average returns following an adjustment—to determine which return is greater—requires averaging returns over an interval much longer than the expected intervals between pellets. Several adjustment-evaluation cycles are required before a new equilibrium is reached, with each adjustment cycle lasting for many visit cycles. The process of equilibration is slow, because the hill must be climbed one step at a time; there are no helicopter rides to the top.
Pure Feed-Forward
Gallistel, Mark, King, and Latham (2001) showed that when step changes in the relative richness of the Poisson scheduling process are frequent, the changes in the apportionment of the investment (changes in the expected visit durations at each location) are themselves step-like (cf. Higa, Thaw, & Staddon, 1993). The shift from expected visit durations appropriate to the prechange schedules to expected visit durations appropriate to the postchange schedules—from the top of the old hill to the top of the new hill—goes to completion within the span of a few visit cycles. Subjects sometimes completely change the expected durations of their visits from one visit cycle to the next, a maximally abrupt adjustment (see, for example, Gallistel et al., 2001, Figure 6). The abruptness of the adjustments—the fact that the top of the new hill is not reached by climbing it—suggests a purely feed-forward model of the kind implied by Heyman's (1982) suggestion that matching is unconditioned behavior.
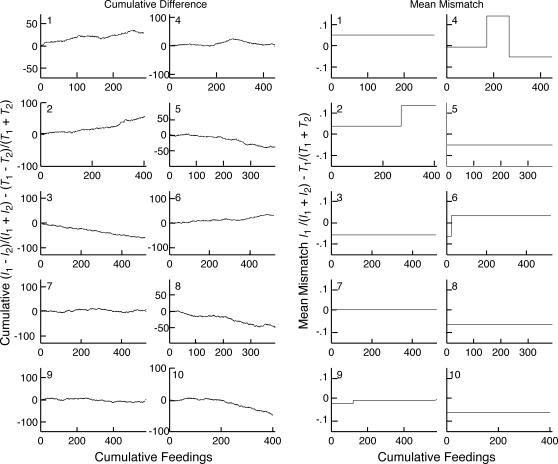
Fig 6. Left: Cumulative feeding-by-feeding difference between the income imbalance and the investment imbalance.
The number in the upper left corner of each panel identifies the subject. The y axis has been scaled so that a difference equivalent to an average difference in the Herrnstein fractions (average mismatch) of .125 would produce a full-scale deflection by the end of the record. Right: Plots of the slopes of the cumulative difference records when parsed with a logit decision criterion of 2. The y axis has been scaled in terms of the difference in the Herrnstein fractions (average mismatch). Positive mismatches constitute overmatching for the subjects whose schedules favored Hopper 1 (Subjects 1–3) and undermatching for those whose schedules favored Hopper 2 (Subjects 4–6).
Gallistel et al. (2001) amplify on Heyman's suggestion by specifying in mathematical form an innate behavior-generating program dependent for its execution only on estimates of expected incomes. The model has the following components:
An on-line, real-time mechanism (algorithm) for detecting changes in income (in the present case, changes in the numbers of pellets obtained from a hopper per unit of session time).
A closely related mechanism for estimating the currently expected income: When it detects a change, the algorithm gives an estimate of the earlier moment at which it estimates the change to have occurred. The income experienced during the (usually small) retrospective interval from the moment-of-change detection back to the estimated moment of change becomes the new (current) estimate of the expected income. Thus, income estimates are not continually updated. Successive income estimates in this model almost always come from nonoverlapping income samples, which is why the change from an old estimate to a new very different estimate can occur in a single step.
A mathematically specified mapping of income estimates into predicted distributions of visit durations. In accord with experimental findings, the distributions of visit durations are assumed to be exponential (Gallistel et al., 2001; Gibbon, 1995). This means that the probability of a subject's leaving the hopper it is currently investigating is independent of how long it has been there (Heyman, 1982; Nevin, 1979; Real, 1983)1. It also means that visit durations are distributed as they would be if departures were decided on by continually flipping a biased coin until it came up heads. Specifying the bias on the coin and the flipping frequency fully specifies the resulting behavior, giving not only the expectation (average visit duration) but also the exponential distribution of visit durations.
The change-detecting algorithm plays two critical roles in this paper. First, we assume it as a component of our mathematical model of the machinery that generates the observed behavior. Second, we also use it to find change points in the cumulative records by which we portray the evolution of matching behavior under different reward-scheduling conditions. The algorithm was first described and used by Gallistel et al. (2001) in the analysis and explanation of matching behavior. It subsequently has been generalized for use in finding change points in the expected value of almost any kind of sequentially obtained data (Balsam, Fairhurst, & Gallistel, in press; Gallistel, Balsam, & Fairhurst, 2004; Gottlieb, 2005, 2006; Papachristos & Gallistel, 2006; Paton, Belova, Morrison, & Salzman, 2006).
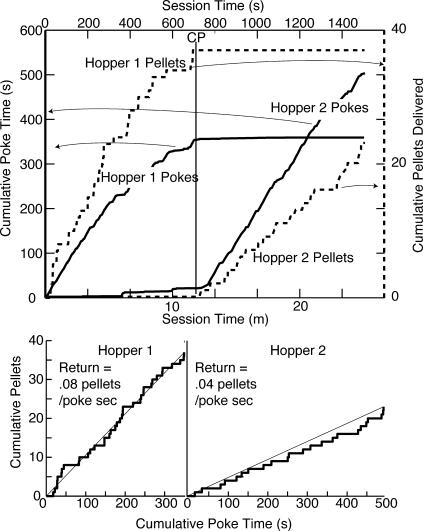
We explain the algorithm as it operates in our matching model by reference to Figure 1, which portrays the cumulative record, n(t), of pellets obtained spanning a change in the rate at which they became available: In this simulation, the first three pellets came from a Poisson process delivering on average one pellet/min; the last three were delivered by a Poisson process with an average rate of 0.1 pellet/min (an expected interval of 10 min between pellets). The real-time algorithm analyzes the incoming data pellet by pellet. In fact, it operates continuously, testing for change even in the absence of any further pellets. (That is why it can detect the apparent cessation of income—see later simulation.) The graph portrays the situation immediately after the sixth pellet is obtained.
Fig 1. Cumulative number of pellets obtained as a function of time.
The change-detecting algorithm operates on this function, as it evolves. In this instance, with simulated data, its evolution spans a step change in the underlying random rate. The current moment is t; the no-change (constant rate) hypothesis is represented by the thin straight line from the origin to the current value of n(t); τm is the past moment at which n(t) deviates maximally from the value expected on the constant-rate hypothesis.
The algorithm continuously tests the plausibility of the null hypothesis that there has been no change in the rate at which pellets are obtained. On that hypothesis, the best estimate of the current rate is the number of pellets obtained (which is six in Figure 1) divided by the interval over which they have been obtained (which is t = 18.21 min in Figure 1). This rate, r ¯, is the slope of the trend line that connects the origin of the cumulative record to its current value (see Figure 1). If there has been a change, the moment in the past at which it occurred may be estimated by finding the moment τm at which the cumulative record deviates maximally from this straight line (see “max dev” on Figure 1). This is the moment, τm, within the retrospective interval from t back to 0 at which the quantity n(τ) − r ¯τ is maximal.
The algorithm asks whether the interval t − τm from τm to the present moment contains its fair share of the pellets delivered in the interval t from 0 to t (because the origin is at 0, the duration of the interval up to t is simply t). If the six pellets delivered in the interval t are distributed at random within that interval, then the probability of finding any one of them within the subinterval t − τm is p = (t − τm)/t = 16.2/18.21 = .89. In other words, roughly 90% or 5.4 of the 6 pellets in the example in Figure 1 ought to be found within that interval, but in fact only three are found there. What are the odds, (1 − P)/P, of this disparity, where P is the probability of observing a number that small or smaller? P is calculated from the cumulative binomial function, with n(t) as the number of observations and p as the probability of a success.
For technical reasons, the algorithm asks what is the log of the odds, log[(1 − p)/p]. The log of the odds against the no-change hypothesis is called the logit. It is a measure of the strength of the evidence that there has been a change. The greater its absolute value, the greater the evidence for a change. The sign of the logit indicates the direction of the change. Again for technical reasons, the algorithm in fact uses what we call the pseudo-logit rather than the true logit; that is, it computes the log of the ratio of the probability of finding that many (i.e., three) pellets or fewer (which probability ≈ .021) to the probability of finding that many or more (≈ .998). The logit is not well behaved when the observed number of rewards is 0 and the expected number is also very close to 0, whereas the pseudo-logit is, because the pseudo-logit, unlike the logit, includes in both the numerator and the denominator of the odds ratio the probability of getting exactly the observed outcome. Notice that, for that reason, the probabilities in the numerator and denominator of the pseudo-logit, unlike the complementary probabilities in a true logit, do not sum to 1.
In the example in Figure 1, the nominal odds against the no-change hypothesis are almost 50∶12 (the pseudo-logit is log10[.021/.998] = −1.68; the true logit is log10[.021/.979] = −1.67; the pseudo-logit is trivially different from the logit when the probability of getting exactly the observed value is low). Whether this evidence is sufficient to decide that there has been a change in the income depends on the decision criterion, which is one of two free parameters in the model. Also, as with any other hypothesis-testing statistic, a decision criterion (commonly called an alpha level) must be specified when the algorithm is used as a methodological tool in the analysis of experimentally obtained cumulative records. (As already noted, the algorithm is both a critical component of our model and a tool that we use to find change points in cumulative records in our later data analyses.)
A pseudo-logit criterion of 1.5 corresponds (approximately) to an alpha level of .05. If we assume that level in the present illustrative example, then the decision criterion is exceeded, and so a change is detected at the moment t. This moment t is the moment of detection, not the moment at which the change is estimated to have occurred, which is τm. The new estimate of the income from this location, Ilatest, which is the estimate that will be used by the mapping from income estimates to behavior until such time as another change is detected, is the number of pellets obtained in the retrospective interval from t back to τm divided by the duration of that interval: Ilatest = 3/(t − τm) = 3/16.2 = 0.19 pellets/min.
Note that this new estimate is off by a factor of almost 2, because the true rate in the second part of the simulated sequence was 0.1 pellets/min. Rather large errors in the estimated rates are to be expected in a model that assumes that the estimates are based on small samples. In our view, this is a feature not a defect in our model. It explains why matching when measured carefully over modest amounts of time in single subjects is only approximately true, as will be seen in the data we report. Deviations this large from true matching are commonly observed.
The detection of a change in the income stream has two consequences: As already noted, it changes the estimate of the current income. Secondly, it truncates at the estimated point of change the data on which the change-detecting algorithm thereafter operates. The algorithm continues to operate after it has detected a change, but it operates only on the data received after the moment at which it estimated the last change to have occurred. Thus, the origin of the cumulative record it operates on is always the moment just after the last change it detected.
The algorithm for detecting changes in income and obtaining small-sample estimates of the current incomes is our model of how subjects process their experience. The second part of our model specifies the relation between the results of this processing (the income estimates) and the observed temporal investments. This mapping from income estimates to observed visit durations is determined by two constraining equations:
| 1 |
| 2 |
Equation 1 takes matching to be an innate behavioral program. It stipulates that the ratio of the expected (average) duration of the visits to Location 1 to the expected duration of the visits to Location 2 be set equal to the ratio of the current income estimates for those locations. The hats (∧) over the income symbols on the right side of Equation 1 do double duty: They indicate that these are estimates (a common statistical notation) and, moreover, that they are assumed quantities, presumably located in the brain, which cannot be directly observed or measured, unlike the average visit durations on the left of the equation, which are what we measure.
Equation 2 makes the sum of the leaving rates, λ1 and λ2, proportional to the sum of the income estimates. This adjusts the temporal scale of the visiting behavior to the temporal scale of the environment. The more often pellets are set up at one or the other location, the more rapidly the subject must circulate between the locations to harvest them efficiently. If it circulates too slowly, set-up pellets go unharvested for long periods; if it circulates too rapidly, it runs back and forth repeatedly to no avail. Subjects should and do scale the rate at which they cycle between the locations to the rate at which pellets are set-up (Gallistel et al., 2001). This scaling explains the seemingly paradoxical Belke (1992) findings on preference transfer (see Gibbon, 1995). It is closely related to if not identical with Killeen's state of arousal that varies with reinforcement density (Killeen & Bizo, 1998; Killeen, Hanson, & Osborne, 1978).
There are only two free parameters in our model: the decision criterion in the algorithm that detects changes in income, and the constant of proportionality, a, in Equation 2. Plausible values of both are circumscribed. The decision criterion must be reasonable, which is to say roughly that its value should lie between 1 and 6 (corresponding to alpha levels between 0.1 and 0.0000013). The value of a should be about 2, because the average period of an appropriately scaled visit cycle should be about half the expected interval between pellets, taken without regard to location.
Experimental Goals
The model just elaborated takes matching as an innate behavioral program dependent on experience only for the income estimates. Therefore, matching should appear in the naive subject as soon as the subject obtains any data on relative incomes (cf. Davison & Baum, 2000; Shettleworth, Krebs, Stephens, & Gibbon, 1988). The first goal of the present research is to determine whether matching is immediately apparent in the foraging behavior of the experimentally naive mouse under widely varying schedule conditions.
One cannot assess matching in a naive mouse until it is hopper trained, that is, until it seeks for pellets in the feeding hoppers with some regularity, and has begun to circulate between the two hoppers. Therefore, our second goal, which is a necessary preliminary to tracking the appearance of matching, is a characterization of the emergence of hopper poking and rapid cycling between hoppers.
The schedule condition in which the income (number of pellets) obtained from a hopper is directly proportional to the investment in that hopper (time spent poking into and out of it) is of particular interest. When the schedules reward one response more often than the other—in our terms, when the return from one location is higher than from the other—then, as Herrnstein and Loveland (1975) pointed out, there are only two patterns of behavior consistent with the matching law: exclusive preference for the better alternative or exclusive preference for the poorer alternative. In either case, the investment fractions match the income fractions because both ratios are at their limiting values of 1 or 0. Any other investment pattern is inconsistent with matching, because the experienced income ratio is the investment ratio multiplied by the scheduled return ratio:
When the scheduled return ratio (R1/R2) is not 1/1, then the income ratio (I1/I2) and the investment ratio (T1/T2) can be equal only if they are both infinite or both 0.
This critical, purely analytic point is sometimes misunderstood to imply that matching must be observed under these conditions for purely analytic reasons. This is a misunderstanding. The scheduling arrangement does not in any way constrain the behavioral result. Matching may or may not be observed. The analytic point is that the only way it can be observed is if the animal chooses to spend its time almost exclusively at one location or the other. For that reason, how subjects behave under this scheduling condition is a critical test of the hypothesis that matching is innate. Thus, a third goal of the present research is to determine whether the predicted investment pattern (almost exclusive investment in one hopper or the other) is present from the beginning in the experimentally naive mouse, as it should be if matching is innate and dependent only on estimated incomes.
Further, in our model the subject takes no account of the impact of its behavior on its income (no account of the B–O association; where O is a measure of food obtained and B is a measure of the behavior invested to obtain it). Thus, our model predicts that when income is proportional to investment, the positive feedback from the investment ratio to the income ratio should make the exclusive preference for one location or the other unstable. As we show later in a simulation, random variations in the investment ratio from one visit cycle to the next, together with the random fluctuations in the pay-offs from those visits, produce large fluctuations in relative income. These behavior-dependent perturbations in relative income feed back positively to produce a still-greater behavioral shift in the same direction. Thus, on our model, one expects to see abrupt swings in preference, from almost exclusive preference for one hopper to almost exclusive preference for the other. These abrupt swings are characteristic of dynamic systems with destabilizing positive feedback from output to input. Such swings are counterintuitive because, as we will show, the abandonment of a high-return hopper for a low-return hopper need not be justified by any local fluctuation in the returns. Such swings are not predicted, so far as we can see, by any model in which behavior is based on the evaluation of returns, that is, on any assessment of the amount of reward produced by a given amount of behavior (the R−>SR contingency).
The situation in which reward depends on investment is, we believe, the most natural (ecologically valid) from the perspective of both economic theory, with its focus on profit (another word for return), and traditional instrumental learning theory, with its focus on R–O associations and the R−>SR contingency. Yet, from the perspective of our model, this is a quasipathological situation that should produce unstable behavior. Thus, the fourth goal of the present research is to determine whether the predicted instability is in fact observed.
The fifth goal is to characterize the abruptness of the swings observed under the hypothesized unstable condition (assuming that the predicted instability is in fact observed) because, as already noted, the abruptness of large changes in investment ratio is a strong constraint on models of matching.
Schedules of Reinforcement
In the experiments we now report, we tracked the emergence of matching behavior in experimentally naive mice under three different schedules of reward. The schedules varied in how closely relative income was tied to relative investment.
The first schedule was the traditional concurrent random-interval (conc RI RI) schedule with unlimited hold. At each location, pellets are scheduled for delivery (set up) at the end of intervals drawn from exponential distributions. These distributions are completely specified by their expectations, which are, in the limit, equal to the average interval between the harvesting of a pellet and the setting up of the next delivery. The scheduling of pellet deliveries at the one location is independent of the scheduling at the other. When a pellet is set up at a given location, the scheduling of further deliveries at that location stops, resuming only when the subject harvests the already-set-up pellet.
With concurrent random interval schedules, the coupling between investment and income depends on the frequency with which the subject visits the locations. This frequency may be expected to increase in the course of conditioning. If, in the early stages, when it is still accustoming itself to the foraging environment, the subject visits the locations at intervals substantially longer than the expected interval to the next pellet setup, then a pellet will usually be waiting for it whenever it tries either location. Thus, regardless of the expectations of the two scheduling algorithms, the subject will experience high returns and approximately equal incomes from both locations, because it rarely visits (invests in) a location, and when it does, it almost always gets an immediate return. When the frequency of visits increases so that the expected interval between visits is less than the expected setup interval, the returns decrease and the incomes become schedule-limited. Then, the ratio of the incomes (relative income) approximates the ratio of the inverses of the schedule expectancies (relative richness, that is, relative set-up rates).
Our second schedule made the incomes as nearly as possible independent of the investments by allowing set-up pellets to accumulate in a queue. The scheduling of further deliveries does not stop when a pellet is set up. If subsequent pellets are set up before an earlier one has been harvested, they join the queue. When a visit is made, the entire queue is delivered, one pellet after the other in rapid succession. Provided only that the subject visits each location at least occasionally (and subjects always did), the income derived from visiting a given location is always schedule limited and independent of investment (how much time the subject spent at a location). This schedule clamps relative incomes, but not relative returns. It does so, in effect, by varying reward magnitude (number of pellets delivered as one reinforcement) from one reinforcement to the next so as to compensate insofar as possible for the effects of the subjects' sampling behavior on the number of pellets that it obtains from a hopper. Under at least some conditions, matching also is seen when reward magnitude is varied rather than reinforcement frequency (Catania, 1963; Keller & Gollub, 1977; Leon & Gallistel, 1998; Neuringer, 1967; but see Killeen, 1985). Moreover, when both are varied, their effects on the investment ratio combine multiplicatively (Keller & Gollub; Leon & Gallistel), which means that increasing reward magnitude by some factor compensates for decreasing reinforcement frequency by that same factor.
The schedules in the third experiment went to the opposite extreme: they made incomes directly proportional to investments, because the scheduling clock at a given location ran only when the mouse was sampling (investing in) that location, that is, only when the mouse had its head in that hopper. This clamps relative returns, but not relative incomes.
Experiment 1
We ran experimentally naive mice in standard mouse testing chambers with two active feeding hoppers at opposite ends of a common wall. The hoppers delivered pellets on concurrent random interval schedules contingent on the mouse poking its nose into the hopper and thereby interrupting an infrared beam across the hopper opening. There was no chamber familiarization or hopper training. The schedules were in force when the experimentally naive mice were first introduced to the chambers and remained in force through 20 daily sessions.
Method
Subjects
Ten adult female C57Bl/6 (purchased from Harlan, Indianapolis, Indiana, USA) mice served as subjects. They were 12–15 weeks of age and weighed 20–22 g when the experiment began.
Apparatus
The experimental environments were Med Associates mouse testing chambers, 22 × 18 cm in plan and 13 cm high, with two opposing metal walls and the other two walls of PlexiglasTM. Three feeding hoppers (Med Associates ENV-203-20) were set into one metal wall and a fourth was set into the middle of the opposing metal wall, but only the two extreme hoppers on the three-hopper side were active. The interiors of the two active hoppers were continuously illuminated by lights within the active hoppers. The chambers were enclosed within Med Associates sound-attenuating boxes (ENV-022M), 56 × 36 × 38 cm in width, depth, and height. The entrance to each hopper was monitored by an infrared beam (IR), the interruption of which delivered a pellet whenever the IR beam was armed by the scheduling algorithm. If the beam was already interrupted when the schedule armed it, a pellet was delivered immediately. Otherwise, it was delivered at the first interruption following the arming of the beam. The pellets were Research Diets NOYES Precision Pellets, PJAI-0020, Rodent Food Pellet, Formula A/I, 20 mg.
Procedure
The mice were deprived of chow on the evening before the day of the first session. After each session, they were weighed and given chow sufficient to keep them at 85% of free-feeding body weight. The sessions lasted only 25 min. In other experiments, with longer sessions, we repeatedly had observed a marked decrease in food-directed behavior toward the end of sessions. Because this would complicate the quantitative analysis of the development of matching, we hoped to avoid it by keeping the sessions short.
The IR beams were armed by MED-PC® software running on the Windows® operating system, with an algorithm that gives a geometric approximation to a Poisson process. In effect, it flips a coin at one-second intervals. When the coin comes up heads, the beam is armed. The coin flipping then halts and remains halted until the armed beam is interrupted by the mouse, at which point the pellet is delivered, and the scheduling algorithm (the coin flipping) resumes. The expected interval to the next arming is 1 over the probability of the coin coming up heads. For example, when the probability is 1/60, the expected interval to the next arming is 60 s. The distribution of arming intervals thus generated is a geometric approximation to the exponential distribution produced by a continuous Poisson (random rate) process. For 4 of the mice, the expected arming intervals on both sides were 90 s (conc RI 90 RI 90); for 3, they were 60 s and 180 s (conc RI 60 RI 180) and for the remaining 3, they were 180 s and 60 s (conc RI 180 RI 60).
Behavioral Measures and Summary Statistics
The raw data record consisted of successive event codes, recording the onsets and offsets of IR beam interruptions and the delivery of pellets, with time stamps specifying to the nearest 20 ms the time at which the event occurred (in seconds since session onset). Using custom MatlabTM functions, we extracted from these records the duration and frequency of pokes and pellets delivered. From these basic measures, we computed proportion of time spent poking and the visit durations. The proportion of time spent poking specified minute-by-minute the proportion of each minute during which the head was in a feeding hopper. The duration of a visit to Hopper i was the interval from the onset of the first poke there, after one or more pokes at j (the opposite hopper), to the termination of the last poke at i (prior to another poke at j). The interval from the termination of the last poke at i to the onset of the next poke at j was the travel time. The measures of visit durations and travel times parcel the session into four mutually exclusive and exhaustive kinds of intervals: visits to Hopper 1, travel from Hopper 1 to Hopper 2, visits to Hopper 2, and travel from Hopper 2 to Hopper 1. One visit cycle consists of these four intervals in sequence; its duration is their sum.
To track changes in these behavioral measures during the course of the experiment, we made cumulative records of them, exploiting Skinner's (1976) insight that a change in the mean value of a repeated measure is manifest as a change in the slope of its cumulative record. The cumulative record is the sum of all the measurements made so far, plotted usually as a function of either the number of the measurement (1st, 2nd, 3rd, etc.) or cumulative session time (cumulative exposure to the experimental arrangement). The slope of this plot is the average measure per trial or per unit of time, that is, the average increment on the y axis divided by whatever the increment on the x axis is from one measurement to the next.
The use of cumulative records resolves a methodological paradox that arises when one attempts to track changes in the average value of successive measurements. In determining whether or not a subject is matching the ratio of its average visit durations to the ratio of the pellet incomes, one compares two ratios (I ¯1/I ¯2 and T ¯1/T ¯2), each composed of two averages. The averages are necessarily taken over time (over repeated visits and repeated feedings). If the ratios are assumed to be stationary (unchanging in time), then the longer the intervals over which the averages are taken, the more precise the estimates of the averages, hence the estimates of the ratios, hence the power of the comparison between the ratios. But if one is looking for changes in the ratios—and particularly if one wants to estimate how closely changes in one ratio (T ¯1/T ¯2) track changes in the other (I ¯1/I ¯2)—then averaging over long intervals is antithetical to one's goals. It smoothes out the changes and makes it hard to say where they occurred. If, for example, one follows the common practice of averaging over entire sessions, then one cannot determine whether changes occur on a time scale shorter than the duration of a session.
The use of cumulative records resolves this methodological paradox. Cumulative records enable one to see changes in averages without averaging. If the generative process being measured is stationary, then the cumulative record of the measures it generates will have a constant slope, a slope equal to the average value of a measurement. If there is a step change (maximally abrupt change) in the process generating whatever is being measured, then there will be an abrupt change in slope. The abruptness of the change in the slope is not smoothed away by averaging, because the cumulative record is a display of the raw data; nothing is averaged prior to plotting it. That is why we make extensive use of cumulative records in the analyses that follow. We supplement this powerful method of visualization with analyses using the algorithm for finding changes in the slopes of cumulative records that we described in the Introduction. In using this algorithm to find change points in our cumulative records, we let the data suggest where the changes are, and we only average between the changes, not across them.
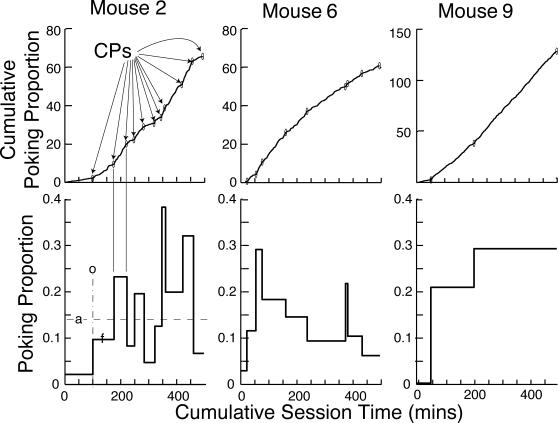
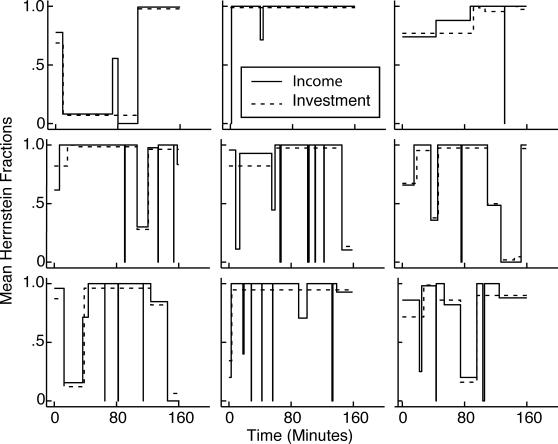
One measure of the intensity of a mouse's food foraging behavior is the proportion of time it spends with its head in a feeding hopper. We use this measure to track the emergence of poking. The upper row of Figure 2 plots for 3 representative subjects the cumulative proportion of each minute that one or another IR hopper-beam was interrupted, as a function of cumulative session time. We used the change-point algorithm to parse the cumulative records into a sequence of straight lines. The slopes of these straight lines are plotted in the lower row of Figure 2. These plots show the successive levels of performance.
Fig 2. Top row: Representative minute-by-minute cumulative records of poking proportion (proportion of each minute during which an infrared beam was interrupted) for 3 representative mice.
The small ovals (CPs) mark the change points found by the change-point algorithm with a logit decision criterion of 4. Bottom row: The slopes of the straight-line segments connecting the change points. These slopes are the mean poking proportion during the successive segments of the parsed cumulative record. Bottom left panel: a = average poking proportion during the last 10 sessions; o = onset of conditioned poking; f = mean poking proportion for the first segment after the onset. The f/a ratio is the first fraction, a measure of the abruptness of a change.
We parse the cumulative records into successive straight-line segments in order to derive descriptive summary statistics. As previously described, the parsing algorithm steps through the record point-by-point, asking at each point whether or not the data up to that point justify the conclusion that there has been a change prior to that point. It does so by finding for each point the previous point that departs maximally from the no-change line. It takes that as the maximally likely estimate of where a change if any occurred and computes the log of the odds against the hypothesis that the data on either side of this putative change point come from the same distribution.
The odds computation depends on the character of the data (binary, integer, or real valued) and on a global assessment of how the measure is distributed. In the case of the minute-by-minute poking proportions, the data are real valued and not normally distributed. Therefore, we use the distribution-free two-sample Kolmogorov-Smirnov test to compute the odds against the hypothesis that the data up to a given point can be represented by a single straight line. When the logit (log of the odds) exceeds our decision criterion, the record is truncated at the estimated point of change, and the analysis begins anew, using only the data after that point.
In parsing the records, we used logit decision criteria of 2 and 4, which correspond to alpha levels of .01 and .0001. The first criterion (logit = 2, p ≈ .01) is a very sensitive one, because the test is performed at each successive point in the record and these records have hundreds of points. It detects transient “changes” that appear to the eye to be just noise. The second criterion is 100 times less sensitive; it detects only those changes that the eye sees as changes. We use two decision criteria in order to determine the effect of the choice of a decision criterion on the resulting summary statistics. Although the choice has a large effect in some individual cases, its impact on the summary statistics is generally minimal (see dashed versus solid lines in Figure 4). Hereafter, we usually only discuss results obtained with the more conservative criterion. The results from the use of the more sensitive criterion are included in plots of summary statistics to enable the reader to assess the impact of making the parser more sensitive.
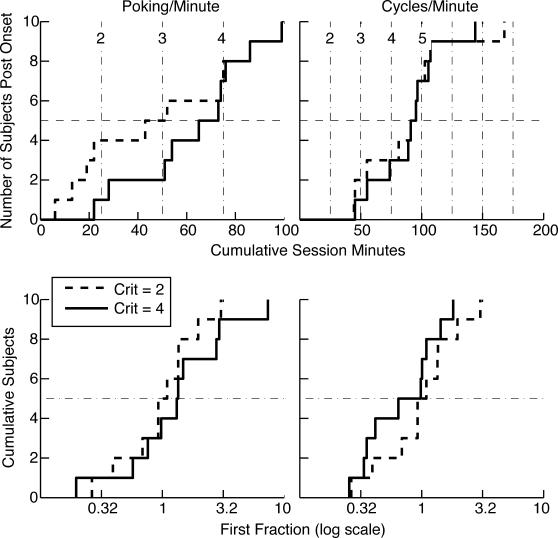
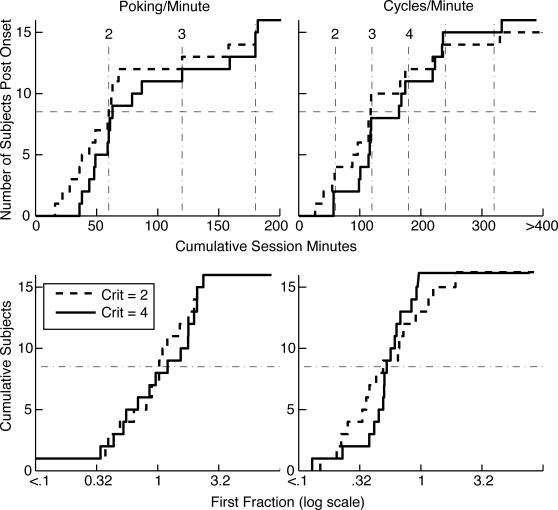
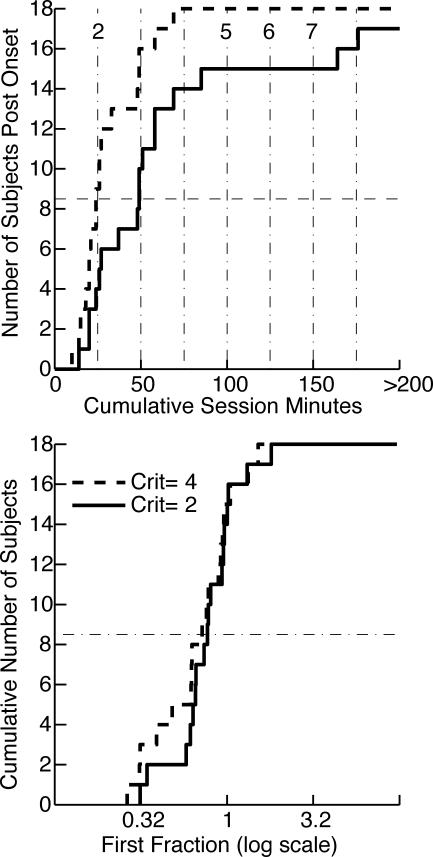
Fig 4. Cumulative distributions of onset latencies and first fractions (the poking proportion immediately after the first increase divided by the asymptotic poking proportion) for poking proportions (poking per min) and cycling rates (cycles per min).
A cumulative distribution shows the number of subjects giving the value on the x axis or less. The x axis value at each upward step gives the datum for one subject. The solid lines are the distributions when a conservative decision criterion is used to parse the cumulative records; the dashed lines are the distributions when a hundredfold-more-sensitive criterion is used. A dashed horizontal line is drawn at 5 to aid in extracting the medians, which are the values on the abscissa at which the cumulative distributions cross this line. In the upper panels, the numbered vertical dashed lines indicate session boundaries. Crit = logit decision criterion used in parsing the cumulative records.
The cumulative records of the minute-by-minute poking proportion begin with a low slope, because our experimentally naive subjects initially spent little time probing the hoppers. At some point during the first four sessions, there was a more or less abrupt increase in the poking proportion, indicated by a sudden steepening of the cumulative record. We call the point at which the slope shows the first increase (as determined by the parsing algorithm) the onset point (o in the lower left panel of Figure 2).
The magnitude of the increase (f in lower left panel of Figure 2) relative to the “asymptotic” level of responding is a measure of the abruptness with which elevated rates of poking appear. ‘Asymptotic’ is in warning quotes because, as this selection of records shows, postacquisition performance is not stable from one 25-min session to the next. In Mouse 2, for example, the postacquisition proportion of time spent poking ranged from 38% to less than 5%, with no clear tendency to increase over sessions. (The proportion on the last two sessions was 13%, the second lowest level of postacquisition responding.) In Mouse 6, there was an initial rapid rise to a high poking proportion (29%) followed by a prolonged decline, with the lowest postacquisition poking proportion (12%) during the final two sessions. Postacquisition instability in measures of behavioral strength is seen in a variety of conditioning paradigms when individual data are analyzed (Gallistel et al., 2004; Papachristos & Gallistel, 2006). (This within-subject instability may be hidden by averaging across subjects before plotting a learning curve, a practice that misrepresents the form of the curve in the individual subjects, see Gallistel et al., 2004). Given the large unsystematic session-to-session fluctuations in postacquisition performance, it is not clear that there is a true asymptote, a stable level of performance attained and maintained by individual subjects. However, to put the size of the initial increase in perspective, it is necessary to have an estimate of the average level of post-acquisition performance. For this purpose, we use the average level of performance over the last 10 sessions (a in lower left panel). Thus, our measure of abruptness is f/a, the ratio of the performance level after the onset to the average level over the last 10 sessions. We call this measure the first fraction.
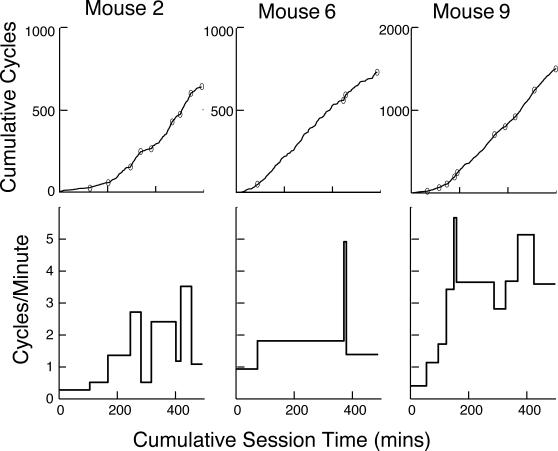
The upper row of Figure 3 plots, for the same 3 subjects, the cumulative number of visit cycles as a function of session time. The cumulative records of this measure were parsed in the same way as the cumulative records of the poking proportion, and the resulting plots of the successive rates of cycling are shown in the bottom row of Figure 3.
Fig 3. Upper row: Representative cumulative records of the number of visit cycles as a function of session time, parsed by the change-point algorithm with a logit decision criterion of 4 (small ovals).
Lower row: Slopes of successive segments of the cumulative record. These slopes are the average cycles per min.
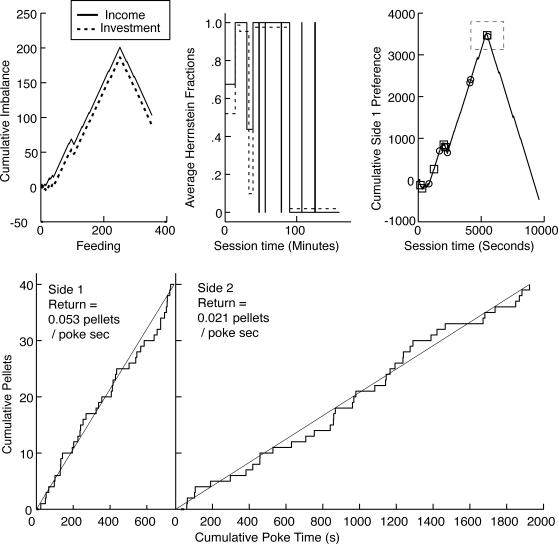
To assess the evolution of the tendency to match the investment fraction to the income fraction, we first compute the feeding-by-feeding income imbalances and investment imbalances. The imbalance is the difference between two complementary Herrnstein fractions. Thus, the income imbalance is I1/(I1 + I2) − I2/(I1 + I2) = (I1 − I2)/(I1 + I2). At any one feeding, the mouse gets a pellet either at Hopper 1 or at Hopper 2, so the possible values of the income imbalance at a single feeding are +1 and −1. The slope of the cumulative income imbalance is the average value of the imbalance. If feedings occur equally often at both Hoppers, the slope is 0; if they occur only at Hopper 1, it is +1; if only at Hopper 2, −1. If they occur 75% of the time at Hopper 1 and 25% at Hopper 2, the slope is +0.5. Similarly, the investment imbalance is T1/(T1 + T2) − T2/(T1 + T2) = (T1 − T2)/(T1 + T2). At any one feeding, this can take on any value between −1 and 1, depending on how the mouse has distributed its visit durations in the interval since the previous feeding. As with the income imbalance, the slope of the cumulative investment imbalance is the average value of this measure. When the slope is 0, the average duration of a visit to Hopper 2 equals the average duration of a visit to Hopper 1. When the slope is .5, the mouse is spending 75% of its total visiting time at Hopper 1 and 25% at Hopper 2, and so on. The mouse is matching when the average investment imbalance equals the average income imbalance, in which case the cumulative records of the two imbalance scores will have the same slope. Thus, a purely visual way to assess matching is to superpose the cumulative imbalance records and compare their slopes (Figure 5). The difference in slope between the two imbalance records is twice the mismatch, that is, twice the difference between the income fraction and the investment fraction.
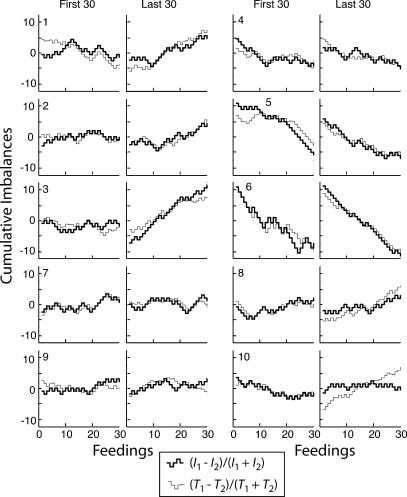
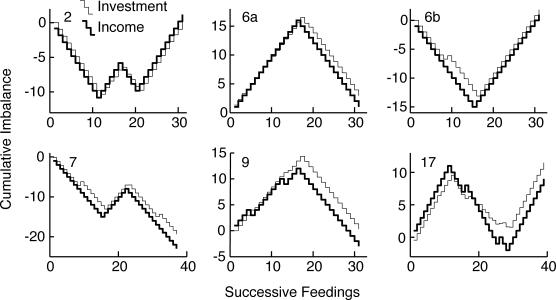
Fig 5. Cumulative records of the feeding-by-feeding income imbalance (heavy lines) and the investment imbalance (light lines) for the first 30 and last 30 feedings.
The imbalance is the difference between two complementary Herrnstein fractions. The number in the upper or lower left corner of the “First 30” panels identifies the subject. For Subjects 1–3, the concurrent random-interval schedules favored Hopper 1 by 3∶1; for Subjects 4–6, they favored Hopper 2, by 3∶1; for Subjects 7–10, the schedule ratio was 1∶1. These records are a sequence of steps because at this resolution one sees every feeding. The imbalances are only recomputed at each feeding, so their cumulative record is flat between feedings and steps up or down at each feeding.
A second way to assess the evolution of matching is to compute the feeding-by-feeding difference between the income and investment imbalances: (I1 − I2)/(I1 + I2) − (T1 − T2)/(T1 + T2). When the mouse is matching the average difference is 0, so the cumulative record of this imbalance difference is flat. The slope of the cumulative imbalance difference is twice the average difference between the income fraction I1/(I1 + I2) and the investment fraction T1/(T1 + T2). If the tendency to match is less initially than later on in training, or if at some point in training a change in the investment fraction lags the change in the income fraction to any appreciable extent, then the absolute value of the slope of the cumulative imbalance difference will be greater than when the investment fraction has been adjusted to match the income fraction. Thus, shifts toward 0 in the slope of the cumulative imbalance difference suggest a lagged adjustment of the investment fraction to the income fraction (a shift in the direction of no difference). The cumulative records of the imbalance difference are plotted and parsed in Figure 6.
Results and Discussion
Conditioned foraging behavior (an elevated poking proportion) and more rapid cycling between hoppers emerged abruptly in most mice, usually at the beginning of a new session (cf. Papachristos & Gallistel, 2006). We judge the onsets to be abrupt because the level of behavior immediately after onset was usually close to the asymptotic level, as shown by the plots of the distributions of first fractions (lower row in Figure 4). In fact, the median first fraction was very close to 1 for both the appearance of increased poking proportions and the appearance of increased rates of cycling between the hoppers.
As may be discerned from the solid line in the upper left panel of Figure 4, the median for the abrupt appearance of a higher proportion of hopper poking in each session minute was at the start of Session 4, although there were two poking-proportion onsets at the start of Session 2 and two more at the start of Session 3. From the corresponding plot in the upper right panel of Figure 4, one sees that the median for the abrupt appearance of a higher rate of cycling between the two hoppers was at the start of Session 5, although there was one such onset at the start of Session 3 and another at the start of Session 4 and one that did not occur until the start of Session 7.
Matching was present from the outset and it did not improve in the course of the 20 sessions. This is seen firstly in Figure 5 where, to facilitate comparison of their slopes, the records of the cumulative income imbalance and the cumulative investment imbalance have been superposed for the first 30 feedings and the last 30 feedings. It may be seen that the slopes match equally well (for all but M10) over the first 30 feedings and the last 30 (and segments thereof).
It also may be seen, however, that in Mice 1–3, the slopes of both imbalance functions are close to 0 over the first 30 feedings whereas they are clearly positive over the last 30 feedings, as they should be given that the concurrent random-interval schedule ratio favored Hopper 1 by 3∶1. The slopes are initially flat because these mice cycled so slowly at the beginning that there was almost always a pellet waiting to be harvested when they got to either hopper. Thus, the effective income ratio was 1∶1 and the matching seen in these subjects initially might be construed to be an artifact of their slow cycling.
The question then becomes, when these subjects began to cycle rapidly enough for the reward schedules to dominate the income fraction, did the adjustment in their investment imbalance lag the change in the income imbalance? The plots of the cumulative feeding-by-feeding imbalance difference in Figure 6 speak to this question. When the cumulative imbalance difference records in Figure 6 are parsed with our customary decision criterion of 4 (using the Kolmogorov-Smirnov test because the differences are real valued and not normally distributed), none of the records has any change points. In other words, using our customary, relatively conservative decision criterion, one would conclude that in none of the 10 mice did the match between investment and income change in the course of the 20 sessions. The Mean Mismatch plots on the right of Figure 6 come from parsing the records with the very sensitive decision criterion of 2. By this analysis, 4 of the 10 mice showed a change in extent of the mismatch between the income fraction and the investment fraction at some point. However, in two instances (Mice 2 and 4) matching was worse after the change (or, in the case of Mouse 4, changes) than it was initially. In the other 2 subjects, the approximation to matching was better after the change than before. However, in 1 of these (Mouse 9), the improvement was from an initial mismatch of −.02 to a terminal mismatch of −.005. In other words, the subject was matching closely at all times. In the 4th subject (Mouse 6), the initial mismatch was −.065 and the terminal mismatch was .035. This is the only subject whose results might be taken to suggest that matching improved by an appreciable amount in the course of training.
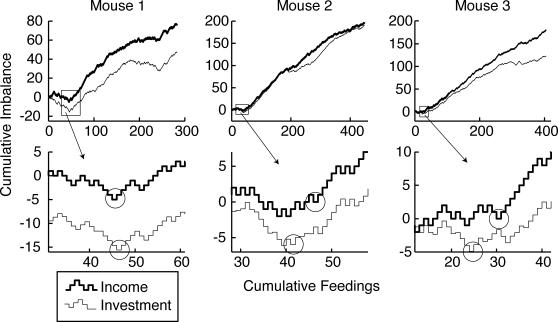
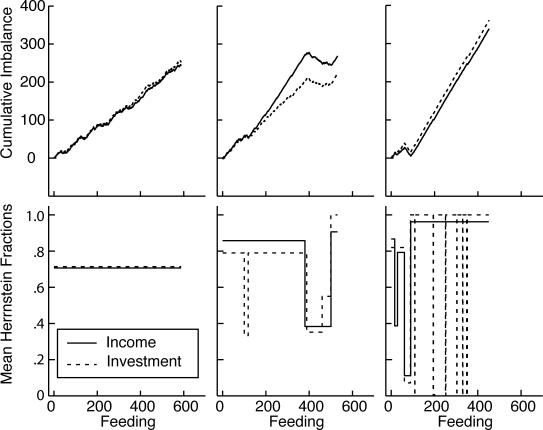
The transitions from balanced incomes and hopper preferences to imbalanced incomes and hopper preferences occurred abruptly in these subjects (M1–M3) when they began to cycle rapidly, as shown in Figure 7. The upper row of Figure 7 plots the complete cumulative income imbalance and cumulative investment imbalance records, while the lower row gives a high-resolution view of these records over the 30 feedings surrounding the transition from approximately flat to positively sloped. The loci of the transition change points found by the parsing algorithm are circled in the lower plots. In these plots, it is apparent that the estimation of a change point, like all statistical estimates, is surrounded by some uncertainty. It is impossible to specify with certainty the particular feeding at which a change should be deemed to have occurred. Nonetheless, it is apparent that the changes in both records are abrupt in all 3 subjects and that they occur at essentially the same time, that is, within the limits to simultaneity judgments imposed by the noise in the data. Because the changes in the income imbalance and the investment imbalance occur at essentially the same time, no increase in their average difference is seen at that time. Such increases, if they were present, would be apparent in the slopes of the cumulative records of their difference in Figure 6. Thus, Figures 5, 6 and 7 all support the conclusion that, with the commonly used concurrent random interval schedules, matching is immediately apparent in the experimentally naive mouse and does not improve over time. The data also support the conclusion that abrupt changes in the income imbalance are accompanied by equally abrupt and essentially simultaneous changes in the investment imbalance (cf. Gallistel et al., 2001).
Fig 7. Cumulative records of the feeding-by-feeding income and investment imbalances for Subjects 1–3.
Upper row: Complete records. Lower row: Thirty feedings surrounding the initial change in slope. Circles indicate the loci of the change points found by the parsing algorithm. For the binary-valued data in the records of income imbalance, the parsing algorithm used the chi square test to compare the proportion of +1 imbalances (feedings at Hopper 1) to the proportion of −1 imbalances (feedings at Hopper 2) before and after a putative change point. For the real-valued and not normally distributed data in the records of investment imbalance, it used the two-sample Kolmogorov-Smirnov test.
Experiment 2
In Experiment 1, the experienced income fraction depended somewhat on the mouse's sampling behavior, particularly in the early stages of training when it sampled each hopper rarely. In this experiment, we eliminated this dependency to the extent possible, by allowing unharvested pellets to accumulate. The Poisson process that scheduled the next pellet set-up did not halt when it set up a pellet. If it set up a second pellet before the already set-up pellet was harvested, the new pellet was added to the queue. There was no limit to how long the queue of to-be-delivered pellets could become. When the mouse finally sampled the hopper, the pellets in the queue were delivered at 0.2-s intervals, one after the other, until the queue was emptied. Thus, provided the mouse sampled both hoppers at least occasionally, the income fraction at any point in training could not diverge far from the programmed value. The programmed values were 1∶3 or 3∶1 for all 16 mice in this experiment.
Method
Subjects
This experiment employed 16 mice with the same specifications as in Experiment 1.
Apparatus
The apparatus used was the same as in Experiment 1.
Procedure
The procedure was the same as in Experiment 1 except that the scheduling algorithm did not halt when it set up a pellet. It continued to run, with scheduled pellets accumulating in a queue, which was emptied when the mouse sampled a hopper. Also, we increased session length to 1 hr because the attempt to eliminate the end-of-session decline in responding did not succeed. The decline seems to occur in anticipation of the end of the session, rather than because the mouse was satiated. The experiment was run in three replications, with 5, 5, and 6 mice, respectively. The numbers of sessions varied from 14 to 18 across replications.
Results and Discussion
Conditioned foraging behavior again appeared more or less abruptly, and its appearance tended to occur at session boundaries, although not so clearly as in the preceding experiment (see the cumulative distributions in Figure 8). Both the onset latency for the increase in the proportion of each minute spent poking and the onset latency for the increase in the cycling rate occurred after roughly the same number of session minutes as in the preceding experiment. For the poking proportions, median onset latencies were near 60 and for cycling rate, near 100 or 120 min. Thus, because session lengths were 60 min in this experiment versus only 25 min in the preceding experiment, onset latencies occurred in an earlier session in this experiment.
Fig 8. Cumulative distribution of onset latencies (top panels) and first fractions (bottom panels).
(The first fraction is the poking proportion immediately after the first increase divided by the asymptotic poking proportion.) Crit = logit decision criterion used in parsing the cumulative records. Dashed vertical lines in top panels are session boundaries. Dashed horizontal lines at the bisection point on the y axis are aids to the extraction of the medians.
For the increase in poking proportion, the first fractions clustered around 1 (medians 1.03 or 1.08, depending on parsing criterion; see Figure 8 lower left), as they did in Experiment 1. In other words, at its first increase, poking proportion went to 100% of its subsequent average value. The onset of rapid cycling was more graded, as indicated by the clustering of first fractions around .5 (median .51 or .47, depending on parsing criterion; see Figure 8 lower right). In other words, at its first increase, the cycling rate went to 50% of its subsequent average value.
Analysis of the cumulative records of the pellets delivered to the two hoppers showed that we succeeded in clamping the income ratio at near the intended 3∶1 or 1∶3 values from the outset. Regardless of the decision criterion used in parsing the cumulative income records, the income fractions showed only minor departures from the intended values.
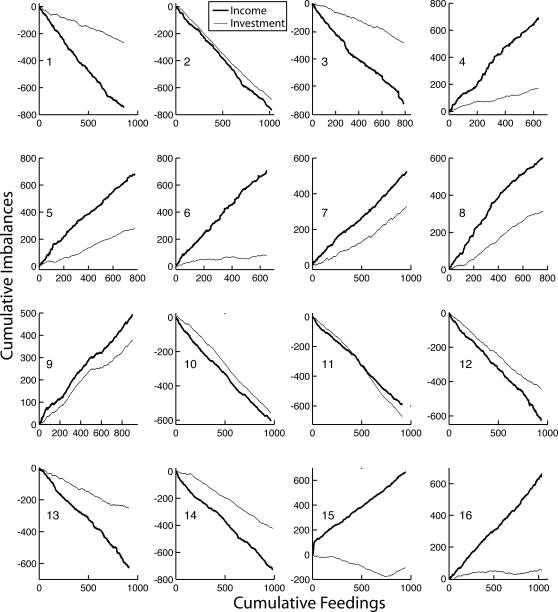
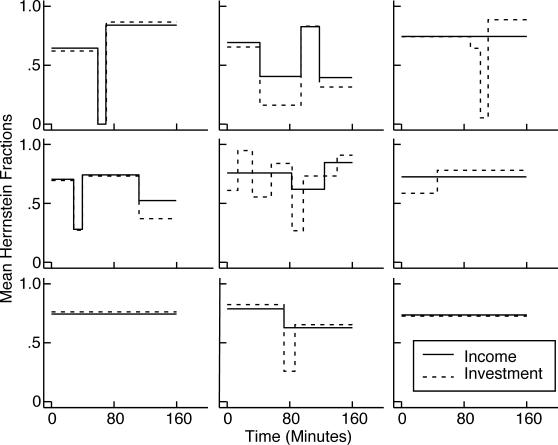
In order to match their investment fraction to their income fraction in this experiment, the mice had to accurately assess the randomly varying intervals between feedings and the varying numbers of pellets received and combine these quantities multiplicatively, because the income from a hopper was the product of the number of feedings per unit of session time and the average number of pellets per feeding. The extent to which subjects matched varied markedly between subjects, as shown by Figure 9, which plots the cumulative records of the feeding-by-feeding income and investment imbalances. Five of the 16 subjects matched very accurately (2, 9, 10, 11, and 12—the numbers on the inside left of the panels in Figure 9 identify the subjects). The close correspondence between the slopes of their income imbalance and investment imbalance records in Figure 9 is the more impressive when it is born in mind that a difference in slope between the income and investment imbalance records is twice the difference in the corresponding Herrnstein fractions (the average mismatch). Eight subjects matched more or less well (3, 4, 5, 7, 8, 13, and 14)—how well is shown in Figure 10. Three subjects did not match, during all or most of the training (6, 15, and 16).
Fig 9. Cumulative feeding-by-feeding imbalance records from Experiment 2.
Heavy lines = income imbalance; light lines = investment imbalance. Numbers at middle-left identify the subjects.
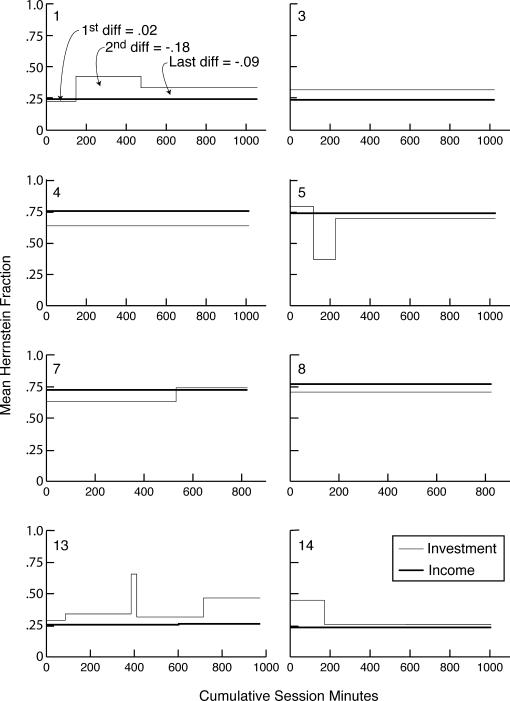
Fig 10. Successive mean Herrnstein income and investment fractions for the 8 mice that matched only approximately, as determined by the parsing algorithm with a decision criterion of 4.
(Four other mice matched almost exactly throughout; and 3 did not match during all or most of training—see Figure 9.) The upper left panel gives the first, second, and last mismatch (income fraction minus investment fraction). The numbers in the upper left corners identify the subjects.
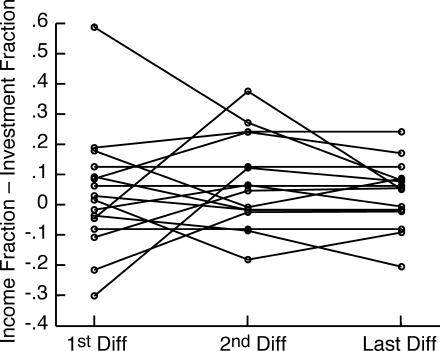
Generally speaking, how well subjects matched did not improve in the course of training. We believe this is apparent in Figure 9. We could not document it using the cumulative feeding-by-feeding difference between the income and investment imbalances, as we did in Experiment 1 (Figure 6), because in this experiment, where pellets can queue, the net income imbalance (the imbalance over several feedings) is not equal to the sum of the feeding-by-feeding imbalances. For example, if the subject gets 15 pellets on arrival at Hopper 1, the imbalance for that feeding is +1; if it next gets 1 pellet at Hopper 2, the imbalance for that feeding is −1. The sum of the imbalances is 0, so the slope of the cumulative imbalance record over those two feedings is zero, but the net imbalance is (15/16) − (1/16) = 7/8. Thus, we cannot compute the mismatch feeding by feeding. We must have recourse to the algorithm for parsing cumulative records into successive segments of presumed constant slope (constant mean Herrnstein fraction), then comparing the slopes as training progresses by plotting them on common axes, as in Figure 10. At any point in training, the estimated mismatch is the difference between the estimated mean income fraction and the estimated mean investment fraction. This is the vertical difference between the two step-plots in each panel of Figure 10 (See “1st, 2nd, and Last Diff” in upper left panel). The first, second, and last differences between these mean Herrnstein fractions for all 16 subjects are plotted in Figure 11. There is no significant tendency for the absolute value of the second or last difference to be smaller than the absolute value of the first difference (both paired-comparison t values < 1.5). The same is true when the records are parsed with a decision criterion of 2 to see whether a very sensitive analysis for changes in slopes can pick up short-lasting large differences at the outset of training.
Fig 11. First, second, and last mismatches (income fraction minus investment fraction).
In summary, when the income ratio is clamped from the outset by allowing scheduled pellets to accumulate in a delivery queue, some mice match very well, some match only moderately well, and some fail to match, but as soon as there are sufficient data to estimate the mismatch, it is on average as small as it will ever be. Thus, under these conditions, too, mice match from the outset, insofar as they match at all.
Experiment 3
In the preceding experiment, we made income independent of investment; in this experiment, we make it completely dependent on investment.
Method
Subjects
This experiment employed 18 mice with the same specifications as in Experiment 1.
Apparatus
The apparatus used was the same as in Experiment 1.
Procedure
The procedure was the same as in Experiment 1 except that the scheduling algorithm for a hopper only ran when the subject's head interrupted the IR beam across the entrance to that hopper. This meant that a schedule only set up a pellet for delivery when the head was in the hopper, so all pellets were delivered at the moment they were set up. For all but 4 of the subjects, the scheduled rates of return were 0.05 and 0.10 pellets per s of poking time. For 2, the ratio of programmed returns was also 2∶1 but the rates were halved (to 0.05 and 0.025 pellets/s); for 2 more, the programmed rates of return were equal (0.05 pellets/s). The actually obtained returns are given in Table 1. The experiment was run in three replications, with 6 mice in each. The number of sessions varied from 14 to 19 across replications. Session length was 25 min, as in Experiment 1.
Table 1. Returns and pellets obtained by subjects in Experiment 3.
| Subject | Returns (pellets/poke-sec) |
Total Pellets Obtained |
||
| Hopper 1 | Hopper 2 | Hopper 1 | Hopper 2 | |
| 1 | 0.11 | 0.06 | 819.00 | 54.00 |
| 2 | 0.11 | 0.06 | 628.00 | 165.00 |
| 3 | 0.11 | 0.06 | 898.00 | 24.00 |
| 4 | 0.12 | 0.06 | 819.00 | 45.00 |
| 5 | 0.11 | 0.06 | 810.00 | 46.00 |
| 6 | 0.11 | 0.05 | 392.00 | 423.00 |
| 7 | 0.07 | 0.11 | 23.00 | 113.00 |
| 8 | 0.06 | 0.10 | 71.00 | 610.00 |
| 9 | 0.06 | 0.11 | 163.00 | 537.00 |
| 10 | 0.06 | 0.12 | 25.00 | 696.00 |
| 11 | 0.06 | 0.11 | 132.00 | 381.00 |
| 12 | 0.05 | 0.12 | 43.00 | 826.00 |
| 13 | 0.10 | 0.04 | 368.00 | 43.00 |
| 14 | 0.12 | 0.05 | 405.00 | 31.00 |
| 15 | 0.06 | 0.06 | 218.00 | 72.00 |
| 16 | 0.05 | 0.02 | 248.00 | 3.00 |
| 17 | 0.06 | 0.03 | 415.00 | 17.00 |
| 18 | 0.05 | 0.04 | 388.00 | 63.00 |
Results and Discussion
As may be seen from the top panel of Figure 12, the onset of an increased proportion of poking time occurred somewhat faster in this experiment than in Experiment 1: the median onset latency fell either at the beginning of the second session or the beginning of the third session, depending on the parsing criterion used. The onset of an increased poking proportion again tended to be abrupt, in that the median first fraction was about 0.75, regardless of the parsing criterion (lower panel of Figure 12), which is to say that when an increase in the poking proportion first appeared it was at 75% of its subsequent average value.
Fig 12. Top panel: Cumulative distribution of the time at which the first increase in poking proportion occurred, for two different parsing criteria.
The dashed vertical lines indicate session boundaries. Bottom panel: Cumulative distribution of first fractions. (The first fraction is the poking proportion immediately after the first increase divided by the asymptotic poking proportion.)
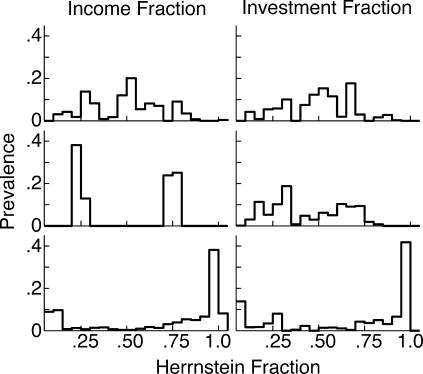
In marked contrast to the preceding two experiments, there was no onset latency for an increase in the cycling rate in this experiment, because the cycling rate did not increase in any subject. In most subjects, it remained at a constant low level (0.39 ± 0.14 cycles/min, at asymptote across all subjects), while in 4 subjects, it decreased to that level from an initially higher level. This asymptotic mean cycling rate is several times slower than in Experiments 1 and 2 (1.73 cycles/min and 1.86 cycles/min, respectively). It is almost three times slower than the slowest rate observed in the 26 subjects in those experiments. Thus, making income proportional to investment greatly increases a subject's tendency to stay at one hopper or the other for prolonged periods rather than cycle rapidly, and that effect is apparent very early. The propensity to devote their time mostly to one hopper is also evident in the two rightmost columns of Table 1, which give the numbers of pellets obtained from each hopper. The ratios of these numbers generally greatly exceed the 2∶1 ratio of rates of return that was programmed for all but 2 of the subjects. It is also seen in Figure 13, which plots the prevalence of the income and preference fractions in the three experiments. The prevalence is the proportion of experiment time during which a fraction of a given magnitude prevailed. For this computation, the fractions are binned at intervals of .05 (0–.05, .05–.1, .1–.15, and so on). In the first two experiments, fractions near .25 and .75 were most prevalent, whereas in this third experiment, the fractions that were most prevalent were at the extremes.
Fig 13. The prevalence of the income and investment fractions in the three experiments.
Prevalence is the fraction of the total time that a given range of fractions prevailed. Ranges are in bins of .05.
Because the subjects in this experiment devoted most of their investment to only one of the hoppers, they, like the subjects in the preceding two experiments, approximately matched their investment fractions to their income fractions throughout the experiment. In Figure 14, the cumulative income- and investment-imbalance plots in most subjects so nearly superpose that only the income plot is apparent, because it obscures the investment plot.
Fig 14. Cumulative income and investment imbalance records.
Where only the income record is apparent, it is obscuring the investment record. The number at upper or lower left of a panel identifies the subject. For Subjects 2, 6, 7, 9, and 17, thin rectangles superposed on abrupt slope reversals indicate the portions of the records shown at high resolution in Figure 15.
The close match between the investment imbalance and the income imbalance is present from the outset, and it does not improve. This is apparent in Figure 14, and it is confirmed by applying the parsing algorithm to the cumulative records of the feeding-by-feeding mismatch scores (income imbalance minus investment imbalance): in 15 of the 18 subjects, there is no change in the mismatch score; in 2, there is a small change for the worse (greater mismatch), and in 1 there is a change for the better.
The tight and stable matching is the more remarkable in that the predicted instability in side preference was observed: In 17 of the 18 subjects, there was at least one reversal of preference; in most subjects, there were several such reversals. In these reversals, the subject abandoned the better side for the worse side for several successive feedings. In some cases, the abandoning of the better side for the worse side was so transient that it is barely discernible in the low-resolution records in Figure 14. However, in all such cases, the period of almost exclusive preference for the poorer alternative lasted at least an order of magnitude longer than average duration of a visit cycle in Experiments 1 and 2. In several cases, it lasted for the better part of a session. In Subject 6, it lasted for more than half the sessions. In short, when income is strictly proportional to investment, subjects do match, which is to say that they spend almost all their time at one hopper or the other, so they get almost all of their income from that hopper. Usually, this is the richer hopper, but the preference for the richer hopper is unstable; sudden shifts to almost-exclusive preference for the poorer hopper are not infrequently observed. In these shifts, both the income imbalance and the investment imbalance go from one extreme to the other within the span of a single interfeeding interval, as shown in Figure 15.
Fig 15. High-resolution cumulative imbalance records covering abrupt reversals.
The numbers inside the panels identify the subject. The portions of the complete records from which these come are indicated by small superposed rectangles in Figure 14. Each step in one of these records corresponds to a single feeding. Where necessary, the records have been vertically displaced to superpose them, facilitating comparison of their slopes.
One of these reversals is examined in detail in Figure 16. The upper panel of Figure 16 plots the cumulative records of the poke durations in the two hoppers (solid lines, left ordinate) and the cumulative records of pellet deliveries (dashed lines, right ordinate), as a function of session time, for the session in which the reversal occurred. These records show the abruptness of the reversal. The estimated point of reversal is indicated by the vertical line in the middle of the plot. Notice that the slope of the cumulative record of pellets obtained after the reversal (the Hopper 2 Pellets record) is less than the slope of the cumulative record of pellets obtained before the reversal (the Hopper 1 Pellets record). These slopes are the incomes (pellets per unit of session time). Thus, the reversal of preference reduced the subject's income.
Fig 16. Analysis of an abrupt reversal in Subject 6.
Upper panel plots the cumulative record of poke durations in the two hoppers (solid lines, left ordinate) and the cumulative record of pellet deliveries (dashed lines, right ordinate), as functions of session time. The vertical line in the middle of the plot indicates the point at which the investments in, and incomes from the two hoppers abruptly reversed. This point of reversal is the vertical line more or less in the middle of the lower panel. To the left of this reversal point, the lower panel plots the cumulative record of pellet deliveries against cumulative poke time in Hopper 1 up to the point of reversal; to the right, the lower panel plots the cumulative record of pellet deliveries in Hopper 2 against poke time in Hopper 2 after the point of reversal. Thin straight lines connect the origins of these records to their end points. The slopes of these lines are the average returns (pellets per s invested in a hopper). Note that the slope of the record on the right (the return from Hopper 2) is everywhere less than the slope of the record on the left (the return from Hopper 1).
The lower panel in Figure 16 plots the cumulative records of pellet deliveries in the two hoppers, as functions of cumulative poke times in the two hoppers, during the session in which the reversal occurred. The vertical line somewhat to the left of the middle of this plot is the point of reversal. The plot on the left is for Hopper 1 up to the moment of reversal; the plot on the right is for Hopper 2 after the moment of reversal. The slopes of these plots are the returns (pellets per s of poking time. The returns differed by a factor of 2 in favor of the abandoned investment in the period immediately surrounding the abandonment. The subject abruptly abandoned the hopper that was providing the higher return in favor of the hopper that provided the lower return, despite the fact that local fluctuations in the returns provided no impetus for this reversal.
There are two striking features of these reversals. First, subjects leave a richer hopper for a poorer hopper, even though in doing so they reduce both their return (the amount of reward per unit of time spent poking) and their income (the amount of reward per unit of session time). Second, they do so abruptly. We stress the abruptness of the reversals in investment because we believe that it presents a significant challenge to models that rely on running averages, as most models do (Dragoi & Staddon, 1999; Sugrue, Corrado, & Newsome, 2004). Figure 15 shows that a complete reversal is often observed between one feeding and the next. Between two feedings, there may be more than one cycle of visits. Figure 17 shows several maximally abrupt reversals, reversals that occur between one visit cycle and the next.
Fig 17. Examples of maximally abrupt reversals.
The investment imbalance (heavy solid line, right ordinate) is plotted against the cumulative investment (cumulative duration of the stays on both sides). Each plot shows a fragment that includes one or more shifts from one extreme to the other in the span of one or two visit cycles. Each step in these stair plots represents the investment imbalance during one visit cycle (consisting of a stay at each hopper). If the step's elevation is close to +1, the investment was almost entirely in Hopper 1; if it is close to −1, the investment was almost entirely in Hopper 2. The width of a step is the total investment on that cycle, that is, the combined duration of the two stays, one at each hopper. The two light lines plot the cumulative excess of the investment in one side over the investment in the other, again as a function of the total investment. The cumulative excess is positive if more time has been spent at Hopper 1 and negative if more time has been spent at Hopper 2. The cumulative excess is plotted either as a continuous function of the cumulative investment (dashed light line) or a step function of the cumulative investment (solid light line). In the latter case, the plot steps at the end of each visit cycle, which is the point at which the excess for that cycle is computed. (The aforementioned heavy line is the discrete derivative of this step plot—the ratio of the signed excess on that visit to the total investment on that visit.) The number at the top of each plot identifies the subject.
In considering the significance of a large change in the investment proportion from one visit cycle to the next, it is important to consider the combined duration of the investments made on the cycle immediately following the shift. If a subject stays only briefly on both sides during a visit cycle, then a large shift in proportion may be ascribed to noise. That is, a shift from an investment proportion of 0.95 to a proportion of 0.05 in the span of one visit cycle is of much greater import when 0.05 = 5 s/100 s than when 0.05 = .05 s/1 s. The large changes in proportion from one visit cycle to the next shown in Figure 17 involve proportions based on large combined investments, as shown by the widths of the postchange steps. Each step in these plots represents one visit cycle. The width of the step is the number of minutes in the combined investment made on that visit cycle.
The widths of the immediate postshift steps in the plots in Figure 17 are measured in minutes. These visits to the newly favored side are orders of magnitude longer than the investments commonly made in any one side within a single visit cycle in Experiments 1 and 2. The median visit durations in Experiments 1 and 2 were 3.8 and 1.5 s, respectively, and the 3rd quartile (75th percentile) was reached at 10.26 and 7.24 s, respectively. Thus, the postchange investments shown in Figure 17 are outside the range of individual investments seen under other conditions. Moreover, the overall rate of reward in this experiment was higher than in the first two experiments. Other things being equal, a higher overall rate of reward shortens the durations of visits (Gallistel et al., 2001). The long visits shown in Figure 17 are a consequence of the subjects' almost-exclusive commitment to one side or the other. The striking thing about this commitment is that it can reverse almost entirely from one visit cycle to the next.
General Discussion
Mice match the ratio of the times they invest in foraging at two hoppers to the ratio of the incomes they have recently received from those hoppers regardless of the coupling between their behavioral investments and the incomes they produce. At one extreme, the incomes are independent of the investments; at the other, they are strictly proportional to them. In either case, in experimentally naive mice, the initial match between the investment ratio and the income ratio is as good, on average, as the final match. There is no tendency for matching to improve as a subject's experience with the two hoppers increases. This suggests to us that matching is innate in Paul Weiss's (1941) sense: “differentiated in [its] essential characteristics independently of the actual intervention of function.” (p. 7). The brain of a mouse that has never foraged between two locations is already programmed to adjust the ratio of the expected visit durations to its current estimate of the ratio of the expected incomes, without regard to the experienced returns, that is, without regard to the amounts of reward it has obtained for the time it has spent or the responses it has made. In Heyman's (1982) terminology, matching is unconditioned behavior; it is insensitive to the R−>SR contingency.
The subjects' seeming indifference to the returns is startling. It appears to be a negation of the most common interpretation of the law of effect, the law that behavior is governed by its consequences. In the instrumental or operant conditioning literature in psychology and the reinforcement learning literature in computer science, this is taken to imply that subjects adjust the mapping between their experience—their current representation of their situation—and their behavior in accord with the effects of that previous behavior. In the computer science literature, this mapping between the perceived current situation and the chosen action is called the subject's policy. The adjustment rule typically imagined is that policies that have led to greater rewards, that is, policies with higher experienced returns have higher value relative to policies with lower experienced returns. It is further assumed that the relative values of policies determine the relative likelihood of their being chosen on the next round (Sutton & Barto, 1998). In psychology, it is usually supposed that the behavior that more frequently produces a reward will grow in relative strength (see, for example, Dragoi & Staddon, 1999). This interpretation of the law of effect is closely related to the rational-agent assumption in economic theory, the assumption that subjects will, on average and in the long run, favor actions that produce higher returns (profits) over actions that favor lower returns.
The assumption that past returns affect future investments, however formulated, requires that subjects assess their returns. Our data suggest that they do not; or, at least if they do, they do not use this assessment when adjusting their investments. Their policy is to match their expected investment ratio to their current estimate of the expected income ratio. That policy does not change.
Our data emphasize the importance of the distinction between a subject's policy and its model of the world, a distinction emphasized in the reinforcement learning literature in computer science, but less so in psychology and economics. The model of the world is the subject's representation of the behavior-relevant aspects of its situation. The policy is the mapping from this representation to its behavior. In the present case, we suggest that the subject's model of the world is its estimate of the currently-to-be-expected incomes from the available foraging locations. What changes with experience are these estimates, not the subject's mapping from them to its temporal (behavioral) investments.
The maximally abrupt changes in investment policy frequently seen in the individual data from Experiment 3 are another theoretically consequential aspect of our data. The abruptness of these changes poses a challenge for models in the family of general linear models (Bush & Mosteller, 1951; Estes & Burke, 1953), to which most models of experience-based decision making belong (Yechiam & Busemeyer, 2005). This includes connectionist models that use the delta rule and most Bayesian learning models. In a general linear model, the expectancies (values, associative strengths, connection weights), that is, the quantities that determine choice or choice probability, are based on averages that are updated trial by trial or response by response. The updating involves a weighted combination of the input on the current trial and the value of the average after the previous updating (the previous trial) (see, for example, Sugrue et al., 2004). The running average produced by this kind of updating can move all the way from one limiting value to the opposite limiting value in a single update only if negligible weight is given to the value on the previous trial. In that case, there is no average; the model tracks the noise in the input; it has no memory for earlier inputs; it remembers only what has just happened. In more complex versions of the running average idea, there are parallel running averages with different rates of decay (e.g., Dragoi & Staddon, 1999).
A distinctive feature of the model of matching that we described in the Introduction and simulate below is that estimates of expected incomes are not continually updated as new data come in. There are no running averages. Rather, there is a process that looks for changes in the income streams. A new estimate of the expected income is made only when this mechanism signals a change. This makes possible two striking features of the data from the third experiment. First, there is the instability, the swings from almost exclusive investment in one hopper to almost exclusive investment in the other. Second, there is the abruptness with which these reversals occur. Similarly large and abrupt adjustments in investment ratios were reported by Gallistel et al. (2001) in rats and by Dreyfus (1991) in pigeons—but only when their subjects frequently encountered changes in the relative rates of reward. Any viable model of matching must be able to produce these abrupt changes, in which subjects switch from one investment ratio to a very different investment ratio within one or two visit cycles (see also Davison & Baum, 2000).
Our model produces abrupt changes because income estimation is discontinuous: an old income estimate is replaced by a new one when a change in the income stream is detected. The new estimate is based only on the subject's experience since the time at which the income stream is estimated to have changed. Because an old estimate is replaced by a new one based on an entirely different sample of the income stream—a sample that is usually not even temporally contiguous with the sample on which the previous estimate was based—the time-allocation ratio can show arbitrarily large step changes.
The change-detecting mechanism also makes it possible for the positive feedback from the investment ratio to the income ratio in Experiment 3 to drive the investment ratio away from the better option toward the poorer option. Although subjects devote most of their time to one hopper, they never stop sampling the other hopper from time to time. Random fluctuations in this sampling, together with the randomness inherent in a random rate of return, will produce apparently significant (in the statistical sense) increases in the income stream from the poorer hopper (see below for illustration). These can divert investment in the direction of the poorer hopper, leading to a decrease in the income from the better hopper, which decrease further diverts investment away from the better hopper toward the poorer hopper.
Generalized Linear Models
The relatively few formalized models of matching that we know of (e.g., Davis et al., 1993; Davison & Baum, 2000; Sugrue et al., 2004) are mostly discrete (see Gibbon, 1995, for one that is not). A discrete model is elaborated by means of a trial-by-trial or response-by-response updating rule (learning rule) for the values (or strengths) of the behavioral options, together with a rule that specifies how these translate into choice probabilities. The updating equation is typically of the form:
| 3 |
where sn is the (underlying) strength on trial n, r is 0 when there is no reinforcement and 1 when there is, and 0 < α < 1. Yechiam and Busemeyer (2005) call this the general linear model. In this model, strength approaches asymptote as sn − αsn → βp(r), that is, as the loss of strength due to discounting by the factor α grows to equal the average increment, which is the increment (β) due to reinforcement times the probability of reinforcement, p(r). The relative magnitudes of the increment parameter, β, and the discount parameter, α, determine how effective the most recent reinforcement is relative to the accumulated effect of past reinforcements: the greater β and the smaller α, the more rapidly the process adjusts. For that reason, it is conceptually helpful to reparameterize Equation 3 with a single learning rate parameter:
| 4 |
where 0 < γ < 1. The greater the learning rate, γ, the more rapidly the system adjusts.
Variants of the general linear model can accurately predict behavior, including transitional behavior, in discrete-trial paradigms (Sugrue et al., 2004), provided that they assume a rapid rate of learning and that the probability of choosing a response is proportional to its relative strength:
| 5 |
The assumption in Equation 5 is the assumption that matching is innate. A MatlabTM script that simulates matching by response-strength updating according to 5 may be downloaded from http://ruccs.rutgers.edu/∼galliste/JEAB_Matching_Simulations.zip. It is based on code initially written in Basic by Peter Killeen. General linear models that predict matching with this response rule do so under assumptions that make the underlying relative strengths proportional to the relative incomes, which is why Sugrue et al. (2004) call these strengths “local incomes.” This must be so, because Equation 5 asserts that the proportion that holds between the observed response frequencies is the same as the proportion that holds between the underlying strengths. When we ran simulations of this model (following Killeen's lead), we found that the returns per response are not equated, even though the response is the event that triggers updating of strength. The returns per time invested are equated, even though this measure of behavior plays no role in the machinery of the general linear model. In short, the ability of a general linear model to simulate matching under these assumptions is consistent with our claim that matching is innate and based on income estimates, not on the equation of returns.
Difficulties in the Application of Discrete Models
In trying to apply discrete models to unconstrained foraging behavior, formulating a workable definition of a trial or a response is difficult. A subjective trial is the interval at the end of which the subject updates the internal variables (response strengths, associative strengths, return or income estimates, and so on) that determine the observed pattern of behavior. If we adopt a discrete updating model, then the need to postulate internally determined, behavior-independent intervals at which updating occurs appears inescapable (Davison & Baum, 2000; Gallistel & Gibbon, 2000; Gibbon, 1981; Lea & Dow, 1984; Rescorla & Wagner, 1972). There does not appear to be a way to make the occurrence of a trial a function of observable events, either environmental events or behavioral events (Gallistel & Gibbon).
Consider then what we might use as the subjective trial duration in analyzing the results at hand. In the first two experiments, the subjects rarely stayed at one hopper for more than a few seconds. Stays of a fraction of a second were common. To get stays that short from a discrete model, we need to assume that subjective trials last only a small fraction of a second; let us say 0.1 s. Then, because the duration of a subjective trial is two or three orders of magnitude shorter than the intervals between rewards, most subjective trials are unreinforced trials. This causes problems, both for models based on returns and for models based on incomes.
In the first case, for models based on returns, the value of the foraging location that the subject is currently visiting is discounted on unreinforced trials (of which there are a great many), while the value of the other location is not. Thus, the hopper the subject is currently visiting rapidly loses relative value during interreinforcement intervals. If we assume the rate of decay per trial that Sugrue et al. (2004) found worked best (a time constant of nine subjective trials, that is 0.9 s), then the hopper being visited loses 90% of its value during any 2-s period without a feeding and more than 99.99% during any period in which the cumulative duration of the unreinforced visits since the last reinforcement exceeds 10 s. (The shorter we assume subjective trials are, the worse this problem gets.) Thus, the relative value of the other option should increase rapidly during unrewarded stays. This should make the probability of terminating a stay increase with the duration of that stay, but that probability does not increase (Gibbon, 1995; Heyman, 1979). Moreover, it should make long stays on one side impossible, but stays of many seconds are in fact common.
In the second case, for models based on incomes, the value of an option not chosen is discounted on every trial. This income-based model is unstable: the longer a subject stays with one option, the more likely it is to continue with it, because the value of the option currently being exercised increases whenever it is reinforced, while the value of the unexercised option is discounted on every subjective trial. Thus, the value of an option not being exercised rapidly becomes orders of magnitude smaller than the value of the option being exercised. This stability problem exists even when modeling discrete-trial probability matching. To surmount this problem, Sugrue et al. (2004) assumed that the running averages of incomes did not decay to zero but rather to some small minimum. In the continuous case, however, there are long sequences of trials where both options are not reinforced, causing both running averages to decay down to the limiting value, making the choices equally probable regardless of the relative rates of reward.
Worse, however, is the problem we confront when we apply the assumption that subjective trials last only a fraction of a second to the results from Experiment 3. In this experiment, the subjects not uncommonly stayed on one side for many minutes. The average interval between rewards measured on a clock that ran only when the subject's head was in the hopper was 10–20 s. During a stay, the head was in the hopper only on the order of 40% of the time, so the interreward intervals measured on a clock that ran only during a stay was on the order of 25–50 s, and sometimes much longer. If a subjective trial lasts on the order of 0.1 s, then between successive reinforced subjective trials, there are commonly hundreds of unreinforced subjective trials, sometimes thousands.
Instead of assuming a fixed value for the duration of a subjective trial, it is tempting to make subjective trial duration proportional to the expected interval between rewards. Then, the greater the temporal density of rewards in an environment is, the shorter the subjective trial duration becomes. That assumption makes the just-described incompatibility between the results of the first two experiments and the results of the third experiment worse, because the overall rate of reward was higher in the third experiment than in the first two, which would make the duration of a subjective trial in Experiment 3 shorter than in Experiments 1 and 2.
Similar difficulties arise in models that update response-by-response rather than trial-by-trial. In our paradigm, which we take to be closer to natural foraging than are paradigms that use an artificial manipulandum, the mouse shuttles back and forth between the two hoppers. When it is at a hopper, it pokes its head in and out. Usually, it does so rather rapidly. However, the durations of pokes vary by two orders of magnitude. Some last only a 50th of a second; some last several seconds. The number of pokes recorded depends strongly on where the mouse pokes in relation to the IR beam. When it pokes only so far that its nose partially interrupts the beam, one gets high frequency poke jitter. Some mice tend to do this, whereas others poke further in.
We cannot call a visit a response, because then there are visits with multiple reinforcements spaced in time. The general linear model is not easily modified to take account of multiple reinforcements for a single response. Even when we treat single pokes as responses, it can happen that more than one pellet is delivered during a single poke. That is sufficiently rare that we could perhaps ignore such instances. But is a .02-s poke to be counted the same as a 2-s poke, despite the 100-fold difference in duration? And what about a 1-s-long sequence of jitter pokes, containing 20 pokes? Should this be counted as 20 responses in 1 s? In short, it is no small challenge to say what aspect of the naturally foraging animal's behavior constitutes a response. Answering that question is a precondition for applying a response-based updating model to our data.
Response definitions that might work for Experiments 1 and 2, where visits lasted at most a few seconds, will not work for Experiment 3, where visits lasted minutes. The problem is similar to the problem that arises with trial-based updating: To get abrupt transitions one needs a high learning rate parameter—a value of γ in Equation 5 on the order of .1 or higher. Then, however, the effects of past reinforcement on strength are strongly discounted after each nonreinforced response, in which case long sequences of unreinforced pokes, which were common in Experiment 3, reduce response strength to a negligible level.
This last difficulty reminds us that both trial-based models and response-based discrete updating models have the property that the longer a run of unreinforced responses grows, the more probable the switch to the other location becomes. The absence of such a pattern in the data is what led Heyman (1982) to suggest that matching was unconditioned behavior.
In summary, running average models of matching have often been developed within the context of discrete-trial or discrete-response paradigms. It is not clear how to apply them to a free-foraging paradigm, for reasons that Lea and Dow (1984) analyzed at some length. The problem is to find a principled way to define a trial or a response. The difficulty does not confront the model we propose, because the income estimates in this model are not running averages and because visit durations are clearly defined.
Simulation
Because the behavior in Experiment 3 is so counter-intuitive, the claim that the model of matching elaborated in the Introduction predicts this behavior may be as mysterious as the behavior itself. To confirm that the model does predict such behavior, and as an aid to understanding its properties, one of us (DG) has developed a computer simulation in MatlabTM, the code for which may be downloaded from http://ruccs.rutgers.edu/∼galliste/JEAB_Matching_Simulations.zip.
Here, we first show how a simulation based on Equations 1 and 2 generates results similar to those seen in Experiments 1 and 3 and then discuss in detail how it can generate an abrupt and persistent change to a less-desirable location, as seen in Experiment 3. In the simulation, pellet delivery and expected stay durations are simulated by random-rate processes; thus, each simulation represents an individual animal's unique experience with a probabilistic environment. The output of the simulation is a second-by-second record of time allocation between two locations (hereafter referred to as hoppers).
To see the model's behavior in its most basic form, consider the left panel of Figure 18. Depicted are the results of a representative simulation when the RI schedule at Hopper 1 is twice as rich as the RI schedule at Hopper 2, and no change detection algorithm is applied to the income stream. The top graph depicts cumulative location preference and cumulative income imbalance. That the two cumulative records fall close to one another means that the simulation has generated matching behavior. This may be seen in a different way in the bottom graph, which depicts the sequence of Herrnstein fractions generated by parsing the cumulative preference and imbalance vectors with the previously described change-point algorithm. Note that the Herrnstein fractions for preference and income are generally close together and that they hover around a value of 2/3, meaning that twice as much time is spent and twice as much income is obtained at Hopper 1.
Fig 18. Representative simulations under three conditions.
Top panels: Cumulative records of feeding-by-feeding income and preference differences. Bottom panels: Mean Herrnstein fraction between change points, after parsing cumulative records with a logit decision criterion equal to 2. Left: Income independent of behavioral investment, no change-detection mechanism. Middle: Income independent of investment, change-detecting mechanism added. Right: Income proportional to behavioral investment, with change detection.
The middle of Figure 18 depicts a second simulation with the same input parameters as the first, except this time with the addition of the change-point algorithm applied to the interreward intervals. This is how the model simulates the conditions of Experiment 1. It might be somewhat surprising that change-points are found at all in this condition, as the models starts out with the assumption that time allocation matches programmed schedules. Why should it change if it's right to begin with? The answer is that both income delivery times and visit durations are probabilistic. Sometimes, by chance, it arises that there is statistical backing in favor of an income that differs from the programmed rate. This is inevitable when a sensitive change-detector operates in a probabilistic environment: sooner or later, it will detect a change when there is none. The lower the decision criterion is, the more often spurious changes will be detected.
The right of Figure 18 depicts a third simulation, identical to the last but with one exception. The clock that decides when to deliver a pellet to a hopper runs only when the animal is at that hopper. This is how the pellet deliveries were scheduled in Experiment 3, producing very long stays at the richer location, with occasional abrupt switches to the poorer location, where the mice sometimes stayed for long intervals. What can be seen in the rightmost graphs of Figure 18 is that the model also generated this general pattern of behavior.
Figures 19 and 20 each depict nine simulations under the conditions of Experiments 1 and 3, respectively. Each panel within the figures is a plot of the investment and income imbalances between change points. These simulations differ from those in Figure 18 in how the simulations were initiated. Here, expected stay durations at the two locations were set as equal until both locations produced a reward, after which the first sequences of expected visit durations were generated. This is more like the situation faced by the experimental mouse that has no way of knowing which location is preferable at the outset. Matching is seen in both figures, but the patterns are otherwise very different. When the clock runs independent of behavior, matching occurs because, within a typical cycle, animals spend about twice as much time at the location that delivers rewards twice as often (Figure 19). When the running of the scheduling clock depends on where the subject is, matching occurs because on each cycle simulated subjects spend the vast majority of time at one location or the other and so get almost all rewards from that location (Figure 20).
Fig 19. Between-change-point Herrnstein fractions at the richer location in nine random simulations, with income independent of behavioral investment.
Change-point logit criterion = 2. Hoppers 1 and 2 delivered rewards on RI 20-s and RI 40-s schedules, respectively.
Fig 20. Between-change-point Herrnstein fractions at the richer location in nine random simulations, with income proportional to behavioral investment.
Change-point logit criterion = 2. Hoppers 1 and 2 delivered rewards on RI 20-s and RI 40-s schedules, respectively, where I is the time on the clock that ran only when the head was in that hopper.
To better understand the unstable behavior of the model in Figure 20, consider the simulation shown in Figure 21. In the top three panels, the simulated animal spent most of its time at the richer location before suddenly shifting to and remaining at the poorer location. The graphs in the left and middle panels are the already familiar plots of cumulative imbalance and average Herrnstein fractions. The graph in the right panel shows cumulative preference for the richer location on a second-by-second basis. Superimposed are change points in the subjective income estimates for the richer location (circles) and the poorer location (squares). Our focus is on the abrupt transition from the richer to the poorer hopper in the part of the record delineated by the dashed rectangular box.
Fig 21. A simulation under the conditions of Experiment 3.
Top Left Panel: Cumulative record of feeding-by-feeding income and preference differences. Top Middle Panel: Between-change-point Herrnstein fractions for income and preference. Top Right Panel: Second-by-second cumulative record of investment imbalance (preference) for the rich hopper (Hopper 1). Preference is 1 if the second was spent at the richer location and −1 if it was spent at the leaner location. Open circles mark changes in income estimates for the richer location. Open squares mark changes in income estimates for the poorer location. The dashed rectangle indicates the period covered by the plots of returns in the lower panels. Bottom Left Panel: Cumulative feeding-by-feeding return for the 40 richer location feedings that preceded the switch to the poorer location. Bottom Right Panel: Cumulative return for the 40 poorer location feedings that followed the switch. The schedules for Hoppers 1 and 2 delivered rewards on RI 20-s and RI 40-s schedules, respectively, where I is the time on the clock that ran only when the head was in that hopper.
The occurrence of this switch is simply a product of chance. After 617 s at the richer location, the simulated animal moved to the poorer location, to remain for 81 s. Although the income estimates from which these stay times derived also happened to differ by almost a factor of eight, the stay durations were both several times longer than average. Usually, an unusual event such as this is needed to prompt a prolonged shift to the poorer hopper. In this case, after 61 of 81 s at the poorer hopper, two rewards were delivered in the span of 4 s. Because these were the first rewards received at that hopper in 753 s of session time (most of which was spent elsewhere), this led to a change to a high income estimate for the poorer hopper. The change was detected because there was such a long period of time preceding the two rewards when none was delivered at that hopper, mostly because visits there were widely spaced and brief. The longer a hopper has gone without delivering a pellet, the lower the estimated income from it becomes, and the easier it is for chance to produce a significant increase in that estimate. This is a kind of negative feedback in that neglecting a hopper for long periods of time sets up conditions that favor a positive change in the income estimate for that hopper, and any such increase counteracts the previous tendency to neglect the hopper.
In this case, the new income estimate for the poorer hopper was sufficiently high that the richer hopper was neglected. After 129 s without reward at the richer hopper (because the simulated subjects spent almost all of that time at the poorer hopper), the income estimate for the richer hopper diminished, leading to even less time spent there. Neglect leading to greater neglect is an example of positive feedback in the model.
The bottom panels of Figure 21 show cumulative returns at the richer and poorer hoppers for the time surrounding the switch from the richer to the poorer hopper. The left panel shows cumulative return at the richer hopper for the 40 feedings immediately preceding the switch, and the right panel shows cumulative return at the poorer hopper for the 40 feedings immediately following the switch. If behavior were based on returns, then there would be no reason for the enduring switch to the poorer hopper, because the return there after the switch is consistently lower than the return at the better hopper prior to the switch. Thus, the model generates shifts from the better investment to the poorer in the absence of evidence that the returns have changed. This is the most paradoxical of the behavioral findings.
In the other situation, where the clock runs independently of behavior (Experiment 1, Figure 19), the probability of reward at a hopper increases as time is spent at the other hopper. Because of this, and because hoppers are never fully neglected, it is difficult for there to be long stretches when no reward is obtained at one of the two hoppers. This prevents both the negative and positive feedback that cause the model to abruptly switch from one prolonged investment to another prolonged investment. For this reason, the model generates different patterns of behavior for the situations corresponding to those of Experiments 1 and 3, patterns of behavior that appear to capture many of the elements of the observed mouse behavior.
The only free parameters in this model are the decision criterion in the change-point algorithm and a, the constant of proportionality between overall income and the cycling rate. The values of both are narrowly constrained by a priori considerations. Models of animal learning and behavior that generate second-by-second simulated data records of free-operant behavior that are difficult to distinguish from the records generated by the subjects themselves are rare. It is of some interest that a model with only two narrowly constrained free parameters can come close to passing Church's “Turing” test (Church & Guilhardi, 2005) of formally specified (hence, simulatable) models of behavior.
Conclusions
The experimentally naive mouse is initially wary of feeding hoppers and pokes into them infrequently. Its rate of poking increases abruptly after a few sessions, usually at the start of a new session. If the income to be obtained by poking is more or less independent of the visit frequency, then it abruptly begins to cycle rapidly between the hoppers, at or soon after the increase in its rate of poking. In contrast, when income is proportional to investment, the initially low rate of cycling remains low and may go even lower, because subjects remain on one side for many successive feedings. This almost never happens when income is more or less independent of investment. Thus, the coupling between investment and income or the lack thereof has a dramatic effect on the pattern of investment. However, in all cases, the investment ratio approximately matches the income ratio, and it does so from the beginning.
When income is proportional to investment, investment is usually concentrated at the richer hopper, which is economically rational. However, this concentration is unstable: subjects not infrequently abandon the richer option to make a prolonged investment in the poorer option, even though the income thus obtained is less than the income they would have obtained had they continued to invest in the richer option. Changes in investment track changes in income very closely and investment can swing from one extreme to the other with maximum abruptness, that is, from one visit cycle to the next.
The results strongly constrain possible models of matching. It is, for example, unclear that these results are consistent with any model that assumes that behavioral change is based on an estimate of the amount of reward obtained for a given amount of behavior (that is, on the estimation of returns). It also is unclear how any model that assumes a running average of either incomes or returns could predict the observed abruptness of the changes in investment. A purely feed-forward model that makes episodic, non-overlapping, small-sample estimates of income accounts for our findings.
Acknowledgments
The authors thank Peter Killeen and three anonymous referees for extensive and very helpful comments and suggestions. This work was supported by NIMH Grant R21 MH63866 to CRG.
Footnotes
It was this finding that led Heyman (1982) to suggest that matching was unconditioned behavior. This finding, that the leaving probability does not depend on elapsed visit time, is inconsistent with the assumption that leaving is sensitive to the reinforcement contingencies in concurrent RI RI schedules because the longer the subject has been at one location, the more probable it is that leaving it for the other location will be reinforced.
See Footnote 3 on why this should not be interpreted as equivalent to a significance level or a Bayes factor. It is functionally equivalent in the sense that it is a measure of the strength of the evidence. In many cases, including the present one, the computation can be reformulated so as to yield a true Bayes factor, but the practical effect of this is only to change the range of useful decision criteria.
Useful decision criteria tend to be higher in change-detection than in other statistical decision settings because there is an inescapable multiple-comparisons problem in change detection: the longer one observes a stationary (unchanging) random process (e.g., coin flipping), the more certain it is that one will observe an improbable sequence (e.g., 10 heads in a row). Thus, our algorithm should not be used for obtaining significance levels. A modified version of it might be used to compute the Bayes factor in a relative likelihood analysis (Glover & Dixon, 2004), provided that one used an appropriate correction for the additional free (data-derived) parameters in the change model, such as the Schwartz criterion (Kass & Raferty, 1995; Schwartz, 1978).
References
- Balsam P.D, Fairhurst S, Gallistel C.R. Unsignaled unconditioned stimuli degrade contingencies by changing cycle time and temporal uncertainty. Journal of Experimental Psychology: Animal Behavior Processes. doi: 10.1037/0097-7403.32.3.284. in press. [DOI] [PubMed] [Google Scholar]
- Belke T.W. Stimulus preference and the transitivity of preference. Animal Learning & Behavior. 1992;20:401–406. [Google Scholar]
- Bush R.R, Mosteller F. A mathematical model for simple learning. Psychological Review. 1951;58:313–323. doi: 10.1037/h0054388. [DOI] [PubMed] [Google Scholar]
- Catania A.C. Concurrent performances: A baseline for the study of reinforcement magnitude. Journal of the Experimental Analysis of Behavior. 1963;6:299–300. doi: 10.1901/jeab.1963.6-299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Church R.M, Guilhardi P. A Turing test of a timing theory. Behavioural Processes. 2005;69:45–58. doi: 10.1016/j.beproc.2005.01.001. [DOI] [PubMed] [Google Scholar]
- Davis D.G, Staddon J.E.R, Machado A, Palmer R.G. The process of recurrent choice. Psychological Review. 1993;100:320–341. doi: 10.1037/0033-295x.100.2.320. [DOI] [PubMed] [Google Scholar]
- Davison M, Baum W.M. Choice in a variable environment: Every reinforcer counts. Journal of the Experimental Analysis of Behavior. 2000;74:1–24. doi: 10.1901/jeab.2000.74-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dragoi V, Staddon J.E.R. The dynamics of operant conditioning. Psychological Review. 1999;106:20–61. doi: 10.1037/0033-295x.106.1.20. [DOI] [PubMed] [Google Scholar]
- Dreyfus L.R. Local shifts in relative reinforcement rate and time allocation on concurrent schedules. Journal of Experimental Psychology: Animal Behavior Processes. 1991;17:486–502. [Google Scholar]
- Estes W.K, Burke C.J. A theory of stimulus variability in learning. Psychological Review. 1953;60:276–286. doi: 10.1037/h0055775. [DOI] [PubMed] [Google Scholar]
- Gallistel C.R, Gibbon J. Time, rate, and conditioning. Psychological Review. 2000;107:289–344. doi: 10.1037/0033-295x.107.2.289. [DOI] [PubMed] [Google Scholar]
- Gallistel C.R, Mark T.A, King A.P, Latham P. The rat approximates an ideal detector of changes in rates of reward: Implications for the law of effect. Journal of Experimental Psychology: Animal Behavior Processes. 2001;27:354–372. doi: 10.1037//0097-7403.27.4.354. [DOI] [PubMed] [Google Scholar]
- Gallistel C.R, Balsam P.D, Fairhurst S. The learning curve: Implications of a quantitative analysis. Proceedings of the National Academy of Sciences. 2004;101:13124–13131. doi: 10.1073/pnas.0404965101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibbon J. The contingency problem in autoshaping. In: Locurto C.M, Terrace H.S, Gibbon J, editors. Autoshaping and conditioning theory. New York: Academic; 1981. pp. 285–308. [Google Scholar]
- Gibbon J. Dynamics of time matching: Arousal makes better seem worse. Psychonomic Bulletin & Review. 1995;2:208–215. doi: 10.3758/BF03210960. [DOI] [PubMed] [Google Scholar]
- Glover S, Dixon P. Likelihood ratios: A simple and flexible statistic for empirical psychologists. Psychonomic Bulletin & Review. 2004;11:791–807. doi: 10.3758/bf03196706. [DOI] [PubMed] [Google Scholar]
- Gottlieb D.A. Acquisition with partial and continuous reinforcement in rat magazine approach. Journal of Experimental Psychology: Animal Behavior Processes. 2005;31:319–333. doi: 10.1037/0097-7403.31.3.319. [DOI] [PubMed] [Google Scholar]
- Gottlieb D. Is the number of trials a learning-relevant parameter? 2006. [Google Scholar]
- Herrnstein R.J. Relative and absolute strength of response as a function of frequency of reinforcement. Journal of the Experimental Analysis of Behavior. 1961;4:267–272. doi: 10.1901/jeab.1961.4-267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein R.J, Loveland D.H. Maximizing and matching on concurrent ratio schedules. Journal of the Experimental Analysis of Behavior. 1975;24:107–116. doi: 10.1901/jeab.1975.24-107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein R.J, Prelec D. Melioration: A theory of distributed choice. Journal of Economic Perspectives. 1991;5:137–156. [Google Scholar]
- Heyman G.M. A markov model description of changeover probabilities on concurrent variable-interval schedules. Journal of the Experimental Analysis of Behavior. 1979;31:41–51. doi: 10.1901/jeab.1979.31-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyman G.M. Is time allocation unconditioned behavior? In: Commons M, Herrnstein R, Rachlin H, editors. Quantitative analyses of behavior: Vol. 2. Matching and maximizing accounts. Cambridge, MA: Ballinger Press; 1982. pp. 459–490. [Google Scholar]
- Higa J.J, Thaw J.M, Staddon J.E.R. Pigeons' wait-time responses to transitions in interfood-interval duration: Another look a cyclic schedule performance. Journal of the Experimental Analysis of Behavior. 1993;59:529–541. doi: 10.1901/jeab.1993.59-529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinson J.M, Staddon J.E.R. Matching, maximizing, and hill-climbing. Journal of the Experimental Analysis of Behavior. 1983;40:321–331. doi: 10.1901/jeab.1983.40-321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kass R.E, Raferty A.E. Bayes factors. Journal of the American Statistical Association. 1995;90:773–795. [Google Scholar]
- Keller J.V, Gollub L.R. Duration and rate of reinforcement as determinants of concurrent responding. Journal of the Experimental Analysis of Behavior. 1977;28:145–153. doi: 10.1901/jeab.1977.28-145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killeen P.R. Incentive theory IV: Magnitude of reward. Journal of the Experimental Analysis of Behavior. 1985;143:407–417. doi: 10.1901/jeab.1985.43-407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killeen P.R, Bizo L.A. The mechanics of reinforcement. Psychonomic Bulletin & Review. 1998;5:221–238. [Google Scholar]
- Killeen P.R, Hanson S.J, Osborne S.R. Arousal: Its genesis and manifestation as response rate. Psychological Review. 1978;85:571–581. [PubMed] [Google Scholar]
- Lea S.E.G, Dow S.M. The integration of reinforcements over time. In: Gibbon J, Allan L, editors. Timing and time perception: Vol. 423. New York: Annals of the New York Academy of Sciences; 1984. pp. 269–277. [DOI] [PubMed] [Google Scholar]
- Leon M.I, Gallistel C. Self-stimulating rats combine subjective reward magnitude and subjective reward rate multiplicatively. Journal of Experimental Psychology: Animal Behavior Processes. 1998;24:265–277. doi: 10.1037//0097-7403.24.3.265. [DOI] [PubMed] [Google Scholar]
- Nevin J.A. Overall matching versus momentary maximizing: Nevin (1969) revisited. Journal of Experimental Psychology: Animal Behavior Processes. 1979;5:300–306. [Google Scholar]
- Neuringer A.J. Effects of reinforcement magnitude on choice and rate of responding. Journal of the Experimental Analysis of Behavior. 1967;10:417–424. doi: 10.1901/jeab.1967.10-417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papachristos E.B, Gallistel C.R. Autoshaped head poking in the mouse: A quantitative analysis of the learning curve. Journal of the Experimental Analysis of Behavior. 2006;85:293–308. doi: 10.1901/jeab.2006.71-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paton J, Belova M.A, Morrison S.E, Salzman C.D. The primate amygdala represents the positive and negative value of visual stimuli during learning. Nature. 2006 Feb 16;439:865–870. doi: 10.1038/nature04490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Real P.G. A time-series analysis of changeover performance on concurrent variable-interval schedules. Animal Learning & Behavior. 1983;11:255–265. [Google Scholar]
- Rescorla R.A, Wagner A.R. A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In: Black A.H, Prokasy W.F, editors. Classical conditioning II. New York: Appleton-Century-Crofts; 1972. pp. 64–99. [Google Scholar]
- Schwartz G. Estimating the dimension of a model. The Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Shettleworth S.J, Krebs J.R, Stephens D.W, Gibbon J. Tracking a fluctuating environment: A study of sampling. Animal Behaviour. 1988;36:87–105. [Google Scholar]
- Skinner B.F. Farewell, my lovely! Journal of the Experimental Analysis of Behavior. 1976;25:218. doi: 10.1901/jeab.1976.25-218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugrue L.P, Corrado G.S, Newsome W.T. Matching behavior and the representation of value in the parietal cortex. Science. 2004 Jun 18;304:1782–1787. doi: 10.1126/science.1094765. [DOI] [PubMed] [Google Scholar]
- Sutton R.S, Barto A.G. Reinforcement learning. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- Weiss P. Self-differentiation of the basic patterns of coordination. Comparative Psychology Monographs. 1941;17:1–96. [Google Scholar]
- Yechiam E, Busemeyer J.R. Comparison of basic assumptions embedded in learning models for experienced-based decision making. Psychonomic Bulletin & Review. 2005;12:387–402. doi: 10.3758/bf03193783. [DOI] [PubMed] [Google Scholar]