The Effects of Reinforcer Magnitude on Timing in Rats

Abstract

The relation between reinforcer magnitude and timing behavior was studied using a peak procedure. Four rats received multiple consecutive sessions with both low and high levels of brain stimulation reward (BSR). Rats paused longer and had later start times during sessions when their responses were reinforced with low-magnitude BSR. When estimated by a symmetric Gaussian function, peak times also were earlier; when estimated by a better-fitting asymmetric Gaussian function or by analyzing individual trials, however, these peak-time changes were determined to reflect a mixture of large effects of BSR on start times and no effect on stop times. These results pose a significant dilemma for three major theories of timing (SET, MTS, and BeT), which all predict no effects for chronic manipulations of reinforcer magnitude. We conclude that increased reinforcer magnitude influences timing in two ways: through larger immediate after-effects that delay responding and through anticipatory effects that elicit earlier responding.

When anticipating a particularly exciting or agonizing experience, we often encounter ebbs and flows in time perception. Good events cannot come fast enough and time can seem to drag on while we wait, whereas unpleasant events pounce faster than we expect. With nonhuman animals, the realm of the subjective remains inaccessible, but time perception can be assayed through behavioral tasks such as fixed-interval (FI) schedules (Ferster & Skinner, 1957), the bisection task (Church & Deluty, 1977), and the peak procedure (Catania, 1970; Roberts, 1981). In this experiment, we investigated how the magnitude of reinforcement influences timing behavior in rats using a peak procedure.

A motley tapestry of results has emerged from previous empirical studies of reinforcer magnitude and timing. Increased reinforcer magnitude has been variously observed as causing earlier responding (e.g., Grace & Nevin, 2000; Doughty & Richards, 2002), later responding (e.g., Blomeley, Lowe, & Wearden, 2004; Staddon, 1970), or no change (e.g., Hatten & Shull, 1983; MacEwen & Killeen, 1991) on timing procedures. One key variable that modulates how reinforcer magnitude influences response timing is the frequency of magnitude change. When magnitude is dynamically changed from reinforcer to reinforcer within a session, larger reinforcers are followed by longer pauses and delayed timing functions. A handful of experiments have explored this dynamic case, using random changes in reinforcer magnitude on FI schedules (Blomeley et al., 2004; Hatten & Shull, 1983; Jensen & Fallon, 1973; Lowe, Davey, & Harzem, 1974; Staddon, 1970; see also Staddon, Chelaru, & Higa, 2002, Figure 7). In these experiments, reinforcer magnitude was manipulated by altering the duration of access to food in a hopper (with pigeons) or the concentration of condensed milk or sucrose (with rats). All five studies found that larger reinforcers were followed by longer pauses (and lower overall response rates) on the immediately subsequent interval. These results were mostly interpreted as reflecting an inhibitory after-effect of the reinforcer on responding. Smaller reinforcers have smaller after-effects and thus produce shorter pauses, culminating in the extreme case of reinforcer omission (i.e., reinforcer magnitude of zero) that produces almost no pause (Mellon, Leak, Fairhurst, & Gibbon, 1995; Staddon & Innis, 1969).

In contrast, chronic variation of reinforcer magnitude across sessions produces no effect on timing. In this situation, animals receive the same reinforcer magnitude for multiple consecutive sessions. Early experiments indicated that chronically increasing the quantity of reinforcement (food pellets or milk concentration) produced higher overall response rates on FI schedules, but did not entirely resolve whether the distribution of those responses changed over the course of the interval (Meltzer & Brahlek, 1968, 1970; Strebbins, Mead, & Martin, 1959; see also Bonem & Crossman, 1988). Subsequently, Hattan and Shull (1983) explored both dynamic and chronic manipulations of reinforcer magnitude in a single experiment. In conditions where hopper duration was varied over a range of 1 s to 8 s across sessions, they found that pausing on an FI schedule was clearly not influenced by reinforcer magnitude.

Under standard FI schedules, the reinforcer serves a dual role: as time marker and reinforcing stimulus. Reinforcer magnitude may exert multiple effects on timing, through direct after-effects on responding (as in the dynamic results above) as well as through changes due to the anticipation of a larger reinforcer. Evidence for the latter comes from work by Grace and Nevin (2000) using the peak procedure, which effectively separates these two potential roles for the reinforcer on standard FI schedules. In this timing procedure, animals are presented with two types of trials. On reinforcement trials, a stimulus is presented and a reinforcer is available for the first response after a given interval (i.e, an FI schedule). Occasional probe trials, where the stimulus remains on well past the usual time of reinforcement and no reinforcement is available, are interspersed among the reinforced trials. An inter-trial interval (ITI) separates all trials. Averaged across the probe trials, many animals show a characteristic response pattern. Typically, response rate increases in the early part of a probe trial, peaks around the time reinforcement is ordinarily available, and gradually tapers off, producing a response curve that resembles a Gaussian distribution.

Grace and Nevin (2000) manipulated reinforcer magnitude on a cued peak procedure in the context of an extensive study on response strength and behavioral momentum. Different-colored cues indicated the availability of a large or small reinforcer after a fixed interval on the reinforced trials. They found that, on probe trials, pigeons peaked earlier following the cue that indicated the large reinforcer was (sometimes) upcoming. Despite the presence of multiple reinforcer magnitudes in a single session, these results are the opposite of what happens when reinforcer magnitude is changed dynamically. The key difference from earlier results seems to be the separation of the two possible roles for reinforcement in the peak procedure—as time marker and reinforcer outcome. In the peak procedure, the outcome only served to reinforce behavior, and the time marker was not the previous reinforcer, but a visual cue. Thus, the reinforcer could not have influenced subsequent responding through any immediate after-effects, and some other process must have been at work.

These potentially conflicting sets of results are explained if we suppose that reinforcer magnitude influences timing in two ways: (1) through immediate after-effects that result in delayed responding after larger reinforcers and (2) through anticipation of upcoming reinforcers that results in earlier responding before larger reinforcers. Following this dual-role hypothesis, when a larger reinforcer serves as a time marker, the immediate after-effects are stronger and responding begins later. When a larger reinforcer is predictably available, either through the presence of a discriminative stimulus or from the recent reinforcer history, animals learn to anticipate this upcoming larger reinforcer and begin responding earlier. The effects of unpredictable, dynamic reinforcer changes are then caused exclusively by the former after-effects process (Hatten & Shull, 1983; Jensen & Fallon, 1973; Lowe et al., 1974; Staddon, 1970), whereas Grace and Nevin's (2000) results are an example of the exclusive action of the latter reinforcer-anticipation process. In some situations, these opposing tendencies towards earlier and later responding are placed in direct conflict. For example, with chronic manipulation on an FI schedule (e.g., Hatten & Shull, 1983), reinforcer magnitude serves as the time marker while simultaneously being perfectly predictable, thereby producing both an inhibitory after-effect and an anticipatory effect, so little change is observed in behavior. Thus, all three classes of previous empirical results (dynamic, chronic, and cued) are correctly addressed by this hypothesis. The current study further tests the scope of this dual-role hypothesis by exploring timing performance in rats on a peak procedure, while varying reinforcer magnitude across sessions. By changing reinforcer magnitude across sessions while separating the trials, we expect to isolate the anticipatory effect and observe shorter pauses with a higher reinforcer magnitude.

A deeper understanding of the relation between reinforcer magnitude and timing also can be gleaned by using several measures of timed behavior. Fine-grained analysis of performance on the peak procedure has revealed that individual probe trials can be effectively modeled as three-state systems with a period of low responding (break) followed by a period of high responding (run) followed by a further period of low responding (e.g., Cheng & Westwood, 1993; Church, Meck, & Gibbon, 1994). These two transition points are termed the start and stop times, and, along with the other measures of temporal control on interval schedules, sometimes yield conflicting results (see Zeiler & Powell, 1994). Much of the previous research on the relationship between reinforcer magnitude and timing has used pause or wait time as the dependent measure, perhaps only revealing an incomplete glimpse of the full scope of the relation between these two variables. Gallistel, King, and McDonald (2004) have even suggested that starts (and presumably wait times or pauses) present a mixture of both timed and untimed responses, whereas stops are more precisely timed and thus the more accurate or reliable measure of timing. We attempted to resolve these potential inconsistencies and lacunae by examining four different behavioral measures of temporal control (i.e., wait times, starts, stops, and peak times) in a single experiment. In addition, we refined the reliability of the peak time measure by selecting the strongest from several statistically derived estimates.

The reinforcer in this experiment was electrical stimulation of the medial forebrain bundle—a heterogeneous group of axons providing bidirectional links between the forebrain on the one hand and midbrain and hindbrain structures on the other (Nieuwenhuys, Geeraedts, & Veening, 1982). Rats seek such stimulation avidly, even at the cost of crossing an electrified grid (Olds, 1958) or forgoing their sole daily opportunity to eat (Routtenberg & Lindy, 1965). The effect that entices the subject to repeatedly seek out the stimulation is called “brain stimulation reward” (BSR). Reinforcer magnitude can be reliably manipulated by changing the frequency, current, or duration of the reinforcing burst of stimulation (Gallistel & Leon, 1991; Mark & Gallistel, 1993; Simmons & Gallistel, 1994). A novel concern that is introduced by the use of BSR regards the generalizability of results using this artificial reinforcer. These potential worries are partly defused by studies demonstrating that stimulation of the medial forebrain bundle can compete with, summate with, and substitute for the reinforcing effects of natural goal objects such as sucrose solutions, saline solutions, food, and water (Conover & Shizgal, 1994; Conover, Woodside, & Shizgal, 1994; Green & Rachlin, 1991). A potential interpretive difficulty is also raised by the possible overlap of the brain substrates for reward processing and timing. Both engage the dopaminergic system (e.g., Maricq & Church, 1983; Meck, 1996; Wise & Rompré, 1989; but see McClure, Saulsgiver, & Wynne, 2005; Odum, Lieving, & Schaal, 2002), and Meck (1988) has shown that chronic, subthreshold intracranial stimulation along the medial forebrain bundle produces underestimation of times in a bisection procedure (we will take this idea up in detail in the Discussion). BSR does have an advantage over other forms of manipulating reinforcer magnitude in that the exact time and amount of reinforcement can be precisely controlled. There is no variability in the length of time to collect or consume the reinforcer, as there often is when food reinforcement is delivered (and necessarily must be when hopper duration is manipulated). In addition, there are no issues of satiety or deprivation level that readily complicate the interpretation of reinforcer magnitude with natural reinforcers.

In this experiment, we tested the effects of chronic presentation of two levels of reinforcer magnitude on timing in a peak procedure. In the peak procedure, both ITIs and the occasional peak trial separate reinforcement from the subsequent timed interval. Thus, the dual-role hypothesis (after-effects vs. anticipation) makes the clear prediction that larger reinforcers should be preceded by shorter pauses (anticipation only). This experiment adds to the existing literature on reinforcer magnitude and timing in at least three important ways. First, we bring the advantages of the peak procedure for evaluating timing effects to bear on the question of chronic reinforcer magnitude changes, allowing for a better synthesis of previously disparate results. Second, by exploring multiple measures of timed responding, we paint a clearer, yet more nuanced, picture of how motivational variables influence timing. Finally, the use of BSR as the reinforcing stimulus eliminates varying levels of satiety and deprivation (and thus reinforcer potency) that may act as potential confounding variables with natural reinforcers.

Method

Subjects

Four male Long Evans rats (Charles River Breeders, St. Constant, Québec, Canada), weighing 350–500 g, served as subjects in the experiment. Prior to surgery, subjects were housed in pairs, and they were switched to individual cages following surgery. Lights were on a 12-hr light-dark reverse cycle, and all testing occurred during the dark phase of the cycle. Food and water were available ad libitum. All subjects were treated in accordance with the ethical guidelines of the American Psychological Association for research with nonhuman subjects.

Apparatus

The test boxes were custom-made 34-cm long × 23.5-cm wide × 60.5-cm high operant chambers with three charcoal grey walls and a clear plexiglass panel with a fold-down door that served as the front wall. Two retractable levers (5-cm wide and protruding 1.5 cm from the wall) were located centrally on the opposite right and left walls, 11 cm off the wire-mesh flooring. A small cue light was located 6 cm above each of the levers. Only the left lever was extended and active in the experiment. Responses were recorded with a temporal resolution of 0.1 s by a local computer that also controlled presentation of stimuli and delivery of stimulation trains through custom software.

Procedure

Surgery

Electrode implantation surgery was performed under deep sodium pentobarbital anesthesia (Somnotol, 60 mg/kg, i.p.) with atropine sulphate (0.5 mg/kg, s.c.) administered preoperatively to help maintain a patent airway. Bilateral monopolar electrodes were stereotaxically aimed at the lateral hypothalamus (2.8 mm posterior to Bregma, 1.7 mm lateral to the sagittal suture, and 8.4 mm below the dura mater). The stimulating electrodes were made from 000 stainless-steel insect pins, insulated with Formvar to within 0.5 mm of the tip, and secured to the skull by dental acrylic. Two jeweler's screws also were secured to the skull to serve as the current return for the electrodes and help secure the electrode headstage. At the end of the surgery, an opioid (buprenorphine, 0.05 mg/kg, s.c.) was administered for postoperative analgesia.

Training

Rats were allowed at least two weeks to recover from the surgery before training began. Rats were trained by successive approximation to press a lever for a train of electrical brain stimulation. The stimulation consisted of a 0.5-s train of constant current (400 µA) cathodal 0.1-ms pulses. Training initially began with a continuous reinforcement schedule with rats receiving BSR for every lever press, but was gradually extended until rats were responding on a FI 10-s schedule, whereby BSR was available for the first response after 10 s had elapsed. All rats readily learned to press the lever under these contingencies within three sessions. Reinforcer magnitude was manipulated by changing the stimulation frequency while maintaining a constant current and duration of the electrical stimulation (Conover & Shizgal, 1994; Gallistel & Leon, 1991). The stimulation frequencies for the high and low reinforcer magnitudes were determined independently for each rat. The high reinforcer was selected as the highest frequency that maintained reliable lever pressing without motor or aversive side effects, and the low reinforcer was selected as the frequency 0.05 log units above the highest level at which rats would no longer respond. These selections were made in a single session after lever pressing was established. Table 1 displays the high and low reinforcer frequencies individually selected for each rat.

Table 1. Details of the experimental protocol in all three conditions of the experiment. The first column under each condition presents the pulse frequency (N) of the brain stimulation reward for each rat (i.e., reinforcer magnitude). The remaining columns give the exact number (and percent) of reinforced and peak trials actually received by each rat totalled over the final five sessions for each of the three experimental conditions.

Rat	Condition 1: High reinforcer magnitude				Condition 2: Low reinforcer magnitude				Condition 3: High reinforcer magnitude
	N	Rf. Trials	Peak Trials	% Peak	N	Rf. Trials	Peak Trials	% Peak	N	Rf. Trials	Peak Trials	% Peak
V1	63	734	187	20.3	50	752	179	19.2	63	744	185	19.9
V2	100	623	300	32.5	63	649	289	30.8	100	656	268	29.0
V3	79	618	319	34.0	63	645	281	30.3	79	659	285	30.2
V4	100	624	310	33.2	63	655	293	30.9	100	641	282	30.6

Testing

The testing phase consisted of exposing rats successively to high and low reinforcer magnitudes, using a high–low–high ABA reversal design. Prior to testing, all rats first received at least 12 sessions of the peak procedure with the high reinforcer magnitude. Rats were then tested repeatedly using the peak procedure with the same reinforcer magnitude (high or low) until, by visual inspection of response rates, behavior was stable for five consecutive sessions (range of 7–16 test sessions for each condition). Each session consisted of approximately 200 trials; every trial began with the onset of the small stimulus light. On reinforced trials, the first lever press that occurred after 20 s had elapsed from light onset (FI 20 s) was immediately followed by a train of electrical brain stimulation. On peak trials, no stimulation was available and the stimulus light remained illuminated for a full 60 s. Table 1 details the number of reinforced and peak trials that each rat received over the final 5 days of testing with the high and low reinforcer magnitudes. Peak and reinforced trials were randomly intermingled, and a 5-s ITI separated every trial. Responses from the first trial of each session were discarded because that trial was not immediately preceded by reinforcement (or a peak trial) as were all subsequent trials.

Data analysis

Three different data analysis methods were utilized ranging from the patently straightforward to the moderately complex. The first method simply measured the wait time: the time to the first response on a given trial. The second method involved fitting a set of three variants of Gaussian functions to the mean response rate for each rat for each condition (further models were explored, but only the three most instructive are included in the text). In the simplest case, all the responses emitted by a rat during the 60-s peak trials were collected in 1-s bins, and a standard three-parameter single Gaussian (SG) function (peak time, rate, and spread) was iteratively fit to the midpoint of each bin, using least mean squares. The second model (SGR: Single Gaussian + Ramp) expanded on this simple case by adding a linear ramp—a popular strategy in the literature to deal with the increase in responding late in peak trials (see, e.g., Buhusi & Meck, 2002; Cheng & Westwood, 1993; Matell, King, & Meck, 2004; Roberts, 1981; Saulsgiver, McClure, & Wynne, 2006). The final fitted function decoupled prepeak and postpeak responding by fusing together two half-Gaussians through spline interpolation, allowed for kurtosis, and switched to a quadratic tail (DGKQ: Dual Gaussian with Kurtosis and a Quadratic Tail). This last model used the following equation for response rate (r) before the estimated peak time (T_p):

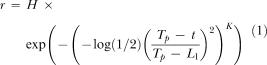1

where H was the peak rate parameter, t was the trial time, K was the kurtosis parameter, and L₁ was the estimated point of half-maximal responding (prepeak). For points after the estimated peak time, the same equation was used with L₂ in place of L₁, thereby giving independent estimates of half-maximal responding for both the rise (start) and fall (stop) of the Gaussian curve. Finally, the latter stages of the trial also included a term for a rising quadratic tail (for full equations of all models, see Appendix).

This family of Gaussian models for the data were compared using the Akaike Information Criterion (AIC):

2

where k was the number of parameters, n was the number of observations, and RSS was the residual sum of squares (Akaike, 1974). The AIC measures the tradeoff between the number of parameters and the variance accounted for by a model, with lower values indicating a relatively better model. The residuals from all fits also were evaluated for serial autocorrelation by means of the Durbin-Watson (DW) statistic (Durbin & Watson, 1971). These two evaluative measures provide complementary information about the utility of different models; the AIC guards against the inclusion of an excessive number of parameters, whereas the DW statistic guards against using not enough parameters to satisfactorily account for the data. On the basis of these two evaluative measures, the best model was selected.

Finally, the third data analysis method focused on responding over the course of individual peak trials. Each peak trial was modeled as a “break-run-break”, three-state system: Rats were assumed to start with a low rate of responding, display a burst of rapid responding in the middle of the trial, and return to another low rate of responding for the remainder of the trial (Cheng & Westwood, 1993; Church et al., 1994; Gallistel et al., 2004; Schneider, 1969). Two transition points (“start” and “stop” times) separating the lower and higher rates of responding were identified for every peak trial. These points were determined by exhaustive search for the two response times that maximized the metric t₁(r − r₁) + t₂(r₂ − r) + t₃(r − r₃), where t₁, t₂, and t₃ were the times from the beginning of the trial to the start point, between the start and stop points, and from the stop point to the end of the trial, respectively; r₁, r₂, and r₃ were the corresponding response rates, and r was the overall response rate for that trial (Church et al.). The only additional constraint was that the start point necessarily preceded the stop point.

All simple computations (e.g., means) were calculated in Microsoft Excel, and more advanced statistical tests and fits (e.g., multi-factor ANOVAs) were conducted using Statistica 6.0 (StatSoft Inc., Tulsa, OK) and MATLAB (The MathWorks, Natick, MA). An alpha level of .05 was selected for all inferential statistics.

Results

Wait-time results

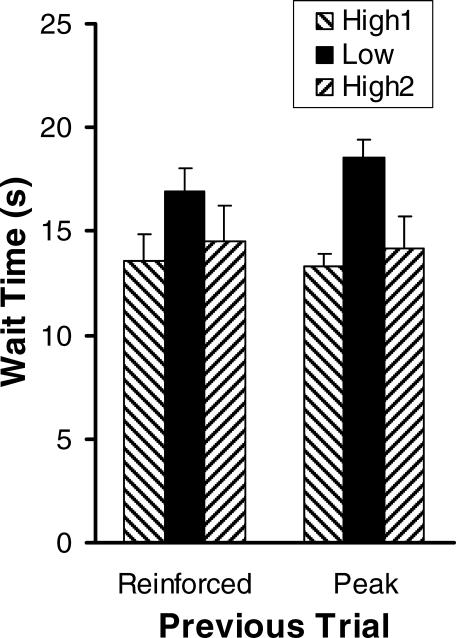
Our first analysis approach focused on the wait time: the time to the first response in a trial. Figure 1 depicts the mean wait time for low- and high- reinforcer conditions, plotted separately according to whether the previous trial was a reinforced or peak trial. Regardless of the status of the previous trial, all rats paused longer when reinforcement was the lower magnitude BSR. The effect was reversible as pausing was shorter for both high-reinforcer conditions for all 4 rats. A two-way (Reinforcer Magnitude × Trial Type), repeated-measures ANOVA corroborated the reliability of these visible trends. There was a main effect of reinforcer magnitude, F(2,6)  =  24.83, p < .01, but no effect of trial type, nor an interaction (both ps > .05). This lack of an interaction is notable because it confirms that the peak procedure did limit the influence of the immediately previous reinforcer as a time marker, successfully separating the after-effects of reinforcement from the anticipatory effects. Planned comparisons confirmed that wait times during the two iterations of the high-reinforcer condition were not significantly different from one another, t(3)  =  1.14, p > .30, and that the two high-reinforcer conditions produced reliably shorter wait times than the low-reinforcer condition, t(3)  =  9.61, p < .01.

Fig 1. Mean wait time (s) as a function of reinforcer magnitude and previous trial type.

For data in the left columns, the previous trial was reinforced, and for data in the right columns, the previous trial was nonreinforced (peak).

Peak fits

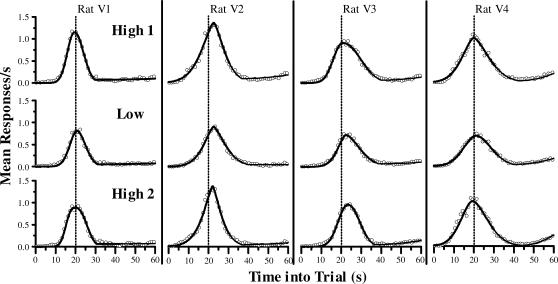
Our second analysis method involved fitting a family of Gaussian models to the mean response rates. The three models were, from fewest to most parameters: Single Gaussian (SG), Single Gaussian summed with a linear Ramp function (SGR), and Dual Gaussian with a single Kurtosis parameter plus a Quadratic tail (DGKQ). Figure 2 plots the mean response rate as a function of time into the peak trial for each of the rats in all three conditions. The curves are the fits from the best Gaussian model: the DGKQ model (see below). Results from individual animals are plotted in separate columns, and results from the three reinforcer conditions are plotted on separate rows. With both high (top and bottom rows) and low (middle row) reinforcer magnitudes, all animals showed a very clear pattern of responding. Rats began responding at a lower rate, increased responding throughout the first part of the trial, and peaked at around the time that BSR would sometimes be available (20 s: dashed line) before gradually tapering off. There was a second increase in responding in the final few seconds before the trial ends—a common finding with fixed peak and intertrial times (see Church, Miller, Meck, & Gibbon, 1991). For all three Gaussian models examined, the fitted functions matched the obtained response rates extremely well, accounting for a high proportion of the variance for all 4 rats (all R² values > .93).

Fig 2. Mean response rate as function of time into peak trial for each rat in each reinforcer condition in 1-s bins.

Each column presents data from an individual rat. Each row presents averaged data from the final five sessions for each of the three levels of reinforcer magnitude (High 1, Low, and High 2). The curves plot the result from the best-fitting Gaussian model (DGKQ: Dual Gaussian with a Kurtosis factor and Quadratic tail; see Methods) to the response-rate data. The dotted line in each plot represents the time at which reinforcement was available to rats on nonpeak trials (20 s).

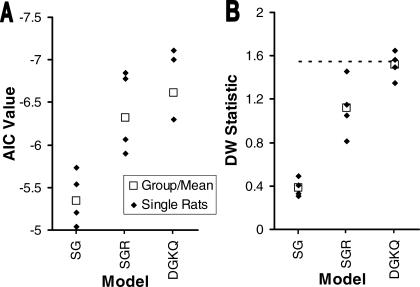
To select the most appropriate Gaussian model for this dataset, we examined two statistics comparing the relative validity of the three different Gaussian models. Figure 3 plots the Akaike Information Criterion (AIC) and Durbin-Watson statistic (DW) for each of the Gaussian models. As illustrated in Figure 3A, the DGKQ model received the best (lowest) AIC value. There was a general trend across the models that a greater number of parameters improved the AIC-measured tradeoff between model complexity and goodness of fit. The second panel (Figure 3B) depicts the DW statistic for the same set of models. Again, there was a gradual improvement with the more complex models (as might be expected because there is no penalty for additional parameters in the DW statistic). For all three models, however, the majority of fits still showed significant residual autocorrelation, mostly due to the rise at the end of peak trials. The SG model, in particular, provides such a comparatively poor fit to the data for both statistics (AIC and DW) because that is the only model considered that cannot account for the rising tail at all (see Figure 2).

Fig 3. Evaluative criteria comparing the three different Gaussian models.

(A) Akaike Information Criteria (AIC) calculated across all rats and all reinforcer conditions for each of the models for both datasets. Lower AIC scores indicate better models. Note that the y-axis is inverted. (B) Durbin-Watson (DW) statistic calculated independently for each rat, averaged across reinforcement condition. Points below the dashed line denote significant autocorrelation at a .05 alpha level. SG  =  Single Gaussian; SGR  =  Single Gaussian plus linear Ramp; DGKQ  =  Dual Gaussian with a Kurtosis parameter plus Quadratic tail.

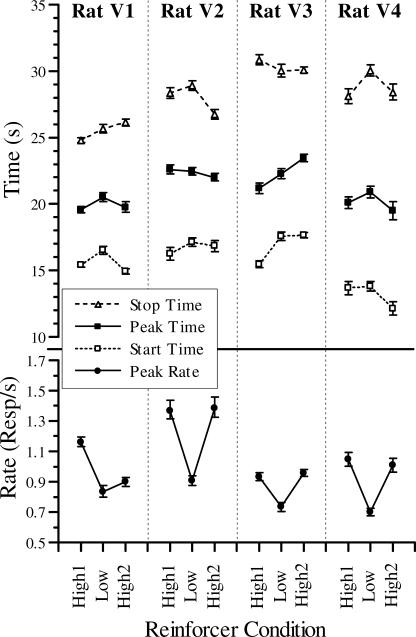
On the basis of these two statistics, we selected the DGKQ model as the most appropriate for this dataset because it had both the best (lowest) AIC values and the best DW statistics. Figure 4 presents parameter results for the peak rates, peak times, plus start and stop half-max times, including 95% confidence intervals, for the DGKQ model (cf. Table 2). The latter two half-max measures are the times at which the fitted Gaussian has risen (start) or fallen (stop) to half of its maximal value. The confidence intervals are the 2.5 and 97.5 percentiles of fits to 1000 datasets generated by repeatedly randomly resampling the residuals. There was a very large effect of reinforcer magnitude on peak rates (bottom row in Figure 4); rats responded much more vigorously on peak trials during sessions with the larger reinforcer magnitude. The start half-max times (open squares of upper panel in Figure 4) showed a moderate effect of reinforcer magnitude with both iterations of the high reinforcer producing earlier start half-max times in 3 of 4 rats; only the second iteration of the high reinforcer for Rat V3 was similar to the low- reinforcer condition. The peak times and stop half-max times (solid squares and open triangles, respectively, in Figure 4) both showed no consistent trends. The peak times from 2 rats (V1 and V4) and the stop half-max times for 1 rat (V4), were possibly a little shorter for the high-reinforcer results, but there was no consistent pattern across the four datasets. The parameters represent different measures (rates and times) and are plotted on different ordinates, but the confidence intervals give a good visual context for evaluating the relative size of the effects.

Fig 4. Fitted peak times, peak rates plus start and stop half-max times as a function of reinforcer magnitude for each rat from the model that best fit the data (DGKQ: Dual Gaussian with a single Kurtosis parameter and a Quadratic tail).

Error bars are 95% confidence intervals as calculated by a bootstrapped resampling method. Note that the parameters are plotted on different y-axes.

Table 2. Statistical results (p values) from a series of paired t tests (df  =  3) comparing averaged performance on the two high-reinforcer conditions versus the low-reinforcer condition. Bolded values are significant at an alpha level of .05.

Model	Peak Rate	Peak Time	Start Half-max	Stop Half-Max
Single Gaussian (SG)	.005	.03	.009	.08
Single Gaussian + Ramp (SGR)	.006	.03	.006	.15
Dual Gaussian with Kurtosis + Quadratic Tail (DGKQ)	.02	.15	.008	.24

To evaluate the statistical reliability of the visible trends in the fitted parameters and compare with results from other models, Table 2 presents comparative statistics for the fitted parameters from the three Gaussian models. The table contains the p values from a series of paired t tests (df  =  3) comparing the average of the two high-reinforcer conditions against the low-reinforcer condition for peak times, peak rates, and start and stop half-max times (see Figure 4). Bolded values are significant at an alpha level of .05. The clearest pattern emerged from the results of the fitted peak rates. As can be seen in Figures 2 and 4 as well as Table 2, all 4 rats showed significantly higher peak rates during both high-reinforcer conditions than during the low-reinforcer condition. This difference offers independent corroboration that our manipulation of the stimulation frequency did indeed alter reinforcer magnitude in the anticipated direction. The start and stop half-max times also produced straightforward results; with all three models, start times were reliably earlier with a larger reinforcer magnitude and stop times were unaffected. The peak times presented the most interesting and variable case. For the two single Gaussian models (SG and SGR), there was a significant effect of reinforcer magnitude on peak time, with higher reinforcer magnitude producing earlier peaks. With the best model (DGKQ), this effect was muted and there was no reliable effect of reinforcer magnitude on peak times. Thus, in this instance, the relative inflexibility of the single Gaussian models produced an artifactual result for peak times that was sharply reduced when a better model was fit to the dataset.

Single-trial analyses

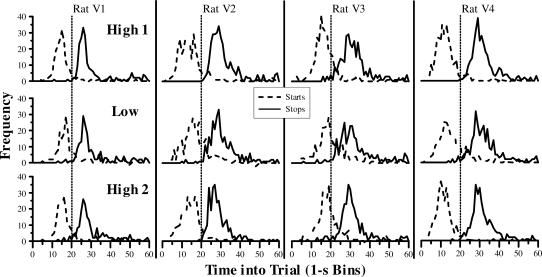
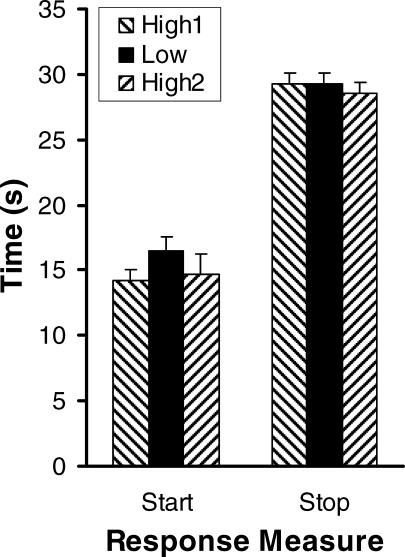
The results from the analysis of responding on individual trials matched the wait-time and peak-fit results quite strongly. Figures 5 and 6 present the results from fitting the individual trials as a three-state system with two periods of low responding surrounding a period of higher responding. The frequency distribution for the two transition points between low and high responding—the start and stop times—are plotted separately for each rat in Figure 5. For all 4 rats, start times clustered around 10–15 s into the trial and stop times clustered around 30 s. There seemed to be a tendency for the start time distributions to be shifted to the right (later) with the low reinforcer magnitude (middle row), but the stop time distributions were largely unaffected. Figure 6 confirms this observation by plotting the median start and stop times, averaged across all 4 rats. Sessions with the lower reinforcer magnitude clearly had later start times, but stop times were not influenced by reinforcer magnitude. Two one-way repeated-measures ANOVAs provided statistical corroboration for this finding; there was a main effect of reinforcer magnitude on start times, F(2,6)  =  11.82, p < .01, but no effect of reinforcer magnitude on stop times F(2,6)  =  1.80, p > .20. A planned comparison confirmed that start times with the low reinforcer magnitude were later than the two conditions with the high reinforcer magnitude, t(3)  =  9.80, p > .01.

Fig 5. Frequency distributions of start and stop times from the single-trial analysis.

Each row plots the cumulated frequency in 1-s bins of starts (dashed curves) and stops (solid curves) across the final five sessions with each reinforcer magnitude condition (High 1, Low, and High 2). The dotted vertical line represents the time at which reinforcement became available to rats on nonpeak trials (20 s).

Fig 6. Median start and stop times (+ SEM) from the single-trial analysis, averaged across all 4 rats at each reinforcer magnitude condition (High 1, Low, and High 2).

Discussion

In this experiment, we established that chronic variation of BSR magnitude substantially changed some measures of rats' timing performance in a peak procedure. Wait and start times were both significantly shorter with a high reinforcer magnitude than with a low reinforcer magnitude. Stop and peak times, however, were not reliably influenced by the reinforcer magnitude manipulation. These results provide further evidence for one prong of the dual-role hypothesis for reinforcer magnitude effects on timing suggested earlier: When a larger reinforcer is predictably available, animals start responding earlier in the interval (anticipation effects). These results pose a considerable challenge to the three most popular theoretical accounts of timing (SET: Scalar Expectancy Theory, Gibbon, 1977; MTS: Multiple Time Scale model, Staddon & Higa, 1999; and BeT: Behavioral Theory of Timing, Killeen & Fetterman, 1988), which all predict no effect of chronic reinforcer magnitude manipulations.

The major theoretical approaches to timing have varied widely in their treatment of the relationship between motivation and timing, spanning the range from complete independence to complete interdependence, but their predictions for chronic reinforcer magnitude effects on timing are identical: no effect. SET (Gibbon, 1977), for example, explicitly eliminates all motivational variables from consideration in determining performance on a timing task. According to SET, all reinforcing stimuli generate different levels of expectancy or “hope” (H) determined by their motivational salience (e.g., magnitude of reinforcer or level of deprivation). This general expectancy for a reinforcer is transformed into an immediate expectancy, h(t), based on the expected delay to reinforcement delivery (x) in a hyperbolically increasing fashion: h(t)  =  H /(x-t). In the model, behavior is determined by a ratio comparison between the immediate expectancy at a given point in time, h(t), and the undifferentiated expectancy, h(0), from the beginning of a trial:

3

Whenever the expectancy ratio, r(t), surpasses a threshold (b), responding is initiated. Note that the motivational parameter (H) appears in both numerator and denominator of this ratio, thus cancelling out and playing no role in the initiation or maintenance of timed responding (see also Gallistel & Gibbon, 2000). As a result, for our experiment, SET makes the straightforward prediction that reinforcer magnitude should have no effect on timing in a peak procedure—a prediction that is not borne out by the data from this experiment. This claim about motivational impotency in timing does draw some empirical support from Roberts (1981) who found that manipulating the probability of reinforcement (a motivational factor) altered the peak response rate without changing the peak response time (cf. Grace & Nevin, 2000).

A potential elaboration of SET that might explain reinforcer magnitude effects observed in this experiment is the partial-reset hypothesis (Mellon et al., 1995). To explain reinforcement omission effects (short pauses after omitted reinforcers), the timing mechanism (accumulator) is assumed to be only partially reset by the omitted reinforcers. As a result, the timing function is shifted earlier on subsequent trials, and shorter pausing ensues. Modifying the partial-reset hypothesis, so that smaller reinforcers also only partially reset the accumulator, adequately explains results from dynamic schedules when shorter pauses follow smaller reinforcers (e.g., Blomeley et al., 2004; Lowe et al., 1974; Staddon, 1970). For our results, however, this hypothesis fails. A partial reset following a low reinforcer would result in earlier responding following the low reinforcer—the opposite of what we find with chronic reinforcer magnitude manipulation in the peak procedure. Further elaboration of the theory would be required to account for these results (see below for a plausible suggestion).

The MTS habituation model of interval timing, in contrast, takes reinforcer magnitude as the constitutive input variable to the memory traces that lie at the core of the theory (Staddon et al., 2002; Staddon & Higa, 1999). Behavior in MTS is determined by a decaying memory trace (through a sum of exponentials) that initiates responding once it passes below a threshold. This threshold is dynamically adjusted based on the remembered trace level of previous reinforcers. According to the model, a larger-than-usual reinforcer results in a larger memory trace that decays below the response threshold at a later time, thus initiating responding at a later time. This prediction of the model is supported in dynamic environments—where the reinforcer magnitude changes regularly—when a larger-than-usual reinforcer results in greater pausing and a delayed timing function (e.g., Staddon, 1970). With repeated presentations of the same (larger) reinforcer magnitude, as in our experiment, however, the threshold recalibrates to the new remembered reinforcement, and the reinforcer magnitude effect should mostly disappear. Thus, like SET, MTS predicts no effect on timing for chronic reinforcer magnitude manipulations.

The third major timing account, BeT (Killeen & Fetterman, 1988), also ties its core assumption to properties of the reinforcement received by the animal. According to BeT, animals pass through a series of sequential states driven by a Poisson pacemaker. These states become associated with adjunctive behaviors, thus providing the substrate for timed responding. As opposed to SET, the rate of the pacemaker in BeT is tied directly to the overall rate of reinforcement. Higher reinforcement densities due to increased frequency or magnitude of reinforcement should result in a faster pacemaker rate, though the empirical evidence for the relation between reinforcer magnitude and pacemaker rate is mixed (see Bizo & White, 1994; Fetterman & Killeen, 1991; MacEwen & Killeen, 1991). For the current experiment, when rats are first exposed to the low reinforcer magnitude condition (Phase 2), BeT clearly predicts longer wait, peak, and stop times. As the animal is repeatedly exposed to the smaller magnitude reinforcer, however, reinforcement becomes associated with an earlier behavioral state and the timing function should recalibrate to the new pacemaker rate, eliminating the initial increase in the timing measures. If the assumption is made that the recalibration is incomplete (perhaps due to insufficient exposure to the new reinforcer magnitude), then BeT does correctly predict the increase in start and wait times (see Fetterman & Killeen, 1995). Incorporating the further (unsubstantiated) assumption that later sequential states recalibrate more quickly would even allow the model to account for the unchanged peak and stop times. The converse set of predictions holds true for the reexposure to the high reinforcer magnitude (Condition 3). Our empirical data do not allow us to adequately address the question of recalibration rates.

Despite wide variation in the core assumptions about the relationship between motivation and timing, all three models assume a veridicality in timing behavior that chronic variations in reinforcer magnitude should not influence (beyond transient effects). Either the models screen off motivational effects altogether (SET) or else the models suppose a recalibration process that eventually eliminates the motivational effects (MTS and BeT). From our results, there is mixed support for this shared assumption. Some measures of timing (pauses and starts) indeed were influenced by reinforcer magnitude, but stop and peak times were not. On the basis of different results from the peak procedure, this relative invariance of stop times led Gallistel et al. (2004) to suggest that stop times are the best measure of timing on the peak procedure. This decision about what measure is best certainly depends very strongly on theoretical predispositions. If the view is held that motivation does not influence timing variables (e.g., SET), then the ever-invariant stop times are clearly the purest measure of timing behavior. If the view is held that motivational factors should influence timing (e.g., BeT), then the best measures of timing are those (pauses, starts, or derived pacemaker rates) that are influenced by motivation and not the less-sensitive stop time.

One way to reconcile this dataset with the two theories that incorporate thresholds to determine response times (MTS and SET) is to assume that there are two independent thresholds to start and stop responding on peak trials. Motivational factors (e.g., reinforcer magnitude) influence the threshold to start responding, but not the threshold to stop responding on peak trials. According to this view, chronic exposure to low reinforcer magnitude decreases the threshold below which the decaying memory trace must dip or, equivalently, increases the threshold above which the expectancy ratio must rise before responding is initiated, resulting in considerably longer pauses and later start times (Figures 1, 5, and 6). Moreover, the small, but significant effect of reinforcer magnitude on peak times (Table 2) with single Gaussian models is readily explained by this two-threshold idea. When peak time is estimated by a symmetric model fit to the response function, the peak time effectively becomes tied to the start and stop thresholds, so if reinforcer magnitude affects only one threshold, the whole fitted function shifts and illusory peak shifts will be produced. Such a two-threshold idea has also gained support in the context of SET from analyses of the patterns of variance and covariance for starts and stops in the peak procedure (Church et al., 1994; Gibbon & Church, 1990).

Reinforcer magnitude can then be taken as influencing the start threshold in the two manners hypothesized in the Introduction: through inhibitory after-effects and anticipatory effects. When reinforcer magnitude is changed unpredictably within sessions (dynamic) and the reinforcer serves as the time marker (Blomeley et al., 2004; Hatten & Shull, 1983; Staddon, 1970), then the inhibitory after-effects of reinforcement increase (for SET) or decrease (for MTS) the threshold for responding, and later pauses ensue after larger reinforcers. The MTS model already accounts for these dynamic results without any additional assumptions (Staddon et al., 2002); adding the assumption of a start threshold that is altered by reinforcer magnitude is necessary for MTS in the chronic case, but serves to even further amplify the already predicted reinforcer magnitude effects on dynamic schedules. When, as in our experiment, reinforcer magnitude is changed across sessions but does not also serve as the time marker, anticipation of the larger reinforcer decreases (for SET) or increases (for MTS) the threshold for response initiation, resulting in shorter wait and start times (cf. Grace & Nevin, 2000). This tendency towards earlier responding also explains why larger reinforcer magnitudes result in poorer performance on DRL schedules, another putative timing procedure (Doughty & Richards, 2002). An analogous dual-role mechanism (immediate after-effects vs. anticipatory effects) has been proposed to account for the effects of interval duration on pausing on certain types of cyclic-interval schedules (Ludvig & Staddon, 2004, 2005).

An empirical question remains outstanding: What would the effect of reinforcer magnitude on timing be if the reinforcer were dynamically and unpredictably varied but did not also serve as the time marker? Presumably, in that instance, there would be neither after-effects of the reinforcer nor any anticipatory effects, and thus no influence of reinforcer magnitude on timing. No results from such a procedure have been reported, possibly because the anticipated result is a null effect.

One potential alternate explanation for the effects of reinforcer magnitude on the wait and start times in this experiment might be that BSR shares the same biological substrate as timing (Meck, 1988). According to this view, the electrical stimulation directly drives the internal clock that underlies time perception, and thus changes in responding are not due to the reinforcer magnitude effects. Indeed, Meck showed that subthreshold trains of stimulation in the medial forebrain bundle shifted the psychometric function for time earlier—interpreted as an increase in the speed of an internal clock. Following that logic, in our experiment, perhaps the higher frequency trains of electrical stimulation directly increased clock speed (Meck). Three key reasons mitigate such a possibility. First, even if stronger trains of BSR were inducing the clock to run faster, presumably that effect would be transient (cf. Maricq & Church, 1983; Meck, 1996) and would not persist across sessions to influence the steady-state behavior that we observed. Furthermore, Meck (1988) had the subthreshold stimulation occurring throughout the timed interval, whereas in this experiment, the train of electrical stimulation was restricted to the end of the interval. It is not clear how such a restricted burst of stimulation could drive the clock throughout the interval. Finally, if clock speed were indeed directly altered by BSR magnitude, then all measures of timing should be equally affected, including the stop and peak times, which did not change reliably in this study.

A more plausible relation between the results of Meck (1988) and the present experiment would actually be the converse: The subthreshold stimulation that Meck gave enhanced the reinforcer, and the anticipation of larger reinforcers led to earlier responding and a shifted psychometric function. This suggestion gains support from previous results that have established that natural reinforcers and BSR can summate (Conover & Shizgal, 1994; Conover, Woodside, & Shizgal, 1994). In addition, although the subthreshold stimulation in Meck's experiment did not directly overlap with the food reinforcer, similar stimulation does produce longer-lasting increases in tonic dopamine levels (Hernandez et al., 2006), which could certainly have mediated an enhanced reinforcer a few seconds later. The question then becomes: Could the rats have learned to anticipate these larger reinforcers in the Meck experiment? If the subthreshold stimulation could also have served as a discriminative stimulus, then that provides a plausible mechanism for rats to know when a larger (summated) reinforcer is upcoming. There is evidence that reinforcer magnitude (Bonem & Crossman, 1988), time intervals themselves (Ludvig & Staddon, 2004, 2005), and even electrical stimulation of the nearby ventral tegmental area (Druhan, Fibiger, & Phillips, 1989; Druhan, Martin-Iverson, Wilkie, Fibiger, & Phillips, 1987a, 1987b) can serve as discriminative stimuli, making it highly probable that rats can use subthreshold electrical stimulation of the MFB as a discriminative stimulus for reinforcer magnitude. Such a combined discriminative stimulus/reinforcer enhancer role for subthreshold stimulation would account for Meck's results without resorting to an internal clock or modified pacemaker that shares the same biological substrate as BSR.

An important general lesson from the curve-fitting results is that the peak time is a potentially biased measure whenever a single Gaussian model is fit to peak-procedure data. Any manipulation that significantly alters only one end of the response distribution (before or after the peak), even if it does not actually alter the peak time, will create a spurious peak shift (cf. Knealing & Schaal, 2002). Numerous papers have relied on the single Gaussian summed with a linear ramp (SGR) model for quantifying peak shifts in the peak or related procedures (for a representative sampling, see Buhusi & Meck, 2002; Cheng & Westwood, 1993; Matell et al., 2004; Roberts, 1981; Saulsgiver et al., 2006). For example, Saulsgiver et al. presented data on how amphetamine affects responding in the peak procedure. Using the SGR model, they found a leftward shift in peak times (i.e., earlier peaks) due to amphetamine, but attributed that shift mostly to a rate-dependency effect, whereby the rate of responding early in the trial was increased, but later responding (after the peak) was unaffected. Using the dual Gaussian (DGKQ) approach detailed here would have allowed them to better dissociate effects on early responding (i.e., start times) from the effects on peak times. Furthermore, the strong similarity of those results and those of the current experiment hint that dopamine effects on timing may be due to increased reinforcer magnitude with dopaminergic agonists and not necessarily due to direct effects on timing. Even more problematic, however, are the cases where peak shifts as derived from the SGR model are taken as constitutive data for psychological interpretations of timing, as is the case with much recent data from the so-called “gap” procedure—where the stimulus is interrupted during peak trials (e.g., Buhusi & Meck, 2002; Buhusi, Perera, & Meck, 2005). McClure et al. (2005) also reached similar conclusions when comparing fitted functions for evaluating performance on a different timing procedure (the bisection task). In future experiments with the peak or related procedures, it would be wise to exercise caution when interpreting shifts in peak times derived from single Gaussian models and to use appropriate statistical procedures when evidence of asymmetry is seen.

As Zeiler and Powell (1994) showed, the conclusions one draws about timed behavior in animals depend strongly on the dependent measures examined (see also McClure et al., 2005). Focussing on stop times alone, reinforcer magnitude does not seem to influence timing. Shifting focus to start and wait times reveals that reinforcer magnitude does indeed influence timing in two ways: later responding following larger reinforcers and earlier responding before larger reinforcers. These results present a challenging, though not irreconcilable, dataset for the major theories of timing. The best explanation for this pattern of results lies in supposing that reinforcer magnitude plays a dual role in influencing timing, producing both immediate after-effects and anticipatory responses.

Appendix A

Full equations for all six models fitted to the peak datasets are presented below. Only Models 1, 2, and 5 are extensively discussed in the text and figures, but similar conclusions regarding the superiority of Model 5 (DGKQ) hold even with all six models.

Model 1. Single Gaussian (SG)

Where:

t is the mid point of the time bin of the trial time (s),

r is the response rate (responses / s),

H is the maximum response rate (responses / s),

L₁ is the start half-max: the time when the Gaussian has risen halfway to its peak value (s),

L₂ is the stop half-max time: the time when the Gaussian has fallen halfway from its peak value (s),

log() is the natural logarithmic function (base e).

A1

Model 2. Single Gaussian summed with a linear Ramp function (SGR)

Where the Single Gaussian variable and parameter definitions are continued for this model and:

R is the slope of the linear ramp function with an intercept of zero (responses / s).

A2

Model 3. Single Gaussian with a Quadratic tail (SGQ)

Where the Single Gaussian variable and parameter definitions are continued for this model and:

T_q is the point in time at which the Single Gaussian is joined to the Quadratic (s),

S is the coefficient for the quadratic (responses / s).

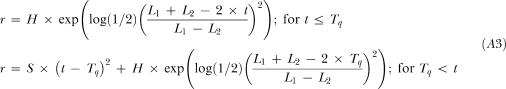A3

Model 4. Dual Gaussian with a Quadratic tail (DGQ)

Where the Single Gaussian with a Quadratic tail variable and parameter definitions are continued for this model and:

T_p is the peak time for the Single Gaussian (s).

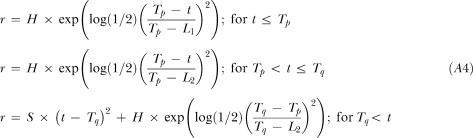A4

Model 5. Dual Gaussian with a single Kurtosis parameter plus a Quadratic tail (DGKQ)

Where the Dual Gaussian with a Quadratic tail variable and parameter definitions are continued for this model and:

K is the kurtosis parameter (dimensionless).

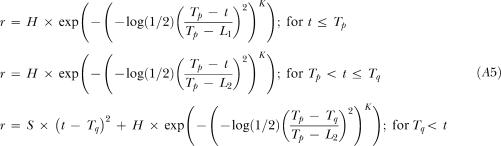A5

Model 6. Dual Gaussian with Dual Kurtosis parameters plus a Quadratic tail (DGDKQ)

Where the Dual Gaussian with a Quadratic tail variable and parameter definitions are continued for this model and:

K₁ is the kurtosis parameter for times less than the peak time, T_p (dimensionless),

K₂ is the kurtosis parameter for times greater than the peak time, T_p (dimensionless).

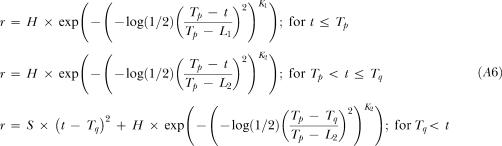A6