Brain size does not predict general cognitive ability within families

Abstract

Hominid brain size increased dramatically in the face of apparently severe associated evolutionary costs. This suggests that increasing brain size must have provided some sort of counterbalancing adaptive benefit. Several recent studies using magnetic resonance imaging (MRI) have indicated that a substantial correlation (mean r = ≈0.4) exists between brain size and general cognitive performance, consistent with the hypothesis that the payoff for increasing brain size was greater general cognitive ability. However, these studies confound between-family environmental influences with direct genetic/biological influences. To address this problem, within-family (WF) sibling differences for several neuroanatomical measures were correlated to WF scores on a diverse battery of cognitive tests in a sample of 36 sibling pairs. WF correlations between neuroanatomy and general cognitive ability were essentially zero, although moderate correlations were found between prefrontal volumes and the Stroop test (known to involve prefrontal cortex). These findings suggest that nongenetic influences play a role in brain volume/cognitive ability associations. Actual direct genetic/biological associations may be quite small, and yet still may be strong enough to account for hominid brain evolution.

Hominid brains have roughly tripled in volume in less than 3 million years, and little of this can be explained by body size increases (1–4). Because larger brains take longer to mature (5), have very high metabolic costs (6), and reduce the efficiency of bipedal locomotion (because the pelvic aperture must still allow birth) (7), increasing brain size must therefore have provided counterbalancing adaptive benefits (8). Seven recent studies using magnetic resonance imaging (MRI) to estimate brain volume have shown a substantial correlation (mean r = ≈0.4) between brain size and general cognitive performance (9–16). Although these findings are consistent with the hypothesis that the payoff for increasing brain size was related in some way to greater general cognitive ability (g), they do not control for potentially confounding between-family (BF) environmental influences.

Family background, socioeconomic status (SES), cross-assortative mating, and cultural influences potentially affect both anatomy and behavior in the same direction independently, which could thereby result in noncausal associations between brain size and cognitive ability. These BF influences can be controlled for by asking whether WF sibling differences in brain size are associated with WF sibling differences in cognitive performance. This technique has been used to show that height/IQ correlations are probably not genetically mediated (17–20), but that myopia/IQ correlations apparently are genetically influenced (21). To date, there is only one brief abstract of a WF MRI study of brain/cognitive ability associations in the literature (16), which found no significant WF correlation between general cognitive ability (g) and MRI brain volume in 40 male siblings (no details were provided). Two additional WF studies used head circumference as a proxy for brain volume (22, 23). The largest (n = 28,992) found that the WF correlations between head circumference and IQ were only 57% the size of BF correlations (22). Because this was a study of very young subjects (ages 4 and 7), variability in maturation rate might have caused a spurious WF association in this sample. Thus, there is no unequivocal evidence that BF associations are attributable to a direct causal influence of brain size on IQ.

Because the causal nature of brain/behavior correlations is important to both human evolutionary studies and to medical research, we report here the details of a WF study of 75 healthy females (36 analyzable sibling pairs) using high resolution MRI (4× finer than any previous study of this kind) combined with a diverse battery of cognitive tests. If brain size truly causes differences in cognitive function, this should be apparent WF as well as BF.

Materials and Methods

Healthy female sib pairs were recruited locally and were screened for pregnancies, siblings more than 6 years older or younger, dyslexia, brain trauma, brain disease, psychiatric history, medication that might affect concentration, and uncorrected hearing or vision problems. Mean age of the subjects was 23.2 years (SD = 5.1; range, 18–43), and they averaged 14.9 years of schooling (SD = 2.1; range, 11–21). The mean sibling age difference was 2.7 years (SD = 1.2; range, 1.0–5.6). Informed consent was obtained following protocols approved by both University of California at San Francisco and University of California at Berkeley human subjects committees.

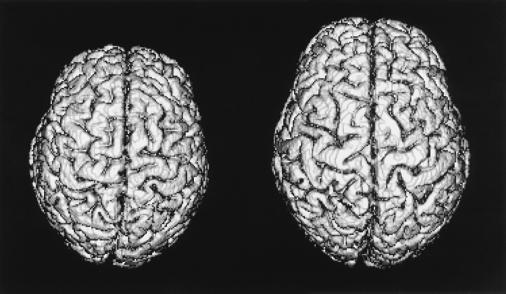
MRI scans were performed on each subject with a 1.5 tesla GE Signa scanner, using an axial three-dimensional SPGR (spoiled-gradient) sequence (Time of Echo 8 ms, Time of Repetition 32 ms, 45° flip angle), resulting in 124 contiguous slices 1.5 mm thick (pixel dimensions = 0.94 mm × 0.94 mm). After removing personal identifying information, non-brain tissues were removed from the images by using standard thresholding and seed-growing methods available in vida image processing software (24). The following volumes were extracted from these images: Total brain (BRAIN), prosencephalon (PROS), prosencephalon gray and white matter (GRAY, WHITE), cerebellum (CEREBELLUM), brainstem (BRAINSTEM), total prefrontal (PREFRONTAL-TOTAL), and gray and white prefrontal (PREFRONTAL-GRAY, PREFRONTAL-WHITE). BRAIN, CEREBELLUM, and BRAINSTEM were obtained by summing pixels within appropriate regions (4). GRAY and WHITE were estimated by iteratively fitting the sum of two Gaussian curves onto histograms of pixel intensities of PROS (the area under these curves is an estimate of the respective tissue volumes), using an algorithm developed and implemented at the Lawrence Berkeley National Laboratory by Sundar Amartur and Thomas F. Budinger. PROS was calculated as GRAY + WHITE. Area under the gray curve extending below the value used for the initial segmentation threshold was used as a partial-volume correction factor (included in BRAIN, PROS, and GRAY). Prefrontal volumes (PREFRONTAL-TOTAL, PREFRONTAL-GRAY, PREFRONTAL-WHITE) were derived by reformatting the images to include only those portions of the frontal cortex anterior to the corpus callosum, in a plane perpendicular to the longest axis of the corpus callosum (in midsagittal view). Reformatted files were interpolated by using vida's nearest-neighbor algorithm. PREFRONTAL-GRAY and PREFRONTAL-WHITE were estimated as per GRAY and WHITE. PREFRONTAL-TOTAL was calculated as PREFRONTAL-GRAY + PREFRONTAL-WHITE. Within-rater reliabilities of all of these measures were r > 0.95. Means and SDs for these variables are shown in Table 1. Fig. 1 shows surface-rendered three-dimensional volumes of the largest- and smallest-brained individuals in the sample, who differ by more than 400 ml. The average WF sibling difference in BRAIN was 62 ml (range, 0.3–219 ml). Substantial average sibling differences were found for all variables.

Table 1.

Between- and within-family correlations among neuroanatomic variables, along with total-sample means and SDs^*

	BRAIN	PROS	GRAY	WHITE	CEREBELLUM	BRAINSTEM	PREFRONTAL			Total sample
							TOTAL	GRAY	WHITE	Mean	SD
BRAIN		0.99‡	0.71‡	0.58‡	0.55‡	0.72‡	0.66‡	0.63‡	0.53‡	1196	77
PROS	0.99‡		0.71‡	0.60‡	0.41†	0.69‡	0.66‡	0.62‡	0.53‡	1041	70
GRAY	0.83‡	0.84‡		−0.14	0.39†	0.31	0.40†	0.62‡	0.01	703	53
WHITE	0.73‡	0.74‡	0.25		0.13	0.62‡	0.47‡	0.17	0.73‡	338	43
CEREBELLUM	0.64‡	0.52‡	0.49‡	0.33		0.38†	0.34	0.34	0.26	132	12
BRAINSTEM	0.45‡	0.37†	0.25	0.35†	0.53‡		0.44†	0.33	0.46‡	24	3
PREFRONTAL
TOTAL	0.50‡	0.50‡	0.39†	0.42†	0.30	0.20		0.91‡	0.85‡	128	17
GRAY	0.46‡	0.46‡	0.51‡	0.18	0.31	0.14	0.94‡		0.56‡	88	11
WHITE	0.46‡	0.47‡	0.16	0.64‡	0.24	0.24	0.89‡	0.67‡		40	8

*Between-family correlations below the diagonal, within-family above. Correlations calculated on age-corrected variables. 

^†P < 0.05. 

^‡P < 0.01. 

Figure 1.

Three-dimensional reconstructions of the smallest- and largest-brained individuals in this data set. The total brain volumes for these two individuals are 1,014.7 ml vs. 1,418.6 ml, respectively.

Each subject was given a diverse set of cognitive tests: a modified, timed version of Raven's Progressive Matrices (RAVEN) (4, 25); verbal fluency (VERBALFL) (26); vocabulary (VOCAB) (27); Wisconsin Card Sort Test (perseverative errors), computer-administered (WCST-PERS) (4, 28, 29); simple reaction time (SIMPLE-RT) (4); semantic verification reaction-time test (OBJECT-ID) (4); sentence verification reaction-time using different types of complex syntax (SENTENCE) (4); difference in average verification reaction time between sentences with identical words but differing syntax (SYNTAX) (4); Stroop test (STROOP) (30, 31); Trails B minus Trails A (TRAILS) (32); and number of correct responses (MRT-N) and median reaction time on correct responses (MRT-SPEED) on a computerized version of the Vandenberg and Kuse Mental Rotation Test (4, 33).

Information relevant to the subject's socioeconomic background (SES) was also collected, as well as recalled age-at-menarche (MENARCHE). SES was estimated from parent's years in school, parents occupation (during the first 2 years subject was in high-school), and an updated version (4) of Home Index of Status Items (34). Family's SES job rating [using a standard SES index (35)] was that of the parent with the highest rated job. Variables were turned into standard scores and were averaged to yield one composite (4).

To avoid confusion in interpreting correlation matrices, scores on tests in which better performance resulted in a lower score (e.g., reaction time tasks) were reversed (multiplied by −1). The data were then divided into WF and BF data sets. WF data were obtained by calculating the signed, sibling differences for each variable, with the order of subtraction (older sib minus younger sib) consistent across all variables. Because age effects on cognitive test scores can be nonlinear, age correction was performed by regressing out difference-in-age, (difference-in-age)², and (difference-in-age)³ from all variables [using multiple regression and partial correlation techniques (19, 37)]. The resulting WF data were then double-entered into the analysis: for each sib pair, age-corrected older-minus-younger data as well as the transpose of these data (i.e., the data multiplied by −1) were both entered as two separate rows of data. This double-entry method was done because the order of subtraction for a given set of siblings is arbitrary, yet the correlations calculated on different orderings may vary somewhat. This double-entry method results in the best estimate of within family associations because it is, in effect, an average correlation for all possible sib orderings [double-entry methods are routinely used in behavioral genetic studies (36)].

BF data were obtained by calculating sibling averages (older sister plus younger sister divided by 2) for the variables of interest. Age correction was then performed on this data by regressing out average age, (average of age)², and (average of age)³ from all variables (using the same techniques described for WF data above). Note that BF age correction is based on average family age whereas WF age correction is based on sibling differences in age. We used this method (rather than regressing out age effects from the individual scores before calculating BF and WF data sets) because age can have different effects within families than it does between (e.g., sibs closer in age might be more competitive than sibs farther apart). Some of the cognitive tests in this study do in fact show weak negative (nonsignificant) WF associations with age. Because it is important to eliminate all age effects, the results reported below are based on age correction applied separately within WF and BF data sets.

Variance within both WF and BF data sets associated purely with speed-of-response by the subjects was removed by regressing out SIMPLE-RT from within each data set (38). Twenty-five percent of the WF age and SRT corrected cognitive test variance and thirty-two percent of the BF variance was explained by the first principal component (1st PC), which was calculated independently in the two data sets. 1st PC was therefore used as a measure of general cognitive ability (g). The 1st PC loadings on each of the cognitive tests are reported in Tables 2 and 3 (for BF and WF data, respectively). The BF and WF pattern of loadings are very similar. RAVEN and SENTENCE loaded highly on 1st PC both BF and WF, even though RAVEN is entirely nonverbal whereas SENTENCE has a strong verbal component. Although it is true that they both have spatial processing components, MRT-SPEED (which is a strongly spatial task) loads only weakly on 1st PC, which suggests that 1st PC is not simply a spatial factor but instead reflects a more general cognitive processing ability.

Table 2.

Between-family (BF) correlations of cognitive to neuroanatomic variables^*

	BRAIN	PROS	GRAY	WHITE	CEREBELLUM	BRAINSTEM	PREFRONTAL			1st PC loadings
							TOTAL	GRAY	WHITE
1st PC	0.45‡	0.41†	0.33	0.31	0.42†	0.42†	0.27	0.23	0.28
VOCAB	0.12	0.10	0.07	0.08	0.20	0.09	0.06	−0.03	0.16	0.60
RAVEN	0.44†	0.41†	0.36†	0.28	0.36†	0.35†	0.22	0.20	0.21	0.88
MRT-SPEED	0.24	0.21	0.09	0.26	0.23	0.23	0.11	0.09	0.11	0.26
MRT-N	0.39†	0.37†	0.22	0.38†	0.28	0.29	0.26	0.16	0.33	0.55
STROOP	0.19	0.21	0.12	0.22	0.00	−0.12	0.37†	0.35†	0.32	0.16
TRAILS	0.33	0.31	0.19	0.30	0.29	0.32	0.37†	0.28	0.40†	0.65
VERBALFL	0.27	0.25	0.24	0.14	0.26	0.17	0.12	0.09	0.15	0.48
WCST-PERS	0.31	0.26	0.14	0.28	0.44†	0.36†	−0.02	−0.01	−0.03	0.43
OBJECT-ID	−0.06	−0.10	−0.05	−0.10	0.16	0.20	0.05	0.05	0.05	0.30
SENTENCE	0.27	0.24	0.21	0.17	0.26	0.31	0.14	0.13	0.12	0.87
SYNTAX	0.21	0.21	0.31	−0.01	0.09	0.22	0.13	0.22	−0.02	0.55

*All variables corrected for age and Simple-RT. 

^†P < 0.05. 

^‡P < 0.05. 

Table 3.

Within-family (WF) correlations of cognitive to neuroanatomic variables^*

	BRAIN	PROS	GRAY	WHITE	CEREBELLUM	BRAINSTEM	PREFRONTAL			1st PC loadings
							TOTAL	GRAY	WHITE
1st PC	−0.05	−0.05	−0.06	−0.01	−0.01	−0.04	−0.04	−0.07	0.01
VOCAB	0.02	−0.01	−0.06	0.06	0.18	−0.17	−0.07	−0.16	0.06	0.46
RAVEN	−0.17	−0.17	−0.02	−0.23	−0.05	−0.18	−0.22	−0.22	−0.16	0.69
MRT-SPEED	−0.27	−0.26	−0.42†	0.12	−0.23	−0.17	0.12	0.02	0.21	0.22
MRT-N	0.00	0.00	−0.02	0.03	−0.01	−0.04	0.02	−0.05	0.10	0.47
STROOP	0.15	0.17	−0.21	0.49‡	−0.07	0.26	0.42†	0.27	0.52‡	0.31
TRAILS	−0.11	−0.08	−0.07	−0.03	−0.20	0.04	−0.11	−0.10	−0.10	0.62
VERBALFL	−0.13	−0.14	0.04	−0.24	−0.04	−0.17	−0.13	−0.06	−0.18	0.67
WCST-PERS	0.04	−0.03	−0.08	0.04	0.37	0.01	0.02	−0.08	0.14	−0.05
OBJECT-ID	−0.09	−0.10	−0.08	−0.04	−0.06	0.06	−0.11	−0.08	−0.11	0.61
SENTENCE	0.19	0.16	0.11	0.10	0.26	0.17	0.08	0.08	0.07	0.73
SYNTAX	0.27	0.29	0.19	0.20	0.05	0.04	0.34	0.34	0.26	0.20

*All variables corrected for age and Simple-RT. 

^†P < 0.05. 

^‡P < 0.01. 

Pearson's product-moment correlations were then calculated on the variables within each data set (note that, although WF data included 36 × 2 = 72 cases due to double-entering, significance levels for WF correlations were calculated by assuming n = 36). WF and BF results therefore represent logically independent components of the original sample data: WF based on sibling differences, BF on sibling averages.

Because many of the neuroanatomical variables are not independent (e.g., BRAIN, PROS, GRAY), significance levels are not corrected for multiple comparisons. Calculations were performed by using statview 4.5 (this version can incorrectly reverse the sign of factor scores; this problem was manually corrected when it occurred) (39).

Results

Our results show a BF correlation between 1st PC and BRAIN of r = 0.45 (P < 0.01; Table 2), which is consistent with published correlations between MRI brain volume and IQ (9–16). None of the neuroanatomical subdivisions correlate higher with 1st PC than does BRAIN. Partial correlations (37) of the cognitive tests with BRAIN after controlling for 1st PC are not significant, suggesting that 1st PC explains most of the observed BF relationship between BRAIN and the test scores. BF correlations between individual cognitive tests and prefrontal variables are significant only for STROOP and TRAILS. This finding is particularly significant, because a variety of evidence points to these tests being mediated by prefrontal cortex (40). Prefrontal correlations with 1st PC are positive but do not reach statistical significance. Ignoring family pairings, the correlation between 1st PC and BRAIN for all 75 individuals lacking brain abnormalities is r = 0.24 (P < 0.05).

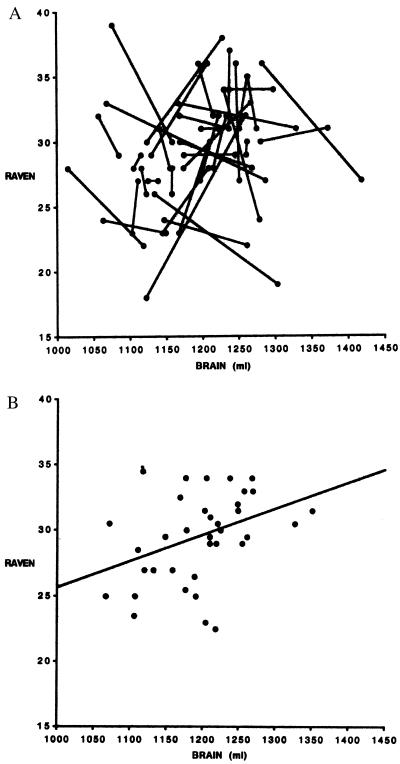
In sharp contrast to the BF findings, WF correlations between neuroanatomical variables and 1st PC are very small and show little variation, ranging from r = −0.07 to 0.01 (Table 3). As a graphic example of these WF vs. BF differences, compare Fig. 2a with Fig. 2b, both of which show scatterplots comparing BRAIN and RAVEN (for clarity, these show the raw scores uncorrected for age and SRT). Fig. 2a shows this relationship for all 72 individuals, with sib pairs connected by lines. Fig. 2b shows the same variables plotted by using the BF (sibling averages) data. Although a weak relationship is evident in Fig. 2b, the slopes of the lines in Fig. 2a do not show any consistent pattern (either positive or negative) between the two variables. If a positive WF association existed, the lines connecting the sib pairs should tend to have a positive slope, yet they clearly do not. This pattern was typical for the variables that showed significant BF correlations.

Figure 2.

(a) The association of BRAIN to RAVEN with family relationships indicated. Data points connected by lines represents sister pairs. The randomness of the within-family relationships of the variables is immediately apparent. For simplicity, these variables are not corrected for age or SIMPLE-RT. (b) The between family relationship of BRAIN to RAVEN. Each data point represents the mean values for one pair of sisters. For simplicity, these variables are not corrected for age or SIMPLE-RT (the relationship is slightly stronger when calculated with corrected data). The line is a least squares regression: RAVEN = 5.66 + 0.02 (BRAIN), r = 0.39 (P < 0.05).

In addition to these correlational analyses, we compared the average differences in cognitive test scores between larger vs. smaller BRAIN sibs for the 12 pairs who differed the most in BRAIN (average difference = 132 ml), but still found no significant differences (4). However, significant WF correlations are found between STROOP and three neuroanatomical variables: WHITE (r = 0.49; P < 0.01), PREFRONTAL-TOTAL (r = 0.42; P < 0.05), and PREFRONTAL-WHITE (r = 0.52; P < 0.01).

It is unlikely that the low WF correlations with BRAIN are methodological artifacts for a number of reasons. Consideration of Fig. 2 a and b makes it difficult to see how any legitimate method of quantifying WF associations could result in significant WF effects. Nevertheless, randomization studies were performed to estimate the likelihood of obtaining a large difference between BF and WF correlations for BRAIN vs. 1st PC purely by chance (4). In one study, we sought to determine the distribution characteristics of BF-minus-WF correlation differences obtained by using the data calculation methods described above. To do this, four sets of random numbers (36 in each set, to match the number of family pairs in this study) were chosen and arbitrarily assigned to represent sib 1-variable A, sib 1-variable B, sib 2-variable A, or sib 2-variable B. WF and BF correlations were then calculated by using these data. This whole process was repeated 1,000 times. The average BF-minus-WF difference from these random data was only 0.007 (SD = 0.237), and only 14 trials (P = 0.014) resulted in a difference ≤0.50 (which was found for the BRAIN-1st PC data in this study). This demonstrates that the basic methodology of calculating BF and WF correlations used in this study is highly unlikely in and of itself to result in higher BF-minus-WF correlations. However, the actual data might have unique characteristics [e.g., differing reliabilities of the cognitive tests and other variables (19)] that might influence the BF-minus-WF difference. We therefore carried out another randomization study in which the actual subjects were randomly paired with individuals who were not their siblings, forming new “nonfamily” pairs. BF and WF correlations for 1st PC to BRAIN where then calculated on these nonfamily pairs. This process was repeated 100 times, allowing us to estimate the likelihood of obtaining a given BF-minus-WF difference in this data simply by randomly pairing individuals together. We found that a BF-minus-WF difference greater than 0.50 occurred only five times of the 101 randomly paired data sets. The average BF-minus-WF difference for these random pairings was only 0.11 (σ = 0.23). These studies show that methodological artifacts do not easily explain the large BF-minus-WF difference in our data.

Additional reasons to doubt that methodological issues explain our findings include the following. First, although WF data has less variance than the BF data (which might therefore predict lower WF correlations), the degree of WF variance reduction across different cognitive tests is not significantly associated with increases in the difference between BF vs. WF correlations (4). Second, when we estimate and account for the effects of reduced variance within families and the different reliability of WF and BF correlations by using published formulas devised for this purpose (19, 41), our conclusions are not changed. Third, the pattern of intercorrelations among the neuroanatomical variables is very similar both BF and WF (Table 1), as are many of correlations between pairs of cognitive tests (e.g., RAVEN and VOCAB are correlated: r = 0.54 BF, and r = 0.40 WF). Overall, the Spearman rank-order correlation between the WF and BF cognitive test intercorrelations is r_s = 0.30 (P < 0.02). If methodology is the primary cause of the large BF vs. WF differences observed between BRAIN and 1st PC, it should generally affect all correlations, not mostly those between a neuroanatomical and a behavioral variable. Lastly, as noted, performance on the STROOP test is significantly correlated with prefrontal variables both WF and BF. All of these findings suggest that methodological differences do not explain the moderate-BF/zero-WF pattern in our 1st PC/BRAIN results.

Discussion

The STROOP findings are consistent with the idea that differences in prefrontal cortex volume causally influence STROOP scores. This test measures the extent of linguistic interference in naming colors, when ink color and word name are mismatched (e.g., the word “red” written in blue ink). It is generally considered to be a test of the ability to extract (and focus on) the relevant information from an environment (30). Because myelinization [thought to be the major cause of gray/white tissue contrast in MRI (42)] occurs relatively late in the prefrontal cortex (43), and because neural organization in general is known to be sensitive to environmental input during development (44–46), it is possible that prefrontal regions are more susceptible to within-family environmental effects than other regions, and that some form of environmental/genetic interaction may underlie the observed correlation between prefrontal volumes and STROOP.

Our findings with respect to total brain volume and overall cognitive performance do not suggest there is a strong, direct, causal influence between the two. We do, however, raise four important points concerning this conclusion.

First, it is possible that some confounding WF influence, possibly reflecting sibling competition, is attenuating WF associations. Older sibs scored better on the cognitive tests than their younger siblings by 0.57 standard deviations for 1st PC (even after age correction applied to the 72 subjects as individuals). Although simple WF and BF age effects were removed before calculating the correlations, age could still affect the WF results if it interacts with brain/behavior relationships in complex ways. If we look only at the six pairs that differ by more than 4 years in age, the WF correlations between BRAIN and the 11 cognitive variables average r = 0.22 (1st PC to BRAIN was r = 0.18) whereas correlations for the 30 sib pairs less than 4 years apart (n = 30) average only r = −0.02 (1st PC to BRAIN was r = −0.07) (4). A randomization study suggested that the probability of obtaining an average correlation of at least r = 0.22 for 11 correlations between sets of six random numbers is P = 0.054 (based on 10,000 replications). Additionally, older sibs with smaller than average brains have significantly higher 1st PC scores than younger sibs with smaller than average brains (mean unpaired difference t value = 1.846, P < 0.04, one-tailed), which is consistent with the idea that older sibs are applying their inherent abilities to these tests more than younger sibs. Recall also that there were weak negative WF correlations (nonsignificant) between age and some cognitive tests (4). These findings suggest the possibility of some sort of sibling interaction that increases as sibling age difference decreases. Such an effect probably explains only a portion of the WF/BF difference, but the possibility needs to be addressed in future studies.

Our second point is that, for the reasons outlined in the abstract, it is still highly unlikely that there would be no genetic correlations of any kind between brain volume and behavioral ability. It may well be that the particular tests used in this study are only distant proxies for those applied by natural selection over the last 3 million years. Other cognitive functions, such as social competence (47, 48) and the complexity and range of concepts that can be processed effectively at a given time, might well show stronger associations with brain size. Our prefrontal results also suggest that genetically mediated volume/behavior associations may occur between localized neuroanatomical regions and specific tasks. It is possible that other cognitive tests used in this study might correlate with the size of localized regions that we did not specifically quantify (e.g., MRT tasks and RAVEN might correlate with parietal association areas, which are thought to be involved in the processing of these tasks).

Additionally, it could be that the causal connection between brain volume and g is so weak that it could not be reliably detected without prohibitively large sample sizes, while still being perfectly adequate, given the large number of generations involved, to account for hominid brain size evolution. A genetic correlation between brain size and g of just r = 0.05 would require an average selection differential (mean of selected individuals minus population mean) of just 0.0059 SD—equivalent to less than 1/10th of an IQ point [this calculation assumes an increase of 1,000 ml over 2.5 million years (3), 20-year average generation length, average brain size SD of 90 ml, and heritabilities of 0.3; the formula is from Falconer (49)]. This level of selection is well within that observed for various characteristics (including IQ) in humans (50–52) while being virtually undetectable in any given generation without massive sample sizes. Our point is not to suggest that hominid brain evolution was necessarily regular and gradual, but rather that strong associations between brain anatomy and behavior are not needed to produce dramatic evolutionary changes. Adding ≈8 ml of extra brain tissue per generation should not rate as a major evolutionary problem.

We also note that large between-species correlations do not necessarily predict or require large within-species correlations. The correlation between log brain size and log age-at-menarche in primates is r = 0.85 (n =49, P < 0.0001) (5), but the same correlation among the subjects in this study (i.e., within-species) was only r = 0.10 (BF) and r = −0.21 (WF) (variables corrected for age-at-testing).

Our third point is that nonrandom associations of independent genetic influences on two variables may occur through various mating tendencies: for example, if large brained individuals tended above chance to mate with high IQ individuals. This would result in a BF correlation but would have no effect on WF correlations because meiosis randomizes genes within families. Further work will need to be done to determine the extent to which this might explain our present findings.

Finally, we note that, although it is theoretically possible for SES (which is primarily a BF influence) to affect brain and behavior independently (resulting in a significant BF − WF difference, as found in this study), SES does not explain our findings. The SES data, unique to this study, allow the conclusion that, although family SES correlates strongly with BF 1st PC [r = 0.55, P < 0.01, similar to other studies (53)], it does not with BRAIN (r = 0.05, P > 0.79). This does not rule out the influence of other BF variables, but they would have to be uncorrelated with SES and yet strongly correlated with both brain size and cognitive performance. Environmental influences responsible for secular trends in, for example, height, brain size, and even IQ might be relevant here (54).

In summary, although total brain volume and cognitive ability are positively associated in the general population, the same is not true among sisters in the same families. Similar results have also been reported for males (16). This suggests that the direct, gene-based, causal association between the total brain volume and cognitive ability may be of minimal functional significance in modern populations, even if large enough to be evolutionarily relevant. However, significant correlations between STROOP and prefrontal regions found among sisters in the same families suggests that brain/behavior associations may exist for specific tasks in localized neuroanatomical regions.

Abbreviations

g

general cognitive ability

BF

between-family

SES

socioeconomic status

WF

within family

1st PC

first principle component