Some transformations of color information from lateral geniculate nucleus to striate cortex

Abstract

We have recorded the responses of single cells in the lateral geniculate nucleus (LGN) and striate cortex of the macaque monkey. The response characteristics of neurons at these successive visual processing levels were examined with isoluminant gratings, cone-isolating gratings, and luminance-varying gratings. The main findings were: (i) Whereas almost all parvo- and konio-cellular LGN cells are of just two opponent-cell types, either differencing the L and M cones (L_o and M_o cells), or the S vs. L + M cones (S_o cells), relatively few striate cortex simple cells show chromatic responses along these two cardinal LGN axes. Rather, most are shifted away from these LGN chromatic axes as a result of combining the outputs (or the transformed outputs) of S_o with those of L_o and/or M_o cells. (ii) LGN cells on average process color information linearly, exhibiting sinusoidal changes in firing rate to isoluminant stimuli that vary sinusoidally in cone contrast as a function of color angle. Some striate cortex simple cells also give linear responses, but most show an expansive response nonlinearity, resulting in narrower chromatic tuning on average at this level. (iii) There are many more +S_o than −S_o LGN cells, but at the striate cortex level −S_o input to simple cells is as common as +S_o input. (iv) Overall, the contribution of the S-opponent path is doubled at the level of the striate cortex, relative to that at the LGN.

We (1–4) and many others (e.g., 5–8) have studied the chromatic response characteristics of cells in the lateral geniculate nucleus (LGN) and at the first processing stages within the striate cortex of the macaque monkey. We are revisiting the problem to test predictions from our recent color model (9) and from our psychophysical studies (10, 11) that certain transformations of color information should occur between the LGN and the cortex. Most previous studies of LGN and cortical cells, including our own earlier ones, used different stimuli in examining cells at the two levels, thus making direct comparisons between LGN and cortex difficult to quantify.

To examine this issue more precisely, we have recorded from a considerable sample of cells in the LGN and striate cortex of macaque monkeys, by using identical stimuli in examining cells at these two successive processing levels. The stimuli also were identical in chromaticity to those used in our psychophysical studies (10, 11). These measurements should allow us to determine any changes in the chromatic information from the LGN to the cortex. Furthermore, they should also facilitate comparisons to psychophysical measurements of color appearance.

Methods

Macaque monkeys (Macaca mulatta and M. fascicularis) were initially tranquilized with ketamine HCl (10–15 mg/kg, i.m.). Anesthesia was maintained with a continuous i.v. infusion of sufentanil citrate (during surgery, 8–12 μg/kg/h; during recording 5–8 μg/kg/h). After surgery, paralysis was induced and maintained with pancuronium bromide (0.1–0.15 mg/kg/h, i.v.). Electrocardiogram, electroencephalogram, body temperature, and expired CO₂ were continuously monitored. All of the procedures were approved by the local Animal Care and Use Committee and were in accord with National Institutes of Health guidelines.

Extracellular recordings were made from single neurons in the LGN and the striate cortex (V1). All recordings were from units whose receptive fields were within the central visual field. Action potentials (spikes) were recorded with a resolution of 1 msec. Visual stimuli were generated and controlled by a Sun/TAAC (Sun Microsystems, Mountain View, CA) image processor, with on-line data analysis being performed by the Sun. The stimuli were presented on an NEC monitor (Nippon Electric, Tokyo) with a spatial resolution of 1,000 × 900 pixels, a 66-Hz refresh rate, and a mean luminance of 70 cd/m².

The chromatic response properties of each cell were characterized with drifting gratings that varied sinusoidally in chromaticity. These were presented for 2 sec each, in random order within a testing series. Typically, we first determined the spatial frequency tuning of a neuron and, in the case of cortical cells, the orientation tuning. The chromatic testing then proceeded with grating patches of the optimal spatial frequency and orientation. The grating patch was centered on the receptive field (RF) of the cell and was slightly larger than the classic RF. Many cortical cells and almost all LGN cells showed low-pass spatial frequency tuning for chromatic patterns. These cells were therefore tested with spatially uniform patches. The gratings drifted, and uniform patches were modulated, at a temporal frequency of 3.8 Hz.

The background chromaticity of the monitor was white (Illuminant C). Stimuli consisted of shifts from the background white to various gratings, each of which was modulated around this white point so that the space-and-time-average luminance and chromaticity were always constant. The chromatic stimuli were specified in a color space developed by MacLeod and Boynton (12) and elaborated by Derrington, Krauskopf, and Lennie (5), which we refer to as the MBDKL color space. In this space, stimuli are defined by vectors based on the characteristics of cones (13) and LGN cells (5). The primary axes in a horizontal (isoluminant) plane of this space are the L/M-opponent axis (0°-180°) and the S_o axis (90°-270°). Along the L/M axis the L- and M-cone contrasts were 8% and 16%, respectively; along the S_o axis, the S-cone contrast was 83%. The intermediate angles were defined as combinations of these unit vectors, e.g., 45° has equal contributions from the 0° and 90° vectors.

Three types of stimuli were used: (i) Isoluminant chromatic modulations were made along various color axes in MBDKL space of either drifting gratings or temporally modulated, spatially uniform patches. The contrasts of the isoluminant patterns were chosen so that the excursions in different color directions around the circle from 0° to 360° produced sinusoidal changes in cone activation for each cone type (see Inset in Fig. 1). (ii) Cone-isolating modulations were made along the L and M cone axes (in addition to the 90°-270° isoluminant grating, which is a modulation along an S-cone isolating axis). The L and M cone contrasts for these cone-isolating but not isoluminant gratings were 22% and 24%, respectively. (iii) Black–white intensity modulations were made of 20% luminance contrast. The maintained firing rate was measured on trials in which no pattern was presented. These various stimuli were presented in a sequentially random order during a single test series, with multiple repetitions.

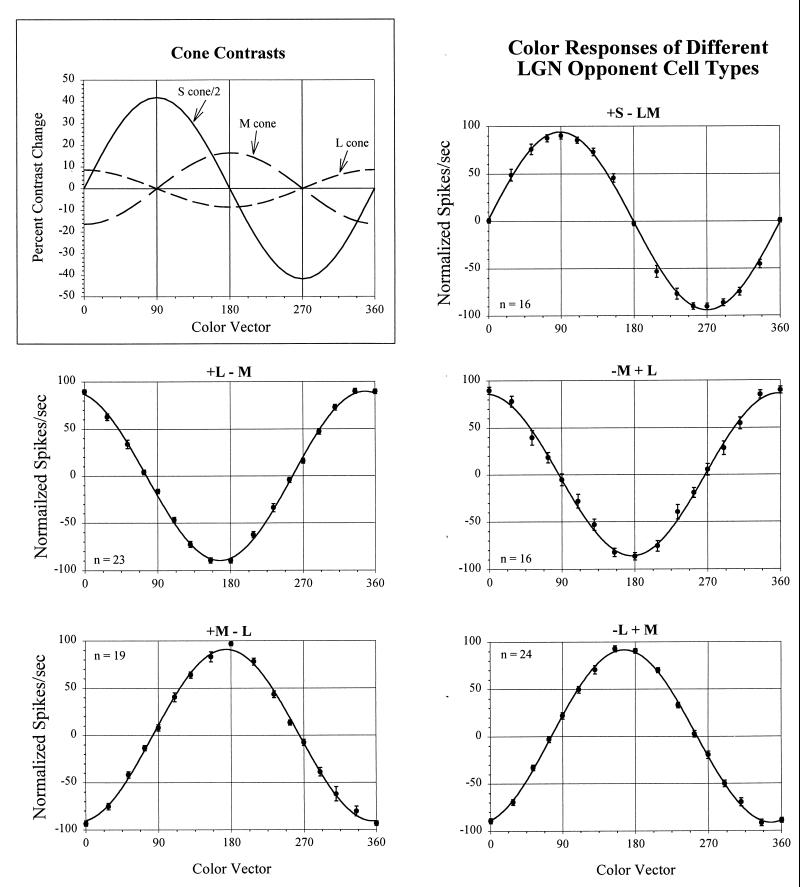
Figure 1.

The cone contrasts produced by stimuli of different color vectors and the responses of LGN cells to these patterns. (Inset) The changes in cone contrast produced by the shift from the background white to the stimuli along different color vectors. Note that the variations in contrast for each cone type are sinusoidal functions of the color vector. The other panels show the average normalized responses (+/− 1 SE) of each of the different LGN opponent cell types, fit with sinusoids. (Positive and negative spikes/second refer to responses to opposite phases of the stimuli, respectively). The cell types are designated in terms of the cone inputs to center and surround of their receptive fields, with + and − referring to activation in response to increments and decrements, respectively. Note that the L/M opponent cells peak close to the 0°-180° MBDKL axis, although the cells with L-cone centers are somewhat off this axis. Note that the responses of +S-LM cells align precisely with the 90°-270° axis. In this cell sample, only two −S + LM (not shown) cells were found.

The spike discharge during each stimulus presentation was recorded, and the data from each cycle of the grating were folded over to obtain an average firing rate as a function of time during one cycle, a peri-stimulus-time-histogram (PSTH). The PSTH was then Fourier analyzed to obtain the mean firing rate and the amplitude and phase of the first harmonic of the response to each stimulus. LGN cells and striate cortex simple cells have a modulated discharge to a drifting grating, and thus a larger first harmonic than mean response (14, 15). Complex cells, on the other hand, have a larger mean than first harmonic response. The response measure in all of the analyses was therefore the first harmonic for LGN and simple cells, and the mean firing rate for complex cells.

In addition to examining the responses to chromatic gratings, we carried out quantitative receptive field mapping by using the reverse-correlation technique (with multiple stimuli presented in shifted versions of an M-sequence). The procedures involved and some of the results of the RF studies have been reported elsewhere (4). Relevant to the present paper are the RFs of cells for increments (+S) and decrements (−S) of S-cone-isolating stimuli.

The data presented here are from 100 cells in the parvo- and konio-cellular layers of LGN and 314 cells in the striate cortex. We have analyzed separately the data from simple and complex striate cortex cells, but we find no differences between them with respect to the issues being studied here. We therefore include both simple and complex cells in our cortical sample.

Results

Chromatic Tuning.

We recorded the responses of LGN and striate cortex cells to isoluminant stimuli of eight different color axes. The responses as a function of color angle were then fit with a sine wave (because the cone contrasts varied sinusoidally as a function of color angle, see Fig. 1 Inset). The optimal chromatic tuning for the cell was derived from the phase of the best-fitting sinusoid. Many cortical cells are better fit with a sinusoid raised to some power greater than one, as we discuss below, and in those cases the optimal tuning was determined from the phase of the exponentiated sinusoid.

Tuning of LGN Cells.

Fig. 1 shows data from a sample of LGN cells of each of the different opponent types from the parvocellular layers. The responses of each cell to the various chromatic gratings were normalized and then averaged together with the responses of other cells of the same opponent-cell type. The four subtypes of LM opponent cells all difference the outputs of L and M cones but have different RF structures, in terms of which cone types feed into the RF center and surround, and whether the excitatory responses are to increments (+) or decrements (−) in cone absorption. Thus a +L − M cell fires to an L-cone increment in its RF center and an M-cone decrement in its RF surround. One opponent cell type, the +S − LM, differences the output of the S cones from the sum of L and M cones.

Relevant to the issue we are concerned with here is the chromatic tuning of these various cells. Note that all of the LM opponent cells are tuned to, or slightly off from, the 0°-180° MBDKL axis, with little variability within the populations or across the different subtypes. The standard errors often do not exceed the size of the data points in the figure. The M-center cells (+M − L and −M + L) on average peak at 180° and 0°, respectively. The L-center cells (+L − M and −L + M) on average peak slightly off this axis, at ≈345° and 165°, respectively. (This difference between these cell types is not in agreement with another recent report of LGN cell color tuning (16), for reasons that are not apparent to us.) Although there is this small variability in peak amongst the LM opponent cells, what is more striking is how similar they are in their chromatic selectivity.

The S − LM opponent cells have a very different chromatic peak, at 90°, with very little variability in the population. The absence of any cells in the parvocellular LGN layers that peak at points other than near the 0°-180° and 90°-270° axes is particularly notable. This can also be seen in Fig. 2, which shows the percentage of cells in the LGN and in the striate cortex that have color peaks in different locations in MBDKL color space. It is clear that not just the averages, but all of the individual LGN cells are tuned very close to one of two discrete chromatic regions.

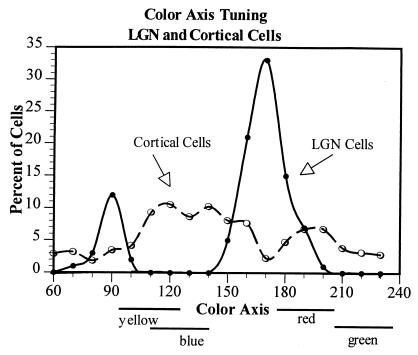
Figure 2.

The distribution of color axis tuning of a population of 100 LGN cells and 314 cells in striate cortex. The data from cells tuned to opposite phases along a given color axis have been combined, so for instance 90° = 90° + 270°. Note that LGN cells are clustered around the L/M (0°-180°) and the S-LM (90°-270°) axes in their color tuning, as was also shown in Fig. 1. Striate cortex cells, on the other hand, are tuned to all of the various chromatic axes, with a slight tendency, however, to be tuned off the LGN axes, and thus more in the regions of the perceptually unique hues, which are also off the LGN axes.

Tuning of Striate Cortex Cells.

In contrast to the sharp clustering of LGN cells into just two main chromatic classes, cells in striate cortex were found to peak in all chromatic regions (Fig. 2). This is consistent with our (3) earlier report and that of Lennie et al. (6) but not with those of others who have reported the presence of discrete red, green, yellow, and blue chromatic cell types in cortex (e.g., 17, 18).

Examination of the chromatic peaks of cells in this large striate cortex population, however, shows that although V1 cells are found to peak at many different chromatic loci, they tend to cluster off the 0°-180° and 90°-270° LGN axes. This is contrary to an earlier report (6) which, however, examined responses to optimum combinations of luminance and color variations rather than to isoluminant patterns. This relation between the color peaks of LGN and striate cortex cells is of particular interest to us because we have postulated (9) that there should be a rotation of color selectivity from the geniculate to the cortex, such a rotation being required to account for our color-scaling data (10, 11).

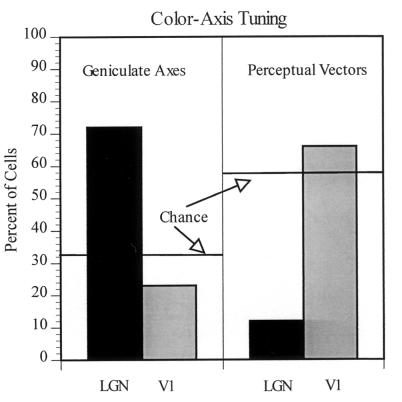
By grouping the cells according to their chromatic peaks, it is possible to evaluate the relationship of LGN cells and V1 cells to (i) the cardinal LGN axes, centered at 0°, 90°, 180°, 270°, and (ii) the perceptual unique hue regions, centered at ≈10°, 125°, 220°, and 290° for red, blue, green, and yellow, respectively (10, 11). To examine how the peak activity regions shift from LGN to V1, and the relation of this shift to the perceptual color axes, we have grouped LGN cells and V1 cells into regions of +/− 15° around the cardinal LGN axes and around the perceptual vectors, respectively. It can be seen in Fig. 3 that most LGN cells show peak tuning to the cardinal axes but relatively few to the regions of the perceptual color vectors. (The numbers do not add to 100% because the red perceptual axis is only slightly off the 0° cardinal axis; cells tuned from −5° to +15° are thus considered to be tuned to both the 0° cardinal vector and the red perceptual vector). On the other hand, far fewer V1 cells are tuned to the LGN cardinal regions than to regions of equal size in color space centered around the perceptual color vectors.

Figure 3.

The distribution of cells in LGN and V1 that are tuned to +/−15° of the cardinal vectors (0°, 90°, 180°, and 270°) versus the regions of the perceptual color vectors (10°, 125°, 220°, and 290° for red, blue, green, and yellow, respectively). It is apparent that, on average, striate cells are shifted off the LGN cardinal vectors toward the perceptual color vectors (regions indicated below the x axis). The color tuning of our LGN L/M cell population was shifted slightly from the canonical 0°-180° axis. Approximately 90% of the L/M cells were tuned to +/−15° from the −10° to 170° and the 90°-270° axes.

Linearity of Response.

Fig. 1 shows the extent to which LGN cells fall into just two classes in terms of their axes of chromatic preference. It also demonstrates the extent to which the processing of color information is very linear up to and at this stage in the visual system. The different isoluminant stimuli we used produce sinusoidal variations in cone activation as a function of color angle for each class of cone. Any linear combination of cone outputs, whether they be summed in a spectrally nonopponent organization, or subtracted one from another in an opponent organization, would also result in a function that varied sinusoidally with color angle. The function might be different in phase, and thus peak chromatic tuning, and/or in amplitude, but it should still be sinusoidal. The color-axis tuning data for each of the different LGN cell types shown in Fig. 1 are fit with sine waves, which can be seen to provide very good fits to the data. Thus the processing from cones up through the responses of these parvocellular (and koniocellular?) LGN cells is quite linear.

To explore the question of response linearity further, we fit the responses as a function of color angle of each cell in the LGN and the V1 populations with a sinusoid raised to the best-fitting exponent, n, [similar to other (19, 20) recent models of cortical cells], where

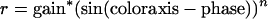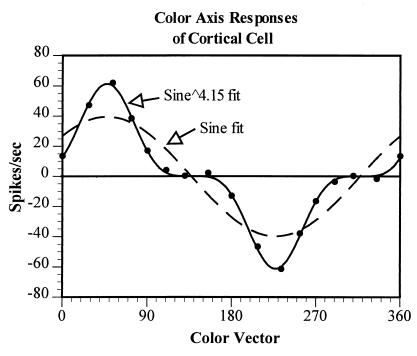
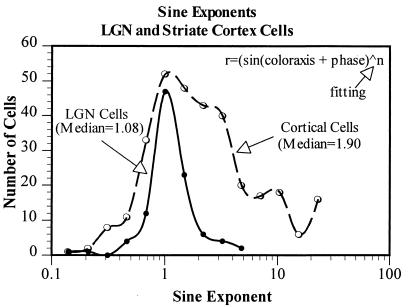
Although some V1 cells show as sinusoidal an output with color angle as do LGN cells, many others do not. Fig. 4, for example, shows the responses of a V1 cell to gratings of different color axes. It can be seen that the data are very poorly fit by a sinusoid but well fit by a sine raised to the power of 4.15. The expansive nonlinearity revealed here clearly narrows the chromatic tuning of this cell. In Fig. 5, we show the distribution of the best-fitting exponents for the whole population of LGN and V1 cells. The responses of almost all LGN cells are well fit by sinusoids of exponent of ≈1, thus indicating quite linear processing. The median exponent of the V1 population, however, is 1.9, reflecting the fact that approximately one-half of striate cortex cells exhibit a significant expansive nonlinearity in their chromatic responsivity.

Figure 4.

The responses of a V1 simple cell to gratings of the various isoluminant colors. The variation in response as a function of color vector is poorly fit with a sinusoid but well fit with a sine raised to a power of 4.15. This result indicates the presence of an expansive nonlinearity at this cortical level, one consequence of which is the narrowing of the color tuning of the cell.

Figure 5.

The distribution of best-fitting exponents to the color-tuning data from all of the LGN and striate cortex cells. LGN cells are quite linear and thus their data are fit with sinusoids of exponents close to 1, that is, with a sine wave. Some striate cortex cells show similar linear responses, but approximately one-half are best fit with sinusoids to higher powers, indicating an expansive nonlinearity (with consequent narrower color tuning). The median best-fitting exponent for the color responses of the LGN cells is 1.08 and for the striate cortex cells it is 1.90.

+S and −S signals.

Several investigators (e.g., 5, 21, 22) who have reported on the relative numbers of +S − LM (+S_o) and −S + LM (−S_o) opponent cells in the LGN have found a large imbalance. There are many more +S_o than −S_o cells in the path to the cortex. In fact some (23) have suggested that there are no −S_o cells at all in the LGN. This imbalance is not surprising given the differential retinal connectivity of S cones compared with L and M cones (24). In the sample of LGN cells from the parvocellular (and koniocellular?) layers reported here, we found 16 +S_o cells and just two −S_o units.

Not only are there very few −S_o cells in the LGN, but there is little evidence of −S input to other cell types. It has been reported that S cones do not feed into cells in the magnocellular LGN path at all (25), nor into the L/M opponent parvocellular cells (26). We find S-cone input into the surrounds of the RFs of some parvocellular LGN cells (thus accounting for the deviation of the average responses of L-center cells to slightly off the 0°-180° axis, as shown in Fig. 1), but this input is relatively minor.

The situation in the striate cortex is quite different. There are few cells in striate cortex that resemble either +S_o or −S_o LGN cells in having only an S-cone input into the RF center or into an RF subregion. Thus there is a paucity of cortical cells tuned to the 90°-270° axis (Fig. 2). However, most V1 cells receive either +S_o or −S_o inputs (or both) in conjunction with inputs from other LGN types. It is the combination of S_o input with input from L_o and M_o cells that rotates the color axes of most V1 cells away from the 0°-180° and 90°-270° LGN axes. We have elsewhere (4) reported studies of the temporal dynamics of this integration of the S_o input with that of the L/M cells.

The best evidence for the presence and the polarity of input originating in S cones comes from RF mapping with cone-isolating stimuli. Some results from these RF-mapping studies are reported elsewhere (4). What is relevant here is the evidence for the presence of −S as well as +S input to V1 cells. The RFs of 169 V1 cells were mapped with cone-isolating stimuli each of which produced a change in activation of only L or M or S cones, respectively. Fifteen of these cells (9%) had no S input, 52 (31%) had an RF region excitatory to +S, 63 (37%) had an RF region excitatory to −S, and 39 (23%) had separate excitatory RF regions for both +S and −S. Thus, in sharp contrast to the situation in the LGN, we find slightly more −S than +S input to cells in V1. Because this S input is also often delayed relative to the inputs of the cells from the L/M systems (4), we have speculated that the S_o signal from the LGN might be inverted, and delayed, by a circuit within the striate cortex.

Proportion of S System.

In our color model (9), we postulated not only that the output of the S system would be added and subtracted from that of the L/M opponent cells in the cortex to rotate the color axes, but that the proportion of the S signal in the total response would be doubled at the cortex relative to that at the LGN. We have a direct measure of whether that may be so in the responses of LGN and V1 cells to the cone-isolating stimuli. The cone contrasts of the L-, M-, and S-isolating gratings were not the same, so the absolute sizes of the responses of cells to these respective patterns is not very meaningful. However, the differences in the relative responses of LGN versus V1 cells to these three cone-isolating gratings are informative.

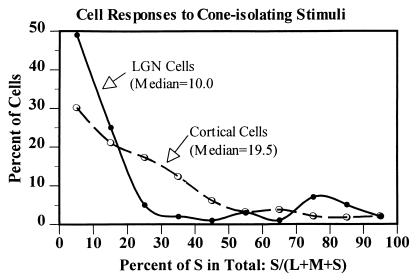
Most LGN cells (with the exception, of course, of the S-opponent cells) showed little or no response to the S-isolating gratings. Consequently, the ratio of the S response to the overall sum of the responses to all three cone-isolating patterns [S/(L + M + S)] for most LGN cells was quite small, <10% (Fig. 6). For many cells in the striate cortex, however, the S input was 20–30% of the total. Overall, the median proportion of S response to the total L + M + S response was 10% in LGN cells and 19% in V1 cells. This near doubling of the S contribution to the responses of the cells at the striate cortex is in agreement with the prediction from our color model (9). It is also consistent with the suggestion we have made (4) that a local cortical circuit may generate a −S signal which, in addition to the +S signal from the LGN, would result in a doubling of the total S input to striate cortex cells.

Figure 6.

We recorded the responses of LGN and V1 cells to L-, M-, and S-cone isolating gratings and computed the ratio of each cell's response to the S-cone isolating grating to the sum of its responses to all three (L + M + S) stimuli. Shown are the distributions across cells of this S/(L + M + S) ratio. Note that most LGN cells have very little S input, whereas many striate cortex cells are more responsive to S-cone isolating stimuli. From LGN to cortex, the average proportion of the total L + M + S response that originates in S cones is approximately doubled.

Discussion

In the experiments reported here, we have examined how several aspects of the chromatic responses of macaque monkey cells differ between the LGN and the next visual processing level, the striate cortex. Our investigation was prompted by predictions we had made (9) about the transformations in chromatic properties, which might occur between LGN and cortex, and by our psychophysical measurements of color appearance (10, 11).

In the history of the study of the visual system and of many other aspects of behavior as well, there has been gradually increasing realization of the complexity of the processes involved and of the number of processing stages required. The earliest theories of color vision were essentially one-stage theories in which the decoding of color takes place in the receptors. Helmholtz (27) postulated three color receptors, red, green, and blue, with discrete paths from each to the brain. References to red, green, and blue cones perpetuate this erroneous notion, despite all the more recent evidence indicating (i) that the cones do not have their peak sensitivities in the red, green, and blue regions, (ii) that cones are not chromatically selective but rather absorb light of all visible wavelengths, and (iii) that there is no discrete path from any receptor to the brain. Hering's postulate (28) of three spectrally opponent processes, red–green, yellow–blue, and black–white, was initially also a one-stage model, although more recent modifications of it (26) had the opponent interactions occurring at a postreceptoral neural processing level. Our early evidence (1, 2) for two color-opponent cell types and one color-nonopponent cell type in the primate LGN provided evidence supporting the modified Hering–Hurvich–Jameson model of color processing. We characterized these different opponent cell types, on the basis of the color appearance of those spectral regions that produced maximum excitation and inhibition, as red–green cells (those differencing the outputs of the L and M cones) and blue–yellow cells (those differencing the S cones from the sum of L and M cones). These color terms for the cell types unfortunately persist, despite more recent evidence (10) that the LGN opponent-cell axes do not precisely correspond to the perceptual red–green and blue–yellow axes.

Considerable anatomical, physiological, and psychophysical evidence demonstrates that the two-stage model of color vision described above is inadequate. For instance, the L_o and M_o cells multiplex color and luminance information, which needs to be separated at some later stage, and the spectral peaks of the opponent LGN cells deviate from the perceptual color regions in systematic ways. To account for these and other problems with a two-stage model, we (9) postulated a third processing stage at the cortical level. The current study examines several of the predictions made by our version of a three-stage model.

Three of the predictions made in our color model concerned characteristics of the S_o system. We suggested that: (i) almost all third-stage color-selective cells should have combined inputs from the S_o and the L_o and M_o systems; (ii) there should be −S_o input at this stage as well as the +S_o input seen at the LGN; and (iii) the proportion of S_o input should be doubled at the cortex relative to that at the LGN. In addition, our studies of color scaling (10, 11) predict a narrowing of color tuning, perhaps by an expansive contrast-response nonlinearity, at a cortical color processing stage.

The data presented here along with that reported earlier (4) support each of these predictions. (i) Both the color axis tuning of V1 cells and responses to S cone-isolating stimuli demonstrate that the large majority of V1 cells combine inputs from the different LGN systems, rather than responding along the LGN cardinal color axes. (ii) Not only do many V1 cells receive −S_o input, but −S_o input is slightly more common than +S_o input, despite the virtual absence of −S_o cells in the LGN. (iii) S input is almost doubled in strength at the cortex relative to the LGN. We also find that most color-tuned striate cortex cells have narrower chromatic tuning than LGN cells. This result can be accounted for by an expansive nonlinearity.

Our earlier psychophysical studies and the physiological data presented here provide strong support for the idea that the S system (S cones and the S-opponent pathway to the cortex) does not constitute the blue–yellow color system but rather serves, in effect, as a color modulator for all the color systems: red–green, blue–yellow, and black–white. The L and M cones are by far the most prevalent in the retina, and they play the predominant role in all aspects of photopic vision, including providing high foveal acuity for luminance variations. The S system, on the other hand, appears to play a role solely in chromatic vision. Because chromatic aberrations preclude our obtaining veridical high spatial frequency chromatic information, the visual system can get by with a limited number of S cones and S_o cells. But this sparse system, increased in strength at the cortex, plays a critical role in all the various perceptual color systems.

Abbreviations

LGN

lateral geniculate nucleus

S_o, S-LM opponent cell

L_o, L-M opponent cell

M_o

M-L opponent cell

RF

receptive field

MBDKL

MacLeod–Boynton–Derrington–Krauskopf–Lennie color space