Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1999 Oct 12;96(21):11707–11712. doi: 10.1073/pnas.96.21.11707

Simulation of biomimetic recognition between polymers and surfaces

Aaron J Golumbfskie *, Vijay S Pande †, Arup K Chakraborty *,‡,§,
PMCID: PMC18350  PMID: 10518514

Abstract

Many biological processes, such as transmembrane signaling and pathogen–host interactions, are initiated by a protein recognizing a specific pattern of binding sites on part of a membrane or cell surface. By recognition, we imply that the polymer quickly finds and then adsorbs strongly on the pattern-matched region and not on others. The development of synthetic systems that can mimic such recognition between polymers and surfaces could have significant impact on advanced applications such as the development of sensors, molecular-scale separation processes, and synthetic viral inhibition agents. Attempting to affect recognition in synthetic systems by copying the detailed chemistries to which nature has been led over millenia of evolution does not seem practical for most applications. This leads us to the following question: Are there any universal strategies that can affect recognition between polymers and surfaces? Such generic strategies may be easier to implement in abiotic applications. We describe results that suggest that biomimetic recognition between synthetic polymers and surfaces is possible by exploiting certain generic strategies, and we elucidate the kinetic mechanisms by which this occurs. Our results suggest convenient model systems for experimental studies of dynamics in free energy landscapes characteristic of frustrated systems.

It is common in biology for a protein to recognize and bind to a specific pattern of binding sites localized in a region of a surface. It is not our purpose to explain how the intricate chemistries resulting from evolution allow such specific recognition to occur. Rather, in this paper, we explore whether there are minimal universal strategies that would allow synthetic polymers to mimic recognition. Such strategies might be profitably exploited in applications (1, 2). To deduce candidates for such strategies, we were inspired by some coarse-grained observations regarding biological systems. Proteins are composed of many types of monomers and have sequences that are not periodically repeating (3–6). Similarly, the pattern of different binding sites on cell surfaces is not periodically repeating. These observations led us to ask whether competing interactions (because of preferential interactions between different types of monomers and surface sites) and disorder are essential ingredients for biomimetic recognition in synthetic systems. [We note that Muthukumar (7, 8) has also thought about questions pertinent to pattern recognition between polymers and surfaces, and Khokhlov and coworkers (9) have considered designing polymer sequences for efficient binding to uniform surfaces that do not bear patterns.]

Disordered heteropolymers (DHPs) are synthetic macromolecules with chemically different monomer units distributed along the backbone in a disordered sequence that is described statistically.‖ Like proteins, they are composed of different monomers, with sequences that are aperiodic and quenched (the sequences cannot change in response to the environment). Unlike proteins, which carry a specific pattern encoded in their sequence distribution, DHP sequence distributions correspond to statistical patterns. The meaning of statistical patterns will be made precise shortly. Imagine a DHP chain interacting with a surface bearing many types of sites that are distributed in a manner that is described statistically. Such surfaces resemble cell surfaces wherein the pattern of binding sites is not periodically ordered. They are different from cell surfaces in that they bear statistical, rather than specific, patterns. Let the DHP segments exhibit preferential interactions with the surface sites; i.e., particular segments prefer to interact with certain types of sites, and others exhibit a different preference. Studying such a system allows us to explore whether competing interactions and quenched disorder are sufficient ingredients for biomimetic recognition.

Recent theoretical studies (10–12) suggest that the occurrence of a phenomenon akin to recognition when the statistics characterizing the DHP sequence and that of the surface site distribution are related in a special way (i.e., matched). Specifically, these thermodynamic studies suggest that frustration (because of the competing segment–surface interactions and quenched disorder) and statistical pattern matching lead to one of the hallmarks of recognition, a sharp discrimination between surfaces to which a given type of DHP sequence binds strongly and those onto which it does not adsorb. These suggestions notwithstanding, it is unclear whether DHPs can sharply discriminate between different regions of a single surface bearing various types of statistical patterns in time scales that are of pragmatic interest. In other words, is statistical pattern matching sufficient for biomimetic recognition to occur? We present results of dynamic Monte-Carlo (MC) simulations that show that the answer to this question is “yes,” provided the statistical patterns are designed properly. Our results show how a mixture of DHPs bearing different statistical patterns can be separated on a surface by discriminatory adsorption onto regions that bear complementary statistical patterns. The simulations also show dramatic differences in chain dynamics in the “wrong” and pattern-matched regions of the surface.

Methods

To illustrate the basic physical ideas, let us first consider DHPs and surfaces with only two types of segments and sites (A and B). The simplest measures of the statistical pattern for a two-letter DHP are provided by the average composition f and a parameter, λ = PAA + PBB − 1; elements of the matrix, Pij, represent the conditional probability of finding a segment of type i, given that a segment of type j immediately precedes it (13). Negative values of λ imply a statistical tendency for the two types of segments to alternate within some correlation length (statistically alternating), while positive values lead to a propensity for like segments to be adjacent (statistically blocky). The magnitude of λ is a measure of the correlation length (e.g., |λ| = 1 implies the correlation length is the entire length of the chain, and λ = 0 refers to a random or uncorrelated sequence). The matrix P is directly related to the reactivities between monomers that constitute the DHP, and hence is determined by their chemical identities (13); thus, the statistical pattern encoded in DHP sequences can be selected by choosing the appropriate chemistry. For two-letter DHPs, we obtain chains with a desired value of f by a successive random process; these sequences are then screened by the desired λ to obtain particular statistical patterns. We will focus here on λ = 0.4 (±0.05) and λ = −0.4 (±0.05).

Surfaces with two types of sites on a neutral background can also bear simple statistical patterns. For example, within a certain length scale there may be an increased propensity to find adjacent sites of the same type (statistically patchy) or of different types (statistically alternating). The simplest statistical measures of the patterns carried by such surfaces are the correlation length, the total density of A and B type sites on the surface (loading), and the ratio of the number of sites of A and B types (always equal to unity in our work). We generate statistically patterned surfaces of this type by obtaining equilibrium realizations of a two-dimensional Ising-like system by using an MC algorithm. We simulate a lattice Hamiltonian with only nearest-neighbor interactions and MC moves that are exchanges of the identity of two sites. Typically, 108 MC steps were run, well after equilibrium was established. For generating statistically patchy (alternating) surfaces, interactions between sites of the same type are taken to be attractive (repulsive) and those between sites of the opposite type are repulsive (attractive). Neutral sites are noninteracting. The correlation length is determined by the temperature, Td, at which we carry out the MC simulation and the loading. Large values of Td lead to essentially random surfaces and, for a fixed loading, statistical patterns with larger correlation lengths are obtained by reducing Td. It is worth noting that patterned surfaces of this sort can be created in practice by self-assembly of mixed molecular adsorbents (14–16).

Consider a surface comprised of four quarters, each of size 100 × 100 lattice units. Let two quarters have essentially random distributions of A (red) and B (yellow) type sites. Let the other two quarters be realizations of statistically patchy and alternating surfaces generated by the methods described earlier. Such an arrangement is shown in Fig. 1, where all quarters of the surface are characterized by an average total loading of 20%, and the correlation length is ≈1.4 for the statistically patterned regions.

Figure 1.

Figure 1

Open in a new tab

Surface bearing different statistical patterns. The two different types of sites are colored red and yellow, with the neutral background being blue. The top right (bottom left) quarter is statistically alternating (blocky); the other quarters are statistically random. The black and white trajectories are two-dimensional projections of the center of mass positions of statistically alternating and blocky DHPs, respectively. 1 (2) and 1′ (2′) are starting and ending positions of the statistically blocky (alternating) DHP.

We have carried out MC simulations with the Verdier–Stockmayer algorithm for chain motion to study the dynamic behavior of DHPs in the vicinity of such surfaces. We simulate a Hamiltonian with nearest-neighbor interactions. We restrict attention to situations where the segment–surface site interactions are much stronger than the intersegment interactions, and hence the latter are taken to be nonspecific and of the excluded volume type. The preferred segment–surface interaction strengths are taken to be −1, and the ones that are not preferred equal +1 in units of kTref, where k is the Boltzmann constant and Tref is a reference temperature. DHP segments of type A prefer to interact with red sites on the surface, and those of type B prefer the yellow surface sites (see Fig. 1). The simulations are carried out at a temperature T for chains of length 32, 100, and 128. We consider the dilute solution limit below the chain overlap threshold. It is possible that additional kinetic barriers could arise at higher concentrations. The results show that for fixed f and surface loading the important design variables are λ, Td, and T/Tref (determined by the chemical identities of segments and surface sites and preparation conditions).

Results

Phenomenology of Statistical Pattern Matching.

Statistically blocky (alternating) DHPs are statistically better pattern matched with the statistically patchy (alternating) part of the surface. The first question we ask is: If the surface shown in Fig. 1 is exposed to a fluid solution containing a mixture of statistically blocky and statistically alternating DHPs, will the chain molecules selectively adsorb on those regions of the surface with which they are statistically pattern matched? Such recognition because of statistical pattern matching requires not only that the “correct” patch be strongly favored for binding thermodynamically, but also that the “wrong” regions of the surface not serve as kinetic traps.

Fig. 1 depicts typical trajectories at T/Tref = 0.6. All points on these trajectories do not correspond to adsorbed states. Both the statistically alternating and blocky DHPs begin on randomly patterned parts of the surface and ultimately find their way to the region of the surface that is statistically pattern matched with its sequence statistics. The length of our simulations roughly corresponds to 1 sec,** over which separation or recognition is achieved with >90% efficiency (of 1000 trials). These results show that biomimetic recognition between polymers and surfaces is possible because of statistical pattern matching. It seems possible to exploit this notion to design inexpensive devices that can separate a large library of macromolecules into groups of statistically similar sequences. Sensor applications are also suggested.

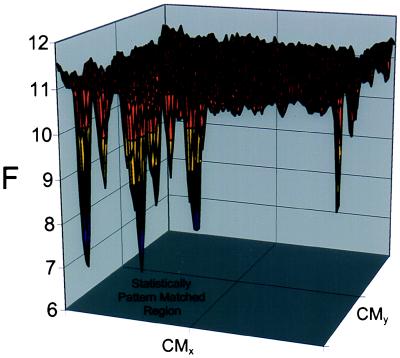
In the trajectories shown in Fig. 1, the DHPs do adsorb onto the wrong parts of the surface. However, these adsorbed states are short-lived compared with the time it takes to evolve to the strongly adsorbed state. Once a chain is strongly adsorbed onto a region that is statistically pattern matched with its sequence, the chain center of mass essentially does not move on simulation time scales (see below). The reason for this is made clear by the free energy landscape shown in Fig. 2. We calculate the free energy by computing the negative logarithm of the probability of finding the center of mass in a given location. This landscape was computed at T/Tref = 0.7, and the trajectory was sufficiently long (2.4 × 1010 MC steps) for adequate sampling. The “wrong” regions of the surface correspond to local free-energy minima, which are separated by relatively small barriers from each other. In contrast, in the statistically pattern-matched region, there exist a few deep global minima; each of these minima, in turn, is very rugged. It is important to note that T/Tref is an important design variable determined by the chemical identity of segments and surface sites. Large values of this parameter will not allow the chains to adsorb anywhere to appreciable extent because the entropic penalty associated with adsorption dominates the free energy. At sufficiently low values of this ratio, the “wrong” regions of the surface serve as kinetic traps, and long-lived metastable adsorbed states exist in these regions. Thus, it is clear that because of both kinetic and thermodynamic considerations there should be an optimal value of T/Tref. We have carried out simulations for T/Tref = 0.45, 0.6, and 0.75. Of these conditions, we find that 0.6 leads to the best discrimination and recognition. More work is needed to provide quantitative criteria for the optimal value of T/Tref.

Figure 2.

Figure 2

Open in a new tab

Free energy (in arbitrary units) versus center of mass (CM) position for a statistically alternating DHP interacting with the surface in Fig. 1. The two deep free-energy minima along the right edge of the surface (wrong region) are the results of periodic boundary conditions.

The importance of both kinetics and thermodynamics for statistical pattern matching is further emphasized by the following point. Thermodynamic arguments (10–12) suggest that DHPs with random sequences (λ = 0) sharply discriminate between surfaces with random site distributions that have different loadings. We find that the likelihood of kinetic trapping in the wrong regions of the surface is rather high when uncorrelated sequence and surface site distributions are statistically pattern matched by adjusting the loading. In particular, let us compare the following two situations: (i) a surface with random site distribution bearing regions with loadings of 20% and 40% being exposed to DHPs with random sequences that thermodynamically strongly favor the region with a loading of 40%; (ii) the surface shown in Fig. 1 exposed to the statistically alternating sequences. We note that the equilibrium adsorbed fraction in the region with a loading of 40% in case i and that for the statistically alternating DHPs in the statistically alternating region in case ii are roughly the same. Our simulations (>40 trials in each case) show that the window of T/Tref for successful recognition (>80% efficiency) is 50% wider for case ii. The reason for this is that, in the former situation, the free-energy landscape that the chains negotiate is virtually uncorrelated, and thus rife with local optima that lead to kinetic trapping (21).

Having illustrated the basic phenomenology of biomimetic recognition that is a result of statistical pattern matching, we now turn to a detailed description of the kinetics that characterize this phenomenon.

Kinetics of Statistical Pattern Matching.

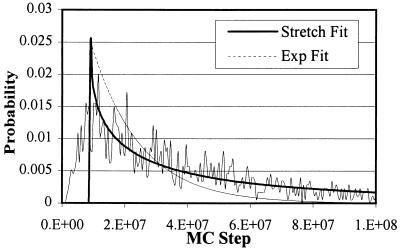
Fig. 2 suggests that, for the system we are considering, chain dynamics on various time scales and different spatial locations should be quite different and interesting. Begin by considering the first passage time, which we define to be the time taken for a chain starting in the random part of a statistically patterned surface to adsorb in the pattern-matched region with the energy being below a certain cut-off value. Fig. 3 shows the distribution of first passage times for chains of length 32, with the energy cut-off being −20 kTref. It is clear that, after the usual turn-on time, the distribution is decidedly nonexponential; a stretched exponential with a stretching exponent equal to 0.43 fits the simulation results. The nonexponential character of the distribution of first passage times is indicative of highly cooperative chain dynamics. The event we are considering is tantamount to two events that occur in succession. These are chain motion to the edge of the statistically pattern-matched region of the surface followed by strong adsorption in one of the deep free-energy minima in the statistically pattern-matched region. We have computed the first passage times for these two events separately. Significantly, we find that the distribution of first passage times for the first event is exponential, and that for the second is nonexponential. This implies that, as the chain traverses the wrong parts of the surface, the center of mass motion is diffusive. This is because the free-energy minima and barriers it encounters in these regions of the surface are relatively small. In contrast, it appears that strong adsorption in the statistically pattern-matched region is highly cooperative with many important free-energy barriers encountered enroute to the bottom of one of the deep free-energy valleys that exist in this part of the surface. What is the physical origin of this behavior in the statistically pattern-matched region?

Figure 3.

Figure 3

Open in a new tab

Distribution of first passage times for a statistically alternating DHP of length 32. On the ordinate, 2.E+07 = 2 × 107, etc. The exponent for the stretched exponential fit is 0.43.

It is interesting to observe that single-particle MC dynamics (data not shown) on the free-energy landscape shown in Fig. 2 is exponential. This indicates something very important for understanding the nature of the dynamics. Single-particle dynamics on the free-energy landscape in Fig. 2 would reproduce the first passage time distribution obtained from the full-chain dynamics if motion of the center of mass was always the slowest dynamic mode. Our results suggest that this is not true.

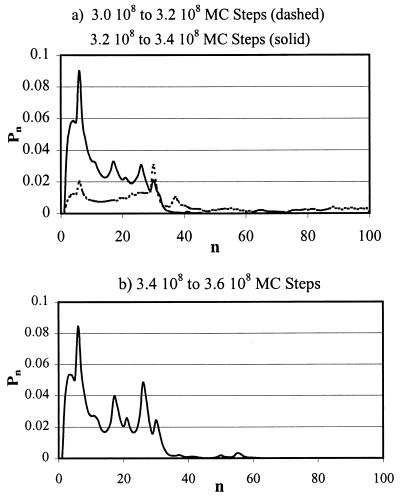
Adsorbed macromolecules are characterized by loops. A loop is a length of contiguous unadsorbed chain segments between two consecutive adsorbed segments. The distribution of these loops fluctuates in time, and hence loop fluctuations are dynamic modes. Prior to considering the dynamics of these modes, let us examine the distribution of these loops as trajectories evolve starting from wrong parts of the surface. We have carried out extensive MC simulations‡‡ with chains of length 100. All trajectories show the qualitative features depicted in Fig. 4, where we plot the probability distribution Pn for an arbitrary segment to be part of a loop of length n for a statistically alternating DHP. Each panel shows Pn averaged over different time (MC step) windows. The dashed curve in Fig. 4a shows that when the center of mass of the chain is in the wrong part of the surface, Pn is essentially structureless. This implies that all possible macromolecular shapes are being adopted as the chain samples the wrong parts of the surface. Remarkably, the other curves in Fig. 4 demonstrate that, as the chain center of mass enters the statistically pattern-matched region, Pn begins to show structure. Ultimately, as shown in Fig. 4b, it exhibits a spectrum of peaks that correspond to preferred loop lengths and hence macromolecular shape in the adsorbed state. This observation of adsorption in preferred shapes because of statistical pattern matching is very similar to recognition in biology, and we shall make it vivid shortly. Loops with the preferred lengths appear to be quenched in time, and so for ease of reference, we will call them quenched loops.

Figure 4.

Figure 4

Open in a new tab

The probability distribution of loops (Pn). (a) Dashed curve, center of mass in the wrong parts of the surface; solid curve, center of mass has entered the statistically pattern-matched region. (b) Shape-selective adsorption has occurred.

There is a simple physical reason for the lack of quenched loops in the wrong regions of the surface, while these types of loops seem to dominate the behavior in the statistically pattern-matched region (see also ref. 12). In the wrong region of the surface, arbitrary adsorbed conformations with the same number of contacts have roughly the same energy. This is because there are no particular arrangements that lead to much higher degrees of registry between adsorbed segments and their preferred sites, compared with other conformations. Thus, the distribution of loops fluctuates strongly, thereby gaining entropy while maintaining roughly the same energy. In the statistically pattern-matched region of the surface, however, the situation is different. While most adsorbed conformations are of relatively high energy, as in the wrong region of the surface, now there exist a few conformations that can bind segments to their preferred sites with high probability in certain regions because the statistics of the sequence and surface site distributions are matched. These few pattern-matched conformations are much lower in energy than all others, and thus the chain sacrifices the entropic advantage associated with loop fluctuations and “freezes” into one of these conformations. The better the statistical pattern matching, the greater the suppression of loop fluctuations.

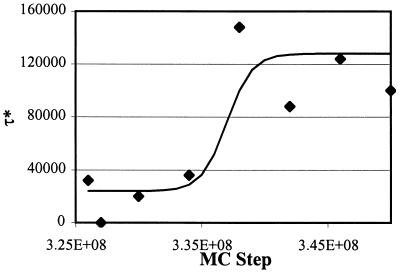
Let us return to the puzzle of why single-particle dynamics on the free-energy landscape calculated for the chain center of mass does not reproduce the correct dynamical behavior. Consider the time correlation functions 〈Pn (t) Pn (t + τ)〉 that describe how loop (and hence, shape) fluctuations decay for n = 17, 26, and 30. We focus on these values of n because Fig. 4 shows that the dominant shape is characterized by loops with these lengths. Our simulation results show that, for motion in the wrong parts of the surface, these correlations decay much more rapidly than the time scale on which the chain center of mass moves. Thus, the modes corresponding to loop fluctuations are the fast dynamic modes. After some time in the statistically pattern-matched region, the chain’s center of mass finds the location corresponding to one of the deep free-energy minima in this region. Now, the center of mass essentially does not move during the simulation (for chains of length 32, the center of mass ceases to move, and for chains of length 100, the diffusion coefficient becomes two orders of magnitude smaller than that in the wrong parts of the surface). On much longer time scales, the centers of mass of these finite chains will be able to escape from these minima and find other deep minima in the statistically pattern-matched region. However, these long times are not relevant to our simulations, and for very long chains, these events would occur over time scales that are not experimentally relevant. The point is that localization of the center of mass implies that this dynamic mode has equilibrated from a practical standpoint. Our simulations show that, after the chain center of mass has equilibrated in the statistically pattern-matched region, the time correlation functions describing loop fluctuations decay over very long times. In fact, ultimately, once shape-selective adsorption occurs, they do not decay to zero and simply oscillate around a finite value. Thus, these modes, which were the fastest dynamic modes in the wrong part of the surface, become the slowest modes once the center of mass reaches a location corresponding to a deep free-energy minimum. This explains why single-particle dynamics on the free-energy landscape appropriate for the center of mass cannot describe the correct dynamics. Fig. 5 shows how the relaxation time for loops of length 26 changes as a typical trajectory evolves in the statistically pattern-matched region.

Figure 5.

Figure 5

Open in a new tab

Growth of the relaxation time (τ*) in the statistically pattern-matched region for loops of length 26. The points correspond to simulation results; the solid line is meant only to guide the eye. τ* is calculated to be the time when 〈P26(t) P26(t + τ)〉 has decayed to 5% of its final value. τ* in the wrong regions of the surface are not reported because the adsorbed states are not sufficiently long to extract meaningful values of τ* (which, in effect, is zero).

The observations noted above imply the following physical picture. Once the center of mass of the chain is located in the region corresponding to a deep free-energy minimum, the chain has to acquire the shape (conformation) that is most favorable on energetic grounds. To do this, it must arrange its loops in a specific way. The necessary conformational rearrangements occur in a highly cooperative way, and there are important entropic barriers associated with this reorganization. These entropic barriers, which correspond to arranging the chain to acquire a specific shape (a hallmark of recognition), lead to the nonexponential character of the first passage time distribution.

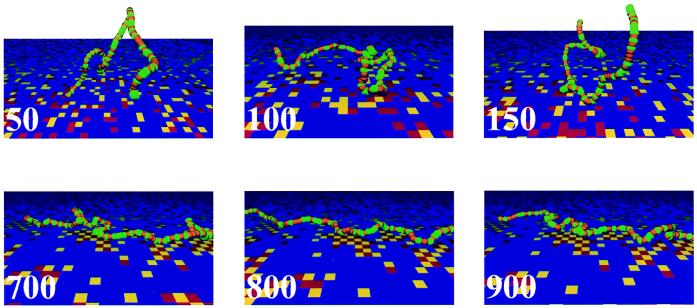
To make some of the results discussed above vivid, we have animated trajectories of our simulation runs. Fig. 6 shows snapshots from such a movie for a 128-segment statistically alternating two-letter DHP. The trajectory starts with the chain above the statistically random part of the surface. The DHP does adsorb somewhat on this region of the surface. The adsorbed conformations are characterized, as usual, by loops, trains, and tails, which exhibit large fluctuations. For example, both the loop length distribution and the distance on the surface between loop ends fluctuate rapidly. The first three frames of Fig. 6 depict this. With time, this DHP evolves toward the statistically alternating region of the surface and adsorbs strongly. Now, the chain dynamics are dramatically different (last three frames in Fig. 6). Several chain segments adsorb on preferred sites on the surface. The resulting loops are quenched in time in that there are essentially no fluctuations of these loops on the time scale of our simulations. Within these quenched loops live annealed loops that exhibit small conformational fluctuations.

Figure 6.

Figure 6

Open in a new tab

Red and yellow colors correspond to different types of surface sites, and green and orange correspond to different types of DHP segments. In the first three frames, the chain is in the wrong region of the surface. In the last three frames, the chain is strongly adsorbed in the statistically pattern-matched region.

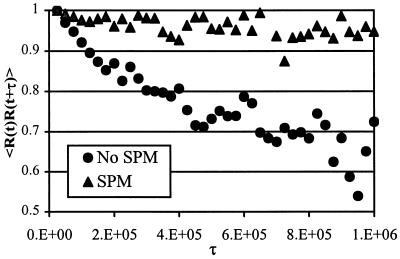
Our results demonstrate that the system we have been considering exhibits dramatic differences in dynamics on different scales of space and time. These are classic signatures of dynamics in free-energy landscapes characteristic of frustrated systems. For example, these features are similar to the behavior of spin glasses (22) and protein-folding phenomena (23–26). Detailed experimental studies of our system may, however, be more tractable, as a simple polymeric system is easier to synthesize, manipulate, and characterize. Single-molecule spectroscopy (27, 28) of the DHP should be able to measure the correlation functions that we have computed. The problem seems ideal for this tool, which is most revealing when the ergodic hypothesis is violated. A convenient correlation function from the standpoint of single-molecule spectroscopic experiments is 〈R(t + τ)⋅R(t)〉, where R is the chain end-to-end vector. This quantity reflects correlations between shape fluctuations, and thus measures how chain conformation evolves in time. In Fig. 7, we show how 〈R(t + τ)⋅R(t)〉 decays with time in the wrong and statistically pattern-matched regions. In the former region, the correlations decay as usual. In the statistically pattern-matched region, we find that conformational fluctuations are strongly correlated over long times.

Figure 7.

Figure 7

Open in a new tab

The temporal decay of correlations for the end-to-end vector in the wrong (no SPM) and statistically pattern-matched (SPM) regions.

Concluding Remarks.

We have described MC simulation results, which suggest that biomimetic recognition can be attained in synthetic polymer–surface systems by exploiting certain universal strategies, namely, competing interactions and quenched disorder. In particular, we find that statistically patterned DHPs can recognize complementary statistically patterned regions of surfaces with high efficiency. This notion of recognition because of statistical pattern matching can perhaps be profitably exploited in separation applications (as illustrated by our simulations) and for sensor technology. Our results demonstrate that frustration leads to interesting dynamics in these systems. Thus, we suggest that they be employed as model systems to study dynamics in frustrated systems using single-molecule spectroscopy. Synergy between such experiments and theoretical ways of computing correlation functions may prove worthwhile because frustrated systems with quenched disorder are important in many contexts (e.g., refs. 22–26).

Our results also suggest an intriguing connection between the experimentally realizable system that we study and some provocative ideas concerning the competition between self-organization and selection in evolution. Populations can be considered to evolve on fitness landscapes due to mutations (21). Kauffman (21) has suggested the NK model (which characterizes the varying degrees of ruggedness of fitness landscapes) to study how the competition between the ability to self-organize and selection influences the manner in which populations evolve. Population evolution on fitness landscapes caused by a finite mutation rate is analogous to the finite temperature dynamics of physical systems on free-energy landscapes (21). The model we study is a kind of NK model. We have described the motion of a statistically alternating DHP on a free-energy landscape corresponding to a surface that has random regions and a region that is statistically pattern matched with the DHP. We find that this type of chain (analog of genotype), which has the ability to self-organize is naturally led to a free-energy minimum in the statistically pattern-matched region. Consequently, members of this ensemble of DHP sequences develop specific characteristics—namely, a specific distribution of loop lengths or shape. In contrast, when we simulate statistically blocky DHPs in the vicinity of this surface, we find that Pn does not develop any structure. This is because this ensemble of DHPs cannot self-organize (the free-energy/fitness landscape does not have the structure shown in Fig. 2). Experimental studies of the physically realizable situation that we study may provide insights (by analogy) to issues pertinent to evolution models.

Our findings also lead us to speculate whether in the early origins of life recognition was affected by statistical pattern matching, with specific sequences for binding and recognition resulting from evolutionary refinement of ensembles of statistically pattern-matched sequences.

Acknowledgments

We thank Profs. K. Dill, E. Shakhnovich, and D. Rokhsar for critical reviews of this manuscript. This work was supported by the National Science Foundation, the U.S. Department of Energy, and the Miller Institute.

Abbreviations

DHP

disordered polymer

MC

Monte-Carlo

Footnotes

See commentary on page 11690.

‖

If a number of DHPs made up of the same monomers are synthesized in a reactor, each DHP chain will have a different sequence. However, every such sequence belongs to the same statistical distribution determined by the reactivity ratios (11).

**

On the monomeric scale, local motions occur in 10−10 to 10−11 sec, depending on solvent viscosity and monomer size (17, 18). Our MC moves correspond to the motion of a statistical segment length (b). For Rouse–Zimm dynamics, the time for local MC moves scales as b2 (17, 18). Estimates of the value of b for synthetic polymers lead us to conclude that the microscopic time corresponding to our simulations is 10−8 to 10−9 sec [in agreement with previous estimates (19, 20)]. We have used 10−8 sec to report numbers cited in the text.

‡‡

In these simulations, the surface is composed of three quarters with a random site distribution, and one quarter that is a realization of a statistically alternating surface. The statistically patchy quarter has been removed only for convenience. We have checked that inclusion of a statistically patchy quarter leads to no qualitative differences as the statistically alternating DHPs adsorb to this type of a surface to the same extent as to a random surface.

References

  • 1.Todd R J, Johnson R D, Arnold F H. J Chromatogr A. 1994;662:13–26. doi: 10.1016/0021-9673(94)85291-X. [DOI] [PubMed] [Google Scholar]
  • 2.Sigal G, Mammen M, Dahmann G, Whitesides G M. J Am Chem Soc. 1996;118:3789–3800. [Google Scholar]
  • 3.Irback A, Peterson C, Potthast F. Proc Natl Acad Sci USA. 1996;93:9533–9538. doi: 10.1073/pnas.93.18.9533. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Pande V S, Grosberg A Y, Tanaka T. Proc Natl Acad Sci USA. 1994;91:12972–12979. doi: 10.1073/pnas.91.26.12972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Dewey G. Fractals in Molecular Biophysics. Oxford: Oxford Univ. Press; 1997. [Google Scholar]
  • 6.Chan H S, Dill K A. Annu Rev Biophys Biophys Chem. 1991;20:447–490. doi: 10.1146/annurev.bb.20.060191.002311. [DOI] [PubMed] [Google Scholar]
  • 7.Muthukumar M. J Chem Phys. 1995;103:4723–4731. [Google Scholar]
  • 8.Kong C Y, Muthukumar M. J Chem Phys. 1998;109:1522–1527. [Google Scholar]
  • 9.Zheligovskaya E A, Khalatur P G, Khokhlov A R. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Top. 1999;59:3071–3078. [Google Scholar]
  • 10.Srebnik S, Chakraborty A K, Shakhnovich E I. Phys Rev Lett. 1996;77:3157–3160. doi: 10.1103/PhysRevLett.77.3157. [DOI] [PubMed] [Google Scholar]
  • 11.Bratko D, Chakraborty A K, Shakhnovich E I. Chem Phys Lett. 1997;280:46–52. [Google Scholar]
  • 12.Chakraborty A K, Bratko D. J Chem Phys. 1998;108:1676–1682. [Google Scholar]
  • 13.Odian G G. Principles of Polymerization. New York: Wiley; 1991. [Google Scholar]
  • 14.Leduc M R, Hayes W, Frechet J M J. J Polym Sci A. 1998;36:1–10. [Google Scholar]
  • 15.Berndt P, Fields G B, Tirrell M. J Am Chem Soc. 1995;117:9515–9522. [Google Scholar]
  • 16.Stranick S J, Parikh A N, Tao Y T, Allara D L, Weiss P S. J Phys Chem. 1994;98:7636–7646. [Google Scholar]
  • 17.deGennes P G. Scaling Concepts in Polymer Physics. Ithaca, NY: Cornell Univ. Press; 1979. [Google Scholar]
  • 18.Hu Y, Macinnis J M, Cherayil B J, Fleming G R, Freed K F, Perico A. J Chem Phys. 1990;93:822–836. [Google Scholar]
  • 19.Byrne A, Kiernan P, Green D, Dawson K A. J Chem Phys. 1995;102:573–577. [Google Scholar]
  • 20.Termonia Y. Macromolecules. 1997;30:5367–5371. [Google Scholar]
  • 21.Kauffman S A. The Origins of Order: Self-Organization and Selection in Evolution. New York: Oxford Univ. Press; 1993. [Google Scholar]
  • 22.Fischer K H, Hertz J A. Spin Glasses. Cambridge, U.K.: Cambridge Univ. Press; 1991. [Google Scholar]
  • 23.Shakhnovich E I, Gutin A M. Nature (London) 1990;346:773–775. doi: 10.1038/346773a0. [DOI] [PubMed] [Google Scholar]
  • 24.Wolynes P G, Onuchic J N, Thirumalai D. Science. 1995;267:1619–1620. doi: 10.1126/science.7886447. [DOI] [PubMed] [Google Scholar]
  • 25.Chan H S, Dill K A. Phys Today. 1993;46(N2):24–32. [Google Scholar]
  • 26.Brooks C L, III, Karplus M, Pettitt B M. Proteins: A Theoretical Perspective of Dynamics, Structure, and Thermodynamics. New York: Wiley; 1988. [Google Scholar]
  • 27.Xie X S. Acc Chem Res. 1996;29:598–606. [Google Scholar]
  • 28.Moerner W E, Orrit M. Science. 1999;283:1670–1674. doi: 10.1126/science.283.5408.1670. [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES