A model of the detection of warmth and cold by cutaneous sensors through effects on voltage-gated membrane channels

Abstract

Warmth and cold sensations are known to derive from separate warm and cold cutaneous thermoreceptors in the form of differentiated afferent nerves. The firing rate of warm-sensing nerves increases as the temperature increases; the firing rate of cold-sensing nerves increases if the temperature is reduced. I postulate that the primary sensitivity of the warm sensors derives from voltage-gated Ca²⁺ membrane channels configured such that an increase in temperature opens channels and increases the ion influx while a reduction in temperature increases the ion influx through voltage-gated Na⁺ channels in the cold sensory nerve ends. In either case, the initial cation influx causes a small cellular depolarization that further opens Ca²⁺ channels, admitting more cations in a positive feedback process that leads to the depolarization of the membrane, thus initiating an action potential pulse. Monte Carlo calculations based on a well defined model of such processes, which include effects of noise, demonstrate quantitative agreement of the model with an extensive body of data.

The sensations of warmth and cold are known to follow from the excitation of separate warm and cold cutaneous thermoreceptors as measured by the firing rates of the afferent nerves that form the receptors. For each modality, the firing rates depend statically upon temperature, T, and dynamically on the rate of temperature change, dT/dt, with positive coefficients for warm receptors and negative coefficients for cold receptors (1). Hence, in the homeotherm skin, the firing rate of the afferent nerves that serve the warm-receptors increases with increasing temperature while the firing rate of the nerves that serve the cold sensors is reduced (1–3). The systems adapt to long-term temperature changes and an increase in external calcium concentration results in a feeling of warmth (4, 5).

I show, through Monte Carlo calculations that include noise effects, that these properties of the warm-cold sensory system can be understood quantitatively as the consequences of simple characteristics of voltage-gated membrane channels in the sensory nerve systems that admit Ca²⁺ and Na⁺ cations into afferent nerve cell that generate the observed action pulses.

The warm-receptors in mammals appear to be differentiated C-fibers, unmyelinated afferent nerve fibers ≈1–2 μm in diameter (6, 7), while the cold receptors are differentiated Aδ fibers (8), myelinated axons ≈3 μm in diameter. The afferent cold fibers differentiate near their end, at the sensory site, into 5 or 10 short unmyelinated fibers (1). The warm-fibers differentiate similarly (9). I assume that the sensory regions consist of these differentiated “fingers.” The cold-receptor fingers are found at a depth of ≈150 μm in the human skin, near the interface between the dermis and epidermis. The warm-receptors may be somewhat deeper (10, 11).

The density of receptors in humans varies according to the location, and there are usually more cold sensors than warm sensors. While there are, typically, from one to five cold points per cm² on the skin of the hand, there seems to be less than one warm point per cm². Elsewhere, such as on the face, the densities are larger, of the order of 10 cold spots per cm² and, perhaps, 2 warm spots (1) per cm². These warm and cold points are generally considered to be associated with single receptors.

The body of data shows that the detailed character of the warm-cold response varies from species to species and varies over the body area of specific species. Hence, the model can be expected to reproduce only the qualitatively similar characteristics of the different systems.

A Boltzmann Description of Ion Channels

The model assigns channel characteristics such that a small increase in temperature increases the opening probability of Ca²⁺ channels in the warm sensors and a small decrease in temperature increases the opening probability of Na⁺ channels in the cold sensors. The cation influx then opens more channels in a positive feedback mode that results in depolarization and an axon action pulse. This model does not differ functionally from standard Hodgkin-Huxley formulations (12).

Occupation Probabilities.

The macromolecules that I consider as gates for the admission of the cations can be considered as nearly classical systems with a set (13) of different configurations, p. Each state will have a characteristic energy, U′_p = U′_p,0 + Q_peV_m, and an entropy factor, S_p, which is essentially a statistical weight. Here Q_peV_m is the energy of interaction with an electric field, where Q_p is a charge number, e is the electronic charge, and V_m is the transmembrane potential difference. I can consider that this energy is the interaction energy of a dipole moment, Q_ped_m with an electric field, E = V_m/d_m, where d_m is the thickness of the membrane. It is convenient to subsume the statistical weights into the energies, U_k = U′_k + k_BTln(S_k), where k_B is Boltzmann’s constant and T is the Kelvin temperature.

The probability, P(j), of the occupation of the state, j, at thermal equilibrium takes the Boltzmann form,

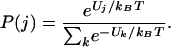1

Transition Rates.

I write the transition rate from state j to state k as ω_j→k and for state k to j as ω_k→j; then, dP_j→k/dt = P_j ω_j→k and dP_k→j/dt = P_kω_k→j. At equilibrium, I take, dP_k→j/dt = dP_j→k/dt, from detailed balance. Hence,

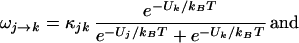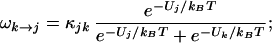2

thus, ω_j→k + ω_k→j = κ_jk, where I take κ_jk as constant over the small range of membrane potentials important to my calculation.

Changes in the configuration of the protein gates generated by a change in temperature or energy will take place over characteristic rearrangement times of the order of τ_r = 1/κ, where I can describe the time variation of such transitions by the relation

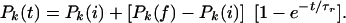3

Here, P_k(i) is the initial probability of finding the system in the state k and P_k(f) the final probability. Since depolarization pulses take place over times of the order of 1 ms, the characteristic time constants for transitions of the gate proteins can be expected to be of the order of 1 ms or less (13, 14), and I take τ_r = 0.5 ms.

Warm Sensors.

I assume that, at the resting potential (≈−70 mV), the lowest energy warm sensor configurations are closed, while higher energy configurations are open and admit Ca²⁺ ions. Over the small range of membrane potentials, ΔV_m ≈ 5 mV, near the resting potential that is important in my calculations, the open probability, P_open < 0.05, and I can write the exact multilevel expressions as

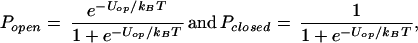4

where U_op is an appropriately weighted average of the differences between the energies of the open and closed states.

Cold Sensors.

For the cold sensors, I postulate two sets of channels. One set is similar to the Ca²⁺ channels described. However, the gates that trigger the cold sensation admit Na⁺ ions selectively and are normally in a kind of reversed configuration. The open states have lower energies and the closed states higher energies. Then, in the notation of Eq. 4, U_op < 0, and the channels are normally open at the resting potential.

Currents Through the Channels

The mean rate of passage of cations into the cell, 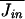will be proportional to K_open, the number of open channels. 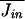= κ[c_out]K_open = κ[c_out]P_openK_tot, where κ is a rate constant, [c_out] is the concentration of cations outside of the cell, and J_in is the current in ions per second passing into the cell. I neglect the dependence of the current through the channel on the potential difference across the membrane since my results are determined largely by potential excursions that are <10 mV.

At equilibrium, the average efflux of cations from the cell must counterbalance the average influx; for T = T₀ and U = U₀, = 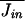. There will then be a “dark current” even in the absence of a perturbation. However, when the energy or temperature is perturbed, U₀ → U and/or T₀ → T, J_in will be modified, and a mean net ion current, J_s, will be generated such that

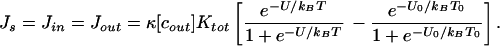5

Warm Sensors.

The energy change, ΔU = U − U₀ = ΔVQe, where Q = Q_op − Q_cl is the difference between the dipole moments of the open and closed states of the Ca²⁺ channels, represents a decrease in the energy difference between the two states if Q is negative and the potential change is positive and depolarizing. Such a change increases the number of open warm-sensor gates which further increases the cation influx. That increased cation flux further reduces the negative membrane potential, thus opening more gates in a positive feedback process that leads to the complete depolarization of the membrane. Hence, I identify this model with the warm-sensory systems that increase their firing rate with an increase in temperature.

Cold Sensors.

For the Na⁺ channels found in the cold sensors, I take U₀ < 0, and the closed state lies higher than the open state. Hence, a decrease in temperature increases the Na⁺ influx current, reducing the transmembrane potential. If Q is negative, that increase in potential will open further gates, generating a larger influx current which in turn opens more gates. But, for plausible parameters, this action alone will not lead to a very large increase in current since the great majority of the gates are open at equilibrium and there are relatively few closed gates to be opened by a change in potential. Therefore, this Na⁺ current is limited and probably insufficient to generate a complete depolarization of the membrane over the sensitive area of the fingers.

Thus, the nominally open temperature sensitive gates must be augmented by a second set of Ca²⁺ gated channels, largely closed at equilibrium with U′₀ > 0. Though a decrease in temperature will reduce the number of open gates from this set reducing the Ca²⁺ influx, the increased Na⁺ influx current is greater than the reduction in Ca²⁺ current. However, I take Q′ negative for the calcium channels so that an increase in potential will open more channels. For larger potential changes, the proportion of open calcium gates will increase greatly, thus increasing the current in the positive feedback that leads to complete depolarization.

Stochastic Fluctuations.

For either warm or cold sensors, the system is at an unstable equilibrium at the base temperature and will be driven from the equilibrium point by stochastic effects. Hence, the firing rates at equilibrium reflect the magnitude of the noise. Effects of the “shot-noise” fluctuations in the number of cations transferred into the cell and the variations in that transfer that follow from fluctuations in the number of open channels are subsumed in a noise current, ξ(t).

For short period, dt, there will be a mean influx of ions, M′ = J_indt, and an efflux, M′′ =J_outdt, with a variance of M′ + M′′ equal to σ′ = 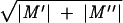. Also, there will be a variance in the number of open calcium channels, N_op, such that σ ≈ 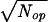; for the Na⁺ channels, σ ≈ 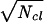. If the mean life, τ, of the open states is smaller than dt by a factor p such that τ ≈ dt/p, the variances will be reduced by a factor of about .

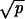With plausible channel numbers, the fluctuations in the number of channels does not contribute very much more to the noise than the shot-noise fluctuations in the number of ions transported. For definiteness, in my calculations, I account for the channel noise current ξ(t) by multiplying the shot noise by a factor of four.

In a time Δτ, the noise current contribution will be M_n = ∫₀^Δτξ(t)dt.

Feedback.

The incremental charge M_s = J_sΔτ conveyed across the membrane in the time Δτ will, in turn, generate a feedback potential ΔV_fb = (M_s + M_n)(ze/C_m), where C_m is the transmembrane capacitance of the sensor fingers and the charge of the ion is ze. The sensitivity of the system follows from the amplifications that result from this positive feedback where the potential generated by the cation charge opens further the normally closed ion channels.

Negative Voltages and Negative Temperature Excursions.

The evolution of the transmembrane potential will be symmetric with respect to small positive and negative drifts in the potential. Hence, if the incremental membrane potential ΔU is small and the temperature is near the base point, the net charge transfer, and the consequent incremental membrane potential, is, initially, as likely to drift under the stochastic effects of the system noise to negative values as positive. My Monte Carlo calculations show that, if there is no constraint on the negative values, the system will be eventually be trapped in such values and rendered inactive.

However, for Ca²⁺ currents, the negative excursion is sharply limited by the very small normal Ca²⁺ ion concentration in the interior of the cell. To take that limitation into account for the Monte Carlo calculations, I use a Michaelis-Menton relation as a recipe which sets the pumping rate to zero when there are no more ions to pump.

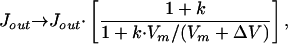6

where ΔV = ΔM⋅ze/C_m is the transmembrane potential change generated by an incremental change, ±ΔM, in the number of ions with a charge ze transferred to the sensitive region—the fingers—interior to the cell; V_m = M_m⋅ze/C_m is the potential corresponding to the number of ions in that region, M_m, when the system is inactive at the resting potential; and k = 0.1 is a saturation factor.

Leakage Effects: The Cable Equation.

The charge, σ, transmitted through the membrane in the sensory areas of the nerve, and the potential, V₀, generated by that charge, will be dissipated as the charge leaks back through the membrane as a consequence of the conductance of the membrane and moves down the axon as a consequence of the conductance of the neuron cytoplasm (15, 16).

From cable theory, I find for an initially localized charge, σ,

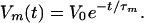7

The calculations are insensitive to the value of the time-constant, and, from plausible axon parameters, I take τ_m = 20 ms.

Inactivation and Adaptation

Sodium channels generally go to closed and inactive states after the depolarization peak and remain inactive for a few milliseconds afterward (15). I do not specifically assume such an inactivation for the channels I consider, but any large inactivation with time constants no longer than a few milliseconds does not change our results significantly.

Hensel (1) has emphasized that the firing rates of both warm and cold sensors depend upon both the temperature and the temperature history; adaptation effects are important. I accommodate this long term adaptation by postulating an “inactive” state with a long time constant.

In particular, I assume transitions from the active (largely open) states to the inactive state when the membrane is depolarized and then transitions from the inactive to active (largely closed) states when the membrane is repolarized. For the polarized membrane, in a given time, Δt, I add a number of active channels ΔK = K₀Δt/τ_adp, where K₀ is total number of available channels at equilibrium and the sensory cell is firing with a mean pulse period of Γ, and τ_adp ≫ Γ is an adaptation time constant which I took as 180 s in my calculations.

Then, upon a depolarizing pulse, I reduce the number of active channels, K, ΔK′ = −K Γ/τ_adp.

Thus, the mean number of active channels over a cycle is unchanged when the pulse period is equal to Γ. If the pulse period is greater than Γ, the number of active channels will increase and the pulse frequency will increase. Conversely, if the pulse period is less than Γ, the number of active channels will decrease and the pulse frequency will be reduced. The system will adapt to changes and reach a steady state such that, after a time, t ≈ t_adp, ΔK ≈ 0, over a cycle.

Numerical Calculations

Calculations of the properties of the sensory systems were conducted numerically by using Monte Carlo techniques and replacing the differential equations with difference equations using a time difference Δt = 1/8 ms. In particular, I calculated (i) the variation of the depolarization voltage of warm and cold sensory cells with time showing the development of the pulses; (ii) the variation of pulse firing rate for small variations of temperature—changes of <10°C—for both warm and cold sensors; (iii) with an added parameter for each mode, the accommodation effects—the effect of the thermal history of the system on the firing rates; and (iv) the effect on the firing rates of varying the calcium ion concentration in the plasma about the sensory cells by adding calcium and by subtracting calcium through the use of a chelating agent.

It is interesting to note that the calculations described piecemeal in the previous discussion can be arranged as a Langevin equation in the membrane potential V_m; β(V_m/dt) = αV_m + γ + ξ(t), where α, β, γ, and ξ are defined by the prescriptions, 1–11, and ξ(t) is the stochastic noise described above.

I take the active element of both warm and cold sensors as a set of 10 axon fingers each with a diameter of 2 μm and a length of 10 μm, giving a total surface area of 630 μm². For a membrane capacitance as 1 μF/cm², the capacitance of the set of 10 fingers is C_m = 6.3 pF.

The Warm Sensor Ca²⁺ Channels.

I take the channel density as ≈40 channels per μm². Thus, there are ≈25,000 channels in the sensory fingers. When open, each channel can pass a current of 0.064 pA or 2 × 10⁵ ions per second.

I assign a transition dipole moment for the gate of μ = Qd_me = 8 × 10⁻²⁷ Cm for a gating charge of Q = 6. I chose the value U₀ = 7.25 k_BT for the energy level spacing of the warm-sensor. At the base temperature, where the mean efflux and influx are equal and the system is at equilibrium, which is taken as T₀ ≈ 33°C to fit observations, ≈3.6 × 10⁶ ions per second will be transmitted through the 20 channels that are open, on the average, at any time.

The Cold Sensor Na⁺ Channels.

For the Na⁺ parameterization, I take U₀ = −3 k_BT, and I take the density of such rather special “reversed” channels as ≈2 per μm² so that there are ≈1,260 channels in the fingers. Taking the current through an open channel at 0.125 pA, a factor of 20 less than for a typical Na-channel (15) (but such reversed channels are hardly typical), J_max ≈ 160 pA or ≈10⁹ Na⁺ ions per second. At the base temperature, T₀, taken as ≈39°C (3), ≈1,200 channels are open on the average at any time—and but 60 are closed. While the model can accommodate small positive values of the Na⁺ gating charge, Q, as well as negative charges, I choose Q(Na⁺) = 0 for simplicity.

The Cold Sensor Ca²⁺ Channels.

For these sensors, I take the Ca²⁺ channel density as 80 channels per μm² or, thus, ≈50,000 total channels. Each such channel—when open—can pass a current of 0.13 pA or 4 × 10⁵ ions per second.

As for the warm Ca²⁺ sensors, I assume a gating charge of Q = 6 and a value U₀ = 7.25 k_BT for the energy level spacing of the warm-sensor. At the base temperature, taken as T₀ ≈ 38°C, where the mean efflux and influx are equal and the system is at equilibrium, ≈1.4 × 10⁷ ions per second will be transmitted through the 36 channels that are open on the average at any time.

Pulse Generation

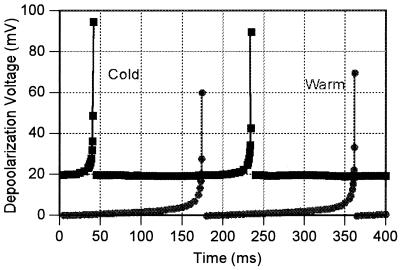
Using the procedures and the parameter values described in the last section, the Monte Carlo calculations show a variation of the potential with time of the form shown in Fig. 1. As a consequence of the limitations of my approximations, I did not follow the depolarization pulse beyond depolarization or describe the repolarization.

Figure 1.

Typical segments of the variation of the transmembrane potential of the sensory fingers as a function of time as calculated from Eqs. 1-7 with the parameters discussed here. The cold sensor variation is off-set by 20 mV for clarity. The solid lines at the pulse are to guide the eye. Each plot is calculated for the “neutral” temperature of ≈37°C, where the two frequencies are about the same.

Variation of Rates with Temperature

Warm Sensor Temperature Variation.

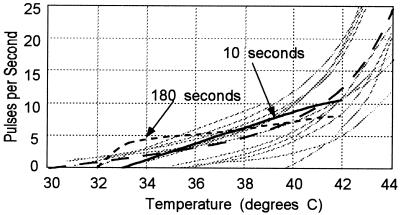
The diagrams of Fig. 2 show the firing rates of warm sensors as a function of temperature (1) for small temperature variations from a neutral point taken as 37°C. The gray lines show measured values of the firing rates for 10 different afferent nerves from the infraorbital region of the cat nose, and the dashed line shows the average of the measurements of 22 such fibers where the fibers have long been held at a constant temperature. The large physiological variation between fibers is evident. The dotted curve shows the calculated response from this model over the first 10 s after the temperature was changed from the neutral temperature. The solid curve shows the results of measurements made 180 s after the temperature is set, a delay sufficient to allow the accommodation mechanisms to erase the effects of any previous temperature history.

Figure 2.

Pulse firing frequencies for warm sensory nerves from the infraorbital region of the cat as a function of temperature.

The data on the firing rates of real systems, as illustrated in Fig. 2 by the gray lines, show values of dν/dT near the neutral temperature of 37°C, where ν is the firing frequency, that are significantly smaller than the results of the calculation; the temperature resolution of the model is greater than that found in nature. This follows from my implicit assumption that the channels and associated pumps perform identically in identical geometries. In nature, I can expect some biological variation which will reduce the resolution of the system. The pulse-to-pulse time variability is small; the period between pulses at the neutral temperature of 37°C is 0.16 ± 0.005 s.

Cold Sensor Temperature Variation.

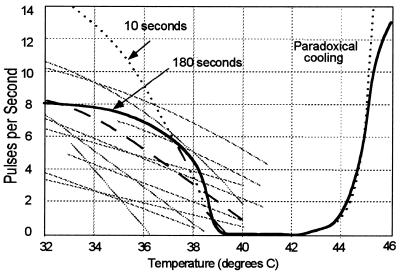
The diagrams of Fig. 3 show the firing rates of cold sensors as a function of temperature. Again, the gray lines show measured values for 10 different afferent nerves held at constant temperature, taken from a larger set (1, 17) from the infraorbital region of the cat nose, and the dashed line shows the average of the measurements of the set of such fibers. Again, there is a large physiological variation between fibers. As for Fig. 2, the dotted curve shows the calculated response from this model for measurements made over 10 s after the temperature was changed from the neutral temperature of 37°C. The solid curve shows the calculated results for a period of 10 s beginning 180 s after the temperature is raised—or lowered—from the previous temperature to allow the accommodation mechanisms, described in detail later, to erase effects of the thermal history of the sensors.

Figure 3.

Pulse firing frequencies for cold sensory nerves from the infraorbital region of the cat as a function of temperature.

As for the warm sensors, the variation of counting rate with temperature, |dν/dT| near the neutral temperature, is greater than that observed experimentally, again because of the idealized equivalence of channels and pumps and geometry. The variation of the period between pulses, at the neutral temperature of 37°C, is ≈0.16 ± 0.05 pulses per second, 10× greater than that for the warm sensors.

For large positive temperatures, in the presence of noise fluctuations of the potential, the incremental opening of Ca²⁺ channels can exceed the closing of Na⁺, channels leading to an overall influx of cations and a positive incremental transmembrane potential change, ΔU, which leads, in turn, to a further increase in cation current and, in time, a depolarization pulse. Such an increase in the cold sensation, as seen in Fig. 3, with increasing temperature has long been known (18) and is called Paradoxical Cold. The calculated increase takes place at ≈45°C, which is in good agreement with the threshold for the cold sensation in humans and the observed increase in firing rates of fibers from the lingual area of cats (19).

Adaptation.

Hensel (1) presents diagrams (his figure 4.1) which show schematically a “generalized response of cutaneous single warm and cold receptors to… rapid temperature changes” (ref. 1, p. 35). My calculations (not shown) faithfully reproduce the qualitative features of Hensel’s summary description for both the warm and the cold sensors.

Bursts.

For large negative temperatures, the afferent cold sensors appear to fire in bursts (20) where the frequency of the bursts varies with temperature in the same manner as the single pulse frequency varies at smaller negative temperatures. I consider that these follow from mechanisms outside of our model.

Effects of Changes in Calcium Concentration.

The intravenous injection of calcium is known to reduce the firing rate of cold receptors (21) and increase the firing rate of warm receptors in cats (7), thus mimicking an increase in temperature. And calcium given to humans intracutaneously or intravenously gives rise to a distinct warm sensation (4, 5). Conversely, the addition of the chelating agent EDTA (the bisodium salt of ethylene diamine tetraacetic acid), which reduces the concentration of calcium ions, results in an decrease in the firing rate of the warm sensors and an increase in the pulse rate of the cold sensor, thus mimicking a decrease in temperature.

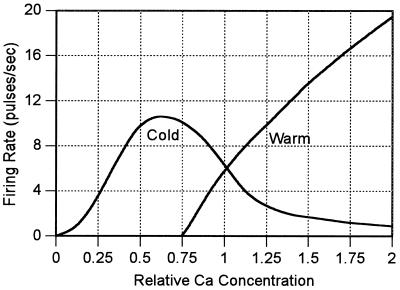
Fig. 4 shows the calculated variation of the firing rate of warm and cold sensors at the neutral point as a function of external calcium concentration. Here, I assume that the current passing through an open calcium channel is proportional to the external calcium concentration. The calculations simulate the results of measurements taken over the first 10 s when changes in the Ca²⁺ concentration and adaptation processes are not important.

Figure 4.

The calculated firing rate of the warm and cold sensors defined by this model at the neutral point of 37°C as the proportional concentration of Ca²⁺ ions in the external environment of the cells is varied from a normal value of one.

Sensitivity

Humans (22–25) show sensitivities to temperature changes in the skin of ≈0.02°C near the neutral point of ≈38°C. There is both temporal summation and area integration; to a good approximation, a warm-cold response is proportional to the time integral of the temperature signal up to a period of 3 s and to a spatial summation up to areas which vary over the body but are of the magnitude of 25 cm² on the forearm or back.

From the average experimental firing rates shown in Figs. 2 and 3, the mean firing frequency for both the warm and cold cat sensory nerves varies by ≈1 pulse per s per degree at the neutral temperature of 37°C, where the firing rate of each is ≈6 pps. Then, for a change of 0.02°C, the mean rates change only by ≈0.02 pps or ≈0.35%. The fiber-to-fiber firing rate variances, illustrated by the gray curves in the figures, are much larger. However, taking the variance in the slope of the firing rate with temperature dν/dT as 0.25 pulse per s per s, the data from one pair of warm-cold fibers would establish the temperature to an accuracy defined by a standard deviation of about σ₁ = 0.25°C, assuming the signal derives from the change in firing rate and not the absolute rate. If the information could be processed efficiently, a sensitivity of 0.02°C could be derived from 100 such pairs.

Taking the error in the warm or cold determination as proportional to the square-root of the total number of pulses from a set of sensors, I would expect the threshold to vary inversely as the square root of the product of the area and the sensing time—up to some integration limit. The variation seems to be better described by a proportionality to the inverse area (27) and the inverse of the length of the signal up to a time of ≈3 s or perhaps 20 pulse periods. Integration inefficiencies and the presence of noise from other sources could account for the difference between the calculated and observed variations.