Optimization of neural network architecture using genetic programming improves detection and modeling of gene-gene interactions in studies of human diseases

Abstract

Background

Appropriate definition of neural network architecture prior to data analysis is crucial for successful data mining. This can be challenging when the underlying model of the data is unknown. The goal of this study was to determine whether optimizing neural network architecture using genetic programming as a machine learning strategy would improve the ability of neural networks to model and detect nonlinear interactions among genes in studies of common human diseases.

Results

Using simulated data, we show that a genetic programming optimized neural network approach is able to model gene-gene interactions as well as a traditional back propagation neural network. Furthermore, the genetic programming optimized neural network is better than the traditional back propagation neural network approach in terms of predictive ability and power to detect gene-gene interactions when non-functional polymorphisms are present.

Conclusion

This study suggests that a machine learning strategy for optimizing neural network architecture may be preferable to traditional trial-and-error approaches for the identification and characterization of gene-gene interactions in common, complex human diseases.

Background

The detection and characterization of genes associated with common, complex diseases is a difficult challenge in human genetics. Unlike rare genetic disorders which are easily characterized by a single gene, common diseases such as essential hypertension are influenced by many genes all of which may be associated with disease risk primarily through nonlinear interactions [1,2]. Gene-gene interactions are difficult to detect using traditional parametric statistical methods [2] because of the curse of dimensionality [3]. That is, when interactions among genes are considered, the data becomes too sparse to estimate the genetic effects. To deal with this issue, one can collect a very large sample size. However, this can be prohibitively expensive. The alternative is to develop new statistical methods that have improved power to identify gene-gene interactions in relatively small sample sizes.

Neural networks (NN) have been used for supervised pattern recognition in a variety of fields including genetic epidemiology [4-12]. The success of the NN approach in genetics, however, varies a great deal from one study to the next. It is hypothesized that for complex human diseases, we are dealing with a rugged fitness landscape [9,13], that is, a fitness landscape with many local minima which make it more difficult to find the global minimum. Therefore, the inconsistent results in genetic epidemiology studies may be attributed to the fact that there are many local minima in the fitness landscape. Training a NN involves minimizing an error function. When there are many local minima, a NN using a hill-climbing algorithm for optimization may stall on a different minimum on each run of the network [9].

To avoid stalling on local minima, machine learning methods such as genetic programming [14] and genetic algorithms [15] have been explored. Genetic programming (GP) is a machine learning methodology that generates computer programs to solve problems using a process that is inspired by biological evolution by natural selection [16-20]. Genetic programming begins with an initial population of randomly generated computer programs, all of which are possible solutions to a given problem. This step is essentially a random search or sampling of the space of all possible solutions. An example of one type of computer program, called a binary expression tree, is shown in Figure 1.

Figure 1.

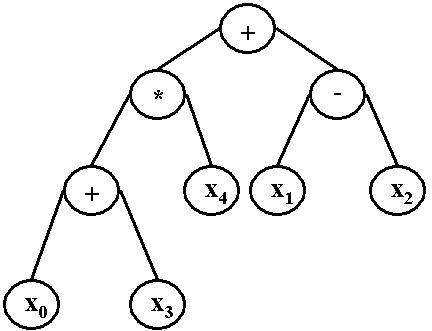
Binary expression tree example of a GP solution. This figure is an example of a possible computer program generated by GP. While the program can take virtually any form, we are using a binary expression tree representation, thus we have shown this type as an example.

Next, each of these computer programs are executed and assigned a fitness value that is proportional to its performance on the particular problem being solved. Then, the best computer programs, or solutions, are selected to undergo genetic operations based on Darwin's principle of survival of the fittest. Reproduction takes place with a subset of the best solutions, such that these solutions are directly copied into the next generation. Crossover, or recombination, takes place between another subset of solutions. This operation is used to create new computer programs by combining components of two parent programs. An example of a crossover event between two solutions is shown in Figure 2.

Figure 2.

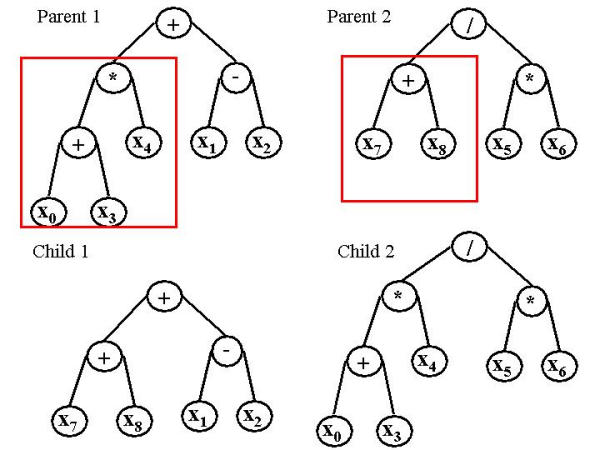
GP crossover. This figure shows a crossover event in GP between two binary expression trees. Here, the left sub-tree of parent 1 is swapped with the left sub-tree of parent 2 to create 2 new trees.

Thus, the new population is comprised of a portion of solutions that were copied (reproduced) from the previous generation, and a portion of solutions that are the result of recombination (crossover) between solutions of the parent population. This new population replaces the old population and the process begins again by executing each program and assigning a fitness measure to each of them. This is repeated for a set number of generations or until some termination criterion is met. The goal is to find the best solution, which is likely to be the solution with the optimal fitness measure.

Koza [17,18] and Koza et al. [19] give a detailed description of GP. A description of GP for bioinformatics applications is given by Moore and Parker [13]. Evolutionary computation strategies such as GP have been shown to be effective for both variable and feature selection with methods such as symbolic discriminant analysis for microarray studies [13,16,21]. Koza and Rice [14] have suggested GP for optimizing the architecture of NN.

The goal of this study was to implement a GP for optimizing NN architecture and compare its ability to model and detect gene-gene interactions with a traditional back propagation NN. To achieve this goal we simulated data from a set of different models exhibiting epistasis, or gene-gene interactions. We applied the back propagation NN (BPNN) and the GP optimized NN (GPNN) to these data to compare the performance of the two methods. We considered the GPNN to have improved performance if 1) it had improved prediction error, and/or 2) it had improved power compared to the BPNN. We implemented cross validation with both the BPNN and GPNN to estimate the classification and prediction errors of the two NN approaches. Based on our results, we find that GPNN has improved prediction error and improved power compared to the BPNN. Thus, we consider the optimization of NN architecture by GP to be a significant improvement to a BPNN for the gene-gene interaction models and simulated data studied here. In the remainder of this section, we will provide background information on the BPNN, the GPNN strategy, and the cross validation approach used for this study.

Back propagation NN (BPNN)

The back propagation NN (BPNN) is one of the most commonly used NN [22] and is the NN chosen for many genetic epidemiology studies [4-12]. In this study, we used a traditional fully-connected, feed-forward network comprised of one input layer, zero, one, or two hidden layers, and one output layer, trained by back propagation. The software used, the NICO toolkit, was developed at the Royal Institute of Technology, http://www.speech.kth.se/NICO/index.html.

Defining the network architecture is a very important decision that can dramatically alter the results of the analysis [23]. There are a variety of strategies utilized for selection of the network architecture. The features of network architecture most commonly optimized are the number of hidden layers and the number of nodes in the hidden layer. Many of these approaches use a prediction error fitness measure, such that they select an architecture based on its generalization to new observations [23], while others use classification error, or training error [24]. We chose to use classification error rather than prediction error as a basis for evaluating and making changes to the BPNN architecture because we use prediction error to measure the overall network fitness. We began with a very small network and varied several parameters including the number of hidden layers, number of nodes in the hidden layer, and learning momentum (the fraction of the previous change in a weight that is added to the next change) to obtain an appropriate architecture for each data set. This trial-and-error approach is commonly employed for optimization of BPNN architecture [24,25].

A Genetic Programming Neural Network (GPNN) Strategy

We developed a GP-optimized NN (GPNN) in an attempt to improve upon the trial-and-error process of choosing an optimal architecture for a pure feed-forward BPNN. The GPNN optimizes the inputs from a larger pool of variables, the weights, and the connectivity of the network including the number of hidden layers and the number of nodes in the hidden layer. Thus, the algorithm attempts to generate appropriate network architecture for a given data set. Optimization of NN architecture using GP was first proposed by Koza and Rice [14].

The use of binary expression trees allow for the flexibility of the GP to evolve a tree-like structure that adheres to the components of a NN. Figure 3 shows an example of a binary expression tree representation of a NN generated by GPNN. Figure 4 shows the same NN that has been reduced from the binary expression tree form to look more like a common feed-forward NN. The GP is constrained in such a way that it uses standard GP operators but retains the typical structure of a feed-forward NN. A set of rules is defined prior to network evolution to ensure that the GP tree maintains a structure that represents a NN. The rules used for this GPNN implementation are consistent with those described by Koza and Rice [14]. The flexibility of the GPNN allows optimal network architectures to be generated that contain the appropriate inputs, connections, and weights for a given data set.

Figure 3.

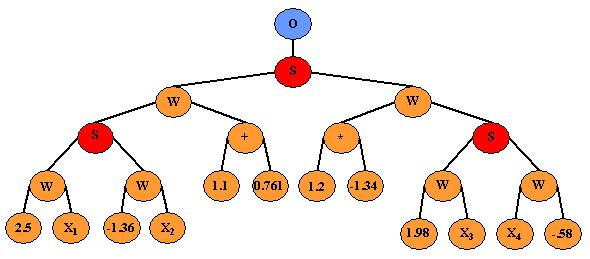
GPNN representation of a NN. This figure is an example of one NN optimized by GPNN. The O is the output node, S indicates the activation function, W indicates a weight, and X₁-X₄ are the NN inputs.

Figure 4.

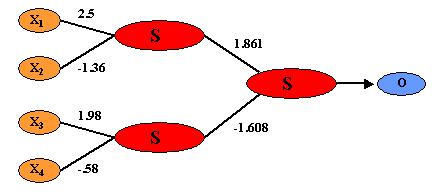
Feed-forward BPNN representation of the GPNN in Figure 3. To generate this NN, each weight in Figure 3 was computed to produce a single value.

The GP has a set of parameters that must be initialized before beginning the evolution of NN models. First, a distinct set of inputs must be identified. All possible variables can be included as optional inputs, although the GP is not required to use all of them. Second, a set of mathematical functions used in weight generation must be specified. In the present study, we use only the four basic arithmetic operators. Third, a fitness function for the evaluation of GPNN models is defined by the user. Here, we have designated classification error as the fitness function. Finally, the operating parameters of the GP must be initialized. These include initial population size, number of generations, reproduction rate, crossover rate, and mutation rate [14].

Training the GPNN begins by generating an initial random population of solutions. Each solution is a binary expression tree representation of a NN, similar to that shown in Figure 3. The GP then evaluates each NN. The best solutions are selected for crossover and reproduction using a fitness-proportionate selection technique, called roulette wheel selection, based on the classification error of the training data [26]. A predefined proportion of the best solutions will be directly copied (reproduced) into the new generation. Another proportion of the solutions will be used for crossover with other best solutions. Crossover must take place such that the rules of network construction still apply. Next, the new generation, which is equal in size to the original population, begins the cycle again. This continues until some criterion is met at which point the GPNN stops. This criterion is either a classification error of zero or the maximum number of generations has been reached. In addition, a "best-so-far" solution is chosen after each generation. At the end of the GP run, the one "best-so-far" solution is used as the solution to the problem [14,16].

While GPNN can be effective for searching highly nonlinear, multidimensional search spaces, it is still susceptible to stalling on local minima [14]. To address this problem, GPNN can be run in parallel on several different processors. Several isolated populations, or demes, are created and a periodic exchange of best solutions takes place between the populations. This is often referred to as an "island model" [27]. This exchange increases diversity among the solutions in the different populations. Following the set number of generations, the best-so-far solutions from each of the n processors are compared and a single best solution is selected. This solution has the minimum classification error of all solutions generated [28].

Cross-Validation

While NN are known for their ability to model nonlinear data, they are also susceptible to over-fitting. To evaluate the generalizability of BPNN and GPNN models, we used 10 fold cross-validation [29,30] (CV). Here, the data are divided into 10 parts of equal size. We use 9/10 of the data to train the BPNN or the GPNN, and we use the remaining 1/10 of data to test the model and estimate the prediction error, which is how well the NN model is able to predict disease status in that 1/10 of the data. This is done 10 times, each time leaving out a different 1/10 of data for testing [29,30]. A prediction error is estimated as an average across the 10 cross-validations. Cross-validation consistency is a measure of the number of times each variable appears in the BPNN or GPNN model across the 10 cross-validations [21,31,32]. That is, we measured the consistency with which each single nucleotide polymorphism (SNP) was identified across the 10 cross-validations. The motivation for this statistic is that the effects of the functional SNPs should be present in most splits of the data. Thus, a high cross-validation consistency (~10) lends support to that SNP being important for the epistasis model. Further detail regarding the implementation of cross-validation can be found in the Data Analysis section of the paper.

Results

Three different analyses were conducted to compare the performance of the BPNN and the GPNN. First, a trial-and-error procedure for selecting the optimal BPNN architecture for a subset of the data was performed. This step established the motivation for optimizing the NN architecture. Next, the ability to model gene-gene interactions by both the BPNN and GPNN was determined by comparing the classification and prediction error of the two methods using data containing only the functional SNPs. Finally, the ability to detect and model gene-gene interactions was investigated for both the BPNN and GPNN. This was determined by comparing the classification and prediction errors of the two methods using data containing the functional SNPs and a set of non-functional SNPs. The details of the implementation of these three analyses are reported in the Data Analysis section of the paper. The results of these three analyses are presented in the following sections.

Trial-and-error procedure for the back propagation NN (BPNN)

The results of our trial-and-error optimization technique for selecting the traditional BPNN architecture indicate the importance of selecting the optimal NN architecture for each different epistasis model. Table 1 shows the results from the traditional BPNN architecture optimization technique on one data set from each epistasis model generated with the two functional SNPs only. A schematic for each of the best architectures selected is shown in Figure 5. Note that the optimal architecture varied for each of the epistasis models. For example, the optimal architecture for Model 1 was composed of 2 hidden layers, 15 nodes in the first layer and 5 nodes in the second layer, and a momentum of 0.9. In contrast, for Model 2 the optimal architecture included 2 hidden layers, 20 nodes in the first layer and 5 nodes in the second layer, and a momentum of 0.9. Different architectures were optimal for models 3, 4, and 5 as well. Similar results were obtained using the simulated data containing the two functional and eight non-functional SNPs as well (data not shown). This provides further motivation for automating the optimization of the NN architecture in order to avoid the uncertainty of trial-and-error experiments.

Table 1.

Trial and Error Optimization of BPNN with only functional SNPs

HL	U/L	M	Epistasis Models
			1	2	3	4	5
0	0	.1	0.48786	0.49460	0.49560	0.49160	0.49545
0	0	.5	0.48786	0.49460	0.49560	0.49160	0.49545
0	0	.9	0.48786	0.49460	0.49560	0.49160	0.49545
1	5	.1	0.47317	0.45883	0.49568	0.49160	0.49553
1	5	.5	0.36422	0.34229	0.48754	0.49010	0.49543
1	5	.9	0.31206	0.23181	0.34522	0.44670	0.48905
1	10	.1	0.47430	0.46820	0.49607	0.49150	0.49559
1	10	.5	0.35916	0.36446	0.49284	0.49020	0.49542
1	10	.9	0.31209	0.23193	0.34524	0.44660	0.49136
1	15	.1	0.48495	0.47508	0.49599	0.49160	0.49552
1	15	.5	0.37511	0.36221	0.49364	0.49150	0.49542
1	15	.9	0.31217	0.23203	0.34525	0.44670	0.49399
1	20	.1	0.48630	0.49240	0.49583	0.49160	0.49549
1	20	.5	0.40750	0.34406	0.49469	0.49070	0.49544
1	20	.9	0.31217	0.23216	0.34511	0.44660	0.49402
2	5:5	.1	0.49965	0.49997	0.49997	0.50000	0.49996
2	5:5	.5	0.49628	0.49980	0.49996	0.49990	0.49995
2	5:5	.9	0.31205	0.23704	0.41740	0.44670	0.49471
2	10:5	.1	0.49623	0.49980	0.49987	0.49980	0.49972
2	10:5	.5	0.49024	0.49854	0.49929	0.49950	0.49847
2	10:5	.9	0.31201	0.23158	0.35430	0.45450	0.49477
2	15:5	.1	0.49398	0.49944	0.49954	0.49940	0.49913
2	15:5	.5	0.48697	0.49578	0.49850	0.49530	0.49700
2	15:5	.9	0.31199	0.23584	0.35993	0.44740	0.49465
2	20:5	.1	0.49160	0.49849	0.49946	0.49840	0.49889
2	20:5	.5	0.48700	0.49212	0.49808	0.49290	0.49596
2	20:5	.9	0.31199	0.23157	0.34657	0.44750	0.49519

Results from the trial and error optimization of the BPNN on one dataset from each epistasis model. We used 27 different architectures varying in HL – hidden layer, U/L – units per layer, M – momentum. The average classification error across 10 cross-validations from each data set generated for each of the five epistasis models are shown. The best architecture is shown in bold and in Figure 5. This was the most parsimonious architecture with the minimum classification error.

Figure 5.

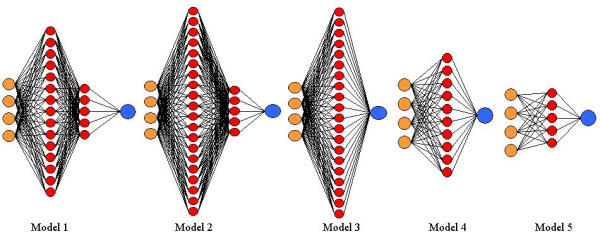
Optimal architecture from BPNN trial and error optimization. This figure shows the result of the BPNN trial and error procedure on one data set from each epistasis model. This shows the NN architecture for the best classification error selected from Table 1.

Modeling gene-gene interactions

Table 2 summarizes the average classification error (i.e. training error) and prediction error (i.e. testing error) for the BPNN and GPNN evaluated using 100 data sets for each of the five epistasis models with only the two functional SNPs in the analyses. GPNN and the BPNN performed similarly in both training the NN and testing the NN through cross-validation. In each case, the NN solution had an error rate within 4 percent of the error inherent in the data. Due to the probabilistic nature of the penetrance functions used to simulate the data, there is some degree of noise simulated in the data. The average error in the 100 datasets generated under each epistasis model are 24%, 18%, 27%, 36%, 40% for Model 1, 2, 3, 4, and 5, respectively. Therefore, the error estimates obtained by the BPNN or GPNN are very close to the true error rate. There is also little opportunity for either method to over-fit the data here, since only the functional SNPs are present in the analysis. These results demonstrate that the BPNN and GPNN are both able to model the nonlinear gene-gene interactions specified by these models.

Table 2.

Results from the BPNN and GPNN analyses of datasets with only functional SNPs.

Epistasis Model	BPNN		GPNN
	Classification Error	Prediction Error	Classification Error	Prediction Error
1	0.238	0.233	0.237	0.237
2	0.180	0.179	0.181	0.181
3	0.268	0.268	0.287	0.301
4	0.370	0.386	0.375	0.398
5	0.405	0.439	0.405	0.439

Detecting and modeling gene-gene interactions

Table 3 shows the average classification error and prediction error for the BPNN and GPNN evaluated using 100 data sets for each of the five epistasis models with the two functional and eight non-functional SNPs. GPNN consistently had a lower prediction error than the BPNN, while the BPNN consistently had a lower classification error. The lower classification error seen with the BPNN is due to over-fitting. These results show that when non-functional SNPs are present, the BPNN has a tendency to over-fit the data and therefore have a higher prediction error than GPNN. GPNN is able to model gene-gene interactions and develop NN models that can generalize to new observations.

Table 3.

Results from the BPNN and GPNN analyses of data sets with both functional and non-functional SNPs

Epistasis Model	BPNN		GPNN
	Classification Error	Prediction Error	Classification Error	Prediction Error
1	0.008	0.340	0.237	0.237
2	0.008	0.303	0.242	0.243
3	0.009	0.398	0.335	0.360
4	0.013	0.477	0.387	0.431
5	0.012	0.486	0.401	0.479

Table 4 shows the power to detect the two functional SNPs for GPNN and the BPNN using 100 data sets for each of the five epistasis models with both the two functional and eight non-functional SNPs in the analyses. For all five models, GPNN had a higher power than the BPNN to detect both SNPs. These results demonstrate the high power of GPNN in comparison to a BPNN when attempting to detect gene-gene interactions in the presence of non-functional SNPs.

Table 4.

Power (%) to detect each functional SNP by BPNN and GPNN analyses of data sets with both functional and non-functional SNPs

Epistasis Model	BPNN		GPNN
	SNP 1	SNP 2	SNP1	SNP 2
1	88	90	100	100
2	80	82	100	100
3	41	50	100	100
4	3	0	92	87
5	0	1	44	47

Discussion

We have implemented a NN that is optimized by GP using the approach outlined by Koza and Rice [14]. Based on the results of the trial and error architecture optimization, we have shown that the selection of optimal NN architecture can alter the results of data analyses. For one example data set from each of the epistasis models, the best architecture was quite different, as shown in Table 1 and Figure 5 for functional SNP only data. This was also the case for data containing functional and non-functional SNPs (data not shown). Since we only tried 27 different architectures, there may have been more appropriate architectures for these data sets. In fact, since enumeration of all possible NN architectures is impossible [24], there is no way to be certain that the global best architecture is ever selected. Thus, the ability to optimize the NN architecture using GPNN may dramatically improve the results of NN analyses.

Using simulated data, we demonstrated that GPNN was able to model nonlinear interactions as well as a traditional BPNN. These results are important because it is well known that traditional BPNN are universal function approximators [22]. When given the functional SNPs, one would expect the BPNN to accurately model the data. Here, we have shown that GPNN is also capable of accurately modeling the data. This demonstrates that GPNN is able to optimize the NN architecture such that the NN evolved is able to model data as well as a BPNN.

GPNN had improved power and predictive ability compared to a BPNN when applied to data containing both functional and non-functional SNPs. These results provide evidence that GPNN is able to detect the functional SNPs and model the interactions for the epistasis models described here with minimal main effects in a sample size of 200 cases and 200 controls. In addition, these are the two criteria we specified for considering GPNN an improvement over the BPNN. Therefore, in situations where the functional SNPs are known and the user is attempting to model the data, either GPNN or a BPNN would be equally useful. However, in situations where the functional SNPs are unknown and the user wants to perform variable selection as well as model fitting, GPNN may be the preferable method. This distinction can be made due to the increase in power of GPNN and the fact that GPNN does not over-fit the data much like the traditional BPNN.

We speculate that GPNN is not over-fitting because while the GPNN is theoretically able to build a tree with all of the variables as inputs, it is not building a fully connected NN. This may be preventing it from over-fitting the way that the BPNN has done. Secondly, it is possible that the strong signal of the correct solution in the simulated data caused the GP to quickly pick up that signal, and propagate trees with components of that model in the population. Because we have mutation set to 0%, there is never a large change to the trees to lead them to explore in the other areas of the search space. As a result, the GPNN converges quickly on a small solution instead of exploring the entire search space. We plan to explore whether GPNN over-fits in certain situations and if so, to develop strategies to deal with this issue, such as the three-way data split discussed by Roland [33].

In an attempt to estimate the power of these NN methods for a range of genetic effects, we selected epistasis models with varying degrees of heritability. Heritability, in the broad sense, is the proportion of total phenotypic variance attributable to genetic factors. Thus, higher heritability values will have a stronger genetic effect. The five disease models we used varied in heritability from 0.008 to 0.053. To calculate the heritability of these models, we used the formula described by Culverhouse et al. [34]. Heritability varies from 0.0 (no genetic component) to 1.0 (completely genetically-specified).

We selected models with varying heritability values to obtain a more accurate comparison of the two NN methods in the presence of different genetic effects. Interestingly, the results showed that GPNN had greater than 80% power for all heritability values tested in the range of 0.012 to 0.053. In addition, GPNN had 100% power for all models with a heritability of 0.026 or greater. However, the BPNN had greater than 80% power only for heritability values greater than 0.051. Therefore, the BPNN has low power to detect gene-gene interactions that have an intermediate to weak genetic effect (i.e. heritability value in the range from 0.008 to 0.026), while GPNN maintains greater than 80% power, even for an epistasis model with a relatively weak genetic effect (i.e. 0.012). The power of GPNN falls below 80% for a heritability value that is very small (i.e. 0.008). Thus, GPNN is likely to have higher power than the BPNN for detecting many gene-gene interaction models with intermediate to small genetic effects.

While GPNN has improved power and predictive ability over the BPNN, there are some advantages and disadvantages to this approach. An advantage of GPNN is its modeling flexibility. With commercial BPNN software, such as the BPNN used here, the user must define the inputs, the initial values of the weights, the number of connections each input has, and the number of hidden layers. Often, the algorithm parameters that work well for one data set will not be successful with another data set, as demonstrated here. With the GP optimization, the user only needs to specify a pool of variables that the network can use and the GP will select the optimal inputs, weights, connections, and hidden layers. An important disadvantage of GPNN is the required computational resources. To use GPNN effectively, one needs access to a parallel processing environment. For a BPNN, on the other hand, a desktop computer is the only requirement. Another disadvantage is the interpretation of the GPNN models. The output of GPNN is a NN in the form of a binary expression tree. A NN in this form can be difficult to interpret, as it can get quite large (up to 500 nodes).

While we have demonstrated the ability of GPNN to model and detect gene-gene interactions, further work is needed to fully evaluate the approach. For example, we would like to know whether using a local search algorithm, such as back propagation or simulated annealing [35], to refine the weights of a GPNN model is useful. This sort of approach has been employed for a genetic algorithm approach to optimizing NN architecture for classification of galaxies in astronomy [36]. However, as described above, a local search could lead to increased over-fitting. Next, the current version of GPNN uses only arithmetic operators in the binary expression trees. The use of a richer function set, including Boolean operators and other mathematical operators, may allow more flexibility in the NN models. Third, we would like to evaluate the power of GPNN for a variety of high order epistasis models (such as three, four, and five locus interaction models). Finally, we would like to develop and distribute a GPNN software package.

Conclusions

The results of this study demonstrate that GP is an excellent way of automating NN architecture design. The NN inputs, weights, and interconnections are optimized for a specific problem while decreasing susceptibility to over-fitting which is common in the traditional BPNN approach. We have shown that GPNN is able to model gene-gene interactions as well as a BPNN in data containing only the functional SNPs. We have also shown that when there are nonfunctional SNPs in the data (i.e. potential false positives), GPNN has higher power than a BPNN, in addition to lower prediction error. We anticipate this will be an important pattern recognition method in the search for complex disease susceptibility genes.

Methods

Data simulation

The goal of the data simulation was to generate data sets that exhibit gene-gene interactions for the purpose of evaluating the classification error, prediction error, and power of GPNN and a traditional BPNN. As discussed by Templeton [1], epistasis, or gene-gene interaction occurs when the combined effect of two or more genes on a phenotype could not have been predicted from their independent effects. Current statistical approaches in human genetics focus primarily on detecting the main effects and rarely consider the possibility of interactions [1]. In contrast, we are interested in simulating data using different epistasis models that exhibit minimal independent main effects, but produce an association with disease primarily through interactions. We simulated data with two functional single nucleotide polymorphisms (SNPs) to compare GPNN to a BPNN for modeling nonlinear epistasis models. In this study, we use penetrance functions as genetic models.

Penetrance functions model the relationship between genetic variations and disease risk. Penetrance is defined as the probability of disease given a particular combination of genotypes. We chose five epistasis models to simulate the data. The first model used was initially described by Li and Reich [37] and later by Culverhouse et al. [34] and Moore et al. [38] (Table 5). This model is based on the nonlinear XOR function that generates an interaction effect in which high risk of disease is dependent on inheriting a heterozygous genotype (Aa) from one SNP or a heterozygous genotype from a second SNP (Bb), but not both. The high-risk genotype combinations are AaBB, Aabb, AABb, and aaBb with disease penetrance of 0.1 for all four. The second model was initially described by Frankel and Schork [39] and later by Culverhouse et al. [34] and Moore et al. [38] (Table 6). In this model, high risk of disease is dependent on inheriting two and exactly two high-risk alleles, either "a" or "b" from two different loci. For this model, the high-risk genotype combinations are AAbb, AaBb, and aaBB with disease penetrance of 0.1, 0.05, and 0.1 respectively.

Table 5.

Penetrance functions for Model 1.

	Table penetrance			Margin penetrance
	AA (.25)	Aa (.50)	aa (.25)
BB (.25)	0.00	0.10	0.00	0.05
Bb (.50)	0.10	0.00	0.10	0.05
bb (.25)	0.00	0.10	0.00	0.05
Margin penetrance	0.05	0.05	0.05

Each cell represents the probability of disease given the particular combination of genotypes [p(D|G)]. This model has a heritability of 0.053.

Table 6.

Penetrance functions for Model 2.

	Table penetrance			Margin penetrance
	AA (.25)	Aa (.50)	aa (.25)
BB (.25)	0.00	0.00	0.10	0.025
Bb (.50)	0.00	0.05	0.00	0.025
bb (.25)	0.10	0.00	0.00	0.025
Margin penetrance	0.025	0.025	0.025

Each cell represents the probability of disease given the particular combination of genotypes [p(D|G)]. This model has a heritability of 0.051.

The subsequent three models were chosen from a set of epistasis models described by Moore et al. [38] (Table 7,8,9). All five models were selected because they exhibit interaction effects in the absence of any main effects when allele frequencies are equal and genotypes are generated using the Hardy-Weinberg equation. In addition, we selected models within a range of heritability values. As mentioned previously, heritability, in the broad sense, is the proportion of total phenotypic variance attributable to genetic factors. Thus, higher heritability values will have a stronger genetic effect. We selected models with varying heritability values to obtain a more accurate comparison of the two NN methods in the presence of varying genetic effects. The heritabilities are 0.053, 0.051, 0.026, 0.012, and 0.008 for Models 1, 2, 3, 4, and 5 respectively. Although the biological plausibility of these models is unknown, they represent the worst-case scenario for a disease-detection method because they have minimal main effects. If a method works well with minimal main effects, presumably the method will continue to work well in the presence of main effects.

Table 7.

Penetrance functions for Model 3.

	Table penetrance			Margin penetrance
	AA (.25)	Aa (.50)	aa (.25)
BB (.25)	0.00	0.04	0.00	0.02
Bb (.50)	0.04	0.02	0.00	0.02
bb (.25)	0.00	0.00	0.08	0.02
Margin penetrance	0.02	0.02	0.02

Each cell represents the probability of disease given the particular combination of genotypes [p(D|G)]. This model has a heritability of 0.026.

Table 8.

Penetrance functions for Model 4.

	Table penetrance			Margin penetrance
	AA (.25)	Aa (.50)	aa (.25)
BB (.25)	0.00	0.02	0.08	0.03
Bb (.50)	0.05	0.03	0.01	0.03
bb (.25)	0.02	0.04	0.02	0.03
Margin penetrance	0.03	0.03	0.03

Each cell represents the probability of disease given the particular combination of genotypes [p(D|G)]. This model has a heritability of 0.012.

Table 9.

Penetrance functions for Model 5.

	Table penetrance			Margin penetrance
	AA (.25)	Aa (.50)	aa (.25)
BB (.25)	0.00	0.04	0.08	0.04
Bb (.50)	0.06	0.04	0.02	0.04
bb (.25)	0.04	0.04	0.04	0.04
Margin penetrance	0.04	0.04	0.04

Each cell represents the probability of disease given the particular combination of genotypes [p(D|G)]. This model has a heritability of 0.008.

Each data set consisted of 200 cases and 200 controls, each with two functional interacting SNPs. SNPs generally have two possible alleles, and in our study, they were simulated with equal allele frequencies (p = q = 0.5). We used a dummy variable encoding for the genotypes where n-1 dummy variables are used for n levels [40]. We simulated 100 data sets of each epistasis model with two functional SNPs. Based on the dummy coding, these data would have four variables and thus four NN inputs. Next, we simulated 100 data sets of each model with eight non-functional SNPs and two functional SNPs. Based on the dummy coding, these data would have 20 variables and thus 20 NN inputs. These two types of data sets allow us to evaluate the ability to either model gene-gene interactions or to detect gene-gene interactions.

Data analysis

In the first stage of analysis, we posed the following question: Is GPNN able to model gene-gene interactions as well or better than a traditional BPNN? First, we used a fully connected, feed-forward BPNN to model gene-gene interactions in the simulated data containing functional SNPs only. The BPNN was trained for 1000 epochs. Although there are an effectively infinite number of possible NN architectures, for each data set we evaluated the classification ability of 27 different architectures. We chose the best architecture as the one that minimized the classification error and was most parsimonious (i.e. simplest network) in the event of two or more with equal classification error. We began with a very small network (4 inputs: 1 output) and varied the number of hidden layers (0,1,2), number of nodes in the hidden layers (5:0, 10:0, 15:0, 20:0, 5:5, 10:5, 15:5, 20:5), and learning momentum (0.1, 0.5, 0.9). We used this optimization procedure to analyze 100 data sets of each epistasis model. We used 10 fold cross-validation to evaluate the predictive ability of the BPNN models. After dividing the data into 10 equal parts, the architecture optimization procedure is run on the first 9/10 of the data to select the most appropriate architecture. Next, the best architecture is used to test the BPNN on the 1/10 of the data left out. This is done 10 times, each time leaving out a different 1/10 of the data for testing. We then estimated the prediction error based on the average predictive ability across the 10 cross-validations for all 100 data sets generated under each epistasis model.

Next, we used the GPNN to analyze the same 100 data sets for each of the five epistasis models. The GP parameter settings included 10 demes, migration of best models from each deme to all other demes every 25 generations, each deme had a population size of 200, 50 generations, a crossover rate of 0.9, reproduction rate of 0.1, and mutation rate of 0.0. Fitness was defined as classification error of the training data. As with the BPNN, GPNN was required to use all four inputs in the NN model for this stage of the analysis. Again, we used 10 fold cross-validation to evaluate the predictive ability of the GPNN models. We then estimated the prediction error of GPNN based on the average prediction error across the 10 cross-validations for all 100 data sets for each epistasis model.

The second aspect of this study involves answering the following question: In the presence of non-functional SNPs (i.e. potential false-positives), is GPNN able to detect gene-gene interactions as well or better than a traditional BPNN? First we used a traditional BPNN to analyze the data with eight non-functional SNPs and two functional SNPs. We estimated the power of the BPNN to detect the functional SNPs as described below. In this network, all possible inputs are used and the significance of each input is calculated from its input relevance, R_I, where R_I is the sum of squared weights for the i^th input divided by the sum of squared weights for all inputs. Next, we performed 1000 permutations of the data to determine what input relevance was required to consider a SNP significant in the BPNN model. The range of critical relevance values for determining significance was 10.43% – 11.83%.

Next, we calculated cross-validation consistency [21,31,32]. That is, we measured the consistency with which each SNP was identified across the 10 cross-validations. The basis for this statistic is that the functional SNPs' effect should be present in most splits of the data. Thus, a high cross-validation consistency (~10) lends support to that SNP being important for the epistasis model. Through permutation testing, we determined an empirical cutoff for the cross-validation consistency that would not be expected by chance. We used this cut-off value to select the SNPs that were functional in the epistasis model for each data set. For the BPNN, a cross-validation consistency greater than or equal to five was required to be statistically significant. We estimated the power by calculating the percentage of datasets where the correct functional SNPs were identified. Either one or both of the dummy variables could be selected to consider a locus present in the model. Finally, we estimated the prediction error based on the average predictive ability across 100 data sets for each epistasis model.

Next, we used the GPNN to analyze 100 data sets for each of the epistasis models. In this implementation, GPNN was not required to use all the variables as inputs. Here, GPNN performed random variable selection in the initial population of solutions. Through evolution, GPNN selects those variables that are most relevant. We calculated the cross-validation consistency as described above. Permutation testing was used to determine an empirical cut-off to select the SNPs that were functional in the epistasis model for each data set. For the GPNN, a cross-validation consistency greater than or equal to seven was required to be statistically significant. We estimated the power of GPNN as the number of times the functional SNPs were identified in the model divided by the total number of runs. Again, either one or both of the dummy variables could be selected to consider a locus present in the model. We also estimated the prediction error of GPNN based on the average prediction error across 100 data sets per epistasis model.

Authors' contributions

JSP, LWH, and BCW performed the computer programming of the software. MDR participated in the design of the study, statistical analyses, and writing of the manuscript. JHM participated in the design and coordination of the study and preparation of the final draft of the manuscript. All authors read and approved the final manuscript.