Sensitivity of T cells to antigen and antagonism emerges from differential regulation of the same molecular signaling module

Abstract

Activation of T helper cells is necessary for the adaptive immune response to pathogens, and spurious activation can result in organ-specific autoimmunity (e.g., multiple sclerosis). T cell activation is initiated by membrane-proximal signaling that is predicated on the binding of the T cell receptor expressed on the T cell surface to peptide major histocompatibility complex (pMHC) molecules presented on the surface of antigen-presenting cells. These signaling processes regulate diverse outcomes, such as the ability of T cells to discriminate sensitively between stimulatory pMHC molecules and those that are characteristic of “self,” and the phenomenon of antagonism (wherein the presence of certain pMHC molecules impairs T cell receptor signaling). We describe a molecular model for membrane-proximal signaling in T cells from which these disparate observations emerge as two sides of the same coin. This development of a unified mechanism that is consistent with diverse data would not have been possible without explicit consideration of the stochastic nature of the pertinent biochemical events. Our studies also reveal that certain previously proposed concepts are not dueling ideas but rather are different stimuli-dependent manifestations of a unified molecular model for membrane-proximal signaling. This model may provide a conceptual framework for further investigations of early events that regulate T cell activation in response to self and foreign antigens and for the development of intervention protocols to inhibit aberrant signaling.

Antigen-presenting cells display complexes of major histocompatibility gene products and peptides obtained from either endogenous proteins or those characteristic of pathogens. Interaction of T cell receptors (TCRs) with pathogen-derived peptide major histocompatibility complex (pMHC) molecules underlies T cell recognition of antigen. T cell-mediated, organ-specific autoimmunity can result from T cell activation in response to endogenous pMHC molecules.

Recent experiments have shown that T cells are sensitive to minute amounts of stimulatory (agonist) pMHC molecules in a sea of endogenous ligands (1–3). T helper (CD4⁺) cells can stop rolling and transiently increase cytosolic calcium levels in response to even one agonist pMHC molecule. Ten agonists appear to be sufficient for sustained calcium release and the formation of the immunological synapse [a patterned collection of proteins at the intercellular junction that is considered a marker of robust stimulation (4–6)]. Cytotoxic (CD8⁺) T cells also seem to be very sensitive (2, 7, 8), and as few as three agonist pMHC molecules have been demonstrated to be sufficient for killing target cells (2).

Signaling induced by agonist ligands can be severely impaired if certain pMHC molecules, called antagonists, are present. Antagonists are obtained by mutating residues of the WT pMHC for a given TCR. Although antagonists were discovered more than a decade ago (9), and despite a wealth of information on their inhibitory consequences (e.g., refs. 10–12), a molecular understanding of how they function remains elusive.

We reasoned that both the sensitivity of T cells to small amounts of antigen and the inhibition of signaling by antagonists must result from differential modulation of the same membrane-proximal signaling events. Thus, we sought a common set of principles underlying these disparate phenomena. Specifically, we aimed to develop a unified molecular model from which the extraordinary sensitivity of CD4⁺ T cells to antigen and antagonism emerges naturally as different stimuli-dependent responses.

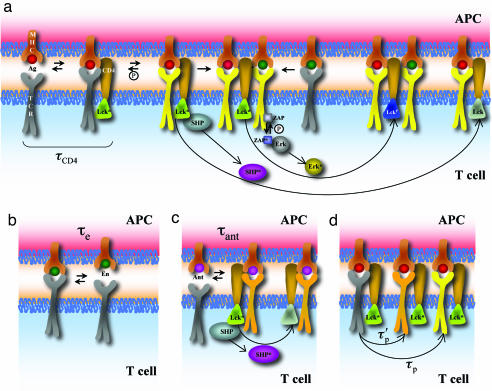
Because of thymic selection, endogenous ligands bind TCRs much more weakly than pathogen-derived pMHC molecules. The extraordinary sensitivity of T cells to agonists, and the weak binding of TCRs to endogenous ligands, have led to suggestions that these ligands may be implicated in T cell activation (1, 3, 13–16). For CD4⁺ T cells, the basic model that is emerging is one in which agonist and endogenous ligands act cooperatively, rather than additively, to trigger TCRs, thereby amplifying signaling when agonists are limiting (1, 3, 16). Spatial localization of a kinase, Lck, in a signaling complex nucleated by agonist binding to TCRs has been considered to play a key role in enabling certain endogenous ligands that associate with such complexes to trigger TCRs (Fig. 1 and ref. 3). Experiments have also provided evidence for cooperative interactions between agonist and endogenous ligands in triggering CD8⁺ T cells (17, 27).

Fig. 1.

Schematic representation of the bare model. (a) Cooperative interactions between agonist and endogenous ligands in phosphorylating TCRs (1, 3, 16) and feedback regulation of Lck (12, 19). Agonist peptides (red) bind TCRs (gray) for a sufficiently long time to recruit Lck (dark green) in a time scale equal to τ_CD4. Lck can phosphorylate TCRs (yellow represents such TCRs). Fully phosphorylated TCRs bind ZAP70 (light blue) with high efficiency, and Lck can phosphorylate ZAP70 (dark blue represents activated ZAP70), which in turn results in ERK activation (ERK → ERK*). Endogenous peptides (green) can associate with signaling complexes nucleated by agonists, and TCRs that bind to these endogenous pMHC molecules can be phosphorylated by the proximal Lck. Lck can activate the phosphatase SHP (purple, when activated), which can deactivate Lck (light green represents its deactivated state). ERK* can phosphorylate Lck, and SHP cannot act on this form of Lck (dark blue). (b) TCR–endogenous pMHC complexes are extremely short-lived (with a lifetime of τ_e) and thus rarely recruit Lck. (c) As described in text, we hypothesize that the short-lived antagonist (lifetime τ_ant) pMHC–TCR can recruit Lck but cannot carry out full phosphorylation of TCRs or nucleate signaling complexes as agonists can. The recruited Lck could activate SHP. (d) Agonist pMHC–TCR complexes recruit Lck, which phosphorylates the ITAMs partially or fully with the time scales τ′_p and τ_p, respectively.

In the context of CD8⁺ T cells, the importance of feedback regulation of Lck in determining the outcome of membrane-proximal signaling (e.g., antagonism) has also recently been emphasized (12, 18). Lck activates its own inhibitor, SHP1, but this inhibitory effect is prevented if activated ERK phosphorylates the serine 59 site on Lck (12). By combining these ideas with additional phenomenological ansatz and asserting that endogenous pMHC molecules play no role in activation of CD8⁺ T cells, mathematical modeling has shown that sharp changes in stimulatory potency can occur upon changing the number of agonist ligands (18). Contrary to the assumption in ref. 18, experiments support a role for endogenous ligands in triggering CD8⁺ T cells (17, 27), but the evidence for feedback regulation of Lck in modulating membrane-proximal signaling is strong (12).

In our quest for a unified molecular model for membrane-proximal signaling in T cells, we carried out extensive computer simulations and theoretical analyses of various molecular hypotheses regarding membrane-proximal signaling in CD4⁺ T cells. We initially discovered that naïvely combining ideas that separately provide satisfactory descriptions of the sensitivity of T cells to antigen (1, 3, 16) and antagonism due to feedback regulation of Lck (12, 18) does not result in an integrated model. This is because stochastic fluctuations prevent such a model from simultaneously describing both the sensitivity to antigen and antagonism. Analysis of the stochastic effects then suggested the mechanistic feature that is required for an internally consistent molecular model; this feature has recently been observed in unrelated experimental work. Thus, our studies have led us to describe a signaling module that can be differentially regulated by stimuli to result in the diverse functional outcomes observed in experiments. This mechanism may provide a unified conceptual framework.

Molecular Models

Because there is now strong experimental support for cooperative interactions between endogenous and agonist ligands when agonist is limiting, the corresponding molecular models (1, 3, 16) constitute our starting point. In the first model we studied, we combined such a model with feedback regulation of Lck, in accordance with Germain and coworkers (12, 18).

The models we have studied previously for describing cooperativity between agonist and endogenous ligands have the following features. The binding of a TCR to an agonist ligand (see supporting information (SI) Table 13 in SI Appendix, reactions 1 and 11) results in a relatively long-lived complex that enables the recruitment of the kinase Lck via the binding of the coreceptor CD4 (reaction 15). Thus, Lck is spatially localized in the signaling complex (Fig. 1). Additional pMHC molecules can then associate with the TCR–agonist pMHC–CD4/Lck complex (reaction 20). The molecular details of how this association occurs are not understood, but many computational models for this interaction exhibit qualitatively similar results (S. Y. Qi, A. R. Dinner, M. Krogsgaard, Mark M. Davis, and A.K.C., unpublished data). Regardless of this detail, because there are many more endogenous pMHC molecules, statistically, the additional pMHC molecule is likely to bear an endogenous peptide. Calculations suggest that when a TCR binds to this endogenous pMHC molecule (reaction 2), immunoreceptor tyrosine activation motifs (ITAMs) of the CD3 and ζ chains associated with the TCR can be phosphorylated (reactions 31 and 32) with a high probability because Lck is spatially localized proximal to this TCR, thereby enabling some endogenous ligands to contribute to productive signaling. In the absence of agonists, Lck recruitment occurs with very low probability upon the binding of a TCR to endogenous pMHC (reactions 3–6) because of the short half-life of this interaction (19).

We have elaborated this class of models in the following ways (Fig. 1). We now explicitly model sequential phosphorylation of the ITAMs of the TCR complex (SI Table 13 in SI Appendix, reactions 31 and 32). As in Lee et al. (20), the TCR complex can be in three states of progressively higher degrees of phosphorylation: not phosphorylated, partially phosphorylated, and fully phosphorylated. Two phosphorylated ITAMs are required for a molecule called ζ-associated protein 70 (ZAP70) to bind (21), and so, in our coarse-grained model, a higher degree of receptor phosphorylation favors ZAP70 binding (reaction 22) and subsequent phosphorylation (reaction 33). We discuss later why representing multiple ITAMs by just two sites that can be phosphorylated should not affect the qualitative mechanistic conclusions gleaned from our calculations. We also simplified the Ras-mediated MAP kinase pathway by subsuming these steps into one [ERK is activated by phosphorylated ZAP70 (reaction 24)]. Activated ERK is used as a counter of signal output.

We model the effects of feedback regulation of Lck on the basis of molecular events. According to Stefanova et al. (12), and as implemented in Lee et al. (20), Lck activates SHP1 (SI Table 13 in SI Appendix, reaction 34), which in turn inhibits Lck activity via the Y394 site (reaction 28); activated ERK can prevent the last interaction by phosphorylating the S59 site in Lck (reaction 25).

We hypothesized that antagonist ligands bind TCRs with a half-life (SI Table 13 in SI Appendix, reactions 7–10) that is sufficiently long to frequently recruit Lck (Fig. 1). This capability distinguishes antagonist ligands from endogenous ligands that bind TCR with a half-life that is too short for Lck recruitment to occur with high probability. However, in our hypothesis, antagonists do not bind TCRs for a time scale that is long enough to both recruit Lck and stimulate full ζ phosphorylation with the same efficiency as agonist ligands. Also, unlike agonists, antagonist pMHC–TCR complexes are not sufficiently long-lived to nucleate the signaling complexes that enable certain endogenous ligands to trigger TCRs. Thus, consistent with previous ideas (12, 18), we expected that the presence of antagonists would selectively increase SHP1 activation over ERK activation. This in turn would lead to increased Lck deactivation, thereby inhibiting signaling stimulated by agonists and synergistic endogenous ligands. We refer to this hypothesis for a unified molecular model for membrane-proximal signaling in CD4⁺ T cells (Fig. 1) as “the bare model” because it contains only features that have been previously (albeit, separately) described.

We tested this hypothesis (and related hypotheses) by carrying out computer simulations using a stochastic algorithm (see Methods) developed by Gillespie (22). The use of a stochastic algorithm is important because even if the intracellular molecules are present in high copy numbers, the numbers of agonist ligands can be small. Furthermore, as we demonstrate later, ignoring fluctuations in the lifetimes of complexes and phosphorylation events can lead to incorrect mechanistic conclusions. We do not consider formation of the immunological synapse because we are concerned here with early signaling events that precede synapse formation. Our simulations require as input a set of rate coefficients for the various reactions, as well as the number of molecules of each species. TCR and pMHC expression and binding kinetics are taken from experimental measurements (5, 19). We study the sensitivity of our results to a wide range of the unknown rate coefficients and copy numbers of various species.

Results

The bare model exhibits sensitivity to minute amounts of agonists in a sea of endogenous ligands (see SI Fig. 5 in SI Appendix) without frequent spurious triggering (i.e., the average level of ERK signaling upon addition of a few agonists far exceeds the basal level stimulated by endogenous pMHC alone by an amount significantly greater than the magnitude of the fluctuations). This is because adding feedback regulation and a more detailed description of ITAM phosphorylation to previously studied models (16) does not alter this observed characteristic. Is this model consistent with known facts about the phenomenon of antagonism?

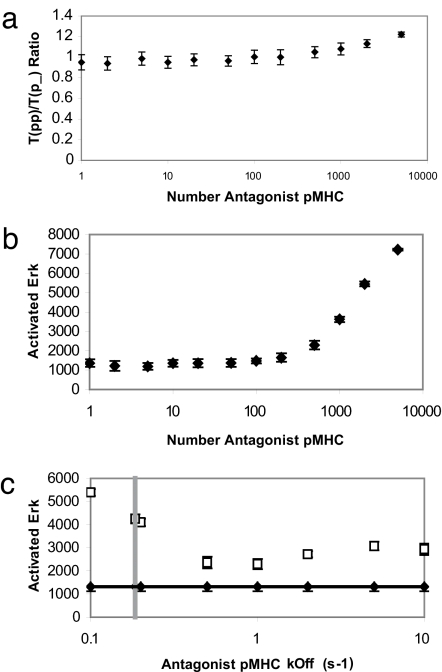
It is well established (10, 11) that the presence of antagonists lowers the ratio of fully phosphorylated to partially phosphorylated receptors (as measured by the ratio of p23 to p21). Fig. 2a shows that the bare model is not consistent with this experimental finding, given that the ratio of full to partially phosphorylated receptors increases as the number of antagonists exceeds a threshold. Fig. 2b shows that the amount of activated ERK (and therefore stimulatory potency) also increases when the number of antagonists exceeds a threshold. This result too contradicts experimental findings, inasmuch as antagonists have not been found to be stimulatory at any dose. The results in Fig. 2 are robust to changing unknown parameters over a wide range of values (see SI Figs. 6–9 in SI Appendix).

Fig. 2.

Results for the bare model. (a) The ratio of fully to partially phosphorylated TCRs in the bare model at time t = 250 s increases slightly as the number of antagonist pMHC ligands present is increased. There are 100 agonists and 5,000 endogenous pMHC. The other parameters used, and sensitivity (or lack thereof) of the results to variation in these parameters, are described in SI Appendix. (b) ERK activation increases with antagonist number past a certain threshold (between 200 and 500 antagonist pMHC). The parameters are the same as in a. (c) The increase in ERK activation with inclusion of “antagonist” pMHC ligands is robust over rates of antagonist dissociation from TCRs varying from 0.1 s⁻¹ to 10 s⁻¹. Filled diamonds are for 100 agonists and 5,000 endogenous pMHC; open squares include an additional 500 antagonists. The vertical dotted gray line indicates the very narrow window in which Eq. 4 is satisfied (τ_ant from Eq. 2 is equal to the inverse of the dissociation rate on the x axis).

There is now strong support for the idea that cooperative interactions between agonists and certain endogenous ligands underlie the sensitivity of T cells to minute amounts of antigen (1–3, 16, 17, 27). Experimental evidence for feedback regulation of Lck also appears to be compelling, and it provides a rationale for antagonism (12). Although these models describe the individual phenomena well, when combined, a unified mechanism providing a satisfactory description of both the sensitivity of T cells to antigen and the phenomenology observed upon addition of antagonist ligands is not obtained (Fig. 2).

To understand the reason underlying this puzzle and to determine how to remedy the bare model, we analyzed the key requirements for this model to function as desired. These conditions are as follows. (i) Synergistic endogenous ligands that are part of signaling complexes nucleated by agonists must bind TCR for a sufficiently long time for the spatially localized Lck to fully phosphorylate ITAMs with high probability. (ii) Antagonists must bind TCR for a time that is long enough for the recruitment of Lck, followed by largely partial phosphorylation of the TCR complex. Is it easy to meet both of these requirements simultaneously? To answer this question, we expressed these requirements in terms of the mean (or most probable) values of the time scales characterizing the pertinent processes. The time scales were represented by the following variables: τ_e, lifetime of an endogenous pMHC–TCR complex; τ_ant, lifetime of an antagonist pMHC–TCR complex; τ_Lck, time required for CD4/Lck recruitment; τ_p, time required for full ITAM phosphorylation, given that Lck is spatially localized in the vicinity of the receptor; and τ′_p, time required for partial ITAM phosphorylation, given that Lck is spatially localized in the vicinity of the receptor. Conditions i and ii noted above can then be expressed by Eqs. 1 and 2, respectively:

Because endogenous pMHC molecules bind TCR for a time that is too short to recruit CD4/Lck with high probability, whereas antagonists can recruit the coreceptor upon binding TCR according to our hypothesis, the two conditions noted above must be satisfied simultaneously with the following requirement:

Combining Eqs. 1–3 by simple algebraic operations allowed us to obtain the following equation, which encapsulates how the mean values of the relevant time scales must be related for the bare model to be satisfactory:

where the symbols represent the following ratios of the time scales defined above:

Eq. 4 is a stringent condition because all of the quantities involved in it lie between 0 and 1, and ε appears on both sides of the equation. However, the condition can be met by specific choices of ε, δ, and η. For example, choosing ε close to unity should enhance the production of partially phosphorylated receptors by antagonists; then, δ can be chosen such that ε + δ > 1, and η must then be a bit smaller than δ.

However, our computer simulations of the bare model with parameters chosen to be in this narrow range (and its vicinity) (Fig. 2c) do not yield satisfactory results. This is because the time scales characterizing various processes are not always equal to the mean values but rather are distributed around these most-probable values. Stochastic computer simulations (Fig. 2) show that these fluctuations make the stringent condition embodied in Eq. 4 impossible to satisfy. Although, we have not carried out the impossible task of searching the space of other parameter values “completely,” we have demonstrated the robustness of this qualitative result over a wide range of conditions (SI Appendix and data not shown).

The bare model is obtained by combining two ideas that separately describe individual phenomena, T cell sensitivity and antagonism, perfectly well. The combination fails to serve as a unified model because fluctuations make it difficult to simultaneously satisfy the requirements that (i) antagonist pMHC molecules largely produce partially phosphorylated receptors and (ii) endogenous ligands (that bind TCRs with a shorter half-life) largely stimulate full phosphorylation when they are associated with signaling complexes nucleated by agonists (Fig. 1).

The reason for this difficulty can be understood in molecular terms as follows. Synergistic endogenous ligands that associate with signaling complexes nucleated by agonists can trigger TCRs that bind to them. However, both full and partially phosphorylated receptors will be generated because the lifetimes of various bonds (e.g., the TCR–endogenous pMHC complex) and the times required for full and partial phosphorylation (τ_p and τ′_p) are distributed around the mean values. Because of the shorter half-life of TCR–antagonist pMHC complexes, they recruit Lck less efficiently compared with agonists. However, once Lck is recruited, both full and partially phosphorylated receptors are generated because of the distribution of lifetimes of various bonds and values of τ_p and τ′_p. Because antagonists bind TCRs for a mean time scale longer than for endogenous ligands, once the prerequisite for receptor triggering (Lck recruitment) is met, antagonists are more likely to stimulate a higher ratio of full to partially phosphorylated receptors. This qualitative effect is robust to including additional ITAMs in our model, and it dominates when the number of antagonists exceeds a threshold value in the bare model, leading to the results shown in Fig. 2 a and b.

Fluctuations prevent the bare model from functioning as a unified molecular model because mean values of certain time scales are not well separated. This difficulty could be ameliorated by a molecular mechanism that results in a wider separation of certain time scales. One way this could happen is if, in addition to facilitating efficient recruitment of Lck, the long half-life of TCR–agonist pMHC complexes enables molecular events that change the activity of Lck such that it phosphorylates ITAMs more rapidly (shorter τ′_p and τ_p). The shorter half-life with which antagonists bind TCRs may preclude these molecular events from occurring, leading to relatively larger values of τ′_p and τ_p. In this scenario, endogenous ligands that can synergize with agonists have two advantages compared with antagonists in generating fully phosphorylated receptors. Antagonists have to recruit Lck upon binding pMHC, and they have a less-active kinase to carry out ITAM phosphorylation. Addition of such a mechanism to the bare model may result in a proper unified model for membrane-proximal signaling.

Two experimental studies support the possibility of such a molecular mechanism. Long-lived TCR–pMHC interactions can lead to the recruitment of the molecule Unc 119, which in turn converts Lck from a partial to a fully activated state (23). More recently, a molecule called TsAD has been discovered to have similar effects (24). TsAD is an adaptor protein that interacts physically with Lck's SH2 and SH3 domains and in so doing promotes further activation of Lck by competitive inhibition of intramolecular interactions in Lck that are inhibitory.

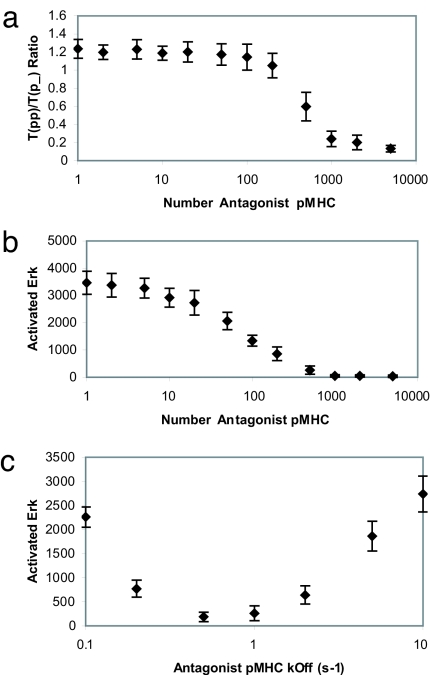
We combined this idea that recruited Lck can change activity (by undergoing two chemical modifications) with the bare model to produce what is referred to henceforth as “the unified model.” Computer simulations show that this model is sensitive to minute amounts of agonists and that cooperative interactions with endogenous ligands play a key role in amplifying signaling (see SI Fig. 12 in SI Appendix). Fig. 3 shows that the unified model is also consistent with the experimentally observed phenomenology of antagonism. As the number of antagonists increases past roughly a 1:1 ratio, we find that the ratio of fully phosphorylated to partially phosphorylated receptors decreases (smaller p23/p21 ratio), as does the amount of activated ERK (counter for downstream signal strength). High doses of antagonists are not stimulatory.

Fig. 3.

Results for the unified model. (a) The ratio of fully to partially phosphorylated TCRs in the unified model at time t = 250 s decreases with increasing numbers of antagonist pMHC. (b) ERK activation is suppressed by antagonist ligands in the unified model. (c) Phenomenon of antagonism in the unified model depends on antagonist pMHC–TCR dissociation rate. Antagonism is maximized (i.e., ERK activation is minimized) at an intermediate value of pMHC–TCR dissociation rate.

In SI Figs. 13–16 in SI Appendix, we describe how the above results depend on the choice of various parameters (e.g., the concentration of SHP1, Lck, and other unknown rate coefficients). The results in Fig. 3 are robust over a wide range of parameters. A noteworthy point is that if the SHP1 activation rate or concentration, or that of the phosphatase that acts on activated ERK, is lowered, antagonists are less effective. We have also carried out computer simulations in which the entire pool of Lck is not associated with CD4, and the qualitative results (see SI Figs. 18 and 19 in SI Appendix) are the same as in Fig. 3. Thus, different ratios of free and CD4-associated Lck will lead to similar results.

Fig. 3c shows results suggesting that antagonist pMHC–TCR complexes are characterized by a narrow range of half-lives. The efficacy of downstream signaling (ERK activation) goes through a minimum as the off-rate characterizing the antagonist in our simulations is varied. This is because if the off-rate decreases past a threshold, then the ligand begins to act as a weak agonist. On the other hand, if the off-rate increases past a threshold, it begins to act like an endogenous ligand that can synergize with agonists to amplify TCR signaling. This may be why mutations to WT peptides that result in antagonists are rare compared with those that produce null, weak, or super agonist ligands.

Discussion

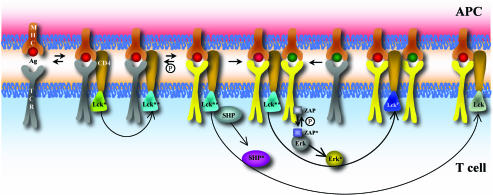
Our computer simulations and theoretical analyses have led us to a well defined molecular model (Fig. 4) for membrane-proximal signaling in CD4⁺ T cells that is simultaneously consistent with the observed sensitivity of T cells to minute amounts of agonists and with the phenomenon of antagonism. In this model, TCR binding to agonist pMHC molecules results in a complex that is sufficiently long-lived to allow recruitment of Lck and a series of steps that converts Lck from a partially active to a fully active state [possibly due to Unc 119 or TsAD (23, 24) or other molecular interactions]. The resulting complex enables endogenous ligands that act cooperatively with agonists to generate many fully phosphorylated receptors, which in turn results in rapid activation of ERK that leads to productive downstream signaling and protection of Lck from the inhibitory effects of SHP1. Thus, endogenous ligands amplify signaling from minute amounts of agonists (1, 3, 16). Antagonist ligands bind TCR with a half-life that is too short to both recruit Lck and stimulate its conversion to a state of higher kinase activity; therefore, these ligands do not stimulate full receptor phosphorylation efficiently. Antagonist ligands have two disadvantages compared with synergistic endogenous ligands: (i) they need to recruit Lck, and (ii) the recruited Lck is less active than in signaling complexes nucleated by agonists. However, Lck recruited by antagonists can activate SHP1, which can function to inhibit Lck and signaling stimulated by agonists and synergistic endogenous ligands (12, 18). This effect dominates when antagonists exceed a threshold value.

Fig. 4.

Schematic representation of the unified model. The colors and symbols are exactly the same as in Fig. 1a, except that Lck can potentially be converted to a state of higher activity (teal) if a TCR is bound to the corresponding pMHC for a sufficiently long time (details in text).

In this model, the concepts of cooperative interactions between self and agonist ligands amplifying signaling (1, 3, 16), kinetic proofreading (25), and feedback regulation of Lck (12) are combined in precise ways to yield a molecular model that is consistent with diverse experimental data. Removing cooperative interactions between agonists and endogenous ligands from the model contradicts experimental findings (1, 3, 16, 17, 27). Removing SHP1 abrogates feedback regulation of Lck (12), and computer simulations of such a model do not reproduce the phenomenology of antagonism (see SI Fig. 17 in SI Appendix). This result is because, although antagonists do produce more partially phosphorylated receptors, there is no mechanism to inhibit signaling stimulated by agonists and their synergistic endogenous ligands. We show that combining the ideas of cooperativity between agonists and endogenous ligands and feedback regulation of Lck does not lead to a self-consistent model from which antagonism and T cell sensitivity to antigen emerge as stimuli-specific consequences. An additional ingredient, steps that change the activity of Lck if TCR–pMHC interactions are sufficiently long-lived, seems to be required in order to create a unified model. This requirement is an example of kinetic proofreading (25), defined to mean that a series of steps can occur only if certain interactions are sufficiently long-lived. But our finding reflects kinetic proofreading with a twist. The beneficiaries of the longer half-life of TCR–agonist pMHC interactions are the synergistic endogenous ligands, because it helps them generate fully phosphorylated receptors more readily. It is also worth remarking that the nucleation of signaling complexes that allow agonists and endogenous ligands to cooperate in triggering TCRs also requires a series of steps akin to kinetic proofreading, and hence such steps are important for ligand discrimination.

The model we have developed predicts that, to function as antagonists, pMHC ligands must bind TCRs with half-lives restricted to a rather narrow range. From a biological standpoint, this is important because, if it were not so, significant parts of the endogenous pMHC repertoire could act as antagonists and inhibit T cell activation in response to pathogens.

It is also important to emphasize that the mechanistic model suggested by our studies emerged from careful consideration of stochastic effects. This consideration allowed us to establish why the seemingly reasonable bare model does not work over a wide range of parameters and suggested a mechanistic ingredient that results in a molecular model that provides a proper description of diverse phenomena in the same parameter space.

Our results provide an example of how ignoring stochastic fluctuations can lead to mechanistically incorrect conclusions in T cell signaling. However, once the topology of the signaling network is formulated based on careful consideration of stochastic molecular events, it is useful (and computationally inexpensive) to construct an approximate model and examine its consequences by using the mathematical language of differential equations. We have carried out such calculations with a model that includes the essential features shown in Fig. 4 (e.g., agonists and synergistic endogenous ligands act cooperatively and stimulate full phosphorylation of receptors, whereas antagonists do not). These calculations make interesting predictions regarding how T cell activation potency depends on the number of synergistic endogenous, agonist, and antagonist ligands (see SI Fig. 22 in SI Appendix). These scaling relationships could be tested by experiments in which T cells are stimulated by controlled mixtures of agonist, synergistic endogenous, and antagonist ligands presented on CHO cells and supported lipid bilayers (3). The amounts of agonists would have to be low (as in vivo and in ref. 1), otherwise the effects we have described may be obscured. It would also be interesting to test the results shown in Fig. 3, as well as our prediction that reduction in phosphatase levels could abrogate antagonism in a specific system.

If these results test affirmatively, it will be important to pursue further work to elaborate the unified molecular model we propose for membrane-proximal signaling in T helper cells. Such a model could help provide a better understanding of T cell activation, T helper cell-mediated autoimmune disorders, and the design of therapeutics.

Methods

To include the effects of stochastic fluctuations, we model the dynamics of the T cell chemical reaction network with a master equation (26),

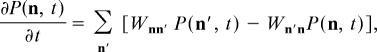where n is a vector whose components indicate the (integer-valued) number of molecules of the various chemical species present in the network, P(n, t) is the probability that the system is in the state described by n at time t, and W_nn′ is the probability per unit time of a transition from state n to state n^′. In this article, the transition matrices W consist of sums of terms corresponding to the various types of chemical reactions making up the reaction network with “mass action”-like kinetics. For instance, a reaction of the form A + B = C will lead to W taking the form

where … indicates the terms in W that correspond to other chemical reactions. The factor kn′_An′_B indicates that the probability per unit time of this reaction occurring is proportional to the number of A molecules present times the number of B molecules present, with rate constant k; this factor is referred to below as the “reaction propensity” r(n′) for the reaction A + B = C, given the initial state n′. The Kronecker deltas indicate that the transition n′ → n is only possible via the reaction in question if the state represented by n has exactly one less A molecule, one less B molecule, one more C molecule, and the same number of all other species as the state represented by n′.

In lieu of an analytic solution for P(n, t) of such master equations, which is generally elusive if the system being described contains many species and reactions, we obtain information about P(n, t) through a Monte Carlo simulation technique known as the Gillespie algorithm (22). This algorithm generates trajectories n(t) of the system in exact accord with the probability distribution P(n, t).

The various types of reactions involved in the different models we simulate, the kinetic parameters, and copy numbers of different molecules, the number of trajectories used to compute average quantities, and the sensitivity of our results to changing parameters are described in detail in SI Appendix. Parameters that reflect the binding of TCR to pMHC are known, and these values are used. However, many pertinent parameters are unknown, and so we carry out an extensive parameter-sensitivity analysis. The purpose of these computations is to establish that the qualitative results we describe are robust over wide ranges of parameter space. Although it is impossible to carry out computations that test parameter sensitivity completely, combined with our analysis of time scales and stochastic fluctuations, our results suggest that the bare model does not provide a satisfactory description of experimental results in a wide range of parameter space, whereas the unified model does.

Abbreviations

ITAM

immunoreceptor tyrosine activation motif

pMHC

peptide MHC

TCR

T cell receptor.