Assess the nature of cholesterol–lipid interactions through the chemical potential of cholesterol in phosphatidylcholine bilayers

Abstract

Cholesterol plays a vital role in determining the physiochemical properties of cell membranes. However, the detailed nature of cholesterol–lipid interactions is a subject of ongoing debate. Existing conceptual models, including the Condensed Complex Model, the Superlattice Model, and the Umbrella Model, identify different molecular mechanisms as the key to cholesterol–lipid interactions. In this work, the compositional dependence of the chemical potential of cholesterol in cholesterol/phosphatidylcholine mixtures was systematically measured at high resolution at 37°C by using an improved cholesterol oxidase (COD) activity assay. The chemical potential of cholesterol was found to be much higher in di18:1-PC bilayers than in di16:0-PC bilayers, indicating a more favorable interaction between cholesterol and saturated chains. More significantly, in 16:0,18:1-PC and di18:1-PC bilayers, the COD initial-reaction rate displays a series of distinct jumps near the cholesterol mole fractions (χ_C) of 0.15, 0.25, 0.40, 0.50, and 0.57 and a peak at the cholesterol maximum solubility limit of 0.67. These jumps have been identified as the thermodynamic signatures of stable cholesterol regular distributions. In contrast, no such jumps were evident in di16:0-PC bilayers below χ_C of 0.57. The observed chemical potential profile is in excellent agreement with previous Monte Carlo simulations based on the Umbrella Model but not with the predictions from the other models. The data further indicate that the cholesterol regular distribution domains (superlattices) are not the hypothesized condensed complexes. Those complexes were mainly implicated from studies on lipid monolayer that may not be relevant to the lipid bilayer in cell membranes.

Cholesterol plays a vital role in determining the physiochemical properties of cell membranes. The presence of cholesterol in a lipid membrane can drastically increase lipid acyl chain order, induce cholesterol regular distributions (superlattices) or lipid raft domains, and modulate the activities of surface-acting enzymes (1–4). Despite significant technical advances in membrane research in recent years, the detailed nature of cholesterol–lipid interactions is a subject of ongoing debate. Existing conceptual models, including the Condensed Complex Model, the Superlattice Model, and the Umbrella Model, identify different molecular mechanisms as the key to cholesterol–lipid interactions in biomembranes. Clearly, there is an urgent need to establish a general cholesterol–lipid interaction theory that can explain how cholesterol supports or modulates important functions in cell membranes and perhaps can predict the behavior and functional role of cholesterol in complex membranes.

Condensed Complex Model.

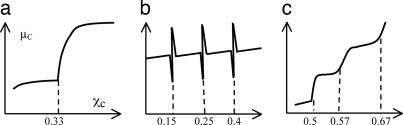
This model was initially proposed based on a study of lipid monolayers at the air–water interface (5). The model hypothesizes the existence of low free-energy stoichiometric cholesterol–lipid complexes that occupy smaller molecular lateral areas (5, 6). At a stoichiometric composition, a sharp jump in cholesterol chemical potential (μ_C) has been predicted (6, 7), as shown in Fig. 1a. Because the proposed condensed complex has a compact low-energy structure, the model explicitly predicted that cholesterol can form condensed complexes with lipids with which it can mix favorably, such as phosphatidylcholine (PC) with long saturated chains or sphingomyelins. It has also been suggested that cholesterol super lattices as well as lipid rafts are examples of the proposed condensed complexes (6, 8). According to this model, the ability to form cholesterol–lipid condensed complexes represents an essential feature of cholesterol–lipid interactions.

Fig. 1.

Schematic of the μ_C as a function of χ_C predicted by various models. (a) The Condensed Complex Model predicted a jump in μ_C at a stoichiometric composition (7). (b) The Superlattice Model predicted dips in free energy at superlattice compositions (13), which also implied sharp spikes in μ_C. (c) The Umbrella Model predicted a cascade of jump in μ_C, and each jump corresponds to a stable cholesterol regular distribution (14).

Superlattice Model.

The superlattice distribution was initially proposed based on the observation of a series of “kinks” or “dips” in the ratio of excimer to monomer fluorescence of pyrene-PC in PC bilayers at some particular mole fractions (9, 10). The bulky pyrene moieties were thought to form hexagonal superlattices to maximize separation from each other. Later, data on cholesterol/phospholipid mixtures containing fluorophores indicated that cholesterol could also form superlattices in lipid bilayers (3, 11, 12). This model is mainly a geometrical one that predicts the existence of a regular distribution of cholesterol at certain critical compositions in lipid bilayers. This model suggests that the difference in the cross-sectional area between cholesterol and other lipid molecules can result in a long-range repulsive force among cholesterols and thereby produce superlattice distributions (3, 9). Many superlattice structures have been predicted from a set of algebraic equations based on a geometric-symmetry argument. At the cholesterol mole fractions where superlattices occur, dips in free energy have also been suggested (13). Because μ_C can be calculated by taking the derivative of the free-energy profile (14), this model also implies that the μ_C should have sharp spikes at those predicted mole fractions (Fig. 1b). The Superlattice Model emphasizes that the long-range repulsive force among cholesterols plays the dominant role in cholesterol–lipid interactions.

Umbrella Model.

Cholesterol consists of a small 3β-OH polar headgroup and a bulky hydrophobic tetrameric ring, and a short acyl chain. The Umbrella Model suggests that the mismatch between the small cholesterol polar headgroup with its large nonpolar body determines the preferential association of cholesterol with certain membrane molecules (14, 15). The model was initially proposed to explain the data of cholesterol maximum solubility in lipid bilayers. In a bilayer, cholesterol relies on the coverage by the large polar headgroups of the neighboring phospholipids to prevent the unfavorable free energy of exposure of the nonpolar part of cholesterol to water. Because it costs much more free energy to cover a cholesterol cluster than a single cholesterol, a crucial property of cholesterol emerges, i.e., cholesterol molecules have a strong tendency not to cluster or at least not to form large clusters. To reduce the free-energy cost, cholesterol in a bilayer distributes in a manner so as to minimize cholesterol cluster size in the high-cholesterol region. This mechanism has been formulated as a multibody interaction among lipids. Monte Carlo (MC) simulations based on this interaction showed that cholesterol can form a “hexagonal” pattern at a cholesterol mole fraction (χ_C) = 0.50, a “dimer” pattern at 0.571, and a “maze” pattern at 0.667 (Fig. 2). The simulation also showed that the formation of a stable regular distribution is always accompanied by a jump in μ_C (14). Thus, a jump in μ_C is a thermodynamic indicator of the formation of a regular distribution. In addition, with the assumption that the energy cost of covering a cholesterol cluster increases nonlinearly with the cluster size, a cascade of jumps in μ_C has also been predicted (Fig. 1c). Note that μ_C is a gradually increasing function of χ_C in between the jumps of μ_C, indicating the overall favorable mixing of cholesterol with PC. In the low-cholesterol region (χ_C <0.45), a MC simulation study showed that cholesterol can form a series of regular distributions if two requirements are met: (i) a strong tendency for cholesterol to stay as monomer; and (ii) a multibody interaction of phospholipid acyl chains with cholesterol, which tends to minimize the acyl chain contact with cholesterol (15).

Fig. 2.

Six regular distributions of cholesterol that have been successfully simulated previously by using MC simulation based on the Umbrella Model. Filled circles, cholesterol; open circles, acyl chains of PC. (a) χ_C = 0.154. (b) χ_C = 0.25. (c) χ_C = 0.40. (d) Monomer pattern at χ_C = 0.50. (e) Dimer pattern at χ_C = 0.571. (f) Maze pattern at χ_C = 0.667, which is the maximum solubility limit of cholesterol in PC.

Because different models have different predictions for the chemical potential profile, an experimental measurement of μ_C can be used to test the validity of the models. In the work reported here, the μ_C in 1,2-palmitoyl-sn-glycero-3-phosphocholine (DPPC; di16:0-PC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC; 16:0,18:1-PC), and 1,2-oleoyl-sn-glycero-3-phosphocholine (DOPC; di18:1-PC) bilayers was measured systematically by using an improved cholesterol oxidase (COD) activity assay. The three PCs were specifically chosen to test the cholesterol interaction with lipids of saturated, mixed, and unsaturated acyl chains. The results were used to judge the merits of each model and to explore the fundamental nature of cholesterol–lipid interactions.

Results

COD Initial-Reaction Rate in the High-Cholesterol Region.

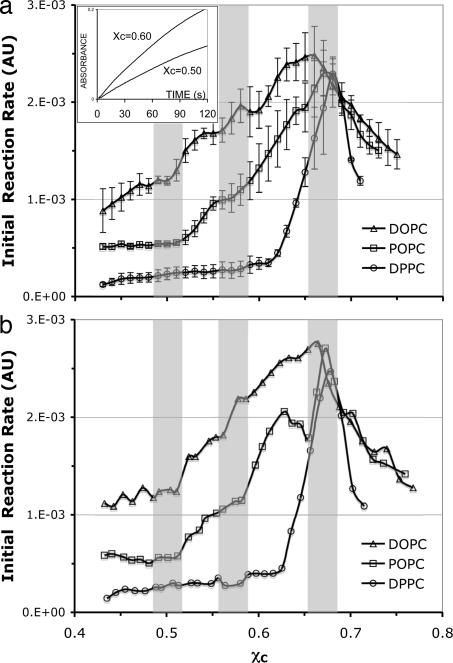
The initial rate of COD activity was obtained by fitting the first 40 s of the reaction progress curves in a coupled enzyme assay (16). Two reaction progress curves of the DOPC/cholesterol mixture are shown in Fig. 3a (Inset). The procedure of the assay and data analysis have been described in detail elsewhere (16). Fig. 3 shows the COD initial rate as a function of cholesterol mole fraction in the high-cholesterol region (χ_C >0.45). The initial rate has a global peak around χ_C ≈0.67 in all three PC bilayers. These global peaks indicate the maximum solubility of cholesterol in the bilayers (16, 17). As χ_C approaches the maximum solubility limit, μ_C in lipid bilayers increases sharply until it equals μ_C in cholesterol monohydrate crystals and results in a sharp increase of the COD initial-reaction rate. Above the maximum solubility limit, the bilayer phase and the cholesterol crystal phase coexist, and μ_C should remain constant. Once the crystal phase appears, the COD initial-reaction rate no longer follows the behavior of μ_C, and it displays a sharp decline as discussed previously (16). The position of the global peak can therefore be used to determine the cholesterol maximum solubility. In Fig. 3a, the peak positions for DOPC, POPC, and DPPC bilayers are 0.66, 0.67, and 0.68, respectively. These values are in excellent agreement with the previous measurements by x-ray diffraction, light scattering, and fluorescence spectroscopy (17, 18).

Fig. 3.

COD initial-reaction rate as a function of cholesterol mole fraction in the high-cholesterol region. The shaded bars indicate the locations of expected jumps at 0.50 and 0.571 and the cholesterol maximum solubility limit at 0.667 predicted by the Umbrella Model. The width of the bars reflects the experimental uncertainty in χ_C in our samples (±0.015). (a) Average curves, each obtained from three independent sample sets. (Inset) COD reaction progress curves of DOPC/cholesterol mixtures. The reaction rate is higher at χ_C = 0.60 than that at 0.50. (b) Individual curves. The jumps at 0.5 and 0.57 appear sharper.

An obvious feature of Fig. 3 is that the COD initial rate is highest in DOPC bilayers and lowest in DPPC bilayer at the same χ_C. Because the initial rate largely reflects μ_C in the bilayer, it indicates that μ_C is lowest in a PC bilayer with all saturated chains (DPPC), higher in a PC bilayer with mixed chains (POPC), and highest in a PC bilayer with all unsaturated chains (DOPC). A higher μ_C reflects a stronger tendency for cholesterol to escape from the bilayer. This result indicates that cholesterol interacts more favorably with saturated chains than unsaturated chains, which is consistent with the experimental findings that cholesterol has a low affinity for unsaturated acyl chains and can selectively form associations with saturated chains (19).

Fig. 3a shows the average curves of COD initial rates in DOPC, POPC, and DPPC bilayers, each obtained from three independent sample sets. The COD initial rate shows several interesting jumps. In POPC bilayers, the initial rate has clear jumps at χ_C = 0.52 and 0.58. In DOPC bilayers, the initial rate shows jumps at χ_C = 0.51, 0.57, and 0.62. In contrast, the initial rate in DPPC bilayers only has a large jump at χ_C = 0.63 and a tiny jump at 0.58. Previous MC simulations showed that the location of a jump (i.e., the lipid composition of the corresponding regular distribution) is at the beginning of the sharp rise in μ_C (14). Therefore, the locations of jumps in the COD initial-reaction rate were determined by using the same criterion in this work. It should be pointed out that these jumps are usually steeper in individual sample sets, as shown in Fig. 3b. Because of the experimental uncertainty in cholesterol mole fraction in our samples (±0.015), the sharpness of the jumps in the average curves (Fig. 3a) is smoothed out considerably. The vertical shaded bars in Fig. 3 indicate the positions of expected chemical potential jumps at χ_C = 0.50 and 0.571 and cholesterol maximum solubility limit at 0.667 predicted from the MC simulations based on the Umbrella Model. The width of the bars represents the experimental uncertainty in χ_C in our samples (±0.015). In Fig. 3, the locations of the jumps and peaks do not fall exactly on the predicted values. To evaluate the degree of agreement, additional experiments using small sample sets covering the jump at 0.50 and the peak at 0.667 were performed. The locations were determined for each sample set, and the mean values were then calculated. The mean ± SD (n) of the jump at 0.50 was 0.495 ± 0.016 (n = 6) and 0.497 ± 0.015 (n = 7) for DOPC and POPC, respectively. Here, n is the number of independent sample sets measured. For the peak at 0.667, the results were 0.671 ± 0.011 (n = 6), 0.668 ± 0.012 (n = 7), and 0.677 ± 0.011 (n = 5) for DOPC, POPC, and DPPC, respectively. Therefore, the measured locations agree favorably with the predicted values within the standard deviations of the data.

COD Initial-Reaction Rate in the Low-Cholesterol Region.

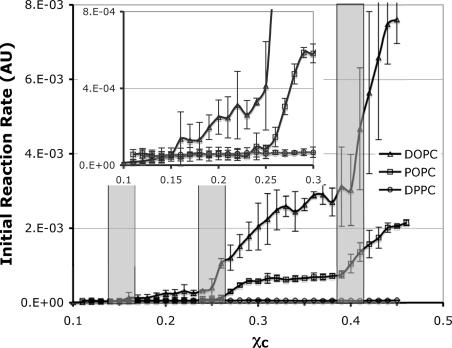
Fig. 4 shows the COD initial rate in the low-cholesterol region (χ_C <0.45). To resolve small jumps at very low cholesterol concentrations, three times more COD (0.3 unit per sample) was used for the low-cholesterol samples. Similar to the high-cholesterol region, the dominant feature of the figure is that the initial rate is highest in DOPC bilayers and lowest in DPPC bilayers. The differences in rate are quite spectacular. For example, at χ_C = 0.35, the rates in POPC and DOPC bilayers are ≈11 and 44 times higher than that in DPPC bilayers, respectively. The data indicate that cholesterol interaction with unsaturated acyl chains is very unfavorable compared with saturated chains in this region. Although the COD initial rate generally increases with χ_C in all three PC bilayers, the rate behaves quite differently in different bilayers. Clear jumps can be seen at χ_C = 0.25 and 0.40 in DOPC and POPC bilayers, whereas the rate in DPPC bilayers is featureless and flat. A close look at low χ_C showed that the rate also has a small but distinct jump at χ_C = 0.15 in DOPC but not in others (Fig. 4 Inset).

Fig. 4.

COD initial-reaction rate as a function of χ_C in the low-cholesterol region. The shaded bars indicate the locations of expected jumps at 0.154, 0.25, and 0.40 predicted by the Umbrella Model. The width of the bars reflects the experimental uncertainty in χ_C.

Discussion

What Does a Jump or a Lack of a Jump in μ_C Mean?

Based on a MC simulation study, it has been shown that the formation of a stable regular distribution is always directly associated with a jump in μ_C (14). Thus, a jump in μ_C is a thermodynamic indicator of a stable regular distribution formation. These stable lipid domains can be quite large, containing a few hundred molecules. On the other hand, if the magnitude of multibody interaction is not sufficiently large to produce a stable regular distribution and to cause a jump in chemical potential, much smaller and unstable dynamic domains can still exist (18).

Jumps in μ_C in the High-Cholesterol Region.

Here, the result will be discussed under the framework of the Umbrella Model because other models offer little or no explanation about the detailed molecular interactions for a particular regular distribution. The behavior of μ_C in the high-cholesterol region can provide some crucial details about the cholesterol–lipid interaction. According to the MC simulations with the Umbrella Model, the molecular driving force for the regular distribution at χ_C = 0.50 is that the free-energy cost of covering a cholesterol dimer is significantly higher than that of covering a cholesterol monomer (14). If the difference is sufficiently large, cholesterol would stay as monomer as long as it could, which can result in a monomer regular distribution pattern at 0.50 (Fig. 2d). The height of the jump in μ_C is directly related to that energy difference. Because an unsaturated chain containing a cis double bond is more “bulky” or less “compressible” than a saturated chain, DPPC with both saturated chains should have the largest “headgroup/body” ratio (or excess headgroup capacity to cover neighboring cholesterol clusters) among the three PCs. Therefore, it is reasonable to assume that DPPC can cover a cholesterol dimer more easily (i.e., at a lower free-energy cost) than does POPC or DOPC. Thus, the driving force to form a regular distribution at χ_C = 0.50 is weakest in DPPC and strongest in DOPC. This assumption is indeed the case, as shown in Fig. 3: No jump is seen at χ_C = 0.50 in DPPC bilayers, and the jump was larger in DOPC than in POPC (Fig. 3b). Similarly, the driving force to form the dimer regular distribution pattern at χ_C = 0.571 (Fig. 2e) is that the free-energy cost of covering a larger cholesterol cluster is much higher than that of covering a cholesterol dimer. As shown in Fig. 3, a small jump was observed at χ_C = 0.58 in DPPC, and bigger jumps were present in POPC and DOPC bilayers. The data show that all three PC are capable of covering cholesterol clusters up to the solubility limit (≈0.67), but the free-energy cost of the coverage in DOPC increases much more rapidly as a function of χ_C than the others do because of the chain unsaturation.

It is interesting that the COD initial rate in DPPC bilayers jumps at χ_C = 0.63. In several measurements with DPPC and DOPC, jumps ≈0.63 have also been observed. Because a regular distribution is a highly ordered distribution, as χ_C approaches, enters, and exits a regular distribution composition, the lateral distribution of the bilayer goes through a disorder—order–disorder transition, accordingly. Often, this transition in membrane order can alter the fluorescence properties of certain membrane fluorophores. Previously, small dips in fluorescence energy transfer efficiency and diphenylhexatrience-labeled PC fluorescence anisotropy have been found at 0.63 in DOPC bilayers (18). Whether or not this previously unassigned critical composition of 0.63 may represent a regular distribution made of “trimer” or “tetramer” pattern remains elusive. More study is needed to verify this interesting possibility.

Jumps in μ_C in the Low-Cholesterol Region.

In the low-cholesterol region, the COD initial rate showed three jumps (0.15, 0.25, and 0.4) in DOPC bilayers, two jumps (0.25 and 0.4) in POPC bilayers, and no jump in DPPC bilayers. These behaviors again can be understood through the Umbrella Model. Based on a MC simulation study, Huang (15) suggested that the driving force of cholesterol regular distributions in the low-cholesterol region is very different from that in the high-cholesterol region. In the low-cholesterol region, a series of regular distributions can be formed if two opposing types of interactions are present: a large interaction against any cholesterol clustering, and a smaller unfavorable acyl chain multibody interaction, which increases nonlinearly with the number of cholesterol contacts. A delicate balance must be maintained among the magnitudes of the two interactions. The combined effect of both interactions must still favor the cholesterol/phospholipid mixing. The first interaction likely originates from the requirement for PC to cover cholesterol. The headgroup/body ratio of a PC should be in some “optimal” range to create a strong tendency for cholesterol to avoid clustering in that particular bilayer. This strong tendency can be verified experimentally by checking whether cholesterol forms the monomer (i.e., hexagonal) regular distribution at χ_C = 0.50. Thus, forming a stable regular distribution at χ_C = 0.50 would meet the first necessary condition for forming regular distributions in the low-cholesterol region because it indicates that cholesterol tries to avoid forming dimer clusters in the bilayer due to the high free-energy cost of covering a cholesterol dimer cluster. The second necessary interaction is likely from the reduction of acyl chain conformation entropy resulting from cholesterol contact (15). Because cholesterol does not form stable regular distributions at χ_C = 0.50 in DPPC bilayers, the first necessary condition is not met, which explains why there is no stable regular distribution at the low-cholesterol region in DPPC. On the other hand, cholesterol does form regular distributions at χ_C = 0.50 in POPC and DOPC bilayers. COD initial-reaction rate curves show that cholesterol forms regular distributions at 0.25 and 0.4 in both bilayers. The data clearly demonstrate the direct correlation between the regular distribution at χ_C = 0.50 and the regular distributions in the low-cholesterol region (0.40, 0.25, and 0.154).

No Indication for a Condensed Complex.

Because the formation of condensed complexes is most likely in DPPC bilayers, and it should be accompanied by a jump in chemical potential as predicted by the Condensed Complex Model, the lack of any jump when χ_C <0.57 in DPPC (Figs. 3 and 4) indicates that there is no evidence of condensed complexes in DPPC bilayers when χ_C <0.57. Furthermore, the jumps (and regular distributions) above 0.57 also occur in DOPC and POPC, and they are not specific between DPPC and cholesterol. Therefore, there are unlikely to be condensed complexes but rather the regular distributions at very high cholesterol content as predicted by the Umbrella Model. It has been reported that the interactions between cholesterol and sphingomyelin are also not specific, and the driving force for the affinity between cholesterol and sphingomyelin is likely the hydrophobic interaction described by the Umbrella Model (20).

Regular Distributions (Superlattices) Are Not Condensed Complexes.

In Figs. 3 and 4, the COD initial-reaction rate shows a series of jumps in POPC and DOPC bilayers. Could the corresponding cholesterol regular distributions (i.e., superlattices) be the condensed complexes, as suggested previously (6, 8)? A careful analysis of data will show that regular distributions cannot be condensed complexes: (i) In Figs. 3 and 4, there is no jump in the initial rate in DPPC bilayers when χ_C <0.57, but four jumps appear in DOPC bilayers in the same region. Obviously, the data indicate that the tendency to form cholesterol regular distributions is much stronger in DOPC bilayers, which are bilayers with which cholesterol has a less favorable interaction, indicated by the high chemical potential. The condensed complexes, on the other hand, are supposed to be low free-energy aggregates of cholesterol and lipids, which occupy a smaller membrane lateral area. According to the Condensed Complex Model (8), the condensed complexes should be formed in a PC bilayer with which cholesterol can mix very favorably, such as with DPPC or sphingomyelins, but not with DOPC or POPC. The data obtained in this work directly contradict the model. It is well known that PC with unsaturated chains occupies more lateral area. Therefore, the regular distributions in DOPC or POPC bilayers are not structurally “condensed.” In addition, the μ_C is higher in DOPC or POPC than that in DPPC. Thus, the observed regular distributions in DOPC and POPC actually have higher free energies than the cholesterol/DPPC mixtures with the same χ_C. (ii) Cholesterol regular distributions lack lipid specificity. The same regular distribution can exist in DOPC, POPC, and other bilayers. The lack of lipid specificity is inconsistent with the idea of a stoichiometric complex. (iii) Cholesterol is a relative simple molecule. It is conceptually difficult to justify that cholesterol can form six different low free-energy stoichiometric complexes with one type of lipid (e.g., DOPC), and μ_C in the complexes continuously increases with χ_C. So far, MD simulations have failed to show what the structure of condensed complex is and why free energy would be low in such complexes.

A Cholesterol-Containing Monolayer at the Air–Water Interface May Not Be Relevant to a Bilayer.

Studies of lipid monolayers at the air–water interface have made important contributions to our understanding of lipid–lipid interactions in lipid bilayers and are particularly useful to estimate the lateral area occupied by membrane molecules (21). However, it should be pointed out that cholesterol–lipid interactions in a monolayer are very different from those in a lipid bilayer. At an air–water interface, the hydrophobic body of cholesterol is suspended in the air, and only the hydrophilic hydroxyl group touches the water. A pure cholesterol monolayer can easily be formed at an air–water interface, whereas it is not possible to have a pure cholesterol bilayer because the hydrophobic bodies of cholesterols would be exposed to water in such bilayer. In water, pure cholesterol forms cholesterol monohydrate crystals, not bilayers. Thus, in a lipid monolayer at the air–water interface, the key cholesterol–lipid interactions described by the Umbrella Model (i.e., the requirement of covering cholesterol hydrophobic bodies by neighboring PC headgroups) do not exit. Because the coverage requirement plays such a key role in determining molecular association and domain formation in a bilayer, one would expect that the cholesterol lateral distribution in a monolayer is different from that in a bilayer. Thus, a conclusion from a cholesterol-containing monolayer study might not be applicable to the corresponding bilayer systems. The condensed complex was originally proposed based on a monolayer study at the air–water interface, which could partially explain the discrepancy between the model and data in this bilayer study.

Superlattice Model.

The Superlattice Model correctly describes a general picture of cholesterol/PC mixing: Cholesterol tends to keep a distance from each other in a PC bilayer. The model also predicts many highly symmetrical regular distribution patterns (superlattices) at some well defined lipid compositions, and a number of those distributions have been verified experimentally through various techniques (13, 22). However, the model does have a few deficiencies: (i) It incorrectly hypothesized that the cross-sectional area difference between cholesterol and other lipid molecules can result in a long-range repulsive force among cholesterol and produce superlattice distributions. Although this mechanism does favor the mixing of cholesterol with phospholipids, it is not necessarily able to produce a regular distribution. For example, the cross-sectional area difference between cholesterol and DPPC chains is larger than that between cholesterol and DOPC chains. However, three stable regular distributions exist in DOPC and none in DPPC in the low-cholesterol region (Fig. 4). MC simulations have demonstrated that multibody interactions are required for superlattice formation. (ii) The Superlattice Model predicts superlattices from equations based on geometric symmetry, not based on a quantitative free-energy calculation. The model does correctly predict the superlattices at χ_C = 0.154, 0.25, 0.4, and 0.50 but failed to predict the regular distribution at χ_C = 0.571 (dimer pattern) and 0.667 (maze pattern) because these two patterns do not have the symmetry it seeks. In addition, it predicts many other superlattices that are unlikely to exist, particularly at low-cholesterol mole fractions. (iii) It has been hypothesized that a superlattice distribution has a local minimum in free energy. The corresponding chemical potential profile (Fig. 1b) has been proven to be incorrect in this work. However, this free-energy minimum prediction was not a fundamental assumption of the model, which is largely a geometrical model without any explicit assumptions of specific molecular interactions among the lipid molecules.

Umbrella Model.

In this work, the Umbrella Model and the consequent MC simulations have been proven quite successful in predicting and explaining the cholesterol mixing behavior with PCs: (i) The measured chemical potential profiles have excellent agreement with the calculated profiles from the MC simulation based on the model (Fig. 4e in ref. 14), which shows that the Umbrella Model captures the key cholesterol–lipid interaction. (ii) The jumps in μ_C at χ_C = 0.154, 0.25, 0.40, 0.50, 0.571, and 0.667, predicted by the Umbrella Model, have all been observed experimentally, which indicates that stable regular distributions can exist at these compositions. (iii) The Umbrella Model naturally explains the detail molecular interactions required for each regular distribution. The result of the present work strongly supports the explanation of the driving forces for regular distributions. It shows that both the headgroup/body ratio of PC and the acyl chain conformational entropy play key roles in cholesterol superlattice formation. (iv) Unlike the Condensed Complex Model, which assumes specific chemical complex formation between cholesterol and other lipids, the Umbrella Model suggests that the key cholesterol–lipid interaction is a hydrophobic interaction that arises from the shape of a cholesterol molecule: a small polar headgroup and a large nonpolar body. The model can be generalized and applied to the interactions between other small headgroup molecules (such as diacylglycerol or ceramide) and large headgroup lipids (such as PC or sphingomyelins). A recent study showed that ceramide displaces cholesterol from POPC bilayers following a 1:1 relation. This behavior of ceramide is well explained by the Umbrella Model (16). In addition, the Umbrella Model also provided a possible driving force for the formation of lipid rafts (18).

Biological Significance.

This work confirms that cholesterol–lipid interactions are deeply rooted in the detailed structures of lipid molecules. As shown in Figs. 3 and 4, one cis double bond difference in lipid structure can result in enormous differences in membrane organization and chemical activities of lipids. The data also show that a small change in membrane composition can produce a dramatic change in membrane protein activity. For example, in DOPC bilayers at χ_C = 0.25, a 2 or 20 mol% increase in χ_C resulted in a 3- or 20-fold increase of COD initial-reaction rate, respectively. The jump of chemical activity at χ_C = 0.25 in POPC could be significant because POPC resembles many natural lipids. First, maintaining the cholesterol mole fraction in a cell membrane above 0.25 would cost the cell a lot more energy because of the high μ_C. Second, it has been reported that cholesterol homeostasis is regulated by the membrane μ_C through a sensitive negative-feedback mechanism (23). If such jumps are also present in cell membranes, they could serve as a sharp cutoff-regulating signal, which could provide a possible explanation of why χ_C in most cell membranes is below 25 mol%.

Conclusion

The measured chemical potential profiles of cholesterol in PC/cholesterol bilayers are in excellent agreement with the predictions from the Umbrella Model. The data indicate that regular distributions (superlattices) are not condensed complexes. The results in this work also question the applicability of the Condensed Complex Model to lipid bilayers. The Superlattice Model is correct in providing a general description of regular distribution behavior of cholesterol in PC bilayers based on a simple symmetry argument. However, this model is incorrect in predicting that the long-range repulsion among cholesterol is the driving force of superlattice formation and in the prediction of free-energy profiles.

Methods

Materials.

POPC, DOPC, and DPPC were purchased from Avanti Polar Lipids (Alabaster, AL). Cholesterol was purchased from Nu-Chek Prep (Elysian, MN). Lipid purity (>99%) was confirmed by thin-layer chromatography, and concentrations of phospholipid stock solutions were determined with a phosphate assay as described previously (16). Aqueous buffer (5 mM Pipes/200 mM KCl/1 mM NaN₃, pH 7.0) was prepared from deionized water (≈18 MΩ) and filtered through a 0.1-μm filter before use. Recombinant cholesterol oxidase expressed in Escherichia coli (C-1235), peroxidase (P-8250) from horseradish, and other chemicals for the cholesterol oxidation measurements were obtained from Sigma (St. Louis, MO).

Liposome Preparation.

Liposomes were prepared by the rapid solvent exchange (RSE) method (24), and the procedure has been described in detail previously (16). After the RSE procedure, the samples were placed in a programmable water bath (model 1187P; VWR, West Chester, PA), preheated to 50°C for the subsequent heating and cooling cycle. The samples were first cooled to 24°C at a rate of 10°C/h and again heated to 50°C at the same rate. The samples were then kept at 50°C for an additional 1 h before finally being cooled to room temperature at a rate of 1.5°C/h. Finally, the liposomes were stored at room temperature with mechanical shaking for 10 days in the dark before the cholesterol oxidation measurements. The majority of liposomes made by the RSE method are large unilamellar vesicles and can set down in a test tube under gravity in a few hours (24).

Cholesterol Oxidation Measurements.

COD is a water-soluble monomeric enzyme that catalyzes the conversion of cholesterol to cholest-4-en-3-one. The initial rate of oxidation of cholesterol by COD enzyme was determined at 37°C through a coupled enzyme assay. For all experiments, each sample contained the same amount of cholesterol (60 μg), and the lipid compositions of samples were adjusted by adding appropriate amounts of PC. The procedure of the assay, reaction progress curves, and data analysis have been described in detail elsewhere (16). It has been shown that a COD enzyme first physically associates with lipid bilayers without perturbing the membrane structure (4). The enzyme then goes through conformation changes and provides a hydrophobic binding cavity that allows a favorable partitioning of the cholesterol from the membrane into the COD cavity. The initial-reaction rate of the oxidation should depend on COD concentration, cholesterol concentration (i.e., substrate concentration), the binding affinity of COD for lipid vesicles, and the cholesterol chemical activity in a lipid bilayer (4). Because the COD concentration and cholesterol content in our samples were kept constant, they should not contribute to the change of the initial rate. Ahn and Sampson (4) have showed that the binding affinity of COD for vesicles is only a weak function of χ_C (4). Thus, the sharp increases of the initial rate in Figs. 3 and 4 essentially reflect the behavior of the chemical activity of cholesterol, which relates to μ_C in lipid bilayers by exp(μ_C/kT). μ_C is directly related to the cholesterol interaction with surrounding lipids and the lateral organization within the bilayer (25). In addition, the binding affinity of COD is higher for DPPC bilayers than DOPC bilayers (4), and it should contribute to a slightly higher initial rate in DPPC. Therefore, the observed low initial-reaction rate in DPPC bilayers should mainly be the result of the low μ_C in DPPC bilayers.

Signal-to-Noise Issue.

In this work, to resolve fine structures in the μ_C dependence on membrane composition, significant effort was made to reduce the noise in the COD initial-rate measurement. Major improvement of the signal-to-noise ratio was achieved from the combination of making liposomes by using the RSE method, temperature cycling and long-term incubation of samples, and precise control of liquid volumes and temperature. Compared with the ethanol injection and the extrusion method, RSE is a convenient method with no lipid-binding, solvent contamination, or lipid-demixing concerns (16). We tested the ethanol injection method with a set of DOPC/cholesterol samples covering the initial-rate jump at χ_C = 0.25 and found that the data obtained were noisier and the COD initial-reaction rates were much lower than those with RSE samples (data not shown), which is consistent with a previous report that ethanol reduces COD activity (16). However, the overall shape and position of the jump were essentially identical to those from the RSE samples shown in Fig. 4, which indicated that the RSE method did not introduce a measurable composition-dependent change in COD accessible surface area. The increase of COD activity as a function of χ_C has been reported previously (4, 26). Our data are at a higher resolution and provide significant details.

Abbreviations

χ_C

cholesterol mole fraction

COD

cholesterol oxidase

DOPC

1,2-oleoyl-sn-glycero-3-phosphocholine

MC simulation

Monte Carlo simulation

μ_C

chemical potential of cholesterol

DPPC

1,2-palmitoyl-sn-glycero-3-phosphocholine

PC

phosphatidylcholine

POPC

1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine

RSE

rapid solvent exchange method.