Drug target interaction energies by the kernel energy method in aminoglycoside drugs and ribosomal A site RNA targets

Abstract

It is possible to use the full power of ab initio quantum mechanics in application to the interaction of drugs and their molecular targets. This idea had barely been realized until recently, because of the well known growth in computational difficulty of the use of quantum mechanics, with the number of atoms in the molecule to be studied. Because the biochemical molecules of medicinal chemistry are so often large, containing thousands or even tens of thousands of atoms, the computational difficulty of the full quantum problem had been prohibitive. Two things have happened, however, that change this perspective: (i) the advances of parallel supercomputers, and (ii) the discovery of a quantum formalism called quantum crystallography and the use of quantum kernels, a method that is well suited for parallel computation. Such advances would allow the quantum mechanical ab initio calculation of the molecular energy of peptides, proteins, DNA, and RNA, obtaining results of high accuracy. In this approach the computational difficulty of representing a molecule increases only modestly with the number of atoms. The calculations are simplified by adopting an acceptable approximation that allows a full biological molecule to be represented by smaller “kernels” of atoms. These results suggest that problems of medicinal chemistry, such as the rational design of drugs, may be illuminated by quantum mechanical analysis. The general case is illustrated by specific examples, namely, the HF/STO-3G calculations of three aminoglycoside drugs that attach to ribosomal A-site RNA nucleotide targets.

This article combines structural crystallographic information with quantum-mechanical theory. One goal is to show that the kernel energy method (KEM) is of practical use in the calculation of drug-target interaction energies. In particular, this is a challenging problem for the common case of very large molecular targets involving proteins, DNA, or RNA. Another objective is to simplify computational chemistry calculations and enhance the information that may be derived from a crystallographic experiment. This article focuses on example calculations of the interaction energies of individual drug-ribosomal RNA targets.

The KEM may be described as the determination of the quantum mechanical molecular energy by the use of the parts of a whole molecule, which are referred to as kernels. Because the kernels are much smaller than a full biological molecule, the calculations of kernels and double kernels are practicable. Subsequently, kernel contributions are summed in a manner affording an estimate of the energy for the whole molecule. Thus, the task of obtaining a quantum mechanical energy has been simplified for biological molecules as large as the various configurations of RNA, combined with drugs studied in this article. The computational time is much reduced by using the KEM, and the accuracy obtained appears to be quite satisfactory, as shown in previous work.

The first applications of the KEM (1) involved a large number of peptides of various shapes and sizes. These studies showed that the KEM that was applied to these molecules did so with good accuracy. The good accuracy was also retained throughout a wide range of basis functions and computational methods (2). Subsequently, the KEM was applied to the protein, insulin (3), various A, B, and Z DNA (4), and RNA (5), again achieving good accuracy and favorable results. The overall theoretical background for the application of quantum mechanics with crystallography may be found in refs. 6–13. References that review the quantum mechanical methods related to this work may be found in ref. 6.

This article is devoted to calculating the energy of various drug–RNA interactions. Only one each of the basis sets and computational methods that were previously tested within the KEM are applied. All calculations here use a limited basis and the Hartree-Fock approximation.

Review of the KEM

Given that the problem of drug-target interactions would be interesting to study by use of the techniques of quantum mechanics, the problem they present is often the considerable size of targets composed of proteins, DNA, and RNA. That is the problem addressed here, by using the KEM approximation, whose main features are now reviewed.

In the KEM, the results of x-ray crystallography are combined with those of quantum mechanics. This leads to a reduction of computational effort and an extraction of quantum information from the crystallography. Central to the KEM is the concept of the kernel. These are the quantum pieces into which the full molecule is mathematically broken. All quantum calculations are carried out on kernels and double kernels. Because the kernels are chosen to be smaller than a full biological molecule, the calculations are accomplished efficiently, and the computational time is much reduced. Subsequently, the properties of the full molecule are reconstructed from those of the kernels and double kernels. Thus a quantum realization of the aphorism that the whole is the sum of its parts is obtained.

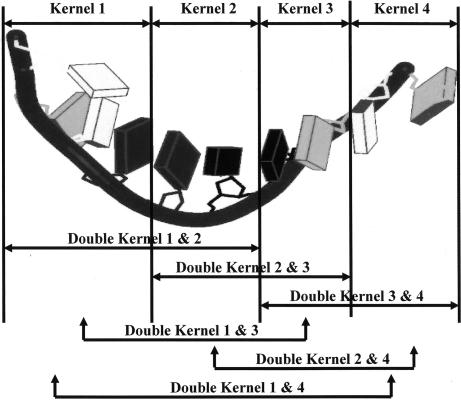
It is assumed that the crystal structure is known for a molecule under study. With known atomic coordinates, the molecule is mathematically broken into tractable pieces called kernels. The kernels are chosen such that each atom occurs in only one kernel. Schematically defined kernels and double kernels are shown in Fig. 1, and only these objects are used for all quantum calculations. The total molecular energy is reconstructed therefrom, by summation over the contributions of the double kernels reduced by those of any single kernels that have been overcounted.

Fig. 1.

An abstract sketch of RNA showing the definitions of the single and double kernels.

If all double kernels are included, the total energy is,

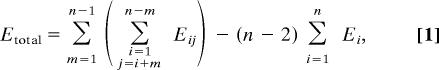where E_ij = energy of a double kernel of name ij, E_i is the energy of a single kernel of name i, i, j, and m are running indices, and n is the number of single kernels.

Here, Eq. 1 is applied to the calculation of the molecular interaction energies of three different amino glycoside drugs and their ribosomal RNA targets. The purpose of the calculations is to obtain kernel contributions to the energy when it is not computationally feasible to treat the entire drug–RNA target molecule, as a whole. When a structure of interest has known crystallographic coordinates, one may easily define kernels, which altogether represent the entire composite molecule. The use of the single kernels and double kernels is an approximation that is made to obtain a simplification in the quantum calculation. The validity of this approximation, in the case of a variety of peptides, proteins, DNA, and RNA structures, has been shown in previous work (1, 3–5). In this article we depend on the known ab initio accuracy of the KEM to show how it may be used to obtain drug–RNA target interaction energies. Such fundamental information, as we indicate below, can be used as the basis of rational drug design.

The Interaction Energy

The definition of the interaction energy between any pair of kernels is:

where, the subscript indices name the pair of kernels in question, I_ij is the pair interaction energy, E_ij is the energy of a double kernel, and E_i and E_j are the energies of a single kernel. The sign of the interaction energy, I_ij, indicates whether the kernels i and j attract (negative I) or repel (positive I). The total interaction energy is a sum of the pair interaction energies of the individual double kernels. The total drug-target interaction energy is:

where the sum is over all pairs of kernels belonging to a drug and its target. The magnitude of a given pair interaction energy I_ij determines its relative importance to the total drug-target interaction energy I_drug-target. The relative importance of each double kernel of given sign I_ij^± to the total interaction of the same sign I^± can be written as the fraction:

The sum of fractional interaction energies of either sign, by definition satisfy:

Knowledge of the list of the double kernel interaction energies is critical to rational drug design. That list determines the total drug–target interaction energy as well as the analysis of exactly which kernels contribute most importantly. Such knowledge may be obtained for the hundreds, or even thousands, of different chemical substitutions at various sites around the drug periphery, and the effect on the interaction between the drug and the target can be computed. Such computational information can effectively replace the perhaps thousands of laboratory synthesis experiments that would be needed to obtain related information. Moreover, it would be extremely difficult to obtain by experimental methods the double kernel interaction energies that flow naturally from implementation of the KEM to the problem.

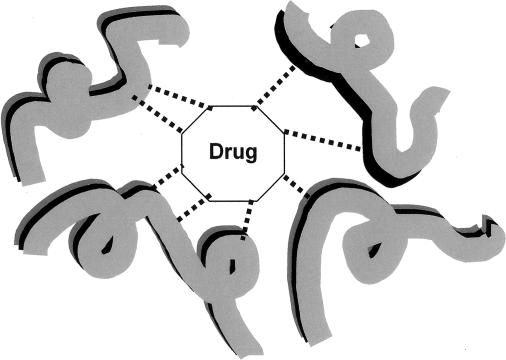
The importance of the interaction energy for rational drug design may be envisioned by consideration of Fig. 2. The efficacy of drugs is based on a geometrical “lock and key” fit of the drug to the target, complimented by an electronic interaction between the two. As indicated in Fig. 2 by dashed lines, there will be several interactions between the drug and the kernels that constitute its target. The KEM delivers the ab initio quantum mechanical interaction energy between the drug and its target. This is computationally practical for molecular targets containing even tens of thousands of atoms. That is the great advantage of using the KEM for rational drug design. Moreover not only is the total interaction energy obtained, so, too, as a natural consequence of the KEM approximation, are the individual kernel components of the interaction energy. That is to say, the interaction energy of the drug with each individual kernel in the target is obtained. Thus the contribution from each kernel to the efficacy of binding to the drug, which may be large or small, and attractive or repulsive, may be obtained. In this way the most important interactions between the drug and the kernels of the target become evident. Although not shown in Fig. 2, and not used in the calculations here, the drug itself can be broken into multiple kernels, and the relative importance of different portions of the drug's structure to total interaction energy can be assigned.

Fig. 2.

An abstract sketch indicating the interaction of a putative drug molecule with its target, a very large medicinal molecular structure. The drug fits geometrically within a reactive “pocket” of the target. The dashed lines indicate interactions with the various kernels that compose the target. The interaction may be either positive or negative, and both types of interaction (attractive and repulsive) are expected to occur.

Results

Antibiotic Drug in Complex (1O9M) with a Model Aminoacyl Site of the 30s Ribosomal Subunit.

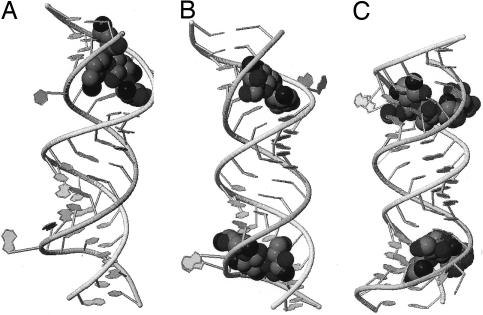
The ribosome is a well known target for antibiotic drugs. The crystal structure of one such drug, compound 2 of ref. 14, when attached to an A-site RNA construct is published in the Protein Data Bank as 1O9M and in the Nucleic Acid Database as ID DR0012, has been solved (14), and is shown in Fig. 3A. The solvent water molecules included in the crystal structure are not shown in Fig. 3. Using the crystal structure we calculate by the KEM the relevant energy quantities. These include the total energy of the complex made up of RNA, solvent, and drug, and the separate RNA, solvent, and drug molecules. We obtain interaction energies descriptive of the drug–RNA target interaction and the hydrogen-bonding network within the RNA molecule.

Fig. 3.

Pictures obtained by crystallography of RNA targets and the drugs compound 2 (14), complex named 1O9M (A), Tobramycin, complex named 1LC4 (B), and Lividomycin, complex named 2ESJ (C). In each case the RNA backbone is displayed as a ribbon, with nucleotide bases indicated as planes, and the drug is drawn as a space-filling figure.

In Table 1, we display the calculated energy results for the 1O9M drug–RNA target and solvent complex. The total complex consisting of 1,673 atoms has been “broken” into 16 kernels. Of these kernels, 1–14 represent the RNA target and kernel 15 represents the drug. The total energy of the complex is listed in Table 1. The number of atoms in the complex and the topological structure of the kernels is maintained, but the results differ according to atomic coordinates that are used for the calculations. In the first calculation all coordinates for nonhydrogen atoms are taken directly from the known crystal structure, and hydrogen atoms are attached to the heavy atoms automatically by using the computer program HyperChem. In the second case the crystallographic positions of the heavy atoms are maintained, and the hydrogen atom positions are energy-optimized by use of molecular mechanics within HyperChem. In a final optimization all atoms of the antibiotic drug are allowed to relax within the fixed field of all atoms of the RNA target. The total energy of the complex listed moves toward increasingly lower energy, with successive rounds of geometrical optimization. As must occur for an effective drug, the final optimization represents an attractive interaction between drug and target as discussed below.

Table 1.

Energy calculations by HF/STO-3G

Complex	EKEM*, au
1O9M, 1,673 atoms
Antibiotic/ RNA	−66,311.1086
Geometry optimization of hydrogen atoms	−66,385.7810
Geometry optimization of H, then H2O and antibiotic atoms	−66,386.3373
1LC4, 1,766 atoms
Ribonucleic acid	−68,724.7950
Geometry optimization of hydrogen atoms	−68,728.2160
Geometry optimization of tobramycin atoms	−68,728.1913
2ESJ, 1,844 atoms
Lividomycin–RNA	−71,946.4952
Geometry optimization of hydrogen atoms	−71,950.2442
Geometry optimization of lividomycin atoms	−71,950.5981

Geometry optimization was by mm⁺ (molecular mechanics).

*All double kernels are included. The energy includes the whole complex of RNA, drug, and solvent.

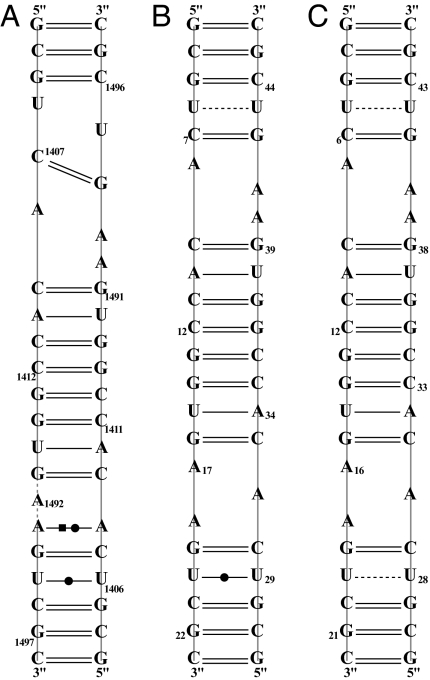
Fig. 4A is a picture of the hydrogen-bonding network in effect among the RNA nucleotide base pairs. The hydrogen-bond network here has been established experimentally from knowledge of the crystal structure and is based on the distances between hydrogen-bond donor and acceptor atoms. The important point is that each of the experimentally established hydrogen bonds must correspond to a negative interaction energy between the donor and acceptor components on either side of the hydrogen bond.

Fig. 4.

The RNA hydrogen-bonding network and the sequence identifications of the types of base pairs for 1O9M (A), 1LC4 (B), and 2ESJ (C).

Table 2 lists the 1O9M interaction energies associated with the experimental hydrogen-bonding network pictured in Fig. 4A. The first column indicates the kernels to which the base pairs belong, and the 1O9M column displays the calculated interaction energies between the kernels of a given double kernel. The hydrogen atom positions have been energy optimized. As must occur, if all hydrogen bonds considered are attractive, the interaction energies between the kernels are all negative. All H-bonding interactions, within the RNA target, must be negative, but the drug–RNA target interactions may be either positive or negative.

Table 2.

Double kernels and interaction energies between kernels corresponding to hydrogen-bonding pairs

Double kernel pair name	Interaction energy, au
	109M	1LC4	2ESJ
K1: K14	−0.116033	−0.095886	−0.081550
K2: K13	−0.041978	−0.024955	−0.044950
K3: K12	−0.054845	−0.060662	−0.045143
K3: K11	−0.032792	−0.029212	−0.045289
K4: K11	−0.081617	−0.076607	−0.071812
K4: K10	−0.045040	−0.045076	−0.046997
K5: K10	−0.013254	−0.035825	−0.047486
K6: K9	−0.012364	−0.024290	−0.048055
K7: K8	−0.047890	−0.047845	−0.093947

The coordinates of hydrogen atoms have been energy optimized. In supporting information (SI) Tables 4–6, the residue pair names are correlated with the double kernel pair names here.

The interaction energies between the drug kernel and the kernels of RNA are listed in SI Table 7. The hydrogen atom positions have been energy optimized. SI Table 7 lists the calculated KEM energies for each double kernel, each of its two single kernel components, each double kernel interaction energy, and it names the double kernels. The single kernels that make up the RNA target are numbered 1 to 14. The antibiotic drug is number 15. The bottom of SI Table 7 indicates the total drug-RNA target interaction energy.

Antibiotic in Complex (1LC4) with RNA Olignecleotide Containing the A-Site Sequence of the 30s Ribosomal Subunit.

A second drug compound that attacks the ribosomal RNA of the A site is 4,6- disubstituted 2-deoxystreptamine aminoglycoside tobramycin with the Protein Data Bank ID code 1LC4 (the Nucleic Acid Database ID code DR0007). The crystal structure of tobramycin complexed with the RNA olignecleotide containing the A-site sequence has been solved (15) and is shown in Fig. 3B. As before in case 1O9M above, we used the crystal structure to calculate by the KEM all of the relevant energy quantities, including total energies and interaction energies, which will be displayed.

In Table 1 are the calculated energy results for the 1LC4 drug RNA complex. This complex is composed of 1,766 atoms broken into 16 kernels. One of the kernels (kernel 15) is made up exclusively of atoms from the drug, and the remaining 14 kernels constitute the RNA of the A-site sequence. The total energy of the complex is listed. Table 1 shows results for crystal structure coordinates of the heavy atoms, with automatic hydrogen atom attachments as before, the optimization of hydrogen atom geometries, and the optimization of all of the drug's atomic coordinates.

In Fig. 4B we have the experimental hydrogen-bond network displayed in a similar manner to the analogous Fig. 4A for 1O9M. Each of the hydrogen bonds in Fig. 4B must correspond to an attractive interaction energy. Calculations show that is the case. The relevant interaction energies associated with the hydrogen bonds within the RNA molecule are shown in Table 2. The interaction energies between the drug kernel and the RNA kernels are given in SI Table 8, and the bottom of SI Table 8 gives the total interaction energy of drug and RNA target.

Antibiotic in Complex (2ESJ) with RNA Olignecleotides Containing the A-Site Sequence of the 30s Ribosomal Subunit.

Our final example (Lividomycin) of an aminoglycoside antibiotic complexed with oligonucleotides containing the decoding A site of ribosomes is that of 2ESJ (16) in the Protein Data Bank (Nucleic Acid Database ID code DR0022). The crystal structure of this case too has been solved, as we show in Fig. 3C, and has been used to calculate all relevant energy quantities with the KEM.

Table 1 contains the calculated energy results. In this case the number of atoms (1,884) is collected into 16 kernels. Notice the calculated energy is lowered with each case of increased optimization of atom coordinates. Fig. 4C displays the experimental hydrogen-bonding network associated with the RNA target molecule. Table 2 shows that the double kernels, corresponding to the RNA hydrogen bonds, all possess negative interaction energies, as required. The double kernel interaction energies are shown in Table 3. The total drug–RNA target interactions are attractive. SI Table 9 shows component contributions to double kernel interaction energies.

Table 3.

The interaction energy between drug and RNA target molecules

Kernel i–Kernel j (RNA–drug)	Iij, au
	109M	1LC4	2ESJ
1–15	0.001038	−0.003927	−0.006886
2–15	−0.007456	−0.007742	−0.008110
3–15	−0.001053	−0.001445	−0.003022
4–15	−0.000074	−0.000608	0.002682
5–15	−0.000026	0.000471	−0.001714
6–15	0.000263	0.010766	0.017184
7–15	0.000203	−0.000647	0.000150
8–15	−0.000201	−0.008514	−0.006457
9–15	0.000111	−0.002917	−0.019590
10–15	−0.000002	−0.000724	−0.003054
11–15	−0.000446	0.000105	−0.000525
12–15	−0.002968	0.000293	−0.009168
13–15	0.000189	0.013930	0.009784
14–15	−0.000818	−0.000703	0.000281
I (Drug–RNA)	−0.0112	−0.0017	-0.0284

Kernels 1–14 belong to RNA, kernel 15 is the drug molecule. In SI Tables 7–9 the calculated (double and single) kernel energies Eij, Ei, and Ej are correlated to the interaction energies Iij listed here.

Discussion and Conclusions

The drug and ribosomal RNA target molecules of this article were treated within the context of the ab initio Hartree-Fock approximation. The basis set used was a limited basis of Gaussian STO-3G type. A limited basis was chosen simply to make the energy calculations as convenient as possible. Previous numerical experience has shown that the KEM can be applied to a wide variety of molecular types with good accuracy. Therefore it is expected that such accuracy would apply in this instance.

We have shown how to begin with a crystal structure and obtain therefrom quantum mechanical information not otherwise known from the structure alone. Such information includes the energy of the structure, the interaction energy between a drug and its target, and the analysis of such interaction energy in terms of the contribution of each contributing kernel pair. Thus the relative importance of individual kernels to the drug interaction efficacy can be assessed. This forms the basis of rational drug improvement from use of a leading drug structure.

Let us, for example, assume the knowledge of a lead compound that displays the usual list of necessary properties including adsorption, distribution, metabolism, excretion, and toxicity. The critical factor that computational chemistry can contribute is the interaction energy between a putative drug and its target. If the target is a molecular structure containing thousands, or even tens of thousands of atoms, and if an ab initio quantum mechanical description of the interaction is to be obtained, then clearly an approximation such as that of the KEM is indicated. Thus, targets composed of peptides, proteins, DNA, RNA, and various of their molecular composites can contain enormous numbers of atoms. Because the straightforward computational difficulty of a fully quantum mechanical calculation rises in proportion to a high power of the number of atoms in the molecular system, such calculations have typically been computationally impractical. The use of the KEM alleviates such computational difficulty by means of a formalism that divides a large molecular system into kernels, which are much smaller than the molecular system considered as a whole. Computations with each of the kernels are thus a relatively smaller problem and can be assigned individually to separate nodes of a parallel processor. Thus a kind of 2-fold advantage accrues to the KEM, because individual calculations are piecewise smaller than otherwise, and they may be computed in parallel with modern computers designed for that purpose. The entire molecular system is reconstituted from a sum over kernels. What has been shown by the calculations here is that the KEM may be applied for purposes of rational design of drugs to the large molecules of medicinal chemistry. The examples used to make this point are three different drugs and their A-site ribosomal RNA targets. Ab initio results of expected high accuracy, within computational times of reasonable practicality, are obtained. Therefore, in general the KEM will be well suited for obtaining the interaction energy between drug molecules and their target medicinal chemical molecules of large size.

We turn now to the matter of the hydrogen-bonding network within the three RNA target molecules of this article. Those hydrogen-bonding networks have been established by crystallography (see Nucleic Acid Database, http://ndbserver.rutgers.edu/index.html, in Derivative Data: Hydrogen Bonding Classifications), based on the experimental distances between hydrogen-bonding donor and acceptor atoms. Adopting the experimentally established network allows one to substantiate the validity of the KEM method for description of the interaction energies that prevail between hydrogen-bonded kernels within these molecules. The interaction energy between a pair of kernels should be negative if that pair is stabilized by the presence of hydrogen bonds. Moreover the magnitude of the interaction energy would be a measure of the hydrogen-bonding stabilization. The interaction energies between pairs of kernels are data that are automatically generated in application of the KEM. Thus an examination of the interaction energies associated with the kernels related to the hydrogen bonding network of Fig. 4 are readily available. Table 2 lists all of the relevant interaction energies, arising from kernel pairs, which would contain the hydrogen bonds indicated in Fig. 4. In every instance, the interaction energy is negative, consistent with a stabilizing hydrogen-bonding interaction between the kernels. Thus the energetics available from the KEM finds independent qualitative confirmation in the experimental hydrogen-bonding network obtained from crystallography. This is important in that it provides confidence in the accuracy expected for the application of the KEM to calculation of the drug-target interaction energy, which is the main point of this article. That quantum mechanical energies are calculable, for large drug molecular complexes, has been demonstrated by the results of Table 1. And importantly, that the total interaction energies may be analyzed according to the individual contributions of each of the kernel pairs that make up the drug-target interaction is demonstrated by the results of Table 3. It is the availability of such analysis that would allow rational design of drugs based on the structure of a lead compound. Substitutions in the lead compound can be analyzed for their efficacy in contributing to an optimized interaction energy. The interaction energies give a direct indication of which target kernels are most important to the interaction with the drug, by either attractive or repulsive interactions. Both types of interaction can be important to the drug design. Testing by KEM calculation of hypothetical chemical substitutions on a lead compound might replace hundreds, or even thousands, of laboratory synthesis experiments. Moreover, direct access to the same interaction energies as obtained by the KEM would not be readily accessible by experimental means.

The results of Table 1 indicate the value of optimizing the hydrogen atom positions, which are not ordinarily given by the results of crystallography for the large structures of medicinal chemistry. The hydrogen atom positions may be optimized by energy minimization. Molecular mechanics may also be used, but in a more rigorous application a fully quantum mechanical optimization would be indicated. Table 1 also indicates that interaction energies are improved by having all atoms of a drug in their optimal positions within the field of the target atoms.

In previous work (1–5) we have shown the KEM provides an effective simplification in the task of solving the Schrödinger equation for the case of large biological molecules. The examples used to make this point included peptides, protein (insulin), DNA, and RNA (1, 3–5). A great saving of computational time is associated with the KEM, and high accuracy is achieved. These remarks hold true for any of the basis sets tested from limited size to very large size and for any of the quantum approximate models tested, including semiempirical, HF, DFT, MP2, CIS, and CCSD cases (2). Clearly, such successful applications associated with the KEM applied to the basic molecules of medicinal chemistry imply its usefulness for studying a variety of medical problems. The point of this article then is to demonstrate that the KEM can be useful for the rational design of drug molecules. To make this point we have calculated the interaction of three drugs with ribosomal RNA targets. These examples correspond to numerous atoms ranging from 1,673 to 1,884, and so it represents a seemingly difficult computational problem, which has been overcome by means of the KEM. The key ideas that result and are useful for drug design are the interaction energy between a drug and its large molecular target and all of the component interaction energies for the individual double kernels.

There is a point worth mentioning, in connection with the kernels and double kernels, as they are defined abstractly in Fig. 1. In the KEM the fragment calculations are carried out on double kernels and single kernels whose ruptured bonds have been mended by the attachment of H atoms. A satisfactory occurrence in the summation of energies is that the total contribution of hydrogen atoms introduced to saturate the broken bonds tends to zero. This happens because the effect on the energy of the hydrogen atoms added to the double kernels effectively cancels that of the hydrogen atoms added to the pure single kernels, which enter with opposite sign. This cancellation of the mending hydrogen atom energy effects contributes to the accuracy achieved by the KEM.

This article describes a case wherein the KEM was used to make ab initio calculations for drug–ribosomal RNA targets, whose size as measured in number of atoms, somewhat <2,000, would have made it inconvenient to calculate the molecules in their entirety. In future calculations molecular complexity will present many instances such that the capacity of presently available computers and computer programs is far exceeded. In such cases, the modestly increasing computer time as N (number of atoms) grows, which characterizes the KEM may be viewed as a valuable circumstance. In the KEM the molecule is not calculated as a whole. It is only the kernels and double kernels that are calculated, and they are chosen to be very much smaller than the whole molecule. Moreover, because the method constructs a whole from the sum of parts, it is especially suitable for parallel computation. Altogether, the results of this article show that the KEM makes practical the quantum mechanical study of drugs interacting with ribosomal RNA targets of considerable size.

The KEM suggested here for drug design would also apply with advantage to a host of other problems in which the object of calculation concerned the true quantum mechanics of large molecules. These include the rational design of proteins, the study of protein folding, and molecular self-assembly.

Abbreviation

KEM

kernel energy method.