Predicting protein–protein interactions based only on sequences information

Abstract

Protein–protein interactions (PPIs) are central to most biological processes. Although efforts have been devoted to the development of methodology for predicting PPIs and protein interaction networks, the application of most existing methods is limited because they need information about protein homology or the interaction marks of the protein partners. In the present work, we propose a method for PPI prediction using only the information of protein sequences. This method was developed based on a learning algorithm-support vector machine combined with a kernel function and a conjoint triad feature for describing amino acids. More than 16,000 diverse PPI pairs were used to construct the universal model. The prediction ability of our approach is better than that of other sequence-based PPI prediction methods because it is able to predict PPI networks. Different types of PPI networks have been effectively mapped with our method, suggesting that, even with only sequence information, this method could be applied to the exploration of networks for any newly discovered protein with unknown biological relativity. In addition, such supplementary experimental information can enhance the prediction ability of the method.

The molecular bases of cellular operations are sustained largely by different types of interactions among proteins. Thus, a major goal of functional genomics is to determine protein interaction networks for whole organisms (1). However, only recently has it become possible to combine the traditional study of proteins as isolated entities with the analysis of large protein interaction networks by using microarray and proteomic approaches (2, 3). Such kinds of studies are significantly important because many of the functions of complex systems seem to be more closely determined by their interactions rather than by the characteristics of their individual components (4). For example, metabolic pathways, signaling cascades, and transcription control processes involve complicated interaction networks (5). Recently, interaction networks have begun to be appreciated because it is necessary to address the general principles of biological systems by means of systems biology (6). Moreover, the study of protein interaction networks has been driven by potentially practical applications in drug discovery, because it might provide great insights into mechanisms of human diseases. This study may revolutionize the pipeline of drug discovery, because drugs discovered based on the protein interaction network may specifically modulate the disease-related pathway rather than simply inhibit or activate the functions of an individual target protein (7, 8). Determining accurate cellular protein interaction networks with experimental methods in combination with computational approaches therefore has become a major theme of functional genomics and proteomics efforts (9).

An impressive set of experimental techniques has been developed for the systematic analysis of protein–protein interactions (PPIs), including yeast two-hybrid-based methods (10), mass spectrometry (11), and protein chips (12) and hybrid approaches (13). Several binding reaction-detected methods, based on the presumption that the binding of one protein to another provokes a variety of biophysical changes, have been developed (14). These technologies recently identified hundreds of potentially interacting proteins and complexes in several species such as yeast (15), Drosophila (16), and Helicobacter pylori (17). Ulrich et al. (18) presented a large-scale two-hybrid map of >3,000 putative human PPIs. These data will serve as an important source of information regarding individual protein partners and offer preliminary insight into the global molecular organization of human cells.

However, current PPI pairs obtained with experimental methods cover only a fraction of the complete PPI networks (19). Therefore, computational methods for the prediction of PPIs have an important role (20). A number of computational methods have been developed for the prediction of PPIs. Computational methods based on genomic information, such as phylogenetic profiles, predict PPIs by accounting for the pattern of the presence or absence of a given gene in a set of genomes (21, 22). The main limitation of these approaches is that they can be applied only to completely sequenced genomes, which is the precondition to rule out the absence of a given gene. Similarly, they cannot be used with the essential proteins that are common to most organisms (23). The prediction of functional relationships between two proteins according to their corresponding adjacency of genes is another popular approach. This method is directly applicable only to bacteria, in which the genome order is relatively more relevant (24). Park et al. (25) tried to find protein interaction partners by viewing interactions between protein domains in terms of the interactions between structural families of evolutionarily related domains. Sprinzak and Margalit (26) put forward another indirect interaction prediction method, digging out signature feature related to interactions rather than domain interaction information from the protein sequences via protein classification. However, these methods are not universal, because the accuracy and reliability of these methods depend on the information of protein homology or interaction marks of the protein partners.

It is virtually axiomatic that “sequence specifies structure,” which gives rise to an assumption that knowledge of the amino acid sequence alone might be sufficient to estimate the interacting propensity between two proteins for a specific biological function (27). Accordingly, prediction of PPIs based only on sequence information is an ideal approach for both the computational and experimental senses. The advantage of such a method is that it is much more universal. However, it is a major challenge in computational biology, and only a few groups have engaged in the development of methodology for such a prediction approach. Joel and David (28) endeavored to solve this problem by using a machine learning method with several physiochemical descriptors. Loris (29) developed a fusion technique of classifiers to predict PPIs. Nevertheless, these methods are not robust and reliable because they have not adequately considered the local environments of the residues in the sequences. Moreover, the prediction models were constructed based on limited PPI pairs (<3,000 pairs) but with hundreds of variants. Therefore, on one hand, they are apt to encounter the problem of overfitting and results that are data-dependent; on the other hand, these methods have not been used to predict PPI networks among a great many proteins.

In the present work, a machine learning method based on a support vector machine (SVM) combined with a kernel function and a conjoint triad feature abstract was developed for the prediction of PPIs based only on the primary sequences of proteins. To reduce the problem of overfitting, >16,000 PPI pairs were used to generate the prediction models. The prediction results of our method are more robust than those of recently published sequence-based PPI prediction models (28, 29). Notably, different levels of networks of PPIs have been effectively reproduced with this approach, indicating that, even with only sequence information, this sequence-based approach could be applied to explore the networks for newly discovered proteins with unknown biological functions.

Results

Our method for PPI prediction was developed based on an SVM. The detailed procedure of an SVM can be found in refs. 30–34. In our approach, each protein sequence is represented by a vector space consisting of features of amino acids [supporting information (SI) Fig. 3], and the PPI pair is characterized by concatenating the two vector spaces of two individual proteins. To reduce the dimensions of vector space and suit synonymous mutation, the 20 amino acids were clustered into several classes according to their dipoles and volumes of the side chains. The conjoint triad method abstracts the features of protein pairs based on the classification of amino acids. A kernel function that is especially designed propitious to the symmetrical property of PPI has been adopted for binary classification on a large data set.

Classification of Amino Acids.

Electrostatic (including hydrogen bonding) and hydrophobic interactions dominate PPIs. These two kinds of interactions may be reflected by the dipoles and volumes of the side chains of amino acids, respectively. Accordingly, these two parameters were calculated, respectively, by using the density-functional theory method B3LYP/6–31G∗ and molecular modeling approach. The result is listed in SI Table 2. Based on the dipoles and volumes of the side chains, the 20 amino acids could be clustered into seven classes. Amino acids within the same class likely involve synonymous mutations because of their similar characteristics.

Conjoint Triad Method.

For predicting PPI by sequences, one of the main computational challenges is to find a suitable way to fully describe the important information of PPI. To solve this problem, we proposed a descriptor named conjoint triad, which considered the properties of one amino acid and its vicinal amino acids and regarded any three continuous amino acids as a unit. Thus, the triads can be differentiated according to the classes of amino acids, i.e., triads composed by three amino acids belonging to the same classes, such as ART and VKS, could be treated identically, because they may be considered to play similar roles while processing PPI. The PPI information of protein sequences can be projected into a homogeneous vector space by counting the frequencies of each triad type. The process of generating descriptor vectors is described as follows.

First, we use a binary space (V, F) to represent a protein sequence. Here, V is the vector space of the sequence features, and each feature (v_i) represents a sort of triad type; F is the frequency vector corresponding to V, and the value of the ith dimension of F (f_i) is the frequency of type v_i appearing in the protein sequence. For the amino acids that have been catalogued into seven classes, the size of V should be 7 × 7 × 7; thus, i = 1, 2, … 343. The detailed definition and description for (V, F) are illustrated in SI Fig. 3. Clearly, each protein has a corresponding F vector. However, the value of f_i correlates to the length (number of amino acids) of protein. In general, a long protein would have a large value of f_i, which complicates the comparison between two heterogeneous proteins. To solve this problem, we defined a new parameter, d_i, by normalizing f_i with Eq. 1:

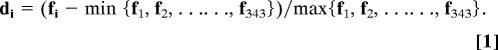The numerical value of d_i of each protein ranges from 0 to 1, which thereby enables the comparison between proteins. Accordingly, we obtain another vector space (designated D) consisting of d_i to represent protein. Next, we concatenate the vector spaces of two proteins (D_A and D_B) to represent their interaction features (D_AB) (Eq. 2):

Thus, a 686-dimensional vector [343 (for one protein) plus 343 (for another protein)] has been built to represent each protein pair.

Kernel Function.

The kernel function K(·,·) dominates the learning capability of the SVM. Considering the fact that PPI is symmetrical, i.e., {D_AB} and {D_BA} represent the same interaction pairs between proteins A and B, we designed a kernel function, K(D_AB, D_EF) (Eq. 3), which is denoted as a S-kernel function in the following:

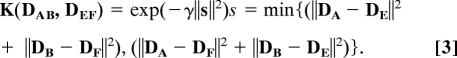SVM Parameter Optimization.

As in other multivariate statistical models, the performances of the SVM for classification depend on the combination of several parameters. In general, the SVM involves two classes of parameters: the capacity parameter C and kernel type K. C is a regularization parameter that controls the tradeoff between maximizing the margin and minimizing the training error. The kernel type K is another important parameter. In the S-kernel function used in this study (Eq. 3), γ is an important parameter to dominate the generalization ability of SVM by regulating the amplitude of the kernel function. Accordingly, two parameters, C and γ, should be optimized. The parameter optimization was performed by using a grid search approach within a limited range. To minimize the overfitting of the prediction model, 3-fold crossover validation was used to investigate the training set. Predict accuracy defined by Eq. 4 that is associated with mean-square-error was used to select the parameters:

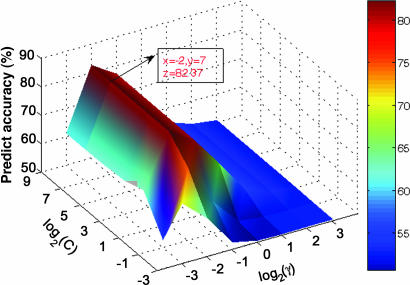
During SVM classification, each data point represents a protein pair (D_AB, y); if the protein pair is experimentally interactive, y is assigned 1, otherwise y is −1. Fig. 1 shows the profile of predicting the accuracy of the threefold crossover validation on the training set versus the variations of parameters C and γ. Obviously, the prediction accuracy profile has a maximum peak at (C, γ) = (128, 0.25), indicating that the optimal values of C and γ for constructing SVM models are 128 and 0.25, respectively.

Fig. 1.

Accuracy surface of threefold crossover validation on training set versus the variations of parameters C and γ.

Prediction Ability.

Using the optimal values of C and γ, the PPI prediction model was constructed based on the training set by using the SVM learning algorithm with the S-kernel function. To minimize data dependence on the prediction model, five training sets and five test sets were prepared by the sampling method described in Materials and Methods. Each training set consisted of 32,486 protein pairs; half of the protein pairs were randomly selected from the data of positive PPI pairs, and the other half were randomly selected from the negative protein pairs. Each test set was constructed with another 400 protein pairs. Thus, five prediction models were generated for the five sets of data. The prediction results are listed in Table 1. For all five models, the precisions are >82.23%, the sensitivities are >84.00%, and the prediction accuracies are >82.75%. On average, our method may produce a PPI prediction model with an accuracy of 83.90 ± 1.29%. To test the reliability of our S-kernel function, we also constructed PPI prediction models by using four other kernel functions, namely, radial basis, polynomial, sigmoid, and linear functions, on the same PPI data sets. The prediction accuracies of those four kernel functions were 80.5%, 72.9%, 50.0%, and 62%, respectively (SI Table 3). The results indicate that the prediction model constructed with our kernel function is more accurate than the models constructed with the other kernel functions. Considering the potential errors of gathering a large amount of PPI data from different sources and experimental errors, it can be concluded that the prediction ability of our method may compare with that of experiments like the yeast two-hybrid method. Moreover, the prediction models constructed by our method may be extended to predict PPIs encoded in a pairwise PPI network, as we demonstrate below.

Table 1.

Prediction results of the test sets

Test set	Accuracy, %	Precision, %	Sensitivity, %	Mean square error
1	84.25	84.42	84.50	0.63
2	82.75	83.59	84.00	0.69
3	83.25	84.82	85.50	0.67
4	83.25	82.23	84.00	0.67
5	86.00	86.00	86.00	0.56
Sum*	83.90 ± 1.29	84.21 ± 1.41	84.80 ± 0.91	0.64 ± 0.05

Precision is the true positive/(true positive + false positive). Sensitivity is the true positive/(true positive + false negative).

*Mean and variance are averaged by the results of five test sets.

Network Prediction.

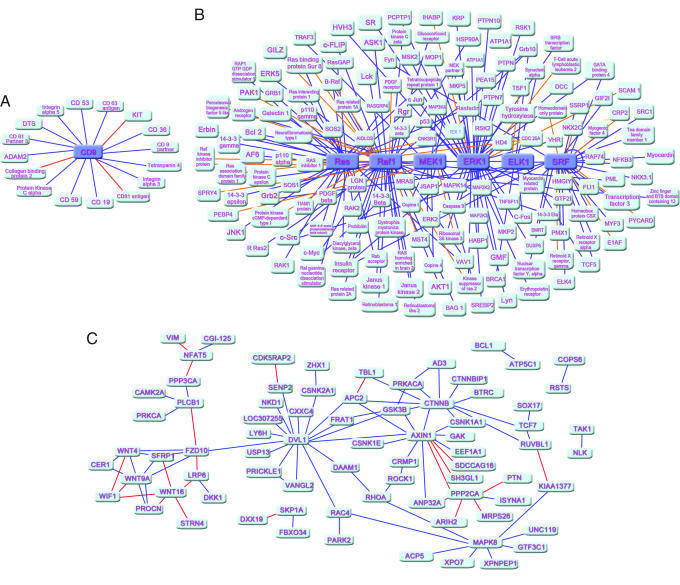
The most useful application of a PPI prediction method is its capability of predicting PPI networks. To our knowledge, PPI prediction methods based on protein sequences have not been reported in the application of network prediction. So, we extended our method to predict PPI networks assembled by pairwise PPIs. Three kinds of PPI networks have been predicted by our method: the one-core network, which is constructed by a core protein interacting with numerous other proteins (Fig. 2A); the multiple-core network consisting of an interacting pathway of several core proteins, which interact with other proteins (Fig. 2B); and the crossover network, which consists of several multiple-core networks and/or one-core networks with complicated interaction among these networks (Fig. 2C).

Fig. 2.

Predicted results of PPI networks of a one-core network for CD9 (A), a multicore network for the Ras-Raf-Mek-Erk-Elk-Srf pathway (B), and a crossover network for the Wnt-related pathway (C). Core and satellite proteins are colored indigo blue and light blue, respectively. Lines connecting core proteins and satellite proteins are divided into two classes: dark blue, true prediction; orange, false prediction.

The one-core network is the simplest because one protein radially interacts with other proteins. CD9, an important tetraspanin protein, interacts with many associated factors, forming a typical one-core network (35). The prediction result revealed that 13 of the 16 PPI pairs could be addressed by our method (Fig. 2A), indicating that this method is capable of digging out partners of a protein encoded in a network composed of pairwise PPIs.

The Ras-Raf-Mek-Erk-Elk-Srf pathway is a currently accepted consensus network that has been implicated in a variety of cellular processes (36). So far, >100 cytoplasmic proteins have been reported to be involved in this pathway connected by means of a typical multicore network. Ras, Raf, Mek, Erk, Elk, and Srf serve as core proteins, which determine the signal transduction. Of the 189 PPI pairs in this network, 161 PPI pairs were predicted correctly by our method (Fig. 2B). The distribution of false frequency for each core protein is listed in SI Table 4. This result suggests that our method also can be used to predict PPIs encoded in a more complicated network.

Biologically, general PPI networks are crossover networks. If a computational method can predict such networks, it should be useful in practical applications. The Wnt-related pathway is essential in signal transduction, and the related network is a typical crossover network, of which the protein interaction topology has recently been demonstrated by Ulrich et al. (18) using yeast two-hybrid experiments (18). To illustrate the capability of our method in predicting such networks, we tried to reproduce the network of Wnt. The prediction result showed that 73 interactions among the 96 PPI pairs in the network were covered by our method (Fig. 2C), suggesting that our method can be applied in the prediction of general PPI networks.

In practice, primary experimental information may be used in PPI network prediction. To test whether the additional experimental clues can enhance the prediction ability of our method, we repredicted the network of Ras-Raf-Mek-Erk-Elk-Srf pathway by adding the existing interaction information of 30% interaction pairs. Indeed, the additional experimental information can increase the prediction ability; the accuracy increased from 84% to 90% (SI Fig. 4).

Discussion

We have presented a computational approach for PPI prediction. The SVM learning algorithm was used to develop methodology. Notably, we advanced a strategy to construct the vector space (V) for representing the PPI information. The protein sequence was characterized by a conjoint triad descriptor, which considered the properties of each amino acid and its vicinal amino acids. The PPI information encoded in the protein sequences was projected into the vector space by calculating the frequencies of the conjoint triads (SI Fig. 3). Because the 20 amino acids have been catalogued into seven classes according to their physicochemical properties (SI Table 2), the dimensions of vector space could be dramatically reduced, from 20 × 20 × 20 to 7 × 7 × 7. Accordingly, the reduced variance dimension may partially overcome the overfitting problem, by which a good prediction model can be constructed based on even a limited amount of data (e.g., currently available data for PPI pairs). In addition, the conjoint triad descriptor implicitly includes the information of synonymous mutation for PPI, which widens the prediction range.

Threefold crossover validation was used to increase the prediction accuracy, and the two important parameters for SVM learning, C and γ, were optimized as 128 and 0.25 (Fig. 1). The prediction ability of our method was first evaluated five times on five test sets. The result indicates that this method may produce a stable prediction model with higher accuracy than other similar methods (Table 1) (26, 27). Moreover, the data set for constructing prediction models is much larger than others, suggesting that our prediction models are more reliable. Considering the symmetrical nature of PPI, i.e., A–B interaction equals B–A interaction, we designed a kernel function-symmetrical kernel function (S-kernel function) for the SVM (Eq. 3). The advantage of S-kernel function is obvious when comparing the prediction accuracy with other kernel functions (SI Table 3).

Accurately predicting PPI networks is the most important issue for PPI prediction methods. So far, PPI prediction methods based only on protein sequence information have not been applied to the prediction of PPI networks. We used such a method to predict networks composed of pairwise PPIs. The results indicate that our method may reproduce most of the PPIs encoded in three typical networks (Fig. 2). Most importantly, this method can be used to predict the most complicate PPI network, the crossover network (Fig. 2C).

Computation Environment.

All calculation programs implementing SVM were written in C++ based on the core of the libsvm 2.8 package (www.csie.ntu.edu.tw/∼cjlin/libsvm) and run on a 128-CPU Origin 3800 server (Silicon Graphics, Mountain View, CA).

Materials and Methods

Data Set Preparation.

PPI information was from the Human Protein References Database (HPRD), version 2005_0913 (www.hprd.org). This version of HPRD contains 16,443 nonredundant entries of experimentally verified PPIs obtained from a manual search of the literature. More than 95% of the interactions in the database are based on individual in vivo (e.g., coimmunoprecipitation) or in vitro (e.g., GST pull down) experiments (37). The data quality of this database is high enough for the construction of PPI prediction models. All of these PPI pairs were used in preparing the positive data set. The selection of a negative data set is essential to the reliability of the prediction model. However, it is difficult to generate such a data set because we have limited information about proteins that are really noninteractive. Unlike the random way for selecting a negative data set (38), we used a relatively rational strategy to select the negative data set, which was composed by the proteins appearing in the positive data set. Any protein pair appearing in the positive data set could be selected as a candidate for a negative pair in an exclusive way, for example, AB and IJ are positive interaction pairs, thus AI, AJ, BI, or BJ could be the negative pairs. Additionally, other requirements were considered: (i) the total number of negative pairs should equal that of the positive pairs (16,443 in this study) and (ii) the contribution of the proteins composing the negative set should be as harmonious as possible.

The training set consisted of 32,486 protein pairs, half from the positive data set and half from the negative date set. A test set was constructed with another 400 protein pairs. Both the positive and negative pairs were randomly selected.

Dipole and Volume Calculations.

The structures of the 20 amino acids were extracted from the standard fragment library of Insight2005 (Accelrys, San Diego, CA). Dipoles of the side chains of the amino acids were calculated by using the density-functional theory method of B3LYP/6–31G∗ encoded in Gaussian03 (39), and the volumes of the side chains were calculated by using Sybyl6.8 (Tripos, St. Louis, MO).

Prediction for PPI Networks.

The core protein in a one-core network was removed from the PPI data set, and the rest of the PPI proteins were used to build a prediction model with the optimal parameters. Afterward, PPIs between the core protein and satellite proteins were predicted by the prediction model. A similar method was used to construct prediction model for a multicore network by removing the core proteins from the PPI data set, and PPIs between the core proteins and satellite proteins were predicted by the model. For a crossover network, all proteins in the network were removed from the PPI data set during construction of the prediction model, and then PPIs in the network were predicted by the model.

Abbreviations

PPI

protein–protein interaction

SVM

support vector machine.