Mechano-electrical Transduction: New Insights into Old Ideas

Abstract

The gating-spring theory of hair cell mechanotransduction channel activation was first postulated over twenty years ago. The basic tenets of this hypothesis have been reaffirmed in hair cells from both auditory and vestibular systems and across species. In fact, the basic findings have been reproduced in every hair cell type tested. A great deal of information regarding the structural, mechanical, molecular and biophysical properties of the sensory hair bundle and the mechanotransducer channel has accumulated over the past twenty years. The goal of this review is to investigate new data, using the gating spring hypothesis as the framework for discussion. Mechanisms of channel gating are presented in reference to the need for a molecular gating spring or for tethering to the intra- or extracellular compartments. Dynamics of the sensory hair bundle and the presence of motor proteins are discussed in reference to passive contributions of the hair bundle to gating compliance. And finally, the molecular identity of the channel is discussed in reference to known intrinsic properties of the native transducer channel.

Introduction

Hair cells are specialized epithelial cells that serve as the mechanosensory cells of the inner ear. The apical surface consists of an array oflarge microvillae, called stereocilia, that together form the mechanosensory hair bundle. Mechanically-gated channels (MET) are located near the tops of these stereocilia. Channel gating and therefore the open probability is regulated by deflection of the hair bundle. It is widely assumed that the overall organization and function of the MET cellular mechanism is common to all hair cells. The basis for this general view comes from the characteristic staircase pattern of hair bundles (Fig. 1), the polarized directional sensitivity observed in all sensory hair bundles and the in vitro experiments showing that hair bundle deflection results in extremely rapid channel activation followed by bimodal adaptation, which reduces current amplitude. In addition, measurements of hair bundle stiffness during MET channel activation suggest a common spring-based mechanism for gating. Deciphering the properties of mechanotransduction intrinsic to the ion channel from those imparted onto the channel by accessory structures and the passive hair bundle properties is a challenge not yet totally realized. Similarly, there are difficulties in separating mechanical bundle responses that correspond to channel gating and the various forms of MET adaptation. Recent studies using multidisciplinary approaches reveal new details of the mechanism and a more complex picture for the MET machinery ensemble has emerged. Not all data collected from different hair cell types can be readily reconciled into a clear and common molecular model. Questions remain about fundamental properties of the gating and adaptation mechanisms, about the nature and identity of their constituent parts, and about the diversity of the ensemble in the different hair cell types. This article reviews the most current information on these issues, using the gating spring model as a theoretical frame-work of channel activation as the basis for discussion.

Fig. 1.

Hair bundles are dynamic structures that come in various sizes and shapes. (a–c) are scanning electron micrographs of cultured rat inner (a), mature rat outer (b) and mature mouse vestibular (c) hair bundles from rat. (d)isa transmission electron micrograph (TEM) where long arrows point to side links, short arrows to the rootlets (rt). CP is cuticular plate. The schematic of (e) shows the typical staircase pattern of hair bundles with the directionally sensitive placement of the tip-link. (f) TEM of the stereociliary pair shows the tenting on the apical surface of the stereocilia as well as the tip-links. Arrows indicate insertional plaques. The inset is a surface plot rendering of the freeze-etching view of the helical structure of the tip-link (from Kachar et al., 2000), made using the Image J image-processing program. (g) Schematic representation of the hair bundle depicting the active turnover process, termed treadmilling. (h) Schematic depicting the location of myosins, in particular the myosin XVa proposed to be critical in setting stereocilia height. Other myosins include myosin VI, VIIa and Ic.

Hair Bundle Structure

Initial treatment of the sensory hair bundle has been to consider it as a series of passive rods interconnected by an array of side-links (Fig. 1) (Tilney & Saunders, 1983; Furness & Hackney, 1985; Tilney, Tilney & DeRosier, 1987). Hair bundles pivot at the ankles and are thought to move as a unit (Crawford & Fettiplace, 1985). Size and shape of hair bundles are presumed to determine passive hair bundle properties such that tall bundles are more compliant than shorter hair bundles (Fig. 1)(Cotton & Grant, 2004; Silber et al., 2004). Side links are thought to bind stereocilia together and to be important in determining the overall hair bundle maturation and stiffness; however, there is limited evidence on the relative importance of the side links (Basthtanov et al. 2004; Michel et al., 2005).

The gating-spring theory separates hair bundle responses into a passive bundle component and a gating component contributed by the MET channel (Eq. 7). Is the bundle really passive? A variety of evidence would suggest the hair bundle is a dynamic structure constantly turning over and reshaping itself while maintaining its exquisite mechanosensitivity. To date, (Fig. 1) five myosin isoforms have been identified. Myosin XVa is present at the tops of the stereocilia and appears to be critical in regulating stereocilia height (Rzadzinska et al., 2004). Myosin VI and VIIa are localized along the stereocilia walls (Hasson et al., 1995). Myosin VIIa is thought to be related to the side-links, whereas VI has been observed in the stereocilia but also in a pericuticular necklace, where a role in endocytosis is implicated (Dance et al., 2004; Swiatecka-Urban et al., 2004). Myosin VIIa can alter the position of the MET activation curves, thus despite presumably not being located near the MET channel it can have dramatic effects on the process of transduction (Hasson et al., 1995; Richardson et al., 1997; Kros et al., 2002; Rhodes et al., 2004). The kinetics of myosin VII specialize it to generating and maintaining tension, thus implicating its role in maintaining tension between rows of stereocilia via the sidelinks (Henn & De La Cruz, 2005), suggesting a calcium-dependent regulation of interstereociliary connections. Myosin 1C has been observed in the stereocilia in some hair cells located in regions where MET channels are postulated (Garcia et al., 1998; Steyger, Gillespie & Baird, 1998). Genetic modifications of this isozyme have implicated it as a major component of the hair cell adaptation process (Holt et al., 2002). In addition to the number of identified myosin isozymes in or near the sensory hair bundle, the actin core of the stereocilia has also been shown to be very dynamic, turning over from top down at higher than expected rates (Rzadzinska et al., 2004; Lin, Schneider & Kachar, 2005). A picture is emerging that suggests the hair bundle is a dynamic entity constantly re-shaping itself in response to environmental stimuli. Understanding the mechanisms and regulation of this plasticity and its relationship to the functioning of mechanosensitivity is work for the future, but certainly present knowledge suggests the sensory hair bundle is much more complex than simple passive descriptions might indicate. In addition, recent modeling data indicate that the bundle may not simply rotate about its base but that there may be movement between stereocilia serving to recruit rows of stereocilia as the mechanical displacement is increased (Cotton & Grant, 2004; Silber et al., 2004). Despite the relatively simple description of the passive hair bundle presented below, the gating-spring theory adequately reproduces most published data.

Channel Gating

Despite the differences in size and shape of hair bundles, excitatory stimulation is consistently toward the tall edge and inhibitory stimulation is away from it (Fig. 1). A more complete description of directional sensitivity is that the MET response is proportional to the cosine of the angle away from the direction of maximal response (Shotwell, Jacobs & Hudspeth, 1981). A morphological correlate that can explain the polarization in sensitivity is the tip-link (Fig. 1) (Pickles, Comis & Osborne, 1984). The tip-link is located appropriately for exerting force onto the transducer channel and is found only along the axis of maximum sensitivity of the bundle (Pickles, 1993). Treatments that destroy the tip-link, like BAPTA, which lowers calcium concentrations (1 lM free calcium), result in a loss of mechanosensation and provide the only correlative data linking the MET channel and the tip-link (Assad, Shepherd & Corey, 1991). Of course we do not know whether such treatments cause other, as yet unknown ultrastructural changes. However, additional circumstantial evidence is the recovery of mechanosensation that has been linked to the recovery of the tip-link (Zhao, Yamoah & Gillespie, 1996). The mechanism by which the tip-link is lost remains a mystery, although Cadherin 23, a tip-link candidate, is known to form homomeric connections that are sensitive to external calcium levels. Recent data also questions what state the MET channel is in (i.e., open or closed) when the tip-link is destroyed (Meyer et al., 1998). Whether the tip-link is selectively removed from the hair bundle or additional side-links or cytoskeletal attachments are lost is also debatable. Because of the correlation between tip-link and MET current as well as the unique location of the link, it has been posited that the tip-link may serve to directly gate the MET channel (Fig. 2a), either being the physical correlate of the gating spring (see below) or directly being attached to the channel to be in series with this gating element (Pickles & Corey, 1992). Tip-links are approximately 200 nm long and 5 nm wide, existing in a coiled helical structure (Fig. 1) (Kachar et al., 2000). More recent arguments based on structural assessments indicate the tip-link does not have the appropriate elastic properties to be the gating spring, however, the possibility remains that the tip-link may be coupled to the channel (Kachar et al., 2000). Recent evidence has posited that Cadherin 23 (cdh23) is a component of the tip-link, at least during developmental stages (Siemens et al., 2004; Sollner et al., 2004). Models extrapolating from the crystal structure of a conserved domain of cdh23 suggest that the mechanical properties of cdh23 do not fulfill the requirements of the gating spring but it may still serve to deliver the stimulus to the channel (Sotomayor, Corey & Schulten, 2005). As the modeling included the most rigid portion of the cdh23 structure, further analysis incorporating multiple interconnected cdh23, as proposed for the tip-link, are needed to clarify its possible role as the gating spring. As cadherins are transmembrane proteins, if this protein is directly coupled to the MET channel one might expect it to be at an intracellular site (Fig. 2). Cdh23 has also been identified as a component of side-links, again at least during development (Michel et al., 2005). This same study and two others show a loss of immunoreactivity in the tip-link region during development so that it is undetectable in the mature animal (Boeda et al 2002, Lagziel et al., 2005, Michel et al., 2005). By contrast, other studies show that cdh23 is present in the adult (Siemens et al., 2004; Sollner et al., 2004, Rzadzinska et al., 2004). At present there is little doubt that there is a reduction in cdh23 expression in the hair bundle as it matures. It still remains to be fully clarified whether differential results described above are a function of sensitivity of the antibodies, the detection systems or whether they do really represent change in protein composition.

Fig. 2.

The mechanism of MET channel activation is unknown. These schematic representations illustrate that a variety of possible mechanisms exist. In each panel the arrow indicates the direction of the applied force. (A) shows the traditionally accepted view that the tip-link is directly associated with the MET channel and exerts force perpendicular to the membrane onto the channel. (B) demonstrates that the tip-link does not need to be associated with the channel but could simply exert force onto the lipid membrane. (C) similarly demonstrates that, dependent on geometry, the force exerted onto the lipid may be parallel to the lipid just as well as perpendicular. (D) further demonstrates that accessory structures like myosins may be linked to the membrane and not the channel. This configuration can produce adaptation. Neither existing data nor existing theoretical arguments can distinguish between these possibilities.

How then is the channel gated? Many mechanoreceptive channels sense the force translated via the membrane (Fig. 2). That is, the force is parallel to the plasma membrane and created in part by the energy differences between hydrophobic and hydrophilic interactions of channel protein and bilayer (Kung, 2005). In fact, many of these channels do not require tethering to either the cytoskeleton or to an extra-cellular stimulus (Fig. 2). In hair cells, the force is typically depicted as being translated perpendicular to the plasma membrane via a tether; the role of lipids has yet to be explored (Fig. 2). The channel is typically depicted as having connections to both the cytoskeleton via myosins and/or some other accessory proteins and to the extracellular matrix, via the tip-link (Gillespie & Corey, 1997). This hypothesis gained credibility with the identification of the tip-link, the concept being that tip-links pull on the channel or on the membrane where the channel is located (Hudspeth, 1989). However, no direct evidence exists to answer this basic question and the possibility that the force is translated to the membrane via the tip-link but to the channel via the plasma membrane still remains. An interaction between the channel and the plasma membrane becomes more appealing with the recent data suggesting the lipid composition of the stereocilia is specialized to contain large amounts of phosphatidylinositol 4,5-bisphosphate (PIP2), a lipid previously shown to associate directly with other mechanosensitive channels (Patel, Lazdunski & Honore, 2001; Hirono et al., 2004; Chemin et al., 2005). Of course, a third possibility is that the channel is not associated with the tip-link at all and that the correlation between tip-link loss and loss of mechanosensitivity is an epi-phenomenon, due to mechanical disruption of the hair bundle and not to some causative association. The gating-spring theory does not require tethering. Existing data does not separate between the possibilities portrayed schematically in Fig 2. Existing data and theoretical arguments cannot distinguish between force being exerted perpendicular or parallel to the membrane, between the tip-link being directly associated with the channel or simply being a lever applying force to the membrane. Indeed, a possible scenario exists in which the channel is untethered but where accessory proteins between the cytoskeleton and plasma membrane and between extracellular proteins and the plasma membrane regulate tension in this membrane and thus exert the force onto the channel. New experimental approaches are needed to resolve these fundamental issues.

Further confounding the issue of whether the MET channel is tethered to the tip-link, to the cytoskeleton or is nontethered, are data suggesting that when the tip-link is destroyed the MET channel can remain open (Meyer et al., 1998; Meyer et al., 2005) or it can close permanently (Assad et al., 1991; Crawford, Evans & Fettiplace, 1991; Zhao et al., 1996; Ricci, Crawford & Fettiplace, 2003). That both can occur might suggest the channel has coupling (whether direct or indirect) to both cytoskeletal and extracellular proteins and that both couplings can lead to channel gating albeit in different modes (Meyer et al., 2005). The channels then operate most effectively when both tethers are present but can operate in the absence of either. More experiments are required to evaluate this possibility in particular, focusing on mechanical correlates to the different modes of operation and perhaps on whether gating compliance varies depending on which linkages remain. An improved understanding of the mechanism of tip-link loss would add insight into its role in channel gating.

Channel Location

A further complexity in determining the mechanism by which MET channels are activated is the identification of the location of the MET channel. Significant data, based on extracellular current flow, sensitivity to local application of antagonists and calcium imaging suggest the channels are located near the tops of the stereocilia (Hudspeth, 1982; Jaramillo & Hudspeth, 1991; Denk et al., 1995; Lumpkin & Hudspeth, 1995). Identification of the tip-link led to the suggestion that the channels might be located at either or both ends of this tip-link. Structural investigations of the tip-link suggested the channels may be located only on the tops of the shorter stereocilia based on the manner in which the protein inserts into the membrane (Kachar et al., 2000). This top location also seems likely given the tenting of the membrane often observed in electron micrographs (see Fig. 1), suggesting force exertion at this site. However, present theories regarding mechanisms of slow adaptation require some channels to be located on the sides of the stereocilia so that putative motor molecules can move along the actin filaments (myosin would not be able to climb the actin if it were at the top of the stereocilia) (Holt et al., 2002). Two-photon calcium imaging supports the hypothesis that channels are located at both ends of the tip-link (Denk et al., 1995). This positioning would predict a negative cooperativity between channels upon activation (due to gating compliance, see below), and would also require adaptation motors associated with one channel to drive adaptation for at least two. At present, evidence does not exist for either of these possibilities.

A third possibility for channel location is at a region slightly below the tip-link where the stereocilia of adjacent rows come into close proximity of one another. Antibody staining for the amiloride-sensitive component of this channel provides the major evidence for this location (Hackney et al., 1992). This location would also account for the calcium imaging results (Denk et al., 1995). In this case, the tip-link may be necessary to keep the stereocilia in close approximation rather than directly stimulating the MET channels. Here, the mechanism of channel stimulation—tether vs. stretch—is less clear. This work however, remains to be confirmed to at least demonstrate staining across species or end organs.

Gating-Spring Identity

Regardless of how force is translated to the MET channel, it must be fast. Both indirect (Corey & Hudspeth, 1983b) and direct (Crawford, Evans & Fettiplace, 1989; Ricci et al., 2005) evidence demonstrated activation kinetics to be at least in the microsecond range. Attempts at measuring activation kinetics from mammalian hair cells (at room temperature), failed due to the channel kinetics being faster than the stimulus rise-time (indicating kinetics faster than 10 lsec) (Ricci et al., 2005). The rapid kinetics limit possible mechanisms of activation and have focused attention on direct coupling of force to a mechanically gated channel. The gating-spring theory suggests that a) an elastic element couples force to the MET channel and b) upon opening, the channel's gate in series with the spring reduces bundle stiffness (Fig. 3). But what is the gating spring? Initial hypotheses suggested the tip-link could serve this purpose but as mentioned previously, structural investigations and modeling suggest the stiffness of the link and its elasticity do not match the needed parameters (Kachar et al., 2000; Sotomayor et al., 2005). The possible identification of a channel subunit has led to a new hypothesis. Transient receptor potential (TRP)-candidates proposed for the transducer channel (TRPN1, Sidi, Friedrich & Nicolson, 2003); TPRA1, (Corey et al., 2004; but see Shin et al., 2005) may intrinsically provide the right elastic engagement via their ankyrin repeats located at their intracellular N-termini (Howard & Bechstedt, 2004). The number of ankyrin repeats (TRPN1, 29 and TPRA1 17; Sotomayer et al., 2005) are just appropriate for forming superhelical structures making up a complete, or at least a significant part of a curved loop that may have a stiffness comparable to that of the gating spring (1 mN/m; Howard & Bechstedt, 2004; Sotomayer et al., 2005). This correlation must be interpreted carefully though, given the large number of free parameters in both the estimates regarding ankyrin and in the measurements of gating-spring stiffness. For example, the values cited refer to a single subunit possessing an ankyrin repeat, while it is likely that the channel is made of at least four subunits. Also heteromeric channels are likely, given tonotopic differences in channel properties (Ricci et al., 2003). The number of repeats has dramatic effects on the estimated stiffness where 17 repeats is significantly more stiff than 29. Given that multiple subunits with multiple length repeats are possible, the potential combinations for gating are considerable (Sotomayor et al., 2005). As will be shown, gating-spring stiffness estimates are based on channels being equal and summing linearly, while data in support of this are limited and if inaccurate may significantly underestimate gating-spring stiffness.

Fig. 3.

Voltage-clamp recordings of mechanoelectric transduction currents and hair bundle movements that underlie the gating-spring theory. (A) Upper panel shows mechanical stimulus paradigm and lower panel, MET currents obtained from a hair cell in response to flexible fiber stimulation. (B) Measured hair bundle motion in response to force stimulation. Note the notch at the onset and the slower increase in movement with larger stimuli. (C) Plotting the applied force against displacement at the timepoint of peak current response results in a nonlinear plot that underlies the gating-spring hypothesis. The region of minimal slope corresponds to the steepest portion of the MET activation plot (D) and indicates a reduction in hair bundle stiffness at these positions. (D) Differentiating the force plot results in a stiffness plot (blue trace) that clearly shows a minimum in stiffness that correlates well with the steepest portion of the activation plot. Note that the stiffness axis start is nonzero. A single Boltzmann function was used to fit the activation plot (see Eq 3).

A final question mark surrounds whether ankyrin repeats are involved in gating of these TRP channels. A possibility not yet considered is that the ankyrin repeats serve as the extent spring (Shepherd & Corey, 1994). This concept was first developed to provide a mechanical correlate to data, suggesting that adaptation was not complete (Fig. 3). The extent spring was thought to be an additional link between the channel and the cytoskeleton that limited the distance traveled by the channel. If a mechanical correlate to this extent spring exists, the ankyrin repeats are as good a candidate for that role as they are for the gating spring. Nonetheless, if TRP channels containing ankyrin repeats are involved in mechanotransduction, identifying the function of these repeats, whether it be as a gating spring, an extent spring, or simply a structural element, is critical. As stated earlier, it remains to be explored whether the gating spring may be part of the lipid environment or of the hair bundle architecture rather than being directly associated with the MET channel.

Gating-Spring Model

Whatever the identity of the gating spring, or its precise mode of engagement of the transducer channel (Kung, 2005; Lin & Corey, 2005), its biophysical consequences are well understood and may explain many observed properties of the transduction process in hair cells. Tension in the gating spring, resulting from the deflection of a hair bundle, is then transferred onto the transducer channels. The gating-spring theory was developed to explain data in which activation of MET channels results in a reduction in hair bundle stiffness (Fig. 3). Figure 3 demonstrates that a reduction in stiffness corresponds to the steepest portion of MET channel activation. The data also demonstrates a linear (Hookean) force displacement plot for regions where all channels are open or closed.

Two- and three state models of the MET channel, based on the idea of gating-spring activation, describe how free energy differences between closed and open states depend on the displacement of the hair bundle by modulating the potential energy of the elastic gating-spring that, in its most simple version, obeys Hooke's law (Corey & Hudspeth, 1983b). Other properties for the gating spring have been proposed (Sachs & Lecar, 1991; Markin & Hudspeth, 1995), but so far no clear experimental evidence is available to justify more complex engaging models (cf. Regan, 1994). The gating-spring model has been formulated for three-state models of the transducer channel (Corey & Hudspeth, 1983b; Markin & Hudspeth, 1995) and also in relation to differential activation caused by a slack gating spring (van Netten & Kros, 2000). However, here only the two-state case, having one open and one closed state, is presented, as it exhibits most of the salient features of the gating-spring model. In the two-state model, the free energy of each state (A_o,c for the open, resp. closed state) has, in addition to its intrinsic state energy, (ε_o,c for the open, resp. closed state) a contribution formed by the potential energy, which is proportional to the gating spring constant, k_gs, and to the square of the gating spring's extension, x (Fig. 4, cf. Corey & Hudspeth, 1983b; Howard & Hudspeth, 1988):

$$A_{\mathrm{c}}=\frac{1}{2}{k}_{\mathrm{gs}}{(x+d)}^2+{\epsilon }_{\mathrm{c}},x>x_c$$ (1a)

$$A_{\mathrm{o}}=\frac{1}{2}{k}_{\mathrm{gs}}{x}^2+{\epsilon }_{\mathrm{o}},x>x_o$$ (1b)

A transition between the discrete states is assumed here to be related to a displacement swing, d, at the site of the channel where the gating spring engages. Energy differences between the two states, ΔA, can then be seen from Eqs. 1 to be linearly related to the extension of the gating spring x:

$$\Delta A=A_{\mathrm{c}}-A_{\mathrm{o}}=z\cdot (x-x_0),$$

where the product of gating-spring constant, k_gs and swing of the channel, z = k_gsd termed gating force is used. The position, x₀, at which the open probability is 0.5, is given by x₀ = (ε_o − ε_c)/z + (x_o + x_c)/2, where x_c and x_o are the position at which the closed and open states are engaged respectively (Fig. 4–model). If the ratio of probability of the open to that of the closed state is governed by the Boltzmann-factor, implying that p_o/(1 − p_o = exp (ΔA/kT), the open probability of the channel, p_o, can be derived and is a single Boltzmann function:

$$p_{\mathrm{o}}=1∕(1+\exp (-z(x-x_0)∕\mathit{kT})$$ (2)

Fig. 4.

Mechanical and electrical properties of a two-state gating spring model of the MET channel. (A) Free energies as a function of hair bundle position of the two states. A_o is the free energy of the open state (dashed line) and A_c that of the closed state (dash-dotted line). The channels average free energy A_ch (continuous line;) A_ch = p_oA_o + p_cA_c). The energy specifically related to gating is indicated as A_g (dotted line). Note that A_ch also equals A_ch = A_o + A_g (Eq. 4). The closed state is engaged at, X ≥ X_c; whereas the open state is activated at X ≥ X_o. (B) Forces acting on a single transduction channel, as resulting from the free energies shown in (A) F_ch = dA_ch/dX is the sum of F_o = dA_o/dX and F_g = dA_g/dX (C) Stiffness resulting from forces depicted in (B). S_ch = dF_ch/dX is the sum of S_o = dF_o/dX and S_g = dF_g/dX. The gating compliance is the reduction of S_ch with respect to k_gs. (D) Open probability as obtained from the free energy difference of A_c and A_o (Eqs. 3 and 4). Parameters: ε_o = 3.5 kT; ε_o = 0 kT; ; X_o = −30 nm; X_c = −5 nm, so that D = X_o − X_c = 25 nm; k_gs = 10 μN/m.

Lever Action of the Hair Bundle and Operational Range

To interpret the open probability of Eq. 2 in terms of displacements of the hair bundle, X, from its equilibrium position, a linear geometrical relationship between bundle displacement, X, and tip link extension, x, is usually assumed (x = γX; Howard & Hudspeth, 1988). Based on the idea of hair-bundle force transferring via their almost parallel directed tip-links, in saccular hair cells γ is estimated to be about 0.1–0.15 (Markin & Hudspeth, 1995) while in mammalian hair cells more widely ranging values have been reported (OHC's: 0.05–1.0; VHC s: 0.02–0.04; Geisler, 1993; Pickles, 1993; Markin & Hudspeth, 1995; van Netten & Kros, 2000). Since γ is usually smaller than 1, a lever function is therefore effectively employed. A displacement reduction is then accompanied by a force multiplication with the same factor, if comparing properties at the site of the gating molecule and at the hair bundle's tip. Reserving capitals for parameters as sensed at the bundle level, and small fonts for those at the molecular level, the molecular gating force, z = k_gsd = Z/γ, where Z denotes the gating force measured at the hair bundle's tip. Energy should be the same in both frames of reference so that ZX = K_gsD · X = k_gsd · x = zx with the consequence that K_gs = k_gsγ². The open probability in terms of parameters Z, X and X₀, measured at the hair bundle's tip is therefore:

$$p_0=1∕(1+\exp (-Z(X-X_0))∕\mathit{kT}).$$ (3)

This concise description of modulation of open probability with hair bundle displacement reflects several basic features observed in measured transducer currents. First, the open probability changes sigmoidally with hair bundle displacement (Fig. 3). As follows from Eq. 3, open probability changes approximately 75% around the set point, X₀ on the displacement axis within a space constant or operational displacement range given by Λ₇₅ = 4kT/Z, (Markin & Hudspeth, 1995), or alternatively, if about 90% modulation is achieved the bundle moves within an operational range given by: Λ₉₀ = 6kT/Z (van Netten et al., 2003). Using the values of the gating forces (tens to hundreds of femto-Newton, (see section on Gating Forces) the model predicts operational ranges of hair bundle displacement in the range of 100 nm to several micrometers (Fig. 3).

Consequences of Thermal Activation

The probabilistic nature of the gating-spring model, which stems from thermodynamic equilibrium between a molecular channel, gating spring and their surroundings, does not impose an intrinsic threshold on transduction (Corey & Hudspeth, 1983a). Thermal energy is enough to overcome the energy barriers between open and closed states. This stochastically induced thermal activation may be advantageous in serving to enhance “hopping” between conformational states (Jaramillo & Wiesenfeld, 1998). Slight modulation of the energy levels of the states of the channel is already enough to evoke a small change in open probability, so that no threshold energy in the strict sense can be defined for transduction. Never-theless, several measures of energy can be defined in the gating process. Since the modulation of the energy levels must compete with thermal energy, which equals kT/2 per degree of freedom, we may expect the relevant energy levels of gating to be of the same order of magnitude as kT, which is equivalent to about 4.1·10⁻²¹ (J) at room temperature. Relevant distances at the level of the channel will be of molecular dimensions, which are on the order of nanometers. The magnitude of the forces relevant for gating of a channel can therefore be predicted to be approximately kT10⁻⁹ (m) (pico-Newton). If forces of this magnitude act over nanometer distances, the typical stiffnesses to be expected are then of the order of pN/nm. In the following sections a systematic approach is given in terms of the energies and forces related to gating within the context of the gating spring model. These quantities will all be shown to be within the realm of thermal noise energy dictated values.

Energy Related to Gating

An important property of the gating process is the energy associated with it. Several definitions may be used. A more general thermodynamic treatment of the activation of the transducer channel than given above (Howard & Hudspeth, 1988; leading to Eq. 3) allows defining its (Helmholtz) free energy, A_ch, in terms of the open probability p₀ of the channel (van Netten & Kros, 2000):

$$A_{\mathrm{ch}}=A_{\mathrm{o}}+\mathit{kT}\ln \left(p_{\mathrm{o}}\right)$$ (4)

This result can be obtained from a minimal number of assumptions and is independent of the number of closed conformational states assumed in the activation model. In the case of a Hookean gating spring engaging the two-state channel, the first term is A_o =½K_gsX² + ε_o, as assumed in Eq. 1b. The variation in the potential energy (A_o, Eq. 1b) of the gating spring depends on its stiffness, and the excursions that the bundle makes. For an estimate of these excursions we may use the operational range Λ₉₀ = 6kT/Z. Using average values of 10 μN/m for the gating's spring stiffness, K_gs, and 25 nm for the swing of the channel, D (Howard & Hudspeth, 1988; van Netten & Kros, 2000; van Netten et al., 2003), K_gsD² equals about 1.5 kT and the related change in potential energy is then $\Delta A_{o,90}=\raisebox{1ex}{${\left(6\mathit{kT}\right)}^2$}\!\left/ \!\raisebox{-1ex}{$\left(2K_{\mathit{gs}}{D}^2\right)$}\right.\approx 12\mathit{kT}$. The free energy of a channel described by the second term of Eq. 4 is proportional to the logarithm of open probability, thereby defining a measure of the free energy difference involved in the gating process. It is clear from Eq. 4 that the numerical value of this second term is critically dependent on the extent of modulation of the open probability, p_o. Several investigations indicated that the elastic gating elements may slacken for (fast) negative hair bundle deflections (Assad & Corey, 1992; Hudspeth, 1992; van Netten & Kros, 2000); implicating that the open probability does not decrease beyond a certain value, contrary to what is found in voltage-gated channels (e.g. (Bezanilla & Stefani, 1994). Lower values of absolute open probability are difficult to obtain from whole-cell patch-clamp recordings. From such measurements, in which only a single channel was operational, a limiting lower value of the open probability was estimated in outer hair cells to be about one hundredth (van Netten & Kros, 2000). This means that the gating-related term of the free energy is modulated within a range of 0.01 to 1, corresponding to a gating-related free energy of about 5 kT. Total variations in the free energy, ΔA_ch, in the channel-spring complex may consequently vary in the range of tens of kT, and are obviously dominated by the potential energy variations in the gating spring, ΔA_o,90.

A different definition of the energy related to gating, ZX₀ has been used to characterize stretch-sensitive (MS) channels (e.g., Kloda & Martinac, 2001). Applying this alternative definition to frog saccular- (Howard & Hudspeth, 1988) and mammalian cochlear hair cells (van Netten & Kros, 2000) resulted in a range of about 1.5 to 1.9 kT. Using this definition, hair cells seem to require less free energy of activation than non-vertebrate MS-channels, which, depending on the type investigated, may have values ranging from 5 to > 30 kT.

Forces Related to Gating

Measurements of hair bundle mechanical properties have largely been made with flexible fibers, (Fig. 3) whose stiffness is comparable to that of the hair bundle (Strelioff & Flock, 1984; Crawford & Fettiplace, 1985; Howard & Ashmore, 1986; Ricci, Crawford & Fettiplace, 2002; Kennedy, Crawford & Fettiplace, 2005). Stiffness is a hair bundle's dominant mechanical impedance component as it resets its position after a stimulation to be ready for the next. Asymmetric forces in the excitatory and inhibitory direction of cochlear hair cells were reported (Strelioff & Flock, 1984) but it was not until observations were made on frog hair cells that a clear link between bundle forces and mechanical gating of the transducer channels was suggested (Howard & Hudspeth, 1988). Hair bundles stepped into the excitatory direction moved transiently toward the short edge of the bundle, implying a reduced force was required to move the bundle, force being dependent on stimulus magnitude. Thus, if the forces during this movement are plotted versus the bundle's step size a nonlinear relationship is found (Fig. 3). Nonlinearity of the force-displacement relation could be abolished by aminoglycosides, known open channel blockers (Kroese, Das & Hudspeth, 1989; Denk, Keolian & Webb, 1992; Ricci, 2002; Marcotti, van Netten & Kros, 2005). The prediction is that, when present in the (open) channel pore, these molecules effectively prevent a channel from making a conformational swing to the closed position.

The observed nonlinear force relationship is predicted by the gating spring model when considering the averaged tension in the gating spring in the two conditions, open and closed, weighted with their respective probability (Howard Hudspeth, 1988)(Fig. 3). A more straightforward approach results from again considering the free energy A_ch (Eq. 4) of a channel-spring complex. Differentiating the free energy A_ch, (4), with respect to bundle position, X, yields the force on the channel, F_ch:

$$F_{\mathrm{ch}}\left(X\right)=\frac{{\mathit{dA}}_{\mathrm{ch}}}{\mathit{dX}}=K_{\mathrm{gs}}X+\mathit{kT}\frac{d\ln \left(p_{\mathrm{o}}\left(X\right)\right)}{\mathit{dX}}.$$ (5a)

The first term expresses the tension in a single gating spring when the channel is in its open conformational state (cf. Eq. 1b) while the second term is the force related to gating. Equation 5a can equally well be used for describing gating forces in multi-kinetic state models. It also provides a straightforward way to estimate gating forces from experimentally determined p_o-X curves. Using the expression for open probability of the two-state model defined in Eq. 3 the gating-related (second) term of Eq. 5a can be readily evaluated, so that the force on a single channel can be written as:

$$F_{\mathrm{ch}}\left(X\right)=K_{\mathrm{gs}}X+Z(1-p_{\mathrm{o}}\left(X\right))$$ (5b)

. This shows that the contribution to the force, as resulting from gating (second term) has a maximum value Z (when p₀ = 0), clearly reflecting the previously defined gating force (e.g., Eq. 3). The magnitude of molecular gating forces, Z, as obtained from fitting the gating-spring model, are of the order of tens to hundreds of fN (Russell & Kossl, 1992; Jaramillo & Hudspeth, 1993; Markin & Hudspeth, 1995; van Netten & Kros, 2000), which, when considering the lever action of the hair bundle, corresponds at the molecular level to forces (z) of up to the order of ten pico-Newtons and are thus comparable to those found to move the transmembrane voltage sensors that gate Na⁺ channels (French et al., 1996) or unbind motor molecules (Nishizaka et al., 1995), while they present lower values found for receptor-ligand bonds (Merkel et al., 1999). Recently much larger gating forces have been observed in rat outer hair cells, forces that are more difficult to explain by a simple gating process (Kennedy et al., 2005).

Altogether it may be concluded that the mechanisms of hair cell transduction and the forces related to them do not yet converge to a comprehensive picture. Whether discrepancies are due to technical differences, species differences or, more interestingly, differences in the inherent frequency responses of hair cells being investigated remains to be determined.

Gating Compliance

The nonlinear relationship of force-displacement curves can also be expressed in terms of stiffness, which is the derivative with respect to bundle displacement, X, of the force on a transducer channel, F_ch(X) (Eq. 5b), and therefore equals the second order derivative of the free energy:

$$S_{\mathrm{ch}}\left(X\right)=\frac{{\mathit{dF}}_{\mathrm{ch}}}{\mathit{dX}}=\frac{d^2{A}_{\mathrm{ch}}}{{\mathit{dX}}^2}=K_{\mathrm{gs}}+\mathit{kT}\left(\frac{d^2\ln p_o}{{\mathit{dX}}^2}\right).$$ (6a)

Equation 6 holds for multi-state models, but when applied to the two-state model we can use Eq. 5b and take the derivative to X to get the stiffness of a single channel-spring complex:

$$S_{\mathrm{ch}}\left(X\right)=K_{\mathrm{gs}}-Z^2{p}_{\mathrm{o}}\left(X\right)(1-p_{\mathrm{o}}\left(X\right))∕\mathit{kT}.$$ (6b)

If a hair cell contains N_ch identical operational channels which are mechanically acting in parallel, the contribution to the hair bundle is N_ch multiplied by S_ch(X), so that the stiffness of a hair bundle may be expressed as:

$$\begin{array}{cc}\hfill S_{\mathrm{hb}}\left(X\right)=& S_{\mathrm{piv}}+N_{\mathrm{ch}}{K}_{\mathrm{gs}}-N_{\mathrm{ch}}{Z}^2{p}_{\mathrm{o}}\left(X\right)\hfill \\ \hfill & (1-p_{\mathrm{o}}\left(X\right))∕\mathit{kT}.\hfill \end{array}$$ (7)

Here S_piv denotes the stiffness of passive components (see Discussion below), most likely resulting from the stereociliar pivots (Crawford & Fettiplace, 1985) and other interstereociliar cross links of a single hair bundle. Its constant value sums to the constant contribution of N_ch gating springs (second term). The third term describes the so-called gating compliance. It is a reduction in stiffness and can be considered a mechanical analogue of the gating charge associated with voltage-dependent channels. Since its first observation in frog saccular hair cells (Howard & Hudspeth, 1988) it has also been experimentally demonstrated in mammalian outer and vestibular hair cells (Russell & Kossl, 1992; Geleoc et al., 1997), the overall cupular dynamics governed by hair cells in the fish lateral line organ (van Netten & Khanna, 1994), and in turtle hair cells (Ricci et al., 2002). In the latter case, though, the existence of other force components in the hair bundle may have contributed to the decrease in stiffness, as the reduction in stiffness could not fully be explained by the gating-spring model. It can be seen from Eq. 7 that the minimum value of S_hb is reached if p_o = 0:5 (at X = X₀), thus reducing the stiffness with an extent equal to N_chZ²/ (4kT), which amounts to fractions of a 0.6 mN/m, assuming Z = 350 fN, and N_ch = 80). The simplifying assumption that the MET channels exist in parallel and are operationally identical is unlikely to be quantitatively valid. The possible different locations of the channels would contribute to inhomogeneities of channel engagement. Also the assumptions that the channels are in parallel is likely an oversimplification based on the structure of the hair bundle (Cotton & Grant 2004 Silber et al., 2004). Although the hair bundle is considered to rotate only around its base, it is possible that there are micromechanical movements that serve to recruit rows of stereocilia as stimulus is increased, suggesting the channels are in fact in some combination of series and parallel. Errors due to the above assumptions mean that stiffness associated with the channel may be significantly underestimated. Recent experimental investigations, though, rather point in the direction of a parallel engagement via tip links in saccular hair cells (Karavitaki & Corey, 2005).

For certain types of hair cells the reduction in stiffness associated with gating is comparable to the constant passive component, so that a hair bundle may become unstable due to an effective negative stiffness. This instability phenomenon has been reported for isolated hair bundle preparations of the frog within a range of hair bundle deflections of about 20 nm (Martin & Hudspeth, 1999). In combination with the action of Ca²⁺-dependent adaptation motors it is suggested to enhance a hair cell's sensitivity (Martin, Mehta & Hudspeth, 2000). Recently, in rat outer hair cell bundles, negative hair bundle stiffness and even negative hair bundle forces (pushing in the same direction as the excitatory displacement) have been observed (Kennedy et al., 2005), exceeding the expected gating forces by more than a factor of 10. The explanation of this most likely requires the existence of additional Ca²⁺, dependent force mechanisms in the outer hair cell bundle, possibly similar to effects found in turtle hair cells (Ricci, Crawford & Fettiplace, 2000; Fettiplace, Ricci & Hackney, 2001). In gerbil hair cells, large, voltage-evoked hair-bundle motions could be explained by relating them to fast somatic motility (Jia & He, 2005), in this case excluding contributions from the hair bundle. Reconciliation of these disparate results is required for understanding the mechanical contributions of the hair bundle to signal processing in the cochlea. Another possibility, which seems to hold for both mouse outer- and vestibular hair cells, is that individual channel-spring complexes are close to instability, so that S_ch (Eq. 6b) is zero or negative (cf. van Netten & Kros, 2000). It has been shown that this condition is favorable in terms of the signal-to-noise ratio of mechano-electrical transduction (van Netten et al., 2003). This concept is closely related to the intrinsic thermally induced noise of transducer channels or channel chatter (Holton & Hudspeth, 1986; Ricci, 2002; van Netten et al., 2003). The gating compliance of a complex consisting of a transducer channel and a gating spring has been shown to be a direct measure of the noise-limited information about bundle position that can be transferred by transducer currents. The thermal noise limits the accuracy of mechano-electrical transduction in terms of a minimum detectable displacement of the hair bundle to X_min = 2kT/Z per channel, which is inversely proportional to the gating force Z, and typically amounts to just a few nanometers per hair cell (van Netten et al., 2003).

Complex Hair Bundle Responses

There are several confounding issues that must be taken into account when bundle movements are being measured and interpreted in terms of the gating-spring theory. First, the ability to detect gating-related movements requires that the responsible active forces in the bundles be similar or greater than the passive stiffness-related forces of the bundles. It is possible that this is not always the case or that the relative contribution of active and passive bundle components can vary, thus leading to different response measurements. For example, in the less stiff frog saccule hair bundles, spontaneous hair bundle oscillations and regions of negative stiffness in the force-displacement relationship are observed, whereas in the stiffex turtle auditory hair bundles, spontaneous oscillations or negative stiffness regions are rarely observed, despite having very robust MET currents and adaptation (Martin et al., 2000; Ricci et al., 2000). Also, in mouse cochlear hair cells, where passive bundle stiffness is expected to be high, no signs of spontaneous hair bundle movements have been observed during different stages of maturation (Géléoc et al. 1997; van Netten et al. 2003).

Second, gating compliance is only one type of active component in the bundle. To date at least four additional movements have been observed. First, a rapid movement away from the tall edge ascribed to fast adaptation in turtle (Ricci et al., 2000) but also observed in frog (Howard & Hudspeth, 1987; Benser, Marquis & Hudspeth, 1996; Ricci et al., 2000; Cheung & Corey, 2005). In mammals this movement appears to be of the opposite polarity and thus implies further complexity (Kennedy et al., 2005). Second, a slow movement toward the tall edge of the hair bundle associated with slow motor form of adaptation (Howard & Hudspeth, 1987; Assad, Hacohen & Corey, 1989; Ricci et al., 2002). Third, a voltage-dependent, calcium- and channel-independent movement away from the tall edge has been identified in both turtle and frog, the functional correlate and mechanisms underlying this movement are unknown (Ricci et al., 2000; Cheung & Corey, 2005). And fourth, a slow movement, away from the tall edge of the bundle, with time constants on the order of 100s of milliseconds, termed sag , has been identified whose function is also unknown (Ricci et al., 2002). Parceling out which movement corresponds to what function is difficult, particularly given that most of the interpretations are based on correlation with current responses and not direct tests of mechanisms. The ability to elicit bundle movements of opposite polarity without significant effects on the MET current illustrates the problem with this correlative approach (Ricci et al., 2002). Recent evidence from the rat cochlea again points to this problem where previously measured movements associated with channel gating now present a time course more appropriately associated with fast adaptation and the estimates of gating force are much greater (Kennedy et al., 2005).

Dissecting Intrinsic and Extrinsic Channel Properties

The gating-spring theory is a general formulation, much like the Hodgkin-Huxley model of the action potential that describes the relationship between hair bundle stiffness and MET channel gating (Corey & Hudspeth, 1983b). It requires no specific molecular correlate and it does not imply whether modeled properties are intrinsic to the MET channel or imposed by accessory structures. The model has successfully reproduced data from a variety of hair cell types, under many experimental conditions. The general formulation provides a useful framework in which to design and test more specific hypotheses regarding channel gating. It is likely that many of the tenets of the model are oversimplifications and that some of the assumptions are not valid in their entirety, yet these problems do not detract from the usefulness of the model. Being a general model, the gating-spring theory can and has been used to assign specific roles to particular proteins or parts of proteins. Since many molecular configurations can be accommodated by this model (for example figure 2) care must be taken when applying simple mathematical expressions to specific molecular mechanisms.

Given that the MET channel is sensitive to the force exerted onto it and that this force is shaped by the complex mechanical properties of the hair bundle and also by the accessory structures associated with the channel, can we clearly define properties of the transduction channel as being intrinsic to the channel or some function of its environment? Complicating this question are the relatively crude methods used for stimulating sensory hair bundles. Fluid jets, stiff fibers, or even optical traps are interpreted as being able to control the position of the hair bundle, an assumption valid only at the macroscopic level. It is quite clear that changes in the micromechanical environment are not being controlled by these stimuli from the maintenance of adaptation processes and active oscillatory behavior that remains despite apparent macroscopic control of the hair bundle position (Ricci, Wu & Fettiplace, 1998). This error is somewhat analogous to a space-clamp error in voltage-clamp where significant errors in interpretation can be made because of the inability of the recording system to maintain a constant voltage at the channel of interest. The difficulty in ascribing properties directly to the channel is elucidated by exploring the effects of calcium on presumed intrinsic channel properties. Activation kinetics, normally considered a property of the channel, exhibit a calcium-dependence (Ricci et al., 2005) that may be a direct result of calcium interacting with the channel or of calcium altering hair bundle stiffness; evidence exists for both. Intuitively this can be understood so that if hair bundle compliance is changed by external calcium then the force exerted onto the channel will be altered and activation kinetics will change. The story gets more complex in that altering activation rates alters adaptation properties such that the calcium-dependence of adaptation may become indirect (Wu, Ricci & Fettiplace, 1999). Furthermore, fast adaptation, which in mammalian hair cells can occur on the time scale of microseconds, has recently been proposed to operate via a myosin 1c pathway (Lemasurier and Gillespie, 2005; Stauffer et al, 2005) and perhaps not via a direct conformational change of the channel (Cheung & Corey, 2005; Crawford et al., 1989; Ricci et al., 2000). This hypothesis points out the significance of understanding the role accessory proteins have in shaping the stimulus sensed by the MET channel. Technological developments are required to aid in the separation of these various mechanical components before we can fully resolve these issues.

Channel Properties

So, at present, properties associated with channel gating or even mechanosensitivity cannot be directly ascribed to the channel because the role of accessory proteins and the hair bundle cannot be clearly separated. How then can the channel be characterized? This question is important for two reasons. First, in order to identify the molecular nature of the channel, the expressed channel must have properties consistent with the native channel. Since expressed channels are unlikely to be associated with accessory proteins found in the hair bundle, intrinsic channel properties are required. And second, considerable data is accumulating to suggest that tonotopic variations in MET channel properties are important for mechanical tuning and amplification (Ricci & Fettiplace, 1997; Ricci et al., 2000, 2003, 2005; Ricci, 2002; Kennedy et al., 2003). In order to determine the mechanisms underlying this tonotopy, it is necessary to isolate intrinsic channel properties. A reasonable assumption here is that the properties of the channel pore are inherent to the channel. Both biophysical and pharmacological characterizations of the pore region have yielded important information regarding MET channel properties that are likely intrinsic to the channel protein. The channels' conductance is nonspecific but selective for cations; they are highly permeable to calcium (Corey & Hudspeth, 1979; Ohmori, 1985; Crawford, Evans & Fettiplace 1991; Ricci & Fettiplace, 1998; Farris et al., 2004). Anomalous mole fraction behavior suggests an interaction between monovalent and divalent ions (Lumpkin, Marquis & Hudspeth, 1997) that may underlie in part a requirement for the unusual endolymph composition (Ricci & Fettiplace, 1998). Calcium also blocks the channel at a distance approximately half way through the membrane electric field (Kros, Rusch & Richardson, 1992; Gale et al., 2001; Farris et al., 2004). The channel shows little voltage-dependent rectification in high external calcium concentrations (Crawford & Fettiplace, 1985; Ohmori, 1985; Kros et al., 1992; Gale et al., 2001; Farris et al., 2004). The channels have large single-channel conductances (Ohmori, 1984; Geleoc et al., 1991; Crawford et al., 1997) that vary with external calcium and characteristic frequency (Ricci et al., 2003), leading to the suggestion that tonotopy might be due to the existence of different subtypes of channels. Interestingly, no difference in calcium permeability was observed between channels with different conductances, nor have any pharmacological differences that could be ascribed to the channel been observed (Ricci, 2002; Farris et al., 2004). Investigations of pore dimensions using relative amine permeabilities resulted in diameters of around 1.2 nm, large as channels go but not nearly as large as other mechanosensitive channels (Sukharev et al., 1997; Farris et al., 2004). Here too, no observable difference was found in amine permeability between cells that had MET channels of different conductances (Farris et al., 2004), suggesting additional complexities in channel permeability.

Corresponding to the large pore size is a pharmacological profile of open-channel blockers whose efficacy is dictated by the molecular dimensions of the compound (Farris et al., 2004). These blockers come from diverse classes of compounds that include calcium-channel blockers, cyclic nucleotide-channel blockers, transient receptor potential-channel blockers, local anesthetics, aminoglycoside antibiotics, gap junctional blockers, nicotinic channel blockers and compounds such as methylene blue and FM1-43 that are not typically channel blockers (Glowatzki et al., 1997; Gale et al., 2001; Farris et al., 2004). Amiloride is one of few compounds demonstrated to bind mechanically-gated channels in a voltage-dependent manner and provides unique evidence that the channel has multiple open states (Jorgensen & Ohmori, 1988; Lane, McBride & Hamill, 1993; Rusch, Kros & Richardson, 1994). Although unique, the pharmacological profile does not point to any particular candidate channel. However, together this profile must provide a useful fingerprint for the channel when testing possible channel candidates.

Single-channel recordings also support the existence of a second MET open state that has a different conductance and is voltage-dependent (Ricci et al., 2003). FM1-43 data showing that the open-channel blocker is ineffective from the inside also supports the existence of a second open state, as does the recent work done with aminoglycosides (Gale et al., 2001; Marcotti et al., 2005). Here, too, the drug was ineffective at blocking from the internal face of the channel. The existence of this state becomes critical when attempting to interpret data regarding hair bundle movements or the presence of adaptation at positive potentials. Present interpretations assume that depolarizations simply reduce the calcium gradient in the stereocilia and that bundle movements and the loss of adaptation result from the reduced calcium (Assad et al., 1989; Ricci et al., 2000, 2002; Cheung & Corey, 2005). If, however, a voltage-dependent open state exists, then it is possible that adaptation does not occur from this state (and so is not a result of a change in calcium) and also that bundle movements may be due to conformational changes in the channel rather than associated with adaptation. Also, the gating, spring theorem works for two, state and three, state models (Markin & Hudspeth, 1995; van Netten & Kros, 2000; van Netten et al., 2003), however, the three-state model is for two closed states. The model parameters will need to be readdressed if the existence of an additional open state can be confirmed.

Candidate Channels

How then does the native channel compare to candidate channels? Recently, channels from the TRP family have been implicated as possible components of the MET channel. Given their diversity of function and burgeoning presence in a variety of sensory systems, the likelihood of their involvement in audition is high. The first TRP channel found in hair cells was the OSM4 channel, an osmotically activated channel whose function in hair cells remains unclear (Liedtke et al., 2000). The first evidence for TRP channel involvement in mechanosensation was found in Drosophila where the NOMP C mutant was identified (Walker, Willingham & Zuker, 2000). An ortholog to NOMP C was found in zebrafish (Sidi et al., 2003) but no mammalian homolog has been identified. TRPN1, the zebrafish channel, has recently been localized to kinociliary bulbs rather than the expected stereocilia, suggesting a focus in transduction but not necessarily as the channel (Shin et al., 2005). Unfortunately there is little biophysical data on these channels to compare to the MET channel. Recently the TRPA1 channel has received a lot of attention as the potential MET channel (Corey et al., 2004; Gillespie, Dumont & Kachar, 2005; Lin & Corey, 2005). A variety of technically diverse data support this contention including in situ hybridization, immunocytochemistry, genetic strategies and RNAi to antagonize expression of the channel (Corey et al., 2004). Although no piece of data stands alone to demonstrate that this is the correct protein, together the data provide a strong case that TRPA1 is involved in mechanosensation. As with the TRPN1 channel, the TRPA1 immunocytochemistry places the channels in the sensory hair bundle but in unexpected places, like the kinocilium, not consistent with existing models of transduction, though its localization is broader than the TRPN1 (Corey et al., 2004). Similarly, the in situ hybridization gives somewhat unexpected results with TRPA1 localized to nonsensory cell types (Corey et al., 2004). Several reports on the biophysical and pharmacological properties of TRPA1 expression are worth noting. Pharmacologically, the channel behaves like a TRP channel, blocked by Gd and ruthenium red, but also blocked by aminoglycosides and amiloride (Nagata et al., 2005), consistent with the MET channel blockade but with variable IC50 values. The TRPA1 channel exhibits rectification that is not present in MET channels with high external calcium and is opposite that displayed by MET channels in low external calcium (Crawford et al., 1989; Bandell et al., 2004). In addition, the relative calcium permeability of the TRPA1 is 0.8 (Story et al., 2003) as compared to the hair cell that is 4.6 (Ohmori, 1985). The single-channel conductance values reported by Nagata et al. (2005) are similar but when compared in comparable external calcium solutions are lower than those reported in hair cells (Ricci et al., 2003). Thus, although evidence exists suggesting TRPA1 is involved in mechanosensation, as a homomeric channel it does not compare well with native properties. It is likely that other subunits will be identified that when expressed at appropriate stoichiometries will reproduce native channel properties.

Are there still other channel classes to be considered? Data exists for a number of channel types to be present in hair cells whose function remains a mystery and who have some resemblance to the MET channel. For example, epithelial sodium channels (ENaC) can be mechanically-gated, (Goodman et al., 2002) and are sensitive to amilo-ride block (Alvarez de la Rosa et al., 2000; Kellenberger & Schild, 2002; Drummond, Gebremedhin & Harder, 2004). Antibody staining for the amiloride-sensitive channel locates the channel in the stereocilia (Hackney et al., 1992; Furness, Hackney & Benos, 1996). However, knockout mice that lack the alpha subunit for the ENaC channel have normal hearing, vestibular function and MET currents (Rusch & Hummler, 1999), suggesting this subunit was not part of the MET channel machinery. Recent work has identified a DRASIC channel that is part of the ENaC family that is amiloride and mechanosensitive (Hildebrand et al., 2004). This channel was also localized to hair cells at the RNA and protein level. Yet, here too, a knockout mouse showed no hearing loss initially, though loss developed with age (Hildebrand et al., 2004). As the human homolog of DRASIC is the acid-sensing ion channel, it is possible that this class of channels needs further investigation as well. And finally, cyclic nucleotide-gated channels show similar pharmacology and some have similar calcium permeabilities as the MET channel (Frings, Lynch & Lindemann, 1992; Balasubramanian, Lynch & Barry, 1995; Bucossi, Nizzari & Torre, 1997; Farris et al., 2004) and their presence has been detected in some hair cells (Letts et al., 1998; Drescher et al., 2002). However, the pharmacological profile is not precise, as some blockers, like pseudecatoxin, are ineffective on the MET channel and the biophysical properties also show some variability (Farris et al., 2004). Thus, a variety of channel types remain as candidate channels and considerably more work needs to be done to sort out which is the MET channel and also to determine the role of these other channels in mechanotransduction.

Summary

In summary, the gating-spring theory provides an excellent framework in which to discuss electrical, mechanical, structural and molecular data regarding mechanisms of mechanoelectric transduction. Care must be taken in doing this since there are simplifying hypotheses in the model that are probably incorrect and there are also a number of different molecular mechanisms that are supported by the model. Nonetheless, the model provides a means for evaluating new data and creating new hypotheses regarding mechanisms. Recent evidence suggests that the hair bundle is a dynamic structure. Identifying the mechanisms involved in maintenance of hair bundle structure and regulation of stereocilia growth and turnover are critical to our overall understanding of mechanotransduction. New tools are required for understanding the coupling of hair bundle mechanics and MET current responses. The molecular identification and manipulation of the proteins involved in mechanosensation are needed to provide the direct testing of existing theories regarding MET channel identity, gating and adaptation. A great deal of progress has been made over the past years in identifying proteins essential to the transduction process. As more proteins are identified new questions are raised and new processes identified. However, fundamental issues regarding hair cell mechanotransduction remain to be resolved and technological advances are now enabling these questions to be addressed more directly than ever before.

Fig. 5.

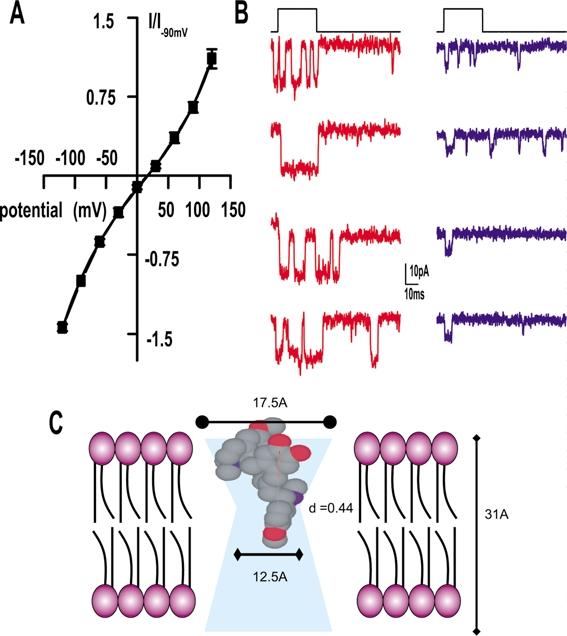
The native MET channel is a nonspecific cation channel that shows little rectification in high external calcium solutions. (A) Plot of the MET current against voltage. The reversal potential of +7 mV demonstrates the nonselective nature of the channel. Little rectification is observed. The data were fit with the single-site binding equation that allows for the estimate of the location of a binding site (presumably a calcium binding site) within the pore (Woodhull, 1973; Kros et al., 1992; Farris et al., 2004). A location approximately 0.5 of the distance into the electric field was obtained. (B) Examples of single-channel recording responses from four stimulus cycles from a high (red) and low (blue) frequency cell. Larger currents are obtained from high-frequency cells than from low-frequency cells. (C) Schematic representation of the MET channel pore illustrating the estimated molecular dimensions of the channel. Curare is shown acting as an open-channel blocker in the pore of the channel and represents the prominent mechanisms of block (Farris et al., 2004).