Dynamic Gain Changes During Attentional Modulation

Abstract

Attention causes a multiplicative effect on firing rates of cortical neurons without affecting their selectivity (Motter, 1993; McAdams & Maunsell, 1999a) or the relationship between the spike count mean and variance (McAdams & Maunsell, 1999b). We analyzed attentional modulation of the firing rates of 144 neurons in the secondary somatosensory cortex (SII) of two monkeys trained to switch their attention between a tactile pattern recognition task and a visual task. We found that neurons in SII cortex also undergo a predominantly multiplicative modulation in firing rates without affecting the ratio of variance to mean firing rate (i.e., the Fano factor). Furthermore, both additive and multiplicative components of attentional modulation varied dynamically during the stimulus presentation.

We then used a standard conductance-based integrate-and-fire model neuron to ascertain which mechanisms might account for a multiplicative increase in firing rate without affecting the Fano factor. Six mechanisms were identified as biophysically plausible ways that attention could modify the firing rate: spike threshold, firing rate adaptation, excitatory input synchrony, synchrony between all inputs, membrane leak resistance, and reset potential. Of these, only a change in spike threshold or in firing rate adaptation affected model firing rates in a manner compatible with the observed neural data. The results indicate that only a limited number of biophysical mechanisms can account for observed attentional modulation.

1 Introduction

Recent experiments have shown that attention can modify neuronal responses to relevant stimuli (e.g., Moran and Desimone, 1985; Motter, 1993; Hsiao, O’Shaughnessy, & Johnson, 1993). The analysis presented here was motivated by the effect of attention on neuronal firing in visual area V4 (McAdams & Maunsell, 1999a, 1999b). When attention was directed into receptive fields of these neurons, their firing rates were scaled multiplicatively (almost doubled) without affecting orientation selectivity, and the ratio of spike count variance to mean (i.e., the Fano factor) was unaffected.

Our aim was to examine whether similar attentional effects on firing rate are seen in other sensory areas besides visual cortex. A finding that the effects are similar will support the idea that the mechanisms of attention are common throughout cortex. Our second motivation was to understand the unusual nature of the change in gain: multiplying a random variable (in this case, spike count) by a factor g increases its mean and standard deviation by g, but its variance increases by g². In contrast, data from V4 cortex (McAdams & Maunsell, 1999b) indicate that the Fano factor is unaffected, which suggests that the effect of attention is not a simple change in gain. We reasoned that the biophysical mechanisms might be inferred by investigating which of them could produce a gain change without affecting the Fano factor.

We analyzed the responses of 144 neurons in the somatosensory cortex (SII) of two monkeys trained to switch their attention between a tactile pattern recognition task and a visual dimming detection task (Steinmetz et al., 2000; Hsiao et al., 1993). Because the tactile stimuli (letters) used in this study did not fall along a continuum, we were unable to compute the change in gain experienced by a single neuron. Instead, we measured the extent of attentional modulation over the entire population of neurons and separated the effect of attention into multiplicative and additive components. In addition, the temporal modulation of the multiplicative and additive components during the trial was examined by repeating this procedure over short time intervals across the trial.

We then examined six mechanisms that affect the mean firing rate and variability in a standard integrate-and-fire cortical neuron model (Troyer & Miller, 1997; Shadlen & Newsome, 1998; Salinas & Sejnowski, 2000), with the aim of finding which mechanisms could account for the observed data. Candidate mechanisms were chosen based on their biophysical feasibility and their ability to be modulated rapidly over the timescale required for attention (hundreds of milliseconds). To simplify our analysis, we assumed that the model neuron receives inputs with fixed firing rates and that attentional modulation acts either by modifying an intrinsic biophysical parameter (e.g., spike threshold) or changing the input synchrony. The results indicate that attentional modulation alters either the spike threshold or firing rate adaptation.

2 Methods

2.1 Neurophysiology and Behavioral Tasks

Two macaque monkeys, M1 and M2, were trained to perform both tactile and visual discrimination tasks (Hsiao et al., 1993; Steinmetz et al., 2000). In the visual task, three white squares appeared on a computer screen, and after a random interval, one of the two outer squares dimmed slightly. To obtain a reward, the monkey was required to detect the dimming and indicate which of the squares dimmed by turning a switch. In the tactile task, the monkey discriminated raised capital letters (6.0 mm high) embossed on a rotating drum (Johnson & Phillips, 1988) that were scanned from proximal to distal across the center of a fingerpad (at 15 mm/sec). To obtain a reward, the animal responded when the letter scanning across the fingerpad matched a target letter displayed on a computer screen. For monkey M1, the target letter remained constant throughout the collection of data from a single neuron. For monkey M2, the task was made more difficult by changing the target letter randomly after each response. Single-unit recordings were obtained from the SII cortex of both monkeys using standard methods. These data have been analyzed for attentional modulation of the firing rate (Hsiao et al., 1993) and synchrony (Steinmetz et al., 2000).

2.2 Statistical Methods

To estimate the 95% confidence intervals shown in Figures 3 and 4, we used a bootstrap method. A random subset of neurons was drawn with replacement, and the slope and intercept were computed as a function of time for that subset. Nonparametric estimates of the variance in the computed slope and intercepts were obtained by repeating the procedure several times. To estimate the significance of the trends in the gain modulation, gaussian random vectors were generated using the means and variances estimated from the bootstrap data. As a result, these random vectors have no temporal trends. We then performed a multivariate analysis-of-variance (manova1, Matlab 7.0) between the bootstrap data and the randomly generated data to determine the significance of the observed trends in gain.

Figure 3.

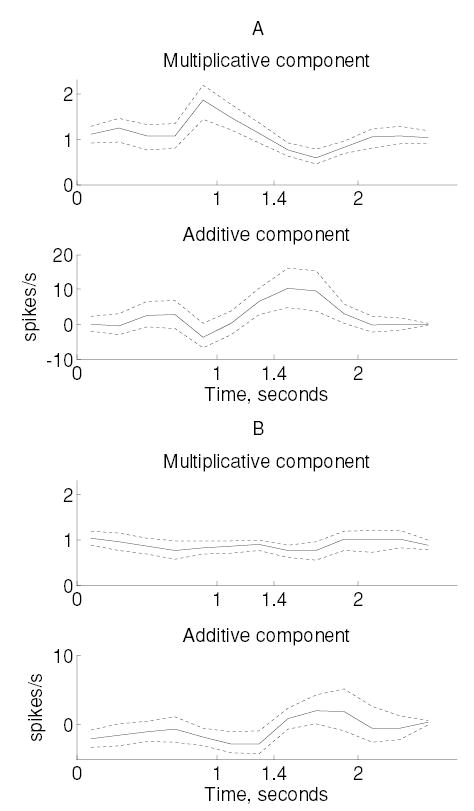
Multiplicative and additive components of attentional modulation observed in monkey M1 within two subpopulations. (A) Neurons that increased their firing rates during the first 600 ms of the stimulus. (B) Neurons from monkey M1 that significantly decreased their firing rates during the tactile (attended) task. Dotted lines indicate 95% confidence intervals computed using bootstrap.

Figure 4.

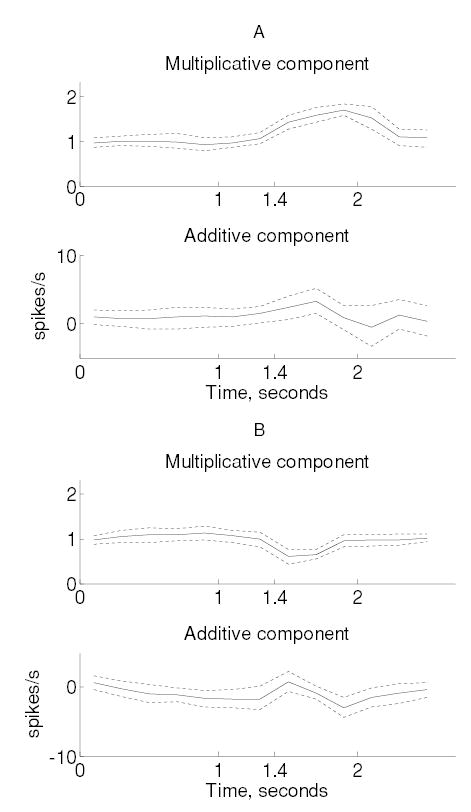
Multiplicative and additive components of attentional modulation for monkey M2 neurons, plotted analogous to the monkey M1 data (see Figure 3).

2.3 Conductance-Based Integrate-and-Fire Model

We used a conductance-based integrate-and-fire model as a simplified model of neuronal firing. This model reproduces the Poisson-like variability exhibited by cortical neurons (Salinas & Sejnowski, 2000; Shadlen & Newsome, 1998; Troyer & Miller, 1997). Parameters of this model were examined for their ability to account for the experimental data.

The model is driven by excitatory and inhibitory inputs that arrive randomly. Each input spike triggers an exponentially decaying change in conductance that leads to the characteristic postsynaptic current—excitatory postsynaptic current (EPSC) or inhibitory postsynaptic current (IPSC)—at the soma. The membrane potential in the model is governed by a linear differential equation (2.1), driven by postsynaptic currents and by intrinsic adaptation and leak currents. When the membrane potential crosses the threshold V_θ, a spike is registered and the potential is held at a reset potential, V_reset, for a time equal to the refractory period:

$$\begin{array}{l}C\frac{dV}{dt}=-g_L(V-E_L)-g_{SRA}(V-E_K)-g_{AMPA}(V-E_{AMPA})\\ -g_{GABA}(V-E_{GABA}).\end{array}$$ (2.1)

In the above equation, C is the membrane capacitance, and g_L is the conductance due to leak channels. The membrane potential is influenced by three types of currents: a current due to fast excitatory synapses (AMPA), a current due to fast inhibitory synapses (GABA), and a spike rate adaptation current (SRA). The conductances g_SRA, g_AMPA, and g_GABA are the sums of the conductances evoked by past output spikes and excitatory and inhibitory input spikes, respectively (see Table 1). The arrival of the inputs is stochastic, and as a result, the membrane potential executes a random walk toward the threshold (Troyer & Miller, 1997). In the baseline condition, the model produces a firing rate of 40 spikes per second when driven by 160 excitatory inputs and 40 inhibitory inputs firing at 40 spikes per second. Input synchrony was controlled as described below. Model parameters for the baseline condition are listed in the appendix and are based on in vitro electrophysiology (McCormick, Connors, Lighthall, & Prince, 1985).

Table 1.

Conductance Changes Accompanying Each Type of Spike in Equation 2.1.

Current (Spike Type)	Conductance Change Due to Spike
SRA (output spike at $t=t_j^{out}$)	$g_{SRA}^j={\overline{g}}_{SRA}exp\left(-\frac{t-t_j^{out}}{{\tau }_{SRA}}\right),\hspace{0.17em}t>t_j^{out}$
AMPA (excitatory spike at $t=t_j^E$)	$g_{AMPA}^j={\overline{g}}_{AMPA}exp\left(-\frac{t-t_j^E}{{\tau }_{AMPA}}\right),\hspace{0.17em}t\hspace{0.17em}>\hspace{0.17em}{t}_j^E$
GABA (inhibitory spike at $t=t_j^I$)	$\begin{array}{l}{g}_{GABA}^j=\\ \frac{{\overline{g}}_{GABA}}{D}\left(exp\left(-\frac{t-t_j^I}{{\tau }_{GABA}^1}\right)-exp\left(-\frac{t-t_j^I}{{\tau }_{GABA}^2}\right)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>t_j^I\end{array}$

Note: D is adjusted to make $g_{GABA}^j={\overline{g}}_{GABA}$ at t = 0.

2.4 Input Synchrony

We used a method in which the synchrony of the inputs could be systematically modulated independent of their firing rates (Salinas & Sejnowski, 2000). Briefly, each input is modeled as a random walk to threshold. When the random walk reaches threshold, a spike is registered, and the random walk is reset. Synchrony between spikes is controlled using the degree of correlation between the random walks. However, changing the correlation between random walks also affects the firing rate. Therefore, we adjusted the standard deviation of individual steps in the random walks to maintain a constant firing rate (Salinas & Sejnowski, 2000). Synchrony between excitatory-excitatory (E-E), excitatory-inhibitory (E-I), and inhibitory-inhibitory (I-I) input pairs was controlled using the corresponding correlations φ_E, φ_EI, and φ_I between the random walks.

3 Results

3.1 Observed Changes in Population Firing

We recorded the responses of 178 neurons from the somatosensory cortex (SII) across two monkeys, M1 and M2. Eighty percent (144/178) of these neurons were selected for further analysis based on the following criteria. First, at least two trials were required in both attended and unattended conditions (176/178). Among these neurons, we found that poorly isolated cells had a very high spike count variance (due to huge variations in the number of recorded spikes from trial to trial); these cells were eliminated by requiring the variance of the spike count to be less than 10 times the mean (144/176). All cells had a firing rate greater than 5 impulses per second. Our analysis was restricted to a 2.6 second time window during which the target stimulus was scanned across the skin. The target letter contacted the skin at a time t = 1.4 seconds after trial onset.

Because the raised letter stimuli used in this study did not fall along any continuum, we were unable to compute the change in gain experienced by a single neuron. Instead, we measured the extent of attentional modulation over the entire population of neurons. We separated the effect of attention into multiplicative and additive components by plotting the spike count for each neuron in the attended condition versus the spike count in the unattended condition. In the plot, a deviation in slope from unity would indicate a multiplicative modulation (i.e., gain change) due to attention over the entire population of neurons, whereas a constant shift (positive or negative y-intercept) would indicate an additive modulation.

Since neurons in SII cortex are known to exhibit both increases and decreases in firing rates with changes in attention (Hsiao et al., 1993), we separated the neurons into three categories in M1 and M2 (t-test for unequal variances for firing rates, p < 0.05): (1) neurons that did not show any significant modulation during the first 600 ms after the stimulus onset—52% (31/60) in M1 and 27% (23/84) in M2; (2) neurons that increased their firing rates during this period—27% (16/60) in M1 and 44% (37/84) in M2; and (3) neurons that decreased their firing rate during this period—22% (13/60) in M1 and 29% (24/84) in M2. Neurons from the second and third categories were selected for analysis of dynamic changes in gain and variability.

Figure 1 shows the change in firing rates with a shift in attention during a 200 ms time period that resulted in the maximum gain change for neurons in monkeys M1 (see Figure 1A) and M2 (see Figure 1B) from the second category (i.e., those that increased their firing rates in the tactile task). Thus, for example, a neuron in monkey M1 with a firing rate of 10 impulses per second in the visual (unattended) task will have a firing rate of 14.8 impulses per second in the tactile task, with the multiplicative component contributing to most of the increase.

Figure 1.

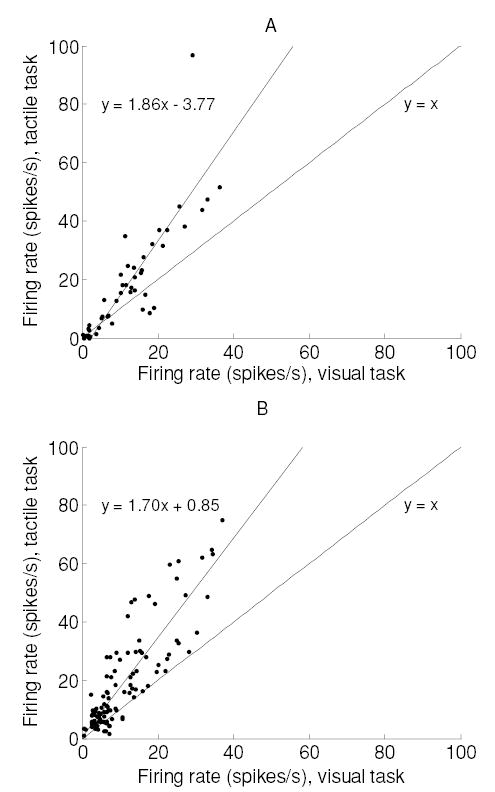
Effect of attention on the firing rate during the 200 ms period of maximum gain change. (A) Monkey M1. Spikes are counted between t = 1.8 and 2.0 seconds. (B) Monkey M2. Spikes are counted between t = 0.8 and 1.0 seconds. Data in both panels are from neurons that increased their firing significantly during the peak firing epoch ( p < 0.05, t-test). Best-fitting slopes, with 95% confidence intervals, were 1.85 ± 0.23 (M1) and 1.70 ± 0.11 (M2). The corresponding y-intercepts were 3.77 ± 4.26 (M1) and 0.85 ± 2.18 (M2).

We then plotted spike count variance against the mean spike count in the same time period for the unattended and attended conditions (see Figure 2). The mean firing rate in the attended condition (M1, 20.4; M2, 22.6 spikes/s) was more than 1.5 times larger than in the unattended condition (M1, 12.9; M2, 12.8 spikes/s). Furthermore, the relationship between the mean spike count and the spike count variance is unaffected by the attentional state (i.e., the regressions in Figure 2 are not significantly different from one another). These results agree well with attentional effects observed in the visual cortex (see Figure 4 of McAdams & Maunsell, 1999b).

Figure 2.

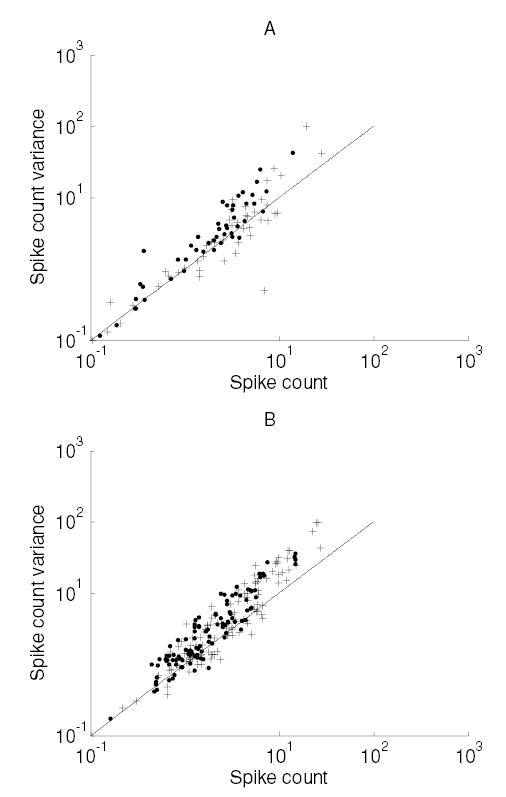
Effect of attention on the variability of neuronal responses. (A) Monkey M1. (B) Monkey M2. Plots show the spike count variance versus spike count for neurons whose spike rate was increased by the focus of attention (data from neurons as in Figure 1). Crosses correspond to neurons in the attended condition, and dots correspond to the unattended condition. Fitted powers (with 95% confidence intervals): M1: attended, 1.0 ± 0.13; unattended, 1.1 ± 0.11. M2: attended, 1.2 ± 0.09; unattended, 1.1 ± 0.08. Coefficients (with 95% confidence intervals): M1: attended, 1 ± 0.24; unattended, 1.4 ± 0.21. M2: attended, 1.2 ± 0.16; unattended, 1.5 ± 0.13.

3.2 Dynamic Modulation of Additive and Multiplicative Components

We examined the temporal variations of additive and multiplicative modulation by repeating this procedure for successive 200 ms windows across the duration of the trial. Additive and multiplicative effects were modulated dynamically during the trial in both monkeys (see Figures 3 and 4). Although trends in both additive and multiplicative modulations were significant (MANOVA, p < 0.0005; see section 2), the effects were predominantly multiplicative in both monkeys (except among neurons in monkey M1, which experienced a decrease in firing rate). The time course of multiplicative and additive modulation was different in the two monkeys. In monkey M1, multiplicative gain reaches a maximum 0.6 seconds before stimulus onset, whereas the additive component peaks roughly 0.2 seconds after stimulus onset. In monkey M2, maximum multiplicative gain occurred 0.5 seconds after stimulus onset, and additive gain peaked 0.3 seconds after stimulus onset. Similar modulations were observed among the subpopulation of neurons that decreased their firing rates. Despite the changes in multiplicative and additive modulation across the trial, we did not observe significant modulations in the Fano factors in any subpopulation of neurons.

3.3 Mechanisms of Gain Change in a Model Neuron

The analysis of SII data shows that in general, many neurons exhibit a multiplicative gain change when the animal shifts its focus of attention (see Figure 1), and that the Fano factor is unaffected by the gain change (see Figure 2). We performed computer simulations on a model cortical neuron to identify which mechanisms could account for a multiplicative gain change without affecting the Fano factor. With independent Poisson inputs, the standard balanced conductance-based model generates Poisson-like output with a Fano factor of 1.0 (Shadlen & Newsome, 1998). To replicate the Fano factor of 2.0 seen in our data, we increased the level of input synchrony and set φ_E = φ_I = 0.2. This corresponds to a 20% common drive for all inputs, a correlation that is commonly seen in neuronal data (e.g., Britten, Shadlen, Newsome, & Movshon, 1992; Shadlen, Britten, Newsome, & Movshon, 1996). We confirmed that our simulations did not depend on the exact Fano factor chosen by repeating them for other levels of input synchrony (data not shown).

We selected parameters of the model neuron such that the output firing rate would approximately equal that of the individual inputs over a physiological range (0–100 spikes/s). We then analyzed six putative mechanisms, each corresponding to a single parameter in the model (e.g., firing threshold), in two steps. First, the mechanism was used to double the firing rate from 40 to 80 spikes per second while leaving the input firing rates unchanged. Second, we examined the ability of the mechanism to modulate the slope of the input-output relationship without affecting the Fano factor (see Figure 5). A multiplicative modulation in the input-output relationship corresponds to a gain change across a population of neurons, each receiving inputs firing at different rates. Thus, we were able to determine whether a given mechanism produced an effect on the firing rate that was consistent with data. Note that although the analysis is shown for populations of neurons that undergo an increase in gain, it is equally applicable to a population of neurons that experience a decrease in gain. Table 2 summarizes the effect of each mechanism on the slope of the input-output relationship and the Fano factor.

Figure 5.

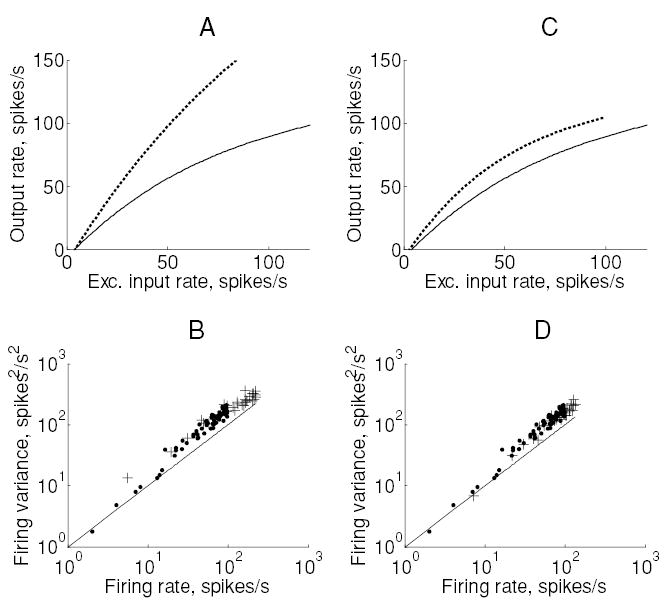
Two types of gain change observed in the conductance-based integrate-and-fire model neuron. (A) Input-output relationship for two different values of threshold. The solid line corresponds to the baseline value (−54 mV) and the dotted line to a lowered threshold (−55 mV). (B) Spike count variance plotted against output rate for each of these data points (dots: baseline; crosses: lowered threshold). The solid line represents the relationship (y = x) expected of a Poisson process. (C, D) Corresponding plots for gain produced by increasing the membrane time constant by four times to 80 ms.

Table 2.

Parameter Changes Required to Double the Output Firing Rate and Their Effects on Gain and Fano Factor.

	Parameter	% Change in Parameter Needed	Fano Factor at 40 Spikes/S After Change	Multiplicative Gain (Slope at 40 Spikes/S)	Consistent with Data?
1	Reset potential	Not possible	NA	NA	No
2	Synchrony of E inputs	+50%	3.85	1.8X	No
3	Synchrony between all input pairs	Not possible	NA	NA	No
4	Membrane time constant	+300%	1.5	1X	No
5	Adaptation conductance	−100%	2.0	2X	Yes
6	Threshold	−1.8%	2.0	2X	Yes

Note: Missing values indicate that it was not possible to double the firing rate using that parameter.

Figure 5 indicates the two types of gain change produced in the model neuron. A slight change in threshold produced a multiplicative gain change without affecting the Fano factor (see Figures 5A and 5B). On the other hand, changing the membrane time constant had an additive effect on the input-output relationship, without affecting the Fano factor. We found that two of the six mechanisms had only weak effects on the firing rate but adverse effects on output variability; these were the reset potential and synchrony between all input pairs (see Figure 6).

Figure 6.

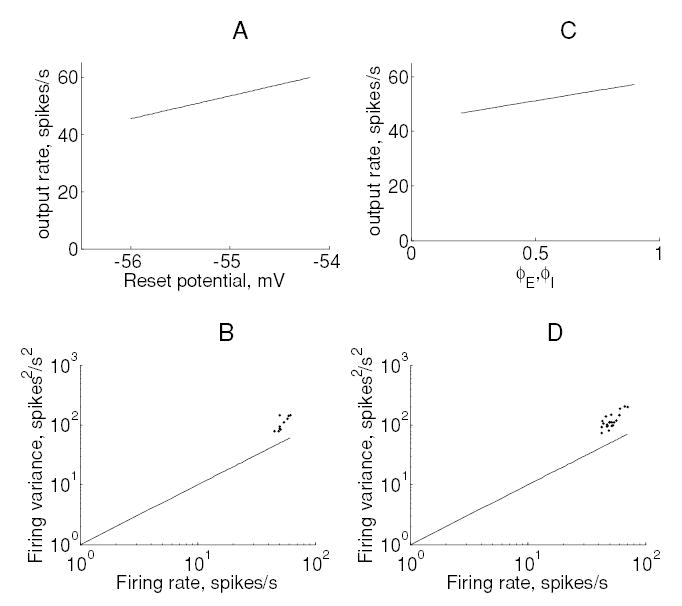
Effect of reset potential and synchrony between all pairs of inputs on output firing. (A) Output rate versus reset potential. (B) Output spike count variance versus output firing rate for these data. (C, D) The corresponding figures for increases in synchrony between all pairs of inputs (E-E, I-I, E-I). Input synchrony was increased without affecting the input firing rates (see section 2).

Changes in synchrony between all input pairs result in a cancellation of the effect of excitatory and inhibitory inputs; this effect has been discussed in detail by Salinas and Sejnowski (2000). On the other hand, changes in excitatory input synchrony produced a multiplicative gain change but a disproportionate increase in output variability (see Figures 7A and 7B and Table 2). Changes in inhibitory input synchrony produced effects that were identical to those produced by changes in excitatory input synchrony (data not shown). Finally, changes in firing rate adaptation produced a multiplicative change in firing while leaving the Fano factor unaffected (see Figures 7C and 7D).

Figure 7.

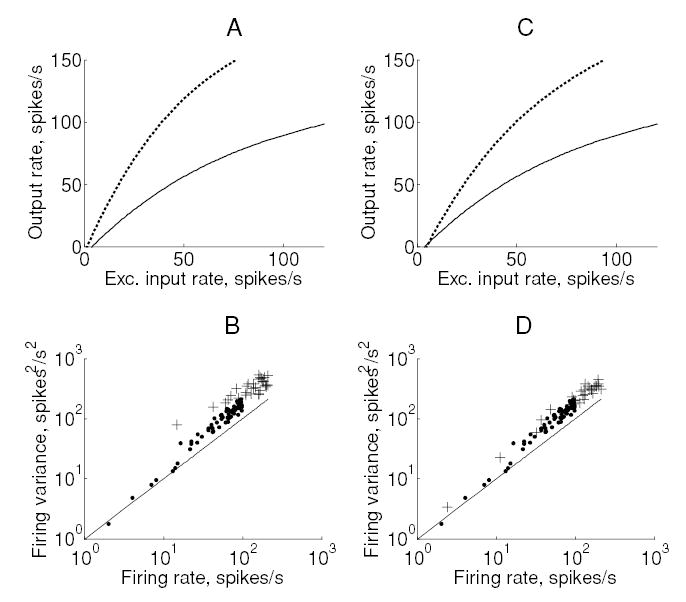
Effect of spike rate adaptation and excitatory input synchrony on output firing. (A) Change in the input-output relationship produced by an increase in synchrony from zero (solid) to φ_E = 0.2 (dotted). (B) Output spike count variance versus output firing rate for the corresponding data points. Changing excitatory input synchrony produced a Fano factor of 3.85 at an output rate of 40 spikes per second. (C, D) Corresponding plots for spike rate adaptation conductance g_SRA. The baseline model firing rate was elevated from 40 to 80 spikes per second by reducing the adaptation conductance to zero.

The results above also indicate that each constraint on attentional modulation can be violated independently; thus, while the membrane time constant did not affect the Fano factor but produced an additive increase in firing, excitatory synchrony produced a gain change but had a large effect on the Fano factor. In summary, of the six mechanisms considered here, only threshold and firing rate adaptation modulated firing rates in a manner consistent with a shift in attention.

4 Discussion

Understanding how neural representations are affected by attentional state is a topic of intense investigation (for a review, see Reynolds & Chelazzi, 2004). However, it is unclear how attentional state affects neural coding and what mechanisms underlie the modulation. Our analysis shows that attention multiplicatively modulates the population firing in a dynamic manner during a trial without affecting the firing variability; in addition, the unique nature of the observed gain change limits the possible mechanisms underlying attentional modulation.

4.1 Dynamic Gain Modulation

Many studies have shown that a shift in the focus of attention modulates neuronal responses over timescales of hundreds of milliseconds (Hsiao et al., 1993; Luck, Chelazzi, Hillyard, & Desimone, 1997; McAdams & Maunsell, 1999b). We observed a similar time course for the gain of neuronal responses (see Figures 3 and 4), which rose to a peak of about 1.5 times and decreased to 1.0 times over a period of about 500 ms. We found different time courses for gain in the two monkeys, which could be due to task-related differences. In monkey M1, the target letter remained constant throughout, whereas in monkey M2, the target letter changed after each trial. Thus, the attentional focus of M1 tended to wax and wane since the animal knew that target letters never followed each other in succession. In contrast, the attentional focus of M2 remained consistently high throughout all tactile trials. Therefore, we hypothesized that the peak in gain observed in monkey M1 prior to stimulus onset may be related to stimulus expectation.

Despite the dynamic modulation of gain, the relationship between spike count variance and mean was unaffected by attentional state. Because the firing rates of neurons varied during the trial, we selected a short interval of 200 ms over which the rate remained relatively constant. Although the Fano factor is known to depend on the counting duration (Rieke, Warland, de Ruyter van Steveninck, & Bialek, 1997), we found little variation over the short timescales required for the analysis (0.1–0.5 ms). The observation that spike count variance is proportional to the mean is thus supported not only across stimulus conditions (Shadlen & Newsome, 1998) but also across variations in attentional state. Therefore, the discharge variability may well be an intrinsic property rather than a function of the input.

4.2 Mechanisms Underlying Attentional Modulation

The main result is that the observed change in gain and variability with attentional state limits the possible mechanisms that can produce this modulation. We selected six biophysical mechanisms that we hypothesized could account for the neural data. Although we did not systematically test whether the effect could be due to some combination of these mechanisms, it is likely that attention functions through one or more of these possibilities.

Out of the six mechanisms considered, only changes in spike threshold or in firing rate adaptation produced a gain modulation without affecting the Fano factor. Primarily, these parameters affect the distance between the threshold and the steady-state membrane potential to bring about a multiplicative gain change. The following mechanisms were found inconsistent with the observed data: changes in (1) reset potential, (2) synchrony between all input pairs, (3) synchrony between excitatory or inhibitory inputs, and (4) membrane time constant. The first two mechanisms affect the variability of the membrane potential about the steady state and produce an increase in the discharge variability. Changing the membrane time constant had an additive effect on firing rate because of the diminishing contribution of leak current with increasing input firing rates.

Biophysical mechanisms underlying attentional modulation have been investigated in relatively few studies. Reynolds, Chelazzi, and Desimone (1999) proposed that attention may increase the effective synaptic strength, although how this might occur biophysically is unclear. Niebur and Koch (1994) first suggested that input correlations may play a role in attentional modulation. Furthermore, input synchrony has a multiplicative effect on firing rate (Salinas & Sejnowski, 2000; Tiesinga, Fellous, Salinas, Jose, & Sejnowski, 2004). However, input synchrony dramatically affects the output variability, as reported here as well as in both computational and in vitro studies (Stevens & Zador, 1998; Salinas & Sejnowski, 2000; Feng & Brown, 2000; Harsch & Robinson, 2000). Finally, Chance and Abbott (2002) have shown in vitro that balanced synaptic input can have a multiplicative effect on firing rate (see below).

Although the observation that attention modulates neuronal gain is relatively recent (McAdams & Maunsell, 1999a), gain modulation itself is a widespread phenomenon (Salinas & Thier, 2000). Simulations using biophysical neuronal models have shown that balanced synaptic input has a modulatory effect on the overall gain and variability (Burkitt, Meffin, & Grayden, 2003). Finally, the impact of Poisson inputs on the output firing rate and variability may differ depending on whether an integrate-and-fire model or a Hodgkin-Huxley model is used (Tiesinga, Jose, & Sejnowski, 2000). Further in vitro studies using dynamic clamp methods need to be performed to develop a statistical description of the output as a function of the inputs (cf. Chance & Abbott, 2002).

4.3 The Neuron Model

We used a conductance-based integrate-and-fire model for cortical neurons with parameters derived from in vitro electrophysiology (McCormick et al., 1985). While the essential features of integration of synaptic EPSPs and IPSPs on the soma are present in the model, the nonlinear dynamics of spiking are lumped together into a threshold (Koch, 1999). The assumption of a fixed threshold is justified because a substantial part of the discharge variability can be attributed to irregular synaptic input (Calvin & Stevens, 1968; Mainen & Sejnowski, 1995; Nowak, Sanchez-Vives, & McCormick, 1997).

We used balanced input to produce high discharge variability in the baseline condition (Shadlen & Newsome, 1998). Due to the balanced input, the membrane potential rapidly achieves a steady-state value after an action potential; the subsequent random walk to the threshold produces a Poisson-like discharge variability (Troyer & Miller, 1997). Cortical neurons are not far from an approximate balance; for example, receptive fields of area 3b neurons in the somatosensory cortex show roughly equal strengths of inhibition and excitation with a median ratio close to 0.8 (DiCarlo, Johnson, & Hsiao, 1998). Our results were independent of balance as long as input synchrony was adjusted to yield the requisite discharge variability at baseline. This is important since changing input balance affects response selectivity, whereas a gain change leaves the selectivity unaffected (e.g., McAdams & Maunsell, 1999a). Therefore, we did not consider input balance to be a putative mechanism if attention affects only the gain of a neuron’s response without changing its selectivity.

We made several assumptions regarding the nature of inputs to the model. First, we used input correlations and balanced synaptic input to obtain the high discharge variability seen in our data (Salinas & Sejnowski, 2000; Shadlen & Newsome, 1998). Second, we assumed inputs to be unaffected by attentional state. Although attentional effects increase progressively along the sensory pathway (Hsiao et al., 1993; Reynolds & Chelazzi, 2004), it is unclear whether attentional modulation in lower cortical areas has a feedforward effect on higher cortical areas. Therefore, we considered the simplified situation in which input firing rates are unaffected by attentional state. We also sought to distinguish the impact of synchrony from that of the firing rate in order to identify how each affects gain and variability. It is unclear whether increasing the gain in a population of neurons will affect their synchrony. It is likely that the underlying mechanisms are constrained further by a network model that reproduces attentional effects on gain and variability reported here, as well as on pair-wise synchrony reported previously (Steinmetz et al., 2000).

4.4 Biophysical Feasibility

Each of the above mechanisms was selected based on its ability to be modulated in a biophysically feasible manner, over durations of hundreds of milliseconds.

4.4.1 Reset Potential

The reset potential is determined by the balance between sodium and potassium conductances. This can be modulated by a specific potassium channel conductance (e.g., M-type K+ channel; Hille, 2001).

4.4.2 Input Synchrony

Increased gamma-band oscillations can lead to increased synchrony, as has been observed recently (Fries, Reynolds, Rorie, & Desimone, 2001). However, we have found that a change in the synchrony alone (without affecting the firing rates) increases the firing variability far beyond physiological levels. Our results are consistent with in vitro experiments (Stevens & Zador, 1998; Harsch & Robinson, 2001) as well as with other theoretical and modeling studies (Salinas & Sejnowski, 2000; Feng & Brown, 2000).

4.4.3 Membrane Time Constant

The leak resistance can be modulated by a change in the properties of K-channels For example, the M-type potassium current can be affected at short timescales and can be modulated by acetylcholine inputs (Hille, 2001).

4.4.4 Adaptation Conductance

Calcium-triggered potassium channels are responsible for adaptation in the firing rates of neocortical neurons (McCormick et al., 1985; Hille, 2001). These channels can be modulated by second messenger effects; for example, acetylcholine or norepinephrine inputs can lead to a change in channel properties over hundreds of milliseconds (Hille, 2001). There is evidence that cholinergic modulation is related to the level of attention (Kodama, Honda, Watanabe, & Hikosaka, 2002; Davidson & Marrocco, 2000). Computational studies also suggest a possible role of feedback modulation in controlling attention, which can be controlled by the extent of firing rate adaptation (Wilson, Krupa, & Wilkinson, 2000; Rothenstein, Martinez-Trujillo, Treue, Tsotsos, & Wilson, 2002).

4.4.5 Threshold

A constant depolarizing current can affect the threshold of production of an action potential (Johnston & Wu, 1995). This can be achieved by a tonic input from other cortical areas. This input need not even be stimulus dependent. A similar observation has been made by Chance and Abbott (2002), in which they find that the level of balanced background synaptic input to neurons in vitro offsets the stimulus-driven current, bringing the steady state closer to threshold, and produces a multiplicative gain change. They too report that the output variability (measured by the coefficient of variation) is unaffected, which is consistent with our findings. An increase in tonic input is consistent with the findings of Luck et al (1997), in which the spontaneous firing rates of neurons in V2 and V4 were found to increase by 30% to 40% when attention was directed into the receptive field.

5 Conclusions

Our results show that in the secondary somatosensory cortex, neurons experience a multiplicative increase in firing rates during attentional modulation while preserving the Fano factor. These effects are similar to those seen in visual area V4 (McAdams & Maunsell, 1999b) and suggest that the mechanisms of attention are common in both sensory areas. While there have been many studies of the effects of attention on perception and the underlying neural responses (Kastner & Ungerleider, 2000), the mechanisms that underlie the modulation of neuronal responses at the single-neuron level are unknown. In this study, we employ a deductive approach to identifying the mechanisms responsible for attentional modulation at the single-neuron level and conclude that attention causes changes in spike threshold or in firing rate adaptation. Further studies are required to understand how changes in these mechanisms account for other effects of selective attention such as the modulation of synchrony with attentional state (Steinmetz et al., 2000).

Appendix

Model neuron parameters at baseline (i.e., output rate = 40 spikes/s, Fano factor = 2.0):

Conductances (in nS)

$${\overline{g}}_{SRA}=3.5;\hspace{0.17em}{\overline{g}}_{AMPA}=2.01;\hspace{0.17em}{\overline{g}}_{GABA}=27.85;\hspace{0.17em}{g}_L=25$$

Time constants (in ms)

$$\begin{array}{l}{\tau }_m=20;\hspace{0.17em}{\tau }_{refrac}=1.72;\hspace{0.17em}{\tau }_{SRA}=100;\hspace{0.17em}{\tau }_{AMPA}=5;\hspace{0.17em}{\tau }_{GABA}^1\\ =5.6;\hspace{0.17em}{\tau }_{GABA}^2=0.28\end{array}$$

Reversal potentials (in mV)

$$\begin{array}{l}{E}_k=-80;\hspace{0.17em}{E}_L=-74;\hspace{0.17em}{E}_{AMPA}=0;\hspace{0.17em}{E}_{GABA}=-61;\hspace{0.17em}\hspace{0.17em}{V}_{rest}=V_{reset}\\ =-60;\hspace{0.17em}{V}_{\theta }=-54\end{array}$$

Numbers of inputs

$$M_E=160\hspace{0.17em}\text{excitatory},M_I=40\hspace{0.17em}\text{inhibitory\hspace{0.17em}inputs}$$

Input rates (in spikes/sec)

$$\text{Excitatory\hspace{0.17em}rate\hspace{0.17em}}{\lambda }_E=40,\hspace{0.17em}\text{inhibitory\hspace{0.17em}rate }{\lambda }_I=\alpha {\lambda }_E,\alpha =1.7$$

Parameters for all random walks

$$N_{reset}=20,\hspace{0.17em}{N}_{\theta }=40,\hspace{0.17em}{N}_{rest}=0$$

Input synchrony

$${\phi }_E={\phi }_I=0.2$$

The subthreshold equation was numerically integrated with a time step of 0.05 ms.