Emergence of tempered preferential attachment from optimization

Abstract

We show how preferential attachment can emerge in an optimization framework, resolving a long-standing theoretical controversy. We also show that the preferential attachment model so obtained has two novel features, saturation and viability, which have natural interpretations in the underlying network and lead to a power-law degree distribution with exponential cutoff. Moreover, we consider a generalized version of this preferential attachment model with independent saturation and viability, leading to a broader class of power laws again with exponential cutoff. We present a collection of empirical observations from social, biological, physical, and technological networks, for which such degree distributions give excellent fits. We suggest that, in general, optimization models that give rise to preferential attachment with saturation and viability effects form a good starting point for the analysis of many networks.

Preferential attachment (PA) has a long tradition as a model to describe social, biological, and technological networks. It is often assumed to be the underlying mechanism at work when power law distributions are observed in data sets. Although the basic PA model and simple variants have had remarkable success in describing various networks, some authors have suggested that these models are not fundamental (1–3), and/or that they do not have the subtle properties necessary to describe empirical observations in real networks (4–6), and often suggest optimization as an alternate mechanism which gives rise to power laws. In a recent technical work, we introduced a mathematical model which implicitly addresses some of these concerns (7, 8).

The purpose of this manuscript is threefold. First, we show how a form of PA can emerge as a consequence of a natural competition model of networks, to a large extent resolving a long-standing controversy between those who view PA as an axiom and those who argue that power laws should arise from a fundamental optimization framework.

Second, we show that the PA model so obtained has two novel features, which we call saturation and viability. The saturation leads to an eventual exponential cutoff of the PA power-law degree distribution. Therefore, we call our model tempered PA (TPA). Previously, saturation was put directly into the PA model (9) and later, into more general network models (10), to explain a broad range of empirical data that exhibit power-laws with exponential cutoffs. Here, we show that saturation and the corresponding cutoffs can arise naturally from an underlying optimization model. Our model exhibits another property, viability, which reflects the fact that not all attempts to create new nodes are successful. The saturation and the viability together determine the value of the power law. Despite the fact that we have not seen viability discussed in previous works, we believe it to be as fundamental a property of network growth as saturation.

The third purpose of this work is to fit empirical observations from a variety of networks. The simple competition model we propose has only a single parameter, and thus both the saturation and viability are functions of this one parameter. However, because these are, in general, two independent effects, it is natural to assume that saturation and viability would be characterized by two independent parameters. Thus we consider the simplest two-parameter TPA model. We show that this model gives very good fits for a variety of social, biological, and technological networks. In particular, the two-parameter TPA model gives an excellent fit to previously unexplained high-quality data of Internet structure compiled by the Cooperative Association for Internet Data Analysis (CAIDA, www.caida.org).

Interestingly, for almost all data sets analyzed, the fits obtained result in the power law portion of the degree distribution having exponent between 1 and 2 (see Table 1). However, the power law in the basic preferential attachment model (11, 12) is 3, and power laws in more general models including mixtures of preferential and uniform attachment achieve exponents greater than 2 (13–17). Our two-parameter TPA model with saturation and viability gives power laws between 1 and 3, and thus provides a much better fit to a large body of empirical observations.

Table 1.

Empirical observations of power-law with exponential decay distributions, p(x) ∼ x^−B exp(−x/C)

System with p(x) ∼ x−B exp(−x/C)	Exponent, B	Cutoff, C
Full protein-interaction map of Drosophila (26)	1.20 ± 0.08	27 ± 4
High-confidence protein-interaction map of Drosophila (26)	1.26 ± 0.25	3.9 ± 0.8
Gene-flow/hybridization network of plants as function of spatial distance (27)	0.75	105 m
Earthquake magnitude (28, 29)	1.35–1.7	≈1021 Nm
Avalanche size of ferromagnetic materials (30)	1.2–1.4	L1.4 (L is sample size)
ArXiv coauthor network (25)	1.3 ± 0.1	53 ± 5
MEDLINE coauthor network (25)	2.1 ± 0.5	≈5,800
PNAS paper citation network (10)	0.49	4.21

It is not the intent of this work to propose that this simple two-parameter TPA model describes a significant fraction of all networks. Instead, we are merely using this model as a prototype of a class of models based on optimization that exhibit saturation and viability effects in addition to preferential attachment. We suggest that the full class of such models provides a good starting point for the analysis of many networks. This class of models may also provide a good starting point for the numerical simulation of network topologies. TPA, like the standard PA processes, requires only minimal computational resources: to simulate a system of size N nodes requires computational time linear in N.

PA vs. Optimization

PA, also called proportional attachment or cumulative advantage, has a long and illustrious history. It is often assumed to be the underlying mechanism at work when power law distributions are observed in data sets. Although introduced by the mathematician Polya in 1923 (18), the concept of PA was popularized by Zipf and Simon in the 1940s and 1950s, respectively, as an explanation for the power law distribution observed empirically in the population sizes of cities (19), and the distribution of wealth amongst members of a society (20). Also in the 1950s, Mandelbrot proposed an alternate view, that power law distributions could arise as solutions to underlying optimization problems. Mandelbrot's focus was on statistical properties of written language, and on optimizing the amount of information transmitted per symbol (1). A series of exchanges between Mandelbrot and Simon soon ensued, published in the journal Information and Control, and launched a still-unresolved public controversy about whether PA or optimization is the more appropriate explanation for emergence of power laws. In recent years, we have seen a flurry of activity on PA, especially in the context of networks, sparked by the model of network growth via PA introduced by Barabási and Albert in 1999 (11). In their model, nodes arrive sequentially and attach to existing nodes with probability proportional to the existing node's current degree. The Barabási–Albert model has been used extensively to describe growth of many classes of networks from social to technological ones. The complementary approach of studying the optimization origins of power laws although dormant for many years, has also recently gained renewed interest (2, 3). For a review of the historical debate, see ref. 21 and references therein; for PA, see ref. 22 and references therein.

Our model resolves the long-standing controversy, unifying both philosophical camps, showing that PA and optimization can be intimately related. Furthermore, it elucidates the potential origins of PA. It is surprising that, until now, despite the decades of study of PA and its widespread uses, no one has investigated or introduced an underlying optimization mechanism that gives rise to it.

Emergence of Preferential Attachment

General Framework.

Rather than assuming the PA premise that the “rich get richer,” we start by considering underlying tradeoffs between constrained resources, as in ref. 3. We first consider the framework at a high-level, illustrating its applicability with a specific idealized example, in rough analogy with growth of the Internet. We later introduce the precise model analyzed mathematically. Consider the Internet at the autonomous systems (AS) level, represented as a collection of nodes {j} linked to one another (the link structure is not important for now), further consider its growth via introduction of new ASes (i.e., new service providers). Each newly arriving entity, labeled t, has to connect to the existing physical network and also establish peering relationships with other existing nodes to route and transmit data packets. Node t will want to make connections that minimize the monetary startup costs required, while still guaranteeing good network performance for its users (this is the tradeoff). Monetary startup costs are not from laying fiber-optic cable to make the physical connection. There are currently thousands of miles of available cable that have already been laid, but are not yet in use (23) (i.e., “dark fiber”), and the Internet backbone currently contains a large amount of excess capacity (24). Startup costs are instead associated with renting “lit” fiber from existing carriers and negotiating peering agreements. We make a simplified model based on these heuristics: node t chooses to fully peer with one other node j, but to reach j it must make agreements to rent lit fiber from n_tj carriers (i.e., n_tj transit intervals). Formally, we can say that the new entity t wants to minimize the cost function

Here, n_tj reflects how many fiber transit intervals a data packet sent from t to j has to traverse. h_j is a measure of network distance from node j to the core of the network, hence reflects the network delay experienced by node j. Also, α is a dimensionless constant which determines the relative weighting between the two metrics, with α>0. Node t wants to connect to j that has the best network performance, relative to the number of transit intervals traversed. Note that we can consider the general form of Eq. 1,

where Λ_tj and h_j are two distinct metrics in competition, and extend the framework to different contexts. For instance, in a systems biology setting, the tradeoff might involve the ability to evolve quickly versus specialization/efficiency. The protein-interaction network of the system could be used as a basis for both metrics. For instance, ease of evolution could be measured by quantifying the extent of modularity of this network. Efficiency could be measured by quantifying the number of distinct modules involved in crucial control pathways.

Formal Model Specification.

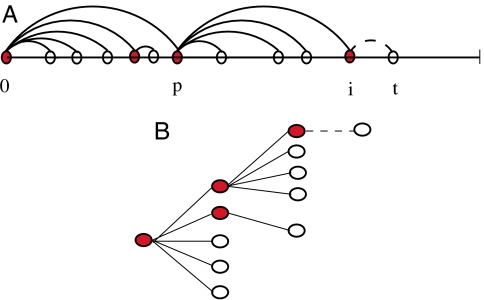
A precise mathematical model for Eq. 1 is constructed by considering a one-dimensional line, as shown in Fig. 1. We begin at time 0 with a single root node, labeled 0. New nodes arrive one at a time, at random positions along the unit line. Each arriving node t chooses to connect to the existing node j, which minimizes Eq. 1. Here, n_tj is the number of nodes already present in the interval between t and j (which can be interpreted as the number of transit intervals required to reach j), and h_j (the network performance degradation experienced by j) is measured by the hop-count of node j to the root node. To simplify our analysis, we add the constraint that x_j < x_t, where x_j is the physical distance of node j to the root (i.e., we require that nodes only connect to nodes that are closer to the root). Finally, ties are broken by connecting to the node with the shortest distance between x_j and x_t.

Fig. 1.

The one-parameter TPA model. (A) An example of the growth process on the line, with 1/α = 4. Node t arrives and wants to minimize the cost function αn_tj + h_j, where n_tj is the number of existing nodes in the interval between t and j, and h_j is the hop-count of node j to the root. The minimization can only be achieved by connecting to the adjacent node i (so that n_ti = 0), or to the parent of i (which has h_p = h_i − 1). If n_tp ≥ 1/α (as is the case illustrated), i gains the new attachment, otherwise p does. Thus as soon as there are 1/α children of node p, node p's attractiveness saturates. (B) The equivalent network structure resulting from the growth process on the line.

It is not hard to show that, given the cost function Eq. 1 and definitions above, node t will connect either to the node i directly to its left (which has cost c_i = h_i because n_ti = 0), or to the parent of i, denoted p (which has cost c_p = αn_tp + h_i − 1, because h_p = h_i − 1). Thus, unlike other optimization models (3), ours requires only local information. Comparing c_i and c_p, if n_tp < 1/α, node t attaches to p; otherwise, it attaches to i. Denoting the degree of a node p as d_p, we see that when d_p < 1/α, any new arrival that lands adjacent to p, or to one of its children, connects to p (node p's attractiveness is proportional to its degree, and its children are “infertile”). If d_p ≥ 1/α, any new arrival that lands adjacent to p, or to one of its closest 1/α children, connects to p. However, if it lands to the right of a farther away child of p, that child acquires the attachment (node p's attractiveness has saturated at 1/α, and all but the closest 1/α children have become “fertile”). Introducing the notation A = ⌈1/α⌉ (i.e., the smallest integer greater than or equal to 1/α), we can summarize the probability of a fertile node p acquiring the next attachment as

where 𝒩(t) is the total number of nodes present at the arrival of node t. Infertile children do not acquire attachments. A node may be initially infertile, but once enough attachments occur that there are at least (A − 1) children between the node and its parent p, that node becomes fertile.

The TPA process thus defined differs from the original PA model in two respects: (i) Each node produces A − 1 infertile children before producing fertile ones. (ii) The preferential attachment of each fertile node saturates at degree A, beyond which the node does not become any more attractive. We call the second effect “saturation,” indicating that fertile nodes become more attractive only up to a certain threshold. Saturation effects clearly occur in real systems with resource constraints. We call the first effect “viability”: each node is either viable or not viable. In general, one expects a distribution of viability: not all children have an equal ability to procreate, not all social contacts have the same networking capabilities, not all businesses have the same abilities to successfully spinoff subsidiary companies, and not all ASes have the same attractiveness to their peers.

As one might expect, TPA leads to a different degree distribution from the standard PA model. Whereas the Barabási–Albert model produces a degree distribution that is a power law with exponent 3 on all scales, our one-parameter TPA model leads to a power law with exponent 2 up to the threshold A, and exponential decay for degrees above A. More explicitly, we find that the probability of observing a node of degree d is p(d) ∝ d⁻² for d ≤ A, and p(d) ∝ exp(−dκ) for d > A, with κ = log(1 + 1/A) (see refs. 7 and 8 for the derivation of this degree distribution).

Obviously, because our competition model contains only a single parameter, both the viability and the saturation thresholds of the corresponding preferential attachment model are functions of this parameter. From the viewpoint of describing real systems, there is no reason to expect the viability and saturation to be determined by a common parameter, and thus it is natural to consider a system with two independent parameters, a viability threshold A₁ and a saturation threshold A₂. Indeed, although it seems reasonable that saturation, which often reflects global resource limitations, may sometimes be characterized by a single cutoff, we believe that viability will have a distribution of values reflecting this distribution of viabilities in the population. Thus, in realistic models, we would expect nodes with a distribution of viabilities and saturations, with each distribution being described by one or more parameters. Nevertheless, for simplicity, we next focus on the model with two independent thresholds, A₁ and A₂, which we will call two-parameter TPA.

Certain limiting cases of the two-parameter TPA model are worth noting. If A₁ = 1 and A₂ = ∞, it is the standard model of PA. If A₁ = 1 and A₂ is finite, it is the standard model of PA with a cutoff. On the other hand, if A₁ = A₂ = 1, it is a uniform attachment model.

The mathematical analysis of the two-threshold model has been undertaken in refs. 7 and 8, where we have shown that the probability of observing a node of degree d is a power law up to A₂, p(d) ∝ d^−γ, with some exponent γ between 1 and 3, whose exact value depends on both A₁ and A₂. More precisely, γ is decreasing in A₁ and increasing in A₂, and is obtained as the largest eigenvalue of an explicit finite-dimensional matrix as given in refs. 7 and 8. For d > A₂, the degree distribution decays exponentially, p(d) ∝ exp(−dκ), where κ is a simple function of γ and A₂.

Finally, if one relaxes the constraint of hard thresholds, i.e., if one allows certain distributions of saturations and viabilities, each again characterized by a single parameter, we would expect that the resulting degree distribution is well approximated by a somewhat smoothed version of that above, namely a power law multiplying an exponential decay, henceforth denoted PLED. Below, we show how such a distribution has been used to fit a wide variety of network data. Then, we look specifically at previously unexplained AS Internet data and show how it is fit remarkably well by the (A₁, A₂) two-parameter TPA distribution, and also by a simple PLED, again with two parameters.

From our perspective, the most interesting open theoretical question is to produce a competition model which is provably equivalent to preferential attachment with independently tunable saturation and viability.

Correspondence with Data

It has been found repeatedly that PLEDs may provide a much better statistical fit to data than do pure power laws. For instance, consider scientific collaboration and citation networks. The in-degree distribution of the network of paper citations for a 20+year collection of papers published in PNAS (10), and likewise the connectivity distributions of coauthor networks from astrophysics, condensed matter, high energy, and computer science databases (25), all are substantially better fit by power-laws with exponential tails than by pure power laws. There are numerous other such examples from a range of fields, spanning earth sciences, ecology, biology, and physics. For some examples of systems where PLEDs are found to provide the best fit to empirical data, see Table 1.

For power laws to continue indefinitely with no upper cutoff or finite-size effects is physically unrealistic if resources are constrained. To explain the exponential decay observed empirically in a range of networks, saturation similar to that in Eq. 3 has been put in at the axiomatic level (9, 10). For instance, the rate at which a paper gains citations, or the level of activity of an individual scientist, is considered to eventually saturate.

In physical systems, the exponential decay of a power-law often arises due to some finite-length scale in the problem, such as the overall system size. PLEDs are a signature of Barkhausen noise in ferromagnetic materials, describing both the distribution of sizes and the duration of avalanches (30). Likewise, in experiments on explosive fragmentation, the distribution of fragment mass is shown to obey a PLED (31). Such a distribution also provides the best fit to the data of the magnitude of earthquakes spanning a >20-year period, as documented in the Harvard Centroid–Moment Tensor Database (28, 29).

We are beginning to understand the complex networked structure of biological systems. Several years ago, it was recognized that protein interaction networks appear to have heavy-tailed degree distributions (32). New technologies for gene-sequencing now allow for more precise determination of this distribution. For instance, consider the protein-interaction network for Drosophila. Giot et al. (26) constructed the full, genome-scale, protein interaction map (consisting of 20,439 unique interactions), as well as the high-confidence protein-interaction map, which isolates only the biologically relevant interactions (consisting of 4,780 unique interactions and 4,679 proteins) (26). The distribution of the number of interactions per protein is analyzed for both the full and the high-confidence map. The authors remark that “neither distribution may be adequately fit by a single power-law. Both may be fit, however, by … Prob(n) ∼ n^−αexp^−βn.” The values for the parameters obtained by a fit to the data (with r² > 0.98 in both cases) are given in Table 1.

As seen in Table 1, the exponents γ for the power-law portion tend to be between 1 and 2, although there are a few instances of γ < 1. Recall that the original PA model has γ = 3 (11, 12). A variety of modified versions of PA have been considered. A combination of PA plus uniform attachment, yielding γ > 2 was proposed by Dorogovtsev et al. (13) and rigorously analyzed in refs. 15 and 16. A “copying model” of network growth was proposed and rigorously shown to give γ > 2 (17). A similar model, worth noting because it considers attachment either to a random node or its parent, also achieves γ > 2 (33). Finally, simulations and heuristic calculations suggest that a modified copying model gives γ > 1 (34, 35). Our two-parameter TPA model is the first to rigorously produce the regime 1 ≤ γ ≤ 3. Furthermore, optimization is a valid scenario in both biological and technological contexts.

Fitting the Internet AS-Level Data

We are interested in the topology of the Internet at the AS-level. There are a number of sources of such data, obtained using different methodologies, which reveal different features of the topology (for instance, “tangential” versus “radial” links). In particular, we concentrate on the topology view extracted from the RIPE WHOIS database (maintained by network operators), as compiled and characterized by CAIDA. See refs. 5 and 6 for access to background and further information on the validity of this data.

The WHOIS data does not fit the standard paradigm that the AS-level topology follows a power law degree distribution. The two standard views that do support the power law paradigm (built from direct traceroute sampling or extracted from BGP tables) both rely on traceroute-like sampling (5). Traceroute sampling has been shown to produce biases that can make an underlying simple random graph appear to have a power law degree distribution (36, 37). Though recent heuristic arguments suggest that, despite these biases, it is possible to use traceroute-like probes to distinguish heavy-tailed degree distributions from an exponential distribution, it is not possible to determine the precise form of the distribution (38). In refs. 5 and 6, the RIPE WHOIS data are put forth as a valid view of the AS-level Internet and the lack of agreement with the power-law paradigm discussed at various points. We show that our TPA model with A1 ≠ A2 provides a remarkable fit to this data. Furthermore, a simple PLED provides a similar fit. For explicit details on the fitting procedure see ref. 39 and supporting information (SI) Appendix.

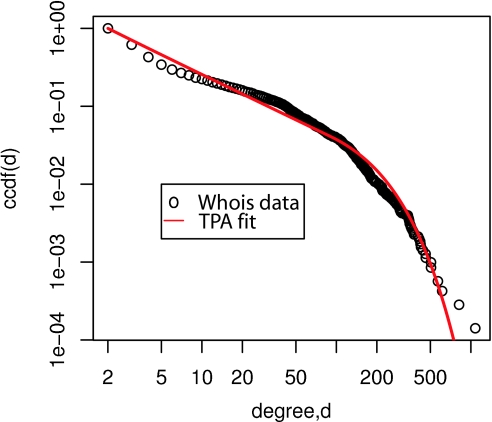
Fig. 2 is a plot of the AS-level connectivity of the Internet constructed from the RIPE WHOIS data. The complementary cumulative distribution function (CCDF), ccdf(x) = 1 − Σ_d=1^x−1p(d), is plotted, along with the CCDF of the best fit provided by the TPA model, obtained for viability A₁ = 187 and saturation A₂ = 90, corresponding to an exponent of γ = 1.83 for the power law portion of the distribution. R² = 0.97 for this fit. We do not include vertices of degree one in Fig. 2. As noted in refs. 5 and 6, technically, nodes should be of degree at least two to qualify for an AS number; therefore, the degree d = 1 data are unreliable. See refs. 5 and 6 for further discussion. See ref. 40 for a detailed discussion of the role of constraints and optimization in the structure of the Internet backbone.

Fig. 2.

CCDF of the “Whois” AS-level connectivity of the Internet. The circles are data compiled by CAIDA from the RIPE WHOIS database (5, 6). The line is the theoretical TPA CCDF with A1 = 187 and A2 = 90 (resulting in the power law portion of the distribution having exponent γ = 1.83).

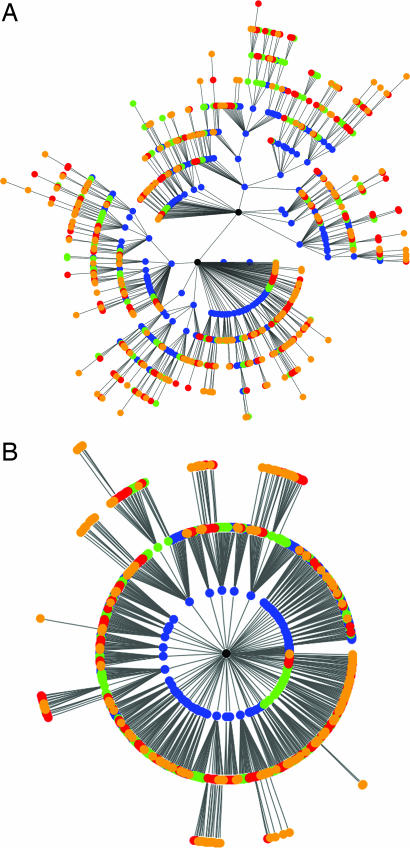
For illustrative purposes we generate an image of a corresponding TPA graph. To render a small graph, we have scaled A₁ and A₂ down, while maintaining the value of γ = 1.83 fixed. Fig. 3 compares this resulting TPA graph with a PA graph of the same number of nodes.

Fig. 3.

Comparison of PA and TPA graphs. Both graphs are grown to n = 1,000 nodes. The oldest N/4 nodes are colored blue, the next quarter green, then red, and finally orange. (A) PA graph. (B) TPA with A₁ = 17, A₂ = 10, thus γ = 1.83. Note the effects of aging in TPA; in contrast to PA, very few of the newest nodes attach to the root. Also, due to the minimization of hop-count, the diameter of the TPA graph is much smaller than that of the PA graph. By varying the choice of parameters A₁ and A₂, it is possible to achieve graphs of appearance intermediate between A and B, or even more extreme than B with respect to the diameter and the number of new nodes attaching to the root.

Discussion and Further Work

We show that an underlying optimization mechanism can give rise to a form of preferential attachment (namely, the one-parameter TPA model). In addition to elucidating underlying causes of PA, the optimization also provides a mechanism for the emergence of saturation, leading to more realistic distributions of power laws with exponential tails. The most intriguing open question is to construct a simple competition model that gives rise to tempered preferential attachment with independent saturation and viability. This more general two-parameter TPA model (with viability and saturation) provides a paradigm for achieving degree distributions with power law exponent 1 ≤ γ ≤ 3 and eventual exponential decay.

The competition framework is very general and we conjecture that, in addition to the metrics defined in Eq. 1, there are several other metrics which would give rise to a form of TPA in other contexts, such as in a system's biology setting or with regards to the economics of trade relations. The metrics presented herein were inspired by analogy with the AS level Internet.

From a practical viewpoint, the TPA model could be extremely useful due its potential widespread applicability, yet the low overhead required for numerical simulation. As shown above, the optimization model giving rise to the one-parameter TPA model is purely local, unlike typical optimization models (for instance, ref. 3) that require that all alternatives be evaluated before the global optimal can be determined. Numerical simulation of the one- or two-parameter TPA model is very similar to simulation of the standard PA process. Both TPA and PA require computational time linear in N to generate a network of size N, but for TPA we must keep track of a small amount of additional information (i.e., which vertices are fertile).

Here, our focus is on degree distributions. Although the degree distribution is an important characteristic of a network, the fine structure is equally important. We have yet to characterize the fine structures resulting via TPA. Our basic model is a tree, and thus has no clustering coefficient; this could be addressed by the modification that each newly arriving node makes m > 1 distinct links to existing nodes.

Finally, similar to PA and the model of ref. 3, our model is an equilibrium one. The values of the controlling parameters (A₁ and A₂) are fixed initially and never change. We expect that to make the model more realistic, these thresholds should change as a function of time or with feedback. In addition, we are interested in considering models where viability is described by a distribution of values, rather than herein, where it is described by a single threshold.

Abbreviations

PA

preferential attachment

TPA

tempered PA

AS

autonomous system.