Two-dimensional ultrasound detection with unfocused frequency-randomized signals

Abstract

A method is described for detecting scattering in two-dimensions using an unfocused ultrasound field created from a continuously-driven source array. The frequency of each element on the array is unique, resulting in a field that is highly variant as a function of both time and position. The scattered signal is then received by a single receiving line. The method, as currently written, is valid under the first order Born approximation. To demonstrate the approach, a series of simulations within the frequency range of 0.10 MHz to 1.25 MHz are performed and compared with a simulated B-Scan in the same frequency range. The method is found to be superior in resolving closely spaced objects, discerning 1.4-mm separation in the radial and 0.5-mm separation in the axial direction. The method was also better able to determining object size, resolving scatters less than 10% of wavelength associated with the center frequency.

I. INTRODUCTION

Ultrasound imaging methods have generally employed temporal bandwidth and frequency to determine image resolution; the former setting the axial resolution and the latter determining the radial beamwidth. Imaging has therefore turned to increasingly higher frequencies as a way to achieve higher imaging resolution via a more localized focus in the transmission and/or receiving array ^1-3. These high-frequency approaches, however, are generally performed at the expense of higher beam attenuation as a function of frequency, limiting their application to more superficial locations.

Alternatively, the ability to detect small phase distortions in an ultrasound field opens the possibility of imaging objects smaller than the focal size. Various ultrasound methods for creating images that are small relative to the imaging acoustic wavelength have been investigated. For example, near field imaging ⁴ records information within a distance of several wavelengths from the source in order to collect information from evanescent wave components of the signal, where the magnitude decays exponentially with distance from an object. Time reversal ⁵ uses information from scattering centers in a highly inhomogeneous field to focus beyond that which is obtainable in a homogeneous medium. Spectral methods ^6,7 seek to reconstruct higher spatial frequencies beyond the cutoff frequency using a priori information about the image.

Presently, an alternative method of ultrasound image construction that creates a signal composed of randomized and spatially-separated time-harmonic frequencies is examined. It will be shown that both transmission and interpretation of the resultant signal does not require a focused beam, allowing for a center frequency that is significantly below that which is required by traditional backscattered ultrasound methods. Using a source array, each element emits a signal differing in frequency from any other element. The individual frequencies are selected so that the net signal is comprised of a relatively large bandwidth, but in this manner, the field is unfocused and seemingly incoherent. A single point-like receiver is used to record the time history of the signal scattered from objects in front of the transducer. Reconstruction of the entire planar region of interest (ROI) is performed from analysis of the time trace acquired from this single receiver. To improve the image, the process is repeated a selected number of times, each time using a new randomized frequency pattern. Signal analysis consists of a Fourier-based approach that determines scattering locations using the spatially-unique phasing patterns created by randomization of the array.

The physical basis of the reconstruction is rooted in its ability to create a known pressure field, with a frequency spectrum whose phase is highly varying as a function of position. In this manner, each point within the ROI possesses a unique, or nearly unique, waveform. The receiver records a superposition of these waveforms, as scattered by any objects present in the field. This signal is used to construct an image of the scattering medium by searching for the presence of each unique waveform within the signal.

This paper aims to describe the method as well as perform a preliminary feasibility assessment of the feasibility of the approach. A detailed description of the ultrasound field and the reconstruction of a scattering region is provided. It is shown that the method provides a means for inverting the linear scattering equation, allowing solutions to the corresponding scattering functions over a limited ROI. A numeric study is then performed to assess the method's ability to construct a two-dimensional scattering field from data gathered in a single temporal dimension. The method is evaluated by comparison of two-dimensional image reconstructions with simulated B-scanned images, assuming a transducer having geometry and bandwidth identical to that used by the randomized frequency method. The resolution limits of the two approaches are determined by measuring two closely situated scattering objects. Scattering of multiple objects and larger inclusions is also demonstrated. It will be shown that the random-frequency approach has the potential to detect small objects beyond the abilities of current widely used methods.

II. THEORY

To illustrate the random-frequency approach, the proposed emitter is first approximated as an array of simple sources, each radiating in a continuous fashion at a unique angular frequency ω. The pressure at any point in a homogeneous space due to a single source at r₀ on the radiator is then given by

$$p_{\omega }(\mathbf{r},t)=-{\mathit{ic}}_0{k}_0{\rho }_0{S}_{\omega }{g}_{\omega }({\mathbf{r}}_{{\mathbf{S}}_{\omega }}\mid {\mathbf{r}}_0)$$ (1)

with sound speed c_0, wave number k_0, density ρ₀, source strength S_ω, and the function

$$g_{\omega }({\mathbf{r}}_{{\mathbf{S}}_{\omega }}\mid {\mathbf{r}}_0)=\frac{e^{-\mathit{ik}\mid \mathbf{r}-{\mathbf{r}}_0\mid }}{4\pi \mid \mathbf{r}-{\mathbf{r}}_0\mid }$$ (2)

that will serve as a Green's function for the relevant wave equation.

If the radiating wave encounters a region of spatially varying density ρ and sound speed c, the time-harmonic acoustic pressure may then be described by the acoustic wave equation

$$\rho \nabla \cdot \left(\frac{1}{\rho }\nabla p_{\omega }\right)+\frac{{\omega }^2}{c^2}{p}_{\omega }=0.$$ (3)

Following the structure of Morse and Ingard ⁸, Eq (3) is first multiplied by $\raisebox{1ex}{${\rho }_0$}\!\left/ \!\raisebox{-1ex}{$\rho $}\right.$ and then $-\left({\nabla }^2+\raisebox{1ex}{${\omega }^2$}\!\left/ \!\raisebox{-1ex}{${c_0}^2$}\right.\right)p_{\omega }$ is added to both sides of the equation,

$${\nabla }^2{p}_{\omega }+{k_0}^2{p}_{\omega }=\nabla \cdot \left(\left\{1-\frac{{\rho }_0}{\rho }\right\}\nabla p_{\omega }\right)+\left\{{k_0}^2-\frac{{\rho }_0}{\rho }{k}^2\right\}{p}_{\omega },$$ (4)

giving the form of a harmonically driven distributed source, which in the absence of the scattering region reduces to a Helmoltz equation. Equation (4) may now be written in the form of a Lippmann Schwinger integral equation ⁹

$$p_{\omega }\left({\mathbf{r}}_R\right)=-{\mathit{ic}}_0{k}_0{\rho }_0{S}_{\omega }{g}_{\omega }({\mathbf{r}}_{{\mathbf{S}}_{\omega }}\mid {\mathbf{r}}_R)+{\int \int \int }_{\mathit{ROI}}\left(\nabla \cdot \left(q_{\rho }\left(\mathbf{r}\right)\nabla p_{\omega }\right)+q_{\kappa }\left(\mathbf{r}\right){k_0}^2{p}_{\omega }\right)g(\mathbf{r}\mid {\mathbf{r}}_R)\mathit{dV},$$ (5)

which represents the incident wave plus the scattered wave. The function $q_{\rho }\left(\mathbf{r}\right)=1-\raisebox{1ex}{${\rho }_0$}\!\left/ \!\raisebox{-1ex}{$\rho $}\right.$ provides a measure of the spatial variation in density while $q_{\kappa }\left(\mathbf{r}\right)=1-\frac{{\rho }_0{c_0}^2}{\rho c^2}$ is a function of variation in compressibility. It is further assumed that the scattered field is weak, such that the first order Born approximation holds ¹⁰, as has been widely used in used in ultrasound scattering in standard and modified ¹¹ forms . The scattered pressure recorded at a point receiver located at r_R will be linearly dependent on the initial source function and Eq (5) becomes

$$p\left({\mathbf{r}}_{\mathbf{R}}\right)\approx {\mathit{ic}}_0{k}_0{\rho }_0{S}_{\omega }\left[g_{\omega }(\mathbf{r}\mid {\mathbf{r}}_0)+{\int \int \int }_{\mathit{ROI}}\left[g_{\omega }({\mathbf{r}}_R\mid \mathbf{r})\nabla \cdot \left(q_{\rho }\left(\mathbf{r}\right)\nabla g_{\omega }(\mathbf{r}\mid {\mathbf{r}}_0)\right)+q_{\kappa }\left(\mathbf{r}\right){k_0}^2{g}_{\omega }({\mathbf{r}}_{\mathbf{R}}\mid \mathbf{r})g_{\omega }(\mathbf{r}\mid {\mathbf{r}}_0)\right]\mathit{dV}\right].$$ (6)

.

The integral in Eq. (6) may be expanded using the vector identity

$$\varphi (\nabla \cdot \mathbf{A})=\nabla \cdot \left(\varphi \mathbf{A}\right)-\mathbf{A}\cdot \nabla \varphi$$ (7)

so that by the divergence theorem,

where S is the surface surrounding the ROI, the first term in the identity given by Eq. (7) integrates to zero. The equation presented by Eq. (6) becomes

$$p\left({\mathbf{r}}_{\mathbf{R}}\right)\approx {\mathit{ic}}_0{k}_0{\rho }_0{S}_{\omega }\left[g_{\omega }(\mathbf{r}\mid {\mathbf{r}}_0)+{\int \int \int }_{\mathit{ROI}}\left[q_{\rho }\left(\mathbf{r}\right)\nabla g_{\omega }({\mathbf{r}}_R\mid \mathbf{r})\nabla g_{\omega }(\mathbf{r}\mid {\mathbf{r}}_0)+q_{\kappa }\left(\mathbf{r}\right){k_0}^2{g}_{\omega }({\mathbf{r}}_{\mathbf{R}}\mid \mathbf{r})g_{\omega }(\mathbf{r}\mid {\mathbf{r}}_0)\right]\mathit{dV}\right].$$ (9)

The central problem lies in the classic problem of inverting Eq (9), to provide solutions of the scattering functions q_ρ (r) and q_κ (r). To tailor the field in a way that will allow this inversion to be performed, n simple sources are now considered, each radiating continuously at its own independent frequency ω(r₀). The scattered acoustic pressure at r_R will then be time-dependent as described by

$$p({\mathbf{r}}_{\mathbf{R}},t)=\sum _{{\mathbf{r}}_0}^n{e}^{i\omega \left({\mathbf{r}}_0\right)t}{\int \int \int }_{\mathit{ROI}}\left[q_{\rho }\left(\mathbf{r}\right)P_{\rho }({\mathbf{r}}_{\mathbf{R}},\mathbf{r},{\mathbf{r}}_0)+q_{\kappa }\left(\mathbf{r}\right)P_{\kappa }({\mathbf{r}}_{\mathbf{R}},\mathbf{r},{\mathbf{r}}_0)\right]\mathit{dV}.$$ (10)

where the kernels P_ρ (r_R,r,r₀) and P_κ (r_R,r,r₀), having the dimension of pressure per unit volume, are obtained by combining terms in Eq. (9). Successful reconstruction requires that Eq. (10) be invertible, or at least pseudo-invertible given p(r_R ,t) and the kernels.

The problem of inversion is presently approached by writing the Fourier integral transform of the received signal,

$$\tilde{p}({\mathbf{r}}_{\mathbf{R}},\omega )=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }p({\mathbf{r}}_{\mathbf{R}},t)e^{i\omega t}\mathit{dt},$$ (11)

as a discrete summation of the scattered signal from finite volumes, δV, in space:

$$\tilde{p}({\mathbf{r}}_{\mathbf{R}},\omega )=\sum _{{\mathbf{r}}_0}^n\sum _{\mathbf{r}}^{\mathit{ROI}}{q}_{\rho }\left(\mathbf{r}\right)P_{\rho }({\mathbf{r}}_{\mathbf{R}},\mathbf{r},{\mathbf{r}}_0)\delta (\omega -\omega \left({\mathbf{r}}_0\right))+q_{\kappa }\left(\mathbf{r}\right)P_{\kappa }({\mathbf{r}}_{\mathbf{R}},\mathbf{r},{\mathbf{r}}_0)\delta (\omega -\omega \left({\mathbf{r}}_0\right))\Delta V,$$ (12)

where the Fourier transform properties of the Dirac delta function δ have been used. The scattering strength at a specific location in the ROI, r = r', is analyzed by multiplying both sides of Eq. (12) by

$${\left[\sum _{{\mathbf{r}}_0}^n{P}_{\rho }({\mathbf{r}}_{\mathbf{R}},{\mathbf{r}}^{\prime },{\mathbf{r}}_0)\delta (\omega -\omega \left({\mathbf{r}}_0\right))\right]}^{-1}\text{or}{\left[\sum _{{\mathbf{r}}_0}^n{P}_{\kappa }({\mathbf{r}}_{\mathbf{R}},{\mathbf{r}}^{\prime },{\mathbf{r}}_0)\delta (\omega -\omega \left({\mathbf{r}}_0\right))\right]}^{-1}.$$

Without loss of generalization, the case of solving for q_ρ (r′) will be considered and applied to both sides of Eq (12):

$$\tilde{\tilde{p}}({\mathbf{r}}_{\mathbf{R}},{\mathbf{r}}^{\prime },\omega )=q_{\rho }\left({\mathbf{r}}^{\prime }\right)+\frac{{\displaystyle \sum _{{\mathbf{r}}_0}^n}{\displaystyle \sum _{\mathbf{r}\ne {\mathbf{r}}^{\prime }}^{\mathit{ROI}}}{q}_{\rho }\left(\mathbf{r}\right)P_{\rho }({\mathbf{r}}_{\mathbf{R}},\mathbf{r},{\mathbf{r}}_0)\delta (\omega -\omega \left({\mathbf{r}}_0\right))+q_{\kappa }\left(\mathbf{r}\right)P_{\kappa }({\mathbf{r}}_{\mathbf{R}},\mathbf{r},{\mathbf{r}}_0)\delta (\omega -\omega \left({\mathbf{r}}_0\right))}{{\displaystyle \sum _{{\mathbf{r}}_0}^n}{P}_{\rho }({\mathbf{r}}_{\mathbf{R}},{\mathbf{r}}^{\prime },{\mathbf{r}}_0)\delta (\omega -\omega \left({\mathbf{r}}_0\right))}.$$ (13)

In this form, the equation is separated in to the desired value q_ρ (r′), referred herein as the signal, and the remaining terms, which will be regarded as noise, N. The inverse Fourier transform of Eq. (13) with respect to frequency

$$\tilde{\tilde{p}}({\mathbf{r}}_{\mathbf{R}},t)=q_{\rho }\left({\mathbf{r}}^{\prime }\right)\delta \left(t\right)+\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }N({\mathbf{r}}_{\mathbf{R}},{\mathbf{r}}^{\prime })e^{-i\omega t}d\omega$$ (14)

will produce a localized peak centered about time t = 0 that is proportional in amplitude to q_ρ (r′). The ability to detect this signal will require that the “noise” terms are sufficiently small relative to the signal. If the amplitudes and phases of each noise term are randomized over the frequency spectrum, their contribution in the time domain will generally not be localized, but rather will resemble a stochastically varying signal as a function of time.

With this observation, it is now assumed that the frequency of each simple source on the emitting transducer surface is randomly selected over the range (ω_min, ω_max), where the range is evenly divided based on the number of transducer elements. This construction process is summarized conceptually in Fig. 1. To enhance the signal strength, an additional independent random frequency distribution may be generated at the source and the two resulting signals combined. In this manner, if a series of M signals are recorded and summed, the signal at q_ρ (r′) will increase linearly with M while the noise N will be further randomized over the frequency domain

$${\tilde{\tilde{P}}}_M({\mathbf{r}}^{\prime },\omega )=\mathit{Mq}\left({\mathbf{r}}^{\prime }\right)+\sum _{m=1}^M{N}_m({\mathbf{r}}^{\prime },\omega ),$$ (15)

and consequently further distributed over the time domain. If the transform of N is sufficiently small, the signal-to-noise ratio will be large enough to recover the signal, which is taken to be the value in the time domain at t = 0. This process is repeated for all r′ over the region of interest to form an image.

Figure 1.

(a) A pressure field is generated by driving each of N transducer elements with a unique frequency within the bandwidth of the transducer, creating a complicated broadband field pattern. (b) This field is assumed to encounter variation in density and sound speed within a region of interest (ROI) causing weak scattering, q(r) (1^st order Born Approximation). (c) Each point in the ROI is tested using the inverse of the kernel for the location. The rest of the signal will present itself as noise N. (d) If this process is repeated with a new randomization, the “Noise” averages toward zero, while the signal gets stronger.

III. METHODS

A. Simulated Array

In this preliminary investigation of the randomized frequency method, fields are selected that could feasibly be produced by a 1-dimensional array. An operating frequency range between 0.1 to 1.25 MHz is chosen, motivated in part by the potential medical implications of these frequencies, which are below the range of existing medical diagnostic transducers. The simulated array has a length y = 40 mm and width of x = 10 mm that is segmented into 202 linear sources with no kerf, propagating into an otherwise homogeneous medium containing a region of scattering sources. The transducer surface is assumed to be situated in the x-y plane with the axis of symmetry along the positive z-axis, which extends from the geometric center of the surface.

To simulate the acoustic pressure field, the transducer surface is divided into simple sources with diameters equal to ¼ wavelength corresponding to the highest transmitted frequency in water (c = 1500 m/s). A linear distribution of 202 frequencies between 0.1 MHz and 1.25 MHz is determined with a frequency resolution of 5.7 kHz, allowing each element on the transducer to be assigned exactly one frequency as obtained using a uniformly distributed pseudo-random number generator. Again by random selection, a single element is also selected to serve as the receiver. A scattering field is placed within the ROI, and the scattered signal reaching the receiver is simulated as a discrete approximation to Eq. (10). This calculated signal is stored for later processing. In practice, the simulation is performed by calculating the scattering element-by-element, and then linearly superimposing the individual time-domain waveforms at the receiver to form the resultant signal.

The scattering kernels, P_ρ and P_κ, given in (10) are also determined for every point over the ROI for a particular random field pattern. The Fourier transform of the received signal is calculated using a discrete approximation to the integral given by (11) and the reconstruction indicated by (13) is then performed. The entire process is repeated M times, and the results summed as given by (15). This sum is inverse transformed with respect to time, providing the image intensity at a single point.

B. B-Scan Simulation

B-Scan images are simulated using focused pulses with bandwidths that span the same frequencies used in the randomized imaging, but with time-localized impulse responses within a 0.1 MHz to 1.25 MHz bandwidth. The emitting array is also geometrically identical to that used in the random-frequency case. Images are assembled by acquiring a series of echoes oriented by phase-controlled beam steering. This phasing is restricted to the y-direction only, with phases calculated according to ${\theta }_n=2\pi \sqrt{{(y-{y_n}^{\prime })}^2+Z^2}∕c$, where Z defines the distance of the focal line on the z axis, and y_n' is the location of the center of the n^th element on the array. In each image, twenty-one focal positions a distance z = 30 mm in front of the transducer are created along the line from y= +10 mm to y = −10 mm. Each of these waveforms is propagated into the ROI and the scattered signal recorded by the center element of the array. The received lines are then extended along their respective directions of propagation and combined to produce an image.

Simulation of the propagation and scattering is performed using a wave-vector space time domain method. ^12,13,¹⁴ Related techniques have been described for propagation in inhomogeneous media ¹⁵, including tissues ¹⁶. These previously-described methods involve elimination of a pressure gradient term, which is based upon simplifications of the wave equation laid out by Pourjavid and Tretiak ¹⁷. The present algorithm follows a procedure similar to past work, but provides a full solution to the wave equation, given the pressure field at some initial time t₀ as well as the density and sound speed over all space. The starting point is time-dependent equivalent to Eq. 4,

$${\nabla }^{2}p-\frac{1}{{c_0}^2}\ddot{p}=\nabla \cdot [q_{\rho }\nabla p]-q_{\kappa }\ddot{p}.$$ (16)

The equation is simplified by assuming only changes in compressibility (q_ρ = 0) and by defining f(r,t) = q(r) p(r,t). Equation (16) may be written in terms of the three-dimensional spatial Fourier transforms with respect to p and f, allowing it to be written as an inhomogeneous Helmholtz equation

$$\ddot{P}+K^2{c_0}^{2}P=\ddot{F},$$ (17)

where capitol letters represent respective Fourier transforms, and the wavenumber in Cartesian coordinates is given by K²=k_x²+k_y²+k_z². The integral solution to (17) may be expressed using the 1D Green's function

$$g(t\mid t_0)=\frac{e^{{\mathit{ic}}_{0}K\mid t-t_0\mid }}{c_{0}K},$$ (18)

giving

$$P(\mathbf{k},t)=P_i(\mathbf{k},t)+{\int }_0^{\infty }g(t\mid t^{\prime })\ddot{F}\left(t^{\prime }\right){\mathit{dt}}^{\prime }.$$ (19)

The integral in (19) has the form of a convolution integral with respect to time. Using the property of the convolution integral

$$P_i{\otimes }_t\ddot{F}={\ddot{P}}_i\otimes F,$$ (20)

the solution to the pressure in k-space may finally be expressed as

$$P(\mathbf{k},t)=P_i(\mathbf{k},t)-c_{0}K{\int }_0^{\infty }g(t\mid t^{\prime })F\left(t^{\prime }\right){\mathit{dt}}^{\prime }.$$ (21)

In general, F is not known but rather may be grown using an iterative method to step forward in time by some step Δt. Presently this is performed using Simpson's method in composite form ¹⁸ . Meanwhile the incident field P_i may be projected forward in time using the exponential transfer function, explained in detail in ¹⁹.

The summarized algorithm for calculating the b-scan image is as follows:

1. Provide the initial fields p(r,t₀) and f(r,t₀)

2. Transform with respect to r to give P(r,t₀) and F(r,t₀)

3. Determine P_i(t+dt) and P_s(t+dt).

4. Inverse transform the field to give p f g, p_x, p_y, and p_z

5. Let p=p_i+p_s

6. f = p γ

7. go to step 2

The time-step, dt, in step 3 may be varied, according to the complexity of the media and the location of the ultrasound beam. In the limiting case of a completely homogeneous media, dt may be arbitrarily long. An example of a field propagating past two scatterers is provided in Fig. 2, representing a 2D slice of the acoustic pressure taken out of the three-dimensional field at a given time.

Figure 2.

Slice from a 3-dimensional k-space simulation of a focused, pulsed wave traveling through a medium with scatterers smaller than the imaging wavelengths. Scattering from two objects is present in the image.

IV. RESULTS

To simulate a B-Scan, the acoustic impulse response directly in front of the array was calculated for a given phase-determined beam orientation. This impulse was then projected forward in time via the k-space projection algorithm using a 200-ns resolution. To produce one image it was necessary to repeat the simulation for each of the 21 scan directions. A planar region of interest having dimensions (40, 40) mm, and with a spatial resolution of 0.2 mm was selected within the three-dimensional field volume in the plane x =0. Two 0.2-mm-diameter wires were added to the ROI, representing the smallest linear scattering object that could be simulated under the current (0.2 mm) resolution. Both objects were given a sound speed of 3500 m/s. The distance between the wires was varied to represent separations of 1 mm, 2 mm, 4 mm, 6 mm and 8 mm. The case of a single wire was also calculated.

Images resulting from the B-scans are presented in Fig 3. In all figures, the transducer is located at the top of the figure, with the axis of forward propagation oriented downward. At 1 mm (not shown) and 2 mm separation (3a), little difference was observed between these images and the images produced with the single wire. The images, which were constructed from the envelope of the amplitude of the backscattered signal, appeared as a single object with a diameter of approximately 2 mm, based on the full-width-at-half-maximum (FWHM) on the y and z axes. At 4 mm (3b), the 2 wires appeared as a single object elongated in the direction parallel with the transducer face. By 6 mm (3c), two individual objects are discernable in the image, but with an on-axis artifact. At 8 mm (3d), the objects are clearly separated.

Figure 3.

Simulated B-scan images (f_center = 0.67 MHz) resulting from scattering from two wires (diam = 0.2 mm) separated by (a) 2mm, (b) 4 mm, (c) 6mm, and (d) 8mm

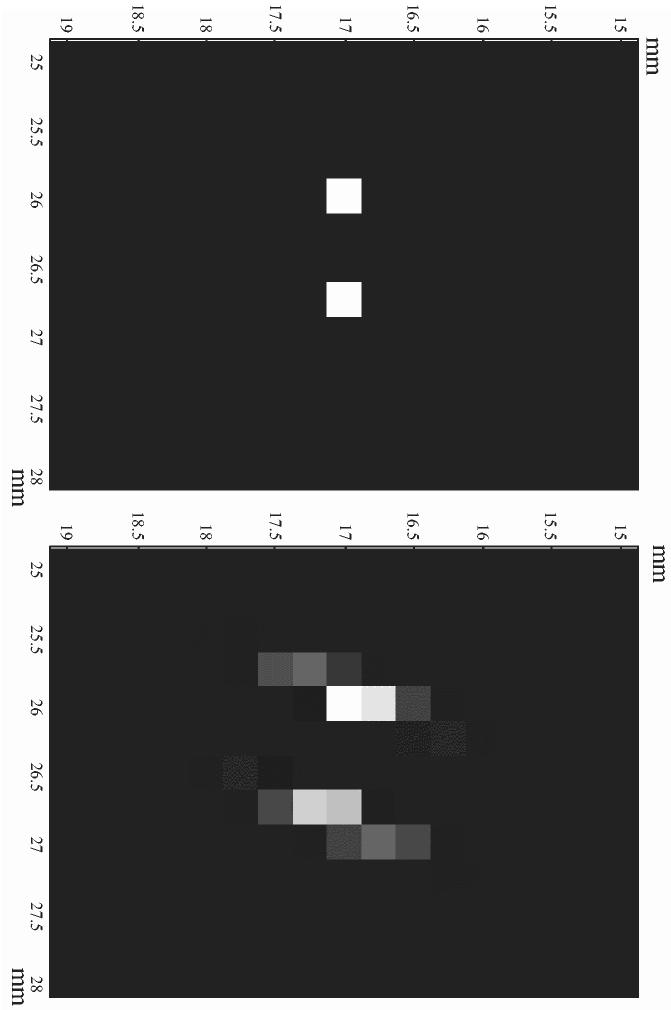
Resolution limits for the spacing between wires was next examined with the randomized method. The transducer was identical in geometry and number of elements to that used in the B-mode simulations and all frequencies were selected within the B-mode bandwidth. Equation (15) was constructed with M = 15 randomized signals. The field was calculated about the wires, using a spatial resolution of 0.2 mm. Based on initial trials, it was observed that a 2-mm separation of the objects, which appeared as a single object in the B-scan, produced two clearly discernable objects, which were also more localized than in the former case. This reconstruction is shown in Fig 4. At 1-mm separation, the objects appeared as a single elongated object, similar to the effect that appeared below 4 mm in the B-scan. The smallest discernable separation for the present configuration was determined to be 1.35 mm (Figure 5), below which the two objects appeared as one. A view over the entire ROI (5a) indicates that artifacts are not present away from the scattering objects, while a magnified view (5b) compares the reconstructed locations with the actual object placement.

Figure 4.

(a) Comparison of the random frequency method (left) with a traditional B-scan (right) using the same frequency bandwidth. (b) A more magnified view compared with the actual position of the scatterers.

Figure 5.

(a) An image of two scatterers separated in the direction parallel to the transducer face at the resolution limit of 1.35 mm over the entire ROI and (b) a magnified view compared with the actual position of the scatterers.

Additional simulations were performed, varying the location of the two objects and their relative positions. Slightly better ability to separate objects was observed along the direction of propagation, where separations of 0.5 mm were observable, but with a distortion in the localization, making the objects appear approximately 0.75 mm apart (Figure 6). This distortion was not apparent beyond 1-mm separation.

Figure 6.

(a) An image of two scatterers separated in the axial direction at the resolution limit of 0.5 mm over the entire ROI and (b) a magnified view compared with the actual position of the scatterers indicates the distortion observed at small separations.

The ability to differentiate between two objects with different scattering strength was next examined. Two point objects (O₁ and O₂) with different speeds of sound were placed within the ROI and reconstructed. In all simulations, the objects were situated 4 mm apart and 17 mm from the transducer surface at locations (17, 8) mm and (17, 11) mm, respectively, as indicated in Figure 7a. A series of reconstructions were performed for a range of O₁ sound speeds equal to 1517 m/s, 1857 m/s, 2143 m/s 2428 m/s 2427 m/s and 3000 m/s, while the speed of sound of O₂ was set at a constant value of 1510 m/s. Figure 7b plots the scattering strength of O₁ relative to the constant O₂ (q₂ = 0.51). This plot is compared with the reconstructed image at the point (17,8) mm relative to the value at (17,11) mm. The plot indicates a similar trend between the scattering strength and the reconstruction, with increased distortion with higher sound speeds. The corresponding error ranged from 4.3% at 1857 m/s to 13% at 3000 m/s.

Figure 7.

(a) Two reconstructed objects in the ROI with scattering strengths q₁ = 0.51 and q₂ = 0.62. The speed of sound of q₂ is varied and the ratio of the measured scattering ratio of the two coefficients q₂/q₁ is plotted as a function of frequency (squares). The reconstructed values are compared with the actual (circles).

A series of reconstructions were then simulated in order to demonstrate the possibility of using the method to detect multiple objects and larger occlusions. Three such examples are provided, representing varying spatial configurations and distances from the source transducer face. The first example (Fig 8a) consists of three scatterers placed diagonally within a relatively small ROI (8 mm × 8mm) plus an additional scattering source situated approximately 4 mm from the others. Each object was given equal scattering strength (q = 0.1). The reconstruction detected all objects with minimal spatial distortion (8b), but with clear variation in the scattering intensity. The second example is presented in Fig 8c as an inverted “V” situated approximately 18 mm from the ultrasound source. Here the objects were detected (8d), but with blurring of the object and enhanced reflection at the extremities. The third example occurred at a mean distance of 27.3 mm from the source (8e) consisting of a linear change in sound speed extending for 3 mm at a diagonal relative to the source. As with the previous example the line was blurred with a half-maximum intensity drop-off of under 1 mm, dimensionally consistent with the separation resolution between two objects.

Figure 8.

A series of simulations with multiple scatterers (right column) and their reconstruction (left column) demonstrating application at distances of (a) 3 mm to 14 mm, (b) 10 mm to 24 mm, and(c) 26 mm to 30 mm in front of the transducer.

V. DISCUSSION

The process of locating an object with a randomized and unfocused field seems, at first, counterintuitive. However, it is in fact the large variation in the imaging field that makes it possible to localize the position of scattering sources. It is particularly interesting that the two-dimensional reconstruction described here can be achieved using only a single receive channel. In the preliminary numeric investigation, it was observed that objects were better defined and more spatially localized, as compared to a synthetic and idealized B-mode signal. The smallest objects considered were less than 0.1X the center wavelength of the signal in the surrounding fluid.

Although in its present basic form, little more than speculation can be applied toward assessing utility to the method; the ability to detect objects would suggest that further investigation is warranted. It is stressed that although the theory was based on a point source/point receiver approximation, the simulations were full three-dimensional simulations, and considered the distortion introduced by finite size elements and radiation in all dimensions. Yet, the conditions displayed in this preliminary work are clearly idealistic, leaving much work still to be performed. For medical and biological application, experimental data is necessary in order to confirm the approach in actual tissues and with noise levels representative of in vivo situations.

Small objects, which can be hard to detect, and even harder to localize using present methods, may be both detectable and localizable with the random-frequency approach. Further, the approach acquires only a single channel of information, leaving the potential to acquire a large amount of data for creating time sequence imaging. One suggested medical use for such “M-mode” images is in conjunction with contrast agents to trace a single bubble along a vessel. While such images would probably not be possible in real time due to the processing time needed for image reconstruction, near-real-time motion image is conceivable. For example, the reconstruction phase of the algorithm typically took approximately 15 seconds, when benchmarked on a Windows XP 64-bit operating platform controlling two dual-core 3-GHz Pentium Xenon processors.

Since the reconstruction approach analyzes changes in density and compressibility separately, there is a prospect of creating separate density and speed-of-sound images. In this configuration, two objects with identical impedances could be placed in the ROI: one varying from the surrounding medium in density and the second varying in speed-of-sound. Provided the objects are adequately separated, traditional backscatter imaging, which is sensitive to impedance mismatch, would display both objects with equal intensity on the one image. In contrast, the randomized frequency reconstruction offers the potential ability to distinguish between the two.

The ability to perform imaging at reduced frequencies may find particular utility in transcranial applications. Clinical methods are presently limited to imaging through the temporal bone acoustic window near the ear, which allows only a limited view of the brain. However, recent research has shown that ultrasound can be delivered through thicker bone and with reduced distortion using shear modes of propagation within the bone itself. ²⁰ Further, reflected signals can return to the transducer in a similar manner and used to form ultrasound images ²¹. Despite reduced beam refraction, absorption in shear propagation is a stronger function of frequency than its longitudinal counterpart ²², and conditions at or below 1 MHz are significantly more favorable than existing transcranial probes that operate at or above 2 MHz. Development of lower frequency reconstruction methods will be necessary to create images with this approach.

It is not expected that hardware will limit the practicality of the method. The approach requires a broadband multi-channel driving system that, in fact, reflects design trends which are increasingly utilizing low cost broadband digital arbitrary waveform circuitry in combination with analog amplification and filtering components to form multi-channel amplifier systems. One such system, capable of over a thousand channels at 50-channels per circuit board has been described by Sokka et al.,²³ with a low cost $20/channel estimate for a broadband (0-10 MHz) system.

VI. CONCLUSIONS

This preliminary study demonstrates the process of two-dimensional object detection by a single receiving channel when using an unfocused field of randomized frequency sources. The algorithm was effective in detecting and separating 0.2-mm-diameter objects placed 1.5 mm from each other when using frequencies in the 0.25 MHz to 1.25 MHz bandwidth. Based on the results, it is concluded that an array could be used for noninvasive monitoring in a variety of acoustic situations. Future experimental work will involve verification of the approach in the laboratory, and examine its ability to detect objects and create images in human tissues. Meanwhile much work is required in optimizing the method for a particular bandwidth, frequency and region of interest.