A Markov Model Approach to Predicting Regional Tumor Spread in the Lymphatic System of the Head and Neck

Abstract

Radiation planning for cancer therapy is becoming more and more dependent on the prediction of microscopic tumor spread to regional lymph nodes for its success. It is known that microscopic spread tends to follow established lymphatic drainage pathways in the head and neck based on the location of the primary tumor. In this paper, we propose a novel model for the prediction of regional lymphatic involvement of head and neck squamous cell carcinoma based on primary tumor location and T-stage. The proposed model operates from first anatomical principles and basic stochastic techniques, and is validated against surgical data.

Introduction

Radiation Oncology is one of the physician’s best tools for treatment of tumors of the head and neck. Recent developments in the field have allowed for more precise dosages of radiation to irregular target volumes of the neck, making it a reasonable alternative to surgery in many cases. The effectiveness of these treatments, however, depends critically on the delineation of these target volumes to include regional lymph nodes to which metastases may have occurred.

Currently, clinicians must draw target volumes by hand. Because tumors metastasize along lymphatic drainage pathways, this process requires them to estimate many variables such as which lymphatic channels the tumor has taken and how far along them it has spread. Lymph nodes to which a tumor has spread cannot always be made visible with any imaging technology and there does not exist a computational tool to estimate their location; although some nodes may be recognized by PET scans, the treatment of occult diseased lymph nodes is critical in preventing recurrence and further metastasis.

Clinicians have defined a number of regions of the head and neck in order to establish some uniformity in terms of related lymphatic chains and node clusters.^{1, 2} These regions frequently make delineation of target volumes easier because entire regions are treated rather than single lymph nodes or smaller clusters. Surgical data has offered some insight into which regions are likely to contain positive lymph nodes in clinical situations and have shown some patterns in terms of regional spread. Generally, the longer a tumor is present and the larger it grows, the more likely distant lymphatic groups are to be affected.

The goal of the work that follows is to produce a theoretical model that predicts the distribution of microscopic spread in the head and neck as well as probabilities of finding positive nodes in each region. The approach uses a simple sequence of Markov models in conjunction with known lymphatic anatomical information in the Foundational Model of Anatomy (FMA)³ to produce a progression of nodal regions with assigned probabilities of disease. Previous work in this area has attempted to establish rules for the involvement of lymph nodes but has done so based on surgical data and not from first principles.⁴

Nodal Regions of the Head and Neck

Cancers of the head and neck tend to follow a reasonably predictable pattern of growth and spread de-fined most importantly by the anatomical surroundings of the initial tumor. Generally, the lymphatic spread follows the drainage patterns of regional lymph nodes and chains. Although surgical techniques originally incited the establishment of regions of the head and neck,^{5, 6} these regions are also useful in radiation therapy. Our model uses the established regions I–VI as well as proposed regions B (Buccal), P (Parotid), and RP (retropharyngeal)⁷ in order to generalize the predicted lymphatic spread (see Table 1).

Table 1.

Clinical Regions of the Head and Heck

Region	Nodal Group
Ia	Submental
Ib	Submandibular
IIa	(Anterior) Upper Jugular
IIb	(Posterior) Upper Jugular
III	Middle Jugular
IV	Lower Jugular
Va	(Upper) Posterior Triangle
Vb	(Lower) Posterior Triangle
VI	Anterior Compartment
P	Parotid
B	Buccal
RP	Retropharyngeal

Published Data

A small number of surgical studies have been performed on patients with tumors of the head and neck and serve as our primary method of validation. Unfortunately, very few studies detail both the extent of lymphatic metastases and the initial tumor’s T-stage. Because of the nature of the model, however, validation can be performed both with metastatic correlations to T-stage and metastatic correlations to nodal regions separately.

The surveys gathered for use in validation varied both in breadth and depth. Studies or aspects of studies that were deemed too small (n < 20) or too biased (e.g. only included patients with aggressive disease) were discarded. Additionally, studies and study components involving anatomy with which the FMA does not record lymphatic drainage had to be discarded.

Anatomical Information

Anatomical information for the model was retrieved from the FMA, which contains a reasonably complete set of lymphatic drainage pathways in the form of lymph chains for the head and neck with the notable exception of lymph nodes, which tend to vary between patients. Because the purpose of the model is to predict regions of spread, however, the lack of specific nodes was not considered problematic.

One shortcoming of the FMA was the lack of information about the head and neck regions for each of the lymphatic chains. This became particularly problematic because certain lymph chains span multiple regions; for example, the jugular lymphatic chain spans both region VI and region IV. In order to make the model more coherent, we supplemented the FMA’s anatomical data with these clinical regions to form an extended set of lymphatic chains that can be divided into subunits, where a single subunit is a regional part (region) of a lymphatic anatomical entity, for example, the part of the superior deep lateral cervical lymphatic chain in region III. The lymphatic drainage of each tumor site, thus, can be divided into a number of positions, where position i consists of the regional subunits that have exactly i subunits prior to them along any possible drainage pathways from the primary tumor site.

Model Specifications

Assumptions

Because the model is intended to derive predictions from anatomical principles, it assumes several things, the most important of which is that the probability of a metastasis at a particular position in the lymphatic drainage pathways depends only on the presence of cancer in the previous position. This implies that the spread of cancer cannot skip a site in the drainage pathway. Although this assumption is probably not biologically true, we feel that it is necessary to maintain the simplicity of the model and that it provides more clinically relevant data by allowing a physician to discern which nodes are upstream from a particular location of known or suspected disease. Additionally, the model assumes a constant relationship between T-stage and nodal metastasis; this is necessary because, in a radiological treatment scenario, the physician is unlikely to have any additional information about the tumor.

Input

The input to the model is a primary tumor site and a T-stage (1–4). The primary tumor site is used to query the FMA for lymphatic drainage and the lymphatic drainage of its subparts (for example, if the primary tumor site is “Ear” then the lymphatic drainage for the “Pinna” would also be queried), all of which is supplemented with head and neck clinical region information to form a series of lymphatic drainage positions from the primary site.

Structure

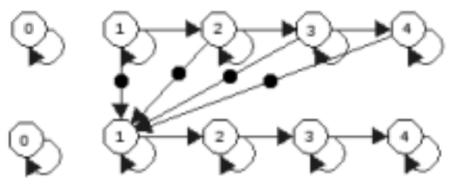
The model itself is made of a series of Markov models, one for each position along the lymphatic drainage pathway of the primary site. An additional “position 0” Markov model represents the primary tumor site has different transition probabilities than the lymphatic regions; the philosophy for this decision is that the initial tumor is unlikely to grow at rates equivalent to those of the diseased lymph nodes. Each other Markov model represents a position along the lymphatic drainage pathway and has five states, 0–4, each representing a state of growth of the cancer at that location. We use the term “state” here instead of “stage” in order to distinguish between the T or N stage of the tumor and an abstract local state of growth. State 0 represents no cancer and state 4 represents considerable disease. Each state s also has associated with it a probability q_s of metastasizing to the next position in the chain such that, given the probability distribution p_i (0 ≤ i ≤ 4) of being in state i at a specific position in the chain, the probability p′that the next position downstream will become diseased from microscopic spread is

$$p^{\prime }=\sum _{s=0}^4{p}_s{q}_s.$$ (1)

For a diagram of the Markov model, see figure 1.

Figure 1.

A diagram of two positions of the Markov model used in the model. Each edge represents a transition probability from one state of growth to another while each dotted edge represents an ‘output’ probability of metastasis, which affects the probability of the next position’s distribution being in state 1.

Execution

Initially, the probability distributions of each of the positions are set to be in state 0 with probability 1 with the exception of the 0th position (the primary tumor site), which has probability 1 of being in state 1. The model is then run for 4 × T iterations (where T is the T-stage of the cancer). The number of iterations was chosen arbitrarily and could be chosen as any monotonically increasing function of T so long as it is not changed after training the model. This flexibility is possible because the length of time represented by an iteration is abstract and the total time of growth is likely unknown. After each iteration, the probability of a given position metastasizing to the next position in the chain is calculated using equation (1), adjusted against the probability that it has already metastasized, subtracted from the probability that the next position is in state 0, and added to the probability that the next position is in state 1. The probability ϱ_k that position k in the pathway has already metastasized is followed in order to assure that metastatic probabilities are kept to scale; assume, for example, that the probability of metastasis from position 5 to position 6 was calculated after two iterations to be μ₂. Position 6’s probability distribution will be accordingly updated and ϱ₅ will be set equal to μ₂. After the next iteration, the probability will be μ₃ > μ₂; if μ₂ = 0.5, then the net probability of metastasis will be greater than 1.0. Instead of allowing this, the actual update to position 5’s probability distribution is not μ₃, but (μ₃ – ϱ₅). This causes the probability distribution of each position to reflect the total probability that metastasis has occurred up to that iteration. The probability matrix P used in the Markov models and the probability of metastasis m are given below:

$$\begin{array}{l}P=\left(\begin{array}{ccccc}1.00& 0.00& 0.00& 0.00& 0.00\\ 0.00& 0.50& 0.50& 0.00& 0.00\\ 0.00& 0.00& 0.50& 0.50& 0.00\\ 0.00& 0.00& 0.00& 0.50& 0.50\\ 0.00& 0.00& 0.00& 0.00& 1.00\end{array}\right)\\ m={\left(\begin{array}{ccccc}0.00& 0.60& 0.70& 0.80& 0.90\end{array}\right)}^T\end{array}$$

Additionally, the matrix P′and corresponding m′vector are used for the initial tumor site:

$$\begin{array}{l}{P}^{\prime }=\left(\begin{array}{ccccc}1.00& 0.00& 0.00& 0.00& 0.00\\ 0.00& 0.90& 0.10& 0.00& 0.00\\ 0.00& 0.00& 0.90& 0.10& 0.00\\ 0.00& 0.00& 0.00& 0.90& 0.10\\ 0.00& 0.00& 0.00& 0.00& 1.00\end{array}\right)\\ m^{\prime }={\left(\begin{array}{ccccc}0.00& 0.20& 0.40& 0.60& 0.80\end{array}\right)}^T\end{array}$$

The probabilities of the matrix P were chosen with the philosophy of keeping the model as simple as possible; the probability of a position’s cancer growing or staying the same is one half. The probability of metastasis m was chosen to be simple, but was chosen relatively high because of the tendency for multiple nodal groups in multiple regions to be involved in any cancer (thus for cancer to move relatively easily through a lymphatic pathway). The matrix P′ was chosen in order to give a reasonable distribution of time in each state for a long simulation (e.g. for T = 4, 16 iterations), and the vector m′ was chosen to be a simple linear distribution over the probability space. For a pseudo-code representation of the stochastic process of the model, see figure 2. Note that the model used in this paper was not trained on data but chosen arbitrarily with the above justifications as a proof of concept.

Figure 2.

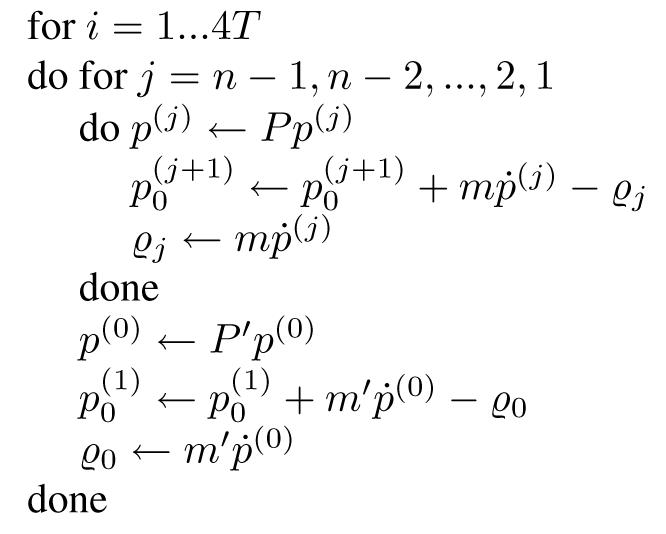
Pseudo-code describing the stochastic process in the lymphatic drainage model.

We define the variables used in the pseudocode as follows:

Let n be the number of positions in the lymphatic pathway downstream from 0.

Let g be the number of states of growth above 0 (4).

Let P and P′ be transition probability matrices and m and m′ be metastasis probability vectors, as described above.

Let {ϱ₀, ϱ₁, ..., ϱ_n-1} be the set of probabilities that state j has already metastasized (initially 0).

Let {p⁽¹⁾, p⁽²⁾, ...p⁽ⁿ⁾} be the set of vectors that express the probability that a given position is in a given for state of growth; p^(j)_k is the probability that position j is in state k of growth.

Let T be the T-stage of the primary tumor.

Following this procedure, the probability of microscopic presence at any given state j is equal to the sum:

$$\sum _{i=1}^g{p}_i^{(j)}$$

After the model has been run for the appropriate number of iterations, the net probability of presence of cancer at each state is calculated by summing over the probabilities of cancer at each growth state. Note that this is not a Monte Carlo approximation of the probabilities but an exact analytical determination of the model’s distribution given the inputs.

Validation

In order to validate the proposed model, we have compared it to two surgical studies. The studies involved patients with cancer of the oropharynx and hypopharynx (n = 204)⁸ and cancer of the oral cavity including the tongue, floor of mouth, gum, retromolar trigone, and cheek (n = 501).⁹ The results of our model’s predictions (each run with an initial T-stage of 1 or 4), along with the results of each study, are summarized in tables 2 and 3. In both tables the percentages of the model are predicted probabilities of finding microscopic disease in lymph nodes at that site.

Table 2.

Comparison of our model’s predictions with a surgical study of the oral cavity.⁹ Percentages are given.

	I	II	III	IV	V	VI
Tongue (Prophylactic Dissection)
Model (T = 1)	28	19	16	0	0	0
Study	14	19	16	3	0	0
Tongue (Therapeutic Dissection)
Model (T = 4)	50	42	35	23	0	18
Study	32	50	40	20	0	0
Floor of Mouth (Prophylactic Dissection)
Model (T = 1)	28	12	12	19	28	19
Study	16	12	7	2	0	0
Floor of Mouth (Therapeutic Dissection)
Model (T = 4)	50	35	35	42	50	42
Study	53	34	32	12	7	0
Gum (Prophylactic Dissection)
Model (T = 1)	28	19	19	12	19	12
Study	27	21	6	4	2	0
Gum (Therapeutic Dissection)
Model (T = 4)	50	42	42	35	42	35
Study	54	46	19	17	4	0

Table 3.

Comparison of our model’s predictions with a surgical study of oropharynx and hypopharynx.⁸ Percentages are given. Note that prophylactic dissection of the piriform sinus and pharyngeal wall were omitted because of a small sample size (n < 20). Additionally, results on the pharyngeal wall and piriform sinus or omitted because of the absence of lymphatic drainage information in the FMA.

	I	II	III	IV	V	VI
Base of tongue (Prophylactic Dissection)
Model (T = 1)	0	19	19	12	0	6
Study	0	19	14	9	5	0
Base of tongue (Therapeutic Dissection)
Model (T = 4)	0	42	42	35	0	29
Study	10	72	41	21	9	0
Tonsillar fossa (Prophylactic Dissection)
Model (T = 1)	0	28	19	12	0	6
Study	4	30	22	7	0	0
Tonsillar fossa (Therapeutic Dissection)
Model (T = 4)	0	50	42	35	0	29
Study	17	70	42	31	9	0

Discussion

The intent of the model is to demonstrate the plausibility of quantitatively predicting the microscopic spread of tumors using anatomical data and basic stochastic techniques. Accordingly, the model was kept intentionally simple. An ideal model would likely employ different transition matrices for different anatomical units and would be trained based on extensive analysis of surgical data. Each Markov model in the process is essentially a hidden Markov model with probabilities of metastasis as outputs; thus methods exist for training ideal outputs given a set of acceptable probabilities.

In examining the results of the validation, there is a high correlation between the predictions for regions II, III, and IV of the neck and a much lower correlation for region I. Many lymphatic pathways drain from region II to III to IV, which are widely conjectured to be the most predictable of the head and neck’s lymphatics. Regions IV, V, and VI, however, were frequently over-predicted by the model (e.g. the floor of mouth and the gum). This may be due in part to the lack of information concerning the proportion of lymphatic drainage that goes to various lymphatic chains. For example, in the gum (gingiva), the submandibular lymphatic chain (I) drains into both the jugulo-omohyoid chain (III) and the superior deep lateral cervical lymphatic chain (V), but probably does not drain as intensely into the latter as the former. Additionally, the model only attempts to predict metastasis to lymph nodes on established drainage pathways; no attempt is made to explain the microscopic spread to regions that may simply be nearby or that may receive metastases via other means. For example, the base of the tongue (listed in the FMA as “Root of tongue”) drains primarily through the basal lingual lymphatic tree (B) which drains into the jugulo-omohyoid lymphatic chain (III) and the jugulodigastric lymphatic chain (II). Based on the base of tongue’s proximity to region I, it is not surprising that tumors might be found there surgically, but because the lymphatic drainage does not include region I, our model did not predict it.

An additional problem that was encountered was the lack of specificity in the studies and the difference in vocabulary of the FMA. The “tonsillar fossa”, for example, being an anatomical space, is not listed in the FMA, but the “Palatine tonsil” and “Soft palate” might be considered reasonable alternatives. Additionally, because the model treats all parts of a queried anatomical unit equally, the reported probabilities are equivalent to the sum of queries of all of the unit’s parts. For example, a query on the cheek would be equivalent to taking the combined results from a query of the wall of the cheek and of the Parotid gland.

Although the correlation to surgical data is not perfect, we feel that the initial results demonstrate the potential for a similar model to accurately predict regional tumor spread in the lymphatic system. Because the best results were obtained for areas in which lymphatic drainage extends throughout the neck (e.g. the tongue) and because the model tends to over-predict rather than under-predict tumor metastasis, we suspect that the addition of information regarding the relevance of drainage pathways would most improve the results. The relative success suggests that a stochastic approach to metastatic prediction is plausible. Future work would establish a more complete anatomical and probabilistic model.