An Effective General Purpose Approach for Automated Biomedical Document Classification

Abstract

Automated document classification can be a valuable tool for biomedical tasks that involve large amounts of text. However, in biomedicine, documents that have the desired properties are often rare, and special methods are usually required to address this issue. We propose and evaluate a method of classifying biomedical text documents, optimizing for utility when misclassification costs are highly asymmetric between the positive and negative classes. The method uses chi-square feature selection and several iterations of cost proportionate rejection sampling followed by application of a support vector machine (SVM), combining the resulting classifier results with voting. It is straightforward, fast, and achieves competitive performance on a set of standardized biomedical text classification evaluation tasks. The method is a good general purpose approach for classifying biomedical text.

Introduction

Text classification is the process of using automated techniques to assign text samples into one or more of a set of predefined classes. The text samples may be of any length including abstracts, titles, sentences, and full text documents. The techniques used to accomplish this are based on machine-learning algorithms, and typically require a set of training data having known classifications on which to fit a model, which is then used to classify previously unseen data. This simple approach has many potential uses in biomedicine including automated document triage for genomics database annotation¹, pre-filtering of search results for identification of high quality articles for evidence-based medicine², identification of biological entities in free text³, and reduction in human labor needed to conduct systematic drug reviews⁴.

While biomedical document classification benefits from many of the existing developments in more general machine learning and text classification research, biomedical document classification does present its own unique challenges. Much of the computer science research focuses on evaluating effectiveness by measuring algorithm accuracy, the fraction of correct predictions. For biomedical text classification many problems have only two classes: the positive class of documents that has the desired characteristics, and the negative class that does not. In biomedical document classification the percentage of positive documents tends to be low. Clearly, measuring classification accuracy is not useful when 99% of documents are negative.

Furthermore, biomedical tasks typically assign unequal costs to missing a positive document versus mistakenly assigning a negative document as a positive. In these scenarios, the positive documents tend to be rare, and mistakenly classifying any of them as negative is undesirable. Often, utility is the metric of performance, which is defined as:

$$U=u_r\times true\_positives+u_{nr}\times false\_positives$$ (1)

where u_r is the value of correctly predicting a positive document, and u_nr is the (usually negative) value of incorrectly predicting a negative document.

Finally, there are many text classification algorithms and approaches, and it is not always feasible to study and compare a large selection of algorithms to determine the best one to use. Tuning an algorithm’s parameters for a given task may be costly in terms of time and training data. Clearly what is needed is a uniform, easily applied approach that takes into account the disparate costs of positive and negative classification mistakes and works well on a wide variety of tasks.

Here we present our general approach to biomedical text classification. We show that this approach can be applied in a uniform manner, with minimal customization for the individual task. We then compare the performance of our method to previous methods used on the same test collection.

Methods

Our classification system uses word-based feature generation and chi-square feature selection, followed by a support vector machine (SVM) classifier wrapped with cost-sensitive resampling. We then apply and test our method on the four document triage tasks from the TREC 2005 Genomics track data. This collection consists of training and test sets of full text documents. Each document has been assigned positive or negative in four document triage tasks performed by the Mouse Genome Informatics group (MGI at http://www.informatics.jax.org/) when reviewing journal articles for information about mouse gene alleles, embryological expression, GO annotation, and tumor biology.

Classification system

For each document in the training and test collections, the classification system generates a binary feature vector. For each document in the data set used here, the features we included were: 1) every word from the title and abstract with common English word stop list removal and Porter stemming, 2) all assigned MeSH terms, and 3) MGI mouse gene identifiers assigned to the documents by an automated process.⁵ We also removed any document from the process that did not include the MeSH term Mice. This is not an essential step in our general method, but is useful and easy to apply for organism specific classification tasks such as we are studying here.¹ When classifying documents in the test collection, a document without the MeSH term Mice was predicted a negative.

Each component in the binary feature vector is a one or a zero, signifying the presence or absence of a feature. This process may generate tens of thousands of features per data set, and can become unmanageable. We therefore reduce the feature set size by using only the features statistically significantly different between the positive and negative training documents, using a chi-square test with an alpha significance value of 0.05.

We then train an SVM-based classifier, SVMLight⁶ on the classified training document vectors. SVM classifiers have become very popular because of their speed, accuracy, and ability to generalize well by maximizing the margin between positive and negative training data.⁷ However, the theory on which SVMs are based optimizes for accuracy, which can be undesirable for biomedical text classification. SVMLight includes a parameter to trade off the cost of misclassifying positive and negative documents. However, both ourselves and others have found this parameter to be ineffective for biomedical tasks.⁸

Instead, we account for asymmetric document misclassification costs using the document resampling method of Zadronzy, Langford, and Abe⁹, which we summarize below. As far as we are aware, this method of accounting for asymmetric costs has not been applied to either general text or biomedical document classification. In simple terms their theory states that an optimal error rate classifier for a distribution D′ is an optimal cost minimizer for another distribution D_test and the two distributions are simply related by:

$$\frac{D^{\prime }}{D_{test}}=k\times Cost(c)$$ (2)

where Cost(c) is the cost of a misclassifying a sample of class c from distribution D_test, and k is a constant.

This means that to create an optimal cost minimizer, all we have to do is resample the original training samples appropriately and then train our optimal error rate classifier on these samples. For the two class case, to resample the training data, we must select the training data so that the ratio D′/D_test reflects the correct relative misclassification costs for the positive and negative samples.

The resampling process includes a few caveats. First, to avoid over-fitting we need to ensure that the samples remain independent and each is sampled with the correct probability. Standard sampling both with and without replacement do not meet this criteria. Instead cost-proportionate rejection sampling is applied. With this sampling method, each sample is independently included or not given the probability P of including a given sample of class c from the set of classes C, where that probability is determined by the misclassification cost Cost(c) for the sample, divided by the maximum sample misclassification cost:

$$P(c)=\frac{Cost(c)}{max[Cost(c),\forall c∊C]}$$ (3)

This resampling method assumes that the class probability distributions are the same in the test collection as in the training data. This may or may not be the case. If the probability distribution of the test data is unknown, then it is assumed to be the same as in the training data. However, if the training and test class probability distributions are known to be different, as is the case with the TREC Genomics data, we have developed a means to account for this by readjusting the sampling probabilities.

Given that D_train and D_test are the class probability distributions of the training and test data, we define the ratio as a function of the class:

$$F(c)=\frac{D_{test}}{D_{train}}$$ (4)

Substituting equation (4) into (2) and then the result into (3), and canceling the factor of k gives:

$$P(c)=\frac{Cost(c)\times F(c)}{max[Cost(c)\times F(c),\forall c∊C]}$$ (5)

In the common two class case this reduces to a simple formula. Without losing generality, we set the cost of misclassifying a positive sample to Cost(+) and a negative sample to one. Given that the proportion of positive and negative samples in the training and testing sets are P_train(+), P_train(−), P_test(+), and P_test(−), then the resampling probabilities P_r(+) and P_r(−) are:

$$P_r(+)=1$$ (6)

$$P_r(-)=\frac{P_{test}(-)\times P_{train}(+)}{P_{test}(+)\times P_{train}(-)\times Cost(+)}$$ (7)

Note that if the class probability distributions in the training and test sets are equal, then P_r(−) equals 1/Cost(+). Furthermore, we define the positive class weight w_p as the simple arithmetic inverse of P_r(−). This is just for convenience, as it transforms the typically small probabilities produced by Equation (7) into values that are more easily compared and given as classifier input parameters.

Since we are accounting for misclassification cost using a resampling method, it is also advantageous to repeat the resampling a number of times and combine the results. This will diminish the chance of degenerate resampling and increase the consistency and average performance of the system. In order to do this, we perform several repetitions of cost-proportionate rejection sampling followed by SVM classifier training, using the default SVMLight settings with the linear kernel. The result is a set of SVM vector weights which when applied to a test sample feature vector each produce a class prediction for the sample. We combine these predictions using a simple voting scheme, if the majority of predictions are positive then we classify the document positive, otherwise the document is classified negative.

Evaluation

To evaluate our approach we applied our method to the four biomedical document triage tasks used in the TREC 2005 Genomics Track classification task.¹ Performance on each task was computed using a utility measure, which assigned a positive value of U_r for correctly classified positive samples (true positives) and a penalty of minus one for incorrectly classified negative samples (false positives). Since making an error on a positive sample decreases the utility by U_r, this value can be interpreted as Cost(+). Scores were then normalized by the maximum possible score for each task. The values of U_r are shown in Table 1, along with the proportion of positive and negative samples in both the training and test collections for each task. Note the wide range of values for U_r, and the differences in class proportions between the training and test collections for the tumor task. Table 1 also includes the computed resampling probability for the negative classes for each task using equation (7).

Table 1.

Comparison of sample frequency for TREC 2005 Genomics data classification tasks

Task	Corpus	N	N(+)	N(−)	P(+)	P(−)	Ur	Pr(−)	wp
Allele	Train	5837	338	5499	0.0579	0.9421	17.00	0.0622277	16.07
	Test	6043	332	5711	0.0549	0.9451
Expression	Train	5837	81	5756	0.0139	0.9861	64.00	0.0124371	80.42
	Test	6043	105	5938	0.0174	0.9826
GO	Train	5837	462	5375	0.0792	0.9208	11.00	0.0834028	11.99
	Test	6043	518	5525	0.0857	0.9143
Tumor	Train	5837	36	5801	0.0062	0.9938	231.00	0.0080906	123.60
	Test	6043	20	6023	0.0033	0.9967

Results

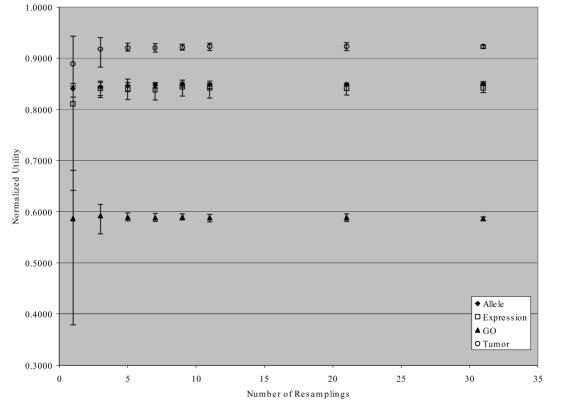
We first determined the correct number of resamplings to use for comparison with prior results on this data. Figure 1 shows the mean, maximum and minimum (shown as error bars) normalized utility scores for each of the four tasks using between one and 31 resamplings, with each set of resamplings repeated 10 times. Both the average performance increases and the variability between the maximum and minimum scores decrease with the number of resamplings. We chose to use 21 resamplings as a good balance between time, utility, and variability, achieving good performance on all four tasks.

Figure 1.

Normalized utility (Un) mean, maximum and minimum by task and number of resamplings

Table 2 presents comparative normalized utility scores (U_n) of several classification systems applied to this test collection. In the table, each classifier system was given the same set of chi-square selected binary features. We compare not only the full approach proposed here, but also the same system without training set correction, SVMLight without resampling at various settings, and the best entry for each task of all entries submitted to TREC 2005. These last are the highest scoring entry for each task which consisted of up to three submissions from each of the 19 participating groups.¹

Table 2.

Comparison of normalized utility scores for various classifier systems

Task	System	Un
Allele	SVMLight default	0.5863
	SVMLight -j option = Ur	0.7050
	SVMLight -j option = wp	0.7050
	SVM with Cost Proportionate Rejection Downsampling x21, P(−) = 1/Ur	0.8464
	SVM with Cost Proportionate Rejection Downsampling x21, P(−) = 1/wp	0.8489
	TREC 2005 Best	0.8710
Expression	SVMLight default	0.1423
	SVMLight -j option = Ur	0.3104
	SVMLight -j option = wp	0.3104
	SVM with Cost Proportionate Rejection Downsampling x21, P(−) = 1/Ur	0.8403
	SVM with Cost Proportionate Rejection Downsampling x21, P(−) = 1/wp	0.8405
	TREC 2005 Best	0.8711
GO	SVMLight default	0.1478
	SVMLight -j option = Ur	0.3998
	SVMLight -j option = wp	0.3891
	SVM with Cost Proportionate Rejection Downsampling x21, P(−) = 1/Ur	0.5891
	SVM with Cost Proportionate Rejection Downsampling x21, P(−) = 1/wp	0.5888
	TREC 2005 Best	0.5870
Tumor	SVMLight default	0.1500
	SVMLight -j option = Ur	0.3489
	SVMLight -j option = wp	0.3489
	SVM with Cost Proportionate Rejection Downsampling x21, P(−) = 1/Ur	0.7337
	SVM with Cost Proportionate Rejection Downsampling x21, P(−) = 1/wp	0.9229
	TREC 2005 Best	0.9433

For all tasks it is clear that SVMLight at the default settings performs very poorly on these tasks. Furthermore, adjusting the cost-factor (-j parameter) helps, but not nearly enough to produce competitive performance. No significant increase in performance is gained on any task by using the distribution adjusted weight w_p in place of the task specified U_r.

On the other hand, our proposed approach of SVM with corrected cost proportionate rejection sampling performs very well on all four tasks. Performance for the full system, using the corrected value 1.0/w_p for downsampling the negative cases produces normalized utilities about equal to the best submitted run for each of the four tasks. In fact, for the GO task, the normalized utility is slightly (insignificantly) greater than the best submitted run.

For three of the four tasks, the difference between using 1/U_r to downsample the negative class and the corrected P_r(−) is minimal. However for the tumor task, which is the task with the largest disparity between positive case frequency in the training and test collections, the difference is quite large. Without correction, performance on the tumor task is somewhat below median compared to other TREC 2005 entries. With correction, performance is comparable to the best submitted run.

Our general system includes the chi-square feature selection method described above. One area of debate with SVM-based text classification is whether the feature set should be reduced as we have done here, or the full feature set given as input to the classifier. Previous work has argued that the full feature set produces better results.⁷ Table 3 shows the performance of our system on each of the four tasks, selecting different numbers of features by varying the alpha threshold of the chi-square association test. While the differences between alpha values of 0.05 and 0.10 are small, including all features produces inferior performance across all four tasks.

Table 3.

Comparison of normalized utility (Un) for various levels of alpha feature selection

Task	alpha
	0.05	0.10	All features
Allele	0.8489	0.8483	0.8310
Expression	0.8405	0.8413	0.6294
GO	0.5888	0.5903	0.5575
Tumor	0.9229	0.9147	0.6645

Discussion

SVM by itself did not produce good results on these biomedical text classification tasks. However, the combination of chi-square binary feature selection, corrected cost-proportionate rejection sampling with a linear SVM, repeating the resampling process and combining the repetitions by voting is an approach that uniformly produces leading edge performance across all four tasks. Other TREC submitted systems performed at this level on only a subset of the tasks.

The optimal number of repetitions may be dependent upon the problem as well as the training data set size. However, for the tasks studied here, even five repetitions results in greater and more stable performance than a single resampling. Furthermore, 21 or so repetitions were more than adequate for these tasks. This is a much smaller amount than the 100–200 resamplings Zadronzny, et al. used in their original paper. However, that work studied numeric and not text data, and the data sets were much larger. More work is needed to understand the relationship between optimal number of resamplings and training set size.

Feature set reduction using chi-square produced consistently better results than using all features. Performance was not particularly sensitive to the choice of alpha, and 0.05 was a good default value. These results are in contrast to the recommendations of others such as Joachims, and may also be somewhat dependent upon the training set size. If the number of features is large as compared to the number of training samples, there may not be enough data to drive the weight of insignificant features to zero. For biomedical document classification, training sets are most commonly created by human review, and therefore extremely large training sets are unusual. Training collections on the order of 100’s to 1000’s of documents as with the TREC datasets are much more common.

It should be noted that the system trains much faster than the standard SVM approach, even with the repeated resamplings. This is because SVM algorithms are polynomial or greater in training time, and the downsampled training sets are much smaller than the original training set. On the tumor task, for example, a training set resampling consists of all 462 positive documents, but only about 8% of the 5375 negative samples, resulting in a resampled size of about 15% of the original. Even at 21 resamplings, this process completes much faster than training on the full set. Classification remains a very rapid process of one vector dot product per resampling and is slower than standard SVM by a simple constant factor equal to the number of resamplings.

Conclusions

The general-purpose biomedical text classification method that we propose here includes features based on document words, as well as MeSH terms and normalized biological entity identifies when available. This feature set is then reduced using a chi-square test for significant differences between positive and negative samples. The reduced binary feature vectors of the training data are then resampled using corrected cost proportionate rejection sampling, with the resulting training data fed into a standard linear kernel SVM implementation. The resampling process is repeated a modest number of times (5 to 31), and the results of the individual trained classifiers combined by voting.

The method requires no task-specific hand-tuning of parameters or knowledge, and can flexibly incorporate available domain specific features such as MeSH terms and normalized named entities. Because of its simplicity, sensitivity to asymmetric error costs, speed, overall high performance, and ability to encompass a wide array of problems and feature types, we recommend this method as a standard, baseline approach to biomedical text classification problems.