Set-based Cascading Approaches for Magnetic Resonance (MR) Image Segmentation (SCAMIS)

Abstract

This paper introduces Set-based Cascading Approach for Medical Image Segmentation (SCAMIS), a new methodology for segmentation of medical imaging by integrating a number of algorithms. Existing approaches typically adopt the pipeline methodology. Although these methods provide promising results, the results generated are still susceptible to over-segmentation and leaking. In our methodology, we describe how set operations can be utilized to better overcome these problems. To evaluate the effectiveness of this approach, Magnetic Resonance Images taken from a teaching hospital research programme have been utilised, are used to reflect the real world quality needed for testing in patient datasets. A comparison between the pipeline and set-based methodology methodologies is also presented.

1. Introduction

The need for non-invasive imaging techniques has been the main reason attributed to the growing importance of Magnetic Resonance Imaging (MRI) [1] in the biomedical field. MRI, with its absence of ionizing radiation, superb soft tissue differentiation and high sensitivity to exogenous contrast agents, permits unequalled imaging of tissue structure and some functional parameters. From the earliest use of MRI, image processing techniques have been critical to optimizing image quality, reducing artifacts and improving tissue differentiation. One of the most important and complex tasks is image segmentation, which has numerous applications, but which is especially important for quantitative image analysis.

Image segmentation in medical imaging refers to the delineation of the tissue of interest from the rest of the tissues in the medical image. The current practice in hospitals to perform this task is through manual tracing of the tissue(s) of interest on a graphics workstation. Trivial as the task may sound, the actual process is tedious and time-consuming; particularly as image acquisition techniques now permit rapid acquisition of thousands of images. Furthermore, it has been shown that while a single human operator can have relatively high inter-examination consistency, there is quite poor inter-operator agreement if there are multiple observers tracing the same examination. Many segmentation algorithms have been proposed throughout the years using MR Image data. However, due to the relatively noisy quality and high artifact level that can be present in MR images, problems have remained with these algorithms.

Two of the main problems are over-segmentation and under-segmentation. Over-segmentation refers to over-cutting that occurs during the segmentation process. This means that fragments of the tissue of interest are omitted from the segmentation result, resulting in incompletely segmented tissue(s) of interest. Under-segmentation, also commonly known as leaking, refers to the inclusion of unwanted regions in the segmentation result. Many causes for these problems have been identified, ranging from the presence of noise, which affects image quality, to the complex geometrical properties of tissues in the human body. Although all of these reasons are to be taken into consideration, in general, these factors cannot be changed significantly; for example, the complex geometrical properties of tissues are intrinsic to the patient. As a result, the focus on tackling the problems of over-segmentation and leaking has shifted to statistical-based algorithms. Hybrid approaches have also been proposed to integrate various algorithms in an attempt to overcome their individual weaknesses. In this paper, we discuss and analyze different hybrid approaches with respect to a prototype implementation targeted at segmentation of the kidney from temporally resolved contrast-enhanced MRI scans.

2. Hybrid Approaches

Many individual segmentation algorithms have been proposed throughout the years. These algorithms include region-growing [2, 3] level-sets [2, 3, 4, 5], deformable models [2, 3, 6, 7, 8, 9], fuzzy-connectedness [2, 3, 10], and so on. Although these algorithms have delivered reasonable results, the segmentations yielded are still very much subject to over- and under-segmentation. Furthermore, these algorithms usually require a substantial amount of initialization processing, thus limiting their potential for routine clinical usage. Although the basic concept for using hybrid approaches lies in the belief that the strengths of one algorithm may overcome the weakness of others, different approaches to integration of such varying algorithms have been proposed. Over the years, many hybrid approaches have used a pipeline methodology, where the output of an algorithm is the input to the next algorithm. To explore the feasibility and potential effectiveness from a different perspective, we propose an alternate method, using a set-based cascading approach to integrate the algorithms has also been proposed. In this approach, the segmentation results from different algorithms are integrated using different set operations to yield potentially improved results.

3. Pipeline Methodology

In the pipeline methodology, the algorithms and components of the approach are arranged in series. Three different components can be found in this approach: the initiator, terminal and processor. The initiator starts the pipeline. Such a component takes in the source image, with the relevant parameters if required, and will perform the first processing task in the pipeline. The results from the initiator are passed on to the processor or the terminal. The terminal, on the other hand, stops the pipeline. It takes in the input from its predecessor, either an initiator or a processor, and returns the final output of the hybrid approach. A processor works as an intermediate component of the system as it takes in input from other components and its output will become input to their subsequent components.

Although the pipeline methodology displays promising results, tThe nature of the pipeline may give rise to pitfalls and errors. The main problem is that the output of the predecessor may be an imperfect segmentation, such that quality of the results generated in subsequent components will be bounded by imperfect segmentation. For example in T.Pavlids and Y. T. Liow’s work [13], the image segmented using a region growing algorithm has many false edges and cannot be fed directly into the next algorithm. Instead it has to be separately processed to differentiate the true and false edges. Hence the performance of this algorithm depends on how well the true edges can be identified.

There are, however, some pipeline approaches that have demonstrated promising results. Some examples involve the integration of the fuzzy-connectedness (FC), Voronoi-Diagram (VD) and deformable model (DM) [10, 11, 12], and the integration of the Gibbs Prior and the deformable model.

In the integration of FC, VD and DM, the initiator of the pipeline makes use of the fuzzy-connectedness algorithm. In this step, an initial segmentation of a region that contains the tissue of interest is first generated using the FC method. Statistical analysis is performed on the sample region generated in the earlier step, in the three color channels, Red, Green, and Blue (RGB), over the two color spaces, Hue, Value, and Chroma (HCV) to derive a homogeneity operator. Following this, the VD algorithm performs classification of the segmentation generated in the predecessor component using the homogeneity operator obtained during the statistical analysis as the multi-channel operator. The final step of the pipeline uses the DM method to obtain a final boundary from the results of the previous steps.

Although this integration approach has obtained promising results, one may argue that the final result is dependent on the previous step, leading to the problem of local minimum. Therefore, to further improve the effectiveness of the integration, the problem of the local minimum needs to be tackled.

4. SCAMIS

In our proposed SCAMIS approach ¹, the integration of different processing stages does not occur at the algorithm-level, but carried out on the results. The algorithms are involved in generating the initial image for further processing and the images generated are subsequently combined using the union operation. This approach aims to tackle the issue of local minimum by assuming that the probability for one algorithm to produce an over-segmented image is higher than the probability for all algorithms in the integration pool to do so. In this way, only one image from one of the algorithms needs to accurately delineate the tissue of interest, in order for the final segmentation to be reasonable. Furthermore, combining segmentation results using the union operation have has shown to yield an image which will contain less, if not equal amount of over-segmentation, manifested as holes, when compared to individual algorithms. Although it may seem trivial that the union operation on the images will reduce over-segmentation at the expense of leaking, in a typical set-based cascading hybrid approach, the leaking is reduced at the later stages either by the intersection or the difference operation. We have implemented and tested a set of different techniques using the set-based cascading approach. These techniques include the SCAMIS-Over-segmentation Prevention (SCAMIS-OP) and the SCAMIS-Under-segmentation Prevention (SCAMIS-UP) approach.

4.1 SCAMIS-OP

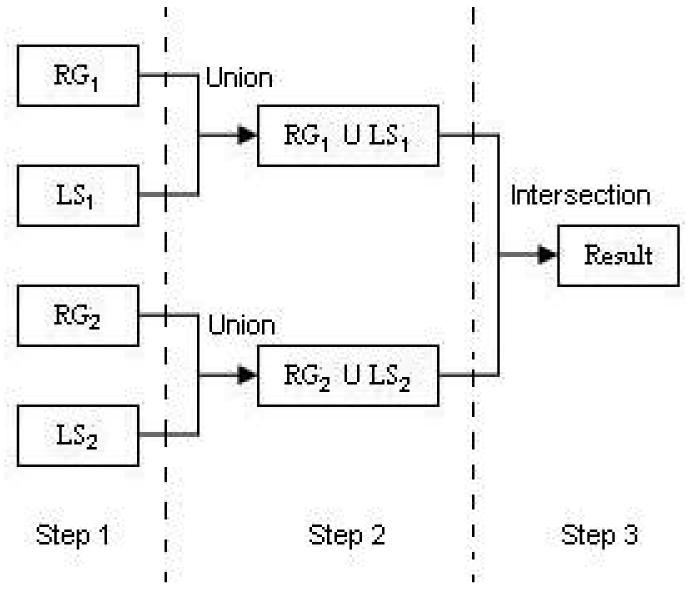
The SCAMIS-OP approach technique has three steps: It works on four images generated using two segmentation approaches which is usually include a region-based approach and a boundary based approach using two seed points which we call S1 and S2. Hence the four images generated are RG1 (region based with S1), RG2 (region based with S2), LS1 (boundary based with s2) and LS2 (boundary based with S1).

Step 1

Segment the image using region based approach with seed point S1 and S2 giving us RG1 and RG2 respectively. Then segment the image using boundary based approach with seed point S1 and S2 giving us LS2 and LS1 respectively.

Step 2

The images RG1 and LS1, and RG2 and LS2 are combined using the union operation. We call the two combined images U1 and U2.

Step 3

The images U1 and U2 are combined using the intersect operation giving us the resultant image, R.

As we have discussed above the union operation will reduce over-segmentation, . however Tthe problem of leaking, however, will also increase as the leaking region are also combined in the images. Hence in step 3 we will reduce leaking. Although this step seems trivial, we are able to obtain satisfactory results as we are using two different seed points and two different segmentation algorithms which work on exactly opposing principles.

4.2 SCAMIS-UP

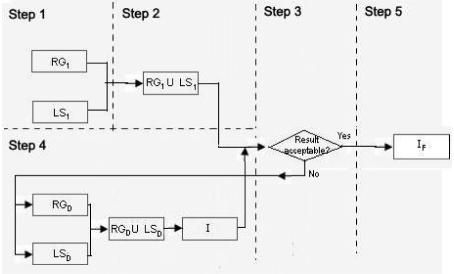
In the set-union-difference approach technique we make use of two segmentation approaches (again a region based and a boundary based approach) with two different seed points each.

Step 1

Segment the image using a boundary based approach and a region based approach. Generate two images RG₁ and RG₂.

Step 2

RG1 and RG2 are then combined using the union operation to reduce over segmentation.

Step 3

This step checks if there is leaking in step 2, if so we proceed to step 4 otherwise stop.

Step 4

For each tissue adjacent to the tissue of interest where leaking occurs, two segmentation images are generated respectively. All the images are then combined using the union operation, before the result is subtracted from the union of RG1 and RG2 o form I.

Step 5

Region growing is then performed on I to yield IF in an attempt to alienate any disjoint regions to the tissue of interest that are generated from the difference operation.

5. Experimental Evaluation

The Insight ToolKit (ITK) [2] identifies three factors that are critical in the evaluation of segmentation methods [14]. These three factors are: precision, which represents repeatability of segmentation taking into account all subjective actions in achieving the result, accuracy, which corresponds to the extent to which the result matches the ideal segmentation, and efficiency, which embodies the practical aspect of the algorithm respectively. Even though these three factors are independent, changes made to the method in an attempt to improve one factor, will still inevitably affect the others. Therefore in evaluating a segmentation method, all the three factors must be taken in consideration instead of independently.

We have performed a preliminary evaluation on the two set-based approaches techniques based on the accuracy of the segmentation methods. We adhered to the main motivation of segmentation, which is to develop segmentation results of quality comparable to human manual cutting of the MR images. Three formulas, over-segmentation rate (OR), under-segmentation rate (UR) and Overall Error rate (ER) are proposed to achieve the accuracy factor. Three variables that are used in the formulas are, the number of pixels that should be included in the segmentation result but are not, denoted by Q_p the number of pixels that should not be included in the segmentation result but are included, denoted by U_P and finally the number of pixels that are included in the desired tissue of interest based on the template image generated by manual cutting, denoted by D_P.

$$OR=O_p/(U_p+D_p)$$ (1)

$$UR=U_p/(U_p+D_p)$$ (2)

$$ER=(O_p+U_p)/D_p$$ (3)

Charts 1 to 6 summarize the results achieved on a set of MR images of the kidney for 10 patients.

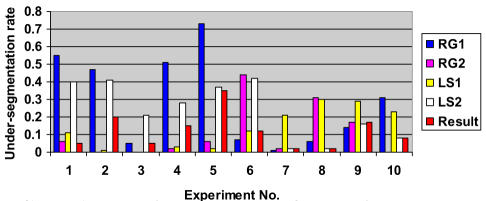
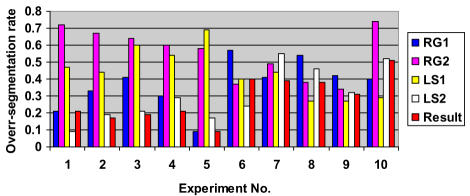
Chart 1.

Experimental results for relative under-segmentation (UR) for SCAMIS-OP

Chart 6.

Experimental results for overall error rate (ER) for SCAMIS-UP

The experiments carried out by on the two set based approach techniques have shown some promising results. From the above tabulated experiment results, we can see that most of the experiments have shown an improvement over the individual segmentation algorithms alone, which demonstrates the effectiveness of our approachestechniques. Although this initial experiment set is small, it has indicated feasibility of the proposed approach in the research on segmentation of MRI images.

6. Conclusion

The pipeline approach is the main hybrid approach proposed to improve on the segmentation results of individual segmentation techniques. Although such approaches techniques [13] show some promising results, auxiliary processing of the intermediate results are often required to ensure that the overall results are reasonable. More recent approaches have also used complicated algorithms and formulas such as the Voronoi classifier to detect the regions and boundaries.

In this paper, a different set-based methodology aiming to reduce complicated calculations and processing of images is proposed. Although the set based approach have shown some promising results, this approach is still new and more experiments need to be conducted to examine how additional preprocessing on the images (e.g., filtering) and choice of segmentation algorithms to could improve on the existing approachresults. More critical comparisons with other algorithms will also be done to further illuminate the strengths and limitations of SCAMIS.

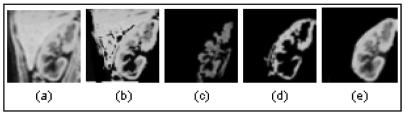
Figure 1.

(a) Original Kidney, (b) Under-Segmented Kidney, (c)&(d) Over-Segmented Kidney, (e) Desired Kidney

Figure 2.

SCARMIS-OP

Figure 3.

SCARMIS-UP

Chart 2.

Experimental results for relative over-segmentation (OR) for SCAMIS-OP

Chart 3.

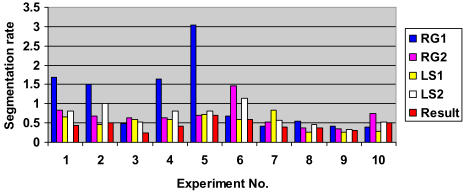
Experimental results for overall error rate (ER) for SCAMIS-OP

Chart 4.

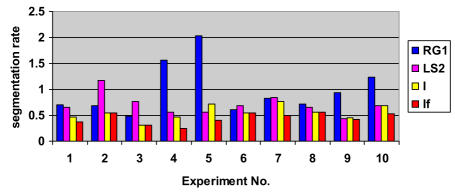
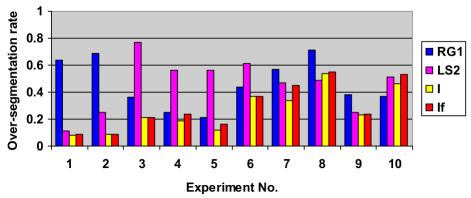
Experimental results for relative Over-segmentation (OR) for SCAMIS-UP

Chart 5.

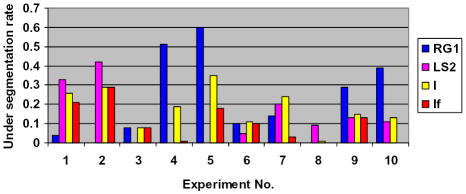
Experimental results for relative under-segmentation (UR) for SCAMIS-UP