Analyzing the Effect of Data Quality on the Accuracy of Clinical Decision Support Systems: A Computer Simulation Approach

Abstract

Clinical decision support systems (CDSS) use data from a variety sources to provide guidance to physicians at the point of care. However, several studies have shown that data from these registries often cannot be trusted to be accurate or complete. For instance, one study shows that accuracy and completeness in medical registries may be as low as 67% and 30.7%, respectively. Consequently, since CDSS rely on this data for generating guidance, the possibility that the medical decisions facilitated by the system may result in negative patient outcomes still exists. To analyze the extent of this problem, we present a two-pronged approach using simulation, followed by regression in order to quantify the relative impact of poor data quality on overall CDSS accuracy. The results from this analysis can be beneficial to developers and hospitals that can use the results to inform the development of procedures for minimizing incorrect medical decisions facilitated by these systems.

Introduction

Guideline-based clinical decision support systems (CDSS) are increasingly being advocated by the medical informatics community as a means to improve patient care and reduce costs [1–3]. Over the years there has been significant progress in developing better systems for a wide range of clinical contexts. One area CDSS research has focused on developing guideline ontologies for accurately representing the complex medical logic where as another area has focused on evaluating the effect of these systems on clinician performance and patient outcomes [1, 4]. Outside of the CDSS literature, there have been several studies on data quality in medical registries which have important implications for CDSSs. These studies have shown that data quality is a significant problem, both in electronic and paper-based registries [5–8]. However, the extent of the overall problem is still unclear.

These results pose a significant problem for CDSS which use electronic and paper registries as principal data sources [9]. Unless CDSS implementations can effectively deal with data quality problems, it is uncertain whether the guidance provided by these systems can be trusted. To our knowledge, only one study has examined this problem [10], and none have provided a generalizable methodology for auditing its extent and severity. The objective of this study is therefore to extend current literature by providing a quantitative methodology for analyzing the effect of data quality on CDSS accuracy. To achieve this aim, we employ a two-pronged approach, first using a simulation model of data generation, data adulteration and CDSS use, followed by regression to quantify the impact of each data element on overall CDSS accuracy. Future work will address the problem of designing controls to detect as well as minimize the data quality problem in clinical decision support systems.

Background

The problem of data quality

The existing literature on data quality in healthcare has focused primarily on assessing the quality of the data in medical registries [5]. These studies have focused on quantifying two main characteristics of data quality: accuracy and completeness, where accuracy is the notion that data are correct, and completeness is the notion that observations are recorded in the medical registry. The results indicate that medical registries have varying rates of data accuracy and completeness. For instance, a study by Wagner et al. indicated that accuracy rates ranged from 67%–100% and completeness rates ranged from 30.7%–100% [7]. Consequently, although it is apparent that data quality is a significant issue - the actual extent of the problem in specific registries is still unknown, and it is unclear whether results of specific studies can be applied to the general problem of data quality and CDSS accuracy.

Dealing with the Uncertainty about Data Quality

Although there is uncertainty about data quality, there are still things that we do know or can reasonably assume about the nature of data and data errors. First, we know much about how data is stored, especially in EMRs. We also have some idea about the distributions of data values as well as how different data elements are related to each other. For instance, having a breast exam date depends on having an EMR entry for breast exam. Collectively, this information allows us to create a probabilistic model of the data generation process.

Similarly, we can get an idea about the nature of data errors from literature as well as interviews with physicians and hospital staff. Physicians and nurses have experience with bad data and can be a valuable resource for determining the nature of data errors. For example, we may note errors in age data occur when a person’s age encoded incorrectly by having the digits switched. For example a 25 year old man is coded as being a 52 year old man. Similarly, we can specify such error transformations for all data elements to create a model of the data adulteration process.

Clinical Decision Support Systems

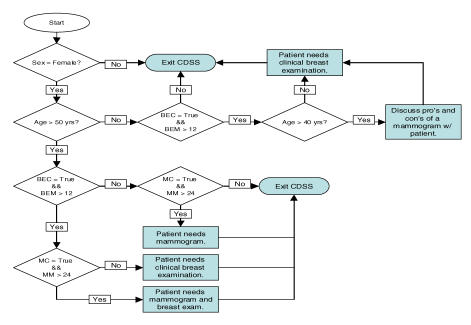
CDSSs use data from various sources, but data is primarily taken from sources such as electronic health records [9]. A CDSS uses this data in conjunction with clinical guidelines to provide guidance to physicians on specific courses of medical action. However, the accuracy of guidance produced by the CDSS assumes that (1) the CDSS implements the correct guideline logic and (2) the data is accurate and complete. But since there are significant questions about the quality of the data in registries such as electronic health records, we cannot assume the latter with any confidence. Given this situation, we need to develop both a way to analyze as well as minimize the effect that poor data quality has on CDSS accuracy. CDSS accuracy can have several definitions. For example, two simple options for measuring CDSS accuracy would be to compare the resulting program execution paths or resulting outputs. However, the choice of program execution paths as a measure of system accuracy is a more conservative estimate of an error in decision making than comparing the outputs of the system. For instance, as we can note with the guideline in Figure 1, a Male encoded as a Female under 50 years of age without a BE produce the same output – but do not result in the same decision logic. Consequently, the comparison of program execution paths would detect this error in decision-making, where as a comparison of outputs would not.

Figure 1.

Breast Cancer Prevention Guideline

Methods

General Description of Analysis Methodology

Using what we know about the data generation process and the data adulteration process we can create a model of what accurate and complete data looks like, as well as what transformations lead to incomplete and inaccurate data. Furthermore, we can also model the CDSS, feeding into it both the unadulterated and adulterated data and comparing outputs to see if data quality had an effect on system accuracy. More precisely, in order to assess the relative impact of the quality of individual data elements on overall system accuracy we propose a methodology with the following five components:

1. Generation of unadulterated patient data: We generate “real patient information” from specified assumptions about the structure and distribution of patient data. We assume that this information is complete, and accurately represents patient states.

2. Adulteration and storage of patient data: Errors are introduced into patient data according to some specific error structure; these could be either errors of completeness or accuracy.

3. Execution of CDSS: Execute the CDSS using both unadulterated and adulterated patient information, and check for accuracy of guidance.

4. Run simulation with varying rates of data accuracy: Repeat simulation under various assumptions the level of data accuracy, which gives us system accuracy percentages and the associated data accuracy percentages.

5. Quantifying the relationship between data accuracy and system accuracy: Regress system accuracy onto data accuracy, which gives us the relative impact of each data element on overall system accuracy.

Analysis Methodology on Example CDSS

To illustrate our methodology, we modeled a simple CDSS which implements one guideline, the U.S. Preventable Services Task Force, 2002, “Screening for Breast Cancer: Summary of Recommendations”, depicted in Figure 1 [11]. We modeled the guideline as requiring six data elements: (1) sex, (2) age, (3) breast exam conducted or not (BEC) (4) months since last breast exam (BEM), (5) mammogram conducted or not (MC) and (6) months since last mammogram (MM). This guideline has a total of seven decision points, and four unique outputs.

The following sections demonstrate how we can apply the methodology presented above to assess the relative impact of the six data elements on the overall quality of this example CDSS implementation.

Generation of unadulterated patient data

The first step in our analysis is the generation of the unadulterated patient data – the data that represents the patient’s actual health status. To generate this information, we specify some structural and distributional assumptions about the data. For instance, we specify that the probability of having had a breast exam depends on the patient being female and over thirty-five years of age. Furthermore we specify some assumptions about the distribution of this data, such as a .5 probability of a patient being female. These assumptions can be informed by looking at medical registries or consulting with physicians about the nature of the patients that visit their practice. For our example we specify the following assumptions about the nature of the unadulterated patient data:

1. Sex: We model sex as an independent variable, with a .5 probability of being female.

2. Age: We model age as an independent variable, taken from a ~Uniform(1,100)

3. Breast Exam (BE): We model breast exam conditional on sex and age. If Sex = Female and Age > 35, then there is a .5 probability that the individual has had a breast exam.

4. Months since last BE: If BE = T, then a month since last BE is generated from ~Uniform(0,36)

5. Mammogram: We model mammogram as conditional on sex and age. If Sex = Female and Age > 35, then there is a .5 probability that the individual has had a mammogram.

6. Months since last Mammogram: If Mamm. = T, then a month since last mammogram is generated from ~Uniform(0,36)

For illustrative purposes, the assumptions about the patient data in our example are relatively simplistic. However, when analyzing a specific instantiation of a CDSS, we can construct a more realistic model of the patient data generation process informed by physician knowledge or medical registries. For instance, modeling patient age as distributed between 18 and 94, with a mode at age 40.

Adulteration and storage of patient data

After the data generation process, we introduce errors of accuracy and completeness into this data. To ascertain the nature of the errors we can survey users of data such as physicians or nurses, or make assumptions based on process information. Next, we construct a set of procedures that introduce these types of errors into our data in the following way:

1. Sex: Errors are introduced into the sex variable when males are coded as females, and vice versa.

2. Age: Errors are introduced into the age variable when age is regenerated from a ~Uniform(1,100)

3. Breast Exam (BE): Errors introduced into BE occur when females who have had a breast exam are coded as not having one, and vice versa.

4. Months since last BE: Errors occur when females who have BE = True have their “months since last exam” re-generated from ~Uniform(0,36). This can be either a woman who has actually had a breast exam as well as one who has not actually had a breast exam, but is marked as having one.

5. Mammogram: Errors introduced into Mamm occur when females who have Mamm = True are coded as not having one, and vice versa.

6. Months since last Mammogram: Error when females who have Mamm. = T have their “months since last mammogram” re-generated from ~Uniform(0,36). This can be either a woman who has actually had a mammogram as well as one who has not actually had a mammogram, but is marked as having one.

Again, we have kept assumptions the errors in our example simple in order to illustrate how the methodology works. We plan to develop a more realistic error structure that better represents the nature of errors for these specific data.

Execution of the Clinical Decision Support System

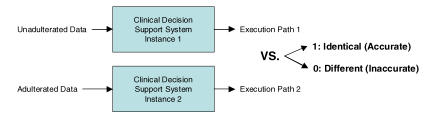
The previous procedures have provided us with two sets of data. One set of data accurately and completely represents patient states (unadulterated), where as another set represents data that may be inaccurate and incomplete (adulterated). We then input these two data sets into identical instances of our example CDSS and compare the resulting program execution paths to determine whether the paths are identical. If paths are not identical – we say that the CDSS did not execute accurately. We illustrate the process of CDSS execution with the two sets of data in Fig. 2.

Figure 2.

Depiction of CDSS Execution

Run simulation with varying data accuracy

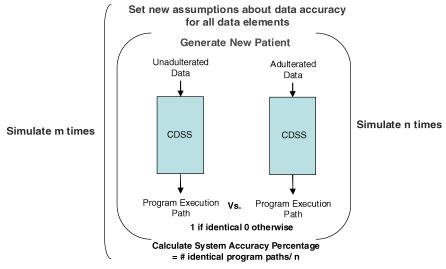
CDSS execution with the two data sets provides a measure of whether one such instantiation of unadulterated and adulterated patient data produces identical program execution paths. However, we are interested in understanding the general behavior of the CDSS under various assumptions about specific instances of patient data and quality of these data elements. We do this by randomly specifying data quality rates for each element (e.g. sex is 98% accurate, age is 93% accurate, etc.) and running the simulation under these data quality assumptions with different patients drawn from our specified distributions. We iterate through n patients and then calculate total accuracy by dividing the total number of identical execution paths over the n iterations. After this, we again randomly specify new data quality assumptions, and run the simulation again using different patients, doing this a total of m times. This process is illustrated in Fig. 3.

Figure 3.

The simulation model

Data accuracy vs. system accuracy

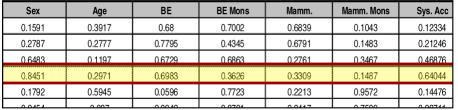
The simulation process in Fig. 3 generates a table consisting of six columns of data accuracy rates and a column of corresponding system accuracy rates. Figure 4 provides a subset of this table for our example. In our simulation we had n=100,000 and m=1,000. We note that for the fourth iteration of m, under the specified data quality assumptions approximately 64% of the program execution paths were identical, as seen in Figure 4.

Figure 4.

Output from simulation

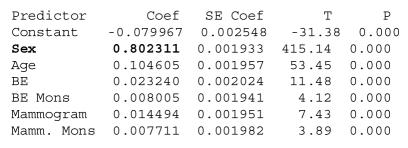
Using this output we regress system accuracy onto the data quality rates to determine the relative effect of these elements on the overall accuracy of the system. Our regression produces the following results, with all coefficients being significant at = .01, and with an Adjusted R-Squared of 99.4%.

We can see that sex is the most important data element for this CDSS, since it contributes the most to the correctness of this guideline. We can roughly interpret the coefficient for sex to mean that for every one percent decrease in the quality of the data element there will be a corresponding .8% decrease in the accuracy of the CDSS. The coefficients for the other data elements also give us the impact of these elements on system accuracy, and can be interpreted in the same way. The results above can be used to inform a variety of actions such as design considerations for better and more error resistant clinical decision support systems. For instance, the idea of a control [12], a central idea in accounting which refers to procedures to verify information using duplicate registers, can also be adapted to the issue of data quality in healthcare. In our context we can refer to a control as any procedure, either electronic or human, that can be used to verify the accuracy or completeness of patient data in order to prevent inaccurate medical decisions. These controls can be used to check whether a data element for a specific patient is logically consistent with other parts of their medical record. For instance, a control could cross check whether a person is actually a female with a test result that only a female patient would have. Another possible control may be one derived from knowledge about the patient population in the form of a probabilistic statement about the likelihood of a certain data value conditional on other aspects of the patient’s medical record. Furthermore, running the simulation again on the more robust implementation with controls will allow us to quantify the improvement in system accuracy.

Discussion and Future Work

As providers begin to adopt healthcare information systems, the issues of data quality and its effect on the system accuracy will become increasingly important. Significant work has been done by the medical informatics community towards building powerful systems for improving patient outcomes. However, there is a paucity of literature providing prescriptive methods for dealing with the underlying data quality problems in medical registries. We believe that the analysis presented in this paper outlines a novel first-cut at dealing with the consequences of poor data quality on the accuracy of medical decisions facilitated by these systems. Through this study we have been able to provide a quantitative methodology to assess a system’s susceptibility to data quality problems. Using this knowledge, we can begin to develop prescriptions such as data-cleanup strategies, controls, and improved medical process design to enhance patient care, by minimizing the effect of poor data quality on clinical decision making.

Although our target system in this study was a CDSS, we believe that with some modifications this methodology can be applied to other classes of healthcare information systems such as computerized physician order entry. Moreover, by relaxing some assumptions about the deterministic nature of medical decision making, we can also analyze combinations of human and electronic healthcare systems. Our goals for extending and improving this methodology include:

1. Defining realistic distributional and structural assumptions about the nature of patient data and errors.

2. Testing the methodology on more complex guidelines in actual care settings.

3. Designing robust controls for minimizing the risk of incorrect medical decisions

We believe that the methodology presented here, even in its current stage, can be a valuable tool for developers of clinical decision support systems as well as hospitals implementing such systems. Developers can use the current methods to assess their system’s susceptibility to data quality problems, and design appropriate controls that can reduce some of these negative impacts. Furthermore, hospitals can use the methodology to determine what data points are critical, and should be verified before implementing the system and relying on its guidance. We believe that future research on this topic will provide a set of useful tools that will ensure that technological interventions in healthcare will improve patient care and medical outcomes.

Figure 5.

Regression output from Example CDSS