Abstract
Acetylcholine excites many neuronal types by binding to postsynaptic m1-muscarinic receptors that signal to ion channels through the Gq/11 protein. To investigate the functional significance of this metabotropic pathway in sympathetic ganglia, we studied how muscarinic excitation modulated the integration of virtual nicotinic excitatory postsynaptic potentials (EPSPs) created in dissociated bullfrog B-type sympathetic neurons with the dynamic-clamp technique. Muscarine (1 μM) strengthened the impact of virtual synapses by reducing the artificial nicotinic conductance required to reach the postsynaptic firing threshold from 20.9 ± 5.4 to 13.1 ± 3.1 nS. Consequently, postganglionic action potential output increased by 4–215% when driven by different patterns of virtual presynaptic activity that were chosen to reflect the range of physiological firing rates and convergence levels seen in amphibian and mammalian sympathetic ganglia. In addition to inhibiting the M-type K+ conductance, muscarine activated a leak conductance in three of 37 cells. When this leak conductance was reproduced with the dynamic clamp, it also acted to strengthen virtual nicotinic synapses and enhance postganglionic spike output. Combining pharmacological M-conductance suppression with virtual leak activation, at resting potentials between −50 and −55 mV, produced synergistic strengthening of nicotinic synapses and an increase in the integrated postganglionic spike output. Together, these results reveal how muscarinic activation of a branched metabotropic pathway can enhance integration of fast EPSPs by modulating their effective strength. The results also support the hypothesis that muscarinic synapses permit faster and more accurate feedback control of autonomic behaviors by generating gain through synaptic amplification in sympathetic ganglia.
INTRODUCTION
The synaptic release of acetylcholine coactivates nicotinic and muscarinic receptors in sympathethic ganglia, initiating a fast nicotinic excitatory postsynaptic potential (EPSP) and slow muscarinic events that include an EPSP, an inhibitory postsynaptic potential (IPSP), and presynaptic inhibition (Eccles and Libet 1961; Libet and Tosaka 1969; Shen and Horn 1996). Here we examine how postsynaptic muscarinic excitation modulates the integration of nicotinic EPSPs arising from preganglionic synapses that converge on sympathetic neurons. To simplify the experimental analysis, virtual nicotinic EPSPs were created on secretomotor B-type bullfrog sympathetic neurons using the dynamic-clamp method (Kullmann et al. 2004). This permitted us to probe the consequences of postsyn-aptic muscarinic excitation with computer-generated fast synaptic conductance changes whose strength and timing could be precisely controlled and then reproduced in different cells.
Muscarinic excitation of sympathetic B neurons is mediated by suppression of M-type K+ conductance (gKM) (Adams and Brown 1982; Brown and Adams 1980) and activation of a cationic leak conductance (gleak) (Kuba and Koketsu 1976; Tsuji and Kuba 1988). In mammals, this pathway includes m1-muscarinic receptors (Marrion et al. 1989) coupled through lipid hydrolysis (Zhang et al. 2003) to M-channels composed of KCNQ2/3 subunits (Selyanko et al. 2002; Shapiro et al. 2000; Wang et al. 1998). Early studies of amphibian B neurons demonstrated that a net decrease in membrane conductance causes muscarinic excitation (Weight and Votava 1970), leading to the proposal that this mechanism could potentiate fast EPSP amplitudes (Schulman and Weight 1976). Subsequent discovery of gKM and its voltage dependency revealed that muscarinic excitation increases postsynaptic excitability, as manifest by repetitive firing in response to depolarizing stimuli (Brown and Adams 1980). However, the consequences for ganglionic integration of enhanced fast EPSP amplitude and repetitive firing have remained unclear. This problem’s significance extends beyond autonomic ganglia.
Muscarinic excitation also occurs in the cerebral cortex (McCormick and Prince 1985), hippocampus (Cole and Nicoll 1984; Dodd et al. 1981), and striatum (Shen et al. 2005). In these circuits, it promotes repetitive firing and oscillatory activity during various physiological and disease states, including memory retrieval (Hasselmo and McGaughy 2004), motor activation (Shen et al. 2005), and epilepsy (Biervert et al. 1998; Cooper et al. 2000, 2001; Singh et al. 1998). However, the complexity of brain circuits makes it difficult to understand in detail how muscarinic regulation of repetitive firing in single cells shapes circuit dynamics (Cobb and Davies 2005).
Our analysis of muscarinic modulation makes use of a theory of ganglionic integration that reduces circuit behavior to that of a single cell (Karila and Horn 2000) together with dynamic-clamp tools capable of testing the theory (Kullmann et al. 2004). Interestingly, previous simulations of a conductance-based model sympathetic neuron predicted that muscarinically enhanced repetitive firing would not influence ganglionic integration (Schobesberger et al. 1999, 2000; Wheeler et al. 2004). Instead, they suggested that muscarine would strengthen subthreshold nicotinic EPSPs and increase synaptic amplification of preganglionic activity (Schobesberger et al. 2000; Wheeler et al. 2004). We now describe new dynamic-clamp experiments to test these ideas using up to ten independent converging nicotinic synapses together with bath-applied muscarine and a virtual cationic leak conductance.
METHODS
All experiments were done on enzymatically dissociated sympathetic B-type neurons from bullfrog (Rana catesbeiana) paravertebral ganglia 9 and 10, maintained in culture for ≤2 wk at room temperature (23°C) on glass coverslips coated with poly-D-lysine (Wheeler et al. 2004). The ganglia were obtained from adult bullfrogs (males and females, 5–7 in.) that were killed by rapid brain stem transection and double-pithing in a procedure approved by the Institutional Animal Care and Use Committee at the University of Pittsburgh.
Electrophysiological recordings and dynamic clamp
Whole cell perforated-patch recordings were made at room temperature using polished pipettes (1–5 MΩ) and amphotericin-B as the ionophore. Details of the dynamic-clamp system were previously described elsewhere (Kullmann et al. 2004). Briefly, the system included an Axoclamp 2B amplifier (Molecular Devices, Sunnyvale, CA), an embedded Pentium III controller running under a real-time operating system (National Instruments, Austin, TX), a Windows-based host computer, and G-clamp version 1.2 software (http://hornlab.neurobio.pitt.edu) written in the LabVIEW-RT 6.1 programming environment (National Instruments). The pipette access resistance (5–15 MΩ) was monitored throughout each experiment and compensated using the bridge circuitry of the current-clamp amplifier. Dynamic-clamp measurements were performed at a feedback loop rate of 20 kHz and filtered at 3 kHz. Conventional current-clamp data were sampled at 10 kHz and filtered at 3 kHz, whereas slow voltage-clamp measurements of steady-state current–voltage (I–V) data were sampled at 5 kHz and filtered at 1 kHz. Rleak was determined as the slope of the linear part of the I–V relation, typically in the range −65 to −85 mV.
Virtual nicotinic synapses were implemented according to Isyn(t) = k × gsyn(t) × (VM − Erev). Synaptic conductance as a function of time gsyn(t) was modeled as the sum of two exponentials, used to fit experimentally measured synaptic currents, with time constants of 1 ms for the rising phase and 5 ms for the falling phase (Schobesberger et al. 2000). The synaptic reversal potential Erev was set to 0 mV (Shen and Horn 1995) and synaptic strength was controlled by adjusting the dimensionless scaling factor k. Threshold-gsyn, defined as the synaptic conductance required to trigger an action potential, was determined with an automated binary search routine that delivered virtual nicotinic EPSPs at a rate of 0.5 Hz (Kullmann et al. 2004). By systematically varying the peak amplitude of the synaptic conductance based on its ability to trigger an action potential, the search routine generally found threshold-gsyn within 10 trials. During this process, the dynamic clamp continually measured membrane potential VM, calculated the appropriate synaptic current Isyn, and injected it into the cell (Kullmann et al. 2004).
The virtual leak conductance gleak, used to mimic the leak component of muscarinic excitation, was implemented as time and voltage invariant with a reversal potential of 0 mV (Schobesberger et al. 2000; Tsuji and Kuba 1988).
To create patterns of virtual nicotinic EPSPs that mimic activity in vivo, the timing of synaptic events was modeled as a Poisson process (Karila and Horn 2000; Wheeler et al. 2004) with Neurosim 2.1 (http://hornlab.neurobio.pitt.edu), a MATLAB program written by Dr. D. W. Wheeler. The program generated the required random numbers and constructed conductance waveforms describing activity of one strong primary synapse and a specified number of weak secondary synapses. During each experiment, G-clamp then scaled the primary and secondary conductance template files relative to threshold-gsyn, as measured for each cell, before combining them into one final template that commanded the dynamic clamp and measured synaptic gain (Wheeler et al. 2004). Scaling of conductance templates was based on the mean value of at least three consecutive measurements of threshold-gsyn. Conductance templates with a mean rate of synaptic activity of 5 Hz were 40 s long (about 200 events per synapse), whereas templates with a mean rate of 0.5 Hz were 60–200 s long (about 30–100 events per synapse).
Solutions and chemicals
The Ringer solution contained (in mM): 115 NaCl, 2 KCl, 1.8 CaCl2, and 4 NaHEPES, adjusted to pH 7.3. The pipette solution contained (in mM): 110 potassium gluconate, 10 NaCl, and 5 Na-HEPES, adjusted to pH 7.2. Patch pipettes were backfilled with this solution plus 250 μg/ml amphotericin-B (Sigma–Aldrich, St. Louis, MO). (−)-Muscarine chloride was also obtained from Sigma–Aldrich.
Data analysis
In vivo synaptic input to sympathetic neurons generally consists of one strong synapse, known as the primary, which invariably elicits an action potential, and a variable number of weak, subthreshold synapses, known as secondaries (Karila and Horn 2000). For simplicity, it was assumed that primary and secondary synapses originate from a common population of preganglionic neurons and therefore that all synapses are active at the same mean rate. As in previous work, synaptic gain was defined as the mean postsynaptic firing rate divided by the mean firing rate of virtual presynaptic neurons (Karila and Horn 2000; Wheeler et al. 2004). In this scheme, when action potentials are generated solely by the strong primary synapse, the synaptic gain = 1 and when additional action potentials are generated by summation of secondary EPSPs the gain rises to >1. Synergy between gKM and gleak was calculated as the difference between the reduction in threshold-gsyn for the combined conductance changes and that for the sum of their individual effects, divided by the latter and multiplied by 100 (Schobesberger et al. 2000). If, for example, the combined conductances reduced threshold- gsyn by 3 nS and the individual effects were 1 nS each, then this would correspond to a synergy of 50% {[(3 nS − 2 nS)/2 nS] × 100}.
Action potential threshold was measured as the maximum second derivative of membrane potential with respect to voltage in phase space (method II in Sekerli et al. 2004).
Grouped data and error bars in figures reflect the means ± SE, except in Fig. 4C where the error bars indicate SDs. Single statistical comparisons between grouped data were made using two-sided t-tests, whereas multiple comparisons were conducted with a repeated-measures ANOVA and Tukey’s test. P < 0.05 was the criterion for significance.
Fig. 4.
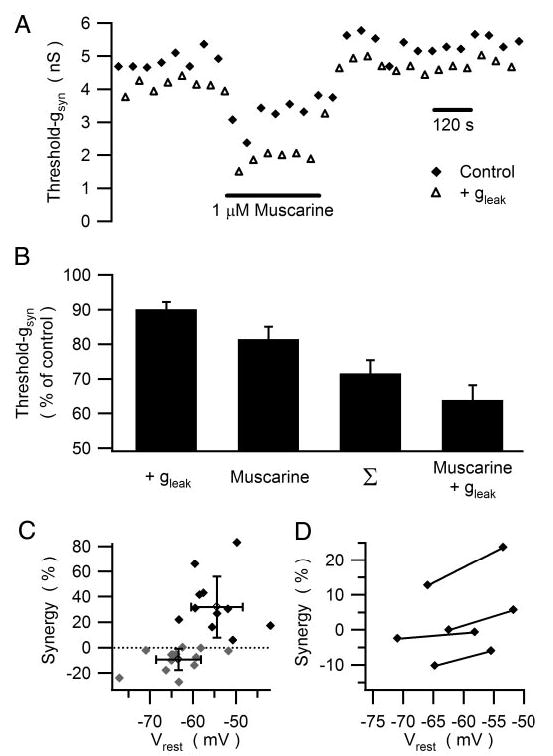
gKM and gleak interact synergistically to lower threshold-gsyn. A: illustration of the time course of an experiment in which muscarine was used to inhibit gKM and the dynamic clamp was used to introduce a 0.25-nS virtual gleak. Threshold-gsyn was repeatedly measured in the presence (open triangles) and absence (filled diamonds) of the leak. These data show that introducing gleak lowered threshold-gsyn and that application of muscarine produced a further decrease in threshold-gsyn. Note, however, that the effect of gleak was larger in the presence of muscarine. B: a similar synergy was observed in 11 experiments where the combination of gleak (0.1–1 nS) and muscarine (1 μM) reduced threshold-gsyn by about 30% more than expected from the sum of the individual effects. C: sorting the data into a group of 11 experiments where synergy >0 was observed and 15 experiments where synergy was absent or slightly negative, revealed that synergy depends on the resting potential. In addition to data from individual experiments, the graph includes the mean ± SD for each group. D: injection of constant depolarizing current to shift Vrest increased the synergy between gleak and gKM in 4 of 4 neurons.
RESULTS
Muscarine strengthens nicotinic synapses by enhancing excitability
In principle, muscarinic EPSPs could serve to modulate ganglionic integration by enhancing the efficacy of nicotinic synapses or by allowing nicotinic EPSPs to drive repetitive postsynaptic firing (Brown and Adams 1980; Schulman and Weight 1976). To distinguish between these possibilities we examined how muscarine modulated the postsynaptic response to virtual nicotinic EPSPs of defined strength.
Bath-applied muscarine increased the efficacy of virtual nicotinic synapses by lowering threshold-gsyn in a manner that was reversible (Fig. 1, A–C) and dose dependent. Muscarine (50 nM) reduced threshold-gsyn to 87.9 ± 4.0% of control (three cells), 1 μM muscarine reduced threshold-gsyn to 63.7 ± 2.6% of control (26 cells, P < 0.002, paired t-test), and 30 μM muscarine reduced threshold-gsyn to 37.2 ± 2.3% (four cells). For 1 μM muscarine, where most data were obtained, the reduction in threshold-gsyn ranged between 31.3 and 86.0% from a mean of 20.9 ± 5.4 nS in control Ringer to 13.1 ± 3.1 nS in muscarine. These effects could not be explained by a hyperpolarizing shift in the threshold membrane potential for spike initiation (Fig. 1A), an action that one might expect to enhance excitation by fast EPSPs. To the contrary, 1 μM muscarine caused a slight depolarization of action potential threshold from −22.4 ± 1.3 to −21.4 ± 1.4 mV (24 cells, P < 0.01, paired t-test). Washout of the agonist often resulted in a transient overrecovery of threshold-gsyn (Fig. 1B), whose time course resembled the well-known overrecovery of gKM seen after its metabotropic suppression (Pfaffinger 1988; Tokimasa et al. 1996).
Fig. 1.
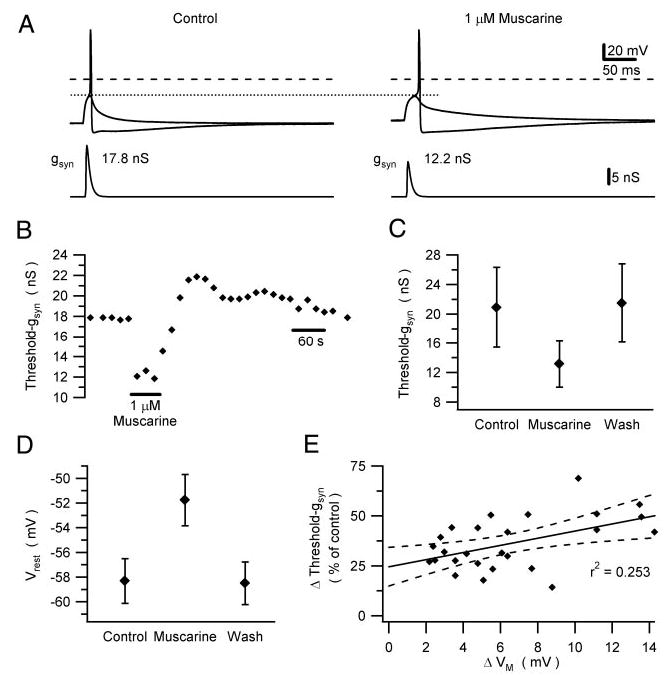
Muscarine enhances the impact of nicotinic excitatory postsynaptic potentials (EPSPs) by reducing threshold-gsyn. A: dynamic clamp experiment in which bath application of 1 μM muscarine lowered threshold-gsyn by 31%. Bottom traces: synaptic conductance used to drive the dynamic clamp. Top traces: membrane potential responses that straddle action potential threshold (stippled line), which did not change in the presence of muscarine. Dashed lines indicate 0 mV. B: time course of the muscarinic reduction of threshold-gsyn of the neuron shown in A. Note the transient overrecovery of threshold-gsyn after washout of muscarine. C and D: grouped data from 26 neurons show that muscarinic reduction of threshold-gsyn (C) is accompanied by depolarization of Vrest (D). E: scatterplot of the data from individual neurons shows a weak correlation between the muscarinic changes in threshold-gsyn and Vrest. Straight line is a linear fit to the data points, with the 95% confidence band indicated by dashed lines.
In addition to reducing threshold-gsyn, 1 μM muscarine depolarized Vrest (Fig. 1D) by 6.5 ± 0.7 mV (26 cells), thereby mimicking the slow EPSP recorded from intact ganglia. Although it could be argued that the muscarinic reduction in threshold-gsyn arises simply from membrane depolarization, the correlation between these two effects (Fig. 1E) was weak (r2 = 0.253, P < 0.01, Pearson correlation test). Previous computational simulations indicate that this behavior originates from the nonlinear voltage- and time-dependent gating of gKM interacting with the resting leak conductance (Schobesberger et al. 2000). To test the idea that membrane depolarization could not fully account for the muscarinic effect on threshold-gsyn, an additional set of experiments was run in which steady current injection was used first to null out the depolarization caused by muscarine and then after washout to mimic the depolarization (Fig. 2, A and B). In seven of seven cells, injection of hyperpolarizing current reduced but did not eliminate the reduction of threshold-gsyn by muscarine. In these same cells, simple injection of depolarizing current also reduced threshold-gsyn, but not to the same extent as muscarine. In addition to these tests, we examined in three of these cells how muscarine and current injection influenced the shape of subthreshold virtual nicotinic EPSPs (Fig. 2, C and D). In every cell, muscarine had very little effect on fast EPSP amplitude while causing a lengthening of EPSP duration. These results confirm the prediction from previous numerical simulations of the same experiment (see Fig. 2 in Schobesberger et al. 1999).
Fig. 2.
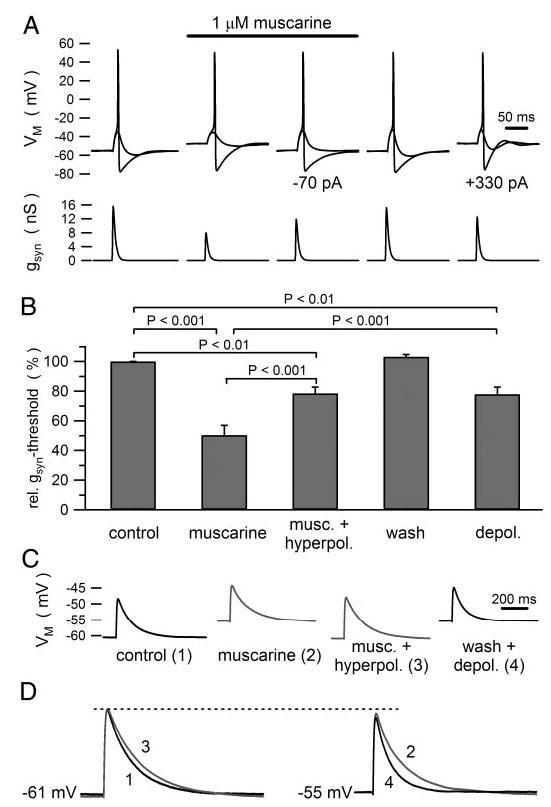
Membrane depolarization does not fully account for the actions of muscarine on threshold-gsyn and fast EPSP waveforms. A: example of a cell where injecting 70 pA of hyperpolarizing current nullified the depolarization produced by muscarine and 330 pA of depolarizing current mimicked the muscarinic depolarization. B: grouped data from 7 cells used for the experiment illustrated in A. Statistical comparisons were based on ANOVA. C: comparison of fast EPSPs produced by a virtual conductance waveform (5 nS peak amplitude). Injected currents were used to nullify the muscarinic depolarization (trace 3) and to mimic it (trace 4). D: superimposition of virtual EPSPs at the control resting potential (traces 1 and 3) and the depolarized potential (traces 2 and 4) show that in both cases muscarine had little effect on peak EPSP amplitude, but prolonged EPSP duration. Note that under control conditions the subthreshold EPSPs in A elicit undershoots, which are inhibited by muscarine, indicating that the EPSPs are not purely passive. In other words, fast EPSPs activate some M-current, which speeds the time course of their decay under control conditions.
Unlike the robust effect of muscarinic excitation on the efficacy of nicotinic stimulation, virtual fast EPSPs never initiated repetitive firing of action potentials either in control Ringer or after exposure to muscarine (Figs. 1A, 5B, and 7A). Nonetheless, B neurons were capable of repetitive firing. Their normal propensity to fire a single action potential in response to a rectangular pulse of depolarizing constant current was readily converted to repetitive firing by addition of muscarine (Fig. 3A). Indeed the conversion from phasic to tonic firing constitutes the classic signature of muscarinic excitation (Adams et al. 1982). In a few cells, the depolarization produced by high muscarine concentrations (≥10 μM) led to spontaneous firing, but this behavior did not require nicotinic or any other form of stimulation.
Fig. 5.
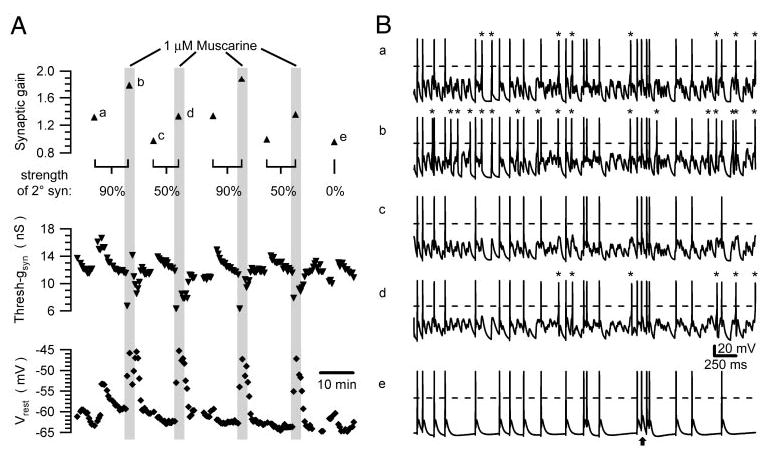
Muscarine reproducibly increases synaptic gain. A: time course of synaptic gain (top), threshold-gsyn (middle), and Vrest (bottom) from a cell that was repeatedly stimulated with a synaptic template incorporating one primary and 9 secondary nicotinic synapses, each firing at a mean rate of 5 Hz. During 4 exposures to muscarine, strengths of the secondary synapses were set to 90 and 50% threshold-gsyn. At the end of the experiment the secondary synapses were eliminated by setting their strength to 0. B: illustration of brief 4-s segments from the synaptic gain measurements denoted a–e in A. In each trace, asterisks mark action potentials elicited by summation of secondary EPSPs and dashed lines indicate 0 mV. By comparing a and b it can be seen that muscarine increased the number of action potentials driven by secondary synapses—this is the effect that produces the increase of synaptic gain. A similar though smaller effect was observed when the strength of the secondary synapses was reduced from 90% threshold-gsyn (Ba, Bb) to 50% threshold-gsyn (Bc, Bd). Turning off the secondary synapses (Be) reduced the gain to slightly <1. This occurred because some primary EPSPs failed to trigger action potentials resulting from refractory occlusion between closely timed events. An arrow marks one example of such a failure where 2 EPSPs were separated by only 3.2 ms.
Fig. 7.
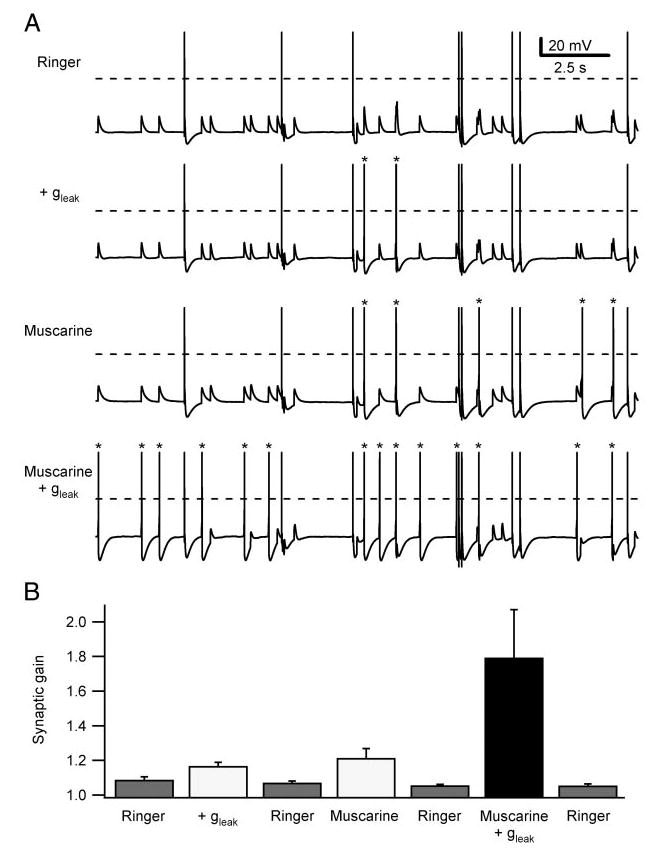
Muscarine and gleak interact synergistically to increase synaptic gain. A: 10-s segments from longer synaptic gain measurements in a cell that was sequentially tested in control Ringer, after introducing a 0.25-nS virtual gleak, after bath application of 1 μM muscarine, and finally with the combination of added gleak and muscarine. Dashed lines indicate 0 mV and asterisks indicate action potentials triggered by secondary EPSPs. Synaptic template contained one primary synapse and 3 secondary synapses scaled to 50% threshold-gsyn and firing at mean rates of 0.5 Hz. Comparing the traces reveals that combined stimulation was much more effective than the individual treatments using the virtual leak and muscarine. B: same synergistic enhancement of synaptic gain was seen in pooled data from 5 neurons treated with 1 μM muscarine and 0.25–0.5 nS gleak. Synaptic gain measurements were conducted with repeated trials to ensure stable conditions during each experiment.
Fig. 3.
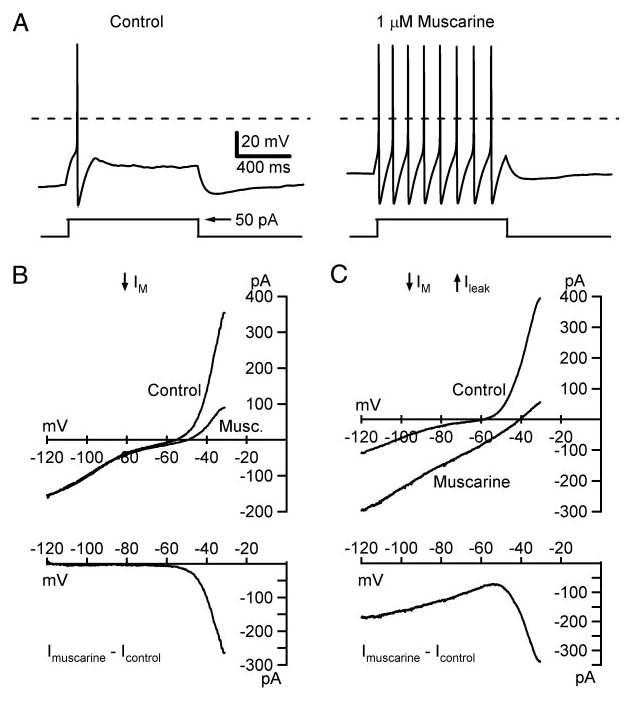
Muscarinic excitation arises from IM and a leak current. A: sympathetic B neurons typically respond to a step-depolarizing current (bottom trace) by generating a single action potential (top trace). Bath application of 1 μM muscarine converts the response to one of repetitive firing. Dashed lines indicate 0 mV. In these experiments, 2 types of steady-state current–voltage (I–V) relations were observed (B, C). Top graphs illustrate the I–V relations in control Ringer and muscarine. Net muscarinic currents, determined by subtraction, are plotted below. B: most cells (92%) responded to muscarine with a nonlinear inward current produced by suppression of gKM at potentials above −70 mV. C: in 3 cells muscarine induced 2-component responses consisting of an inward linear leak current that decreased as the membrane was depolarized from −120 to −60 mV and the inward M-current response at more depolarized potentials. I–V relations in this figure were constructed from voltage-clamp data using a slow ramp command (9 mV/s) from −30 to −120 mV.
Previous studies indicate that muscarine activates a branched signaling pathway in bullfrog B neurons to suppress gKM and activate gleak (Tsuji and Kuba 1988). To assess whether both conductance changes occurred under our experimental conditions, steady-state I–V relations were constructed with either voltage-clamp or current-clamp measurements, which yielded similar data. In 34 of 37 cells, muscarine inhibited only gKM, which was evident in the I–V relation as a voltage-dependent inward current activated positive to −70 mV (Fig. 3B). In the three other neurons, the muscarinic current had two components corresponding to suppression of IM and activation of an inward leak conductance (0.98 ± 0.56 nS) with an extrapolated reversal potential of −20 ± 9.3 mV (Fig. 3C). In all three cells, the leak component of the muscarininc response recovered on washout, thereby indicating it was not an artifact of cell damage or deterioration. Both the increase in leak conductance and the decrease in M-conductance had the effect of linearizing the I–V relation in the region between the resting potential (−55 to −70 mV) and the spike threshold (−20 to −30 mV). This resulted in depolarization and a reduction of the inward synaptic current required to reach threshold for generating an action potential.
The next set of experiments examined how gKM and gleak interact to control the efficacy of virtual nicotinic EPSPs. To assess the impact of each conductance type, we exploited the fact that most neurons in our preparations did not exhibit the muscarinically controlled gleak. Instead we used the dynamic clamp to implement a virtual leak response in neurons that responded to bath-applied muscarine with a pure gKM response. This approach permitted independent manipulation of the two conductances. In the experiment illustrated in Fig. 4A, threshold-gsyn was measured repeatedly in the presence and absence of a small virtual gleak (0.25 nS). Plotting these data against time yielded one baseline describing threshold-gsyn without the leak and a second lower baseline, which reflected the ability of the leak to reduce threshold-gsyn. On application of muscarine both baselines shifted to lower values, but the difference between them increased. This was because muscarine had a greater effect in the presence of the leak conductance. In other words, the increase in gleak and reduction in gKM interacted synergistically to reduce threshold-gsyn. This experimental protocol was repeated 25 times in 15 neurons using different levels of virtual gleak (0.1–1 nS) comparable to those activated by a muscarinic agonist (Tsuji and Kuba 1988). Figure 4B illustrates grouped data from 11 of these trials, collected from seven neurons where the interaction between gleak and gKM was synergistic. In these cases, adding gleak alone reduced threshold-gsyn to 90.1 ± 2.1% of control and suppressing gKM alone reduced threshold-gsyn to 81.4 ± 3.7% of control, whereas combining the two changes reduced threshold-gsyn to 63.9 ± 4.3% of control, which was a greater change than the arithmetic sum of the two individual effects (71.5 ± 3.9% of control). This behavior contrasted to the other 14 trials where no synergy or slight negative synergy was seen. Comparing the positive and negative synergy data (Fig. 4C) revealed a significant difference in resting membrane potentials under control conditions before manipulation of gleak and gKM (positive synergy: −54.4 −1.8 mV; negative synergy: −63.4 ± 1.4 mV; P < 0.001; two-tailed unpaired t-test). The likely explanation again derives from the voltage dependency of gKM (Schobesberger et al. 2000). Hyperpolarized resting potentials are associated with low activation of gKM, whereas more depolarized resting potentials can fall into a region where small depolarizations cause large activation of gKM (Fig. 3B). Accordingly, the effects of gleak and gKM should add supra-linearly when the depolarization produced by the leak causes a large increase in the resting M-current. To test this idea, synergy was measured in four cells with low resting potentials and then a second time after steady currents were injected to produce small depolarizations (Fig. 4D). In all four cases, depolarization led to an increase in synergy between gleak and gKM as assayed by the reduction in threshold-gsyn.
Muscarinic modulation of synaptic gain
Synaptic amplification of activity can arise in sympathetic ganglia from the summation of fast nicotinic EPSPs that are subthreshold in strength (Karila and Horn 2000; Wheeler et al. 2004). Finding that muscarinic excitation enhanced the effective strength of nicotinic synapses therefore implies a concomitant increase in synaptic gain. To test this prediction, B neurons were stimulated with defined patterns of noisy virtual nicotinic synaptic input in the presence and absence of muscarine (Fig. 5). The templates of virtual synaptic conductance used to drive the dynamic clamp and measure synaptic gain were defined by parameters describing nicotinic convergence, the strength of nicotinic synapses, and the mean firing rate of preganglionic neurons. Specific values for these parameters were chosen to be physiologically realistic and to span a range of conditions that elicit different baseline levels of synaptic gain in simulations and dynamic-clamp recordings (Karila and Horn 2000; Wheeler et al. 2004). All synaptic templates incorporated the n = 1 pattern of nicotinic convergence seen in paravertebral sympathetic ganglia (Karila and Horn 2000). To reproduce this pattern, each template contained three or nine secondary synapses whose resting strength was set to either 50 or 90% of threshold-gsyn and one primary synapse whose strength was always set to 10 times threshold-gsyn. Similarly, the average presynaptic firing rate was studied at 0.5 and 5 Hz to reflect a physiologically relevant range.
By testing individual cells with different patterns of virtual synaptic stimulation, we found that muscarine elevated synaptic gain over the entire parameter space for preganglionic activity (Figs. 5 and 6). To obtain reliable estimates of synaptic gain, it was essential to maintain stable recordings for periods long enough to permit repeated trials, interleaving of different stimulus templates, applications of muscarine, and recovery between trials. The cell illustrated in Fig. 5 was tested nine times in this way over a period of 80 min. In this particular experiment, all synaptic templates contained nine secondary nicotinic synapses firing at 5 Hz, but their strength was varied during repeated trials. The results from this cell showed that muscarine reproducibly elevated synaptic gain. In replicate trials with secondary synaptic strength set at 50% threshold-gsyn, 1 μM muscarine increased gain in this cell from 0.97 and 0.99 to 1.33 and 1.35, respectively. When secondary synaptic strength was raised to 90% threshold-gsyn, muscarine increased gain from 1.31 and 1.33 to 1.77 and 1.88, respectively. Synaptic gain dropped to slightly <1 when secondary synapses were turned off by setting their strength to 0. The drop in gain to <1 has been found in other recent experiments to arise from the failure of large EPSPs to trigger firing during the refractory period after each spike (Wheeler et al. 2004). After each stimulus trial we also observed transient changes in threshold-gsyn, but rest periods successfully allowed for recovery back to baseline before the next trial (Fig. 5A). In grouped data (Fig. 6B) using the same stimulus parameters (fpre = 5 Hz, nine secondary synapses), the increase in synaptic gain produced by 1–5 μM muscarine was significant when secondary synaptic strength was set to 50% threshold-gsyn (control 1.054 ± 0.028, muscarine 1.227 ± 0.028, nine cells, P < 0.05, paired t-test) and to 90% threshold-gsyn (control 1.467 ± 0.051, muscarine 1.759 ± 0.064, 10 cells, P < 0.05, paired t-test).
Fig. 6.
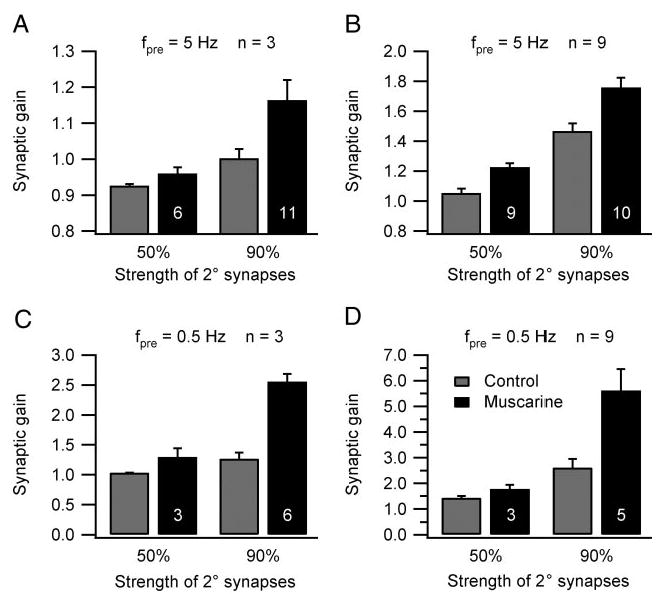
Muscarine increases synaptic gain over a range of physiologically realistic stimulus parameters. Grouped data from experiments where secondary synaptic strength, the number of secondary synapses (n), and the presynaptic firing rate were systematically varied. In each graph, the number in the black bar (1–5 μM muscarine) denotes the number of cells in the comparison and the gray bar to the left is the paired control. All differences were statistically significant except for that using synapses set to 50% threshold-gsyn in C.See RESULTS for additional details.
Using the same approach, we systematically tested the effect of muscarine on synaptic gain elicited by other preganglionic stimuli. With only three secondary synapses and fpre maintained at 5 Hz, muscarine elevated gain (Fig. 6A) from 0.926 ± 0.005 to 0.960 ± 0.018 (50% threshold-gsyn, six cells; P < 0.05, paired t-test) and from 1.003 ± 0.026 to 1.164 ± 0.056 (90% threshold-gsyn 11 cells; P < 0.05, paired t-test). The largest muscarinic effects, which doubled synaptic gain, were recorded when fpre was lowered to 0.5 Hz and secondary synapses were scaled to 90% threshold-gsyn (Fig. 6, C and D). With three secondary synapses, muscarine increased the gain under these conditions from 1.268 ± 0.100 to 2.556 ± 0.130 (six cells; P < 0.05, paired t-test) and with nine secondary synapses, muscarine increased the gain from 2.609 ± 0.340, to 5.615 ± 0.842 (five cells; P < 0.05, paired t-test). Smaller effects were recorded with 0.5-Hz stimulation and secondary synapses scaled to 50% threshold-gsyn (Fig. 6, C and D). With three secondary synapses, muscarine increased synaptic gain from 1.037 ± 0.001 to 1.300 ± 0.144 (three cells) and with nine secondary synapses, muscarine increased synaptic gain from 1.432 ± 0.070 to 1.784 ± 0.157 (three cells).
Synergistic regulation of synaptic gain by gKM and gleak
In the preceding experiments (Figs. 5 and 6), metabotropic suppression of gKM was the most likely mechanism for enhancement of synaptic gain because 92% of the neurons in our cultures did not show the muscarinically activated leak conductance. Nonetheless, analysis of excitability clearly showed that introduction of a virtual leak conductance could lower threshold-gsyn and interact synergistically with suppression of gKM in regulating the response to nicotinic excitation (Fig. 4). A final series of experiments examined whether these effects could also produce significant increases in synaptic gain. B neurons were stimulated with a synaptic template that included three secondary synapses set to 50% threshold-gsyn, one primary synapse, and an average presynaptic firing rate of 0.5 Hz. With this template, separate introduction of either the virtual gleak or muscarine each produced small increases in synaptic gain and adding both together produced a significant increase in gain, greater than the sum of the individual effects (Fig. 7). In grouped data from five neurons, synaptic gain was 1.069 ± 0.008 under control conditions. Adding 0.25 to 0.5 nS of virtual gleak increased the gain to 1.169 ± 0.020, while simultaneously reducing Rleak in the steady-state I–V relation from 1,108 ± 92 to 834 ± 67 MΩ and depolarizing the resting potential from −68.6 ± 1.4 to −54.1 ± 2.2 mV. Adding 1 μM muscarine increased synaptic gain to 1.214 ± 0.055 and depolarized the cells from −67.1 ± 0.9 to −60.6 ± 1.7 mV. Adding the virtual leak and muscarine together increased synaptic gain to 1.794 ± 0.276 (P < 0.05, repeated-measures ANOVA, Tukey’s post hoc test) and depolarized the cells from − 66.1 ± 1.2 to −46.8 ± 3.1 mV.
DISCUSSION
In this study, we analyzed the integrative role of muscarinic excitation in sympathetic ganglia by testing the predictions of a computational model (Schobesberger et al. 2000; Wheeler et al. 2004). To simplify the experimental problem, the dynamic-clamp method was used to create virtual nicotinic synapses whose strength, number, and activity could be precisely controlled. The results show that muscarinic suppression of gKM and activation of a virtual gleak are each sufficient to strengthen the excitatory impact of nicotinic synapses by lowering threshold-gsyn (Figs. 1 and 4). Importantly, the excitatory action of muscarine cannot be explained simply by its depolarizing effect on resting potential (Fig. 2). A direct consequence of excitatory muscarinic modulation in this system is to increase the synaptic gain (Figs. 5–7) that arises through convergence of nicotinic synapses on sympathetic neurons. Both effects were very robust. Although variable in magnitude, the excitatory consequences of muscarinic modulation were consistently evoked over an entire parameter space whose boundaries were chosen to reflect physiological estimates of naturally occurring synaptic strength, nicotinic convergence, and preganglionic activity. Our data also show that combining the changes in gKM and gleak can result in a synergy to produce even larger increases in synaptic strength (Fig. 4) and gain (Fig. 7). These nonlinear interactions between gKM and gleak arise from the voltage and time dependency of gKM. Finally, the results indicate that nicotinic excitation does not act as a physiological trigger of repetitive firing, even though sympathetic neurons are capable of such firing during metabotropic excitation (Fig. 3; also see Adams et al. 1982; Dodd and Horn 1983).
The bridge from metabotropic signaling to synaptic integration
The problem of muscarinic modulation in autonomic ganglia is long-standing and multifaceted. Slow muscarinic EPSPs were first recorded in the 1960s from isolated preparations of the rabbit superior cervical ganglion (Eccles and Libet 1961; Libet and Tosaka 1969) and amphibian lumbar chain ganglia (Koketsu 1969; Nishi and Koketsu 1968; Tosaka et al. 1968). It took ten years to implicate a decrease in K+ conductance (Weight and Votava 1970) and another ten to elucidate the voltage-dependent nature of the M-conductance (Brown and Adams 1980). Most subsequent work focused on the signal transduction pathway, which is now best understood in mammalian sympathetic neurons. Muscarinic suppression of gKM arises through the m1 subclass of receptors (Marrion et al. 1989), which are coupled to the Gq/11 protein, activation of phospholipase C (Delmas et al. 2004), hydrolysis of PIP2 (Suh and Hille 2002; Suh et al. 2004; Zhang et al. 2003), and reduced opening of channels composed of KCNQ2 and KCNQ3 subunits (Delmas et al. 2004; Selyanko et al. 2000, 2002; Shapiro et al. 2000; Wang et al. 1998). By comparison, muscarinic activation of gleak in paravertebral sympathetic neurons was documented repeatedly (Kuba and Koketsu 1976; Mochida and Kobayashi 1986; Tsuji and Kuba 1988), although further details have remained elusive. Possible candidates for this conductance include cyclic nucleotide-gated ion channels (Thompson 1997) and transient receptor potential (trp) channels (Delmas et al. 2004). However, it remains unclear why muscarinic activation of the leak was seen in only 8% of the B neurons that we studied. The rarity of these cells could reflect either a functionally specialized subset of sympathetic B neurons or a technical limitation of our tissue culture and recording methods. In any event, it is important to note that various forms of branched metabotropic signaling pathways are widespread. The observations reported here may therefore prove significant in a number of different cellular contexts.
Previous efforts to understand the role of slow muscarinic excitation in ganglionic integration primarily focused on the afterdischarge of action potentials that is sometimes associated with the slow EPSP (Horn 1992; Nishi and Koketsu 1968). In vivo recordings from lumbar chain ganglia in the cat (Janig 1995) and frog (Ivanoff and Smith 1997) demonstrated after-discharges and slow potentials, although this approach did not elucidate a physiological role for such events, explained in part by problems that arise from the difficulty of working in vivo and the need to introduce exogenous drugs and nerve stimulation to evoke afterdischarges. Another approach was to isolate preparations of amphibian ganglia together with end organs (Jobling and Horn 1996; Thorne and Horn 1997). This demonstrated that metabotropic excitation of postganglionic neurons could elicit detectable consequences in arteries and cutaneous glands, although again the effects were critically dependent on exogenous drugs such as nicotine and d-tubocurarine. All of these results from earlier work are borne out by the present finding that virtual nicotinic EPSPs were incapable of evoking repetitive firing of any kind, let alone the type that has been associated with classical recordings of ganglionic after-discharges. Nonetheless, our conclusion that metabotropically regulated repetitive firing does not contribute to normal ganglionic integration should not be construed as an argument against the practical utility of classifying cell-firing properties as phasic or tonic. Indeed the firing patterns induced by current injection have proven useful as signatures to functionally identify different classes of central and peripheral neurons (Boyd et al. 1996; Cassell et al. 1986; Connors and Gutnick 1990). Our results indicate simply that one must be cautious in extrapolating from such signatures to synaptic integration. In central neurons where convergence is high and individual synapses produce relatively small EPSPs, varying the background level of synaptic activity may function in a manner analogous to steady-current injection and lead to consequences different from those observed in sympathetic neurons.
The view of muscarinic excitation developed herein has its earliest precedent in the observation that slow EPSPs potentiate the amplitudes of fast EPSPs by reducing total membrane conductance and thereby lowering the shunting of synaptic currents (Schulman and Weight 1976). Although very attractive, the data supporting this idea are in retrospect very minimal and recent simulations indicate that effects on EPSP amplitude would be very small and difficult to detect (Schobesberger et al. 1999). These predictions were indeed confirmed by our observations of fast virtual EPSP shape (Fig. 2, C and D). When viewed in the context of synaptic strength, our computational and dynamic-clamp approach has now shown clearly for the first time that by altering postsynaptic excitability, muscarinic excitation can strengthen the impact of nicotinic synapses.
By answering some of the original questions about muscarinic modulation it becomes possible to focus on other unresolved issues, both postsynaptic and presynaptic. First, there is the limitation of the dynamic-clamp method, which implements conductances at the site of recording without mimicking the spatial distribution of synapses over the surface of a neuron. In the case of bullfrog neurons, this problem is insignificant because the cells are monopolar with nicotinic synapses on the soma and axon hillock. In the case of mammalian sympathetic neurons, one must eventually account for the influence of dendrites. Nonetheless, our results demonstrate how muscarinic excitation can modulate integration of fast EPSPs within an isopotential cellular compartment. A second postsynaptic issue is the possible role of calcium-activated K+ conductances (gKCa). Although changes in gKCa do not contribute to the slow muscarinic EPSP, in mammalian sympathetic neurons muscarinic inhibition of N-type calcium currents can reduce their activation by action potentials and may thereby influence synaptic integration (Bernheim et al. 1992; Haley et al. 2000). However, this mechanism is not expressed in bullfrog sympathetic neurons (Bley and Tsien 1990; Jones and Marks 1989) and therefore cannot account for the present results. Finally, it is important to note that our analysis of postsynaptic integration deliberately simplified presynaptic mechanisms by omitting the dynamics of release. It would be interesting to extend the analysis of ganglionic integration to include presynaptic facilitation and depression together with muscarinic receptors that inhibit acetylcholine release (Karila and Horn 2000; Shen and Horn 1996). In the meantime, the present experiments provide evidence that postsynaptic muscarinic excitation can regulate the synaptic gain generated in sympathetic ganglia. The resulting notion that ganglia function as use-dependent amplifiers is likely to be important because the ganglia are embedded in negative feedback loops that control blood pressure, body temperature, and other physiological state variables.
Footnotes
GRANTS
This work was supported by National Institute of Neurological Disorders and Stroke Grant RO1 NS-21065.
References
- Adams PR, Brown DA. Synaptic inhibition of the M-current: slow excitatory post-synaptic potential mechanism in bullfrog sympathetic neurones. J Physiol. 1982;332:263–272. doi: 10.1113/jphysiol.1982.sp014412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams PR, Brown DA, Constanti A. Pharmacological inhibition of the M-current. J Physiol. 1982;332:223–262. doi: 10.1113/jphysiol.1982.sp014411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernheim L, Mathie A, Hille B. Characterization of muscarinic receptor subtypes inhibiting Ca2+ current and M current in rat sympathetic neurons. Proc Natl Acad Sci USA. 1992;89:9544–9548. doi: 10.1073/pnas.89.20.9544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biervert C, Schroeder BC, Kubisch C, Berkovic SF, Propping P, Jentsch TJ, Steinlein OK. A potassium channel mutation in neonatal human epilepsy. Science. 1998;279:403–406. doi: 10.1126/science.279.5349.403. [DOI] [PubMed] [Google Scholar]
- Bley KR, Tsien RW. Inhibition of Ca2+ and K+ channels in sympathetic neurons by neuropeptides and other ganglionic transmitters. Neuron. 1990;4:379–391. doi: 10.1016/0896-6273(90)90050-p. [DOI] [PubMed] [Google Scholar]
- Boyd HD, McLachlan EM, Keast JR, Inokuchi H. Three electrophysiological classes of guinea pig sympathetic postganglionic neurone have distinct morphologies. J Comp Neurol. 1996;369:372–387. doi: 10.1002/(SICI)1096-9861(19960603)369:3<372::AID-CNE4>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- Brown DA, Adams PR. Muscarinic suppression of a novel voltage-sensitive K+ current in a vertebrate neurone. Nature. 1980;283:673–676. doi: 10.1038/283673a0. [DOI] [PubMed] [Google Scholar]
- Cassell JF, Clark AL, McLachlan EM. Characteristics of phasic and tonic sympathetic ganglion cells of the guinea-pig. J Physiol. 1986;372:457–483. doi: 10.1113/jphysiol.1986.sp016020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cobb SR, Davies CH. Cholinergic modulation of hippocampal cells and circuits. J Physiol. 2005;562:81–88. doi: 10.1113/jphysiol.2004.076539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole AE, Nicoll RA. Characterization of a slow cholinergic post-synaptic potential recorded in vitro from rat hippocampal pyramidal cells. J Physiol. 1984;352:173–188. doi: 10.1113/jphysiol.1984.sp015285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connors BW, Gutnick MJ. Intrinsic firing patterns of diverse neocortical neurons. Trends Neurosci. 1990;13:99–104. doi: 10.1016/0166-2236(90)90185-d. [DOI] [PubMed] [Google Scholar]
- Cooper EC, Aldape KD, Abosch A, Barbaro NM, Berger MS, Peacock WS, Jan YN, Jan LY. Colocalization and coassembly of two human brain M-type potassium channel subunits that are mutated in epilepsy. Proc Natl Acad Sci USA. 2000;97:4914–4919. doi: 10.1073/pnas.090092797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper EC, Harrington E, Jan YN, Jan LY. M channel KCNQ2 subunits are localized to key sites for control of neuronal network oscillations and synchronization in mouse brain. J Neurosci. 2001;21:9529–9540. doi: 10.1523/JNEUROSCI.21-24-09529.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delmas P, Crest M, Brown DA. Functional organization of PLC signaling microdomains in neurons. Trends Neurosci. 2004;27:41–47. doi: 10.1016/j.tins.2003.10.013. [DOI] [PubMed] [Google Scholar]
- Dodd J, Dingledine R, Kelly JS. The excitatory action of acetylcholine on hippocampal neurones of the guinea pig and rat maintained in vitro. Brain Res. 1981;207:109–127. doi: 10.1016/0006-8993(81)90682-x. [DOI] [PubMed] [Google Scholar]
- Dodd J, Horn JP. Muscarinic inhibition of sympathetic C neurones in the bullfrog. J Physiol. 1983;334:271–291. doi: 10.1113/jphysiol.1983.sp014494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eccles RM, Libet B. Origin and blockade of the synaptic responses of curarized sympathetic ganglia. J Physiol. 1961;157:484–503. doi: 10.1113/jphysiol.1961.sp006738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haley JE, Delmas P, Offermanns S, Abogadie FC, Simon MI, Buckley NJ, Brown DA. Muscarinic inhibition of calcium current and M current in Galpha q-deficient mice. J Neurosci. 2000;20:3973–3979. doi: 10.1523/JNEUROSCI.20-11-03973.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME, McGaughy J. High acetylcholine levels set circuit dynamics for attention and encoding and low acetylcholine levels set dynamics for consolidation. Prog Brain Res. 2004;145:207–231. doi: 10.1016/S0079-6123(03)45015-2. [DOI] [PubMed] [Google Scholar]
- Horn JP. The integrative role of synaptic cotransmission in the bullfrog vasomotor C system: evidence for a synaptic gain hypothesis. Can J Physiol Pharmacol Suppl. 1992;70:S19–S26. doi: 10.1139/y92-239. [DOI] [PubMed] [Google Scholar]
- Ivanoff AY, Smith PA. On the role of muscarinic and peptidergic receptors in ganglionic transmission in bullfrogs in vivo. Am J Physiol Regul Integr Comp Physiol. 1997;272:R1501–R1514. doi: 10.1152/ajpregu.1997.272.5.R1501. [DOI] [PubMed] [Google Scholar]
- Janig WM. Ganglionic transmission in vivo. In: McLachlan EM, editor. Autonomic Ganglia. Canberra, Australia: Harwood Academic; 1995. pp. 349–395. [Google Scholar]
- Jobling P, Horn JP. In vitro relation between preganglionic sympathetic stimulation and activity of cutaneous glands in the bullfrog. J Physiol. 1996;494:287–296. doi: 10.1113/jphysiol.1996.sp021491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones SW, Marks TN. Calcium currents in bullfrog sympathetic neurons. I. Activation kinetics and pharmacology. J Gen Physiol. 1989;94:151–167. doi: 10.1085/jgp.94.1.151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karila P, Horn JP. Secondary nicotinic synapses on sympathetic B neurons and their putative role in ganglionic amplification of activity. J Neurosci. 2000;20:908–918. doi: 10.1523/JNEUROSCI.20-03-00908.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koketsu K. Cholinergic synaptic potentials and the underlying ionic mechasims. Fed Proc. 1969;28:101–112. [PubMed] [Google Scholar]
- Kuba K, Koketsu K. Analysis of the slow excitatory postsynaptic potential in bullfrog sympathetic ganglion cells. Jpn J Physiol. 1976;26:651–669. doi: 10.2170/jjphysiol.26.651. [DOI] [PubMed] [Google Scholar]
- Kullmann PH, Wheeler DW, Beacom J, Horn JP. Implementation of a fast 16-bit dynamic clamp using LabVIEW-RT. J Neurophysiol. 2004;91:542–554. doi: 10.1152/jn.00559.2003. [DOI] [PubMed] [Google Scholar]
- Libet B, Tosaka T. Slow inhibitory and excitatory postsynaptic responses in single cells of mammalian sympathetic ganglia. J Neurophysiol. 1969;32:43–50. doi: 10.1152/jn.1969.32.1.43. [DOI] [PubMed] [Google Scholar]
- Marrion NV, Smart TG, Marsh SJ, Brown DA. Muscarinic suppression of the M-current in the rat sympathetic ganglion is mediated by receptors of the M1-subtype. Br J Pharmacol. 1989;98:557–573. doi: 10.1111/j.1476-5381.1989.tb12630.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Prince DA. Two types of muscarinic response to acetylcholine in mammalian cortical neurons. Proc Natl Acad Sci USA. 1985;82:6344–6348. doi: 10.1073/pnas.82.18.6344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mochida S, Kobayashi H. Three types of muscarinic conductance changes in sympathetic neurons discriminately evoked by the different concentrations of acetylcholine. Brain Res. 1986;383:299–304. doi: 10.1016/0006-8993(86)90028-4. [DOI] [PubMed] [Google Scholar]
- Nishi S, Koketsu K. Early and late after discharges of amphibian sympathetic ganglion cells. J Neurophysiol. 1968;31:109–121. doi: 10.1152/jn.1968.31.1.109. [DOI] [PubMed] [Google Scholar]
- Pfaffinger P. Muscarine and t-LHRH suppress M-current by activating an IAP-insensitive G-protein. J Neurosci. 1988;8:3343–3353. doi: 10.1523/JNEUROSCI.08-09-03343.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schobesberger H, Gutkin BS, Horn JP. A minimal model for metabo-tropic modulation of fast synaptic transmission and firing properties in bullfrog sympathetic B neurons. Neurocomputing. 1999;26/27:255–262. [Google Scholar]
- Schobesberger H, Wheeler DW, Horn JP. A model for pleiotropic muscarinic potentiation of fast synaptic transmission. J Neurophysiol. 2000;83:1912–1923. doi: 10.1152/jn.2000.83.4.1912. [DOI] [PubMed] [Google Scholar]
- Schulman JA, Weight FF. Synaptic transmission: long-lasting potentiation by a postsynaptic mechanism. Science. 1976;194:1437–1439. doi: 10.1126/science.188131. [DOI] [PubMed] [Google Scholar]
- Sekerli M, Del Negro CA, Lee RH, Butera RJ. Estimating action potential thresholds from neuronal time-series: new metrics and evaluation of methodologies. IEEE Trans Biomed Eng. 2004;51:1665–1672. doi: 10.1109/TBME.2004.827531. [DOI] [PubMed] [Google Scholar]
- Selyanko AA, Delmas P, Hadley JK, Tatulian L, Wood IC, Mistry M, London B, Brown DA. Dominant-negative subunits reveal potassium channel families that contribute to M-like potassium currents. J Neurosci. 2002;22:RC212. doi: 10.1523/JNEUROSCI.22-05-j0001.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selyanko AA, Hadley JK, Wood IC, Abogadie FC, Jentsch TJ, Brown DA. Inhibition of KCNQ1–4 potassium channels expressed in mammalian cells via M1 muscarinic acetylcholine receptors. J Physiol. 2000;522:349–355. doi: 10.1111/j.1469-7793.2000.t01-2-00349.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapiro MS, Roche JP, Kaftan EJ, Cruzblanca H, Mackie K, Hille B. Reconstitution of muscarinic modulation of the KCNQ2/KCNQ3 K(+) channels that underlie the neuronal M current. J Neurosci. 2000;20:1710–1721. doi: 10.1523/JNEUROSCI.20-05-01710.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen W, Hamilton SE, Nathanson NM, Surmeier DJ. Cholinergic suppression of KCNQ channel currents enhances excitability of striatal medium spiny neurons. J Neurosci. 2005;25:7449–7458. doi: 10.1523/JNEUROSCI.1381-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen WX, Horn JP. A presynaptic mechanism accounts for the differential block of nicotinic synapses on sympathetic B and C neurons by d-tubocurarine. J Neurosci. 1995;15:5025–5035. doi: 10.1523/JNEUROSCI.15-07-05025.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen WX, Horn JP. Presynaptic muscarinic inhibition in bullfrog sympathetic ganglia. J Physiol. 1996;491:413–421. doi: 10.1113/jphysiol.1996.sp021225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh NA, Charlier C, Stauffer D, DuPont BR, Leach RJ, Melis R, Ronen GM, Bjerre I, Quattlebaum T, Murphy JV, McHarg ML, Gagnon D, Rosales TO, Peiffer A, Anderson VE, Leppert M. A novel potassium channel gene, KCNQ2, is mutated in an inherited epilepsy of newborns. Nat Genet. 1998;18:25–29. doi: 10.1038/ng0198-25. [DOI] [PubMed] [Google Scholar]
- Suh BC, Hille B. Recovery from muscarinic modulation of M current channels requires phosphatidylinositol 4,5-bisphosphate synthesis. Neuron. 2002;35:507–520. doi: 10.1016/s0896-6273(02)00790-0. [DOI] [PubMed] [Google Scholar]
- Suh BC, Horowitz LF, Hirdes W, Mackie K, Hille B. Regulation of KCNQ2/KCNQ3 current by G protein cycling: the kinetics of receptor-mediated signaling by Gq. J Gen Physiol. 2004;123:663–683. doi: 10.1085/jgp.200409029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson SH. Cyclic GMP-gated channels in a sympathetic neuron cell line. J Gen Physiol. 1997;110:155–164. doi: 10.1085/jgp.110.2.155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorne R, Horn JP. Role of ganglionic cotransmission in sympathetic control of the isolated bullfrog aorta. J Physiol. 1997;498:201–214. doi: 10.1113/jphysiol.1997.sp021851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tokimasa T, Simmons MA, Schneider CR, Akasu T. Hyperpolarizing shift of the M-current activation curve after washout of muscarine in bullfrog sympathetic neurons. Neurosci Lett. 1996;207:97–100. doi: 10.1016/0304-3940(96)12495-2. [DOI] [PubMed] [Google Scholar]
- Tosaka T, Chichibu S, Libet B. Intracellular analysis of slow inhibitors and excitatory postsynaptic potentials in sympathetic ganglia of the frog. J Neurophysiol. 1968;31:396–409. doi: 10.1152/jn.1968.31.3.396. [DOI] [PubMed] [Google Scholar]
- Tsuji S, Kuba K. Muscarinic regulation of two ionic currents in the bullfrog sympathetic neurone. Pfluegers Arch. 1988;411:361–370. doi: 10.1007/BF00587714. [DOI] [PubMed] [Google Scholar]
- Wang HS, Pan Z, Shi W, Brown BS, Wymore RS, Cohen IS, Dixon JE, McKinnon D. KCNQ2 and KCNQ3 potassium channel subunits: molecular correlates of the M-channel. Science. 1998;282:1890–1893. doi: 10.1126/science.282.5395.1890. [DOI] [PubMed] [Google Scholar]
- Weight FF, Votava J. Slow synaptic excitation in sympathetic ganglion cells: evidence for synaptic inactivation of potassium conductance. Science. 1970;170:755–758. doi: 10.1126/science.170.3959.755. [DOI] [PubMed] [Google Scholar]
- Wheeler DW, Kullmann PH, Horn JP. Estimating use-dependent synaptic gain in autonomic ganglia by computational simulation and dynamic-clamp analysis. J Neurophysiol. 2004;92:2659–2671. doi: 10.1152/jn.00470.2004. [DOI] [PubMed] [Google Scholar]
- Zhang H, Craciun LC, Mirshahi T, Rohacs T, Lopes CM, Jin T, Logothetis DE. PIP(2) activates KCNQ channels, and its hydrolysis underlies receptor-mediated inhibition of M currents. Neuron. 2003;37:963–975. doi: 10.1016/s0896-6273(03)00125-9. [DOI] [PubMed] [Google Scholar]


