Background Selection in Single Genes May Explain Patterns of Codon Bias

Abstract

Background selection involves the reduction in effective population size caused by the removal of recurrent deleterious mutations from a population. Previous work has examined this process for large genomic regions. Here we focus on the level of a single gene or small group of genes and investigate how the effects of background selection caused by nonsynonymous mutations are influenced by the lengths of coding sequences, the number and length of introns, intergenic distances, neighboring genes, mutation rate, and recombination rate. We generate our predictions from estimates of the distribution of the fitness effects of nonsynonymous mutations, obtained from DNA sequence diversity data in Drosophila. Results for genes in regions with typical frequencies of crossing over in Drosophila melanogaster suggest that background selection may influence the effective population sizes of different regions of the same gene, consistent with observed differences in codon usage bias along genes. It may also help to cause the observed effects of gene length and introns on codon usage. Gene conversion plays a crucial role in determining the sizes of these effects. The model overpredicts the effects of background selection with large groups of nonrecombining genes, because it ignores Hill–Robertson interference among the mutations involved.

IT has been known for a long time that selection at one site in the genome influences the evolutionary fate of variants at linked sites (Fisher 1930; Muller 1932; Hill and Robertson 1966; Felsenstein 1974; Birky and Walsh 1988; Gordo and Charlesworth 2001). Such effects are expected to be particularly strong in regions of the genome with low levels of crossing over, but normal gene densities. Consistent with this, there are associations between low recombination rates and reduced levels of silent nucleotide site diversity in Drosophila (Begun and Aquadro 1992; Presgraves 2005; Bierne and Eyre-Walker 2006). This has stimulated interest in understanding the forces that influence patterns of diversity along chromosomes, with particular attention having been paid to two extreme alternatives: selective sweeps (Maynard Smith and Haigh 1974; Begun and Aquadro 1992; Betancourt and Presgraves 2002; Kim 2004; Presgraves 2005; Stephan et al. 2006) and background selection (Charlesworth et al. 1993, 1995; Hudson and Kaplan 1995; Charlesworth 1996; Nordborg et al. 1996). These factors can usefully be thought of as causing a reduction in effective population size, N_e, leading to reduced genetic diversity (Kimura 1983).

In addition, a higher level of nonsynonymous divergence in a gene between Drosophila species is correlated with a lower frequency of optimal codons (f_op) (Betancourt and Presgraves 2002; Marais et al. 2004; Bierne and Eyre-Walker 2006). To explain this in terms of selective sweeps, Kim (2004) modeled the effect of the spread of selectively favorable amino acid mutations on N_e for the gene in which they occur. In addition, interference among weakly selected sites may also reduce the efficacy of selection at such sites, as measured by N_es, where s denotes the relevant selection coefficient (Li 1987; Coméron et al. 1999; McVean and Charlesworth 2000; Tachida 2000; Coméron and Kreitman 2002). Such interference has been proposed as an explanation of patterns in the inferred intensity of selection on codon bias within genes of Drosophila. As discovered from whole-genome analyses, less frequent use of optimal codons (i.e., lower codon usage bias) is found in the middle of genes that lack introns, in long genes, and in regions of low recombination (Coméron et al. 1999; Coméron and Kreitman 2000, 2002; Qin et al. 2004).

Background selection causes a similar reduction in N_e, by the removal of weakly selected or neutral variants at sites that are closely linked to sites under purifying selection. When deleterious mutations at the latter sites have N_es > 1, they can be treated as effectively close to equilibrium under mutation–selection balance and contribute to background selection effects (Charlesworth et al. 1993, 1995; Nordborg et al. 1996). Recent results suggest that most amino acid mutations in Drosophila are sufficiently deleterious to fall into this category (Loewe and Charlesworth 2006; Loewe et al. 2006); these are so abundant that they may exert significant effects on sites within the same or neighboring genes.

The basis for this can be understood as follows. Published data on autosomal DNA sequence polymorphisms in regions with normal recombination rates in African populations of Drosophila melanogaster yield a mean nonsynonymous nucleotide site diversity of ∼0.3% (B. Vicoso, personal communication). With a mean of ∼1333 nonsynonymous sites per gene (Misra et al. 2002), this implies an average of 1333 × 0.003/2 ≈ 2 amino acid variants per gene. Even if as few as 50% of these have N_es > 1, then each gene would carry an average of close to one effectively deleterious mutation. In the absence of recombination, Equation 4 of Charlesworth et al. (1993) shows that N_e is then reduced to 37% of its maximal value. This suggests that there may be enough deleterious amino acid variants in Drosophila genes to cause significant background selection on closely linked sites, even in the presence of recombination. This reflects the weak selection coefficients for most amino acid mutations inferred from polymorphism studies (Loewe and Charlesworth 2006; Loewe et al. 2006). Earlier models of background selection assumed stronger selection that leads to less frequent, but more deleterious, variants, on the basis of estimates of the fitness effects of mutations from mutation-accumulation lines (Hudson and Kaplan 1995; Charlesworth 1996).

We use theoretical predictions of the effects of background selection on neutral diversity, which allow arbitrary levels of recombination to be modeled (Hudson and Kaplan 1995; Nordborg et al. 1996). The theory has been extended to include the effects of background selection on fixation probabilities of weakly selected mutations linked to sites under strong selection (Stephan et al. 1999; unpublished results of M. Nordborg, personal communication). This enables the prediction of codon usage bias, from standard results on mutation–selection–drift equilibrium (Li 1987; Bulmer 1991; McVean and Charlesworth 1999). We can thus combine a set of mutation rates and fitness effects with an arbitrary recombinational landscape, for the purpose of predicting the effects of background selection for each point in the landscape.

In the past, such efforts have focused mainly on whole chromosomes to examine whether background selection can explain the relation between local recombination rate and nucleotide diversity for Drosophila (Hudson and Kaplan 1995; Charlesworth 1996) and for humans (Payseur and Nachman 2002a,b; Reed et al. 2005). It was tacitly assumed that background selection at the level of a single gene is negligible. Since gene conversion acts only over short distances, it was also ignored in these studies. While the question of the pattern of chromosomewide variability is important, this article has a quite different goal. We explore whether background selection can cause the patterns of codon bias mentioned above, by predicting the reduction of N_e due to background selection in single genes or in small groups of genes. We investigate the effects of various parameters, including rates of recombination caused by both crossing over and gene conversion, mutation rates, selection coefficients, and gene structure (introns, intergenic distances, and numbers of neighboring genes). All the parameters are chosen as being realistic for D. melanogaster. The results show that background selection may play a significant role in shaping the observed patterns of codon usage bias.

METHODS

Basic model:

A detailed description of the model is given by Nordborg et al. (1996). The main feature of the version developed here is a gene with l bp of coding sequence, where nonsynonymous mutations (occurring only in the first two sites of a triplet of bases, i.e., a codon) have a deleterious heterozygous selection coefficient, s, assigned from previous estimates of the distribution of s (Loewe and Charlesworth 2006; Loewe et al. 2006). Selection on the third site in each codon is assumed to be negligibly weak compared with selection on the first two sites; variability and adaptation for synonymous mutations at such a site are then controlled by the variable B = N_e/N₀, where N₀ and N_e are the effective population sizes in the absence and presence of background selection, respectively. Ignoring the pressure of selection on nonsynonymous mutations at two- and threefold degenerate third positions means that we slightly underestimate the effects of background selection, since we assume that 66.7% of all 576 possible point mutations in all codons are nonsynonymous, whereas the genetic code predicts that 68.6% of all possible point mutations are nonsynonymous, ignoring stop codons.

The strongly selected sites are assumed to be in mutation–selection equilibrium, so that q_i, the frequency of the deleterious allele at site i, is given by

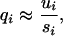(1)

where u_i is the mutation rate per generation at site i from wild type to mutant (Haldane 1927).

B for the weakly selected (synonymous) site under consideration (the “focal site”) is then equal to

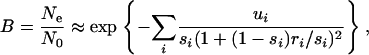(2)

where r_i is the recombination rate between a given strongly selected deleterious site, i, and the focal site. The sum is over all nonsynonymous sites in the gene under consideration and in all relevant neighboring genes. This formula has been shown by simulations to predict the reduction in neutral variability caused by background selection (Nordborg et al. 1996).

A study of the effect of background selection due to a single site subject to mutation and selection (Stephan et al. 1999) showed that the fixation probabilities of mutations at a weakly selected linked site can be predicted by substituting the value of N_e from Equation 2 into the standard formula for fixation probability for a single locus (Kimura 1962). Simulations have confirmed that this result also applies to a large number of strongly selected, linked sites, each subject to mutation and selection (M. Nordborg, personal communication). The level of adaptation at weakly selected, synonymous sites, measured by the frequency of preferred codons at statistical equilibrium under mutation, drift, and selection, is determined by these fixation probabilities (Li 1987; Bulmer 1991; McVean and Charlesworth 1999).

There are, however, conditions on the validity of Equation 2 that need to be considered. First, use of Equation 1 requires N_es_i > 1. This does not necessarily mean that the population is at equilibrium, but implies that the mean allele frequency over the distribution generated by selection, mutation, and drift is well approximated by Equation 1, assuming semidominant effects of mutations on fitness (McVean and Charlesworth 1999). Thus the mean frequency over a group of variants subject to selection is given by Equation 1, so that the formula works well in practice (Nordborg et al. 1996). Second, if selection against deleterious mutations is very weak, there is a significant probability of fixation of a mutation at a weakly selected site in situations when the mutation is linked to a deleterious variant that is drifting to high frequencies or fixation; such cases are ignored in Equation 2. Use of Equations 5 and 6 in the Appendix to Charlesworth et al. (1993) for the case of no recombination shows that this effect will be small if the fixation probability of a deleterious mutation can be neglected relative to the neutral value, as is the case if N_es_i > 1 (Kimura 1983, pp. 43–46). Third, if there is tight linkage among a group of deleterious mutations, Hill–Robertson effects among them undermine the effectiveness of selection, and Equation 2 overestimates the reduction in N_e (Charlesworth et al. 1993; Nordborg et al. 1996). For these reasons, we removed from consideration any sites for which N_es_i ≤ 1 and restricted ourselves mostly to small groups of genes with nonzero levels of gene conversion. To produce our results, we computed B either for all synonymous sites in the focal gene or for 200 evenly distributed synonymous sites in the gene (to save computing time). To condense this into a single value of B for each gene, we computed the arithmetic mean over all synonymous sites for use in some of our plots.

Modeling gene structure and gene conversion:

To incorporate gene structure into Equation 2 requires only specification of the recombination rates, r_i, if we assume a constant mutation rate and selection coefficient across the gene. Our basic approach was to measure the molecular distance d_i between the synonymous focal site and the selected site i while walking over all sites between them. Whenever nonselected sites were encountered, d_i was increased accordingly, without increasing the sum in Equation 2. Three types of sequences affect d_i in this way: synonymous sites, introns, and intergenic regions. Although our computer code is flexible, we assumed that all neighboring genes had the same structure (2000 bp in exons; four introns of 100 bp), independent of that of the focal gene. For a given number of introns, the l bp of the exon sequence were divided into a corresponding number of equally long exons.

To convert d_i into r_i, we used Equation 1 of Frisse et al. (2001), which assumes a mixture of reciprocal crossing over and gene conversion with an exponential distribution of tract lengths. This gives the net recombination rate between the focal site and site i as

(3)

where r_c is the probability of a reciprocal crossover between two bases, d_g is the mean tract length of a gene conversion event, and r_g is the probability of gene conversion at a particular site (the product of d_g and the probability of initiating a gene conversion at a given site). This formula is more exact than that of Andolfatto and Nordborg (1998) and is equivalent to those of Wiuf and Hein (2000) and Langley et al. (2000). It neglects the reduction in r_i from double crossovers over large chromosomal distances, which are not the focus of our study.

Modeling the distribution of deleterious mutational effects (DDME) on fitness:

We assumed that the distribution of heterozygous selection coefficients against deleterious mutations follows a lognormal distribution (Aitchison and Brown 1957; Crow 1988), since this distribution has proved useful for estimating mutational effects in Drosophila (Loewe and Charlesworth 2006). It is characterized by “shape” and “location” parameters, σ_g and μ_g, which correspond to the exponentials of the standard deviation and mean of the natural logarithm of the variate, respectively (Limpert et al. 2001). Unfortunately it is not possible to estimate the DDME in D. melanogaster by this method without making several assumptions. We therefore used estimates from D. miranda and D. pseudoobscura (Loewe and Charlesworth 2006) to choose plausible DDMEs, on the basis of the requirement that these be compatible with the diversity data for both species and also predict a realistic number of dominant, effectively lethal, mutations (Loewe and Charlesworth 2006).

We then used the shape parameters of these DDMEs to estimate the corresponding location parameters. This was done by using nonsynonymous and synonymous nucleotide site diversities (π_A and π_S, respectively) from autosomal genes in high-recombination regions of African populations of D. melanogaster. Means with ∼90% confidence intervals (from a metaanalysis of published data) were kindly provided by Beatriz Vicoso: π_A = 0.295% (0.166–0.560%) and π_S = 2.07% (1.67–2.59%), on the basis of 17 loci weighted by the inverses of their expected sampling variances (Bartolomé et al. 2005). The location parameter for an assumed shape parameter was obtained by equating observed and expected values of π_A/π_S, in a similar way to the procedure of Loewe and Charlesworth (2006). Key parameters of the resulting DDMEs are given in Table 1.

TABLE 1.

Estimates of the DDME for D. melanogaster

Shape	Location	Lethals	Nes(am)	Nes(hm)	Nes (5%)	Nes (95%)	CV	cne %
1.35	2.85 × 10−6	<10−100	3.87	3.54	2.17	6.16	0.308	0.0040
2.72	4.25 × 10−6	10−36	9.46	4.18	1.46	30.3	1.27	4.41
3.67	5.43 × 10−6	4 × 10−22	17.5	4.83	1.46	62.1	2.02	6.68
7.39	1.02 × 10−5	3.4 × 10−10	108	6.39	1.58	394	6.81	9.81
10	1.37 × 10−5	4.3 × 10−8	279	7.58	1.6	910	10.4	10.6
20	2.71 × 10−5	1.7 × 10−5	2,460	9.76	1.84	5,820	9.65	11.7
30	4.07 × 10−5	0.00011	6,530	11.1	1.87	17,000	7.23	12.2
40	5.47 × 10−5	0.00029	11,100	12.0	2.00	34,100	5.98	12.4
50	6.86 × 10−5	0.00053	15,500	12.7	2.02	54,400	5.26	12.6
60	8.27 × 10−5	0.00080	19,500	13.3	2.15	79,300	4.8	12.7
70	9.69 × 10−5	0.0011	23,200	13.7	2.16	101,000	4.48	12.8
80	0.000111	0.0014	26,400	14.1	2.17	126,000	4.24	12.8
90	0.000126	0.0017	29,400	14.4	2.19	148,000	4.6	12.9
100	0.000140	0.0020	32,000	14.7	2.32	171,000	3.91	12.9

All estimates are consistent with diversity data from D. melanogaster. The values underlined, for the predicted frequencies of effectively lethal, dominant mutations, are consistent with genetic data (∼10⁻⁵–0.004/zygote/generation; see Loewe and Charlesworth 2006). Columns denote the shape, σ_g, and location, μ_g, of the assumed lognormal DDME; the number of dominant, effectively lethal mutations per genome per generation predicted by the DDME; the arithmetic (am) and harmonic (hm) mean selection coefficient multiplied by N_e (averaged over the truncated DDME, including all nonneutral, nonlethal mutations); the lower (5%) and upper (95%) 5% percentiles of the truncated DDME; the coefficient of variation of the truncated DDME; and c_ne %, the percentage of effectively neutral nonsynonymous mutations.

We included the DDME in our computations of background selection by constructing an array that contained all deleterious sites to be considered for one computation of B. Then mutational effects were randomly drawn for each site, using the parameters of an estimated lognormal DDME, and stored while B was computed for all neutral sites considered in the focal gene. To average over the large amount of noise, we repeated the procedure 100 times and finally used the arithmetic mean of B for each site from these repeats. This is equivalent to averaging sequence data over 100 different genes, similar to the approach of Coméron et al. (1999; Coméron and Kreitman 2000, 2002).

Since most DDMEs included a significant probability mass in the effectively neutral area (N_es ≤ 1.0), a significant number of nonsynonymous sites are nearly neutral and are thus omitted from the calculations. This makes our DDME-based estimates of B slightly overestimate the true value.

Plausible parameter combinations for D. melanogaster:

We chose our parameters to reflect the properties of autosomal genes in D. melanogaster. Nucleotide site mutation rate estimates (u = 5.8 × 10⁻⁹/bp/generation, with ∼95% confidence interval 2.1 × 10⁻⁹–1.31 × 10⁻⁸) have been obtained from a mutation-detection screen of mutation-accumulation experiments (Haag-Liautard et al. 2007). To cover a range of mutation rates across the genome, we used mutation rates of 2 × 10⁻⁹, 4 × 10⁻⁹, and 8 × 10⁻⁹, respectively, in the calculations described in results. If we combine these with the mean synonymous diversity at autosomal loci in high-recombination regions from African populations (see above), N_e ∼ 1.3 × 10⁶, with a range from 0.65 × 10⁶ to 2.6 × 10⁶, corresponding to the upper and lower limits for the mutation rates that we use. Our results agree with other estimates that suggest a recent N_e of ∼10⁶ (Moriyama and Powell 1996; McVean and Vieira 2001). Estimates of the parameters of the DDME assumed a “standard” mutation rate of 4 × 10⁻⁹. Previous work suggests that the estimates of the shape of the DDME and the product of N_e and location parameter are not very sensitive to the mutation rate (Loewe et al. 2006).

We assumed crossing-over rates of recombining genes that ranged from r_c = 1 × 10⁻⁹ to 3 × 10⁻⁸, with a mean of ∼1 × 10⁻⁸/bp/generation (Betancourt and Presgraves 2002; Hey and Kliman 2002), averaging over the r_c-values for females and males (which do not cross over). Unless otherwise stated, all computations assumed a gene conversion frequency per site (corrected for the lack of events in males) of r_g = 0.25 × 10⁻⁵, on the basis of the mean of estimates from the rosy locus (Hilliker and Chovnick 1981), and a mean tract length of 352 bp (Hilliker et al. 1994).

Gene structures were estimated from the third release of the D. melanogaster genome (Misra et al. 2002; FlyBase 2006). The average length of the sum of all exons in a gene is 2078 bp (27.8 Mb total sequence in exons/13,379 protein-coding genes; Misra et al. 2002), with extremes ranging from 63 to 15,603 bp (Adams et al. 2000). The typical gene has 3.6 introns (48,257 introns/13,379 protein-coding genes; Misra et al. 2002). Most introns have a length between 59 and 63 bp (Mount et al. 1992), but extremes range from 40 bp to >70 kb (Adams et al. 2000). Intergenic distances are ∼6.2 kb on average [subtracting 4 introns of 100 bp from (116.8 Mbp total euchromatin − 27.8 Mb all exons)/13,379 protein coding genes] (Misra et al. 2002). However, gene densities vary from 1/50 kbp to 30/50 kbp (Adams et al. 2000), so that the intergenic distance could be as little as 500 bp in dense gene clusters. We chose our “standard setup” to resemble these findings, by assuming that a typical gene has 2000 bp of exons, 4 introns of 100 bp, and a distance of 6 kb between genes. The possible effects of neighboring genes are ignored, except where specifically mentioned. We assume that two-thirds of sites are nonsynonymous, i.e., 1333 per gene. Mutations to stop codons were ignored. Deviations from this standard setting are mentioned explicitly.

The DDME estimates are shown in Table 1. In computations that assumed constant selection coefficients, we used the harmonic mean heterozygous selection coefficient, s_h, estimated from a DDME with a width of σ_g = 50. This gives N_es_h ≈ 12.7 and c_ne ≈ 12.6%, where c_ne is the fraction of effectively neutral nonsynonymous mutations (for which N_es ≤ 1). s_h can be shown to be the dominant term in a Taylor series expansion of Equation 2 for low recombination rates, when there is a distribution of s-values, which provides a justification for using s_h in Equation 2 as an approximation. This requires a correction for the presence of effectively neutral mutations among the nonsynonymous mutations. We therefore multiplied the overall mutation rate by a factor of 1 − c_ne to obtain the mutation rate used in Equation 2.

Computations:

The model described above was implemented using the statistical script programming language R (Ihaka and Gentleman 1996; Maindonald and Braun 2002), which can be freely downloaded from http://www.r-project.org/. All core functionality was contained in a function “FopBgs,” which takes all possible input parameters and returns a list that contains all potentially informative results. FopBgs was tested by monitoring key parameters while stepping through the important parts of the code and by comparing results with analytical results, for the case with no recombination and for an approximation for the case of crossing over with no gene conversion (Equation 9 of Nordborg et al. 1996).

RESULTS

Edges of exons experience less background selection:

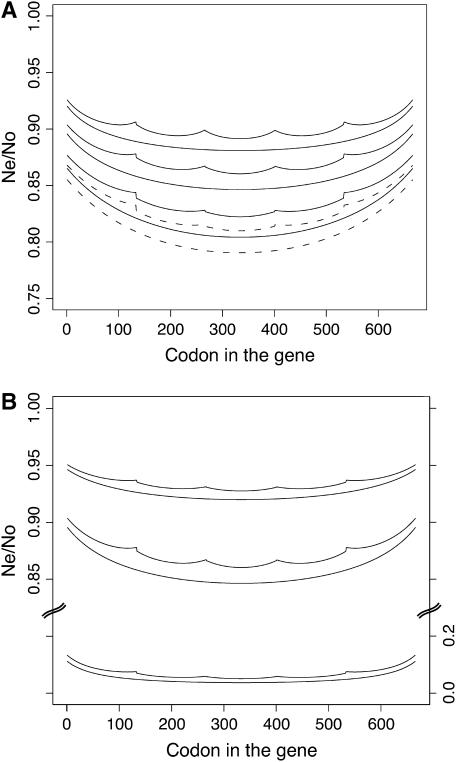
Figure 1 shows the pattern of B-values across genes with the standard structure described above, assuming a fixed selection coefficient. Figure 1A shows the effect of varying the rate of gene conversion, r_g, with standard mutation and crossover rates. Gene conversion reduces the overall effects of background selection, as would be expected from its major role in intragenic recombination in Drosophila (Hilliker and Chovnick 1981). The edges of a gene experience less background selection, as would be expected from the lower density of deleterious sites that they experience—see the discussion following Equations 9 and 10 in Nordborg et al. (1996). The same principle applies to the boundaries of introns. These effects generate a U-shaped pattern for B within each exon. We also found that gene conversion alone, without any reciprocal crossing over, can produce patterns similar to those shown here (data not shown). The presence of introns has a small but notable effect on the mean B for a gene, reflecting the increased recombination rate among the sites contributing to background selection.

Figure 1.—

Background selection in a single gene with the fixed selection coefficient approximation, showing the effects of gene conversion and mutation rates with a crossover rate of 10⁻⁸. The selection coefficient s was set equal to the harmonic mean heterozygous selection coefficient, estimated from a DDME with a width of σ_g = 50, which gives an N_es value of 12.7 and a frequency of effectively neutral mutations, c_ne, of 12.6%. All curves are paired, with the bottom curve representing the coding sequence of a gene without introns and the top curve that of a gene with four equidistant introns. (A) Different gene conversion rates for u = 4 × 10⁻⁹; pairs of solid lines from top to bottom are for r_g = 5 × 10⁻⁶, 2.5 × 10⁻⁶, 0.5 × 10⁻⁶; the dashed line is for r_g = 0. (B) Different mutation rates for r_g = 2.5 × 10⁻⁶; pairs of lines from top to bottom are for u = 2 × 10⁻⁹, u = 4 × 10⁻⁹, and u = 8 × 10⁻⁹. The scale for the bottom two curves is on the right.

Figure 1B shows the effect of varying the mutation rate, for standard selection and recombination parameters. As would be expected from the exponential dependence of B on mutation rate (Equation 2), a high mutation rate greatly increases the effect of background selection. This gives some insight into the expected patterns of differences between genes caused by different mutation rates, assuming fixed selection and recombination parameters (the standard mutation rate was used to estimate N_e and the parameters of the DDME in these cases).

An important question is the sensitivity of these results to the assumption of constant selection coefficients. Figure 2, A and B, shows the same plots as Figure 1, A and B, but with a DDME of width σ_g = 50, averaged over 100 genes, instead of a fixed selection coefficient. Together with the results for other DDMEs (data not shown), this suggests that the general nature of the patterns within genes is robust to the distribution of s, but that the overall effects of background selection are reduced by a wide distribution. The effects of introns and gene boundaries seem to be slightly more pronounced with a wider DDME, but the reduction in B in the center of genes is smaller.

Figure 2.—

Background selection in a single gene: average of 100 samples from a DDME, showing the effects of gene conversion and mutation rate. Otherwise this is similar to Figure 1.

The effects of exon and intron lengths:

Figure 3 shows that the effect of background selection increases with exon length in genes with no introns and no neighbors. The effect is especially large for a high mutation rate and low rate of crossing over and is quite small (<10%) for the standard recombination and mutation rates combined with a realistic exon length and DDME (Figure 3B). Long genes with low crossing over and high or standard mutation rates suffer a considerable reduction in B, since with low recombination there is a large effect of the number of nonsynonymous mutations, as explained in the Introduction. Figure 4 shows that longer introns reduce the mean effect of background selection on a gene, although the effect levels off once introns become >1 kb, except with low recombination rates and high mutation rates.

Figure 3.—

Longer exons experience more background selection. Mean values of B = N_e/N₀ for a gene are shown, assuming no neighboring genes, no introns, and r_g = 2.5 × 10⁻⁶. The thickness of the curves denotes the crossing-over rate (thick, 3 × 10⁻⁸; medium, 1 × 10⁻⁸; thin, 1 × 10⁻⁹), line type represents the mutation rate (dotted, 2 × 10⁻⁹; dashed, 4 × 10⁻⁹; solid, 8 × 10⁻⁹), and the highlighted curve indicates a typical gene (dashed line with medium thickness). (A) Fixed selection coefficient is as in Figure 1. (B) Average of 100 samples from the DDME. The bottom three curves belong to the scale on the right.

Figure 4.—

Longer introns reduce background selection. Mean values of B for a gene of the standard length are shown, assuming no neighboring genes, four equidistant introns, and r_g = 2.5 × 10⁻⁶. Other features of the curves are as in Figure 3. (A) Fixed selection coefficients. The bottom three lines belong to the scale on the right. (B) Average of 100 samples from the DDME. The bottom three lines belong to the scale on the right.

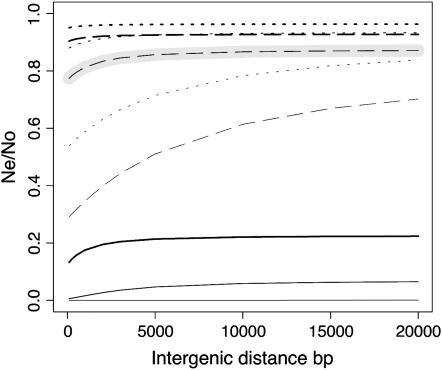
The effects of numbers of neighbors and intergenic distance:

The effect of increasing the number of neighboring genes on the mean level of background selection over a gene is surprisingly small, unless the recombination rate is very low or the mutation rate is high (Figure 5). This probably reflects the rather weak average s-values assumed here, which mean that a small amount of recombination is sufficient to remove the effects of linked genes (Equation 2). This result is encouraging, since it suggests that a quite accurate prediction of B can be obtained from our standard model with only five genes on each side of the focal gene, except in regions of low recombination. It also suggests that a substantial reduction in nucleotide site diversity and codon usage bias is expected in low- but non-zero recombination regions, even if they contain only a small number of genes, since B for the low crossing-over rate and the standard mutation rate asymptotes at about two-thirds of the high recombination value, in the presence of gene conversion at the standard rate (Figure 5B). With the standard mutation and recombination parameters, there is little effect beyond 10 genes on each side of the focal gene. With normal levels of recombination, the pattern of variation in N_e within a gene is affected little by the presence of neighboring genes (Figure 6). Figure 7 shows that regions where there is no crossing over show very large effects of the number of neighboring genes on the mean B for the focal gene, even in the presence of gene conversion.

Figure 5.—

The effect of neighboring genes on the mean B for a gene under background selection. Both plots show a focal gene and assume four equidistant introns of 100 bp length, 6000 bp intergenic distance, 2000 bp coding sequence for all genes, and r_g = 2.5 × 10⁻⁶. Other features of the curves are as in Figure 3. (A) Fixed selection coefficient. (B) Average of 100 samples from the DDME.

Figure 6.—

Neighboring genes do not affect the patterns of background selection within a gene. This plot is like Figure 2A, except that five neighboring genes were located on both sides of the focal gene (with features as in Figure 5).

Figure 7.—

The effect of neighboring genes on background selection without crossing over. Both plots show the mean B for a focal gene, with the same features of neighboring genes as in Figure 5. However, crossing over is assumed to be absent and curve thickness denotes the rate of gene conversion r_g (thick, 5 × 10⁻⁶; medium, 2.5 × 10⁻⁶; thin, 0.5 × 10⁻⁶). Line type represents the mutation rate (dotted, 2 × 10⁻⁹; dashed, 4 × 10⁻⁹; solid, 8 × 10⁻⁹) and the highlighted line indicates a typical gene (dashed line with medium thickness). (A) Fixed selection coefficient. (B) Average of 100 samples from the DDME.

As would be expected from the assumed lack of sites under strong purifying selection in intergenic regions, longer distances between genes (with five genes on each side of the focal gene) reduce the effect of background selection, and this effect is most marked with low recombination and a high mutation rate (Figure 8). Once again, however, the effect asymptotes beyond a certain distance, ∼6 kb for many typical parameter combinations.

Figure 8.—

Longer intergenic distances reduce background selection in a region. This plot shows the fixed selection coefficient prediction for the mean B of a focal gene with varying intergenic distances, when five neighboring genes are located on both sides (with features as in Figure 5) and r_g = 2.5 × 10⁻⁶. Other features of the curves are as in Figure 3.

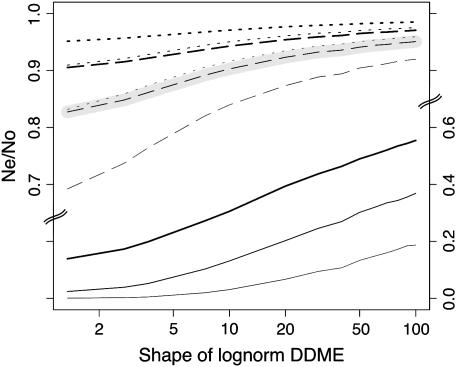
The effects of the DDME width:

To investigate the dependence of B on the DDME, we computed the mean B for a single standard gene, assuming different widths of the DDME and corresponding estimates of the location parameter from Table 1. The results show that the width of the DDME has surprisingly small effects (Figure 9), provided that it is large enough to be compatible with estimates of the rate of occurrence of dominant, effectively lethal mutations (Loewe and Charlesworth 2006).

Figure 9.—

Predictions of background selection are insensitive to uncertainty in realistic DDME width estimates. For each assumed DDME shape (x-axis), a corresponding estimate of the location parameter was made from the diversity data. The standard gene structure without neighboring genes was assumed, with r_g = 2.5 × 10⁻⁶. Other features of the curves are as in Figure 3. The bottom three lines belong to the axis on the right. Note that realistic shapes in this case are in the range 20–100, as narrower shapes predict too few lethal mutations and wider shapes predict too many lethal mutations (on the basis of estimates in Loewe and Charlesworth 2006). Details of the assumed DDMEs can be found in Table 1.

DISCUSSION

We focus on the relation between the theoretical predictions described above and data from genome analyses and population genetic studies of Drosophila.

Patterns of N_e within genes:

Background selection caused by deleterious amino acid mutations within a single gene can reduce the effective population size experienced at linked neutral or nearly neutral sites (Figures 1 and 2). In addition, the dilution of background selection effects by recombination produces patterning along the gene of B, the ratio of N_e at a given site to its value in the absence of background selection, N₀. This is because intergenic and intron sequences are assumed for convenience to be neutral and hence do not contribute to background selection. This produces an increase in B at the ends of genes and at the boundaries of exons with introns (see Equation 9 of Nordborg et al. 1996). While there is evidence for purifying selection on synonymous mutations (Coméron and Guthrie 2005) and on mutations in noncoding sequences (Haddrill et al. 2005), the levels of constraint on such mutations are typically much lower than those for nonsynonymous mutations, so that it seems reasonable as a first approximation to ignore them, especially as the effects of weak selection are rapidly diluted by recombination (Equation 2). This argument does not apply to the splicing signals at the beginning and the end of introns (Mount et al. 1992). These are probably under strong selection and can be accounted for by slightly longer “effective exons.”

Although for plausible parameter sets, it is clear that the mean B over all sites within a gene is always reduced by at least 4% or so, the within-gene patterns in B are likely to be very small and would be very hard to detect in surveys of nucleotide site diversity, which previously have been used to infer differences across the genome in N_e caused by background selection and selective sweeps (Begun and Aquadro 1992; Charlesworth 1996). They may, however, be detectable from patterns of codon bias seen in genomewide analyses of sets of genes, since codon bias is affected by the value of N_e under the standard mutation–selection–drift model (Li 1987; Bulmer 1991; McVean and Charlesworth 1999). According to the Li–Bulmer equation, the equilibrium frequency of optimal codons, f_op (assuming a preferred and an unpreferred codon at each site), for a given strength of selection is given by

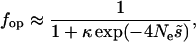(4)

where 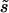is the selection coefficient against heterozygotes for nonoptimal codons (semidominance is assumed), and κ is the ratio of the mutation rates from and to optimal codons, respectively (i.e., the mutational bias).

Without estimates of κ and 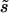, it is impossible to make fully quantitative predictions to compare with the data, but an approximate analysis can be carried out as follows. Differentiating f_op in Equation 4 with respect to N_e, we obtain the following expression for the relation between a small change in f_op as a proportion of its value, (df_op)/f_op, and the corresponding small proportional change in N_e, (dN_e)/N_e:

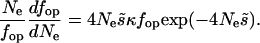(5)

The important parameters can be estimated as follows. In their genome analyses, Coméron and Kreitman (2002) used the frequency of GC content at third coding positions (GC3) in genes of D. melanogaster as a proxy for codon usage bias, since most preferred codons in Drosophila end in G or C. Work on several species of Drosophila has suggested values of κ ∼3 for mutational bias from GC to AT mutations (Maside et al. 2004; Bartolomé et al. 2005); to be compatible with the mean GC3 of ∼0.65 found by Coméron and Kreitman (2002), N_es for selection on GC3 must be ∼0.43. A proportional change in equilibrium f_op (given by the right-hand side of Equation 5) is ∼60% of the corresponding small proportional change in N_e, if f_op = 0.65. Thus, everything else being equal, a change in f_op is associated with a substantially larger change in N_e.

Figure 10 of Coméron and Kreitman (2002) shows that GC3 for the central part of a D. melanogaster gene without an intron is 3–4% lower than the value for the distal parts, but with a good deal of uncertainty as to the exact value of this difference. Figure 2B shows that, with the standard rate of gene conversion and the estimated DDME, a mutation rate of 4 × 10⁻⁹ (slightly lower than the point estimate of Haag-Liautard et al. 2007) gives a value of B for the central part of a gene with no introns that is ∼3% lower than that for the ends, corresponding to a difference of 1.8% in f_op, somewhat smaller than the observed value. Coméron and Guthrie (2005) directly estimated values of N_es from polymorphism and divergence data on D. melanogaster and its close relatives and showed that it was lower for the central regions of long exons; their estimates of f_op for these genes showed a reduction of ∼10% for the central 150 codons as opposed to the 150 codons at the beginning and the end of long genes without introns. One possibility for explaining this underprediction of the observed effects is that gene conversion rates may be higher at the ends of genes than in their centers, as seen for the rosy locus (Hilliker and Chovnick 1981); this could enhance the relative difference in codon bias between the ends and the centers. Another possibility is that the mutation rate is higher than we have assumed. A mutation rate of 8 × 10⁻⁹, which is near the upper confidence interval of the estimates, gives a larger predicted difference in f_op (≈14%, transformed from Figure 2B) than is observed.

Figures 1 and 2 also show that the presence of introns reduces the size of the difference in B between the ends and the middle of genes, because the value of B for the central part of a gene is increased by the presence of introns. This is qualitatively consistent with the results in Figure 10 of Coméron and Kreitman (2002).

Qin et al. (2004) reexamined these patterns in the context of the effects of gene length and level of gene expression, using the effective number of codons (ENC) as an inverse measure of codon usage bias. Somewhat unexpectedly, their analyses showed that codon bias is lowest at either end of the genes, reaches a peak toward ∼50–100 codons from the ends, and then declines toward the middle of the genes (their Figure 6). There is no obvious explanation for the low bias at the very ends of genes, which may reflect constraints on translational efficiency at the beginning and the end of translation (Qin et al. 2004), but the tendency for ENC to increase toward the centers of genes is qualitatively consistent with expectations under both background selection and weak Hill–Robertson effects among synonymous sites (Coméron and Kreitman 2002). The spatial pattern appears to be stronger in genes with higher expression levels; since overall codon bias is well known to be correlated with level of gene expression (Duret and Mouchiroud 1999), this presumably reflects stronger selection for codon bias in more highly expressed genes. From Equation 5, it can be shown that a higher value of N_es is associated with a higher relative sensitivity of f_op to N_e for realistic parameter values, so that any mechanism causing differences in N_e will cause differences in codon bias to be stronger when overall codon bias is higher. Genes with one intron have slightly higher levels of codon usage bias along their length than genes lacking introns (Figure 8 in Qin et al. 2004), consistent with the results in Figures 1 and 2.

The effects of gene length and intron length:

Figure 3 shows that exon length can have a substantial effect on the mean B for a gene, but the magnitude of the effect is very dependent on other parameter values. For selection coefficients drawn from the estimated DDME, and with the standard mutation rate of 4 × 10⁻⁹ and standard recombination parameters, the value for the longest genes in Figure 3B is ∼0.92 instead of the maximal value of 0.97 that would apply to very short genes; i.e., there is an ∼5% reduction in B, corresponding to a 3% reduction in f_op below the maximum. With a mutation rate of 8 × 10⁻⁹ and a standard rate of recombination, B falls from ∼0.45 for short genes to ∼0.15 for long genes (Figure 3B, right scale). This 66% reduction in B corresponds to an ∼31% reduction in f_op, from Equation 5 with f_op = 0.55 and κ = 3.

The results on D. melanogaster of Duret and Mouchiroud (1999, Figure 1 therein) showed that long genes (>570 codons) with high expression levels have ∼11% lower f_op than very short genes (<333 codons). The direct estimates of N_es also suggested a large effect of exon length (Coméron and Guthrie 2005). Our results indicate that other processes will be required to explain these observations, if the mutation rate is 4 × 10⁻⁹; however, if the mutation rate in these genes is somewhat larger, background selection can generate these patterns.

Hill–Robertson interference among weakly selected synonymous sites is one of the other processes that may help explain these observations; simulations showed effects of this kind in regions of normal crossing over (but gene conversion was ignored in the model of Coméron et al. 1999). It is possible that a combination of background selection and Hill–Robertson interference among synonymous sites might produce larger effects at standard mutation rates. Duret and Mouchiroud (1999) argued that it was unlikely that general Hill–Robertson effects (which include background selection) could explain the effects of gene length, since they found no effect of the length of neighboring genes on f_op in Caenorhabditis elegans. However, with the very high linkage disequilibrium observed in C. elegans, probably reflecting a high rate of self-fertilization (Cutter 2006), it is likely that the effective rate of recombination is very low (Charlesworth et al. 1993), so that genes experience background selection effects from many neighbors. This would greatly reduce the effects of immediate neighbors, if codon usage bias is determined by the current recombinational environment.

Coméron and Kreitman (2002, Figure 11 therein) also showed that the GC3 content of a D. melanogaster gene decreases by ∼3% of its maximal value as the proportion of a gene contributed by introns decreases. The results in Figure 4B for the standard parameter set predict an effect of this kind, but the magnitude of the change in f_op is only ∼2%, although bigger effects are again possible with a higher mutation rate. Also, it is possible that including Hill–Robertson interference among synonymous sites would improve the fit to the data.

The effects of intergenic distance and neighboring genes:

It has been argued that a higher local gene density correlates with reduced diversity because of increased levels of background selection in humans (Payseur and Nachman 2002a) and in Arabidopis thaliana (Nordborg et al. 2005). This is consistent with Figure 8, which shows more background selection with shorter intergenic distances in gene clusters of constant size.

Figures 5 and 6 show that neighboring genes have little effect on B and its behavior within a gene, unless crossing over is infrequent. This reflects the fact that background selection caused by the relatively weak selection experienced by most amino acid mutations is very sensitive to recombination. But if crossing over is completely absent, gene conversion on its own fails to prevent the cumulative effects of background selection (Figure 7), so that B is then very sensitive to the number of neighboring genes. With the standard gene conversion, selection, and mutation parameters, Figure 7B shows that B is reduced to 5% of its maximum level with only 40 genes that fail to cross over. It was not possible to produce numerical results for cases with a distribution of selection coefficients for >40 genes, due to computing time constraints, but it seems likely from the nearly log-linear relation between B and the number of genes that 80 genes (close to the number on chromosome 4 of D. melanogaster; FlyBase 2006) would result in an effective population size of ∼0.1% of its size without background selection. These results assume that gene conversion is occurring at normal rates in regions of low crossing over, consistent with observations on SNPs in such regions in D. melanogaster, other than the Y chromosome (Langley et al. 2000; Jensen et al. 2002; Sheldahl et al. 2003). The effect would obviously be even larger in the absence of gene conversion.

These results raise serious questions about the validity of the model for groups of genes that do not cross over. While codon usage bias is greatly reduced in low-recombination regions of the D. melanogaster genome, it is not completely absent, with an ENC of 50.9 on chromosome 4 compared with a value of 56.0 for random nucleotides from noncoding regions (Coméron et al. 1999). Furthermore, the level of SNP diversity on chromosome 4 is ∼20% of the genomic average (Jensen et al. 2002; Sheldahl et al. 2003), much greater than predicted by the model. Similarly, diversity on the nonrecombining neo-Y chromosome of D. miranda is about one-sixtieth of that of its partner, the neo-X chromosome (Bartolomé and Charlesworth 2006).

Limitations of the background selection model:

These observations suggest that the model grossly overestimates the effects of background selection when recombination rates are low. Such an effect has indeed been detected in previous studies using Monte Carlo simulations (Charlesworth et al. 1993; Nordborg et al. 1996). It is probably caused by the fact that, with very close linkage, Hill–Robertson interference develops between the relatively strongly selected sites causing background selection, and so its efficacy is undermined. The more densely that selected sites are packed into a given map length, the greater the extent of Hill–Robertson interference among them, and so the weaker the effective selection acting on each of them. A pattern of this kind can be seen in Figure 9 of McVean and Charlesworth (2000). This suggests a need to carry out more detailed investigations, to determine whether the observed features of low-recombination regions can be adequately accounted for. There is also a need to reinvestigate the predictions of the background selection model for the distribution of N_e over large genomic regions in Drosophila (Hudson and Kaplan 1995; Charlesworth 1996), using estimates of the distribution of selection coefficients from molecular population genetics analyses rather than mutation-accumulation experiments.

Conclusion:

Background selection within genes seems to be sufficient to explain the observed patterns of codon usage bias in genes, if mutation rates are high enough. However, we cannot exclude other explanations, since the absolute magnitude of the strength of background selection is strongly influenced by evolutionary parameters such as local mutation rates, recombination rates, and the distribution of selection coefficients. Other explanations like Hill–Robertson effects among synonymous sites or recurrent selective sweeps can be excluded only if the evolutionary parameters of background selection can be estimated with sufficient accuracy. We therefore suggest that any integrated theory of the patterns of codon bias in genes must include background selection. Further understanding of these complexities will require models that include all relevant factors.