A General Model to Explore Complex Dominance Patterns in Plant Sporophytic Self-Incompatibility Systems

Sylvain Billiard; Vincent Castric; Xavier Vekemans

doi:10.1534/genetics.105.055095

. 2007 Mar;175(3):1351–1369. doi: 10.1534/genetics.105.055095

A General Model to Explore Complex Dominance Patterns in Plant Sporophytic Self-Incompatibility Systems

Sylvain Billiard ^*,†,¹, Vincent Castric ^†, Xavier Vekemans ^†

PMCID: PMC1840071 PMID: 17237502

Abstract

We developed a general model of sporophytic self-incompatibility under negative frequency-dependent selection allowing complex patterns of dominance among alleles. We used this model deterministically to investigate the effects on equilibrium allelic frequencies of the number of dominance classes, the number of alleles per dominance class, the asymmetry in dominance expression between pollen and pistil, and whether selection acts on male fitness only or both on male and on female fitnesses. We show that the so-called “recessive effect” occurs under a wide variety of situations. We found emerging properties of finite population models with several alleles per dominance class such as that higher numbers of alleles are maintained in more dominant classes and that the number of dominance classes can evolve. We also investigated the occurrence of homozygous genotypes and found that substantial proportions of those can occur for the most recessive alleles. We used the model for two species with complex dominance patterns to test whether allelic frequencies in natural populations are in agreement with the distribution predicted by our model. We suggest that the model can be used to test explicitly for additional, allele-specific, selective forces.

THE population genetics of plant species with sporophytic self-incompatibility (SSI) are notoriously difficult to study both empirically and theoretically because of the complex dominance relationships occurring among alleles. Wright (1939) developed a theory for gametophytic self-incompatibility (GSI), a genetic system to avoid self-fertilization involving recognition between a protein expressed in the haploid pollen and two codominantly expressed pistil proteins, and identified negative frequency-dependent selection as the major evolutionary force promoting allelic diversity. According to Wright's theory, selection under GSI is symmetric among alleles, and the only relevant feature of an allele is its current population frequency. In SSI, however, the incompatibility phenotypes of pollen and pistils are determined by the diploid genotypes of the paternal and maternal plants, respectively, and are governed by complex dominance interactions among alleles that introduce asymmetrical selection among alleles (Bateman 1952; Schierup et al. 1997). A general understanding of the population genetics of SSI has also been difficult because different authors investigated different, often nonoverlapping model representations of SSI, sometimes with unstated assumptions, so that their outcomes have been difficult to compare (Table 1). Differences among models comprise: (1) frequency-dependent selection acting on male fitness only (corresponding to Wright's assumption) vs. selection on both male and female fitnesses, named “fecundity selection” in Vekemans et al. (1998); (2) expression of dominance in both pollen and pistils vs. codominance in pistil and dominance in pollen; and (3) occurrence of at most one allele per dominance class along a hierarchical ladder of dominance vs. allowing several alleles per dominance class.

TABLE 1.

Features of the different specific sporophytic self-incompatibility models available in the literature

No. of dominance classes	No. of alleles per dominance class	Dominance relationships	Selection model	Population	Authors	Marked results (see text)
3	1	cod, dom, domcod	FDS_m	Infinite	Bateman (1952)	Alleles from a recessive dominance class reach higher frequencies than alleles from a more dominant class.
n	1	dom	FDS_m	Infinite	Cope (1962)	Identical phenotype frequencies at equilibrium (“isoplethy”).
n	1	domcod	—^a	Infinite and finite	Imrie et al. (1972)	Low no. of alleles maintained in small isolated populations.
3	≥1	domcod	FDS_m	Infinite	Sampson (1974)	Individual allelic frequencies within a dominance class are inversely related to the no. of alleles within this class.
2 and 3	1–4	dom, domcod	FDS_m	Infinite	Charlesworth (1988)	The difference in frequencies between recessive and dominant alleles is lower under the domcod than under the dom model.
3–11	1	cod, dom, domcod	FDS_m	Infinite and finite	Schierup et al. (1997)	The most recessive allele is highly sensitive to drift under domcod.
3 and 11	1	cod, dom, domcod	FDS_m/f	Infinite and finite	Vekemans et al. (1998)	Adding selection on female fitness under domcod causes the most recessive allele to be protected from drift.
2	≥1	domcod	FDS_m	Infinite	Uyenoyama (2000)	Only one allele is maintained deterministically in the pollen-recessive class if more than two alleles are in the pollen-dominant class.

Open in a new tab

FDS_m in finite population simulations and FDS_m/f in deterministic equilibrium frequencies computations.

Previous analyses of deterministic models of SSI have shown the following:

Recessive alleles should reach higher equilibrium frequencies than more dominant alleles, the so-called “recessive effect” (Bateman 1952; Sampson 1974). The reason is that negative frequency-dependent selection tends to homogenize the frequencies of the phenotypic classes (the “isoplethy” hypothesis). Because of dominance, recessive alleles can be present in more phenotypic classes than are dominant alleles, and they thus reach higher total frequencies (Cope 1962).
Within a given class of dominance, individual allelic frequencies should be inversely related to the number of alleles in that class, the so-called “small number effect” (Sampson 1974). This arises because within a given dominance class, alleles are selectively equivalent and are thus expected to reach identical frequencies at equilibrium (as in completely symmetric models of balancing selection such as GSI). In contrast to expectation 1 above, recessive alleles, if present in higher number, could thus potentially reach lower overall equilibrium frequency than dominant alleles.
The recessive effect is substantially less pronounced in models where dominance is acting in pollen (with a single allele per dominance class) and all alleles are codominant in the pistil (domcod model) as compared to models with identical expression of dominance in pollen and pistil (dom model) (Charlesworth 1988; Schierup et al. 1997). In the latter, the strength of the recessive effect was found to increase with an increasing number of dominance classes whereas the reverse was true for the domcod model (Schierup et al. 1997).
The properties of the domcod model denoted in expectation 3 are no longer valid when selection acts on both the male and the female fitnesses (i.e., when the availability of compatible pollen is limited). Under such a selection scenario, the properties of the domcod and dom models are qualitatively very similar (Vekemans et al. 1998).
A peculiar behavior was observed for alleles in the recessive class in a domcod model with two classes of dominance and no selection on female fitness. In many instances where two alleles were introduced in the recessive class, only a single allele could be maintained deterministically (Uyenoyama 2000). Also, with a single recessive allele, the total frequency of dominant alleles was increasing with the number of alleles, varying from ∼0.5 to 0.8 when increasing from 2 to 50 dominant alleles in the population.

Detailed theoretical investigations of SSI in finite populations have been rather scarce and did not model cases with more than one allele per dominance class. Imrie et al. (1972) showed that only a very low number of alleles at the S locus (S alleles) would be maintained in a small population under domcod SSI, but that recurrent migration would lead to a substantial increase in the number of alleles maintained. Schierup et al. (1997) compared different models of SSI with or without dominance, with dominance represented as a linear hierarchy with a single allele per dominance level. The total number of alleles maintained in finite populations was found to decrease with increasing expression of dominance and was interpreted as the result of decreasing overall strength of selection in the presence of recessive alleles that are not expressed in heterozygous genotypes (Schierup et al. 1997). The domcod model showed idiosyncratic evolutionary dynamics of alleles, with most dominant alleles having a higher rate of successful invasion whereas most recessive alleles had a higher rate of loss, leading to continuous evolution toward an increasing absolute level of dominance within populations (Schierup et al. 1997). The introduction of selection on female fitnesses was found to override this running-over process (Vekemans et al. 1998).

Although data on patterns of dominance and distribution of allelic frequencies in natural populations are accumulating slowly, application of the theoretical results to actual data has remained difficult because extant patterns of dominance relationships among alleles at SSI loci are typically more complex than the over-simplified dominance relationships assumed in the models (e.g., Stevens and Kay 1989; Kowyama et al. 1994; Mehlenbacher 1997). However, testing predictions from models on the distribution of allelic frequencies within and among populations is necessary to assess the occurrence of frequency-dependent selection, to test whether selection is acting on male vs. female fitnesses, and to detect the occurrence of additional selective forces, potentially differing among alleles. Additional components of selection could arise, for instance, as a consequence of the association of S-allele lineages to different sets of deleterious alleles at linked loci (the “sheltered load”; Uyenoyama 1997) or of the occurrence of partial overlap among pairs of allelic specificities leading to selection to avoid false rejection of nonself pollen (Richman 2000; Chookajorn et al. 2004). Although the sheltered load hypothesis was initially suggested for GSI systems, it is potentially of major interest in SSI, with the difference that its strength is expected to vary among dominance classes as recessive alleles may occur as homozygotes (Bechsgaard et al. 2004).

Here, we present a flexible model of SSI that allows deterministic computations for any number of dominance classes with any number of alleles per dominance class and full definition of dominance relationships in pollen and pistil between each pair of alleles. Our model also allows specifying whether selection acts on male fitness only or both on male and on female fitnesses. The model allows the computation of expected equilibrium frequencies as well as single-generation genotypic changes in cases with complex patterns of dominance previously determined from nature. We use the model to explore situations with more than two dominance classes and different numbers of alleles per class, both in deterministic models and in finite populations. In both types of models we estimate the relative frequencies of alleles from the most recessive and the most dominant classes. We also estimate frequencies of homozygote genotypes as they are of special interest in the context of the sheltered load hypothesis. In finite populations we monitor the number of alleles per dominance class and the number of dominance classes maintained. We discuss how our results extend the current knowledge about SSI and permit explicit detection of non-frequency-dependent selection components in species with SSI.

MODEL AND METHODS

We consider a sporophytic self-incompatibility system determined by n specificities in a diploid hermaphrodite species. The phenotype of an individual bearing specificities i and j depends on the patterns of expression (relative dominance) of their associated alleles at the pollen and pistil self-incompatibility genes. We suppose that a given allele encodes for a single specificity and a given specificity is encoded by a single allele. An i-specific pollen protein is produced when allele S_i is expressed in the anthers, whereas an i-specific protein is produced at the pistil surface when the S_i allele is expressed in the pistil. The pollen and pistil phenotypes of an individual S_iS_j can then be interpreted as the relative proportions of proteins i and j produced in anthers and pistils, respectively. Note that a given plant may express different specificities in pistils and anthers if the dominance relationships between co-occurring alleles are not the same in the reproductive structures. Moreover, an individual may express two different specificities if the alleles it carries are partially codominant in a reproductive structure, possibly at different intensities in the case of partial dominance. A cross is considered incompatible when pollen and pistil proteins bearing the same specificity come into contact provided there is enough of them in both reproductive structures for recognition to occur.

In the following, we computed the expected genotypic frequencies under any scheme of dominance relationships among n alleles and two contrasting models of frequency-dependent selection:

Frequency-dependent selection occurring through male and female reproductive structures (FDS_m/f), also called fecundity selection by Vekemans et al. (1998).
Frequency-dependent selection occurring only through male reproductive structures (FDS_m) first proposed by Wright (1939). The main hypothesis of this model is that all maternal plants produce the same number of offspring without regard for the quantity of compatible pollen they receive.

Dominance relationships:

We define α and φ, two square matrices of dimension n × n, respectively containing the dominance relationships for all pairs of alleles in anthers and pistils, where n is the number of different specificities actually present in the population. The elements on row i and column j in these matrices are α_ij = 1 − α_ji and φ_ij = 1 − φ_ji, respectively the dominance level of allele S_i over allele S_j in pollen and pistil, with 0 ≤ α_ij ≤ 1 and 0 ≤ φ_ij ≤ 1 for all {i, j}. For instance, if α_ij = 1, S_i is fully dominant over S_j in anthers and if 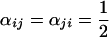Inline graphic , S_i and S_j are codominant. More generally, if α_ij > 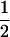, S_i is partially dominant over S_j in anthers.

From genotypes to phenotypes:

We denote A_ij and P_ij, respectively, the anther and pistil phenotypes of an individual with genotype S_iS_j. Phenotypes are defined as vectors of dimension n as follows: 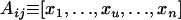Inline graphic with x_u = 0 for 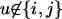, x_i = α_ij and x_j = α_ji = 1 − α_ij if i ≠ j, and x_i = 1 if i = j. We can define in the same way the phenotype of the pistil: 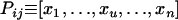with x_u = 0 for 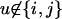, x_i = φ_ij and x_j = φ_ji = 1 − φ_ij if i ≠ j, and x_i = 1 if i = j. Typically, A_ij and P_ij have the form 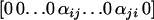Inline graphic , which can be interpreted as the proportion of u-specific protein produced in anthers and pistil of an individual S_iS_j, for all .

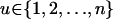Cross compatibilities:

This definition of the phenotype is convenient because a cross between a pollen from an S_iS_j plant and the pistil of an S_kS_l plant is compatible if 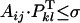Inline graphic , with 0 ≤ σ ≤ 1 a specified threshold value, and the superscript T indicates the transpose of vector P_kl. We denote p_ijkl the variable that takes the value 1 if the cross between a pollen from an S_iS_j plant and the pistil of a S_kS_l plant is compatible and 0 if it is not; in other words, p_ijkl = 1 if 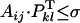Inline graphic or else p_ijkl = 0.

A cross is compatible in four cases:

If i ≠ k, i ≠ l, j ≠ k, and j ≠ l, then 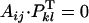and the cross is compatible.
If i = k, i ≠ l, j ≠ i, and j ≠ l, 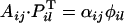and the cross is compatible if 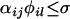. If we specify σ = 0 then the cross is possible only if S_i is fully recessive relatively to S_j or S_l or both.
Symmetrically, if j = l, i ≠ k, j ≠ i, and j ≠ k, 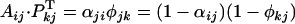, and the cross is compatible if .
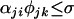If i = k, j = l, and i ≠ j, .

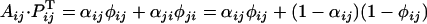While the cross implies two plants with the same genotype S_iS_j, the cross may be compatible if dominance is expressed differently in anthers and pistil; for example, if S_i is fully dominant over S_j in anthers and fully recessive in pistil, then we have α_ij = 1 and φ_ij = 0, and therefore 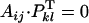Inline graphic and the cross is compatible.

Genotypic frequency change:

We denote f_ij the frequency of genotype S_iS_j in the population, 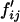Inline graphic the frequency of genotype S_iS_j in the next generation, and 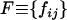a symmetric matrix. We assume an infinite population of diploid hermaphrodite individuals producing an infinite number of pollen and ovules. We also assume that the probability that a given pistil receives a given type of pollen depends only on the frequency of the latter in the pollen pool. We denote w_ijkl the fraction of seeds produced by a cross between S_iS_j pollen and S_kS_l ovules among all seeds. The fraction of seeds produced by a cross between genotypes S_iS_j and S_kS_l is w_ijkl + w_klij. Hence, the frequency of seeds S_iS_k produced by a cross between genotypes S_iS_j and S_kS_l is (w_ijkl + w_klij)/4 if k ≠ l and i ≠ j, (w_ijkl + w_klij)/2 if k = l or i = j, and (w_ijkl + w_klij) if k = l and i = j. Finally, the frequencies of heterozygotes S_iS_j and homozygotes S_iS_i after one generation are

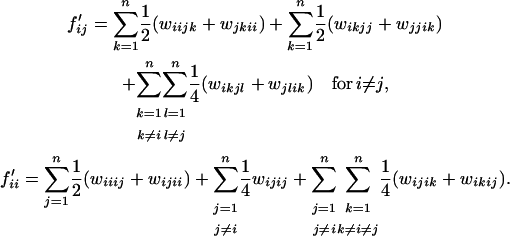(1)

The value of w_ijkl for any two genotypes depends on their population frequencies, on the compatibility indicators p_ijkl, and on the chosen regime of frequency-dependent selection: FDS_m/f or FDS_m.

Under FDS_m/f, a pistil S_kS_l receives compatible pollen with a probability equal to the overall sum of the frequency of compatible pollen 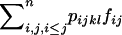Inline graphic . Hence, if compatible pollen is rare (pollen limitation), a given plant may produce less seeds and selection may occur through both male and female reproductive functions. Pollination of a pistil S_kS_l by a pollen S_iS_j occurs with probability f_ij f_kl and fertilization with probability p_ijkl f_ij f_kl. Hence, the contribution of a cross between a pollen S_iS_j and a pistil S_kS_l to the next generation under FDS_m/f is

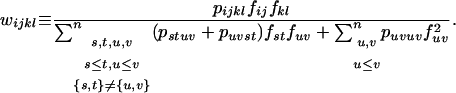(2)

Under FDS_m, every plant receives enough compatible pollen such that all plants produce the same quantity of seeds and selection occurs through the male reproductive function only. The total frequency of compatible pollen with an S_kS_l pistil is 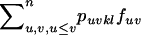Inline graphic such that ovules of an S_kS_l plant are fertilized by pollen from an S_iS_j plant with probability

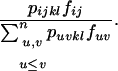(3)

According to FDS_m, a cross between a pollen S_iS_j and a pistil S_kS_l thus contributes to the next generation in proportion

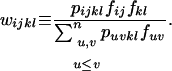(4)

Overall the frequency of allele S_i in the next generation thus equals to 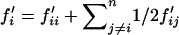Inline graphic , where 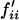and 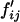can be obtained from Equation 1, where values for w_ijkl can be obtained from either Equation 2 or Equation 4 under FDS_m/f or FDS_m, respectively.

Simple cases:

Three kinds of dominance relationships have typically been used in the literature (Schierup et al. 1997; Vekemans et al. 1998): cod, where all alleles are codominant in pistil and pollen; dom, where alleles occur in a linear dominance hierarchy, identical in both pistil and pollen (two alleles from the same dominance class are codominant and each allele of a given dominance class is either strictly dominant or strictly recessive relative to the alleles of another dominance class); and domcod, where alleles follow the dom model in pollen and the cod model in pistil. Each of these three models can be conveniently represented with our notations, using the following dominance relationships matrices α and φ (here represented for three dominance classes and six alleles, two alleles in each class):

(5)

Hence, for instance, allele S₁ in the domcod model is codominant with allele S₂ only (they are in the same dominance class) and recessive relative to all other alleles in pollen, while it is codominant with all alleles in pistil. Here, we do computations mainly for two kinds of dominance relationships, dom and domcod, for which we state for clarity that class 1 is always the most recessive class. It is, however, possible to numerically compute genotypic frequencies at equilibrium for any dominance relationships between alleles (see below). A Mathematica (Wolfram Research 2004) notebook performing those calculations is available from S. Billiard.

Deterministic equilibrium frequencies:

According to Equations 1, 2, and 4, the frequency change for a given genotype depends on the genotypic frequencies matrix F. We thus computed the frequency of all genotypes after reproduction, during which frequency-dependent selection occurs, using Equations 1 and 2 under FDS_m/f or Equations 1 and 4 under FDS_m. Deterministic equilibrium genotypic and allelic frequencies were computed using recursively Equations 1, 2, and 4 until the frequency change in one generation was <10⁻⁶ for all genotypes. The initial genotypic frequencies are the same for all genotypes and set as the inverse of the total number of possible genotypes 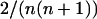Inline graphic .

Allele number in the most recessive class:

This analysis was motivated by the unexpected result of Uyenoyama (2000) who showed that, under FDS_m and domcod dominance relationships with two dominance classes, two alleles could not coexist in the recessive class except when more than two alleles occur in the recessive class or two or less alleles in the dominant class, in which case all recessive alleles can be maintained. We determined if this result still holds for models with more than two dominance classes, for dom and domcod dominance relationships and under both FDS_m/f and FDS_m. For a given set of parameters, we first ran computations until deterministic equilibrium was reached (see previous paragraph). Since all genotypic frequencies are equal at the beginning of the deterministic computations, no alleles are lost deterministically during this step. We then perturbed the system by randomly changing the frequency of all genotypes (multinomial sampling of genotypic frequencies with 1000 trials) and let the population evolve deterministically for an additional 10,000 generations. The deterministic equilibrium after the perturbation did not depend on the sampling. So, we chose to perform the procedure a single time for each single parameter set. We specifically investigated whether (1) allelic frequencies came back to the same equilibrium values as before the perturbation (we considered that the equilibrium frequencies before and after the perturbation were identical if the difference between them was <10⁻⁶) or (2) some alleles tended to disappear. We performed computations for 3, 4, 5, 6, and 10 dominance classes, with one, two or three alleles by dominance class. Only some combinations of these parameters have been examined (see supplemental data at http://www.genetics.org/supplemental/ for the complete list of parameter combinations tested).

Selection strength:

Because frequency-dependent selection acts on genotypes rather than alleles and since an infinite array of genotype frequencies is compatible with a given set of allelic frequencies, measuring the strength of selection for a given allele is not an easy task. In general, the strength of selection can be defined as a function of the frequency change in a generation. When a genotype departs from its equilibrium frequency, negative frequency-dependent selection is expected to bring frequencies back to equilibrium. To measure selection strength for allele i in a synthetic way, we compared its frequency change in a generation normalized by the genetic variance 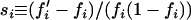Inline graphic for a given deviation from its equilibrium frequency 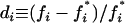, where a superscript asterisk refers to equilibrium values. Practically, random deviations were obtained by sampling 500 diploid individuals from a population at deterministic equilibrium for cases with two alleles by dominance class. Values of d_i and s_i were computed for every simulated population and the procedure was repeated 100,000 times. The strength of selection for allele i was measured as the slope of the linear regression between d_i and s_i.

Stochastic simulations:

For simulations in finite populations with N diploid individuals, we used a three-step life cycle:

Gametogenesis, syngamy, and seed production: Frequency-dependent selection occurred during this step and we used Equations 1, 2, and 4 to compute the genotypic frequencies in the seed pool (assuming that individuals produce an infinite number of seeds).
Drift: Given the genotypic frequencies in the seed pool after frequency-dependent selection, we randomly sampled N seeds to constitute the next generation of adults.
Mutation: The number of mutation events occurring in a generation was drawn from a Poisson distribution with mean 2Nμ, with μ the mutation rate. We used a K-allele model (KAM); i.e., we randomly drew for each mutation event one of the 2N genes, whose allelic state was equiprobably changed to one of K − 1 other possible states, irrespective of dominance classes.

To compute the expected number of alleles in finite populations, simulations were performed for dom and domcod dominance relationships, under both selection regimes, with three dominance classes. We fixed the number of possible allelic states to K = 18 (6 per class) and K = 30 (10 per class) for N = 100 and N = 500, respectively. Those limits were fixed after some preliminary simulations showing that for these population sizes, a higher number of alleles at a given time was never or very rarely reached. Some alleles could be lost by drift or introduced in the population by mutation, and thus n varies but at any given time, n ≤ K. Simulations were also performed with a higher number of possible allelic states, but the results were quantitatively similar (not shown). Simulations were started with K/3 alleles in each class, the total number of alleles at the beginning was thus n = K, and the initial genotypic frequencies were set at deterministic equilibrium without mutation as described above. We ran simulations for 10,000 generations to reach a drift–mutation–selection equilibrium where the mean total number of alleles over time remained stable. We then recorded the number of alleles in each class every generation during 100,000 generations and computed the probability that a given number of alleles were present in a given class during the whole process. An allele was counted if its frequency was >0.01 after drift. We performed 100 independent replicates of the whole process and we present the mean over replicates. Since the process is stationary, that is to say the mean and the variance of the number of alleles in the population do not change with time, our estimation of the expected number of alleles should not be biased.

DETERMINISTIC DYNAMICS AND EQUILIBRIUM

Model verification:

The deterministic equilibrium frequencies obtained using our model were compared to the results available in the literature for models with FDS_m with only one allele in each class (Schierup et al. 1997), n alleles in two classes under domcod (Uyenoyama 2000), n alleles in three classes under domcod (Sampson 1974), and n alleles in four classes under dom (Schierup et al. 2006) as well as with FDS_m/f with 1 allele in each class (Vekemans et al. 1998). Results were identical in all cases, thus confirming that the proposed formalization is a correct generalization of all previous SSI models.

Deterministic dynamics:

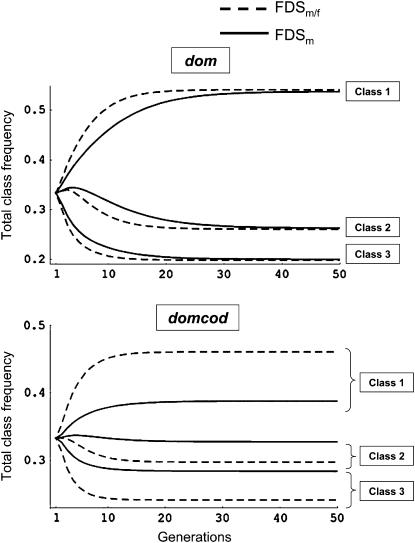
Figure 1 shows the dynamics of allelic frequencies under dom and domcod dominance patterns with three dominance classes and FDS_m/f or FDS_m selection regimes. Although equilibrium was reached more quickly under FDS_m/f than under FDS_m for the dom model, equilibrium allelic frequencies were sensibly the same under both selection regimes. Under domcod, in contrast, the equilibrium values differed greatly between the two selection regimes: The difference between dominance classes was higher under FDS_m/f than under FDS_m. Despite the large difference in the frequencies at equilibrium under domcod, the equilibrium values were reached in approximately the same number of generations under both models of selection. This is due to the fact that selection occurred through male and female fitnesses under FDS_m/f; consequently, although the difference between initial and equilibrium frequencies was greater under FDS_m/f than FDS_m, selection was also stronger and the approach toward equilibrium frequencies was faster.

The recessive effect:

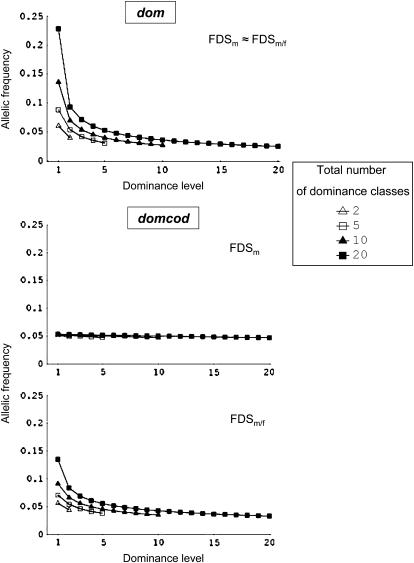
We investigated the recessive effect in models with different numbers of dominance classes and numbers of alleles per class, using both selection regimes. We quantified this effect with either the frequency of a single allele from a given class or with the total frequency of all alleles of that class. Figure 2 shows that equilibrium frequency of a given allele decreases when the dominance level of its class increased under both dom and domcod dominance patterns and for both selection regimes. The effect was, however, weak under domcod with FDS_m. Interestingly, equilibrium allelic frequencies were almost identical between the two selection regimes under the dom model, which generalizes the results obtained by Vekemans et al. (1998) in a simpler model with only one allele by class. In the domcod model in contrast, equilibrium allelic frequencies were sharply different between FDS_m and FDS_m/f with substantially higher difference between the most recessive and the most dominant allelic frequencies under FDS_m/f.

Figure 2 also reveals that the equilibrium frequency of an allele of a given class increases together with the total number of classes. This effect arises as a consequence of fixing the total number of allelic states (the small number effect; Sampson 1974). In such case, the number of alleles by class varies and the total frequency of a class is then equally shared among all alleles of that class. Moreover, the total frequency of a class depends on the total number of alleles considered. For a given number of classes, an increase in the total number of alleles resulted in an increase in the total frequency of the most dominant classes, together with a decrease in the total frequency of the most recessive classes (Table 2).

TABLE 2.

Total frequency of dominance classes at equilibrium under the FDS_m or the FDS_m/f model, for 20 and 40 alleles equally distributed among dominance classes

Dominance patterns	Total allele no.	Selection regimes	Dominance class no.	Dominance level
Dominance patterns	Total allele no.	Selection regimes	Dominance class no.					1	2	3	4	5	6	7	8	9	10	FU
dom	20	FDS_m	2	0.604	0.396									1.53
			5	0.353	0.215	0.167	0.141	0.124						2.85
			10	0.272	0.139	0.108	0.091	0.080	0.072	0.066	0.061	0.057	0.054	5.01
		FDS_m/f	2	0.607	0.393									1.54
			5	0.355	0.214	0.167	0.141	0.123						2.88
			10	0.272	0.139	0.108	0.091	0.080	0.072	0.066	0.061	0.057	0.054	5.03
	40	FDS_m	2	0.597	0.403									1.48
			5	0.335	0.219	0.172	0.146	0.128						2.61
			10	0.236	0.145	0.113	0.095	0.084	0.076	0.069	0.064	0.060	0.057	4.15
		FDS_m/f	2	0.598	0.402									1.49
			5	0.335	0.219	0.172	0.146	0.128						2.61
			10	0.236	0.145	0.113	0.095	0.084	0.076	0.069	0.064	0.060	0.057	4.15
domcod	20	FDS_m	2	0.516	0.484									1.06
			5	0.210	0.205	0.200	0.195	0.190						1.11
			10	0.106	0.105	0.103	0.102	0.101	0.099	0.098	0.097	0.096	0.094	1.12
		FDS_m/f	2	0.561	0.439									1.28
			5	0.282	0.216	0.185	0.165	0.152						1.86
			10	0.182	0.132	0.112	0.099	0.091	0.085	0.080	0.076	0.073	0.070	2.60
	40	FDS_m	2	0.508	0.492									1.03
			5	0.205	0.202	0.200	0.197	0.195						1.05
			10	0.103	0.102	0.101	0.101	0.100	0.100	0.099	0.098	0.098	0.097	1.06
		FDS_m/f	2	0.554	0.446									1.24
			5	0.272	0.216	0.187	0.169	0.156						1.74
			10	0.167	0.131	0.113	0.101	0.093	0.087	0.082	0.078	0.075	0.072	2.31

Open in a new tab

FU is the frequency unevenness, defined as the ratio of the frequencies of the most recessive allele to the most dominant allele.

In spite of the inherent asymmetry among alleles in SSI caused by dominance, the frequency unevenness (FU), as measured by the ratio of the total frequency of the most recessive to the most dominant classes, was very low in some cases, especially under FDS_m and domcod dominance patterns (Vekemans et al. 1998 showed this result for one allele by class). Indeed, in this case FU remained as low as 1.03 when the 20 alleles considered belong to two dominance classes only. Yet, several factors had an impact on FU. For a given set of parameters in Table 2, FU under FDS_m/f was on average 35.5% higher than under FDS_m. Moreover, as revealed by Table 2, the number of dominance classes strongly influenced how even allelic frequencies remained among classes. FU generally increased with the number of classes, reaching overall frequencies for the most recessive class 5.03 times higher than the overall frequencies for the most dominant class with 20 alleles evenly distributed among 10 dominance classes. Table 2 also shows that when the number of alleles by class increases, FU decreases, under both dominance patterns and selection regime. This is due to the fact that the higher the number of alleles, the lower the selection strength difference between alleles of different dominance classes since the number of compatible genotypes is increased for all genotypes. Hence FU tends toward 1 when the total number of alleles increases. Conversely, when there is only one allele in the most recessive class and there are several alleles in the more dominant classes, the recessive effect may be large (Table 3).

TABLE 3.

Homozygote frequencies for the most recessive class(es) in models with two and three dominance classes

			FDS_m				FDS_m/f
dom		domcod		dom		domcod
No. of dominance classes	Dominance level	Allele no. per dominance class^a	Homozygote frequency	Allele frequency	Homozygote frequency	Allele frequency	Homozygote frequency	Allele frequency	Homozygote frequency	Allele frequency
2	1	1-2	0.398	0.671	0.250	0.550	0.405	0.674	0.323	0.612
		1-6	0.258	0.536	0.114	0.371	0.266	0.542	0.148	0.418
		1-10	0.204	0.475	0.076	0.300	0.211	0.481	0.099	0.341
3	1	1-1-1	0.333	0.610	0.182	0.487	0.333	0.610	0.251	0.544
		1-3-3	0.200	0.468	0.071	0.290	0.204	0.472	0.108	0.356
		1-5-5	0.154	0.408	0.045	0.230	0.157	0.412	0.070	0.285
	2	1-1-1	0.024	0.223	0.036	0.286	0.024	0.223	0.028	0.258
		1-3-3	0.005	0.101	0.005	0.125	0.007	0.100	0.006	0.119
		1-5-5	0.002	0.068	0.002	0.080	0.003	0.067	0.002	0.079

Open in a new tab

The number of alleles in the most recessive class is fixed to one, and alleles are equally distributed among other classes.

These results confirmed the generality of the recessive effect when there is a linear dominance hierarchy between alleles in pistil and pollen (dom) or in pollen only (domcod), for models with a larger number of dominance classes and higher numbers of alleles per class than had previously been considered, as well as under the two selection regimes considered.

Homozygote frequencies:

Because of the dominance relationships among alleles in SSI, homozygotes can be formed for alleles belonging to all classes but the most dominant one. As revealed by Table 3, homozygotes for the most recessive allele can reach high equilibrium frequencies even when the total number of alleles is high and they possibly represent an important proportion of individuals carrying the most recessive allele. The homozygote frequency is higher under dom than under domcod for both selection regimes and is lower under FDS_m than under FDS_m/f. Table 3 also shows homozygote frequencies for alleles of class 2 when there are three dominance classes. Homozygotes for class 2 alleles reach much lower equilibrium frequency than the class 1 allele.

ALLELE NUMBER BY DOMINANCE CLASS

Allele number in the most recessive class:

Uyenoyama (2000) showed that under FDS_m and domcod dominance patterns with two dominance classes, very restrictive conditions are required for two alleles to be deterministically maintained in the most recessive class. We used our general model to extend this investigation and explore the conditions under which several alleles can be deterministically maintained in the most recessive class when there are more than two dominance classes for both selection regimes, under dom and domcod dominance relationships (all parameter combinations examined and results are available as supplemental data at http://www.genetics.org/supplemental/).

Under FDS_m/f, two or more alleles in the most recessive class were always maintained and had identical frequency at equilibrium under both the dom and the domcod dominance relationships. The same was true for the dom model under FDS_m. In contrast, under FDS_m in the domcod model, several alleles could be maintained in the most recessive class only if more than two alleles occurred in the most recessive class. When exactly two alleles occurred in the most recessive class, they could still be maintained if (1) there is a single allele in each other dominance class and/or (2) there is a single allele in each class but exactly two alleles in the most dominant class (3 classes), in one of the 3 most dominant classes (4, 5, and 6 classes), or in one of the 4 most dominant classes (10 classes). In all other cases, notably with two alleles in the most recessive class and three alleles in at least one of the other classes, the recessive allele with the lowest frequency ultimately disappeared. Altogether our results thus suggest that the occurrence of a single allele in the most recessive class is a specific property of the FDS_m regime when combined with the domcod dominance relationships.

Number of alleles maintained in finite populations:

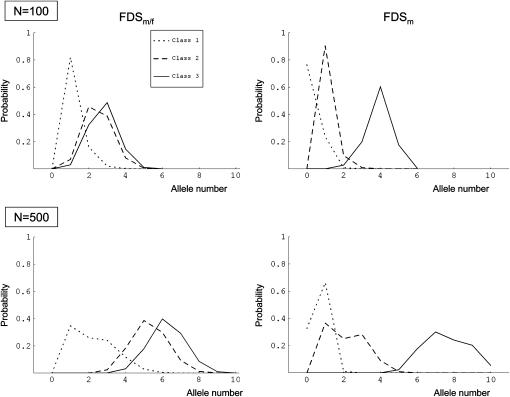
Simulations with three dominance classes, under domcod dominance relationships and for both selection regimes in a population of 100 and 500 diploid individuals, showed that the distributions of the allele number for dom under FDS_m/f and FDS_m were similar to those for domcod under FDS_m/f (Figure 3). The average numbers of alleles under FDS_m/f and FDS_m under dom and domcod are given in Table 4.

Figure 3.— — Distribution of the number of alleles in dominance classes under domcod dominance relationships (distributions patterns for dom under FDS_m and FDS_m/f are similar to the pattern of domcod under FDS_m/f).

TABLE 4.

Mean allele number and selection strength per dominance class in a finite population

No. of individuals	Mutation rate	Dominance pattern	Dominance class	Mean allele no.		Slope (selection strength)
No. of individuals	Mutation rate	Dominance pattern	Dominance class					FDS_m	FDS_m/f	FDS_m	FDS_m/f
100	0.0001	dom	1	1.06	1.07
			2	1.38	1.77
			3	1.55	2.08
			Total	3.99	4.92
		domcod	1	0.26	1.21
			2	1.12	2.5
			3	3.93	2.78
			Total	5.31	6.49
500	0.00002	dom	1	1.09	1.13	−0.077	−0.12
			2	2.91	4	−0.124	−0.197
			3	3.61	4.91	−0.178	−0.279
			Total	7.61	10.04
		domcod	1	0.68	2.25	−0.082	−0.161
			2	2.13	5.32	−0.188	−0.281
			3	7.58	6.22	−0.336	−0.369
			Total	10.39	13.79

Open in a new tab

The slope is obtained by linear regression between selection strength and relative deviation from equilibrium (see text and Figure 4 for details).

Interestingly, the number of alleles maintained in a class increased with dominance. Under FDS_m/f, there was a high probability to observe only one allele in the most recessive class, but this probability decreased with increasing population size. When comparing both dominance models under FDS_m/f, we found that the number of alleles maintained in each class was higher under domcod than under dom (Table 4).

When the population size was large enough, more than one allele could frequently be maintained in the most recessive class under FDS_m/f and domcod (Table 4). Under FDS_m, however, one allele was at best expected in the most recessive class, with many cases where all alleles from this class became lost from the population. Under FDS_m when N = 100, distributions for the number of alleles were quite different between dom and domcod. Under domcod, the most typical outcome was no allele in the most recessive class and mostly one allele in class 2. Under dom, one allele was always maintained in the most recessive class (Table 4). Under domcod, when the size of the population was increased to N = 500 individuals, the probability of loss for the most recessive class was ∼0.33. In the latter case, class 2 became the most recessive class, where a single allele was thus expected to be maintained (vs. one to four alleles maintained when class 1 existed in the population). As a consequence, the distribution of the number of class 2 alleles became bimodal (Figure 3). Although the distribution of the number of class 3 alleles was not bimodal, it was, however, wider than under FDS_m/f presumably because when class 1 was lost, more alleles were present in class 3.

Selection strength:

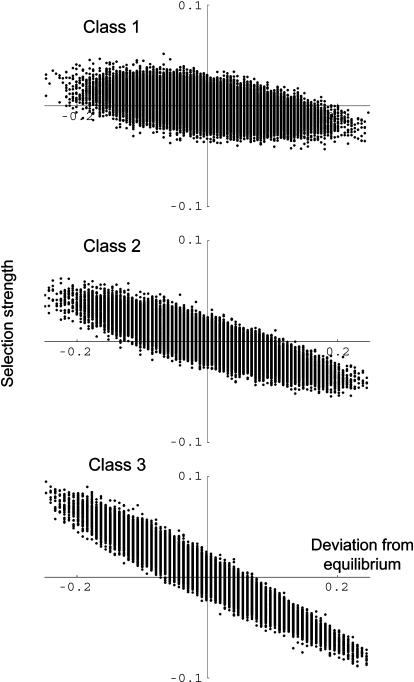
Although selection strength varied extensively according to the genotypic composition of the population (Figure 4), the expected selection strength over all genotypic compositions closely followed negative frequency-dependent selection. Most interestingly, Figure 4 shows that the relationship between selection strength and relative deviation differed among classes. The slope was high for the most dominant class, intermediate for the intermediate class, and low for the most recessive class. In addition, the regression slope was higher under FDS_m/f than under FDS_m (Table 4), in line with the fact that equilibrium was attained more quickly (Figure 1). The slopes were also higher under domcod than under dom under both selection regimes, and they were also higher for alleles in higher dominance classes. This strongly suggested that alleles in the most recessive class are subject to weaker selection than alleles in the dominant classes. This analysis provided a mechanistic explanation for the differences in the number of alleles maintained in a class in finite populations. The stronger selection is, the higher the number of alleles maintained in the population is expected to be. Indeed, even if alleles in the most dominant classes are expected to be the least frequent (Table 2), the most dominant class has the highest number of alleles (Table 4) because those alleles are returned to their equilibrium frequency faster than alleles in the recessive classes. Hence, for a given equilibrium frequency and a given population size, the probability for an allele to be lost by drift is negatively correlated with its dominance level.

APPLICATIONS

Comparison between expected and observed frequencies in natural populations:

The dominance relationships between alleles have been studied in only a few species with sporophytic self-incompatibility and, at best, only partially. An estimation of observed allelic frequencies in a natural population is also available in a few cases only. To illustrate the potential use of our model to test the hypothesis of negative frequency-dependent selection, we applied our model to two cases for which both data sets are available: Sinapis arvensis (Stevens and Kay 1989) and Ipomoea trifida (Kowyama et al. 1994). Assuming that individuals were sampled in a large population at selection–mutation equilibrium, it is possible to test whether the observed allelic frequencies are significantly different from the expectation under our model. For that purpose, we used a likelihood-ratio test to test whether the observed frequencies significantly differ from a multinomial distribution with the expected equilibrium allelic frequencies as parameters. The expected equilibrium allelic frequencies were computed using our general model, with the number of alleles n equal to the number of specificity observed in each population: n = 33 for the population of S. arvensis and, respectively, n = 5, n = 16, and n = 6 for populations M81, M84, and G80 of I. trifida. We computed the log-likelihood ratio

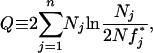(6)

where N_j is the number of copies of allele j observed in the population, N is the total number of sampled individuals, Inline graphic is the expected frequency at equilibrium for allele j, and n is the number of alleles observed in the sample. The observed allelic frequencies are then significantly different from the expectations if Q is higher than a chi square with n − 1 d.f. We also performed the test on each allele independently, considering all other alleles as a single one, and tested if its observed frequency significantly differed from its expected frequency under our models (footnote a in Tables 5 and 6). For that purpose, we also used a likelihood-ratio test with n = 2.

TABLE 5.

Observed and expected frequencies for Sinapis arvensis according to dominance relationships and data from natural populations given in Stevens and Kay (1989)

Allele	Observed	FDS_m/f	FDS_m
1	0.029 (2)	0.070	0.081
2	0.015 (1)	0.023	0.029
3, 24	0.029 (2)	0.038	0.028
4, 6, 12	0.029 (2)	0.020	0.020
5, 9, 14	0.015 (1)	0.020	0.020
7, 13	0.059 (4)	0.020	0.020
8	0.044 (3)	0.018	0.020
10, 11	0.059 (4)	0.038	0.028
15	0.059 (4)	0.034	0.028
16	0.044 (3)	0.038	0.028
17, 27, 28, 35	0.015 (1)	0.020	0.020
18, 19, 29, 30, 34	0.029 (2)	0.020	0.020
20	0.015 (1)	0.046	0.054
23	0.088 (6)	0.020	0.020^a
25	0.015 (1)	0.069	0.104^a
26, 31	0.015 (1)	0.038	0.028
32, 33	0.015 (1)	0.055	0.058
Likelihood ratio		38.961	46.633
P-value		0.185	0.046

Open in a new tab

The number of identified alleles is given in parentheses next to the observed allele frequencies.

Alleles for which the observed frequency is significantly different from the expectations, using a likelihood-ratio test at 5%.

TABLE 6.

Observed and expected frequencies for Ipomoea trifida according to dominance relationships and data from natural populations given in Kowyama et al. (1994)

	Population
M81 (70)				M84 (82)				G80 (62)
Allele	Observed		FDS_m/f	FDS_m	Observed		FDS_m/f	FDS_m	Observed		FDS_m/f	FDS_m
1					0.061	(5)	0.047	0.047
2					0.012	(1)^a	0.059	0.059
3	0.486	(34)	0.468	0.468	0.366	(30)	0.295	0.293	0.371	(23)	0.450	0.449
4					0.037	(3)	0.059	0.059
5					0.073	(6)	0.038	0.039
6					0.024	(2)	0.051	0.050
7					0.012	(1)^a	0.059	0.059
8	0.271	(19)^a	0.137	0.137
9	0.086	(6)	0.114	0.114
10	0.143	(10)	0.181	0.181	0.085	(7)	0.119	0.118	0.323	(20)^a	0.175	0.175
11	0.014	(1)^a	0.100	0.100
12					0.085	(7)	0.037	0.038	0.226	(14)^a	0.080	0.083
13									0.032	(2)^a	0.133	0.132
14									0.016	(1)^a	0.077	0.077
15									0.032	(2)	0.084	0.084
16					0.134	(11)^a	0.043	0.044
17					0.037	(3)	0.037	0.037
18					0.024	(2)	0.037	0.037
19					0.012	(1)	0.047	0.047
20					0.012	(1)	0.036	0.037
22					0.012	(1)	0.037	0.037
X					0.012	(1)	—	—
Likelihood ratio			16.461	16.461			34.76	33.96			31.77	31.159
P-value			0.002	0.002			0.002	0.002			<0.001	<0.001

Open in a new tab

The sample size is given in parentheses next to the population name and the number of identified alleles is given in parentheses next to the observed allele frequencies.

Alleles for which the observed frequency is significantly different from the expectations, using a likelihood-ratio test at 5%.

Example 1—S. arvensis:

Stevens and Kay (1989) obtained genotype frequencies for 34 individuals from a natural population. They found 35 alleles, belonging to three distinct dominance classes in pollen and two dominance classes in pistil. Interestingly, several dominance relationships were asymmetrical. Allele 1, for instance, was one of the most recessive alleles in pistil but one of the most dominant alleles (together with allele 2) in pollen (Stevens and Kay 1989; appendix a). Table 5 reports the observed frequencies from Stevens and Kay (1989) as well as the expected frequencies obtained under FDS_m and FDS_m/f. Overall, the observed frequencies were not significantly different from the expected frequencies under FDS_m/f while they were significantly different from the expected frequencies under FDS_m (Table 5). This discrepancy was mostly due to several large differences between both selection regimes in the expected frequencies at equilibrium, notably for alleles 23 and 25. Allele 25 is the single most recessive allele in pollen and one of the nine most recessive alleles in pistil. Its observed frequency is significantly different from the expected frequency under FDS_m. Surprisingly, although allele 23 was predicted to be one of the less frequent alleles in the population, it was actually one of the most frequent in the samples, suggesting that evolutionary forces other than negative frequency-dependent selection may play a role in the evolution of this allele.

APPENDIX A.

Dominance relationships between alleles in Sinapis arvensis from Stevens and Kay (1989)

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	23	24	25	26	27	28	29	30	31	32	33	34	35
Pairwise dominance relationships in pistil
1	1	0	0	0	0	0	0	0.5	0	0	0	0	0	0	0	0	0	0	0	0.5	0	0	0.5	0	0	0	0	0	0	0.5	0.5	0	0
2	1	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
3	1	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
4	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
5	1	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
6	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
7	1	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
8	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
9	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
10	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
11	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
12	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
13	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
14	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
15	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
16	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
17	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
18	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
19	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
20	0.5	0	0	0	0	0	0	0	0	0	0	0	0	0	0.5	0	0	0	0	1	0	0	0.5	0	0	0	0	0	0	0.5	0.5	0	0
23	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
24	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	1	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
25	0.5	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.5	0	0	1	0	0	0	0	0	0	0.5	0.5	0	0
26	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5
27	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	1	0.5	0.5	0.5	0.5	1	1	0.5	0.5
28	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	1	1	0.5	0.5
29	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	1	0.5	0.5	1	1	0.5	0.5
30	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	1	0.5	1	1	0.5	0.5
31	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5
32	0.5	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.5	0	0	0.5	0	0	0	0	0	0	1	0.5	0	0
33	0.5	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.5	0	0	0.5	0	0	0	0	0	0	0.5	1	0	0
34	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5
35	1	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	1
Pairwise dominance relationships in pollen
1	1	0.5	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
2	0.5	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3	0	0	1	0	0	0	0	0	0	0.5	0.5	0	0	0	0.5	0.5	0	0	0	0	0	0.5	0.5	0.5	0	0	0	0	0.5	0	0	0	0
4	0	0	1	1	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
5	0	0	1	0.5	1	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
6	0	0	1	0.5	0.5	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
7	0	0	1	0.5	0.5	0.5	1	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
8	0	0	1	0.5	0.5	0.5	0.5	1	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
9	0	0	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
10	0	0	0.5	0	0	0	0	0	0	1	0.5	0	0	0	0.5	0.5	0	0	0	0	0	0.5	0.5	0.5	0	0	0	0	0.5	0	0	0	0
11	0	0	0.5	0	0	0	0	0	0	0.5	1	0	0	0	0.5	0.5	0	0	0	0	0	0.5	0.5	0.5	0	0	0	0	0.5	0	0	0	0
12	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
13	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	1	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
14	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
15	0	0	0.5	0	0	0	0	0	0	0.5	0.5	0	0	0	1	0.5	0	0	0	0	0	0.5	0.5	0.5	0	0	0	0	0.5	0	0	0	0
16	0	0	0.5	0	0	0	0	0	0	0.5	0.5	0	0	0	0.5	1	0	0	0	0	0	0.5	0.5	0.5	0	0	0	0	0.5	0	0	0	0
17	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
18	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	1	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
19	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	1	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
20	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
23	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	1	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
24	0	0	0.5	0	0	0	0	0	0	0.5	0.5	0	0	0	0.5	0.5	0	0	0	0	0	1	0.5	0.5	0	0	0	0	0.5	0	0	0	0
25	0	0	0.5	0	0	0	0	0	0	0.5	0.5	0	0	0	0.5	0.5	0	0	0	0	0	0.5	1	0.5	0	0	0	0	0.5	0	0	0	0
26	0	0	0.5	0	0	0	0	0	0	0.5	0.5	0	0	0	0.5	0.5	0	0	0	0	0	0.5	0.5	1	0	0	0	0	0.5	0	0	0	0
27	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	1	0.5	0.5	0.5	1	0.5	0.5	0.5	0.5
28	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	1	0.5	0.5	1	0.5	0.5	0.5	0.5
29	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	1	0.5	1	0.5	0.5	0.5	0.5
30	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5
31	0	0	0.5	0	0	0	0	0	0	0.5	0.5	0	0	0	0.5	0.5	0	0	0	0	0	0.5	0.5	0.5	0	0	0	0	1	0	0	0	0
32	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5
33	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	1	0.5	0.5
34	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	1	0.5
35	0	0	1	0.5	0.5	0.5	0.5	0.5	0.5	1	1	0.5	0.5	0.5	1	1	0.5	0.5	0.5	0.5	0.5	1	1	1	0.5	0.5	0.5	0.5	1	0.5	0.5	0.5	1

Open in a new tab

Example 2—I. trifida:

The genotype of 214 individuals from three populations was determined and 23 alleles were found by Kowyama et al. (1994). We give in Table 6 the expected allelic frequencies obtained under the FDS_m and FDS_m/f models as well as observed frequencies in three populations. The dominance relationships matrix used for the computations is derived from Kowyama et al. (1994) and is given in appendix b. The dominance relationships are approximately symmetric in pollen and pistil for all alleles. For computations in each population, we used a reduced matrix restricted to alleles present in each population. We found almost no differences between the predictions under both selection regimes. The observed frequencies were significantly different from the expectations in each population (Table 6). This departure was due to 2 alleles in population M81, 3 in population M84, and 4 in population G80. Allele 3 was recessive to all other alleles in pistil and pollen and it was, as expected, the most frequent in all populations. Allele 10 was recessive to all alleles except allele 3 and, as a consequence, it was expected to be the second most frequent allele after allele 3 in all populations. However, it was actually not the second most frequently observed allele in populations M81 and M84. Indeed, allele 8 in population M81 and allele 16 in population M84 had a much higher frequency than expected.

APPENDIX B.

Dominance relationships between alleles in Ipomoea trifida from Kowyama et al. (1994)

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	22
Pairwise dominance relationships in pistil
1	1	1	1	1	0	1	1	1	0	1	0	0	1	0	0	0.5	0	0	1	0	0
2	0	1	1	0.5	0	0	0.5	0.5	0	1	0	0	0.5	0	0	0	0	0	0	0	0
3	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
4	0	0.5	1	1	0	0	0.5	0.5	0	1	0	0	0.5	0	0	0	0	0	0	0	0
5	1	1	1	1	1	1	1	1	0.5	1	0	0.5	1	0.5	1	1	0.5	0.5	1	0	0.5
6	0	1	1	1	0	1	1	1	0	1	0	0	1	0	0	0.5	0	0	0.5	0	0
7	0	0.5	1	0.5	0	0	1	0.5	0	1	0	0	0.5	0	0	0	0	0	0	0	0
8	0	0.5	1	0.5	0	0	0.5	1	0	1	0	0	0.5	0	0	0	0	0	0	0	0
9	1	1	1	1	0.5	1	1	1	1	1	0	0.5	1	0.5	0.5	1	0.5	0.5	1	0	0.5
10	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0
11	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0.5	1
12	1	1	1	1	0.5	1	1	1	0.5	1	0	1	1	0.5	0.5	1	0.5	0.5	1	0	0.5
13	0	0.5	1	0.5	0	0	0.5	0.5	0	1	0	0	1	0	0	0	0	0	0	0	0
14	1	1	1	1	0.5	1	1	1	0.5	1	0	0.5	1	1	0.5	1	0.5	0.5	1	0	0.5
15	1	1	1	1	0	1	1	1	0.5	1	0	0.5	1	0.5	1	1	0.5	0.5	1	0	0.5
16	0.5	1	1	1	0	0.5	1	1	0	1	0	0	1	0	0	1	0	0	0.5	0	0
17	1	1	1	1	0.5	1	1	1	0.5	1	0	0.5	1	0.5	0.5	1	1	0.5	1	0	0.5
18	1	1	1	1	0.5	1	1	1	0.5	1	0	0.5	1	0.5	0.5	1	0.5	1	1	0	0.5
19	0	1	1	1	0	0.5	1	1	0	1	0	0	1	0	0	0.5	0	0	1	0	0
20	1	1	1	1	1	1	1	1	1	1	0.5	1	1	1	1	1	1	1	1	1	1
22	1	1	1	1	0.5	1	1	1	0.5	1	0	0.5	1	0.5	0.5	1	0.5	0.5	1	0	1
Pairwise dominance relationships in pollen
1	1	1	1	1	0	1	1	1	0	1	0	0	1	0	0	0.5	0	0	1	0	0
2	0	1	1	0.5	0	0	0.5	1	0	1	0	0	0.5	0	0	0	0	0	0	0	0
3	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
4	0	0.5	1	1	0	0	0.5	0.5	0	1	0	0	0.5	0	0	0	0	0	0	0	0
5	1	1	1	1	1	1	1	1	0.5	1	0	0	1	0.5	1	1	0.5	1	1	0	0.5
6	0	1	1	1	0	1	1	1	0	1	0	0	1	0	0	0	0	0	0.5	0	0
7	0	0.5	1	0.5	0	0	1	0.5	0	1	0	0	0.5	0	0	0	0	0	0	0	0
8	0	0	1	0.5	0	0	0.5	1	0	1	0	0	0.5	0	0	0	0	0	0	0	0
9	1	1	1	1	0.5	1	1	1	1	1	0	0.5	1	0.5	0.5	1	0.5	0.5	1	0	0
10	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0
11	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0.5	1
12	1	1	1	1	1	1	1	1	0.5	1	0	1	1	0.5	1	1	1	0.5	1	0	1
13	0	0.5	1	0.5	0	0	0.5	0.5	0	1	0	0	1	0	0	0	0	0	0	0	0
14	1	1	1	1	0.5	1	1	1	0.5	1	0	0.5	1	1	0.5	1	0.5	0.5	1	0	0.5
15	1	1	1	1	0	1	1	1	0.5	1	0	0	1	0.5	1	1	0.5	0.5	1	0	0.5
16	0.5	1	1	1	0	1	1	1	0	1	0	0	1	0	0	1	0	0	0.5	0	0
17	1	1	1	1	0.5	1	1	1	0.5	1	0	0	1	0.5	0.5	1	1	0.5	1	0	0.5
18	1	1	1	1	0	1	1	1	0.5	1	0	0.5	1	0.5	0.5	1	0.5	1	1	0	0.5
19	0	1	1	1	0	0.5	1	1	0	1	0	0	1	0	0	0.5	0	0	1	0	0
20	1	1	1	1	1	1	1	1	1	1	0.5	1	1	1	1	1	1	1	1	1	1
22	1	1	1	1	0.5	1	1	1	1	1	0	0	1	0.5	0.5	1	0.5	0.5	1	0	1

Open in a new tab

Although some level of concordance can be found, especially for S. arvensis, the two examples above generally enabled us to reject the model's predictions. Although the low number of individuals analyzed relative to the total number of alleles in the population may greatly affect the accuracy of allele frequency estimates, this pattern of discrepancy may actually reveal that additional evolutionary forces are indeed interfering with the strict frequency-dependent selection implemented in our model. Our model may thus be viewed as a “null model,” where frequency-dependent selection is the only evolutionary force taken into account.

DISCUSSION

Generality of the model:

Due to the generality and flexibility of our approach, we were able to investigate a large range of SSI models in a single framework. This enabled us to fill the gaps between previously scattered theoretical investigations (Table 1) as well as to extend previous results to situations with many dominance classes and several alleles per class. This approach has been used to compute equilibrium genotypic and allelic frequencies under a variety of conditions and to compute expected genotypic changes over a single generation on the basis of known genotypic composition from a natural population, as well as to perform exploratory stochastic simulations. These analyses rely on the assumption that the only relevant force acting on S alleles is negative frequency-dependent selection generated by self-incompatibility. Basically we showed that the higher frequency of recessive alleles is a general feature of SSI models, but also that in finite populations the number of dominance classes will evolve according to the population size, and that dominant classes will contain more alleles than recessive classes. We also showed that fecundity selection (FDS_m/f) may have large effects on the dynamics of allelic frequencies as well as on the expectation of the number of alleles, the number of dominance classes, and the number of alleles by class maintained in finite populations. We notably showed that contrary to FDS_m, it is possible to maintain deterministically more than one allele in the most recessive class under domcod and consequently in finite populations.

Because our model uses very general recurrent equations, it can be extended to incorporate direct selection on S alleles, such as, for instance, selection due to the expression of linked deleterious alleles in homozygotes. In line with most other theoretical investigations of self-incompatibility (SI) (but see Charlesworth 1988), we also assumed that self-incompatibility was fully functional (technically, the compatibility threshold σ was set to zero in all our computations). However, partial self-incompatibility is often reported in empirical studies (Nou et al. 1991; Reinartz and Les 1994; Good-Avila and Stephenson 2002; Mable et al. 2005), and examination of its effect using modifications of our model is straightforward.

Generality of the recessive effect:

As was shown by several authors in a number of different specific situations, we observed in deterministic models that alleles from the most recessive class were always more frequent than dominant alleles, and this result was consistent across any number of classes, any number of alleles per class, and both types of selection (Table 2 and Figure 2). However, the strength of this recessive effect varied greatly among models. In the dom model, the effect increased drastically with increasing number of dominance classes, but was little affected by the number of alleles per class. In the domcod model with FDS_m, the recessive effect was weak and did not increase much with the number of dominance classes, whereas the effect was stronger under FDS_m/f. These results are qualitatively identical to those obtained by Schierup et al. (1997) and Vekemans et al. (1998) in models with only one allele per class. We showed that the recessive effect is even higher when the number of alleles by classes is different, especially when there is only one allele in the most recessive class (Table 3). In general agreement with these results, higher frequencies of the most recessive alleles have been observed in most empirical surveys of S alleles in natural populations of species with SSI (Sampson 1967; Stevens and Kay 1989; Kowyama et al. 1994; Mable et al. 2003; Glémin et al. 2005). Using our model, the recessive effect seemed also to be verified for the most recessive alleles in a case with very complex overall patterns of dominance, such as allele 25 in S. arvensis. In other complex cases, it may be difficult to decide unambiguously which allele is dominant or recessive but we can still interpret differences in expected frequencies in terms of relative dominance.

How many alleles per dominance class in finite populations?

This study is the first to investigate models of SSI that allow multiple alleles per dominance class in finite populations (but see Uyenoyama 2000). We consistently found that the number of alleles maintained per dominance class increases with dominance level. This result is not trivial because deterministic computations in models with an identical number of alleles in each class predicted a lower frequency of more dominant alleles, which could potentially cause a higher rate of loss of dominant alleles due to genetic drift. Empirical studies seem to agree overall with this expectation. In Arabidopsis lyrata, where four dominance classes have been recorded, 8 S alleles are known overall in the two most recessive classes, whereas the two most dominant ones comprise 16 S alleles (Prigoda et al. 2005). Similarly, in a single population of this species, 3 and 8 S alleles were found in the most recessive and the most dominant classes, respectively (Schierup et al. 2006). In Brassica insularis, where two dominance classes are known and dominance relationships seem to follow the domcod model, 2 alleles have been identified in the recessive class whereas >18 alleles have been recorded in the dominant class (Glémin et al. 2005). Differences in allele numbers between the most recessive and the most dominant classes are increased under FDS_m/f, as compared to the FDS_m model, and we showed that the overall strength of selection is higher under the former. The higher number of alleles in dominant than in recessive classes could be due either to higher rates of incorporation of new alleles, with dominance conferring a large advantage over recessive alleles when rare (Schierup et al. 1997), and/or to lower rates of loss. Our estimates of the strength of selection on alleles from different classes of dominance indicate a clear trend of increasing selection intensity with increasing dominance (Table 4). SSI systems thus appear as important examples of asymmetric balancing selection. Because individual allelic frequencies within a given dominance class are inversely related to the number of alleles in that class (Sampson 1974), the recessive effect is amplified by this difference in allele numbers, with substantially higher differences in frequencies between dominant and recessive alleles in finite populations, which could explain the very high differences in allelic frequencies observed for I. trifida (Table 6).

An additional mechanism must be taken into account to explain the number of alleles by dominance class under the FDS_m model of selection and domcod dominance relationships. Indeed, as first pointed out by Uyenoyama (2000), under deterministic conditions, two alleles cannot coexist in the most recessive class: As soon as a slight perturbation is introduced, the less frequent allele tends to disappear. Although this arguably occurred under a wide range of parameters, we also showed that some cases exist where two alleles can be maintained in the most recessive class for up to 10 dominance classes. It is interesting to note that this result does not extend to FDS_m/f under which two alleles can typically coexist at deterministic equilibrium under domcod. When the size of the population is small, only one allele is observed in the most recessive class (Figure 4). However, when the size of the population increases, then more than one allele coexist in the most recessive class even under domcod dominance relationships, contrary to results under the FDS_m model (Table 4 and Figure 4). Glémin et al. (2005) found evidence for the occurrence of two alleles in the most recessive class within populations of B. insularis and suggested that it could be due to population substructure. We show here that it is possible to maintain two alleles in the most recessive class in a panmictic population when selection occurs through both male and female reproductive structures. Because of the low density in B. insularis populations, pollen limitation due to low pollinator activity could indeed generate a female component of frequency-dependent selection through fecundity selection (Vekemans et al. 1998), and the FDS_m/f model is likely to be relevant.

How many dominance classes in finite populations?

In finite populations, the number of dominance classes may evolve. Schierup et al. (1997) showed that under the FDS_m regime and domcod, the most recessive alleles could not be maintained in finite populations: Every time a more dominant allele appeared in the population (in their model the number of dominance classes was infinite), the most recessive allele tended to be lost, resulting in a constant turnover of the most recessive allele. Hence, absolute levels of dominance tend to increase over time. Here we reported a phenomenon similar to the results of both Uyenoyama (2000) and Schierup et al. (1997). Indeed, as shown in Figure 3 and Table 4, under FDS_m and domcod, class 1 may be lost. The probability of loss of the most recessive class depends on the size of the population, suggesting that a simple interaction between demography and selection may cause differences in the number of dominance classes in different species. This could be relevant to explain why in the Brassica genus, only two dominance classes are found in Brassica, where domcod patterns of dominance are reported (Thompson and Taylor 1966), whereas at least four dominance classes are known to occur in A. lyrata where patterns of dominance are dom-like (Prigoda et al. 2005). Our results suggest that differences in numbers of dominance classes can be explained by an interaction between demography and selection. The lower number of dominance classes in the Brassica genus could be related, for instance, to the occurrence of an ancient bottleneck, which would be congruent with the observation of lower phylogenetic diversity of alleles in Brassica than in A. lyrata (Schierup et al. 2001).

Measure of selection strength:

The measure we used to quantify selection strength allowed us to better understand the difference in allele number maintained in different dominance classes under different models. Selection strength is a synthetic quantitative measure explaining the different dynamics and expectations at equilibrium in finite populations both for selection regimes and for any kind of dominance relationship. Figure 4 showed that the frequency of an allele is not sufficient to predict its frequency change in a generation under negative frequency-dependent selection because this change will depend upon the exact genotypic composition of the population at this generation. Indeed, the frequency of an allele can increase in a generation even if it is higher than its equilibrium frequency expectation. Sporophytic self-incompatibility systems illustrate how difficult it may be to measure selection under complex selection regimes such as negative frequency-dependent selection, notably since it depends on genotypic rather than allelic frequencies. In finite populations, selection strength reflects the probability of loss for an allele and depends on its dominance class. However, within complex dominance patterns, it can be difficult to determine the absolute dominance level of an allele and it is possible to use selection strength for this allele to estimate its probability of being lost or maintained.

Frequency-dependent selection models and pollen limitation:

We observed large differences in the properties of the FDS_m and FDS_m/f models of selection, in terms of frequencies at equilibrium, dynamics, and expected number of alleles by class. Notably, under FDS_m/f several alleles are expected in the most recessive class, contrary to under the FDS_m model. The fundamental difference between both models is that under the FDS_m model, all plants receive sufficient compatible pollen to fertilize all their ovules, such that all plants produce the same quantity of seeds whatever their S-locus genotype and whatever the genotypes of the other individuals in the population. However, it is known that “pollen limitation” may be frequent in natural populations, i.e., that seed output is limited by the availability of compatible pollen (Larson and Barrett 2000). Under the FDS_m/f model, not all plants produce the same quantity of seeds when the population departs from equilibrium because the probability that a given ovule will be fertilized is proportional to the amount of compatible pollen and thus varies among genotypes at the S locus. It would be interesting to know which of the two models of selection is closer to natural conditions, and we anticipate that this should heavily depend both on the species considered and on ecological conditions. Indeed, when populations are small, because of a recent bottleneck or a recent colonization event, or highly structured or when pollen dispersal is strongly spatially restricted, we could expect pollen limitation to be important. The occurrence of clonality due to vegetative propagation within species with SSI can also increase the incidence of pollen limitation, due to within-ramets incompatible pollination (DeMauro 1993; Young et al. 2002). Under those circumstances, FDS_m/f models could be more relevant.

Causes of the deviation between expected and observed frequencies in natural populations:

Our model enabled us to compute expected frequencies for each allele and each genotype at equilibrium for any kind of dominance relationship. We showed that observed allelic frequencies were significantly different from the expected frequencies under FDS_m for S. arvensis (Table 5) and that alleles 23 and 25 taken independently had frequencies significantly different from their expectations. For I. trifida the observed frequencies were different from their expectations in three populations. Four kinds of causes could explain these discrepancies between expected and observed allelic frequencies. First, the empirical determination of allelic frequencies and dominance relationships within natural populations may be inaccurate. Indeed, in articles from which those data were taken, only a fraction of all pairwise dominance relationships between alleles were actually tested, the others being inferred transitively. Also, errors in allele identification and statistical uncertainty due to low sample size relative to the number of alleles could lead to imprecise estimation of allelic frequencies. In particular, if all alleles are not known, the model will overestimate the allelic frequencies at equilibrium, especially for alleles in the same dominance class as the missing alleles. Second, the sampled population may not be at equilibrium because of drift or perturbations of the habitat or because the colonization of the population is recent. Third, population structure can also cause some deviation from deterministic equilibrium because the intrademe frequencies distribution can be different from that of a panmictic population for intermediate migration rates (Schierup 1998). Fourth, some important model assumptions could be erroneous. Indeed, we assumed that all S alleles are selectively equivalent while there are reports of differential selection on S alleles (Bechsgaard et al. 2004). Also, we have seen that the frequency of homozygotes is not negligible, especially for alleles in the most recessive dominance classes and when the number of S alleles is low. Hence, selection on S-allele-linked deleterious recessive alleles may play an important role in the dynamics of S alleles in sporophytic systems (Uyenoyama 1997) and could explain the discrepancy between expected and observed frequencies in a natural population. Finally, several mechanisms have been described that could occur in addition to frequency-dependent selection and potentially affect predictions for the number of alleles and their respective frequencies.

CONCLUSIONS

The model presented here is very general and allows predicting either genotypic frequencies at deterministic equilibrium (and all statistics derived from genotypic frequencies such as F_is) or the expected genotypic frequencies that change in a generation. We confirmed previously identified characteristics of SSI systems and generalized them to situations with several alleles per dominance class. Moreover, we found emerging properties of such systems in finite populations such as the dynamics of the number of dominance classes and the asymmetry in allele numbers among classes. However, these predictions hold only under the assumptions that the sole mechanism acting is negative frequency-dependent selection due to the particular reproductive system. Hence, the results obtained under this model constitute a direct test of this hypothesis, as illustrated with two example applications. Consequently one can use this model as a tool to detect alternative selection forces that may be allele specific. Furthermore, in this article, the dominance classes were set either as parameters in the deterministic computations or as the result of the maintenance or loss of alleles in a finite population because of drift and frequency-dependent selection. However, the model can be used to examine the evolution of dominance through the selection of a dominance modifier.

Acknowledgments

We thank F. Christiansen for sending a Mathematica notebook to verify our derivations in models with four dominance classes. We are indebted to S. Glémin, to an anonymous reviewer, and to the associate editors for their suggestions to improve the manuscript. S. Billiard especially thanks M. Ballatore without whom this work would not exist. The self-incompatibility team at Lille University is supported by an Action Thématique et Incitative sur Programme grant from the Centre National de la Recherche Scientifique, an Action de Recherches Concertées d'Initiative Régionale grant from Région Nord-Pas de Calais, and a Fonds Européen de Développement Régional grant from the European Union.

References

Bateman, A. J., 1952. Self-incompatibility systems in angiosperms. 1. Theory. Heredity 6: 285–310. [Google Scholar]
Bechsgaard, J., T. Bataillon and M. H. Schierup, 2004. Uneven segregation of sporophytic self-incompatibility alleles in Arabidopsis lyrata. J. Evol. Biol. 17: 554–561. [DOI] [PubMed] [Google Scholar]
Charlesworth, D., 1988. Evolution of homomorphic sporophytic self-incompatibility. Heredity 60: 445–453. [Google Scholar]
Chookajorn, T., A. Kachroo, A. G. Clark and J. B. Nasrallah, 2004. Specificity determinants and diversification of the Brassica self-incompatibility pollen ligand. Proc. Natl. Acad. Sci. USA 101: 911–917. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cope, F. W., 1962. The effects of incompatibility and compatibility on genotype proportions in populations of Theobroma cacao L. Heredity 17: 183–195. [Google Scholar]
DeMauro, M. M., 1993. Relationship of breeding system to rarity in the lakeside daisy (Hymenoxys acaulis var. glabra). Conserv. Biol. 7: 542–550. [Google Scholar]
Glémin, S., T. Gaude, M. L. Guillemin, M. Lourmas, I. Olivieri et al., 2005. Balancing selection in the wild: testing population genetics theory of self-incompatibility in the rare species Brassica insularis. Genetics 171: 279–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
Good-Avila, S. V., and A. G. Stephenson, 2002. The inheritance of modifiers conferring self-fertility in the partially self-incompatible perennial, Campanula rapunculoides L.(Campanulaceae). Evolution 56: 263–272. [DOI] [PubMed] [Google Scholar]
Imrie, B. C., C. J. Kirkman and D. R. Ross, 1972. Computer simulation of a sporophytic self-incompatibility breeding system. Aust. J. Biol. Sci. 25: 343–349. [Google Scholar]
Kowyama, Y., H. Takahasi, K. Muraoka, T. Tani, K. Hara et al., 1994. Number, frequency and dominance relationships of S-alleles in diploid Ipomoea trifida. Heredity 73: 275–283. [Google Scholar]
Larson, B. M. H., and S. C. H. Barrett, 2000. A comparative analysis of pollen limitation in flowering plants. Biol. J. Linn. Soc. 69: 503–520. [Google Scholar]
Mable, B. K., M. H. Schierup and D. Charlesworth, 2003. Estimating the number, frequency, and dominance of S-alleles in a natural population of Arabidopsis lyrata (Brassicaceae) with sporophytic control of self-incompatibility. Heredity 90: 422–431. [DOI] [PubMed] [Google Scholar]
Mable, B. K., A. V. Robertson, S. Dart, C. D. Berardo and L. Witham, 2005. Breakdown of self-incompatibility in the perennial Arabidopsis lyrata (Brassicaceae) and its genetic consequences. Evolution 59: 1437–1448. [PubMed] [Google Scholar]
Mehlenbacher, S. A., 1997. Revised dominance hierarchy for S-alleles in Corylus avellana L. Theor. Appl. Genet. 94: 360–366. [Google Scholar]
Nou, I. S., M. Watanabe, A. Isogai, H. Shiozawa, A. Suzuki et al., 1991. Variation of S-alleles and S-glycoproteins in a naturalized population of self-incompatible Brassica campestris. Jpn. J. Genet. 66: 227–239. [Google Scholar]
Prigoda, N. L., A. Nassuth and B. K. Mable, 2005. Phenotypic and genotypic expression of self-incompatibility haplotypes in Arabidopsis lyrata suggests unique origin of alleles in different dominance classes. Mol. Biol. Evol. 22: 1609–1620. [DOI] [PubMed] [Google Scholar]
Reinartz, J. A., and D. H. Les, 1994. Bottle-neck induced dissolution of self-incompatibility and breeding system consequences in Aster furcatus (Asteraceae). Am. J. Bot. 81: 446–455. [Google Scholar]
Richman, A., 2000. Evolution of balanced genetic polymorphism. Mol. Ecol. 9: 1953–1963. [DOI] [PubMed] [Google Scholar]
Sampson, D. R., 1967. Frequency and distribution of self-incompatibility alleles in Raphanus raphanistrum. Genetics 56: 241–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sampson, D. R., 1974. Equilibrium frequencies of sporophytic self-incompatibility alleles. Can. J. Genet. Cytol. 16: 611–618. [Google Scholar]
Schierup, M. H., 1998. The number of self-incompatibility alleles in a finite, subdivided population. Genetics 149: 1153–1162. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schierup, M. H., X. Vekemans and F. B. Christiansen, 1997. Evolutionary dynamics of sporophytic self-incompatibility alleles in plants. Genetics 147: 835–846. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schierup, M. H., B. K. Mable, P. Awadalla and D. Charlesworth, 2001. Identification and characterization of a polymorphic receptor kinase gene linked to the self-incompatibility locus of Arabidopsis lyrata. Genetics 158: 387–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schierup, M. H., J. S. Bechsgaard, L. H. Nielsen and F. B. Christiansen, 2006. Selection at work in self-incompatible Arabidopsis lyrata: mating patterns in a natural population. Genetics 172: 477–484. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stevens, J. P., and Q. O. N. Kay, 1989. The number, dominance relationships and frequencies of self-incompatibility alleles in a natural population of Sinapis arvensis L. in South Wales. Heredity 62: 199–205. [Google Scholar]
Thompson, K. F., and J. P. Taylor, 1966. Non-linear dominance relationships between S alleles. Heredity 21: 345–362. [Google Scholar]
Uyenoyama, M. K., 1997. Genealogical structure among alleles regulating self-incompatibility in natural populations of flowering plants. Genetics 147: 1389–1400. [DOI] [PMC free article] [PubMed] [Google Scholar]
Uyenoyama, M. K., 2000. Evolutionary dynamics of self-incompatibility alleles in Brassica. Genetics 156: 351–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
Vekemans, X., M. H. Schierup and F. B. Christiansen, 1998. Mate availability and fecundity selection in multi-allelic self-incompatibility systems in plants. Evolution 52: 19–29. [DOI] [PubMed] [Google Scholar]
Wolfram Research, 2004. Mathematica, Version 5.1. Wolfram Research, Champaign, IL.
Wright, S., 1939. The distribution of self-sterility alleles in populations. Genetics 24: 538–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
Young, A. G., J. H. Hill, B. G. Murray and R. Peakall, 2002. Breeding system, genetic diversity and clonal structure in the sub-alpine forb Rutidosis leiolepis F. Muell. (Asteraceae). Biol. Conserv. 106: 71–78. [Google Scholar]

[bib1] Bateman, A. J., 1952. Self-incompatibility systems in angiosperms. 1. Theory. Heredity 6: 285–310. [Google Scholar]

[bib2] Bechsgaard, J., T. Bataillon and M. H. Schierup, 2004. Uneven segregation of sporophytic self-incompatibility alleles in Arabidopsis lyrata. J. Evol. Biol. 17: 554–561. [DOI] [PubMed] [Google Scholar]

[bib3] Charlesworth, D., 1988. Evolution of homomorphic sporophytic self-incompatibility. Heredity 60: 445–453. [Google Scholar]

[bib4] Chookajorn, T., A. Kachroo, A. G. Clark and J. B. Nasrallah, 2004. Specificity determinants and diversification of the Brassica self-incompatibility pollen ligand. Proc. Natl. Acad. Sci. USA 101: 911–917. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib5] Cope, F. W., 1962. The effects of incompatibility and compatibility on genotype proportions in populations of Theobroma cacao L. Heredity 17: 183–195. [Google Scholar]

[bib6] DeMauro, M. M., 1993. Relationship of breeding system to rarity in the lakeside daisy (Hymenoxys acaulis var. glabra). Conserv. Biol. 7: 542–550. [Google Scholar]

[bib7] Glémin, S., T. Gaude, M. L. Guillemin, M. Lourmas, I. Olivieri et al., 2005. Balancing selection in the wild: testing population genetics theory of self-incompatibility in the rare species Brassica insularis. Genetics 171: 279–289. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib8] Good-Avila, S. V., and A. G. Stephenson, 2002. The inheritance of modifiers conferring self-fertility in the partially self-incompatible perennial, Campanula rapunculoides L.(Campanulaceae). Evolution 56: 263–272. [DOI] [PubMed] [Google Scholar]

[bib9] Imrie, B. C., C. J. Kirkman and D. R. Ross, 1972. Computer simulation of a sporophytic self-incompatibility breeding system. Aust. J. Biol. Sci. 25: 343–349. [Google Scholar]

[bib10] Kowyama, Y., H. Takahasi, K. Muraoka, T. Tani, K. Hara et al., 1994. Number, frequency and dominance relationships of S-alleles in diploid Ipomoea trifida. Heredity 73: 275–283. [Google Scholar]

[bib11] Larson, B. M. H., and S. C. H. Barrett, 2000. A comparative analysis of pollen limitation in flowering plants. Biol. J. Linn. Soc. 69: 503–520. [Google Scholar]

[bib12] Mable, B. K., M. H. Schierup and D. Charlesworth, 2003. Estimating the number, frequency, and dominance of S-alleles in a natural population of Arabidopsis lyrata (Brassicaceae) with sporophytic control of self-incompatibility. Heredity 90: 422–431. [DOI] [PubMed] [Google Scholar]

[bib13] Mable, B. K., A. V. Robertson, S. Dart, C. D. Berardo and L. Witham, 2005. Breakdown of self-incompatibility in the perennial Arabidopsis lyrata (Brassicaceae) and its genetic consequences. Evolution 59: 1437–1448. [PubMed] [Google Scholar]

[bib14] Mehlenbacher, S. A., 1997. Revised dominance hierarchy for S-alleles in Corylus avellana L. Theor. Appl. Genet. 94: 360–366. [Google Scholar]

[bib15] Nou, I. S., M. Watanabe, A. Isogai, H. Shiozawa, A. Suzuki et al., 1991. Variation of S-alleles and S-glycoproteins in a naturalized population of self-incompatible Brassica campestris. Jpn. J. Genet. 66: 227–239. [Google Scholar]

[bib16] Prigoda, N. L., A. Nassuth and B. K. Mable, 2005. Phenotypic and genotypic expression of self-incompatibility haplotypes in Arabidopsis lyrata suggests unique origin of alleles in different dominance classes. Mol. Biol. Evol. 22: 1609–1620. [DOI] [PubMed] [Google Scholar]

[bib17] Reinartz, J. A., and D. H. Les, 1994. Bottle-neck induced dissolution of self-incompatibility and breeding system consequences in Aster furcatus (Asteraceae). Am. J. Bot. 81: 446–455. [Google Scholar]

[bib18] Richman, A., 2000. Evolution of balanced genetic polymorphism. Mol. Ecol. 9: 1953–1963. [DOI] [PubMed] [Google Scholar]

[bib19] Sampson, D. R., 1967. Frequency and distribution of self-incompatibility alleles in Raphanus raphanistrum. Genetics 56: 241–251. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib20] Sampson, D. R., 1974. Equilibrium frequencies of sporophytic self-incompatibility alleles. Can. J. Genet. Cytol. 16: 611–618. [Google Scholar]

[bib21] Schierup, M. H., 1998. The number of self-incompatibility alleles in a finite, subdivided population. Genetics 149: 1153–1162. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib22] Schierup, M. H., X. Vekemans and F. B. Christiansen, 1997. Evolutionary dynamics of sporophytic self-incompatibility alleles in plants. Genetics 147: 835–846. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib23] Schierup, M. H., B. K. Mable, P. Awadalla and D. Charlesworth, 2001. Identification and characterization of a polymorphic receptor kinase gene linked to the self-incompatibility locus of Arabidopsis lyrata. Genetics 158: 387–399. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib24] Schierup, M. H., J. S. Bechsgaard, L. H. Nielsen and F. B. Christiansen, 2006. Selection at work in self-incompatible Arabidopsis lyrata: mating patterns in a natural population. Genetics 172: 477–484. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib25] Stevens, J. P., and Q. O. N. Kay, 1989. The number, dominance relationships and frequencies of self-incompatibility alleles in a natural population of Sinapis arvensis L. in South Wales. Heredity 62: 199–205. [Google Scholar]

[bib26] Thompson, K. F., and J. P. Taylor, 1966. Non-linear dominance relationships between S alleles. Heredity 21: 345–362. [Google Scholar]

[bib27] Uyenoyama, M. K., 1997. Genealogical structure among alleles regulating self-incompatibility in natural populations of flowering plants. Genetics 147: 1389–1400. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib28] Uyenoyama, M. K., 2000. Evolutionary dynamics of self-incompatibility alleles in Brassica. Genetics 156: 351–359. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib29] Vekemans, X., M. H. Schierup and F. B. Christiansen, 1998. Mate availability and fecundity selection in multi-allelic self-incompatibility systems in plants. Evolution 52: 19–29. [DOI] [PubMed] [Google Scholar]

[bib30] Wolfram Research, 2004. Mathematica, Version 5.1. Wolfram Research, Champaign, IL.

[bib31] Wright, S., 1939. The distribution of self-sterility alleles in populations. Genetics 24: 538–552. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib32] Young, A. G., J. H. Hill, B. G. Murray and R. Peakall, 2002. Breeding system, genetic diversity and clonal structure in the sub-alpine forb Rutidosis leiolepis F. Muell. (Asteraceae). Biol. Conserv. 106: 71–78. [Google Scholar]

PERMALINK

A General Model to Explore Complex Dominance Patterns in Plant Sporophytic Self-Incompatibility Systems

Sylvain Billiard

Vincent Castric

Xavier Vekemans

Abstract

TABLE 1.

MODEL AND METHODS

Dominance relationships:

From genotypes to phenotypes:

Cross compatibilities:

Genotypic frequency change:

Simple cases:

Deterministic equilibrium frequencies:

Allele number in the most recessive class:

Selection strength:

Stochastic simulations:

DETERMINISTIC DYNAMICS AND EQUILIBRIUM

Model verification:

Deterministic dynamics:

Figure 1.—

The recessive effect:

Figure 2.—

TABLE 2.

TABLE 3.

Homozygote frequencies:

ALLELE NUMBER BY DOMINANCE CLASS

Allele number in the most recessive class:

Number of alleles maintained in finite populations:

Figure 3.—

TABLE 4.

Selection strength:

Figure 4.—

APPLICATIONS

Comparison between expected and observed frequencies in natural populations:

TABLE 5.

TABLE 6.

Example 1—S. arvensis:

APPENDIX A.

Example 2—I. trifida:

APPENDIX B.

DISCUSSION

Generality of the model:

Generality of the recessive effect:

How many alleles per dominance class in finite populations?

How many dominance classes in finite populations?

Measure of selection strength:

Frequency-dependent selection models and pollen limitation:

Causes of the deviation between expected and observed frequencies in natural populations:

CONCLUSIONS

Acknowledgments

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases