An extension of the steepest descent method for Riemann-Hilbert problems: The small dispersion limit of the Korteweg-de Vries (KdV) equation

Abstract

This paper extends the steepest descent method for Riemann-Hilbert problems introduced by Deift and Zhou in a critical new way. We present, in particular, an algorithm, to obtain the support of the Riemann-Hilbert problem for leading asymptotics. Applying this extended method to small dispersion KdV (Korteweg-de Vries) equation, we (i) recover the variational formulation of P. D. Lax and C. D. Levermore [(1979) Proc. Natl. Acad. Sci. USA 76, 3602–3606] for the weak limit of the solution, (ii) derive, without using an ansatz, the hyperelliptic asymptotic solution of S. Venakides that describes the oscillations; and (iii) are now able to compute the phase shifts, integrating the modulation equations exactly. The procedure of this paper is a version of fully nonlinear geometrical optics for integrable systems. With some additional analysis the theory can provide rigorous error estimates between the solution and its computed asymptotic expression.

Introduction

The Korteweg-de Vries (KdV) equation

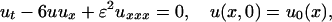1

was solved by Gardner, Greene, Kruskal, and Miura (1) who discovered its close connection with the Schrödinger equation,

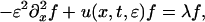and introduced the inverse scattering transformation as a fundamental tool of applied mathematics and physics.

The initial value problem for KdV with small dispersion ɛ↘0, was first analyzed by Lax and Levermore (2, 3) for initial data consisting of a single potential well u₀(x) < 0, and then by Venakides (4) for initial data consisting of a single “hump” u₀(x) > 0. The dispersion coefficient tending to zero (ɛ↘0), corresponds to considering the Schrödinger operator in its semiclassical limit, a regime that allows explicit scattering calculations by the WKB method. In both studies, the inverse scattering transformation procedure led, at each (x,t), to a variational problem over spectral density functions of the eigenvalue parameter λ. The variational problem was shown to possess a unique solution and the weak limit ū(x,t) of u(x,t,ɛ) as ɛ↘0 emerged as a simple linear functional of the maximizing function ψ.

The nonexistence of a strong limit beyond a break time t_crit was shown by the fact that, over wide space-time regions, the weak limit of u² did not equal ū², a fact that demonstrated the emergence of small-scale oscillations in these regions. The analysis of the variational problem by Lax and Levermore (2, 3) revealed the deep significance of the nature of the support of the maximizing function ψ. Under the assumption that the support of ψ is a finite set of intervals, Lax and Levermore derived a formula for the weak limit in terms of the endpoints of these intervals. The number 2N + 1 of the end points (N = 0, 1, 2, … ), and the end points themselves, were dependent on (x,t). At t = 0, it was seen that N = 0 and the unique end point for any given value of x was easily derived from the initial data u₀(x). In space-time regions of constant N, Lax and Levermore showed that the end points were the solution of a nonlinear hyperbolic system in Riemann invariant form. The system turned out to be identical to the modulation equations satisfied by the evolving spectral end points that describe modulated multiphase KdV waves. The latter had been derived earlier by Whitham (5) for single-phase traveling waves and concurrently with the Lax–Levermore calculation by Flaschka, Forest, and McLaughlin (6) (N > 1) for multiphase waves. Thus, Lax–Levermore theory produced overwhelming evidence that the small-scale oscillations in the initial value problem for Eq. 1 consisted of multiphase KdV waves, and that the Lax–Levermore end points should be identified with the spectral endpoints of quasi-periodic N-phase KdV waves. We will refer to the end points as branch points, because in both theories they are the branch points of an algebraic curve. The precise identification between the branch points of the two theories was not made, and a direct derivation of the small-scale oscillations was still lacking.

The open question could be phrased as follows: Derive the leading order asymptotic behavior for the solution u(x,t,ɛ) after break-time, that is after the time at which oscillations emerge. The task would require resolving the small-scale wave structure, i.e., identifying the local wave as a KdV single-phase or multiphase wave and calculating the small-scale wave parameters, i.e., the mean value (weak limit), the wave numbers, the frequencies, and the phase shifts. The local mean value was calculated in Lax–Levermore theory. The wave numbers and frequencies also would follow if the above identification of two types of branch points were made. Even then however, the phase-shifts (i.e., the order one term in the phase function of the oscillatory structure) lay well beyond any existing theory.

A further step toward the above identification was made by Venakides (4) in two ways, first by using Abel sums (7, 8), and later by a sharpening of the derivation of the variational problem in ref. 9. This sharpening led to the introduction of an additional “quantum condition” or quantum constraint on the variational problem. As a consequence, the unique maximizer of the variational problem was replaced by a sequence of nearby maximizers that carried the information not only of the solution average, but also of the structure of the oscillations (9). As a result, a version of Eq. 12 below was derived in ref. 9 that describes the leading asymptotic behavior of the solution u(x,t,ɛ) as ɛ↘0. The derivation (9) relied on an averaging Ansatz and, as stated in that study, there was some uncertainty in the resolution of the phase shifts. During this time the theory for the periodic small dispersion KdV equation (10) also was developed.

Our approach in this paper follows the Shabat (11) (see also ref. 12) reformulation of the inverse scattering transformation as a Riemann–Hilbert problem (RHP). It is motivated by the steepest descent method for oscillatory RHPs introduced by Deift and Zhou (13) and developed further, in particular, in refs. 14 and 15. For simplicity, we consider only the case u₀(x) > 0. The case u₀(x) < 0, as well as the case when u₀ changes sign, also can be handled with slight modifications of the same method (see Remark below). A more detailed version of the results of this paper is given in ref. 16. The extension of the nonlinear steepest descent method of Deift and Zhou consists of introducing a rigorous fully nonlinear version of geometrical optics in the following way.

As in refs. 15 and 16, we introduce in the Shabat vector RHP, which describes inverse scattering, the phase function g (see section 1) as the nonlinear analogue of the phase function in the geometrical optics representation of a linear wave. The form of the function g cannot be easily guessed in this case; we introduce a systematic procedure for determining g, which reduces its calculation to a scalar RHP. The solution of the scalar RHP corresponds to the solution of the eikonal equation and the leading transport equation in linear wave theory (amplitude is coupled to the other wave parameters) with g yielding the local number of phases, wave numbers, frequencies, and the weak limit. Pursuing the analogy to the linear theory, we call the scalar RHP, the eikonal RHP. Once g is determined, we solve the remaining vector RHP explicitly in terms of theta functions.

We present three main results for small dispersion KdV.

First, the leading asymptotic behavior of u(x,t,ɛ), including the phase shifts, is obtained in terms of the modulating branch points described above. The identification between the branch points of refs. 2 and 3 on the one hand, and refs. 5 and 6 on the other, is made precise (there is no use of an Ansatz). Our Eq. 12 indicates that the corresponding formula of ref. 9 has the correct phase shifts to order ɛ. Our method actually allows one to write down higher order correction terms in the asymptotic expansion of u(x,t,ɛ), but this work has not yet been carried out.

Our second result relates to the determination of the branch points. In the Lax–Levermore theory, the calculation of the branch points is reduced to solving the initial value problem for the modulation system. This goal motivated a large body of research both in the former Soviet Union and in the West in the eighties and nineties. Leaving aside the discussion of the work of many authors (see ref. 16) we mention the fact that the KdV modulation equations are themselves integrable, as was first shown by Tsarev (17), and that the local existence of the solution of the modulation system beyond break-time was established constructively for N = 1 by Tian (18). In the present work, we write down explicit first integrals for the solution of the modulation equations, for arbitrary N. If N is known, and (x,t) is fixed, our Eqs. 7 and 8 provide a complete algebraic system of 2N + 1 equations for the 2N + 1 unknown branch points. To find the branch points at some given (x,t), we have to solve this nonlinear algebraic system starting with the value N = 0, and proceeding to N = 1, … until the corresponding function g (see section 1) satisfies conditions (Eqs. 4 a–d) below. The function g corresponds (see below) to the Lax–Levermore–Venakides maximizer. For illustrative purposes (see ref. 16), we have carried out this construction globally in (x,t) when the graph of u₀ has the shape of a tent, u₀(x)= 1 −  x  for  x  < 1, and u₀(x) = 0 otherwise. We remark that we derive Eqs. 7 and 8 for the branch points directly from the RHP and without resorting to the modulation equations. We can derive the modulation equations from the compatibility condition g_xt = g_tx exactly as in Lax–Levermore theory, but they do not play such a prominent role in our calculation.

Our third result consists of establishing a connection between our steepest descent approach and the variational approach of Lax and Levermore.

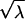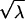We assume a positive, and hence soliton-free, u₀(x) that is analytic and consists of a “hump” of unit height, restrictions that are convenient but not essential to our method. This is the problem considered in ref. 4. After changing from the -plane to the λ-plane, taking the right half -plane onto C/(−∞,0], the Shabat RHP consists of finding a row-vector-valued function m(λ) = m(λ;x,t,ɛ) = (m₁,m₂), analytic for complex λ off the real axis, with boundary values m_± (λ;x,t,ɛ) ≡ m(λ ± i0;x,t,ɛ) ∈ (1,1) + L²(|dλ^1/2|) that satisfy the jump condition

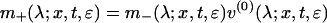on the real axis. The jump matrix v⁽⁰⁾(λ;ɛ) is given by

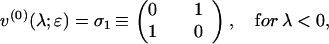(σ₁ reflects the to − symmetry of the RHP in the 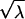-plane), while

Here r(λ;ɛ), λ > 0, is the reflection coefficient for the Schrödinger equation (Eq. 2) at t = 0 and α = 4tλ^3/2 + xλ^1/2. The space and time variables are simply parameters in the solution process. The solution to Eq. 1 is given by

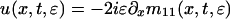where

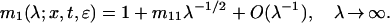We identify r with its WKB approximation (cf e.g., ref. 19)

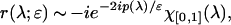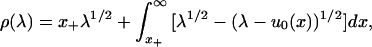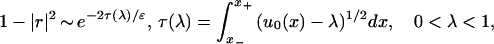the quantities x₋(λ) < x₊(λ) being defined by u₀(x_± (λ)) = λ. Here χ_[0,1] is characteristic function of the interval [0,1]. The jump matrix reduces to the identity for λ > 1 and our problem reduces to a RHP on the interval (−∞,1]. Further reductions of the RHP m₊⁽ⁿ⁾ = m₋⁽ⁿ⁾v⁽ⁿ⁾, where m₊⁽ⁿ⁾ and m₋⁽ⁿ⁾ are the left and right boundary values of m⁽ⁿ⁾ on the oriented contour Σ⁽ⁿ⁾ with jump matrix v⁽ⁿ⁾, will not affect the jump matrix outside 0 < λ < 1.

1. The Eikonal Problem and the Differentiated Eikonal RHP

We introduce the complex phase function,

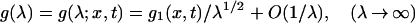to be determined below, by making the change of dependent variable

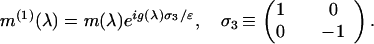The function g is required to be analytic in λ off the set (−∞,1] and satisfy g₊(λ) + g₋(λ) = 0 for λ ∈ (−∞,0), to maintain the jump σ₁ for m⁽¹⁾ across (-∞,0). The formula for u becomes

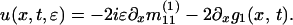2

where m_i⁽¹⁾(λ) = 1 + m₁₁⁽¹⁾/λ^1/2 + O(1/λ); in the region 0 < λ < 1, the RHP transforms to

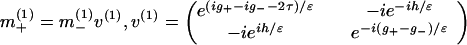3

where h = g₊ + g₋ − 2ρ + 2α.

Our strategy is to determine g in such a way that for each value of 0 < λ < 1, as ɛ↘0, the jump matrix v⁽¹⁾ reduces to one of the following three forms with exponentially small errors,

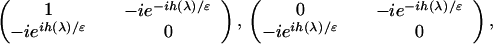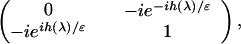where h′ < 0 in the first form, h′ = 0 in the second form, and h′ > 0 in the third form. As can be seen in the more detailed presentation (16), according to the steepest descent method, the first and third forms can be replaced by the identity matrix through the use of an intermediate RHP (m⁽²⁾,v⁽²⁾, Σ⁽²⁾). This reduces the RHP for m⁽¹⁾ to one with a piecewise constant jump matrix (h′ = 0) of the second form, which is exactly solvable. To implement this strategy we require that, at each 0 < λ < 1, exactly one of the conditions (Eqs. 4 a–c) be satisfied, and that condition (Eq. 4d) below be satisfied as required earlier.

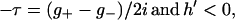4a

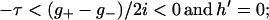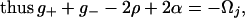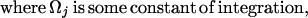4b

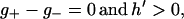4c

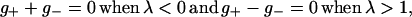4d

In the remaining RHP (m⁽³⁾, v⁽³⁾, Σ⁽³⁾) the contour Σ⁽³⁾ consists of the union of (-∞,0] with the set of λs where Eq. 4b holds. We pose the ansatz that the latter consists of disjoint intervals I_j = (α_j,β_j),j = 0, … , N < ∞, ordered from left to right and lying in the open interval (0,1), with α₀ = 0. For λ in I_j, the jump matrix v⁽³⁾(λ) = −iσ₁e^{−Ω_j/ɛσ₃} where Ω_j = −h(λ). The equalities in Eqs. 4 a–d define a scalar RHP for the function g. This is the eikonal problem.

Differentiating with respect to λ, we obtain a RHP for g′ namely

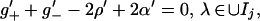4e

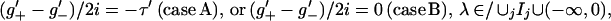4f

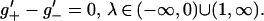4g

This is the differentiated eikonal problem. To have a well-posed RHP for g′, we require additionally that

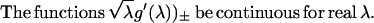5

2. Calculation of the Branch Points α_j and β_j

The solution to the differentiated eikonal RHP is given in terms of the initial data of Eq. 1 by

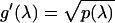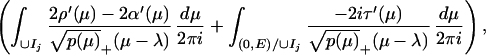6

where E = 1 in case A and E = β_N in case B,

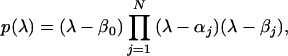with 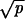determined to be positive for λ > β_N, and ₊ = .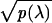

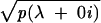We obtain 2N + 1 equations to determine the 2N + 1 unknown branch points β₀,α_j,β_j,j = 1,… N as follows. The condition g(λ) = O(λ⁻½) for large λ implies g′/ 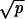= O(λ^−N−1), and leads to the N + 1 moment equations, for k = 0, … , N,

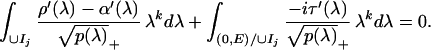7

An additional set of N equations is obtained by integrating g′ around each I_j and by using Eqs. 4a and 4c. In case A we obtain for j = 1, … N,

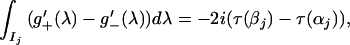8

while in case B, τ(β_N) must be replaced by zero. To calculate the branch points at some (x,t), we solve the above equations for N = 0. If g, as determined from g′ by integration, satisfies the conditions (Eqs. 4 a–c), it is the desired solution of the scalar RHP. If not, we increase the value of N by one and repeat the calculation. We expect that the procedure always terminates with a finite N for generic initial data. For a more systematic determination of N = N(x,t), we construct for each t the separatrix F(t)=[(x,λ): λ = β₀(x,t), α₁(x,t),… ,β_N(x,t), −∞ < x < ∞,] (see Fig. 1a and b).

If a vertical line is drawn at some x, its intersection with the points in the plane on the one side of the curve (the “lower” one) gives the contour Σ⁽³⁾. For example, if x > x₁ in Fig. 1b, then Σ⁽³⁾ consists of a single interval (−∞,β₀(x)): on the other hand, for x₂ < x < x₁, Σ⁽³⁾ consists of two intervals, (−∞,β (x))∪(α,(x),β(x)), etc.

For times t less than the critical value t_crit at which Eq. 1 with ɛ = 0 breaks down, we take N = N(x,t) = 0. Solving Eq. 7 for β₀, we find that F(t)=[(x,λ):λ = u(x,t)], where u(x,t) is the solution of Eq. 1 with ɛ = 0, and we verify that the corresponding function g satisfies Eqs. 4 a–c. For x > x_max(t), we are in case B and for x < x_max(t), we are in case A. For fixed t > t_crit, we construct the separatrix of Fig. 1b starting with x ≫ 1 and N(x,t) = 0. We then move x to the left, calculating the parameters α_j,β_j, and readjusting the value of N as soon as one of the inequalities (Eqs. 4 a–c) is violated. In Fig. 1b, interval I₀ splits into two intervals at x₁ and x₂, whereas interval I₁ collapses to a point and disappears at x₃ and x₄. As noted earlier, we have carried out (see ref. 16) this procedure explicitly in the case of the nontrivial example u(x,0)= 1 −  |x| , when  |x|  < 1 and u(x,0) = 0 otherwise.

3. Calculation of the Ω_j

We obtain a formula for g by solving the eikonal RHP,

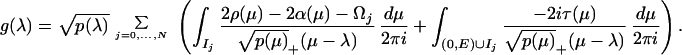The original RHP for m has a 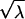symmetry, and we require that g be an odd function of 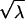to retain the symmetry for m⁽¹⁾; this leads to the condition Ω₀ = 0. We determine the remaining Ω_js from the N moment conditions that g/ 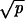= O(λ^−N) must satisfy at λ = ∞. We find for j > 0, Ω_j = xΩ_j1 + tΩ_j2 + Ω_j3, where

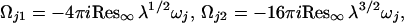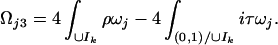9a

In these formulae, ω_i = p_i(λ)/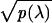 dλ, i = 1, … , N, and p_i(λ) are polynomials of degree ≤N − 1 uniquely determined from the N relations ∫_aj ω_i = δ_ij (contour a_j circles around interval I_j clockwise). Solving the RHP for ∂_xg we obtain

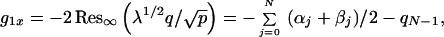where the meromorphic differential (q/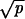)dλ = (λ^N + q_N−1λ^N−1 + … +q₀)/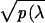dλ, has N coefficients q₀, … q_N−1 uniquely determined by the N relations ∫_a>j(q/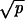)dλ = 0,j = 1, … , N.

From the RHP for ∂_xg and ∂_tg, we obtain the relations

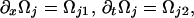9b

that are not at all obvious because Ω₍₁₎, Ω₍₂₎, and Ω₍₃₎ all depend on x and t through ω_j.

4. Calculation of u(x,t,ɛ)

We verify (also see refs. 2 and 15) that the solution to the RHP for m⁽³⁾ is

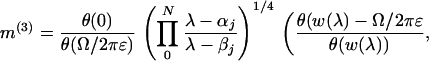10

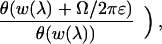where the Riemann theta function θ has period matrix (∫_bjΩ_i) (contour b_j proceeds from β₀ to α_j on the upper half of the lower sheet of the Riemann surface and returns to β₀ on the lower half of the upper sheet), w(λ) = ∫_∞^λ ω, ω = (ω₁, … , ω_N)^t, and Ω = (Ω₁, … , Ω_N)^t. We obtain finally, as ɛ → 0,

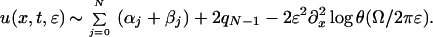11

In a space-time window of scale ɛ about (x,t), we have

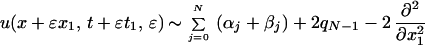12

By using Eqs. 9 a and b, we see that Eq. 12 has precisely the form of a modulated KdV wave (see e.g., ref. 6).

5. A Variational Principle for g′(λ)

We make the change of variable λ = 1 − η², taking the upper complex half-plane onto C/(−∞, 1]. The function g transforms to G(η) = g(λ). We extend the definition of G onto the lower complex η half-plane, by the relation G(−η) = − G(η), and we observe that G is analytic off the real η axis. We transform the RHP for g into a problem for G, observing that G₊ − G₋ = g₊ + g₋ and G₊ + G₋ = −(g₊ − g₋)sgnη. On the real axis, we define the function ψ (η) to equal zero outside the interval (−1,1) while on (−1,1)

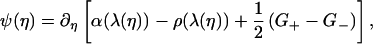13

and one verifies that

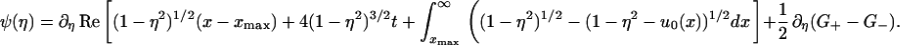14

After a nontrivial calculation, conditions (Eqs. 4 a–c) transform to the variational conditions of ref. 4 (a misprint in equation 1.33, line i of this reference in which a factor η is missing from the second term in the expression for a(η) is corrected below). This allows us to use the variational formulation of Lax–Levermore–Venakides for the derivation of ψ, and hence of g. Indeed, the function ψ(η), restricted to the interval [0,1] is the unique maximizer of the functional Q(ψ) = (2a,ψ) − (2γ,ψ₊) + (Lψ,ψ) where

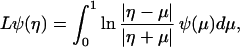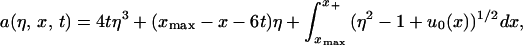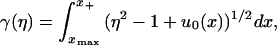ψ₊(η) is the positive part of the function ψ. The benefit of the variational formulation is that, because of the convexity of the maximization problem, the uniqueness of ψ, and hence of G and g, are guaranteed.

Remark.

The RH steepest descent method also can be used to analyze potential wells u₀(x) < 0: here the critical behavior of the RHP takes place on the interval [min_xu₀(x),0], rather than the interval [0,1 = max_xu₀(x)] as in the case of a “bump.” If u₀ consists of a “bump” separated from a well, then the critical region for the RHP is the interval [min_xu₀(x),max_xu₀(x)].

ABBREVIATIONS

KdV

Korteweg-de Vries

RHP

Riemann–Hilbert problem