Abstract
Evidence for a two-metal ion mechanism for cleavage of the HH16 hammerhead ribozyme is provided by monitoring the rate of cleavage of the RNA substrate as a function of La3+ concentration in the presence of a constant concentration of Mg2+. We show that a bell-shaped curve of cleavage activation is obtained as La3+ is added in micromolar concentrations in the presence of 8 mM Mg2+, with a maximal rate of cleavage being attained in the presence of 3 μM La3+. These results show that two-metal ion binding sites on the ribozyme regulate the rate of the cleavage reaction and, on the basis of earlier estimates of the Kd values for Mg2+ of 3.5 mM and >50 mM, that these sites bind La3+ with estimated Kd values of 0.9 and >37.5 μM, respectively. Furthermore, given the very different effects of these metal ions at the two binding sites, with displacement of Mg2+ by La3+ at the stronger (relative to Mg2+) binding site activating catalysis and displacement of Mg2+ by La3+ at the weaker (relative to Mg2+) (relative to Mg2+) binding site inhibiting catalysis, we show that the metal ions at these two sites play very different roles. We argue that the metal ion at binding site 1 coordinates the attacking 2′-oxygen species in the reaction and lowers the pKa of the attached proton, thereby increasing the concentration of the attacking alkoxide nucleophile in an equilibrium process. In contrast, the role of the metal ion at binding site 2 is to catalyze the reaction by absorbing the negative charge that accumulates at the leaving 5′-oxygen in the transition state. We suggest structural reasons why the Mg2+–La3+ ion combination is particularly suited to demonstrating these different roles of the two-metal ions in the ribozyme cleavage reaction.
Keywords: ribozyme function, metal ion activation, RNA cleavage, magnesium ion, lanthanum ion
Ribozymes are rightly classified as metalloenzymes because metal ions in the reaction mixture are obligatory for catalytic activity (1–5). However, the precise role of metal ion cofactors in these systems is not fully understood. The currently debated models describing the involvement of metal ions in ribozyme-mediated cleavage are generally divided into one-metal ion and two-metal ion classes. In a popular single metal ion model a solvated metal hydroxide coordinates to the pro-R oxygen of the phosphate at the cleavage site (6–8). This metal hydroxide is favorably positioned to act as a base to abstract the proton from the 2′-OH in the first step of the cleavage reaction. The resulting 2′-alkoxide then acts as a nucleophile, attacking the electropositive phosphorus by an intramolecular reaction and displacing the 5′-oxygen of the leaving nucleotide. The general two-metal ion model (3) is functionally much the same as the single metal ion model, except that a second metal ion is invoked that coordinates to the 5′-oxygen of the leaving nucleotide to dissipate the accumulating negative charge on this atom in the transition state of the rate-determining step. Similar two-metal ion models have been proposed for a variety of other enzymatic phosphoryl transfer reactions (3, 9–11). In a previous publication, we critically examined the literature on this subject and concluded that all of the available data were at least consistent with a two-metal model (12). Other relevant reviews of metalloenzymes and ribozymes are also available (5, 13–18).
An experimental design that can definitively distinguish between these two general classes of models has been elusive for a variety of reasons. By using a DNA–RNA hybrid hammerhead ribozyme, Hendry and McCall (19) observed a biphasic relationship between the observed rate constant for RNA cleavage and the concentration of Mg2+ ion, which they interpreted as evidence for a strong metal ion binding site and a weak metal ion binding site in a two-metal ion model. We also observed this biphasic behavior as a function of Mg2+ concentration for the fully RNA HH16 hammerhead ribozyme shown in Fig. 1 (12) and estimated apparent dissociation constants for the binding of Mg2+ to these sites at 3.5 mM and >50 mM, respectively (B.W.P., unpublished data). Measuring the binding constant of Mg2+ to the putative weaker site in such experiments, in particular, requires studies at very high divalent salt concentrations. As a consequence it is difficult to differentiate between general polyelectrolyte effects on the structure of the RNA complex and specific binding at the defined site(s) as the Mg2+ concentration is increased in this range.
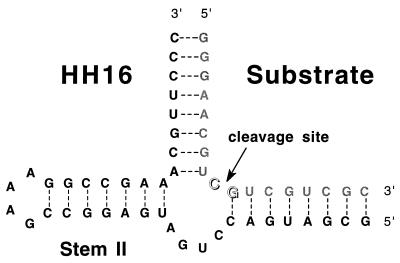
Figure 1.
HH16 hammerhead ribozyme–substrate complex. The base pairing within the ribozyme complex is shown as observed in the crystal structure of the hammerhead ribozyme (7, 8, 20–22).
At these high Mg2+ concentrations, the reaction also proceeds so fast that it is difficult to follow manually under single-turnover reaction conditions. Single-turnover reaction conditions are preferred because (e.g.) a rate-limiting product dissociation reaction could obscure the metal ion concentration dependence of the cleavage reaction in multiturnover measurements. An additional implication is that the extremely weak binding site might only exist in a high-energy conformation near the transition state. Such a metal ion binding site would only be transiently present along the reaction pathway, and nonkinetic detection methods, including x-ray crystallography, would fail to observe its presence.
In this study, we present the results of an experiment that effectively circumvents these problems. Cleavage of the HH16 hammerhead ribozyme (Fig. 1) was carried out in the presence of a constant concentration of Mg2+ ion, with La3+ as a competing metal ion species. kobs, the observed rate constant of the cleavage reaction, was measured as a function of La3+ concentration. In this fashion, bound Mg2+ ions were effectively titrated (displaced) by La3+ ions as the concentration of the latter cation was increased. Because a kinetic parameter was used to monitor the cleavage reaction, the resulting activity titration as a function of total La3+ ion concentration defines the relative concentrations of the metal ion species in the transition state of the rate-determining step.
MATERIALS AND METHODS
The RNA substrate oligomer for the hammerhead ribozyme cleavage reaction was purchased from Midland Certified Reagent (Midland, TX) and purified electrophoretically on a 20% polyacrylamide gel. The hammerhead ribozyme itself was transcribed from a synthetic DNA template by using a published procedure (23). All metal chlorides were obtained as reagent grade salts of >99.9% purity from Aldrich and were not further purified. The final HH16 hammerhead ribozyme–substrate complex used in this study is shown in Fig. 1.
Cleavage reactions were carried out at 37°C in 20 mM Hepes (pH 7.0) under single-turnover conditions, in 50-μl reaction volumes containing a 40 nM concentration of radioactively 5′-end-labeled RNA substrate and an 80 nM concentration of unlabeled ribozyme. The reaction solutions contained 200 mM NaCl to provide an essentially constant ionic strength for the reaction and to neutralize nonspecific electrostatic effects. The ribozyme and substrate RNA oligomers were allowed to hybridize in the reaction solution for 5 min at 37°C, and then cleavage was initiated by adding stock solution mixtures of di- and trivalent metal ions to obtain the required final Mg2+ and La3+ concentrations. Each solution was sampled at designated time intervals by removing 5 μl of the reaction mixture and quenching with 10 μl of a 90% formamide solution containing 50 mM EDTA. The cleaved (and end-labeled) reaction products were separated from the remaining unreacted (and labeled) ribozyme complex on a 20% polyacrylamide denaturing gel and quantitated with a Molecular Dynamics Storm model 860 PhosphoImager. A typical reaction gel is shown in Fig. 2. The reaction rate data obtained were fit to a first-order reaction by using the kaleidograph graphing software program to obtain apparent rate constants for the ribozyme cleavage reaction as a function of the concentration of metal ion cofactor.
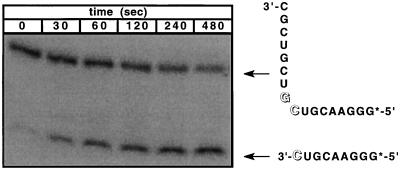
Figure 2.
Gel autoradiogram of the time course of a typical HH16-mediated cleavage reaction with a 5′ end-labeled RNA substrate. The gel bands corresponding to the complex and to the cleaved RNA are indicated at increasing reaction times. These experiments typically resulted in 80–90% cleavage of the substrate over the measured time course of the reaction.
RESULTS AND DISCUSSION
If a general two-metal model is assumed for the ribozyme-catalyzed cleavage process (see Fig. 5), a close examination of the likely mechanism suggests that the two-metal ions involved must play very different roles in the reaction (12). The metal ion that binds at or near the 2′-OH (metal binding site 1 in Fig. 5) should function primarily to change the pKa for the deprotonation of this hydroxyl group. Whether this results from the coordination of the metal ion to the 2′-oxygen itself, leading to a lower pKa for this entity (24), or from the binding of a metal hydroxide species coordinated to the pro-R phosphoryl oxygen, functioning as a specific base to deprotonate the 2′-OH (6), is unclear. Both mechanisms would produce the observed correlation between the pKa values of the aqueous metal ions and the measured cleavage rate constants (12).
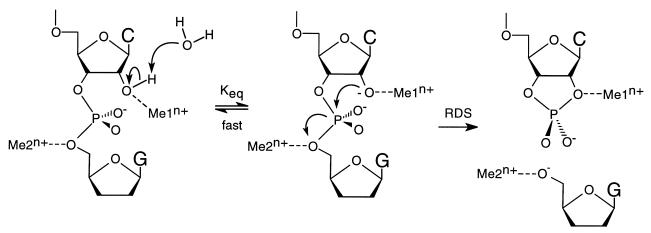
Figure 5.
Modified two-metal ion model for ribozyme cleavage. The metal ion in binding site 1 (Me1n+) coordinates directly to the 2′ oxygen, lowering the pKa of the 2′-OH proton. The 2′-OH proton is lost to the solvent in an equilibrium that is fast relative to the rate-determining cleavage step. The resulting 2′-alkoxide serves as the attacking nucleophile, displacing the 5′-oxygen of the leaving nucleotide (see arrows). The metal ion in binding site 2 (Me2n+) absorbs the developing charge on the leaving 5′-oxygen in the transition state of the rate-determining step. The nature of the metal ion coordination to the pro-R oxygen is not explicit in this model, although there is evidence for such an interaction. RDS, rate-determining step.
Metal ion binding at site 1 modulates the distribution between the protonated and deprotonated forms of the 2′-OH in a thermodynamic process that is fast relative to the rate-determining cleavage event, with binding of the metal ion at this position increasing the rate of cleavage by increasing the equilibrium population of the active (deprotonated) species. The putative second metal cation (which binds at site 2 in Fig. 5) in the two-metal ion model plays a true kinetic role, binding coordinately to the 5′-oxygen of the leaving nucleotide to absorb the negative charge that accumulates on this atom in the transition state of the cleavage reaction. The activation energy barrier for the cleavage reaction is thus lowered by this binding and the reaction is accelerated.
When the diverse roles that must be played by the metal cations in a two-metal ion reaction model are considered, it is highly unlikely that the same cationic species would function optimally at both of the postulated metal ion binding sites. Thus, some selectivity between the two sites would be expected for a reaction system in which two or more different metal ion species are available. We have exploited this putative selectivity difference by establishing a competition for the two putative metal ion binding sites between divalent and trivalent metal cations with very different physical properties.
Choice of Metal Ions.
Mg2+ is likely to be the cation used in ribozyme cleavage reactions in vivo and thus represents a natural choice as the representative divalent ion for this study. A fixed 8 mM concentration of MgCl2 was chosen for our reactions because this concentration falls well above the dissociation constant for Mg2+ for the tighter metal ion binding site and also provides a convenient range of reaction times for following cleavage under single-turnover conditions.
We chose La3+ as the competing cation for a number of reasons. First, the ionic radius of La3+ is roughly the same as that of Ca2+, which has been well characterized in the HH16 system (6, 25). In addition, the La3+ ion is well known as an inhibitor of biochemical processes requiring Ca2+, Mg2+, or other divalent metal ions (26). Finally, in contradistinction to other transition state metal ions that have been commonly used in biochemical reactions, La3+ has a roughly spherical orbital symmetry due to its completely filled outer d orbital, which obviates the need to consider issues related to orbital shape and directionality (27).
The fully hydrated La3+ ion has a pKa of 9.06, which is more than two pKa units lower than that of either Mg2+ (pKa = 11.41) or Ca2+ (pKa = 12.67) (28). The observed correlation between the pKa of the various divalent metal ions tested with the kobs of HH16 cleavage would predict a larger cleavage rate in the presence of La3+ ion than is observed with either of these divalent cations. However, if a metal ion were indeed directly coordinated to the 2′-oxygen, a La3+ in this position might be expected to result in a lower kobs for the reaction, compared with that seen with a divalent metal ion in this position, because the nucleophilicity of the 2′-alkoxide bound to a trivalent metal ion would be greatly reduced relative to that of the same alkoxide bound to a divalent cation.
In support of the first expectation listed above, La3+ has been shown to increase the rate of phosphodiester cleavage by 106 compared with Mg2+ ion in a nonenzymatic phosphodiester cleavage reaction (29). In that work a complexing moiety was engineered into the molecule to increase the coordination of metal ions at the leaving oxygen. These results suggested that a La3+ cation coordinated to the 5′-oxygen of the leaving nucleotide would likely increase kobs for ribozyme cleavage well above the rate seen with the divalent Mg2+ cation. We therefore chose La3+ as a “foil” for Mg2+ in this study because we expected that profound kinetic changes would result when this cation was substituted for Mg2+ in the cleavage reaction and that these effects would be quite different depending on which of the two putative metal ion binding sites was involved.
Titration by Increasing Concentrations of La3+ in the Presence of a Constant Concentration of Mg2+ Is Consistent with a Two-Metal Ion Model.
Fig. 3 shows the effect of increasing (micromolar) concentrations of LaCl3 in the presence of 8 mM MgCl2 on the apparent rate constant for the ribozyme cleavage reaction. The most striking feature of this titration curve is its bell-shaped character, with the midpoints of the two sides of the curve centered at total La3+ concentrations of ≈2 μM and ≈6 μM, respectively. The demonstration of this bell-shaped curve, and of the two titrations that it represents, provides in itself clear and convincing qualitative evidence for the two-metal ion model of ribozyme catalysis. Thus these observations alone show that two-metal ions are involved in controlled the apparent rate of the cleavage reaction and that these two ions must play very different roles in the reaction mechanism.
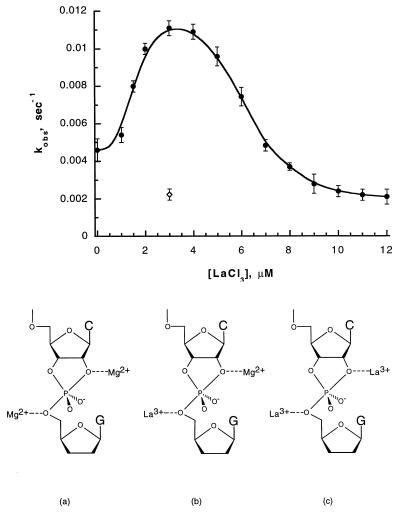
Figure 3.
Kinetic titration curve of kobs for the cleavage of the HH16 ribozyme with increasing concentrations of LaCl3 in a solution containing 8 mM MgCl2 (•). At low concentrations of LaCl3 both metal ion binding sites are occupied with Mg2+, as illustrated in structure a. At intermediate concentrations (1–8 μM LaCl3), the two sites are heterogeneously complexed with one La3+ ion and one Mg2+ ion (structure b). At high concentrations of LaCl3 both sites are occupied by La3+ (structure c). The combination of 3 μM LaCl3 and 8 mM MgCl2 in the reaction solution yields a higher value of kobs than is observed in the presence of either 3 μM LaCl3 alone (⋄) or 8 mM MgCl2 alone (• at [LaCl3] = 0 μM).
Because the biphasic titration of Fig. 3 must represent the replacement of one Mg2+ and then the other by La3+ (Fig. 3, see structures a–c), it is clear that the replacement of the former cation by the latter in the two binding sites produces opposite effects on kobs for the ribozyme-mediated cleavage reaction. With 3 μM LaCl3 and 8 mM MgCl2 present together in the solution (the conditions that apply at the peak of the titration curve), we see that the measured value of kobs is greater than that measured in the presence of either 3 μM LaCl3 or 8 mM MgCl2 alone. Thus in the absence of La3+ ions and at 8 mM MgCl2, Mg2+ ions are expected to fully occupy the tighter metal ion binding site and to partially occupy the weaker binding site (see estimates of Mg+2 dissociation constants given above). A measured value of kobs = 4.5 × 10−3⋅sec−1 corresponds to the cleavage rate constant for this concentration of MgCl2 alone.
As LaCl3 is added to a total concentration of about 3 μM, the first of the two-metal ion binding sites is saturated with La3+ and the measured value of kobs increases to a maximum of ≈11 × 10−3⋅sec−1. We speculate that the Mg2+ ion bound to the 5′-oxygen of the leaving nucleotide (see Fig. 5, binding site 2) is the one that is displaced in this initial titration. The metal ion in this position absorbs the developing charge in the transition state of the rate-determining step of this reaction, and the increased charge of a trivalent metal cation at this binding site would be expected to produce greater transition state stabilization than would a divalent cation.
A second titration is observed as the concentration of LaCl3 increases from 3 μM to 12 μM. The apparent value of kobs diminishes in this region of the La3+ titration curve, approaching a value of ≈2.2 × 10−3⋅sec−1 at LaCl3 concentrations above 12 μM. This value of kobs is also observed for the reaction performed in 3 μM LaCl3 alone (Fig. 3, ◊), confirming that both metal ion binding sites are fully occupied by La3+ ions under these conditions. The observation that La3+ occupation of the binding site near the 2′-oxygen lowers kobs is consistent with direct coordination of a metal ion to the 2′-oxygen, whereas the deprotonation of the 2′-OH by a metal hydroxide species would be expected to produce the opposite effect.
These Results Are Not Compatible with a Solvated Metal Hydroxide Cleavage Mechanism.
With a pKa value of 9.06 for a bound water in the fully hydrated La3+ ion, the low kobs for the cleavage reaction involving the La3+ ion in both positions is not compatible with the observed correlation between the pKa of a water bound to a metal ion and the kobs produced by different divalent metal ions. That correlation has been interpreted in the metal hydroxide model (Fig. 4) as an effect on the concentration of the aqueous metal hydroxide, which then serves as a Brønsted base in the abstraction of the proton from the 2′-oxygen. We have argued (12) that this logic is flawed, because the metal hydroxide complexes formed with metal ions with lower pKa values are weaker bases and, therefore, should be less able to abstract the 2′-OH proton, despite their greater concentration. This conclusion is supported by the data presented in Fig. 3 because the pKa of the 2′-OH is two or more pKa units higher than those of any of the aqueous metal ions studied, making the metal hydroxide poorly suited to the task of deprotonating the 2′-OH. It has been convincingly shown that proton transfer does not occur in the rate-determining step of the ribozyme cleavage reaction (30). The observed pH dependence and the correlation between the pKa values of the aqueous metal ions and kobs must, therefore, reflect the effects of the metal ions on the equilibrium concentration of the active species in solution, i.e., the 2′-alkoxide.
Figure 4.
Solvated metal hydroxide model. The concentration of metal hydroxide coordinated to the pro-R oxygen depends upon the pKa of a water molecule coordinated to the metal ion. Use of hydrated metal ions with lower pKa values would produce a larger Keq,1 but would also result in a smaller Keq,2. Because the active nucleophile in the rate limiting step is the 2′-alkoxide and not the metal hydroxide, the observed pKa correlation is not supported by a solvated metal hydroxide model.
Roles of the Two Metal Cations.
We have proposed that the metal ion in binding site 1 is directly coordinated to the 2′-oxygen. The metal ion would then directly effect the pKa of the 2′-OH and would result in the correlation that is experimentally observed. Although the equilibrium concentration of the resulting 2′-alkoxide would increase, this metal ion binding would also decrease the nucleophilicity of the 2′-alkoxide toward the electropositive phosphorus. However, because the nucleophilic attack does indeed take place in the rate-determining step, the sensitivity of the reaction rate to the strength of the nucleophile will be strongly dependent upon the position of the transition state.
Thus, if the transition state for the cleavage reaction occurs relatively early in the reaction process, kobs would not be overly sensitive to the reactivity of the nucleophile, requiring instead that the 2′-OH simply be deprotonated. This would need to be true at least throughout the series of divalent metal ions previously studied (6). Coordination of a trivalent metal at this position reduces the nucleophilicity of the resulting alkoxide much more dramatically than the differences that would be expected within a series of divalent ions. When the La3+ ion is used in place of Mg2+, a greater equilibrium concentration of the 2′-alkoxide is expected, whether or not direct coordination to the 2′-oxygen is assumed. However, direct coordination of the La3+ ion to the 2′-oxygen would result in the observed reduced rate of cleavage. This result cannot be reconciled with a metal hydroxide abstraction of the 2′-OH proton.
Estimation of the Binding Constants of La3+ to the Metal Ion Binding Sites of the Ribozyme.
This displacement titration method allows indirect estimation of dissociation constants for metal ions that are difficult to measure directly. As discussed earlier, the Kd for the weaker binding Mg2+ ion is experimentally difficult to observe, and we have only been successful at estimating it as >50 mM. The problem arises largely from the unusually high concentrations of MgCl2 that must be added to measure such a high dissociation constant. Because the concentration of La3+ bound to a metal ion binding site is equal to the concentration of Mg2+ bound to this same site at the half-equivalence point, it can be shown mathematically from the individual Kd expressions for these two ions that:
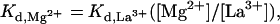 |
1 |
where [Mg2+] is the constant concentration of MgCl2 used in the experiment (8 mM) and [La3+] is the value of the LaCl3 concentration read from the abscissa on the graph of Fig. 3 at the inflection point for each of the two titrations. Eq. 1 is only exact, of course, when (i) the total concentrations of Mg2+ and La3+ in solution are much greater than the concentrations of these ions bound at the metal ion binding site and (ii) the two-metal ion binding sites titrate independently of one another. Assumption i is obviously approximately true in our experiments because the concentration of ribozyme complexes (and thus of metal ion binding sites) used is 40 nM, whereas the total concentration of Mg2+ is 8 mM and the lowest concentration of La3+ used is 1 μM. The overall shape of the bell-shaped titration curve of Fig. 3 suggests that assumption ii is also likely to be correct and that the titration of the two-metal ion binding sites is likely to be noncooperative.
In principle, if the Kd values for one-metal ion are known and the assumptions i and ii listed above apply, then the Kd values for the other metal ion can be calculated from Eq. 1. By using the values of ≈3.5 mM and >50 mM previously estimated for the Kd values for the binding of Mg2+ to the two sites in the absence of La3+, we can use this relation to estimate the Kd values for La3+ at the two binding sites as ≈0.9 μM and >37.5 μM, respectively. (We note that these values apply to a ribozyme titration carried out against a constant background of 200 mM NaCl.) Because these values are relatively small, it would be easier to measure these Kd values directly for La3+ than for Mg2+. Then, with an experimentally measured binding constant for La3+ to the weaker binding site of the HH16 hammerhead ribozyme, an accurate value of the Kd for Mg2+ at that site can also be calculated. Such measurements are currently in progress.
Other Studies of Ribozyme Cleavage Rates with Two Different Metal Ions.
Recently a conceptually similar competition experiment involving two different metal ions was reported for a “leadzyme” ribozyme (31). In that experiment, concentrations of Pb2+ and Nd3+ in the same reaction mixture were varied while keeping the total concentrations of these metal ions constant. An experiment of this sort requires that the binding affinities of the ribozyme for the two catalytically active metal ions be comparable. If these binding constants differ by more than an order of magnitude, the effects of the two different ions on the cleavage reaction will be obscured. In our titration experiment with La3+ against a constant concentration of Mg2+, the binding affinities of the two ionic species for the putative binding sites are obviously very different, and thus such a varying mole fraction strategy could not be employed. In fact, as Fig. 3 shows, the titration of the first putative metal ion binding site begins at concentrations of La3+ as low as 2 μM in the presence of an 8 mM concentration of Mg2+. Thus, for the HH16 hammerhead ribozyme, the apparent binding affinities of La3+ for both binding sites is approximately three orders of magnitude stronger than the binding affinities of Mg2+ for these sites. Because the dissociation constants for the La3+–Mg2+ cation pair are so vastly different, a standard “varying mole fraction” type of experiment would have failed to demonstrate the different binding (and catalytic) effects of these two ions.
Structural Roles of Metal Ions?
We must also consider the structural role(s) that divalent metal ions may play in maintaining a particular functional nucleic acid conformation in aqueous solution. Thus we were concerned that at the low concentrations of La3+ required for catalysis in the absence of Mg2+, the ribozyme might lack sufficient metal ions to support the required conformation of the ribozyme complex during catalysis. In the titration experiment described herein, sufficient Mg2+ ions were present to satisfy such structural requirements, even at low concentrations of La3+. It is interesting to note, however, that as the second metal ion binding site is titrated with La3+, the value of kobs approaches ≈2.2 × 10−3 sec−1, which is the same value obtained in solutions containing 3 μM LaCl3 in the absence of MgCl2 (see Fig. 3). This suggests that structural metal ion requirements, if any, are fully satisfied by La3+ alone, even at micromolar concentrations of this ion.
This conclusion may not be surprising, because the hammerhead is among the smallest ribozymes known and may well have simpler structural requirements than do the larger ribozyme systems. On the other hand, we find that no cleavage of the RNA substrate is observed at millimolar concentrations of LaCl3 (data not shown), either in the presence or in the absence of 8 mM MgCl2. This may mean that at millimolar concentrations the La3+ cation does bind to structural binding sites on the hammerhead ribozyme complex to produce a conformation that is unfavorable to cleavage. (We note that this experiment also serves as a control to show that even relatively elevated concentrations of La3+ ion do not catalyze nonspecific degradation of the ribozyme under our reaction conditions.) By operating at micromolar concentrations of La3+ and (when present) at Mg2+ concentrations that are comparable to the dissociation constant for that ion from such putative structural binding sites, we have been able to avoid such potentially unfavorable conformational effects.
Conclusions.
On the basis of the results presented herein, it is clear that a two-metal ion model for the mechanism of ribozyme action best explains the available data for the cleavage of the hammerhead HH16 ribozyme. Our data support the two-metal ion model illustrated in Fig. 5, requiring that metal ions directly coordinate to the attacking 2′-oxygen and to the 5′-oxygen of the leaving nucleotide. The metal ion coordinated at the 2′-oxygen lowers the pKa of the attached proton, thereby increasing the equilibrium concentration of the attacking nucleophilic alkoxide species. The role of the putative second metal ion positioned at the leaving 5′-oxygen is to absorb the negative charge that accumulates at that position in the transition state.
Since our earlier examination of the mechanistic hammerhead ribozyme literature (12), several papers have been published that support the present version of the general two-metal ion model (11, 30–33). In addition to the leadzyme experiments (32) mentioned above, a very recent paper supporting a two-metal ion model presents data from competition experiments between Mg2+ and Ca2+ on the rate enhancement of the cleavage of the Tetrahymena thermophila L-21 ScaI ribozyme (11). Thus, including the work with the hammerhead ribozyme presented herein, three distinct ribozyme systems have now been shown to exhibit similar two-metal ion dependencies. It is increasingly clear that a general two-metal ion model is operating in these systems and that this model is likely to be common to most, if not all, ribozyme-catalyzed phosphodiester cleavage reactions. In addition, as predicted by Steitz et al. (3), this mechanism may also apply to many of the phosphoryl transfer reactions catalyzed by polymerases and related enzymes in the processes of gene expression and their regulation.
Acknowledgments
We thank colleagues in our laboratory at University of Oregon and elsewhere for many helpful and stimulating discussions and Dr. Mark Young for a careful reading of the manuscript. This work was supported in part by National Institutes of Health Research Grants GM-15792 and GM-29158 (to P.H.v.H.) and by a grant from the Lucille P. Markey Charitable Trust to the Institute of Molecular Biology. B.W.P. was a postdoctoral fellow of the Jane Coffin Childs Memorial Fund for Medical Research. P.H.v.H. is an American Cancer Society Research Professor of Chemistry.
References
- 1.Cech T R, Herschlag D, Piccirilli J A, Pyle A M. J Biol Chem. 1992;267:17479–17482. [PubMed] [Google Scholar]
- 2.Yarus M. FASEB J. 1993;7:31–39. doi: 10.1096/fasebj.7.1.8422972. [DOI] [PubMed] [Google Scholar]
- 3.Steitz T A, Steitz J A. Proc Natl Acad Sci USA. 1993;90:6498–6502. doi: 10.1073/pnas.90.14.6498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pan T, Long D M, Uhlenbeck O C. In: The RNA World. Gesteland R F, Atkins J F, editors. Plainview, NY: Cold Spring Harbor Lab. Press; 1993. pp. 271–302. [Google Scholar]
- 5.Wilcox D. Chem Rev. 1996;96:2435–2458. doi: 10.1021/cr950043b. [DOI] [PubMed] [Google Scholar]
- 6.Dahm S C, Derrick W B, Uhlenbeck O C. Biochemistry. 1993;32:13040–13045. doi: 10.1021/bi00211a013. [DOI] [PubMed] [Google Scholar]
- 7.Pley H W, Flaherty K M, Mckay D B. Nature (London) 1994;372:68–74. doi: 10.1038/372068a0. [DOI] [PubMed] [Google Scholar]
- 8.Scott W G, Klug A. Trends Biochem Sci. 1996;21:220–224. [PubMed] [Google Scholar]
- 9.Freemont P S, Friedman J M, Beese L S, Sanderson M R, Steitz T A. Proc Natl Acad Sci USA. 1988;85:8924–8928. doi: 10.1073/pnas.85.23.8924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Beese L S, Steitz T A. EMBO J. 1991;10:25–33. doi: 10.1002/j.1460-2075.1991.tb07917.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.McConnell T S, Herschlag D, Cech T R. Biochemistry. 1997;36:8293–8303. doi: 10.1021/bi9700678. [DOI] [PubMed] [Google Scholar]
- 12.Pontius B W, Lott W B, von Hippel P H. Proc Natl Acad Sci USA. 1997;94:2290–2294. doi: 10.1073/pnas.94.6.2290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Burke J M. Nat Biotechnol. 1995;29:175–192. [Google Scholar]
- 14.Grassi G, Marini J C. Ann Med. 1996;28:499–510. doi: 10.3109/07853899608999114. [DOI] [PubMed] [Google Scholar]
- 15.Birikh K R, Heaton P A, Eckstein F. Eur J Biochem. 1997;245:1–16. doi: 10.1111/j.1432-1033.1997.t01-3-00001.x. [DOI] [PubMed] [Google Scholar]
- 16.Ramos A, Gubser C C, Varani G. Curr Opin Struct Biol. 1997;7:317–323. doi: 10.1016/s0959-440x(97)80046-2. [DOI] [PubMed] [Google Scholar]
- 17.Jaeger L. Curr Opin Struct Biol. 1997;7:324–325. doi: 10.1016/s0959-440x(97)80047-4. [DOI] [PubMed] [Google Scholar]
- 18.Zhou, D.-M. & Taira, K. (1998) Chem. Rev., in press. [DOI] [PubMed]
- 19.Hendry P, McCall M J. Nucleic Acids Res. 1995;23:3928–3936. doi: 10.1093/nar/23.19.3928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Scott W G, Finch J T, Klug A. Cell. 1995;81:991–1002. doi: 10.1016/s0092-8674(05)80004-2. [DOI] [PubMed] [Google Scholar]
- 21.Scott W G, Murray J B, Arnold J R P, Stoddard B L, Klug A. Science. 1996;274:2065–2069. doi: 10.1126/science.274.5295.2065. [DOI] [PubMed] [Google Scholar]
- 22.Mckay D B. RNA. 1996;2:395–403. [PMC free article] [PubMed] [Google Scholar]
- 23.Hoffman L M, Johnson M G. Biotechniques. 1994;17:372–375. [PubMed] [Google Scholar]
- 24.Uebayasi M, Uchimaru T, Koguma T, Sawata S, Shimayama T, Taira K. J Org Chem. 1994;59:7414–7420. [Google Scholar]
- 25.Dahm S C, Uhlenbeck O C. Biochemistry. 1991;30:9464–9469. doi: 10.1021/bi00103a011. [DOI] [PubMed] [Google Scholar]
- 26.Rosenthal L, Zacchetti D, Madeddu L, Meldolisi J. Mol Pharmacol. 1990;38:917–923. [PubMed] [Google Scholar]
- 27.Sinha S P. Structure and Bonding. New York: Springer; 1989. [Google Scholar]
- 28.Dean J A. Lange’s Handbook of Chemistry. New York: McGraw–Hill; 1992. [Google Scholar]
- 29.Bruice T C, Tsubouchi A, Dempcy R O, Olson L P. J Am Chem Soc. 1996;118:9867–9875. [Google Scholar]
- 30.Sawata S, Komiyama M, Taira K. J Am Chem Soc. 1995;117:2357–2358. [Google Scholar]
- 31.Ohmichi T, Sugimoto N. Biochemistry. 1997;36:3514–3521. doi: 10.1021/bi962030d. [DOI] [PubMed] [Google Scholar]
- 32.Sakamoto T, Kim M H, Kurihara Y, Sasaki N, Noguchi T, Katahira M, Uesugi S. J Biochem (Tokyo) 1997;121:288–294. doi: 10.1093/oxfordjournals.jbchem.a021585. [DOI] [PubMed] [Google Scholar]
- 33.Zhou D-M, Zhang L-H, Taira K. Proc Natl Acad Sci USA. 1997;94:14343–14348. doi: 10.1073/pnas.94.26.14343. [DOI] [PMC free article] [PubMed] [Google Scholar]