Natal dispersal and senescence

Abstract

The potential existence of natal dispersal strategies depending on parental age has been suggested by Hamilton and May [Hamilton, W. D. & May, R. M. (1977) Nature 269, 578–581] for organisms whose survival rates decline with age. When competition between parent and offspring is strong, any individual should disperse a smaller fraction of its offspring when it ages. Here, we verify their verbal prediction. First, we determine the evolutionarily stable dispersal strategy conditional on parental age, associated with a particular senescence curve. We show that such a conditional dispersal strategy should evolve independently from the genotype controlling the offspring dispersal behavior. Second, studying a population of common lizards, we provide empirical evidence of a relation between dispersal of female offspring and maternal senescence, in agreement with our theoretical predictions.

In a spatially structured population, the reproductive success of a breeding individual depends on the fraction of its offspring that stay at the parental site or emigrate to breed elsewhere. As a consequence, numerous allocation decisions for parents, such as offspring sex ratio (1), optimal clutch size (2), or reproductive effort (3), have been predicted to depend on offspring movement. Conversely, the offspring dispersal rate is likely to be, itself, a character under selection (4–7), and its evolution has been shown to depend, in some instances, on other life history traits, such as fecundity or adult survival (5, 7, 8). Therefore, the offspring dispersal rate, or natal dispersal rate, can be considered as a particular allocation decision, being part of the general reproductive strategy adopted by a species.

Life history theory predicts that allocation decisions, made by a breeding individual, should vary with its age for two reasons. First, decisions at one age affect possible decisions later in life because of the cost of reproduction for instance (9). Second, the optimal allocation strategy at each age may depend ultimately on the age-specific survival probability of the parent (10). In agreement with theoretical predictions, empirical studies have shown that reproductive effort, offspring size (11), and offspring sex ratio (12) depend on maternal age in numerous species. However, we are not aware of any study investigating the relation of natal dispersal to maternal age.

Yet, in their seminal paper on the evolution of dispersal, Hamilton and May (4) suggest the possible existence of age-dependent dispersal strategies. According to the assumptions of their simple model, juveniles can establish only in sites freed by the death of an adult. If adults experience senescence and their survival probability declines with age, any individual should disperse a smaller fraction of its offspring when it ages as the probability of local recruitment by philopatric offspring at the parental site increases. Nevertheless, these verbal arguments never have been verified theoretically, nor has such a pattern of dispersal ever been documented in natural populations.

Our aim in this paper is to verify the prediction of Hamilton and May (4). We first develop a general theoretical model. We used the same assumptions as Hamilton and May (4), and we allowed adults to survive from one year to the next, with age-specific survival probabilities, and we determined the evolutionarily stable (ES) dispersal strategy conditional on maternal age, associated with a particular senescence curve. Second, we provide a case study, in a population of common lizards, in which female offspring dispersal was related to maternal senescence and discuss whether the observed pattern may be explained by the same mechanisms as in our theoretical study. Eventually, we broaden our discussion to the adaptive value of conditional dispersal strategies that use age as a cue for habitat quality.

A THEORETICAL MODEL OF AGE-DEPENDENT DISPERSAL

Our assumptions are the same as those of Hamilton and May (4). Consider a stable environment with a fixed number of sites each year. Only one adult can occupy a site. We first suppose that the species is parthogenetic or that the species reproduces sexually but offspring movement is under maternal genotype control. Maternal control of seed dispersal is obvious in plants, and several cases of maternal effects on offspring dispersal have been reported in animal species (13–16). We later relax this assumption and consider a species reproducing sexually in which juveniles control their own dispersal behavior. Each year, each adult produces a large number of offspring, and no site is ever vacant. In such a stable habitat, Hamilton and May (4) showed that some level of dispersal was always selected for, as a result of strong sib competition at the parental site. We suppose that adults are competitively superior to juveniles and that a juvenile can establish successfully at one site only if the adult that previously occupied this site has died. Juveniles compete for sites freed by the death of an adult, and one offspring is chosen at random among the young present at a site to become an adult the following year. Reproductive maturity is attained after 1 year. Adults survive from age x to age x + 1 with probability s(x) and die eventually at the maximal age X_m. Senescence does not affect fecundity. The frequency of individuals with age x in the population is u(x).

Maternal Control of Dispersal

We assume that the fraction d(x) of dispersing offspring born to a mother in a given year is determined by her genotype and depends on her age, x. We are interested in the fate of a rare mutant with the conditional dispersal strategy d = {d(1), d(2), … , d(x), … , d(X_m)}, confronted to the frequent genotype, with strategy: d* = {d*(1), d*(2), … , d*(x), … , d*(X_m)}. d* is an ES strategy (17) if it resists invasion whatever the mutant phenotype d. We first calculated the number of newborn mutant individuals, produced by each age class, that survived to the following year.

The probability that a given philopatric offspring produced by a mutant aged i will successfully establish at the parental site is:

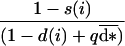1

with 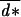= ∑_x u(x)d*(x), the average dispersal rate in the population, and q, the probability of surviving the migration episode.

The probability that a given dispersing mutant offspring successfully establishes in another site previously occupied by an adult with the most frequent genotype is:

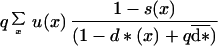2

Because the mutant is rare, we neglected the possibility of a mutant dispersing offspring establishing in a site previously occupied by another mutant adult. Thus, the number of surviving juveniles produced by a mutant aged i, or the realized fecundity of a mutant aged i, was:

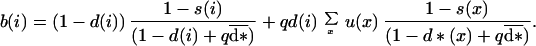3

The asymptotic growth rate of the rare mutant, λ, is given by the dominant eigenvalue of the Leslie matrix (18), where b(i) are age-specific fecundities and s(i) are age-specific survival probabilities (18). The frequent strategy d* is stable against small disturbances and resists invasion by mutants with strategy d close to d* if λ is at a local maximum when d = d*. Then, by using partial derivatives of λ, with respect to the dispersal strategy at each age, a set of necessary conditions for d* being ES (17) is that:

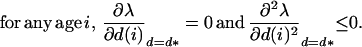4

Because of standard properties of age-structured populations (18, 19), it can be proved that these conditions are, in the present case, equivalent to:

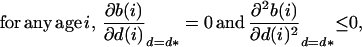5

These conditions apply only for values of the dispersal rates, at each age, lying in the feasible range between 0 and 1. Let us differentiate b(i) as a function of d(i) when d = d*. The first condition in Eq. 5 then can be written for any age i:

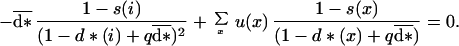6

The second order derivative in Eq. 5 is given by:

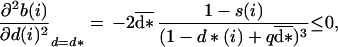7

which is always negative, so that the second condition in Eq. 5 is fulfilled for any age i. Eq. 6 holds whatever i; therefore, for any couple (i, j), we have:

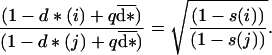8

Incorporating Eq. 8 into Eq. 6, we further obtain after some algebra:

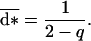9

Therefore, in a population occupied by individuals with the ES conditional dispersal strategy, the average dispersal rate equals the ES dispersal rate obtained by Hamilton and May (4) in the absence of any age structure. But the dispersal rate at each age now differs from the invariant ESS because we find, solving the system of equations defined by Eq. 6, that the ES conditional dispersal strategy satisfies, at each age i:

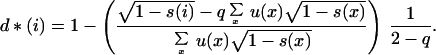10

If the survival probability s(i) decreases with age, Eq. 10 shows that the dispersal rate is expected to decrease as the mother ages, as predicted by Hamilton and May (4). This happens because the chance of success for a philopatric offspring at the parental site, measured by , becomes greater when the parent ages, compared with the constant expectancy of a dispersing offspring, measured by q∑_x u(x), which suffers the cost of dispersal and experiences competition with adults with average survival rate. Note that, whenever < q ∑_x u(x), one individual aged i should disperse all of its descendants out of the parental site because a dispersed offspring has greater chances of success despite dispersal costs. When philopatric offspring have greater chances of success than a migrant, it is, however, beneficial for the individual to disperse a fraction of its descendants away to avoid sib competition, as in the original model of Hamilton and May (4), but this fraction decreases as the individual ages. Eventually, for high cost of dispersal and steep senescence curve, a mother might keep all of her offspring at the parental site at the end of her life.

Note that Eq. 10 holds only if, at each age, the optimal dispersal rate lies strictly between 0 and 1. For some age classes, the optimal dispersal rate may lie at the limit of the feasible range, and the first order derivative in Eq. 5 is then not necessarily equal to 0. If we constrain the value of the dispersal rate for these age classes, the analytical resolution of the problem is then much more complicated because modification of one term in the composite strategy d* affects the optimal value of all other terms in the vector. We were not able to find a general explicit expression for the ES dispersal strategy at each age in this case. But, it still can be found numerically. Note that, in these cases, the average dispersal rate in the population does not necessarily equal 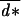= 1/2−q even though it remains close to this value.

Offspring Control

We then relax the assumption of maternal control or asexual reproduction. We suppose that the species is diploid and reproduces sexually and that the offspring genotype controls its dispersing behavior. We further make the same simple assumption, as did Hamilton and May (4), that male offspring always disperse away from the parental site. By using the same derivation as before, a set of conditions for the female dispersal d* being ES becomes, for any age i,

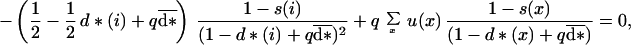11

which defines a system of equations similar to Eq. 6, which can be solved to find the dispersal strategy at each age. We were not able to find an explicit analytical expression for the ES conditional dispersal strategy in this case, so we solved the system of equations numerically.

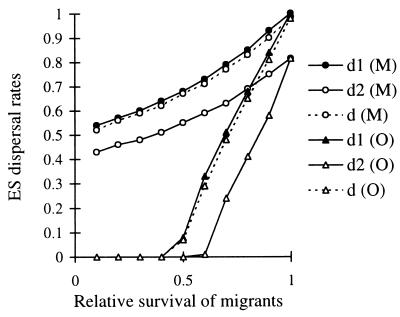
An example of ES conditional dispersal strategies for a species with two age classes is given in Fig. 1, in the case of maternal control and in the case of offspring control of dispersal as a function of the probability of surviving the dispersal event q. As generally stated, the selected average dispersal rate is higher under maternal control, which illustrates a case of parent–offspring conflict (20). Differences between the two cases emerge because the average relatedness between resident offspring in a patch is 1 from the point of view of their mother and ½ from the point of view of the offspring (21). When dispersal cost was lower than ½, we found that age-dependent dispersal strategies evolved as in the case of maternal control. The average dispersal rate in the population was very close to 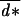= (2q−1)/(4q−1−2q²), which was the ES dispersal rate obtained by Hamilton and May (4) in this case. But, at the limit value of ½ for the dispersal cost, we found that some age classes evolved a low but non-null dispersal rate of their offspring (see Fig. 1), resulting in an average dispersal rate greater than 0 whereas Hamilton and May (4) predicted the evolution of total philopatry in this case, in the absence of age structure. This result occurs because the actual cost of dispersing is different for offspring born to old or young mothers and may be <½ for the latter.

Figure 1.

ES dispersal rates for female offspring as a function of the probability to survive dispersal for a species with two age classes. Survival rate of individuals aged 1–3 years: s₁ = 0.53; survival rate of individuals aged 4 years and more: s₂ = 0.32; frequency of individuals aged 1–3 years in the population: P = (1 − s₂)/(1 − s₁ + s₂). d₁, the dispersal rate of individuals issued from mothers aged 1–3 years; d₂, the dispersal rate of individuals issued from mothers aged 4 years and more; d, the average dispersal rate in the population; M, mother control of dispersal; O, offspring control of dispersal (complete dispersal for male offspring).

Our qualitative prediction of increased offspring philopatry with mother age in a senescent species seems to hold, independent of the genotype that controls the offspring dispersal behavior. Therefore, we predict that offspring dispersal strategy conditional on parent age may be observed in a natural population as long as the following conditions are respected: (i) The habitat is relatively stable; (ii) competition between parent and offspring is intense; and (iii) adults experience senescence. Currently, we are aware of no data that show such trends. Our aim in the second part of the article is to test our theoretical predictions in the case of the common lizard. First, we verify that there are no discrepancies between the biology of the common lizard and the main assumptions of our theoretical model. Second, we investigate how juvenile dispersal changes with maternal age in this species. If we observe a pattern of natal dispersal consistent with our theoretical predictions, we may consider two alternative hypotheses: Either the observed pattern is truly an adaptation as suggested here, or declining dispersal in senescing mothers is simply a consequence of their declining performances. To discriminate between these hypotheses, we compare not only the dispersal rates of offspring born to mothers with different ages but also the performances of the offspring and mother.

A BIOLOGICAL MODEL: THE COMMON LIZARD

Material

The common lizard (Lacerta vivipara) is a small lacertid lizard that inhabits peat bogs and heathlands and is widely distributed across Eurasia. The species is ovoviviparous. More details on the species biology and biotopes can be found in Pilorge (22). The studied population was monitored intensively by hand captures from 1989 to 1994 on the Mont Lozère (Cévennes, 1420 m of elevation) in the South of France.

Justification for the Choice of the Common Lizard as a Biological Model

Stable and Saturated Habitat.

Population sizes showed little variation across years (23) so that the habitat could be considered relatively stable. The experiment was conducted in the part of the studied area showing the highest lizard density (23). The observed rapid readjustment of the density, after an experimental density manipulation (23, 24), suggests that the habitat was saturated.

Competition and Juvenile Dispersal.

The same density manipulation (23) showed that juvenile mortality increased in zones where the density of conspecifics had been increased artificially. This suggests that juveniles suffer strongly from competition with adults. Juvenile dispersal is the most common type of dispersal in the common lizard (25). There is no parental care, and juveniles are independent right from birth. Direct aggressive behavior between mother and offspring has never been observed. However, the existence of potential manipulation of the offspring behavior by their mother cannot be discarded. Juvenile dispersal was found to be influenced by the natal environment as well as by prenatal conditions. In particular, density at the natal site (25), maternal parasitism (26), and maternal nutritional state during gestation (14) were shown to influence juvenile dispersal.

Methods

Senescence.

Our theoretical study suggests that dispersal conditional on maternal age may be observed only if adults experience senescence. So our aim in this analysis was to investigate whether the survival rate of adult females in the common lizard significantly decreased after a given age. The model also assumes that differences in adult survival rates are essentially caused by senescence and not by differences in habitat quality, for instance.

From 1989 to 1994, we followed individuals of one population by capture–recapture every year. Most individuals were of known age because they were captured either at birth or as yearlings since 1986. Only sexually mature individuals, which are 2 years old and older, were considered in the analysis. We used statistical models (capture–recapture models) that give separate estimates of the survival and capture probabilities (27, 28). To test whether habitat heterogeneity is a significant source of variation in survival probabilities among individuals, we started with a general statistical model assuming that age and time were the only sources of variation in both survival and recapture probabilities (29). We measured the fit of this model to the data with a contingency table test (computer program release) (30). Then, to identify the pertinent sources of variation in survival and recapture probabilities, we compared several statistical models with different numbers of parameters (see Table 1). For instance, some models assumed that survival rates were not subject to temporal fluctuations but were different for each age. In a second step, we considered models with a reduced number of age classes. Survival probability was supposed to change only after the ages of 2, 3, or 4 years. Recapture rates were treated similarly except that we did not investigate models with time-invariant recapture rates (23). Each of these models was fitted to the data (computer program surge) (29, 31), and we selected the fitted model with the smallest Akaike’s information criteria (AIC) value (32). Models with similar AIC values also were compared with the selected model by log–likelihood ratio tests.

Table 1.

Survival analysis in adult females

Recapture models		Survival models
		a*t	a + t	a	t	c
a*t	np	25	24	19	19	16
	AIC	508.64	508.00	503.88	504.38	504.94
a + t	np	24	18	14	14	10
	AIC	506.64	499.10	494.54	502.30	497.31
t	np	19	14	10	9	6
	AIC	499.35	494.02	494.27	496.76	496.70

AIC for different time (t)- and age (a)-dependent models of survival and recapture probabilities; np, number of parameters modeled; a*t, a model in which survival (or recapture) varies with age, time, and their interaction; a + t, the same model without interactions. a and t are models in which survival (or recapture) varies only respectively with age or with time. c, designates a model in which survival is assumed to be constant. The lower the AIC, the more appropriate the model to fit the data. 

Maternal Age and Dispersal.

To study offspring dispersal in relation to their mother’s age, we removed pregnant females from the field and kept them in the laboratory until parturition. Therefore, maternal lineages were known. Immediately after birth, females and their young were weighed and measured and then released at the mother’s last capture point (33). Philopatric and dispersing juveniles were defined by individuals moving a distance respectively smaller or larger than a home range diameter (20 m; ref. 34). Return rarely was observed. Because most of the females were of known age, it was possible to relate juvenile dispersal to the offspring’s mother’s age. Because juveniles of a same mother cannot be assimilated to independent statistical units, we used a resampling approach to analyze juvenile dispersal (34). We analyzed only 2 years, 1991 and 1992, in which we had enough offspring with a known dispersal status for each mother age class we defined (i.e., 2, 3, and 4 years old and older).

Maternal Age and Performances.

To discriminate between alternative mechanisms potentially leading to the same pattern of declining offspring dispersal in senescent mothers, we measured the change in some characteristics of adult females when they reach the age of 4 years, as well as the change in their offspring’s characteristics.

We counted the number of alive newborns in the female’s clutch. The corpulence of mothers was measured just after parturition as the ratio of body weight over body length. Offspring survival was estimated by the same method as previously. Offspring endurance was measured after birth by running juveniles until exhaustion on a motorized treadmill (35, 36). Offspring speed was measured by running juveniles at top speed in a race track equipped with photocells every 20 cm (26, 35, 36). Juvenile corpulence was measured as for mothers. Continuous variables such as endurance, speed, and corpulence were compared through variance–covariance analyses, and discrete variables such as fecundity were compared through a logistic linear analysis; both continuous and discrete variables were analyzed with time, weight, and/or size as covariates (37).

Results from an analysis of juvenile behavior also are included here. This analysis was conducted in the course of a study on juvenile ability to discriminate social environment on odor cues alone (J. P. Lena and M. De Fraipont, unpublished work). Juveniles, shortly after birth, were offered the choice to stay outside or to enter shelters when the odor of a foreign female was present in one of the shelters.

RESULTS

Senescence

We concluded that adult females experienced senescence in the studied population of common lizard, with a drop in survival rate at the age of 4 years.

The general statistical model incorporating time and age specificity in survival and capture probabilities fitted well the data (χ_2df² = 0.01, P = 0.996). Therefore, if we except time and age effects, there is no detectable heterogeneity among individuals in survival rates. So habitat heterogeneity is not a significant source of variation in adult survival. Statistical models involving survival rates varying with age and recapture rates varying from year to year best describe our data, according to the AIC criteria (Table 1). Survival probability of females younger than 4 years (0.532, 95% confidence interval 0.460–0.603) was significantly higher than the survival of females aged 4 years and older (0.319, 95% confidence interval 0.190–0.484). The best AIC value was obtained for this model (Table 2), which was significantly different from a model (Table 1) with no age variation (χ_1df² = 5.24, P = 0.022), but not from a model (Table 1) in which survival rates were different for each age (χ_3df² = 3.20, P = 0.362). So we did not lose information by reducing the number of age classes.

Table 2.

Survival analysis in adult females

Age contrast	Survival models
	2 years old vs. older than 2 years	2 and 3 years old vs. older than 3 years	2, 3, and 4 years old vs. older than 4 years
AIC	493.31	491.46	496.69

AIC for different age-dependent statistical models of survival with two age classes. The recapture probability is modeled as a function of time. The number of parameters used in the model is always 7. 

Maternal Age and Offspring Dispersal

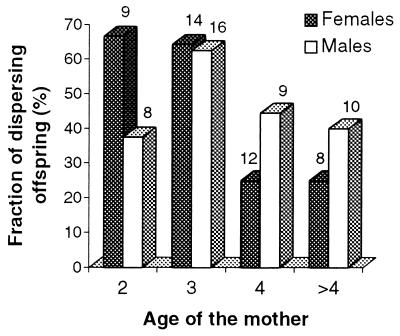
We found that female offspring dispersal rate declined once their mother had reached the age of 4 years and become senescent. Dispersal of male offspring was not significantly related to their mother’s age.

Juvenile females born from 2- and 3-year-old females dispersed significantly more than those born from older females (Fig. 2). All tests calculated on the 1000 samples, representing a random combination of one offspring per adult female, fell in the significant region (P < 0.039). This was not the case for juvenile males (Fig. 2), for which none of the tests fell in the significant region (P > 0.145).

Figure 2.

Female and male juvenile dispersal rates in relation to maternal age (in years) in the common lizard. >4, females older than age 4 years. Number of mothers in each category above bars.

Maternal Age and Performances

Results are summed up in Table 3. Mothers aged less than 4 years did not differ significantly from older mothers for any characteristic we measured. Offspring born to young and old mothers did not show any significant differences in their performances. Juvenile females born to mothers aged 4 years and more had, in only 1 year, a significant higher corpulence than juvenile females born to younger mothers. There was no difference in the other 2 years that we examined. Therefore, nothing allows us to conclude that offspring produced by senescent mothers are of poorer quality than offspring born to young mothers.

Table 3.

Comparison of some characteristics of females aged <4 and >4 years as well as those of their offspring

Variable	Comparison between young and old mothers
Maternal characteristics
Fecundity (101)	F991  =  1.07	P  =  0.30
Corpulence after parturition (101)	F991  =  0.02	P  >  0.50
Offspring characteristics
Male juvenile survival (309)	χ1df2  =  0.10	P  >  0.50
Female juvenile survival (325)	χ1df2  =  0.28	P  >  0.50
Juvenile endurance (322)	F3191  =  0.22	P  >  0.50
Juvenile speed (512)	F5091  =  1.29	P  =  0.26
Male juvenile corpulence (309)	F3031  =  0.81	P  =  0.37
Female juvenile corpulence (325)*	F3154  =  2.88*	P = 0.02
Sensitivity to odor cues (19)	χ1df2  =  4.68	P = 0.03

Sample sizes are given within brackets. 

^*The interaction between the mother’s age and time was significant, not the main effect of the mother’s age. In all other cases, interaction terms involving age were not significant. 

The only significant change that we observed for offspring born to old and young mothers was a behavioral change. In response to an odor cue, juveniles born to old mothers entered the shelters in significantly higher proportions than juveniles issued from mothers aged <4 years. There was a clear change in the way juveniles perceived their social environment depending on their mother’s age.

DISCUSSION

In stable and homogenous habitats, dispersal is supposed to have evolved in response to kin competition (4, 6) or inbreeding depression (38, 39). Our theoretical study is based on Hamilton and May’s model (4), in which the force driving the evolution of dispersal is competition among siblings. However the age-dependent pattern of dispersal obtained here was ultimately linked to another kind of kin competition, namely competition between parent and offspring. If some conditional dispersal strategy can evolve, we predict that offspring philopatry should increase when their mother becomes senescent, which could be viewed as some local terminal investment in reproduction (see also ref. 40). Moreover, we found that age-dependent dispersal evolved whether offspring dispersal was under maternal control or not.

Empirical Test of Theoretical Predictions in the Common Lizard

The studied population of common lizards inhabits a stable and saturated habitat. Dispersal between sites is essentially due to juveniles, and they suffer from competition with adults. The present study showed that adult female survival probability decreased when they aged. Therefore, the common lizard provides a convenient biological model to test our theoretical predictions. We expect offspring philopatry to increase for senescent mothers.

Female Offspring

Dispersal rates of juvenile female lizards declined at the point at which life expectancies of their mothers declined, in agreement with our qualitative prediction. Our aim was to develop a general model, not to make any precise quantitative predictions in the case of the common lizard. Quantitative fit between theoretical predictions and the data presented here is not measurable anyway because the value of the dispersal cost, a key parameter in our model, is unknown for the common lizard. Theoretical predictions for the same adult survival rates as measured in the common lizard are shown in Fig. 1. We can only notice, at this stage, that observed dispersal rates for young and old mothers (respectively 65 ± 20% and 25 ± 19% of their daughters) were more consistent with the range of theoretical predictions in the case of offspring control than in the case of maternal control of dispersal.

We might suspect that a juvenile female generally competes with a group of adult females within the home range and not only with her mother. We need to extend the present model to allow several adults to inhabit the same home range and test under which conditions we can still select for a dispersal strategy conditional on maternal age.

Male Offspring

The male offspring dispersal rate was not related to maternal age. Previous studies have shown that maternal effects on dispersal could be different for male and female offspring in the common lizard (26). Male offspring establishment may not be limited by the presence of their mother. Young males compete with adult females at the beginning of their life, but, once they become adults, their survival and breeding success would essentially be limited by competition with older males. For a juvenile male, a dispersal strategy conditional on its mother’s age then would have little adaptive value.

Another explanation for this sex-specific behavior would be that male and female offspring do not disperse for the same reason (41). Motro (39), considering the effects of both sib competition and inbreeding depression, found that, with a high cost of inbreeding, a sexual dimorphism with respect to dispersal could evolve even if both sexes had the same costs and benefits associated with dispersal. In the common lizard, both male and female offspring may disperse to avoid competition with their young mother. But when the mother is older and female offspring are in majority philopatric, male offspring may still disperse to avoid inbreeding with their sisters. Further studies of inbreeding depression in this population are needed (25).

Alternative Explanations

We observed a pattern of natal dispersal for juvenile females that is consistent with our theoretical predictions. Can we, however, conclude that kin competition is responsible for the evolution of such a dispersal strategy in the common lizard, as assumed in our model? Or, is this pattern a constraint rather than an adaptation, a consequence of senescent mothers being less able to produce dispersing daughters? We found that senescent mothers produced both the same quantity of offspring and offspring with the same performances as young mothers. Aggressive behavior between mothers and offspring is unlikely to be involved in dispersal mechanisms. Therefore, we are aware of no evidence supporting the constraint hypothesis. Instead, the only observed change between offspring born to young and old mothers concerns their perception of their social environment. Sensitivity to odor cues has been shown to be linked to the dispersal behavior of juveniles (J. P. Lena and M. De Fraipont, unpublished work). This observation supports the hypothesis that changing dispersal rates in juvenile females according to the maternal age is an adaptation. Mechanisms by which mothers with different ages may manipulate their offspring, or by which offspring may respond to changes in their mother, currently are unknown. Variation in maternal hormonal level with age and chemical exchanges during gestation are promising potential mechanisms.

In conclusion, the trends observed in the present study suggest that kin competition is probably an important factor for the evolution of dispersal in the common lizard, confirming the findings of other studies on dispersal determinants in the same species (refs. 14 and 26 and J. P. Lena and M. De Fraipont, unpublished work).

Generalization: Maternal Quality as a Source of Habitat Heterogeneity

Senescence Generates Spatial Heterogeneity.

Whether dispersal evolved to escape sib competition (4) or more generally crowding (42), adult survival has no effect on the ES fraction of dispersing offspring in a stable habitat if constant mortality with age is assumed. When adult survival increases, sites occupied by adults are unavailable for juvenile establishment so that the expectation of inheriting a vacant site is decreased by a constant factor, for both dispersing and resident offspring in all populations. Therefore, adult survival cancels out of the analysis and does not affect the ES dispersal rate. In contrast, senescence and varying survival probabilities create spatial heterogeneity among the previously homogenous population, for which expectancies of successful establishment for juveniles now differ greatly among sites, depending on the age of the resident adult. Spatial heterogeneity in a temporally constant environment selects against dispersal behavior (43, 44) because passive dispersal then drives, on average, more individuals from productive sites to poorer habitats than the reverse. However, McPeek and Holt (44) showed that, in such spatially heterogeneous and temporally constant habitats, conditional dispersal strategies were ES. Similarly, we found that dispersal strategies conditional on maternal age were selected for when senescence generates spatial heterogeneity among a previously homogenous habitat.

Mother Age as a Cue for Habitat Quality.

Cases of conditional dispersal are well documented in mammals (see ref. 45 for a review), for whom the emigration rate increases with density of conspecifics, but also have been reported for Seychelles warblers (46), superb fairy wrens (47), collared flycatchers (48), and a number of insect species (reviewed in ref. 49). In all of these examples, the dispersal decision depends on the evaluation of an environmental, demic, or individual feature used as a cue that reflects habitat quality. In the general context of habitat selection, we suggest that maternal age in the present study could be perceived as a cue for habitat quality whenever habitat quality is essentially determined by the intensity of competition between parent and offspring.

This perspective on age-dependent dispersal allows us to broaden our conclusions. First, in a stable environment with strong intraspecific competition, if quality of the habitat closely depends on the maternal presence, maternal general condition rather than maternal age per se might be a reliable cue for a conditional dispersal strategy. In the common lizard, parasitized mothers produce more philopatric female offspring (26). Conversely, in the same species, well fed mothers produce a larger fraction of dispersing offspring, with no sex effect (14). However, there are alternative explanations for these observed patterns of dispersal, such as a differential cost of producing dispersing and resident offspring. Second, whenever maternal age is correlated to any environmental feature affecting habitat quality, maternal age could be used as a cue, and age-dependent dispersal strategies could be selected for even though maternal presence does not alter directly offspring success.

CONCLUSION

We have provided here a theoretical study of age-dependent natal dispersal, as well as an empirical example illustrating our predictions. An effect of the grandmother’s age on the production of winged and wingless offspring has been reported in pea aphids (50), but the mechanisms underlying the observed patterns of increasing or decreasing philopatry were not investigated. More generally, it would be interesting to test whether such patterns of dispersal may be observed in other systems, including, for instance, long-lived perennial plants.