A novel approach to assess post-yield energy dissipation of bone in tension

Abstract

In this study, we proposed a novel approach to assess the energy dissipation during the post-yield deformation of bone. Based on the stress–strain behavior in an incremental and cyclic loading–unloading–reloading scheme in uniaxial tension, we partitioned the post-yield energy dissipation of bone into three distinct pathways: released elastic strain energy (U_er); irreversible energy (U_i); and hysteresis energy (U_h). Among them, U_er depends on the stiffness loss, U_i is the energy permanently consumed, and U_h reflects changes in the viscoelastic behavior of bone in the process of post-yield deformation. As an example, bone specimens from human cadaveric femurs of middle-aged and elderly donors were tested using this approach. The results of this study indicate that there exist age-related differences in post-yield energy dissipation and modulus degradation. These results implicate that this novel approach could detect the age-related differences in energy dissipation of bone and may aid in understanding the underlying mechanisms of such changes.

1. Introduction

Age-related degradation in toughness makes bone more susceptible to fracture (Burstein et al., 1976). The observed decrease in bone toughness with age likely depends on the age-related changes in the post-yield behavior of bone (McCalden et al., 1993). However, underlying mechanisms of post-energy dissipation in bone is still not clear. Previous studies have reported that microdamage accumulation (including both linear microcrack and diffuse damage) may be major mechanisms in energy dissipation during the post-yield deformation of bone (Courtney et al., 1996; Jepsen and Davy, 1997; Kotha and Guzelsu, 2003; Martin et al., 1997; Zioupos and Currey, 1998). In addition, age- or disease-related changes in the collagen network may also contribute to the reduced bone toughness (Jepsen et al., 1996; Wang et al., 2002; Zioupos et al., 1999), indicating the involvement of collagen in post-yield energy dissipation. These previous studies implicate that the post-yield energy dissipation in bone may be associated with several pathways. Thus, partitioning the energy dissipation during the post-yield deformation of bone may help elucidate the underlying mechanism of age-related bone fractures. To address this issue, we proposed a novel methodology to assess the energy dissipation pathways during the post-yield deformation of bone.

2. Materials and methods

2.1. Loading procedure

Using a load–unload–reload scheme as shown in Fig. 1, we proposed to partition post-yield energy into three components during the cycle: the released elastic strain energy (i.e., the area enclosed in HEF or U_er), hysteresis energy (i.e., the area enclosed in the unloading and reloading loop or U_h), and the irreversible energy (i.e., the area enclosed in ABCG or U_i). The released elastic strain energy is mainly due to the modulus loss (Fondrk et al., 1999a, b). The hysteresis energy reflects the viscoelastic behavior of bone in the process of load bearing (Doubal et al., 2004). Finally, the irreversible energy dissipation (U_i) involves at least two possible pathways: formation of new cracks (U_er) and permanent deformation (U_p) in the tissue (Fondrk et al., 1999a, b). The underlying mechanisms involved in these pathways are still unclear. However, previous studies have shown that microdamage accumulation is related to the loss of the stiffness of bone (Burr et al., 1998). In addition, the integrity of the collagen network significantly affects the toughness (Wang et al., 2001) and the post-yield stress–strain behavior of bone (Wright et al., 1981). Moreover, A microstructural barrier (e.g., cement lines), which slows the growth of cracks during fatigue loading, may also affect post-yield behavior of bone (O'Brien et al., 2003).

Fig. 1.

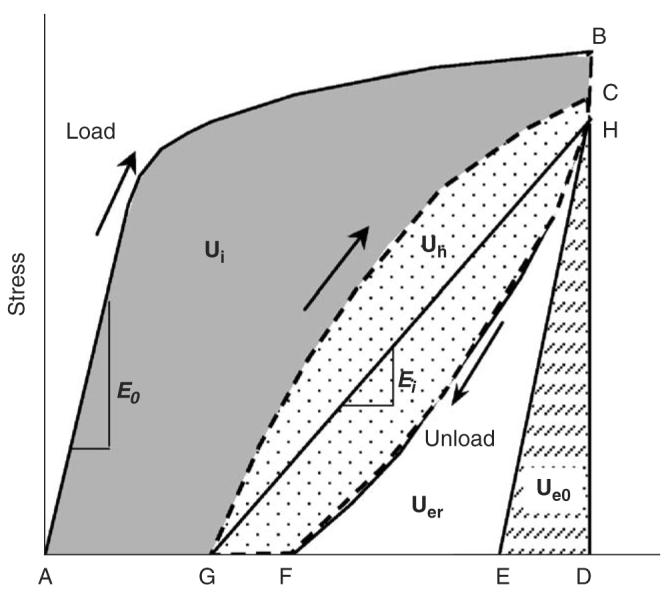
Partitioning the energy capacity of bone: nominal elastic strain energy (U_e0) depending on the initial elastic modulus (E₀); released elastic strain energy (U_er) relating to modulus degradation; hysteresis energy (U_h) reflecting the viscoelastic nature of bone; and irreversible energy (U_i) dissipation, which reflects the free surface energy released by microdamage formation (U_er) and the permanent strain energy (U_p).

To distinguish between these different pathways of energy dissipation, a progressive load–unload–reload scheme in uniaxial tension was implemented as shown in Fig. 2. An incremental displacement of 0.05 mm was imposed on the specimen for each cycle (Table 1). Strain was estimated as the change of the crosshead displacement per 10 mm gage region. In each cycle, the specimen was first loaded under displacement control to the next displacement level at a rate of 5 mm/min; then held steady for 60 s for stress relaxation (from point C to H as shown in Fig. 1). Thereafter, the specimen was unloaded in load control to zero force, and held for 60 s for strain relaxation (from point F to G as shown in Fig. 1), and then reloaded again in displacement control to the next strain level. This process was repeated until failure. All specimens that did not fail at the sixth cycle were loaded to failure without further cycles. The bone specimens were kept moist by wrapping them with gauze soaked with physiological saline.

Fig. 2.

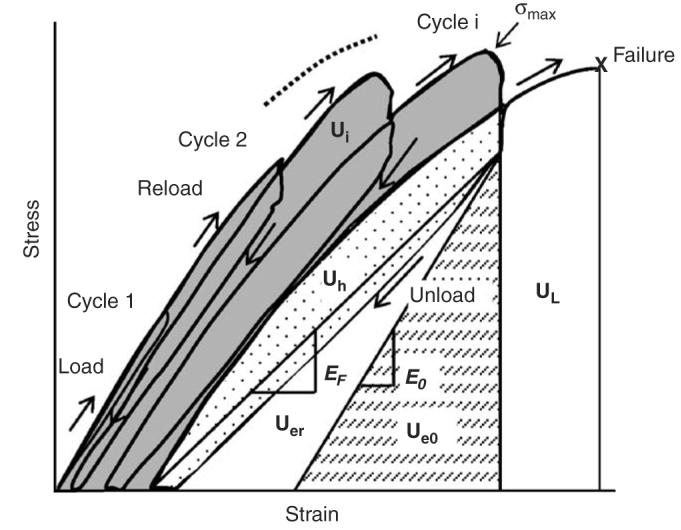
The cyclic loading scheme was used with a displacement increment of 0.05 mm (approximately 0.5% strain) at each successive cycle. The energy terms could be calculated for each cycle. In this example, failure occurred after the fourth cycle, but before the fifth cycle. U_I is estimated as the gray shaded area for the last cycle. The toughness (U_T = U_I + U_er + U_h + U_e0 + U_L) was calculated as a summation of all energy terms including U_L.

Table 1.

Number of survival specimens (no failure) at incremental displacement is greater in middle-aged bone as indicated by the greater number of surviving specimens at greater displacement

Cycle (ith)	Displacement (mm)	Estimated strain	Middle-aged	Elderly
1	0.05	0.005	9	9
2	0.10	0.010	9	9
3	0.15	0.015	9	9
4	0.20	0.020	9	6
5	0.25	0.025	7	4
6	0.30	0.030	4	2
Final	Till failure	>0.030	3	2

In the incremental loading scheme (Fig. 2), the total irreversible energy (U_i) absorbed by the specimen at the previous and present cycles is actually the result of cumulative deformation of each loading cycle, and can be simply calculated as the summation of each U_i of all previous and present loading cycles. On the other hand, U_er and U_h measured at each cycle already represent the cumulative effect. The permanent strain energy portion (U_p) of the total irreversible energy (U_i) was estimated as U_i—U_er. Also, we calculated the toughness (U_T = U_i + U_er + U_h + U_e0 + U_L) and the ultimate strength (σ_max) for each bone specimen as shown in Fig. 2. To investigate the contribution of each post-yield energy term to the total energy dissipation, we used the ratio of each energy term (i.e., U_p, U_er, and U_h) to the overall energy capacity (U_S = U_i + U_er + U_h + U_e0 in Fig. 2) at the final cycle.

The elastic modulus after yielding was calculated as the slope of line HG (presumably between two equilibrium points) in order to avoid the influence of viscoelasticity (hysteresis). Moreover, the modulus degradation at the each cycle was estimated as (1–E_f/E₀), where E₀ is the initial elastic modulus and E_f is the elastic modulus at the cycle.

2.2. Bone specimen preparation

Eighteen tensile specimens were prepared each from 18 male cadaveric femurs that were collected from Texas Willed Body Program and National Disease Research Exchange. The specimens were evenly divided into two age groups (n = 9): middle-aged (49–59 years) and elderly (69–87 years). The ‘dog bone’ specimens (10 mm × 5 mm grip regions and a 10 mm × 2 mm gage region) were prepared longitudinally from the middiaphysis of each femur using a diamond saw and a CNC machine (ProLIGHT 1000, Light Machines, Manchester, NH).

2.3. Statistical analysis

Student's t-tests (one tail) were performed to examine the age-related effects on the post-yield energy dissipation and other aforementioned properties of bone. Significant differences were considered only if p-value was less than 0.05.

3. Results

Table 1 shows the number of survival specimens (no failure) at each incremental loading cycle. It was observed that after 2.0% strain the number of survival specimens in the middle-aged group was consistently higher than that in the elderly one. Also, it was observed that no difference in U_p exists at cycle 3 (Fig. 3), but at the final cycle between the age groups (Table 2). As shown in Table 2, U_p, U_er, σ_u, and modulus degradation of bone deceased significantly with age (p<0:05). U_T and U_h of bone did indicate a trend of decrease with age although their p-values are little higher than 0.05 (p<0:06). It is noteworthy that the age-related differences were very similar in all energy dissipation terms (about 30–35%), while the differences in strength and modulus degradation were somewhat smaller (around 13–15%).

Fig. 3.

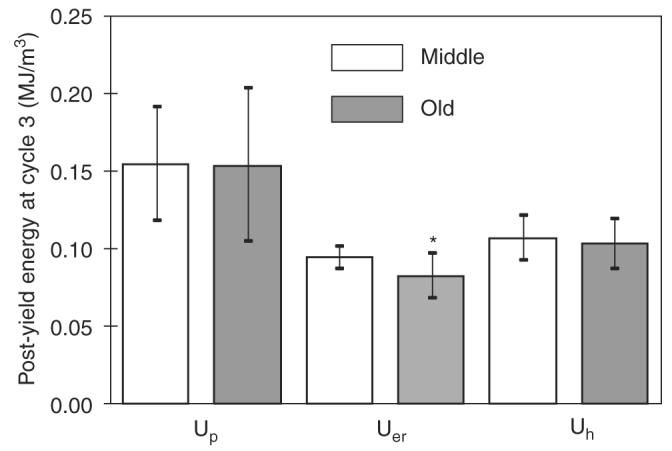
Post-yield energy dissipation at the early stage of post-yield deformation (at cycle 3) does show significant age-related effects in energy dissipation except for the released elastic strain energy (p = 0:027). *indicates significant difference between the two age groups (p<0:05).

Table 2.

Summary of experimental results obtained at the last cycle prior to failure (N = 9)

Properties	Middle-aged	Elderly	p-value
Plastic strain energy Up (MJ/m3)	0.674±0.257	0.403±0.230	0.016
Released elastic strain energy Uer (MJ/m3)	0.298±0.099	0.199±0.126	0.042
Hysteresis energy Uh (MJ/m3)	0.320±0.092	0.229±0.134	0.058
Toughness UT (MJ/m3)	2.48±0.975	1.740±0.856	0.054
Strength σmax (MPa)	88.1±11.4	75.6±13.0	0.023
Final modulus degradation (1–EF/E0)	0.48±0.05	0.41±0.09	0.047

Furthermore, the relative contribution of the post-yield energy terms to the energy capacity of bone did not show significant differences between the age groups in the early cycles (Fig. 3), with permanent strain energy (U_p) having the greatest contribution to energy dissipation. However, significant age-related differences were observed in the total energy dissipation of bone (Table 3). Lastly, with an increase in post-yield deformation, age first affected U_er and then U_p (Table 2 and Fig. 3).

Table 3.

Relative contribution of each final post-yield energy term to the energy capacity of middle-aged and elderly bone (N =9)

Properties	Up/US (%)	Uer/US (%)	Uh/US (%)
Middle-aged	34.4±5.3	15.4±1.5	16.8±1.1
Elderly	28.7±7.3a	13.5±2.3	16.5±1.9

^aSignificantly less than the middle-aged group (p-value<0.05).

4. Discussion

The results of this study indicate that the proposed experimental approach may be of use in distinguishing the different pathways of energy dissipation in the post-yield deformation of bone. Conventional approaches, such as fracture toughness testing, give the bulk properties, but cannot distinguish between contributions of bone constituents to bone toughness. The advantage of the present approach is that it may provide more specific information to help understand changes in the bone constituents as a function of aging or other bone diseases.

There are some limitations to the current approach. First, this approach has only been tested in uniaxial tension. While energy dissipation during tensile yielding is informative, failure of bone certainly occurs in the other modes of loading. Diagnostic tests investigating the effect of damage by overload on mechanical properties of cortical bone indicated similar post-yield behavior in torsion (Jepsen and Davy, 1997) and compression (Morgan et al., 2005), but failure appears to occur at lower strain levels. Second, since the bone specimens did not break exactly at prescribed strain levels, we used the post-yield energy dissipation at the last complete cycle as an approximation of those terms at failure. In fact, such errors could be limited by reducing the incremental loading displacement.

There is one intriguing observation in the experimental results obtained using the proposed approach: That is, age-related decreases are more significant in the post-yield energy dissipation than in the modulus degradation (stiffness loss) of bone, suggesting that aging has more effects on the post-yield energy dissipation than on the stiffness loss of bone.