Correlation of Free Radical Yields with Strand Break Yields Produced in Plasmid DNA by the Direct Effect of Ionizing Radiation

Abstract

The purpose of this study was to determine how free radical formation (fr) correlates with single strand break (ssb) and double strand break (dsb) formation in DNA exposed to the direct effects of ionizing radiation. Chemical yields have been determined of (i) total radicals trapped on DNA at 4 K, G(∑fr), (ii) radicals trapped on the DNA sugar, G_sugar(fr), (iii) prompt single strand breaks, G_prompt(ssb), (iv) total single strand breaks, G_total(ssb), and (v) double strand breaks, G(dsb). These measurements make it possible, for the first time, to quantitatively test the premise that free radicals are the primary precursors to strand breaks. G(∑fr) were measured by EPR applied to films of pEC (10 810 bp) and pUC18 (2686 bp) plasmids hydrated to Γ = 22 mol of water/nucleotide and X-irradiated at 4 K. Using these same samples warmed to room temperature, strand breaks were measured by gel electrophoresis. The respective values for pEC and pUC18 were G(∑fr) = 0.71 ± 0.02 and 0.61 ± 0.01 μmol/J, G_total(ssb) = 0.09 ± 0.01 and 0.14 ± 0.01 μmol/J, G(dsb) = 0.010 ± 0.001 and 0.006 ± 0.001 μmol/J, and G_total(ssb)/G(dsb) ~9 and ~20. Surprisingly, G_sugar(fr) ≈ 0.06 μmol/J for pUC18 films, less than half of G_total(ssb). This indicates that a significant fraction of strand breaks are derived from precursors other than trapped DNA radicals. To explain this disparity, various mechanisms were considered, including one that entails two one-electron oxidations of a single deoxyribose carbon.

Introduction

The events that lead to DNA damage by ionizing radiation result from two different energy deposition processes: the direct and indirect effects.¹ The direct effect involves, in principle, ionization of the DNA itself but in practice includes the most closely bound hydration shell.² The indirect effect refers to the ionization of the solvent, and in biological systems, this means water. Although it is a minor pathway in a dilute solution, the direct effect makes a significant contribution to DNA damage under the prevailing conditions in the nuclei of eukaryotic cells. This is because chromatin is tightly packed, the amount of unbound water is relatively small, and diffusible radical intermediates are efficiently scavenged. It has been estimated that the direct effect contributes 40–50% of the DNA damage responsible for viral³ or cell death.⁴

Although both the direct and indirect effects make significant contributions to DNA damage in vivo, the direct effect still remains poorly characterized. The indirect effect is the dominant process in a dilute solution and so it has been studied extensively using a variety of aqueous model systems.^3,5–13 To study the direct effect, it is necessary to heavily attenuate the otherwise overwhelming indirect effect. This is achieved by dehydration which removes^14,15 the water responsible for the indirect effect and/or by using cryogenic temperatures,^16–21 which prevent diffusion of the intermediate radical species derived from water ionization. At cryogenic temperatures, it is possible to employ EPR spectroscopy to characterize the radical intermediates.^16,20 Studies of this sort suggest that the direct effect dominates at hydration levels of less than about 13 water molecules per nucleotide residue (Γ < 13).^2,14,22 This represents the most closely bound hydration shell whose ionization tends not to produce water radicals but instead rapidly transfers the ionization site (also called the “hole”) to the DNA where it is more stable.

Ionizing radiation produces nonspecific ionizations. According to the Bragg rule, the functional groups present in DNA are ionized in proportion to the numbers of electrons they contain. An accounting implies that 61% of the ionizations take place in the deoxyribose phosphate backbone (sodium salt) with the remaining 39% distributed among the four bases. A single ionization creates a hole and ejects an electron. The electrons are captured exclusively by the pyrimidine bases while the holes are distributed between guanine and deoxyribose. Comparing the results obtained with different model systems suggests that the yield of deoxyribose radicals may be sufficiently large to account for the formation of all single strand break (ssb) events.^23–26 It is, however, possible that EPR invisible intermediates may also contribute to ssb formation.

Low-energy electrons (<20 eV) are able to produce ssb in plasmid DNA by dissociative electron attachment (DEA).^27,28 DEA is a terminal reaction for primary and secondary electrons approaching thermal energies. It is a resonant process that leads to fragmentation at the attachment site, pyrimidine being one known example.²⁹ Most of the ejected secondary electrons produced by ionization are sufficiently energetic to produce excitations or additional ionizations in all functional groups present in DNA.^30–34 Additional excitations are produced by recombination of radical ions. These excited states, produced by nonresonant interactions, may also be precursors to homolytic bond fission and, thus, to strand breaks.

Previous studies that attempted to determine direct strand break yields in DNA either were carried out in dilute aqueous environments with high concentrations of radical scavengers,⁶ or involved “dry” or “hydrated” DNA samples in which the packing and hydration were poorly controlled. Yield of direct strand breaks were measured by Symons et al.²¹ in frozen aqueous solutions of pBR322 plasmids irradiated at 77 K. Their results were difficult to interpret due to the fact that the free radical yields and the strand break yields were determined in two different types of DNA using markedly different DNA concentrations and buffers. Furthermore, the packing was poorly controlled. DNA packing has been shown to exert a large influence on free radical yields and, therefore, most likely on strand break yields as well.^35,36 In a separate study, Ito et al.³⁷ determined the yield of strand breaks induced in plasmid DNA by X-irradiation at 77 K. He observed that the yield of strand breaks induced in dry or hydrated (assuming 20 waters per mole of nucleotide (Γ ~ 20)) plasmid DNA at 77 or 298 K increased significantly with an increase in DNA hydration and that the trend was more pronounced for irradiations at 298 K. In a more recent work by Yokoya et al.,³⁸ yields of ssb and dsb, as well as base lesions, were determined in X-irradiated plasmid DNA films.

Strand breaks can be detected with unusually high sensitivity using plasmid DNA as the target.^{3,5–8,10,12,13,39} The sensitivity derives from the relatively large target size and the assay precision. In their most common form, such assays rely on the differential electrophoretic mobility of conformational isomers that are supercoiled (break free), relaxed (contain at least one ssb), or linearized (contain a single dsb).³ For example, 250 ng of 10 kb plasmid is employed for measuring ssb with a detection sensitivity of ~4 × 10⁻¹⁴ mol. This sensitivity is difficult to match with spectroscopic techniques.

EPR sensitivity varies as the square of the spectral line width. For DNA trapped radicals, the detection limit for our Q-band (ca. 35 GHz) EPR spectrometer with the sample at 4 K is ~5 × 10¹⁰ spins/μg. The DNA sample mass used in our experiments is ~60 μg, giving a sensitivity of ~3 × 10¹² spins or ~5 × 10⁻¹² mol. This lower sensitivity, of course, dictates that the EPR sample mass be 200-fold larger than that used for plasmid based ssb measurement. If one were to attempt this experiment using a conventional EPR spectrometer, operating at X-band (ca. 10 GHz) frequencies with the sample at 77 K, the sample mass would have to be increased by an additional 2 orders of magnitude. Under the latter conditions, the experiments reported here would have required grams of plasmid DNA instead of a few milligrams. The enhanced sensitivity of our EPR instrumentation made it possible to compare free radical yields with ssb yields in samples of manageable size.

Here we report on the X-irradiation of a plasmid target under dehydrated and cryogenic conditions. The advantage of this combined approach lies in its ability to correlate free radical intermediates detected by EPR spectroscopy with stable end products (ssb and dsb), which are diamagnetic and therefore EPR invisible. The hydration level of the plasmid film was maintained at Γ = 22. The total free radical (fr) yield, G(∑fr), was quantified at 4 K using Q-band EPR spectroscopy.²⁰ These samples were returned to room temperature, and then the ssb and dsb yields (respectively G(ssb) and G(dsb)) were quantified using gel electrophoresis.^6,7 It was therefore possible for us to achieve the unprecedented evaluation of G(∑fr), G(ssb) and G(dsb) with the same sample.

Materials and Methods

Preparation of Plasmid DNA

Plasmids pUC18 (2686 bp) and pEC (10 810 bp) were isolated from Escherichia coli K-12 HB101 by the “cleared lysate” procedure,⁴⁰ purified by isopyknic banding in cesium chloride density gradients in the presence of ethidium, followed by gel filtration chromatography using Sephacryl S-1000, and finally dialyzed extensively against TE (10 mmol dm⁻³ tris(hydroxymethyl) aminomethane (Tris) and 1 mmol dm⁻³ ethylenediaminetetraacetic acid (EDTA), pH 8.0).

Sample Preparation

Appropriate aliquots of the plasmid solution (both pEC and pUC18 DNA) were drawn into open-ended silylated suprasil quartz tubes and then allowed to dry and equilibrate in humidity chambers containing a saturated solution of NaOH which gave a relative humidity of 5%.⁴¹ These “dry” samples were then weighed and subsequently taken to the desired level of hydration by allowing them to equilibrate in humidity chambers containing a saturated solution of K₂-HPO₄ which gave a relative humidity of 92%.⁴¹ From the weights determined before and after equilibration, the level of hydration, Γ (moles of water per mole of nucleotide), could be determined accurately for each sample. The mass fraction of film consisting of DNA and the solvation shell is 87 ± 4%. This fraction was determined after EPR measurement by dissolving a known mass in a known volume of water and measuring the OD at 264 nm.

Sample Irradiation and EPR Spectroscopy

Samples were irradiated at 4 K in a Janis Dewar setup⁴² with X-rays generated by a Varian/Eimac OEG-76H tungsten-target tube operated at 70 keV and 20 mA. The dose rate was 24 kGy/h. The dose regime extended from 0 to 3200 Gy for individual pUC18 samples at each dose point in this range. For pEC plasmid samples, the dose regime extended from 0 to 4000 Gy. The samples were raised into the EPR cavity and allowed to equilibrate for several minutes before spectra were recorded. All EPR spectra were taken as first derivatives with a Q-band (35 GHz) Varian E-12 EPR spectrometer. Data were collected using 1000 points per EPR scan, typically spanning a field width of 40 mT. Approximately 30 mT of the scan was devoted to the EPR spectrum of the sample, the remainder being devoted to the spectrum of a ruby marker mounted on the inside wall of the sample cavity.²⁰ Following a simple ramp baseline correction, the spectrum was numerically integrated to obtain the absorption spectrum. This was then baseline corrected and integrated again, yielding the intensity of the absorption. The baseline correction and integration procedure was also carried out on the ruby portion of the EPR spectrum to determine the intensity of the ruby standard. Free radical concentrations were then determined by comparing the intensity of the EPR signal at 4 K to that of the ruby standard for each of the plasmid samples at each dose point. The dose-response characteristics of both pEC and pUC18 plasmid samples were obtained by plotting the free radical concentrations against the radiation dose. The free radical yields, G(∑fr), were then calculated from the slope of the dose-response curves.

In a separate experiment, a dose-response curve for free radical trapping was determined at a dose regime extending from 0 to 1000 kGy for a pUC18 sample hydrated to Γ = 22 waters/ nucleotide. The dose-response curve was then fit to a two-component model.⁴³ In this model, each component represents a set of radical species that are characterized by different values of G and k, namely, the base-centered and the sugar-centered radicals. The relationship between the free radical concentration, C, and the absorbed dose, D is given by the expression

$$C(D)=(G_{\text{b}}/k_{\text{b}})[1-{\text{e}}^{-k_{\text{b}}D}]+(G_{\text{s}}/k_{\text{s}})[1-{\text{e}}^{-k_{\text{s}}D}]$$ (1)

where G_b represents the rate of production and k_b represents the rate of destruction, for the base-centered radicals, and G_s, k_s represent the same for the sugar-centered radicals. From eq 1, the quantities (G_b/k_b) and (G_s/k_s) yield the values of C_mxB and C_mxS , the free radical concentration at saturation of the base-centered and the sugar-centered radicals, respectively. The total free radical yield, G(∑fr), is G_b + G_s. The dose-response curves are fit to the above model using a nonlinear least-squares fitting routine based on the Levenberg–Marquardt method.⁴⁴

Agarose Gel Electrophoresis

Immediately after irradiation and EPR spectroscopy, the samples were dissolved in 1X TE buffer (10⁻² mol dm⁻³ Tris, 10⁻³ mol dm⁻³ EDTA, pH 8.0) to 10-fold their weight in volume. Aliquots of this solution were then mixed with equal volumes of the loading buffer containing 0.1% bromphenol blue and assayed by agarose gel electrophoresis at 4 °C in TBE (89 mmol dm⁻³ boric acid, 89 mmol dm⁻³ Tris, 1 mmol dm⁻³ EDTA). The pEC plasmid samples were run on 0.75% neutral agarose gels at a voltage gradient of 1.5 V cm⁻¹ for 16 h with 0.25–0.5 μg of DNA loaded into each well, whereas the pUC18 plasmid samples were run on 1.4% neutral agarose gels at a voltage gradient of 2.0 V cm⁻¹ for 16 h with 0.1–0.25 μg of DNA loaded into each well. After electrophoresis, the gels were stained in a solution of SYBR Green I dye (Molecular Probes, Eugene, OR) for 1 h at a 1:10 000 dilution of the stock solution. The gels were scanned with a Fluor-S MultiImager MAX (BIO-RAD laboratories). The relative amount of DNA in each of the three plasmid conformations was estimated by integration of the intensity of the pixels comprising each band using the Quantity One quantitation software.

To account for the lower binding constant of SYBR Green I dye to the supercoiled plasmid relative to the open-circle and linear conformations, intensities of supercoiled bands were multiplied by a factor of 1.4. The value of this correction factor was determined using a slightly modified version of the procedure employed by Arnold et al.⁴⁵ in which the fluorescence intensities of equal quantities of supercoiled and linear plasmids are compared.

The plasmids were linearized by digestion with the restriction endonuclease Eco RI (New England Biolabs) at 37 °C for 1 h. The restriction enzyme activity was quenched by the addition of 10 μL of 0.5 M EDTA solution and the mixture kept on ice prior to electrophoresis. An equal amount of unirradiated DNA (1μg) was then added to this enzymatically linearized DNA. Correction factors were calculated for each gel run from the intensities of the fluorescence of the three bands in both of the control lanes containing a linearized plasmid. The value of 1.4 ± 0.05 for the correction factor was obtained from six different sets of experiments.

Calculation of the G Value for ssb and dsb Formation

In the plot of the logarithm of the fraction of supercoiled DNA against radiation dose, the data are fitted to a straight line. The reciprocal of the slope gives D₀. Assuming Poisson statistics for ssb induction, D₀ represents the radiation dose required to give, on average, one ssb per plasmid molecule.

The G value for ssb formation is then given by the expression

$$G(\text{ssb})=1000/[D_0(\text{in\hspace{0.28em}Gy})\times \text{MW}(\text{in\hspace{0.28em}MDa})]\mathrm{\hspace{0.17em} }(\text{in\hspace{0.28em}}\mu \text{mol}/\text{J})$$ (2)

where MW represents the molecular weight of the plasmid sample. The yield for double strand breaks, G(dsb), is determined from the dose-response plot of the fractional abundance of the linear form of DNA. The data set is fitted with a least mean squares polynomial of the form y = ax² + bx + c.

The G value for dsb formation is then given by the expression

$$G(\text{dsb})=b\times 1000/\text{MW}(\text{in}\mathrm{\hspace{0.17em} }\text{MDa})\mathrm{\hspace{0.17em} }(\text{in\hspace{0.28em}}\mu \text{mol}/\text{J})$$ (3)

where b is obtained from the slope of the dose–response curve.

Molecular weights of dry pEC plasmid (10 810 bp) and dry pUC18 plasmid (2686 bp) DNA are determined to be (665 × 10810) Da ≈ 7.189 MDa and (665 × 686) Da ≈ 1.786 MDa, respectively. The average mass of a base pair as sodium salt is assumed as 665 Da.

Results

Free radical yield and strand break yields were measured on the same DNA sample sets. That is, for any given dose point within a dose-response curve, the same sample was used to measure the concentration of free radicals trapped by plasmid at 4 K as was used to measure the fraction of plasmids sustaining strand breaks after warming to room temperature and dissolution in water. A typical EPR spectrum of pUC18 film, X-irradiated and observed at 4 K, is shown in Figure 1. The spectra of pEC are qualitatively the same.

Figure 1.

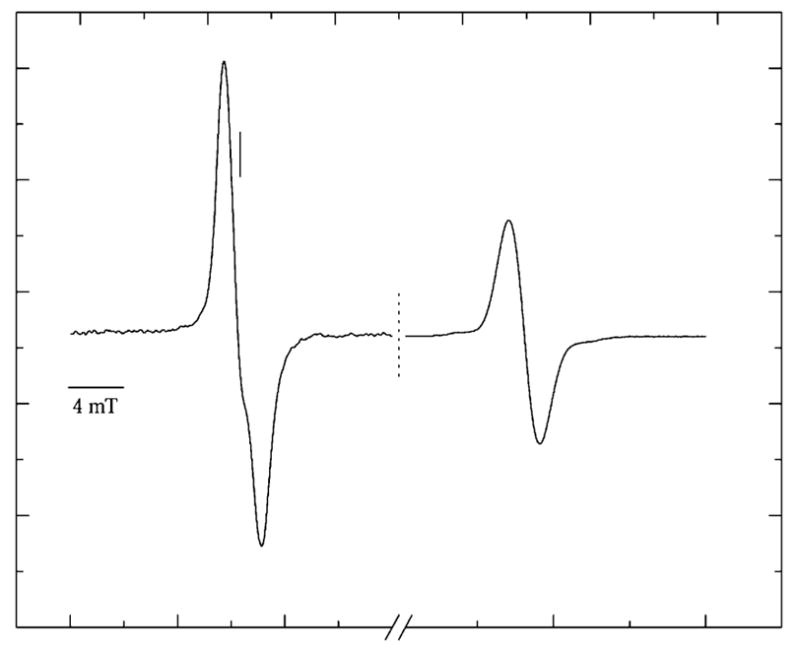
First-derivative, Q-band, EPR spectrum recorded at 4 K of pUC18 plasmid X-irradiated to 2400 Gy at 4 K. The scan is paused at the dashed line, the field sweep center increased by 20 mT, and the signal gain adjusted to record the singlet of the ruby reference at high field. The vertical solid line marks g = 2.0022.

By comparing the intensity of the pUC18 spectrum to that of the adjacent ruby spectrum, the concentration of radicals trapped by DNA at 4 K was determined. The concentration of trapped radicals increases linearly at low dose, as can be seen in Figure 2. The slope of the linear fit, at these low doses, gives the yield of radicals trapped by DNA, G(∑fr). For pEC and pUC18 films at 4 K, G(∑fr) is found to be 0.71 ± 0.02 and 0.61 ± 0.01 μmol/J, respectively.

Figure 2.

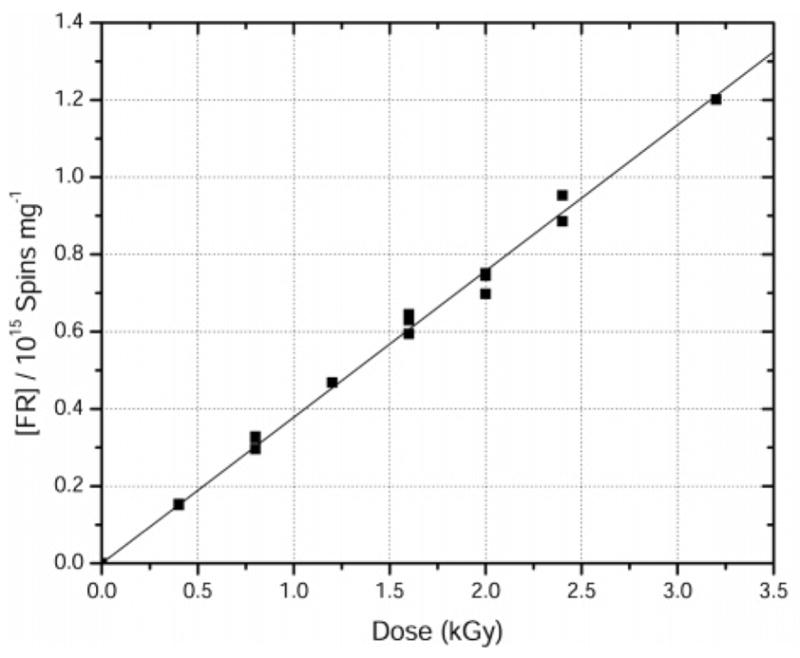
Free radical dose-response curve for X-irradiated pUC18 plasmid films hydrated to Γ = 22 mol water/mol nucleotide. X-irradiation and EPR measurements were done at 4 K. G(∑fr) = 0.61± 0.01 μmol/J.

We note that the standard errors in these yields are increased by the fact that a different sample is used at each dose point. If, instead, the same DNA sample had been used for all the dose points, as is done for the high-dose free-radical-response curve discussed at the end of this section, the standard error would be significantly smaller. The larger errors shown above are more realistic because they reflect the fact that free radical yields are sensitive to DNA packing.^20,35

The yield for single strand breaks, G(ssb), was obtained for both pEC and pUC18 plasmid DNA by plotting the logarithm of the fraction of intact supercoiled DNA against the radiation dose. One data set for pUC18 films is shown in Figure 3.

Figure 3.

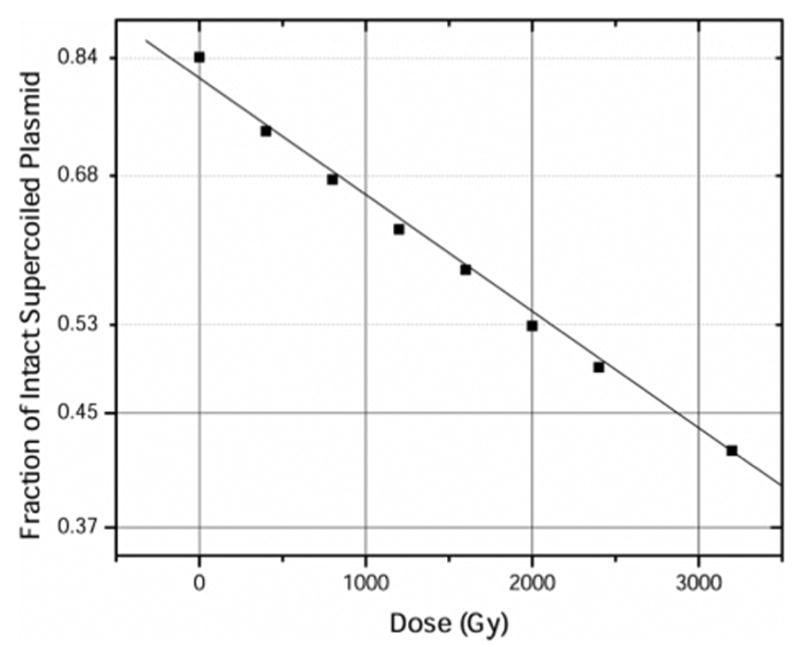
Loss of supercoiled DNA in films of pUC18, X-irradiated at 4 K, warmed to room temperature, and dissolved in 1X TE buffer. The data set is fitted with a straight line of the form y = c e^−mx. From the slope m, G_prompt(ssb) = 0.12 ± 0.01 μmol/J.

This analysis assumed that ssb events are significantly greater than dsb events (which also result in the loss of intact supercoiled plasmid). Likewise, the yield for double strand breaks, G(dsb), was determined from the dose-response plot of the fractional abundance of the linear form of DNA (see Figure 4).

Figure 4.

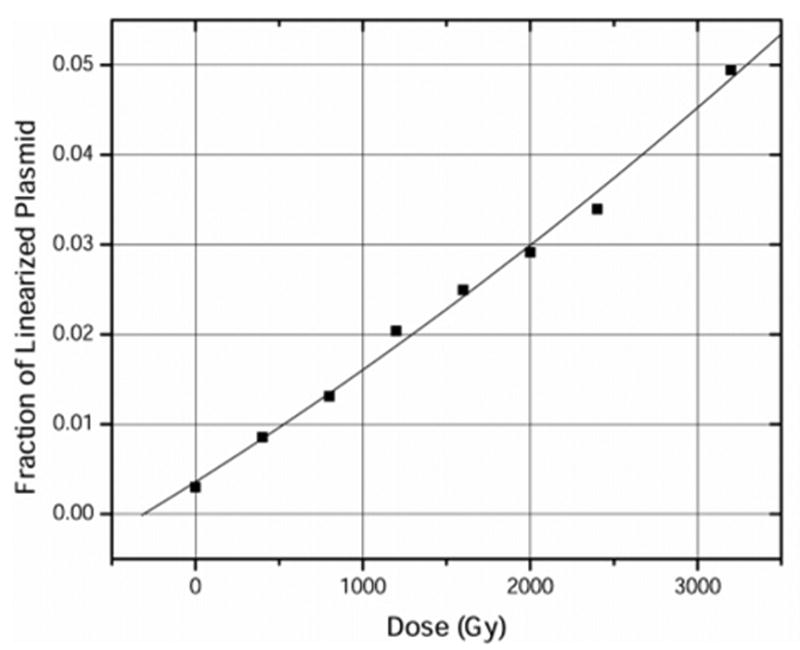
Formation of linearized plasmid in pUC18 plasmid DNA, corresponding to the loss of supercoiled plasmid plotted in Figure 3. The data set is fitted with a least mean squares polynomial of the form y = ax² + bx + c. From the value b, G(dsb) = 0.007 ± 0.001 μmol/J.

The G values for both ssb and dsb formation were calculated as described under Materials and Methods. The total single strand break yield, G_total(ssb), which includes both the prompt and the heat-labile strand breaks, and the double strand break yield, G(dsb), were found to be 0.09 ± 0.01 and 0.010 ± 0.001 μmol/J for pEC plasmid DNA, and 0.14 ± 0.01 and 0.007 ± 0.001 μmol/J for pUC18 plasmid DNA, respectively. These yield values were found to be in excellent agreement with yields obtained for a second set of pEC and pUC18 plasmid samples that were measured by the same procedure. The strand break yields are compared with the free radical yields in Table 1.

TABLE 1.

Yields of ssb and dsb Induced in X-Irradiated Samples of pEC and pUC18 Plasmid DNA Hydrated to a Γ = 22 ± 1 mol Water/mol Nucleotide (Standard Errors Are in Parentheses)

sample	G(∑fr) (μmol/J)	G(ssb)a (μmol/J)	G(ssb)/G(∑fr)b	G(dsb)a (μmol/J)	G(ssb)/G(dsb)b
pEC plasmids
prompt strand breaks	0.71 (0.02)	0.08 (0.01)	0.11 (0.01)	0.010 (0.001)	8 (1)
prompt + heat labile strand breaks	0.71 (0.02)	0.09 (0.01)	0.13 (0.01)	0.010 (0.001)	9 (1)
pUC18 plasmids
prompt strand breaks	0.61 (0.01)	0.12 (0.01)	0.20 (0.02)	0.006 (0.001)	20 (4)
prompt + heat labile strand breaks	0.61 (0.01)	0.14 (0.01)	0.23 (0.02)	0.007 (0.001)	20 (3)

^aThe standard deviations are calculated from six different sets of gel electrophoresis data.

^bThe standard deviation of the quotient in each case is calculated using standard statistical procedure: For (A ± a)/(B ± b) = (D ± d), where “/” indicates division and A/B = D, then d = D ×[(a/A)² + (b/B)²]^1/2.

The high-dose-response data were recorded using a single pUC18 sample hydrated to Γ = 22 mol water/mol nucleotide. The fit shown in Figure 5 is to the two-component model described under Materials and Methods and the parameter values thus derived are listed in Table 2. Based on the goodness-of-fit value, as represented by the R² parameter (R² ≈ 0.999), the dose-response curve is seen to have a fairly robust fit to the model. Central to the discussion below is the finding that the yield of radicals trapped on sugar at 4 K is 1/10 the yield of all radicals trapped by the DNA.

Figure 5.

Corrected dose-response curve for free radical trapping by pUC18 plasmid film hydrated to Γ = 22 mol of water/nucleotide, fit to the two component model given in eq 1. X-irradiation and EPR were done at 4 K. R² is the goodness of fit, and χ² is the reduced χ²-value calculated by the nonlinear least-squares fitting routine used by ORIGIN. Inset: G(∑fr) = 0.62 ± 0.001 μmol/J was calculated from a fit to the initial linear response.

TABLE 2.

Parameters G_b, G_s, k_b, and k_s Obtained by Fitting Eq 1 to the Dose-Response Curve for pUC18 Plasmid Film Sample at a Γ = 22 ± 1 mol Water/mol Nucleotide^a

sample	Gb (μmol/J)	Gs (μmol/J)	Gb/Gsb	kb (kGy−1)	ks (kGy−1)	kb/ksb	G(∑fr) (μmol/J)	Gb/G(∑fr)b
pUC18 plasmids	0.560 (0.008)	0.061 (0.0004)	9.2 (0.1)	0.046 (0.001)	0.00070 (0.00003)	66 (3)	0.621 (0.004)	0.90 (0.01)

^aThe standard deviation of the average and the quotient in each case is calculated using standard statistical procedure.

^bThe standard error for each parameter as reported by the nonlinear least-squares fitting procedure is included in the parentheses. From previous work,²⁰ the relative error in G value is seen to vary from ±5% to ±15%.

Discussion

Using the exact same DNA samples, this study has successfully determined the yields of (i) total radicals trapped on DNA at 4 K, G(∑fr), (ii) radicals trapped on the deoxyribose, G_sugar-(fr), (iii) prompt single strand breaks, G_prompt(ssb), (iv) total single strand breaks, G_total(ssb), and (v) double strand breaks, G(dsb). This makes possible, for the first time, a quantitative comparison of strand breaks with presumed radical precursors using results that are not encumbered by confounding variables inherent to solid-state DNA preparations.³⁶ Of the findings summarized in Tables 1 and 2, the most provocative is that the yield of total single strand breaks exceeds the yield of trapped sugar radicals, i.e., G_total(ssb) > G_sugar(fr). The implications of this inequality will be discussed after comparing our yield measurements with those in the literature.

Free Radical Yields

The free radical yields reported in Table 1, 0.71± 0.02 μmol/J for pEC and ~0.61± 0.01 μmol/J for pUC18 plasmid, represent the first such measurements made on samples of high molecular weight DNA that possess a high degree of homogeneity. The molecular weight and base composition are effectively invariant, the fraction of single stranded regions is effectively zero, and the tertiary conformation is predominantly supercoiled with the remaining fraction in relaxed circular form. The plasmid G(∑fr) values are, however, higher than those reported previously for high molecular weight DNA hydrated to a similar extent. For example, films of sodium salt calf thymus DNA, irradiated and measured at 4 K, give a peak value of G(∑fr) = 0.45 ± 0.05 μmol/J at Γ = 15 waters/nucleotide and G(∑fr) = 0.35 ± 0.05 μmol/J at Γ = 20.³⁵

On the other hand, comparable values of G(∑fr) are observed in crystalline DNA X-irradiated at 4 K. The yields for crystalline samples of 13 different oligodeoxynucleotides fall in the range of 0.55–0.75 μmol/J.²⁰ In crystalline DNA, G(∑fr) is seen to be independent of Γ over the range 4 < Γ < 16.²² These high yields have been attributed to the high density of DNA packing, and their lack of dependence on Γ is related to the relative constancy of DNA density in these crystalline samples.^20,35 The high yields observed for the plasmid DNA films are consistent with the expectation that supercoiled DNA condensed in the form of films will result in a relatively high DNA packing density.

To shed light on the mechanisms of strand break, it is necessary to know the yield of radicals trapped on the sugar moiety of DNA, G_sugar(fr). Sugar radicals are known precursors to strand breaks, whereas base radicals are not.⁴⁶ As seen in Table 2, 10% of the trapped radicals in pUC18 DNA reside on the sugar. Similar results were obtained for four different crystalline DNA oligomers, where between 8% and 19% of the radicals were trapped on the sugar at 4 K.⁴³ While the standard errors in these determinations of G_sugar(fr) are relatively small, we do not yet have a means of assessing the accuracy of the absolute value. With that caveat, we do believe there is merit in comparing the value of G_sugar(fr) = 0.06 μmol/J measured for pUC18 with the total strand break yields measured in the same samples.

Single Strand Break Yields

The values for total single strand break, G_total(ssb), for pUC18 and pEC X-irradiated at 4 K are 0.09 ± 0.01 and 0.14 ± 0.01 μmol/J, respectively. Comparison of these values to others in the literature needs to be done with care because not much is known as to how strand break yields vary with respect to sample preparation and irradiation conditions.⁴⁷ The work of Swarts et al.⁴⁸ has had an important impact on understanding the effects of variable hydration. Those authors measured free base release from lyophilized salmon sperm DNA X-irradiated at room temperature as a function of hydration. Because of the tight correlation between base release and strand break, these yields provide a good, although indirect, measure of G_total(ssb). At Γ = 22.4 and 2.5 waters/nucleotide, Swarts et al. found the yield of free base-release to be 0.055 ± 0.007 and 0.073 ± 0.003 μmol/J, respectively. The yield of free base release for a DNA hexamer and decamer in crystalline form, X-irradiated at 4 K, was found to be 0.058 ± 0.003 and 0.109±0.007 μmol/J, respectively.⁴⁹ The yield of 3′- and 5′- phosphate terminated fragments in a series of crystalline oligomers provides a lower boundary for the yield of strand breaks. The fragment yields varied between 0.06 and 0.16 μmol/J, and radiation temperature, 4 K versus room temperature, appears to have only a small influence on these yields.^24,49,50 G_total(ssb) for solid-state pUC18 X-irradiated at 5.6 °C were measured by Yokoya et al.³⁸ At a nominal Γ of 24.5 (inferred from the measured relative humidity) and relatively high salt conditions, G_total(ssb) was determined to be 0.068 ± 0.006 μmol/J; the value for immediate strand breaks was the same within the margins of error. Given the differences in sample preparation and radiation conditions, the values of G_total-(ssb) reported in Table 1 are consistent with these earlier reports.

Double Strand Break Yields

In this study, the G(ssb)/G(dsb) ratio is found to vary between 8 and 20 in pEC and pUC18 plasmid DNA. It is evident from previous studies^37,51 that a ratio in the 10–20 range is much too small to be accounted for by two ssb occurring independently on opposite strands within close proximity (~10 bp) of each other. Knowing that base radicals are ineffective in causing strand breaks,^50,52 it is now widely accepted that the main source of dsb is spatially correlated ssb (which occur in multiply ionized sites).^37,53 The dose-response curve for the induction of prompt dsb is shown to be linear in this study, indicating that these lesions arise from interactions with a single radiation track, rather than from an accumulation of multiple lesions arising from more than one radiation track. It is well known, from dose-response curves measuring free radical trapping in DNA at low temperature, that track overlap is not detectable until reaching doses above 5 kGy.⁵⁴

Strand Break Mechanisms

Given that sugar radicals are precursors to strand breaks, in pUC18 plasmids X-irradiated at 4 K, 0.06 μmol/J (G_sugar(fr)) out of 0.14 μmol/J (G_total(ssb)) of the total ssb yield is accounted for. This leaves 0.08 μmol/J (0.14 – 0.06) of ssb yield unaccounted for. It follows, therefore, that other mechanisms of comparable importance must exist.

Dissociative Electron Attachment (DEA)

Elegant experiments by Sanche, Huntington, Huels, and co-workers have shown that low-energy electrons (LEE) give single strand breaks in plasmid DNA.^28,29,55,56 These experiments were conducted on very dry DNA at 77 K under high vacuum. Because LEE are major intermediaries of the action by ionizing radiation, there is little doubt that some fraction of the 0.08 μmol/J shortfall is accounted for by dissociative electron attachment, a resonant interaction that results in fragmentation. Not known, however, is the absolute yield of DEA-generated strand breaks.

Homolytic Bond Cleavage by Excited States

When ionizing radiation is absorbed, it does so via both ionization and excitation events, with comparable likelihood. Also, recombination of radical ions produces excitations. Brocklehurst⁵⁷ has pointed out that homolytic bond cleavage by excited states of the sugar phosphate backbone would generate a hydrogen atom that is likely to react with a nearby sugar, the consequence of which would be double strand break. It is suggested that this may explain the low ratio of G(ssb)/G(dsb) (the ratios in Table 1 are typical). In fact, there is compelling evidence of this type of reaction sequence in model compounds of DNA. EPR studies have shown that hydrogen atom adducts, and even radical pairs, are a dominant form of radical damage in crystalline bases whenever extensive hydrogen bonding networks are absent in the crystal lattice.⁵⁸ In these cases, however, the yield of radicals assignable to homolytic bond cleavage is quite low, ~0.001 μmol/J. Therefore, while this mechanism may play a marginal role in hydrated DNA, the possibility that it accounts for more than a very small fraction of strand breaks in the plasmid films appears unlikely.

Hydroxyl Radical Attack

The hole produced by ionizations in the DNA’s solvation shell is involved in two competing reactions: hole transfer to the DNA and formation of OH^•. For those holes initially formed in the tightly bound solvation shell (Γ 10) of DNA, transfer to the sugar and bases occurs rapidly; for the outer lying waters (9 < Γ < 22), the rate at which the water radical cation deprotonates is faster than the transfer rate, and OH^• formation dominates. Sevilla and co-workers have shown that OH^• is not detected in relatively dry DNA (Γ < 8)⁵⁹ but is detected at increasingly higher hydrations, suggesting that all holes produced in the solvation shell do not transfer to the DNA in the regime (8 < Γ < 22). La Vere et al. measured an OH^• yield of 0.07 μmol/J for DNA hydrated to Γ = 20 and irradiated at 77 K.⁶⁰ Some fraction of these OH^• radicals would be expected to react with DNA, but that fraction is unknown. The yield of H₂O₂, measured at very high doses (65 kGy), is 0.0026 μmol/J for DNA hydrated to 23 < Γ < 27 and irradiated at 77 K, suggesting that H₂O₂ formation is a very minor pathway. On the other hand, experiments utilizing OH^• scavengers lead to the conclusion that DNA radicals, due to OH^• abstraction and addition, are not formed at 77 K.⁶¹ We are unable to measure low levels of OH^• radicals in this type of amorphous state because of extremely broad EPR lines that result from a combination of the large variation in g-tensors and working at Q-band microwave frequencies.²² It is conceivable, therefore, that OH^• attack accounts for the shortfall between the yields of strand breaks and DNA trapped radicals.

Doubly Oxidized Sugar

Combination reactions dominate the free radical processes initiated by ionization of DNA.⁵⁸ In the absence of geminate ion recombination and cross combination reactions, the yield of radicals should be ~1.18 μmol/J,⁶² assuming the absorption cross sections for DNA are the same as those for water.³⁴ In pUC18 plasmid at 4 K (G(∑fr) = 0.61±0.01 μmol/J), 52% (0.61/1.18) of the free radicals would be, thereby, lost via combination reactions. Of these, the reactions that recombine holes with electrons result primarily in return to the parent structures, i.e., no damage. In contrast, hole–hole combination reactions result in one site being doubly oxidized; the probability of damage at such a site is very high.

The analysis presented above indicates that, for DNA irradiated at 4 K, 10% of the holes are trapped in the form of neutral deoxyribose radicals and 90% are trapped on the bases. Electron trapping is exclusively by the pyrimidines and hole trapping by the bases is predominantly (perhaps exclusively) by guanine.^63–65 The hole located on guanine (Gua^•+) is mobile^66,67 but the range at 4 K is short, <10 bp. During the recombination events that occur at 4 K, this mobility allows for an increased probability of encounters between neutral deoxyribose radicals and Gua^•+. One-electron oxidation of the carbon-centered radicals on the DNA backbone by Gua^•+ is expected to be energetically favorable.⁶⁸ Such a reaction would result in a second one-electron oxidation at a single site on the backbone.

Quantitative considerations indicate that it is feasible that double one-electron oxidation of sugars at one site is a significant pathway for strand breaks produced by direct ionization. About half of the 0.61 μmol/J radicals lost to combination reactions in pUC18 are presumed to be holes; if half of these combine with one another, the yield would be 0.076 μmol/J (0.61/8). If, as suggested previously,⁶⁹ the range of guanine trapped holes (Gua^•+) is greater than the range of the trapped electron (Pyr^•−), the probability of this event will be increased. Multiple oxidation at a single site has been reported in a recent work by Sevilla et al.²⁵ where evidence is presented for the formation of triple one-electron oxidation at guanine in solid-state DNA. We believe, therefore, that it will be valuable to design experiments that test for the occurrence of two one-electron oxidations at a single site.

Conclusion

Measurement of strand break and free radical yields for the same plasmid samples makes it possible, for the first time, to quantitatively test the premise that free radicals are the primary precursors to strand breaks. The total yield of trapped radicals, G(∑fr), in pEC and pUC18 is 0.71 ± 0.02 and 0.61 ± 0.01 μmol/J, respectively. The yield of prompt plus heat-labile single strand breaks, G_total(ssb) in pEC and pUC18 is 0.09 ± 0.01 and 0.14 ± 0.01 μmol/J, respectively. The ratio of total ssb to dsb in pEC and pUC18 is ~9 and ~20, respectively. For pUC18 films, the yield of radicals trapped on the DNA sugar, G_sugar-(fr), is ~0.06 μmol/J, surprisingly less than half of G_total(ssb). We suggest, therefore, that a significant fraction of strand breaks are derived from precursors other than trapped DNA radicals. Alternate reaction pathways are briefly considered, one of which is a novel mechanism whereby strand breaks are produced by two one-electron oxidations at a single site. The first oxidation is by direct ionization and the second is by a mobile guanine radical cation.