The Role of Hydration in the Distribution of Free Radical Trapping in Directly Ionized DNA

Abstract

The purpose of this study was to elucidate the role of hydration (Γ) in the distribution of free radical trapping in directly ionized DNA. Solid-state films of pUC18 (2686 bp) plasmids were hydrated to Γ in the range 2.5 ≤ Γ ≤ 22.5 mol water/mol nucleotide. Free radical yields, G(∑fr), measured by EPR at 4 K are seen to increase from 0.28 ± 0.01 μmol/J at Γ =2.5 to 0.63 ± 0.01 μmol/J at Γ = 22.5, respectively. Based on a semi-empirical model of the free radical trapping events that follow the initial ionizations of the DNA components, we conclude that two-thirds of the holes formed on the inner solvation shell (Γ < 10) transfer to the sugar-phosphate backbone. Likewise, of the holes produced by direct ionization of the sugar-phosphate, about one-third are trapped by deprotonation as neutral sugar-phosphate radical species, while the remaining two-thirds are found to transfer to the bases. This analysis provides the best measure to date for the probability of hole transfer (~67%) into the base stack. It can thus be predicted that the distribution of holes formed in fully hydrated DNA at 4 K will be 78% on the bases and 22% on the sugar-phosphate. Adding the radicals due to electron attachment (confined to the pyrimidine bases), the distribution of all trapped radicals will be 89% on the bases and 11% on the sugar-phosphate backbone. This prediction is supported by partitioning results obtained from the high dose–response curves fitted to the two-component model. These results not only add to our understanding of how the holes redistribute after ionization but are also central to predicting the yield and location of strand breaks in DNA exposed to the direct effects of ionizing radiation.

INTRODUCTION

Free radical ions, due to either the loss or gain of one electron, are produced in DNA by ionizing radiation through energy deposition in DNA and its surrounding water. From the initial distribution of ionizations, a population of trapped radicals arises through a series of electron transfer reactions. These transfer reactions redistribute some of the initial ionizations from water to DNA and from one DNA component to another. The hole thus transferred to a more stable site gives rise to subsequent reactions that are indistinguishable from those initiated by the direct ionization of DNA. Because it is indistinguishable, the damage that arises from ionization of either DNA or its tightly bound water is called direct-type damage. To understand the chemistry of direct-type damage and the attending radiation biology, it is important to determine the distribution of the precursors to that damage.

The influence of the solvation shell on DNA radiation chemistry has been studied between 4 K and 77 K in a number of laboratories (1–12) by varying the level of DNA hydration in solid-phase samples; the level of DNA hydration is expressed as Γ in mol water/mol nucleotide. Hole transfer dominates only for the water in direct contact with DNA, Γ = 9–10 mol water/mol nucleotide. For the water in the outer portion of the solvation shell, 9 < Γ < 23, HO^• formation dominates (7, 9, 12). Reactions stemming from these hydroxyl radicals and hydroxyl radicals formed in the bulk water (Γ > 23) are indistinguishable from each other; both lead to HO^•-induced DNA damage (3, 10). It is generally believed that clustering is a major determinant of biological impact (13–16); therefore, it is important to determine the degree of track expansion between energy deposition and end-product formation. With respect to one-electron reduction, this should not be too hard to model. The estimated thermalization distance for the electron in liquid water is 2.5–3.0 nm (17). Most of the migration is done by electrons with less than 7 eV of energy (18). The yield of DNA trapped electrons produced by water ionization is effectively equal to the yield produced by direct ionization of the DNA itself. The thermalized electron attaches nearly exclusively to the base stack and at 4 K most likely travels only a few base pairs (19) before trapping out, partially at thymine but primarily at cytosine (20–23). Since there are very few competing reactions at Γ < 16, transfer of excess electrons stemming from water ionization is ~100% efficient (11). Unlike the ejected electrons, the distribution of hole formation and migration is more complex.

Ionization sites, also called one-electron oxidation sites, or holes, are formed in all components of the sample. Low-LET irradiation of fully hydrated DNA deposits approximately an equal amount of energy in the solvation shell as in the DNA itself (24). The initial yield of radicals in liquid water is G = 1.18 μmol radicals/J (25). A mean energy of 20 eV is deposied per electron/hole pair produced in the water (18, 26), occurring on a time scale of 10⁻¹⁷ s (5). The attenuation cross section for DNA is expected to be comparable to that of liquid water (27). A large fraction, 50–75%, of the initial radicals have combined with each other before EPR measurements are made on DNA samples irradiated at 4 K (28). The holes that remain are trapped as deprotonated radical cations, and they are found in each component of the sample: the solvation shell, the DNA backbone, and the DNA bases (5, 7, 9, 12, 29–31).

The observed distribution of trapped holes differs substantially from the distribution of initial sites of ionization based on the Bragg rule. According to the Bragg rule, the probability of ionizing a component is directly proportional to the number of valence electrons making up that component. In principle, therefore, it should be possible to determine how hole transfer between components alters the initial hole distribution to give the final distribution of trapped damage. Here we focus on the early hole transfer processes, defined as the events that lead to free radical trapping at 4 K. Our perspective relies heavily, but not exclusively, on information gained from electron paramagnetic resonance (EPR) spectroscopy.

There are two objectives in our present study, which builds on our earlier work (32). One is to determine how holes partition between the three sample components: solvation shell, sugar-phosphate backbone, and DNA bases. The other is to investigate how this partitioning depends on the level of hydration. Both aims are directed toward gaining a better understanding of the mechanisms of strand break formation and damage clustering caused in DNA by the direct effects of ionizing radiation.

MATERIALS AND METHODS

The preparation and purification of plasmid pUC18(2686 bp) have been described previously (32, 33). Appropriate aliquots of the pUC18 plasmid solution were drawn into open-ended silylated suprasil quartz tubes and then allowed to dry and equilibrate in humidity chambers containing a saturated solution of NaOH that gave a relative humidity of 5% (34). It is assumed that under these conditions DNA contains ~2.5 mol water/mol nucleotide. These ‘‘dry’’ samples were then weighed and subsequently taken to the desired level of hydration by allowing them to equilibrate for a minimum of 3 weeks in humidity chambers containing saturated solutions of KNO₂, NaNO₂, KBr and K₂HPO₄, which give a relative humidity of 45%, 66%, 84%, and 92%, respectively (34). From the weights determined before and after equilibration, the level of hydration (Γ) could be determined accurately for each individual sample. While the samples were briefly exposed to air during weighing and sample preparation (when they were sealed) for EPR, these exposures did not measurably alter the level of hydration. The mass fraction of film consisting of DNA plus solvation shell varies between 92 ± 3% and 87 ± 4% with increasing Γ; the remaining ~10% is assumed to consist of salt. This fraction was determined after the EPR measurement by dissolving a known mass in a known volume of water and measuring the absorbance at 264 nm.

Samples were irradiated at 4 K in a Janis Dewar EPR-accessory (35) with X rays generated by a Varian/Eimac OEG-76H tungsten-target tube operated at 70 keV and 20 mA and filtered by 0.025 mm aluminum foil. The dose rate was 24 kGy/h. The dose regimen extended from 0 to ~1000 kGy for individual pUC18 samples. The samples were raised into the EPR cavity and allowed to thermally equilibrate for several minutes before spectra were recorded. All EPR spectra were taken as first derivatives with a Q-band (35 GHz) Varian E-12 EPR spectrometer. Free radical concentrations were then determined by comparing the intensity of the signal due to DNA radicals trapped at 4 K to that of a ruby standard mounted on the inside wall of the EPR cavity (36). Because the EPR signal due to irradiated quartz grows in very slowly, it was subtracted only in the experiments that extended to very high doses (>50 kGy) (30). No attempt was made to measure the concentration of trapped hydroxyl radicals because its broad signal would be very difficult to detect. Dose–response curves for free radical trapping were determined at dose regimens extending from 0 to ~1000 kGy for pUC18 samples hydrated to Γ of 2.5, 11.5 and 22.5 mol water/mol nucleotide, respectively. The dose–response curves were then fitted to a two component model described previously (30, 32). In this model, each component represents a set of radical species that are characterized by different values of G and k, namely, the base-centered and the sugar-centered radicals. These two components may also be referred to as charged radicals and neutral radicals (31), which allows for the possibility that a minor population of neutral base radicals are included in the component we assign to sugar radicals. In our analysis, the impact of neutral base radicals is assumed to be negligible. Equation (1) describes the relationship between the free radical concentration, C, and the absorbed dose, D. G is defined as the slope of the dose–yield curve in the limit of zero dose (chemical yield), and k is the destruction of radicals per unit dose; G is based on the total film mass. Thus we have the expression

$$C(D)=\left(\frac{G_{base}}{k_{base}}\right)(1-e^{-k_{base}D})+\left(\frac{G_{sugar}}{k_{sugar}}\right)(1-e^{-k_{sugar}D}),$$ (1)

where G_base and k_base represent the rate of production and the rate of destruction, respectively, for the base-centered radicals and G_sugar and k_sugar represent the same for the sugar-centered radicals. The total free radical yield, G(∑fr), is G_base + G_sugar. The dose–response curves are fitted to the above model using a nonlinear least-squares fitting routine based on the Levenberg-Marquardt method (37).

RESULTS

The EPR spectra of variably hydrated pUC18 plasmid DNA X-irradiated at 4 K with a dose of 3 kGy are shown in Fig. 1. The major features of the spectra are relatively well understood from earlier work (22, 38–44). The features in the central region of the spectra are consistent with the presence of one-electron reduced pyrimidines (prominent doublet with a poorly resolved splitting of roughly 2 mT) and one-electron oxidized guanine (consisting of a broader singlet). The wing features of the spectra are due to a sub-population of deoxyribose radicals and become increasingly prominent at higher doses; these are shown in Fig. 2 for plasmid DNA hydrated to Γ of 2.5, 7.5, 11.5 and 22.5 mol water/mol nucleotide irradiated with a dose of 90 kGy.

FIG. 1.

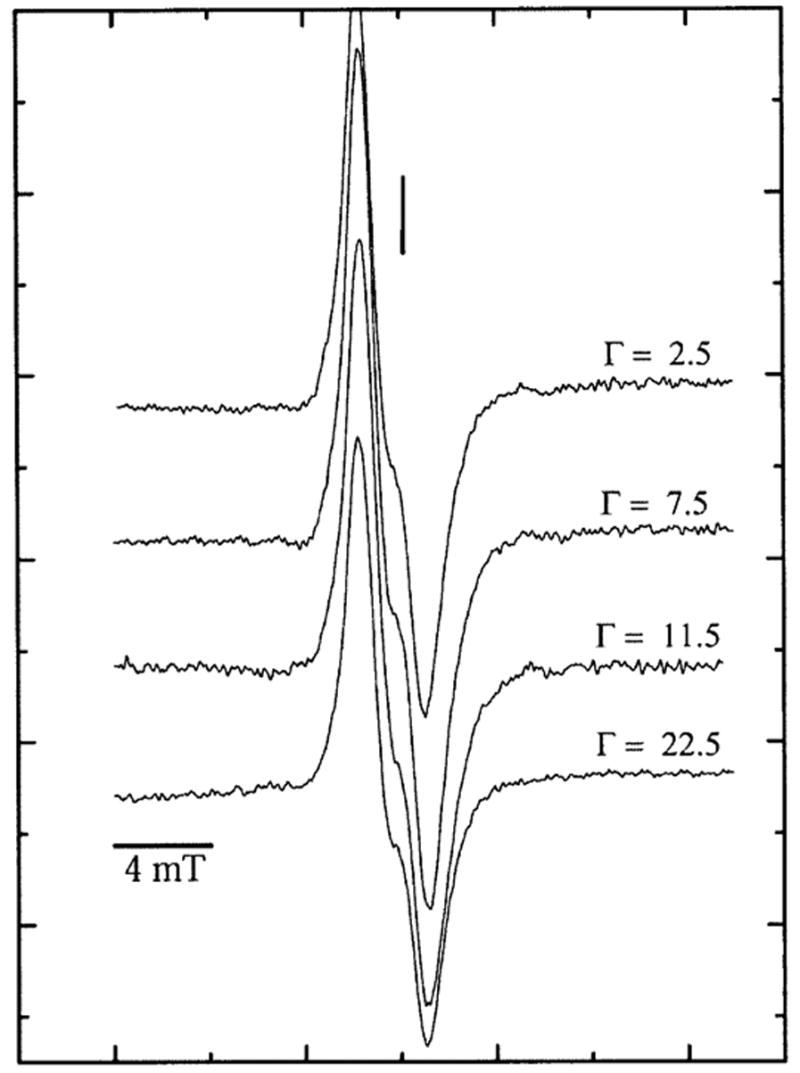
First-derivative, Q-band, EPR spectra of pUC18 plasmid X-irradiated with a dose of 3 kGy and recorded at 4 K at various Γ. The vertical line corresponds to the position of g = 2.0022. The modulation amplitude was 0.40 mT, and the microwave power attenuation was 50 dB, delivering 0.3 nW to the cavity. The signal from ruby, used as an internal standard to determine the free radical concentration, lies about 40 mT up field from the DNA signal and is not shown here.

FIG. 2.

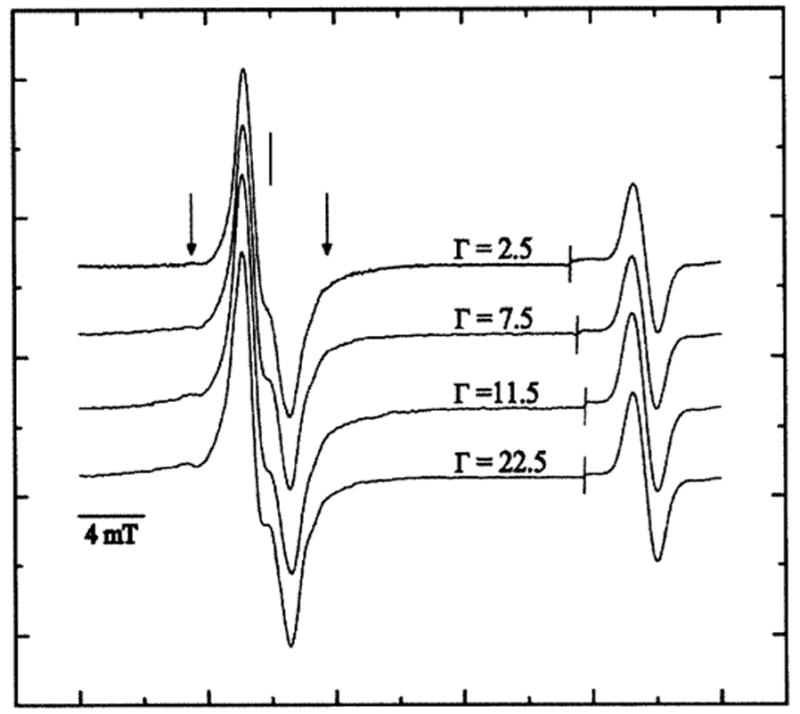
First-derivative, Q-band, EPR spectra of pUC18 plasmid X-irradiated with a dose of 90.0 kGy and recorded at 4 K at various Γ. The spectral width was 40 mT. The scan was paused at the line as shown; the field sweep center was then increased by 20 mT and the signal gain adjusted before continuing the sweep to record the strong singlet of the ruby reference at high field. The vertical line corresponds to the position of g = 2.0022. The vertical arrows indicate the broad wing-line features of the putative sugar radicals.

From the EPR spectra such as those shown in Fig. 1, we would like to extract the fraction of the spectral intensity due to deoxyribose radicals. But deconvoluting these spectra so as to obtain a good quantitative measure of the yield of deoxyribose radicals would be very difficult. This is because of the severe overlap between the spectrum of the base radicals and the deoxyribose radicals, some of which have a spectral width no greater than the base radicals (42). For this reason, we measured the deoxyribose radical yield by taking advantage of their resistance to dose saturation (30). The intensity of the EPR spectrum was monitored as a function of dose, out to very high doses (~1000 kGy), for pUC18 films hydrated to Γ of 2.5, 11.5 and 22.5 mol water/mol nucleotide. For each dose–response curve, only one sample is used. The curves were fitted to a two-component model as described above. The fit for a pUC18 plasmid film at = 2.5 mol water/mol nucleotide is shown in Fig. 3.

FIG. 3.

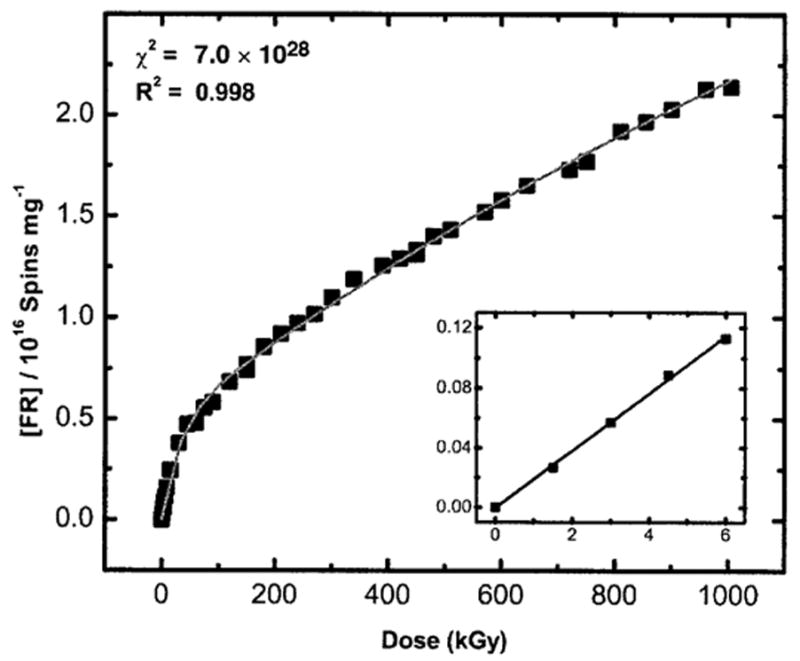
Corrected dose–response curve for free radical (FR) trapping by pUC18 plasmid film hydrated to a Γ = 2.5 mol water/mol nucleotide fitted to the two-component model described previously (30). X irradiation and EPR were done at 4 K. Note that the slope shown in the inset (G) is the yield obtained from a fit to the initial linear response measured at low dose (~6 kGy). The free radical yield, G(∑fr), of this pUC18 plasmid (2686 bp) sample determined from the fit is found to be 0.285 ± 0.006 μmol/J. R² (~0.998) is the goodness of fit and χ² (~7.04 × 10²⁸) is the reduced χ² value calculated by the nonlinear least-squares fitting routine used by ORIGIN.

The parameter values for all three levels of Γ are given in Table 1. From the G_base(fr)/G(∑fr) ratio, we find that 10–11% of the total trapped radicals in these pUC18 DNA samples reside on the sugar and that this fraction is relatively independent of Γ. This finding is consistent with the observation that the qualitative features of the EPR spectra do not vary with the level of hydration. For plasmids at various levels of hydration, the free radical dose–response curves were measured at relatively low doses (shown in Fig. 4). The concentration of trapped radicals is linear with dose in this low-dose range. The total free radical yields, G(∑fr), at each level of hydration were calculated from the slope of the dose–response curves at these low doses. G(∑fr) is found to vary between 0.285 ± 0.006 μmol/J and 0.621 ± 0.01 μmol/J as Γ is increased from 2.5 to 22.5 mol water/mol nucleotide (see Table 1).

TABLE 1.

Parameters G_base(fr), G_sugar(fr), k_base and k_sugar Obtained by Fitting to the Two-Component Model, the Dose–Response Curve for pUC18 Plasmid Film Samples at Various Γ (mol water/mol nucleotide)^a

pUC18 plasmids	Gbase(fr) (μ mol/J)	Gsugar(fr) (μ mol/J)	kbase (kGy −1)	ksugar (kGy−1)	G(∑fr) (μmol/J)	Gbase(fr)/G(∑ fr)	G(∑fr)/Ginitial(fr)
at Γ ~2.5	0.253 (0.008)	0.032 (0.0004)	0.033 (0.001)	0.0004 (0.00003)	0.285 (0.006)	0.89 (0.047)	0.24 (0.01)
at Γ ~11.5	0.416 (0.008)	0.053 (0.0004)	0.034 (0.001)	0.0006 (0.00003)	0.469 (0.008)	0.89 (0.032)	0.40 (0.01)
at Γ ~22.5	0.560 (0.008)	0.061 (0.0004)	0.046 (0.001)	0.0007 (0.00003)	0.621 (0.01)	0.90 (0.019)	0.53 (0.01)

^aThe standard error for each parameter as reported by the nonlinear least-squares fitting procedure is included in parentheses. From previous work (36), the relative error in G(∑fr) is seen to vary from ±5% to ±15%. It is assumed that in the absence of geminate ion recombination and cross combination reactions, the initial yield of radicals is G_initial(fr) ~ 1.18 μmol/J (56).

FIG. 4.

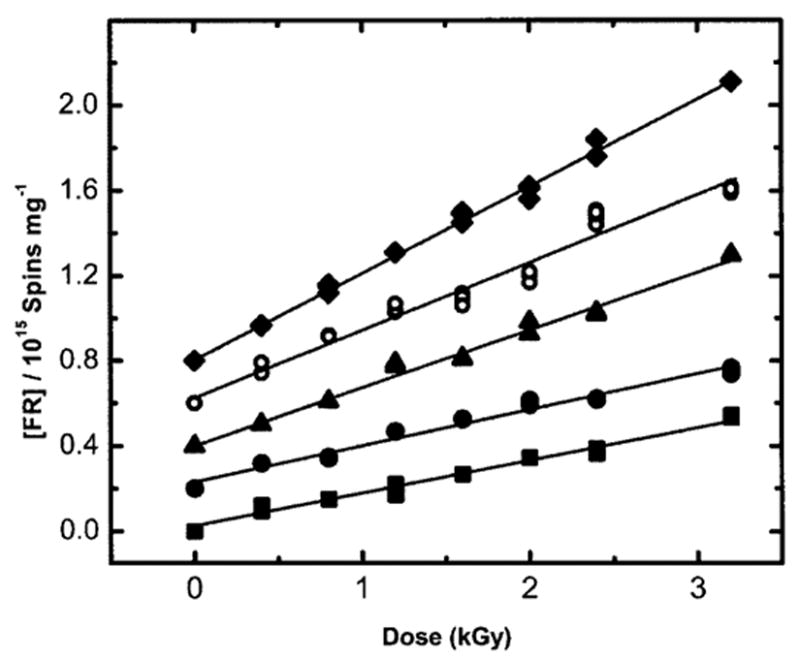
Plot of the free radical (FR) concentration as a function the X-ray dose for irradiated pUC18 plasmid samples at various Γ (mol water/mol nucleotide). The data includes plasmids at (■) Γ = 2.5, (●)Γ = 7.5, (▲) Γ = 11.5, (○) Γ = 15.0, and (♦) Γ = 22.5 mol water/mol nucleotide. The data for Γ = 22.5 have been published previously (32). X irradiation and EPR measurements were done at 4 K. A vertical offset of 0.2 units has been introduced between each curve. The linear region of the dose–response data has been fitted to a straight line by least squares. The free radical yield of the pUC18 sample at each Γ is determined from the slope of this line.

The dependence of the total free radical yield, G(∑fr), on Γ(mol water/mol nucleotide) for X-irradiated pUC18 plasmid samples measured at 4 K is shown in Fig. 5. A similar dependence of free radical yields in DNA films has been observed previously (5).

FIG. 5.

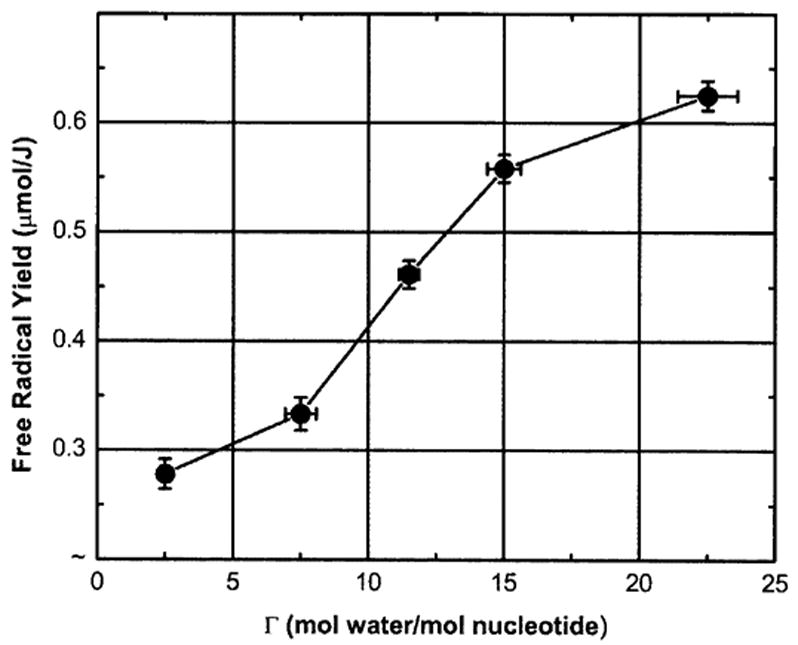
Dependence of the total free radical yield, G(∑fr), on Γ (mol water/mol nucleotide) for X-irradiated pUC18 plasmid samples measured at 4 K.

DISCUSSION

Migration of the sites of one-electron addition (excess electron) and one-electron loss (hole) after energy deposition in DNA and its solvation shell alters the extent to which stable chemical damage is clustered in DNA. In this context, it is important to determine the electron and hole transfer processes that occur at early times after the initial ionization of each DNA component. To this end, we have measured the distribution of those free radicals that can be trapped as early as possible in the chain of events that follow energy deposition. We begin with a discussion of how the yield of total DNA-trapped free radicals, G(∑fr), varies as a function of DNA hydration. Then we make use of the data on partitioning of radicals between DNA components (Table 1) to estimate how holes redistribute between the different components.

Total Free Radical Yield as a Function of Hydration

The total free radical yield, G(∑fr), was found to vary between 0.285 ± 0.006 μmol/J at Γ = 2.5 and 0.621 ± 0.01 μmol/J at Γ = 22.5 mol water/mol nucleotide. These plasmid G(∑fr) values are higher than those reported previously for high-molecular-weight DNA films hydrated over the same range (11) and are consistent with our working hypothesis that increased DNA packing density increases electron/hole scavenging, thereby decreasing the probability of geminate ion recombination (28).

Thus we speculate that supercoiled DNA is able to pack more densely than linear high-molecular-weight DNA and that between a Γ of 7.5 and 15, the plasmid packing density undergoes a substantial increase. While packing density is believed to be the primary variable that affects G(∑fr), it is not the only variable. For example, as proposed by Swarts et al. (45), DNA conformation may play a role; if so, the supercoiling of DNA may affect G(∑fr) by promoting different conformations at different levels of hydration. The fraction of radicals actually trapped is shown in the last column of Table 1. The fraction varies from 0.24 to 0.53, where the fraction is calculated under the assumption that in the absence of geminate ion recombination and cross combination reactions, the yield of radicals should be ~1.18 μmol/J (24, 56) and that the absorption cross sections for DNA are the same as water (46). Recently, a mechanism has been proposed that implicates a specific type of hole-hole recombination between a hole located on the deoxyribose moiety and the guanine (or other base) radical cation as a precursor to strand breaks in directly ionized DNA (32).

The free radical yields reported in Table 1 display the previously observed trend in which these yields increase with increasing hydration and do so with a fractional increase that is greater than that expected if based simply on the increase in target mass. The increase in radical trapping efficiency has been attributed to an increase in DNA packing density as the hydration shell is filled (11, 36). The yield measurements reported here have unusually small standard errors for samples prepared from high-molecular-weight DNA. We attribute this reproducibility to the homogeneity in both DNA molecular weight and conformation, which is gained by working with plasmid DNA, and to the film preparation protocol. Consequently, the relationship between G(∑fr) and the level of DNA hydration is defined more precisely than for previous results (11). This improvement, coupled with the results in Table 1 on the partitioning of radicals between the DNA bases and backbone, provides improved information on how holes redistribute between the components of DNA and its solvation shell.

Redistribution of Holes

The initial distribution of holes (one-electron loss sites) can be calculated using the Bragg rule, according to which the probability of ionization of a given site is proportional to the number of valence electrons comprising that site. Three assumptions are made. First, for each trapped hole there is one trapped electron (one-electron gain site); i.e., the yield of observable one-electron oxidized sites equals that of one-electron reduced sites. Second, the base contains a mean of 67 electrons, which is equivalent to assuming a GC:AT ratio of 1:1 (the actual pUC18 GC:AT ratio is 1.03 (47, 48). Third, energy deposition events involving excitation do not give rise to detectable radicals (5, 6, 49, 50). Using the above assumptions, Table 2 presents the predicted redistribution of initial free radicals between the major components of plasmid DNA. Table 2 is divided into five groups of rows; each group corresponds to one of the five different levels of hydration: Γ = 2.5, 7.5, 11.5, 15 and 22.5.

TABLE 2.

Predicted and Observed Distribution of Radicals Trapped on the Components of DNA

	1	2	3	4	5	6	7	8	9
DNA components at different Γ	No. bound e− (′)	Bound e− (%)	Initial hole distribution (%)	Initial e− adduct distribution (%)	Predicted initial free radical distribution (%)	Neglect outer shell free radical (%)	Renormalize (%)	Observed free radical distribution (%)	Calculated free radical distribution (%)
Γ = 2.5
Bases	48	35	17	50	67	67	67	89	89
Sugar-phosphate	63	45	23	0	23	23	23	11	11
Solvent shell,a Γ ≤ 10	28	20	10	0	10	10	10
Sum	139	100	50	50	100	100	100	100	100
Γ = 7.5
Bases	48	27	13	50	63	63	63		88
Sugar-phosphate	63	35	18	0	18	18	18		12
Solvent shell,a Γ ≤ 10	68	38	19	0	19	19	19
Sum	179	100	50	50	100	100	100		100
Γ = 11.5
Bases	48	23	11	50	61	61	63	89	88
Sugar-phosphate	63	30	15	0	15	15	15	11	12
Solvent shell,a Γ ≤ 10	88	42	21	0	21	21	21
Solvent shell, Γ > 10	12	6	3	3	b
Sum	211	100	50	50	100	97	100	100	100
Γ = 15.0
Bases	48	20	10	50	60	60	65		88
Sugar-phosphate	63	26	13	0	13	13	14		12
Solvent shell,a Γ ≤ 10	88	37	18	0	18	18	20
Solvent shell, Γ > 10	40	17	8	8	b
Sum	239	100	50	50	100	92	100		100
Γ = 22.5
Bases	48	16	8	50	58	58	70	90	90
Sugar-phosphate	63	21	11	0	11	11	13	10	10
Solvent shell,a Γ ≤ 10	88	29	15	0	15	15	18
Solvent shell, Γ > 10	100	33	17	17	b
Sum	299	100	50	50	100	83	100	100	100

^aThe inner solvent shell, Γ ≤ 10, includes the sodium counterion.

^bIt is assumed that holes formed in the outer solvation shell (Γ > 10) do no transfer to the DNA (7, 9).

The last row in each group gives results for the total sample, and the preceding rows separate the DNA into its constituent chemically distinct compartments: the bases, the sugar-phosphate backbone (S-P), the Γ ≤ 10 solvent shell, and the Γ ≤ 10 solvent shell. Each compartment is chosen because of its presumed unique radical-trapping properties. The first column gives the number of electrons comprising each component. These numbers are converted into percentages in the next column. Because the holes comprise half of the total initial radicals (the other half are electron gain centers), these percentages are halved in column 3. Column 4 gives the distribution of electron adducts relative to the total radicals; all of the electrons are assumed to attach to the pyrimidine bases (23, 51–54). Adding the values in columns 3 and 4 gives the values in column 5, the predicted distribution for all of the initially formed radicals. At the higher levels of Γ, particularly 22.5, one expects hydroxyl radical formation and trapping. However, since the EPR spectrum of these radicals is extraordinarily broad at Q-band frequencies, they were not measured. In column 6, the radical population in the Γ > 10 shell is neglected, and in column 7, the percentages are renormalized. Column 7 of Table 2 gives the predicted distribution of initial radicals. To obtain the observed distribution of trapped radicals, shown in column 8, redistribution of the holes must occur.

The observed radical-trapping distribution, 10–11% on the deoxyribose and 89–90% on the bases, can be explained as follows. Net hole trapping is obtained by transferring two-thirds of the holes initially formed on the backbone plus inner solvation shell to the base stack. The arithmetic for net trapping in each component is as follows: solvent, 0% = 18 − 12 − 6; backbone, 22% = 48 − 32 + 6; bases, 78% = 34 + 12 + 32. Converting from percentage holes to percentage total radicals, assuming a 50:50 ratio of holes to electron adducts, we find that 11% of the radicals are trapped on the backbone. This hole transfer is accounted for in column 9, which compares favorably with the observed numbers in column 8.

The fraction of two-thirds comes from solving the simple algebraic equations that relate the initial to the observed distribution (columns 7 and 8). The exact solution to these equations gives transfer probabilities of 0.66 for hole transfer from the backbone and 0.70 for transfer from the inner solvent shell. If the solvent shell is not split into two compartments, thereby assuming all holes transfer to the bases, the respective transfer probabilities of 0.61 and 0.82 are calculated. We see, therefore, that these values are relatively insensitive to just how many waters are placed in the ‘‘inner’’ shell. This analysis provides the best measure to date for the probability of hole transfer into the base stack, increasing our earlier estimate of ~50% transfer (55) to 67% transfer.

There are three important findings in this study. First, the probability of the base stack trapping a hole that is borne on the sugar-phosphate backbone is twice the probability of that hole being trapped on the backbone. Second, holes that transfer from the solvent shell to the DNA end up distributed between the backbone and bases with the same stoichiometry as holes formed by direct ionization of the DNA. (The actual numbers indicate a slight bias for transfer to the base stack, but the current confidence level in these numbers precludes making a distinction.) Third, the probability of DNA trapping a hole that is initially formed in the inner solvent shell is the same as the probability of DNA trapping a hole after ionization of DNA itself.

CONCLUSION

The total yield of trapped radicals, G(∑fr), in pUC18 films increases from 0.28 ± 0.01 μmol/J at Γ = 2.5 to 0.62 ± 0.01 μmol/J at Γ = 22.5 mol water/mol nucleotide, respectively. In fully hydrated DNA, holes initially formed in the hydration layer are predicted to redistribute as follows: approximately two-thirds to the bases and one-third to the sugar-phosphate backbone. This assumes that holes in the outer shell (Γ > 10) do not transfer to the DNA, giving rise to HO^•. Likewise, of the holes produced by direct ionization of the sugar-phosphate, approximately one-third are trapped by deprotonation as neutral sugar-phosphate radical species, while the remaining two-thirds transfer to the bases. This predicts that the distribution of holes formed in fully hydrated DNA at 4 K will be 78% on the bases and 22% on the sugar-phosphate. Adding radicals formed by electron attachment, the distribution of all trapped radicals is predicted to be 89% on the bases and 11% on the sugar-phosphate, which are the observed values.