What angle-resolved photoemission experiments tell about the microscopic theory for high-temperature superconductors

Abstract

Recent angular-resolved photoemission experiments on high-temperature superconductors are consistent with a phenomenological description of the normal state of these materials as marginal Fermi liquids. The experiments also provide constraints on microscopic theories.

The discovery of the copper oxide superconducting materials in 1987 and the intense investigations that followed have raised some fundamental questions in condensed matter physics. These superconductors are characterized by two unexpected features. One is, of course, their unprecedented high transition temperatures (T_c). In addition, it is clear that their normal-state properties are not those of ordinary metals; they are not consistent with the traditional Fermi-liquid quasiparticle picture that is a cornerstone of our understanding of the metallic state.

Many theoretical ideas have been proposed in response to these observations, but it has been difficult, on the basis of the experimental evidence, to identify the correct picture. However, recent angle-resolved photoemission (ARPES) experiments show a remarkable consistency with predictions (1, 2), made in 1989, based on a phenomenological characterization of these materials as “marginal Fermi liquids” (MFL). The aim of this communication is to discuss some aspects of these experiments and to point out what constraints they impose on possible microscopic theories.

The initial motivation for the MFL phenomenology was to understand simultaneously two quite different normal-state properties of these quasi-two-dimensional materials: the Raman scattering intensity, which measures the long wavelength response over a wide range of frequencies, and the nuclear magnetic relaxation rate of planar copper nuclei, which comes from magnetic fluctuations of low frequency and short wavelength. The underlying MFL assumption was that, at compositions for which the T_c is highest (“optimal doping”), a sector of both the charge and magnetic excitation spectra χ(q,ω,T) has unusual properties: (i) The sector is momentum q independent over most of the Brillouin zone, and (ii) it has a scale-invariant form, as a function of frequency ω and temperature T, so that Imχ ∝ [f](ω/T) as follows:

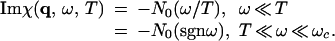1

N₀ is the density of energy states per unit volume, and ω_c is a high-frequency cutoff. A central conclusion (1) is that the single-particle self energy caused by scattering from the excitation spectrum of Eq. 1 has a singular dependence on frequency and temperature but has unimportant momentum dependence. This self energy is calculated to be

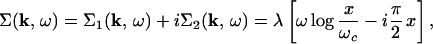2

where x ≈ max(|ω|,T) (for example, x = 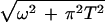), and λ is a coupling constant. The spectra of Eq. 1 could actually have a smooth dependence on q over a substantial part of the Brillouin zone. In that case, λ acquires a weak dependence on k. In the experiments discussed below, λ is in fact constant, within the experimental error. The most important point is that Σ₂ remains proportional to x all around the Fermi surface.

In a Fermi liquid, quasiparticles are well defined, because the single-particle excitation decay rate (Σ₂) is small compared with Σ₁. Because in the present case Σ₂, the imaginary part of the self energy, is only logarithmically smaller than Σ₁, the real part, at T = 0, the appellation MFL was given (1). Here, the singular behavior of Σ leads to the result that there are no Fermi liquid-like quasiparticles; at T = 0, their “residue” z = [1 − ∂Σ₁/∂ω]⁻¹ vanishes at the Fermi surface (k = k_F).

The earliest experimental data revealed that the transport properties in the normal state of the high-T_c superconductors are unlike those of normal Fermi liquids, which have nonzero z. P. W. Anderson suggested (3, 4) that this experimentally observed anomalous normal-state behavior implies a non-Fermi liquid with z = 0. He developed this idea based on the separation of charge and spin energy scales and excitations. The MFL analysis is different and begins with a key assumption, Eq. 1, about the particle-hole excitation spectrum in both charge and magnetic (including spin) channels. Eq. 2 for the self energy follows from Eq. 1 with the following consequences:

•  A Fermi surface is defined at T = 0 as the locus of k points, where z→0 as (log ω)⁻¹.

•  The single-particle scattering rate Σ₂ is proportional to x≈max(|ω|,T).

•  The leading order contribution to Σ₂ is independent of momentum both perpendicular to and around the Fermi surface. As discussed above, a weak smooth momentum dependence does not alter our conclusions.

In general, transport (e.g., electrical or thermal conduction) scattering rates have a different frequency and temperature dependence from that of the single-particle scattering rate Σ₂, because the former emphasize backward scattering (large momentum transfer). However, the combination of momentum independence of Σ and the linear dependence on x of Σ₂ in the MFL form of the self energy, Eq. 2, leads to a resistivity that is linear in T, as is seen in experiments on optimally doped materials. Other consequences of the MFL phenomenology include a temperature-independent contribution (with logarithmic corrections) to the thermal conductivity; an optical conductivity that falls off as with frequency as ω⁻¹ (with logarithmic corrections), more slowly than the ω⁻² dependence of the familiar Drude form; a Raman scattering intensity ∝ max(ω,T)/T; a T-independent contribution to the copper nuclear spin relaxation rate; and (in some geometries) a linear in bias voltage contribution to the single-particle tunneling rate. The MFL phenomenology has often been used to fit experiments, and it is found that the behavior of response functions is generally consistent with MFL as expressed in Eq. 1.

Nevertheless, although there were some direct indications of the correctness of Eq. 2 in early ARPES measurements (5), the MFL behavior of the single-particle excitation spectrum [i.e., Eq. 2] was not adequately confirmed. ARPES experiments measure the single-particle properties directly, in contrast to response functions, which are governed by joint two-particle (that is, particle-hole) properties. The quantity determined in ARPES experiments is the single-particle spectral function 𝒜(k,ω), which depends on the self energy as follows:

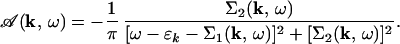3

The MFL behavior of the single-particle excitations has now been verified convincingly in the new ARPES experiments of Valla et al. (6) at Brookhaven National Laboratory and by Kaminski et al. (7) at Argonne National Laboratory. In the past, such measurements have been limited by energy and momentum resolution and large experimental backgrounds in the energy distribution measurements at fixed momentum (EDCs). These problems are now being overcome as new detectors have come on line. In particular, Valla et al. (6) have taken advantage of improved resolution to measure, on optimally doped Bi₂Sr₂CaCu₂O_8+δ, in addition to EDCs, momentum distributions at fixed energy (MDCs). In this way, the frequency dependence of the single-particle spectral function 𝒜(k,ω) is measured at fixed k (EDC) and also the k dependence at fixed ω (MDC).

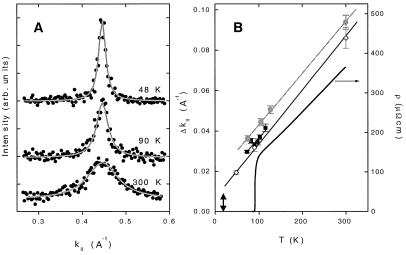
It follows from Eq. 3 that, if the self energy Σ is momentum independent perpendicular to the Fermi surface, then an MDC scanned along k_perp for ω≈0 should have a lorentzian shape plotted against (k − k_F)_perp with a width proportional to Σ₂(ω), and the Σ₂ found in this way from MDCs should agree with that found by fitting EDCs. Furthermore, for an MFL, the width should be proportional to x = max(|ω|,T), where ω is measured from the chemical potential. This behavior has now been verified by Valla et al. (6). The fits of the MDCs at ω = 0 to a lorentzian are shown in Fig. 1A. Fig. 1B shows the linear variation of the width of the lorentzian with temperature.

Figure 1.

(A) Momentum distribution curves for different temperatures. The solid lines are lorentzian fits. (B) Momentum widths of MDCs for three samples (circles, squares, and diamonds). The thin lines are T-linear fits. The resistivity (solid black line) is also shown. The double-headed arrow shows the momentum resolution of the experiment. Figure courtesy of P. D. Johnson (Brookhaven National Laboratory). Reproduced with permission from ref. 6 (Copyright 1999, American Association for the Advancement of Science)].

Preliminary data from both the Brookhaven (8) and Argonne (A. Kaminski, personal communication) groups also show that the contribution to Σ₂, which is proportional to x as determined by scans perpendicular to the Fermi surface, is very weakly dependent on k̂_F; i.e., it varies only weakly with the angle on the Fermi surface. It is important to notice that there is no evidence of a T² contribution to Σ₂ in the neighborhood of the Fermi surface anywhere in the Brillouin zone; the temperature-dependent part is always T linear.

Phenomenological ideas that seek to explain the transport anomalies in the cuprates on the basis of hot and cold spots on the Fermi surface are not consistent with this experimental finding, because they are based on having a T² behavior in the (1,1) direction and a T behavior in the (1,0) direction.

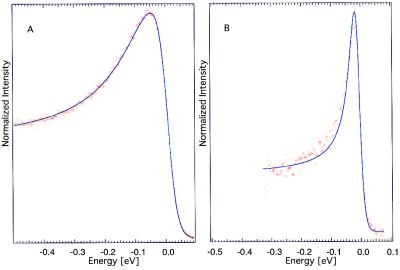
The Argonne group has plotted the EDCs together with fits to the MFL spectral function of Eq. 3 at over a dozen k-points between the (1,1) and (1,0) directions in the Brillouin zone. ImΣ(ω) is taken to be of the form Γ(k̂) + λ(k̂_F)ω. Γ represents an impurity contribution (see below). We show two typical examples in Fig. 2 A and B. These display, respectively, the results at the Fermi surface in the (1,0) and the (1,1) directions in the Brillouin zone that give the widest k̂ variations of Γ and λ. These self-energy parameters for the fit are given in the legend to Fig. 2.

Figure 2.

Fits of the MFL self energy Γ+λℏω to the experimental data. Energies are in meV, with estimated uncertainties of ±15% in Γ and ±25% in λ. (A) The (1,0) direction, Γ = 0.12, λ = 0.27, and (B) the (1,1) direction, Γ = 0.035, λ = 0.35. Figure courtesy of A. Kaminski (Argonne National Laboratory). [Figure courtesy of A. Kaminski (Argonne National Laboratory), used by permission.]

Thus, the results for MDCs as well as EDCs may be summarized by the following expression:

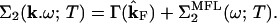4

The first term on the right-hand side of Eq. 3 is independent of frequency and temperature and is properly considered as the scattering rate because of static impurities. This can depend on k̂_F, the direction of k around the Fermi surface, as explained below. The second term is the MFL self energy of Eq. 2, a function only of x = max(|ω|,T); however a weak dependence on k̂ is possible, as discussed earlier. There may be additive analytic contributions of the normal Fermi-liquid type as well.

The dependence of the impurity scattering on k̂_F can be understood by the assumption that in well-prepared cuprates, the impurities lie between the CuO₂ planes and therefore give rise to small-angle scattering (small momentum transfer) only. If the distance of the impurities to the CuO₂ plane is D, then the characteristic scattering angle is δθ≈(2k_FD)⁻¹ [≈O(a/d)], where a and d are the in-plane and c-axis lattice constants). The single-particle impurity scattering rate Γ_k at a point k is then proportional to δθ about that point. For small δ θ, this gives the scattering rate Γ_k proportional to the local density of states at that k. It is known from both band structure calculations and ARPES experiments that the local density of states is about an order of magnitude larger in the (π,0) direction than in the (π,π) direction. Therefore, we expect the impurity contribution to increase as one turns k̂ around the Brillouin zone toward the (π,0) region. This is seen in preliminary data from the Brookhaven group as well as the Argonne group, which also show that the MFL contribution proportional to x has only weak dependence on k̂_F, if any (ref. 8; A. Kaminski, personal communication).

This assumption about the nature of impurity scattering also explains the well-known fact that the impurity contribution to the resistivity of well-prepared optimally doped cuprates is anomalously small. An impurity contribution to the single-particle scattering rate does not necessarily appear in the transport scattering rate, because the latter depends only on large momentum transfers. Thus the transport rate, emphasizing as it does the large-angle scattering, is proportional to δθ³, thus a factor δθ² (perhaps as small as 0.04) smaller than Γ. In fact, it is known that impurities like Zn, which replace Cu in the plane, give a large contribution to the resistivity (9).

Some properties at optimum doping, for example the temperature dependence of the Hall resistivity, do not follow from the MFL self energy, Eqs. 2 and 4. Although the ARPES experiments indicate that the MFL form of the self energy is necessary, it is not sufficient to characterize all of the normal state properties at optimum doping.

The negligible (or weak) experimentally observed momentum dependence of the singular part of the single-particle self energy constrains theories of the normal state of the cuprate superconductors. We have discussed how the MFL phenomenology is consistent with the experiment. There are at least three classes of theories in which (in contrast to MFL) the self energy has strong momentum dependence: (i) Theories that involve strongly momentum-dependent couplings such as antiferromagnetic spin fluctuation exchange (10). (ii) Theories based on breaking of translational symmetry, such as stripe or charge-density wave scenarios (11, 12). (iii) Theories based on an extension from one to two dimensions of anomalous non-Fermi liquid behavior as described in the Luttinger liquid formulation (13). In the first case, coupling involving an excitation whose spectrum is peaked in one part of the Brillouin zone necessarily leads to a momentum-dependent self energy. In the second case, the breaking of translation invariance also results in momentum dependence of all quantities. The third case, the Luttinger liquid, has nonanalytic dependence of the spectral function on momentum, that is on k − k_F, at ω = 0 that is the same as the ω dependence at k = k_F (14). Thus, should the new ARPES results prove robust, these three classes of theories would require important modifications.

In the theory of the MFL, the max(|ω|,T) dependence of both the single-particle and transport rates comes about from a particle-hole fluctuation spectrum that both is scale invariant in frequency and has negligible momentum dependence as in Eq. 1. A direct experimental verification of the basis for MFL, that is, of a scale-invariant fluctuation spectrum as in Eq. 1 is as yet incomplete. Although such a spectrum is observed at long wavelengths in Raman scattering, it has not yet been clearly identified at larger momentum. Experimental methods to measure the charge fluctuation spectrum at large momentum are not well developed. The magnetic part of the spectrum (because of both orbital and spin fluctuations) is in principle observable in neutron scattering. However, the signal-to-noise and background problems for a featureless inelastic spectrum spread over ω_c≈0.5 eV are formidable. At the same time, the fact that a magnetic fluctuation spectrum of the MFL form accounts for the longitudinal NMR relaxation rate of planar copper nuclei near optimum doping does give support to Eq. 1 for large momenta.

It is not clear to us how the observed ARPES spectra (and the fact that the transport scattering rate has the same temperature and frequency dependence as the single particle scattering rate) can come about except in a theory that results in the scale-invariant form essentially as specified by Eq. 1. It is suggestive that a scale-invariant fluctuation spectrum generally arises in a region about a quantum critical point (QCP). The momentum independence of Eq. 1 specifies that if a QCP underlies the MFL behavior, then the associated dynamical critical exponent z_d → ∞. As stressed elsewhere (15, 16), the experimental phase diagram in the temperature-doping plane is consistent with the existence of a QCP at a doping near that of the highest critical temperature. A microscopic theory for a QCP with properties similar to the MFL spectrum of Eq. 1 has been presented and shown also to promote d-wave superconductivity (15, 16). Some unique predictions of that theory await experimental tests.

Abbreviations

ARPES

angle-resolved photoemission

MFL

marginal Fermi liquids

EDCs

energy distribution measurements at fixed momentum

MDCs

momentum distributions at fixed energy