The effect of public health measures on the 1918 influenza pandemic in U.S. cities

Abstract

During the 1918 influenza pandemic, the U.S., unlike Europe, put considerable effort into public health interventions. There was also more geographic variation in the autumn wave of the pandemic in the U.S. compared with Europe, with some cities seeing only a single large peak in mortality and others seeing double-peaked epidemics. Here we examine whether differences in the public health measures adopted by different cities can explain the variation in epidemic patterns and overall mortality observed. We show that city-specific per-capita excess mortality in 1918 was significantly correlated with 1917 per-capita mortality, indicating some intrinsic variation in overall mortality, perhaps related to sociodemographic factors. In the subset of 23 cities for which we had partial data on the timing of interventions, an even stronger correlation was found between excess mortality and how early in the epidemic interventions were introduced. We then fitted an epidemic model to weekly mortality in 16 cities with nearly complete intervention-timing data and estimated the impact of interventions. The model reproduced the observed epidemic patterns well. In line with theoretical arguments, we found the time-limited interventions used reduced total mortality only moderately (perhaps 10–30%), and that the impact was often very limited because of interventions being introduced too late and lifted too early. San Francisco, St. Louis, Milwaukee, and Kansas City had the most effective interventions, reducing transmission rates by up to 30–50%. Our analysis also suggests that individuals reactively reduced their contact rates in response to high levels of mortality during the pandemic.

The Spanish influenza pandemic in 1918–1919 was exceptional in its lethality and the multiple distinct waves of the epidemic seen in many areas. Conservative estimates indicate that 50 million people died worldwide (1), with significant consequent social and economic disruption. However, observations in Europe and the U.S. differ considerably. In Europe, only one autumn wave was seen, whereas many U.S. cities saw two peaks in mortality incidence spaced by only a few weeks. Also, far greater variation in mortality was seen among U.S. cities than was seen, for instance, in the United Kingdom [see supporting information (SI) Appendix]. The origin of these differences is unclear. Here we examine the hypothesis that they result largely from the much wider use of public health measures in the U.S.

A range of interventions was tried in the U.S. in 1918, including closure of schools and churches, banning of mass gatherings, mandated mask wearing, case isolation, and disinfection/hygiene measures. However, a challenge in undertaking this analysis is finding data on public health measures used in different U.S. cities and their precise timing. Here we examine the dynamics of the autumn 1918 waves in 16 cities for which we were able to collate reasonable data on the timing of public health interventions (see http://www.pnas.org/cgi/content/full/0611071104/DC1SI Appendix): Atlanta, Baltimore, Chicago, Fall River, Indianapolis, Kansas City, Milwaukee, Minneapolis, New York, Newark, Philadelphia, Pittsburgh, San Francisco, Spokane, St. Louis, and Washington. For an additional seven cities (Boston, Buffalo, Detroit, Rochester, St. Paul, Seattle, and Toledo), we had data on the start dates of interventions only. Based on the weekly mortality data (2), we estimate the effect of the interventions by correlating the timing of interventions with the incidence patterns seen.

The interest of this study is far from just historical; policy makers around the world are considering how nonpharmaceutical public health measures (3) can be used to contain or mitigate a future pandemic. Key to the decisions to be made in the coming months and years will be the evidence base for the effectiveness of such interventions (4). Much data will come from ongoing prospective studies, but historical analysis (5) is a powerful secondary source of information on the feasibility and effectiveness of public health measures in a crisis situation of the type represented by an acute lethal pandemic.

Results

Correlation Analysis.

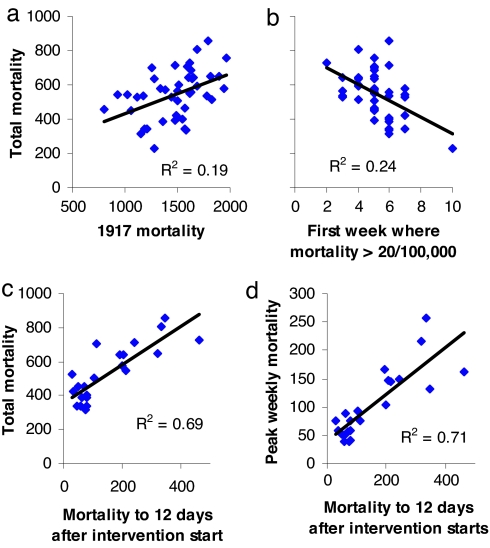
We initially undertook an exploratory analysis of which city-specific demographic or geographic variables were predictive of pandemic mortality in 1918–1919. In the 45 cities for which we had nearly complete weekly mortality data, there was an ≈4-fold variation in excess mortality because of influenza in 1918–1919 (Fig. 1a). Influenza-related excess mortality was positively correlated with prepandemic mortality (e.g., mortality in 1917) and negatively correlated with the day of the start of the epidemic (Fig. 1 a and b). Excess mortality was also positively correlated with the proportion of excess deaths that occurred in the peak week (see SI Appendix). However, the most striking correlations found (for the subset of 23 cities for which we had start dates for interventions) were between excess mortality (either total or peak), and how early interventions were introduced into the epidemic in a city (Fig. 1 c and d and SI Appendix). We optimally wanted to know the number of influenza infections that had occurred by the time controls were introduced, but because infections were not observed, we use a proxy statistic: the number of deaths occurring up to 12 days after controls were started, given that the average delay between infection and death in 1918 was 12 days (see SI Appendix). This proxy variable explained 69% of the variance in total mortality among cities. It can be argued that the absolute numbers of deaths up to 12 days after controls start is confounded with other intrinsic city-specific factors determining mortality. The proportion of deaths that occur up to 12 days after controls start does not suffer the same problem and is still significantly correlated with total excess mortality explaining 44% of between-city variance (see SI Appendix). Many other factors, such as population size or density, were not significantly correlated with excess deaths in 1918–1919 (see SI Appendix).

Fig. 1.

Predictors of excess influenza-related mortality in 1918–1919. Correlation of peak mortality (per 100,000) with all-cause mortality in 1917 (a), total mortality with the week (counting from the week of September 7–13, weekly mortality first exceeds 20/100,000) (b), total mortality with mortality up to 12 days after start date of interventions (c), and peak mortality with mortality up to 12 days after start date of interventions (d). a and b show data for the 45 U.S. cities for which mortality data were relatively complete. c and d show data for the 23 cities for which the start date of public health interventions was known. Peak and total 1918 mortality refers to excess pneumonia- and influenza-related mortality in the period September 7, 1918, to May 10, 1919. Regression shows all slopes to be significantly different from zero (P < 0.01).

Limits to the Impact of Imperfect Transient Interventions.

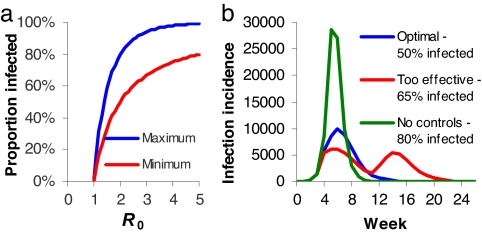
Given this correlation, to what extent might we expect time-limited public health interventions to affect cumulative mortality? Epidemics are characterized by the reproduction number, R, the number of secondary cases each case causes at a particular stage of the epidemic. R is highest at the start of an epidemic, when the population is fully susceptible [and when R = R₀ (6)], but declines thereafter as population immunity builds up. For transmission to be self-sustaining, R needs to be above unity. Interventions act to reduce R. However, an uncontrolled epidemic “overshoots”; more people are infected than the minimum proportion of 1 − 1/R (assuming random mixing) needed to achieve R < 1. The difference can be striking; the 1918 pandemic had R₀ ≈ 2 in the U.S. (7, 8), which would lead to 80% of the population being infected in an uncontrolled epidemic, compared with a minimum of 50% needed to stop transmission. Thus, if control measures are temporary and imperfect, the best they can do is to reduce the total proportion infected to that minimal level of 1 − 1/R (50% for R = 2). Fig. 2a illustrates how this effect becomes more substantial as R decreases.

Fig. 2.

Effects of transient imperfect health interventions on epidemic dynamics. (a) Total proportion of the population infected in an epidemic in the absence of controls or reactive contact reduction compared with the minimal proportion needing to be infected to achieve herd immunity and therefore stop transmission, shown as a function of R₀. Results derived from a simple deterministic susceptible–infected–recovered (SIR) epidemic model (6). (b) Weekly infection incidence over 6 months from a SIR model with 3.5-day infectious period, R₀ = 2, 100,000 population, two seed infections at time 0, and controls imposed from day 25. Green curve, no controls; red curve, overeffective controls that reduce R by 40% and stop on day 75 (leading to a second wave); blue curve, controls that reduce R by 32.5% and stop on day 110 (giving the minimal possible epidemic size).

Paradoxically, there is therefore an optimal maximal effectiveness of imperfect transient control measures; R needs to be reduced to a value that gives an outbreak of exactly the size needed to give sufficient population immunity to make transmission unsustainable once controls are lifted (see SI Appendix). Controls can also be effective, in that they control spread, but then when lifted, there are enough susceptible individuals left for the epidemic to resume; a second peak can result (Fig. 2b), akin to what was seen in some U.S. cities in 1918. In such cases, reintroduction of controls can still achieve the optimal outcome of an overall epidemic size across both peaks, which is just sufficient to provide herd immunity. However, if controls are introduced too late into the first epidemic peak, their overall impact is inevitably minor, irrespective of their efficacy (Fig. 2b).

Estimating the Impact of Controls on Transmission.

Drawing on this theoretical framework, if we want to really examine the extent to which differences in control measures can explain the variability in levels of mortality and epidemic patterns seen between different cities, it is clear we need to go beyond simple correlative analysis and examine more mechanistically how controls could have affected transmission. We use the simple well proven susceptible–exposed–infected–recovered (SEIR) epidemic model (6) and allow for a city-specific reduction in transmission rates for periods when control measures are in force. In addition, we further allow for reactive changes in population contact rates in response to recent mortality in the community.

The model is fitted to excess pneumonia and influenza mortality data from the 16 cities for which we had data on the timing of interventions. The model has the following fitted parameters (see Methods): R₀ (the reproduction number), μ (per-capita mortality), κ (the mortality threshold for reactive social distancing), T (the period over which mortality is averaged in determining the degree of reactive distancing), and p_c (the degree to which transmission is reduced by controls in a specific period). Given the obvious possible confounding among some of these parameters, we explore the effects of making parameters the same for all cities or making them city-specific (Table 1). A priori, we might expect more biological parameters, such as R₀ (although R₀ has strong demographic/social/behavioral determinants), to vary less among cities than more obviously behavioral parameters (e.g., p_c or κ).

Table 1.

Results of fitting eight model variants to weekly mortality data for 16 cities for which data on the timing of interventions were available

Model variant	Mean posterior log likelihood	μ, per-capita death rate, %	R0	κ, threshold for contact reduction (per 100,000)	T, memory period for contact reduction	pc, effectiveness of control measures, %	Reduction in mortality due to controls, %	Reduction in mortality for optimal controls, %
1	−2,318	Per city, 1.1 (0.7–1.8)	Per city, 2.0 (1.4–2.8)	Per city, 99 (10–538)	Per city, 12.2 (0.1–58.1)	Per city, 26 (0–49)	13 (0–36)	47 (0—100)
2	−4,764	Per city, 1.2 (0.7–2.6)	Per city, 1.9 (1.4–2.8)	No reactive contact reduction	No reactive contact reduction	Per city, 37 (0–83)	33 (21–57)	88 (36–100)
3	−4,652	Per city, 1.2 (0.7–2.5)	Per city, 2.1 (1.3–3.2)	Per city, 55 (3.8–185)	Per city, 1.4 (0.1–8.6)	No effect of controls	No effect of controls	No effect of controls
4	−3,168	Per city, 1.1 (0.6–1.8)	Common, 1.96 (1.95, 1.97)	Per city, 186 (7.5–828)	Common, 20.4 (20.1, 20.6)	Per city, 36 (0–55)	28 (7–64)	68 (28–100)
5	−7,627	Per city, 1.2 (0.7–1.8)	Common, 1.79 (1.78, 1.80)	No reactive contact reduction	No reactive contact reduction	Per city, 40 (0–86)	43 (30–72)	92 (35–100)
6	−3,824	Per city, 1.2 (0.7–2.1)	Per city, 1.9 (1.5–2.6)	Common, 22.0 (21.5, 22.5)	Common, 7.25 (7.08–7.40)	Per city, 23 (0.1–68)	6 (2–25)	44 (1–100)
7	−4,609	Per city, 1.1 (0.6–1.6)	Common, 1.99 (1.98, 2.0)	Common, 21.4 (20.8, 21.9)	Common, 13.7 (13.1, 14.1)	Per city, 30 (0–72)	14 (2–30)	51% (24–100)
8	−6,362	Common, 1.21 (1.20, 1.21)	Common, 1.94 (1.93, 1.95)	Per city, 78 (2.7–530)	Common, 7.18 (7.00, 7.36),	Per city, 20 (0–54)	12 (2–51)	38 (0–100)

Markov-Chain Monte-Carlo methods were used for fitting. Model fit is characterized by the mean log-likelihood from the posterior distribution (Fig. 3 gives a qualitative indication of the quality of fit for model variant 4; see SI Appendix also). Where a parameter was estimated on a per-city basis, the average and range across all cities of the mean posterior estimates of that parameter are shown. For parameter estimates assumed to be common to all cities, the mean and 95% credibility estimates of the parameter from the posterior distribution are shown. In addition, the time of introduction of the first infection into each city is fitted as a city-specific parameter for all models (estimates not shown). The last two columns show the average and range (across cities) of the estimated reduction in total mortality achieved by the implemented controls (represented as a percentage of the observed total mortality), and the average and range of reduction in mortality that would have been achieved had the period for which controls were most effective in each city been extended to cover September 1918 to May 1919, respectively.

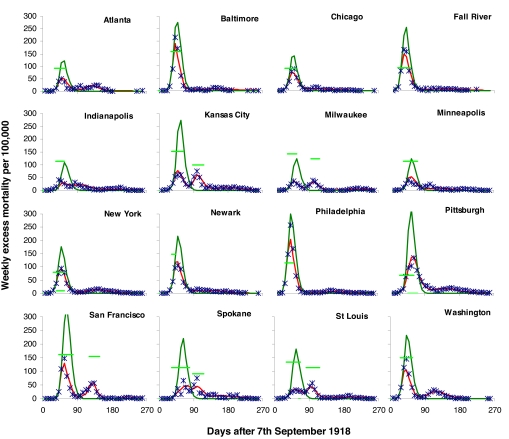
Treating all parameters as city-specific gives an excellent qualitative fit to the data (see SI Appendix). This could be viewed as unsurprising, given that five or more parameters are being fitted per city. At the other extreme, fitting R₀, κ, and T as common to all cities, while giving a much worse fit statistically (Table 1), still qualitatively gives a reasonable match to the temporal patterns in the data (see SI Appendix). Model variant 4 shows an intermediate case, where R₀ and T are assumed to have common values in all cities, and the resulting fit to the data is still very good (see Fig. 3).

Fig. 3.

Weekly excess mortality (per 100,000) resulting from the 1918 pandemic in 16 U.S. cities (blue points), compared with the fit of model variant 4, Table 1 (red curves). This variant fits R₀ and T, the duration of the population “memory” of past mortality, as parameters common to all cities and other parameters as city-specific. Estimated weekly mortality, had controls not been implemented, is also plotted (dark-green curves). The effectiveness and period of implementation of control measures are also shown as light-green horizontal lines; horizontal position and length, indicate start date and duration of interventions, and vertical position indicates estimated effectiveness. The top of the vertical axis is 100% effectiveness, and the bottom of this axis is 0%.

The results in Table 1 represent strong evidence that both organized public health interventions and reactive social distancing are needed to fit the data well. Assuming an effect of interventions alone can give a reasonably qualitative match to the data and requires three city-specific parameters to be fitted (variant 2). Reactive social distancing can give a similar fit quality without assuming an effect of organized interventions (variant 3), but only at the cost of fitting four city-specific parameters, 17 parameters more than variant 2. However, fitting both an effect of interventions and reactive social distancing gives a much better fit than either alone (variant 4) and requires fitting only two more parameters than variant 2.

All of the best-fitting variants (1, 4, and 6 in Table 1) fit either R₀ or κ (the threshold for reactive social distancing) as city-specific parameters. For variants with reactive social distancing, making κ common to all cities gives a substantially poorer fit (compare variants 4 and 7), although variant 7 still fits much better than the other model variants (variants 5 and 8) with the same number of parameters.

Variation in control measures explains some, but not all, of the variation in total excess mortality among cities. It is still necessary to fit μ on a city-specific basis, because not doing so gives a poor fit (variant 8), with the model then being able to explain only 46% of the variance in total mortality among cities.

There is considerable variation in the estimated impact of control measures, as a function of which parameters are assumed to be city-specific (see SI Appendix), but overall a fairly consistent rank-ordering of cities emerges. San Francisco, St. Louis, Milwaukee, and Kansas City comprise the subset of cities with policy effectiveness estimates (i.e., reduction in R) exceeding 30% for every model variant. Conversely, Chicago, Fall River, and Minneapolis are the cities most frequently in the bottom six in a ranking of estimated effectiveness (comparing across model variants).

The duration of interventions is equally important in determining their overall impact; in only two cities, St. Louis and San Francisco, are controls estimated to have achieved at least a 10% reduction in mortality for all model variants. Indeed, in San Francisco, we estimate that controls reduced mortality by at least 25%. The impact of controls on overall mortality is largest for the model variants where we do not assume reactive reductions in contact rates. These limited effects are as expected by the simple theory of imperfect interventions outlined above. The impact of controls on the shape of the epidemics seen was much more major than the effect on overall mortality. For most cities, a single large epidemic peak would have been expected had controls not been imposed (Fig. 3).

Given these estimates, we can ask how much better might cities have done had controls been enforced throughout the pandemic. We examined the impact of maintaining controls at the maximum level of effectiveness estimated for each city throughout the modeled period. Table 1 (last column) indicates that, if this had been feasible, it might have reduced mortality by an average of ≥40%. For the four top-ranked cities for intervention effectiveness listed above, mortality could have been reduced by at least 50% for all model variants, whereas for San Francisco, we estimate that transmission might have been stopped (R < 1), and thus mortality might have been reduced by >95%. These figures, however, do not allow for the mortality that may then have resulted when controls were finally lifted.

Discussion

The most important conclusion from this work is that the timing of public health interventions had a profound influence on the pattern of the autumn wave of the 1918 pandemic in different cities. Cities that introduced measures early in their epidemics achieved moderate but significant reductions in overall mortality. Larger reductions in peak mortality were achieved by extending the epidemic for longer.

We have not demonstrated this correlation only statistically, but we have also presented a plausible quantitative model that explains how such correlations arose. Our theoretical analysis demonstrates that, in the cities that saw double-peaked autumn epidemics, control measures may have been, if anything, too effective, stopping transmission so effectively that substantial numbers of susceptible individuals remained in the population when controls were lifted. This remaining susceptible pool allowed transmission to restart, leading to another epidemic peak and (in some cases) to the resumption of interventions. Conversely, cities in which transmission had been continuing for longer before interventions were introduced saw much smaller or no second epidemic peaks, because insufficient susceptible people remained to restart transmission. The theory of imperfect interventions tells us there is an optimal middle ground, i.e., interventions tuned to give a single peak of minimal size. It appears no U.S. cities found that optimal point, however; indeed, the cities that got closest to the theoretical maximum possible reduction in mortality were those that implemented both early and effective interventions throughout the first peak and then were able to reintroduce these when transmission again increased.

Our conclusion that transmission in 1918 showed strong frequency dependence, namely contact rates spontaneously reduced when recent mortality was high, warrants further comment. Similar reactive social distancing was arguably observed during the severe acute respiratory syndrome epidemic in Hong Kong and Singapore (3, 9). Whether the effect in 1918 was caused by people deliberately reducing contacts or by indirect effects (e.g., caring for the sick, absenteeism, or reactive closure of workplaces) cannot be determined. However, the effect of such reactive distancing is to introduce a form of time-delayed negative frequency dependence (because people respond to deaths, not infections) into the model, which substantially enhances the tendency for oscillatory epidemics. As such, alternative explanations, such as heterogeneous social mixing as a function of age, explain the observed trends much less well (see SI Appendix); whereas social structure can partly reproduce the observed rapid reduction in real-time epidemic growth rates seen in the data, it does so by assuming exhaustion of the subset of the population with the highest levels of susceptibility.

Our assumption that control measures had an effect on transmission that was constant throughout the period during which they were imposed is an obvious simplification. In reality, it is highly likely that some measures (e.g., mandated mask wearing) showed reductions in compliance over time. We also assume the virus did not change in virulence through time; in reality, there is some evidence (5) that the lethality of the 1918 virus had declined by January 1919. However, if anything, a temporal trend of declining virulence would imply an even greater impact of interventions, because the secondary or tertiary peaks in mortality would, in fact, correspond to higher levels of infection than revealed by mortality data. Conversely, it is also possible that the virus evolved antigenically through time, in which case the rise in incidence in spring 1919 can perhaps be explained by partial immune escape of the virus. However, it is difficult to explain between-city variation in epidemic shape by antigenic variation. If a new variant was circulating in November 1918, which was sufficiently novel to cause major epidemics in some cities, we might have expected it to spread successfully to all cities.

Furthermore, we did not attempt to model exogenous secular variation in transmission rates, such as that resulting from increases in mixing during Liberty Loan or Armistice Day parades or from seasonality. Given that annual seasonal influenza incidence in the U.S. often peaks in January, seasonality might play some role in explaining the small peaks in mortality rates seen in January 1919. Generalizing further, we cannot exclude the possibility that there may have been some other factor that varied among cities, and that might have been partly responsible for the observed variation in overall mortality and epidemic pattern. However, it is highly unlikely that such a factor would make nonsignificant the very strong correlation we have uncovered between mortality and the timing of interventions.

Last, we have assumed the whole population was susceptible to infection at the start of September 1918. It is likely there was some degree of population immunity because of transmission in the spring of that year (10), and perhaps because of prior circulation of an H1 virus in the 19th century (11). However, such prior immunity would be significant in explaining intercity variation in mortality only if preexisting immunity levels varied substantially among cities.

Our analysis agrees with earlier work (7, 8, 12) in giving central estimates of the R₀ for 1918 pandemic influenza of ≈2, with a range of 1.4–2.8 (Table 1, excluding model variant 3, which did not fit an effect of controls). However, here we have gone beyond previous analyses of the initial growth rate of the 1918 epidemic and modeled the whole epidemic. We have shown that a combination of reactive behavioral changes in contact rates and the impact of organized public health measures can explain the very different influenza epidemic patterns seen in different U.S. cities in 1918–1919.

Causality will never be proven, because, unsurprisingly, control measures were nearly always introduced as case incidence was increasing and removed after it had peaked. Thus, the broad correlation observed between the incidence and timing of control measures was predefined. However, in a multivariate analysis, only the correlation between mortality and the timing of the start of controls remains significant. What is more persuasive still is that allowing those controls to have an effect on transmission allows epidemic models to fit the observed mortality curves much better than they otherwise might. Indeed, the estimated effectiveness of interventions was sometimes high even for cities where controls were in place only for a short time (e.g., Baltimore). Reactive behavior change and control measures are also confounded in their timing; however, both factors independently contributed substantially to the model fit.

More work is needed to attempt to disentangle the impact of different control measures, although this will be challenging without independent data on efficacy. Furthermore, such a nuanced analysis will arguably require a more sophisticated model framework than we have adopted here. By assuming random mixing of the population and not explicitly representing schools or households, we are easily able to capture only overall reductions in transmission caused by the whole range of control measures used. The availability of more comprehensive data on the interventions implemented in a larger set of U.S. cities may enable some intervention-specific analysis and at the very least will increase the rigor and power of the initial analysis presented in this paper. Our analysis indicates that, whereas control measures can explain much of the variation in the shape of epidemics seen in different cities, they can explain only about half of the variance in overall mortality. Understanding the causes of the remaining variation, whether social or biological, is an important topic for future work.

Extrapolating from 1918 to the present day requires great caution; the U.S. of 1918 was a very different place from today. Household sizes were much larger, and many workers lived in large crowded boarding houses within which transmission can be expected to have been intense. More generally, far more people interacted with large extended families, children spent many fewer years in full-time education, and travel patterns were also very different. Overall infectious-disease-related mortality was much higher than today, and cofactors that might have affected transmission and mortality (such as malnutrition) were much more prevalent. More demographic and socioeconomic data need to be collated for different U.S. cities in 1918 to understand the effect of these differences. More challenging still, collecting data on behavioral responses to the pandemic might enable our hypothesis of reactive social distancing to be tested.

That said, our conclusions, to a degree, are encouraging for ongoing pandemic planning efforts in the U.S. that emphasize the potentially key role that might be played in a future pandemic by exactly the sort of public health measures used in 1918. Our theoretical analysis of the impact of transitory imperfect controls on the total number infected in an epidemic is more sobering, however. Although attack rates (and thus mortality) can be reduced by 30–40% through transitory controls, to achieve reductions beyond this with public health measures alone requires those measures be sustained for as long as it takes for vaccination of the population to be completed, perhaps as long as 6 months. The experience of many U.S. cities in 1918 shows us that the social, political, and behavioral challenges in delivering such long-term intensive policies will be considerable.

Methods

Transmission Model.

The requirements of solving the transmission model many millions of times during the model-fitting procedure impose major restrictions on the sophistication of the model we can use. We therefore model the epidemic in each city using a deterministic susceptible–exposed–infected–recovered model (6) defined by: dS/dt = −λ(t)S; dE/dt = λ(t) S − αE; dI/dt = αE − νI, where S, E, and I are the number of individuals who are susceptible, latently infected, and infectious, respectively. Initially, we assume one infectious individual and N − 1 susceptibles, where N is the population size of the city. The mean latency period, 1/α, is assumed to be 1.5 days, and the mean infectious period, 1/ν, is assumed to be 1.8 days. For values of R₀ between 1.5 and 2, this choice results in real-time epidemic growth rates compatible with those obtained by using more complex models with time varying infectiousness (8). The death rate at time t is defined as D(t) = μ ∫₀^∞ f(τ)λ(t − τ)S(t − τ)dτ where μ is the proportion of infected individuals who die, and f(τ) is the distribution of the delay between infection and death with 1918 pandemic influenza (12). The force of infection, λ(t), is defined by λ(t) = β(t) I(t) Nκ/(κ + M(t)), where β(t) = (1 − p_c)νR₀ when control measures are in force (overlapping sets of controls were assumed to combine multiplicatively), and β(t) = νR₀ at other times, with p_c being the effectiveness of controls. The Hill function in the parameter κ represents frequency dependence in the contact rate, whereby individuals reduce their contacts as a function of the number of deaths occurring in the population in the previous time period T (so M(t) = ∫₀^T D(t − τ)dτ). When κ → ∞, the model reverts to standard homogenous mixing (mass action). The cumulative number of people infected in an epidemic in the absence of controls and with κ → ∞, I_total, satisfies the equation N ln(1 − I_total/N) + R₀I_total = 0. It should be noted that, if the duration of infectiousness differed for lethal and nonlethal cases, then the above model is an approximation, although because case mortality was always <2% in the U.S., the effect of any correction would be very minor.

Model Fitting.

From the mortality data in Collins et al. (2), we use the model to estimate the absolute number of excess pneumonia and influenza deaths per week from September 1918 to May 1919 for the 16 cities being fitted. Where excess deaths are negative, we assume that they are zero in the fitting procedure. We further assume that the weekly data are Poisson-distributed and construct the corresponding log-likelihood (subtracting the saturated log-likelihood). This is almost certainly conservative in judging goodness of fit, in the sense that the variation in the data might be expected to be extra-Poisson, having been derived by using an ad hoc algorithm from raw mortality data (see SI Appendix). Markov-Chain Monte-Carlo (MCMC) methods (13) are used for model fitting, with uniform priors used for all model parameters. All parameters are assumed to be positive definite. MCMC chains were run until convergence was achieved (by visual inspection), and an additional 10⁷ parameter update steps (proposals) were then generated to estimate posterior distribution. We cannot be sure that mixing is perfect, especially in relation to dominant parameters (e.g., R₀ fitted as common to all cities), which, together with being overconservative in our assumption of Poisson variation in the data, may explain the rather tight credibility intervals on some parameters. However, we did run multiple chains from different starting points for each model variant, giving greater confidence in at least the mean posterior estimates of parameters.