Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2007 Apr 2;104(15):6194–6199. doi: 10.1073/pnas.0608558104

The role of lubricin in the mechanical behavior of synovial fluid

G D Jay †,‡,§, J R Torres †, M L Warman , M C Laderer †, K S Breuer †
PMCID: PMC1851076  PMID: 17404241

Abstract

Synovial fluid is a semidilute hyaluronate (HA) polymer solution, the rheology of which depends on HA–protein interactions, and lubricin is a HA-binding protein found in synovial fluid and at cartilage surfaces, where it contributes to boundary lubrication under load. Individuals with genetic deficiency of lubricin develop precocious joint failure. The role of lubricin in synovial fluid rheology is not known. We used a multiple-particle-tracking microrheology technique to study the molecular interactions between lubricin and HA in synovial fluid. Particles (200 nm mean diameter) embedded in normal and lubricin-deficient synovial fluid samples were tracked separately by using multiple-particle-tracking microrheology. The time-dependent ensemble-averaged mean-squared displacements of all of the particles were measured over a range of physiologically relevant frequencies. The mean-squared displacement correlation with time lag had slopes with values of unity for simple HA solutions and for synovial fluid from an individual who genetically lacked lubricin, in contrast to slopes with values less than unity (α ≈ 0.6) for normal synovial fluid. These data correlated with bulk rheology studies of the same samples. We found that the subdiffusive and elastic behavior of synovial fluid, at physiological shear rates, was absent in fluid from a patient who lacks lubricin. We conclude that lubricin provides synovial fluid with an ability to dissipate strain energy induced by mammalian locomotion, which is a chondroprotective feature that is distinct from boundary lubrication.

Keywords: diffusion, hyaluronic acid, microheology, PRG4, Einstein–Stokes relation

Synovial fluid, an ultrafiltrate of blood with additives produced by the synovium, has a number of biological roles. Articular cartilage is nourished by synovial fluid, because cartilage lacks its own blood supply. Synovial fluid also contributes to the lubrication and protection of articular cartilage surfaces. The glycosaminoglycan hyaluronate (HA) is a synovial fluid constituent that is produced by synoviocytes. HA is composed of repeated disaccharide units of N-acetylglucosamine and d-glucuronic acid that has an average molecular mass of 1 × 106 Da and a concentration of 2–4 mg/ml in synovial fluid (1). In articular cartilage, the complex of HA, aggrecan, and link protein contributes to the elastic properties that characterize the bulk behavior of cartilage under pressure (2). Lubrication of mammalian joints under load with near-zero sliding speed (the boundary mode) requires constituents in synovial fluid to lower the adhesion energy between apposed semiflattened cartilage asperities. Unless physically bound to a surface (3), HA alone cannot provide boundary lubrication, because surface lubrication under load becomes independent of synovial fluid's bulk viscous property (4, 5).

Lubrication of cartilage surfaces under load is provided by another abundant synoviocyte-derived component of synovial fluid, lubricin (encoded by the gene PRG4), which is a mucinous glycoprotein with globular amino- and carboxyl-terminal domains and a central region that is extensively modified by O-linked oligosaccharide side chains (6). Lubricin was initially purified from bovine synovial fluid (BSF) on the basis of its ability to lubricate biological and nonbiological surfaces (5). Its concentration in synovial fluid is ≈200 μg/ml (7). Subsequent in vitro studies have indicated that lubricin interacts with HA and works synergistically to provide boundary lubrication of a latex-glass bearing under increasing load (5).

However, it is unknown whether the lubricin–HA interaction contributes to biophysical properties of synovial fluid that are distinct from the ability to contribute to boundary lubrication. Synovial fluid behaves in a non-Newtonian manner, because dynamic interactions between individual HA polymers depend on shear rate (1). The effects of lubricin on the mechanical properties of synovial fluid, were studied by using a multiple-particle-tracking microrheology (MPTM) technique (8). The random walk behavior of tracer particles introduced into synovial fluid was modeled by the Einstein–Stokes relation (9).

Synovial fluid from an individual with genetic deficiency of lubricin (10) provides an opportunity to address the contribution of lubricin to synovial fluid's biophysical properties. The autosomal recessive human disease camptodactyly-arthropathy-coxa vara-pericarditis (CACP) syndrome is caused by truncating mutations in the gene PRG4, leading to no lubricin expression (11). A comparison of synovial fluid from patients with osteoarthritis, rheumatoid arthritis, and CACP indicates that lubricin is the predominant component missing from the latter (12). Despite containing normal amounts of HA, synovial fluid from a patient with CACP syndrome is unable to provide efficient boundary lubrication.‖ Synovial fluid functions as a dynamic network, in which filament-shape fluctuations allow entanglements to appear and disappear at small time intervals in the molecular network of the fluid (13). Given that HA shows little intermolecular association (14, 15), we hypothesized that lubricin will contribute to the structural organization of synovial fluid. The interaction may also give rise to anomalous diffusion, which plays a fundamental role in other biological processes (16). Therefore, we studied pure solutions of HA, BSF, and patient-derived CACP synovial fluid (CACP-hSF) by using MPTM and rheology to determine how the lubricin–HA interaction affects the mechanical properties of synovial fluid. Herein, we demonstrate that lubricin–HA interactions contribute to a chondroprotective mechanical property of synovial fluid that is distinct from its role as a boundary lubricant. We also demonstrate that MPTM and standard viscometry yield comparable results when applied to synovial fluid. We suggest that MPTM will be a useful tool for measuring biophysical properties of clinical samples, without strain and with using very small sample volumes.

Results

The Diffusive Behavior of BSF.

The diffusive behavior of synovial fluid was studied by quantifying the random walk behavior of introduced tracer particles (Fig. 1). This method also permitted indirect measurements of viscoelastic behavior as described in Eq. 1 (see Methods). The diffusive behavior of particles in synovial fluid was characterized by measuring the ensemble-averaged mean-squared displacement (MSD) [〈r2(τ)〉], a time-dependent quantity that is related to the diffusion coefficient (D) by 〈Δr2(τ)〉 = 4Dτ, where τ is the lag time, a measure of the amount of time elapsed between MSD measurements. For Newtonian fluids, the MSD has a linear relationship with the lag time, whereas for non-Newtonian fluids this relationship is nonlinear. Measuring the MSD across a range of lag times reveals the non-Newtonian behavior of synovial fluid, which is characterized by a slope lower than unity at short lag times.

Fig. 1.

Fig. 1.

Open in a new tab

Random walk exhibited by a 200-nm-diameter particle embedded in BSF from start (a) to end (b) after tracking its position over 12 s. Each pixel represents 64.5 × 64.5-nm resolution.

At long lag times (τ > 300 ms), the diffusive behavior of particles in BSF was similar to that of an 80% (wt/vol) glycerol solution. The logarithmic curve of the MSD with respect to lag time was linear with slopes (α) of 0.9 for BSF and 1.0 for glycerol (Fig. 2). At shorter lag times (τ < 300 ms), BSF exhibited a subdiffusive behavior, in that the slope of the curve became less than unity, closer to 0.6 (Fig. 2). Eighty-percent glycerol continued to exhibit linear behavior at shorter lag times. The difference in behavior between BSF and 80% glycerol at shorter lag times likely reflects particle trapping by the HA network in BSF. When BSF was diluted with 80% glycerol, the subdiffusive behavior decreased (Fig. 2). As BSF made the transition from a “semidiluted” to a dilute solution (i.e., 25% BSF by volume), the fluid behavior became increasingly diffusive at the short lag times. This result is best explained by the reduced concentration of synovial fluid HA no longer being able to promote polymer entanglements. At longer lag times the particles are able to diffuse through the network at rates limited by the viscosity of the fluid and, to a lesser extent, the network organization. This result may be seen in Fig. 2, where it is observed that although BSF was increasingly diluted to 25% of its physiological concentration, particle entanglement still occurred at higher lag times.

Fig. 2.

Fig. 2.

Open in a new tab

Time-dependent MSD of 200-nm beads in BSF, 80% glycerol solution, ET-BSF, CACP, and BSF diluted with 80% glycerol. The power law with a slope near unity is exhibited at low and high lag times for all samples except BSF, which exhibits a slope less than unity (α ≈ 0.6) for short lag times (τ ≤ 300 ms).

Lubricin Influences Synovial Fluid Mechanics.

To determine whether the concentration of HA polymers alone is sufficient to cause the subdiffusive behavior of synovial fluid, we examined the diffusive behavior of particles in BSF, in BSF that had been digested with trypsin, and in synovial fluid from a patient with CACP whose HA concentration was normalized. Trypsin will not affect the integrity of HA molecules but will digest synovial fluid protein constituents, including lubricin, that could promote HA polymer entanglement. Enzyme (trypsin)-treated BSF (ET-BSF) adopted a linear relationship with respect to short and long time lags (α ≈ 1) (Fig. 2), which is consistent with trypsin digestion having increased the characteristic mesh size of the network in the synovial fluid. To study the microrheology of synovial fluid that is missing lubricin, CACP-hSF was also tested. The HA concentration in CACP-hSF was equivalent to that of the other tested samples, so that any changes in network formation would be attributable to lubricin deficiency. CACP-hSF at short (τ ≤ 300 ms) and long lag times exhibits a purely diffusive behavior as seen by the MSD with a slope near unity (Fig. 2), even though the bulk viscosity remained high (see below). The ability of trypsin digestion to cause the synovial fluid to lose subdiffusive properties and resemble a simple HA (polyelectrolyte) solution indicates that the protein constituents within synovial fluid provide this unique property. More importantly, the lack of subdiffusive behavior in CACP-hSF, along with the evidence of a direct interaction between HA and lubricin (5), suggests that lubricin is a major synovial fluid protein that provides structure to synovial fluid.

Probability Density Function for the Normalized Displacement of Individual Tracers.

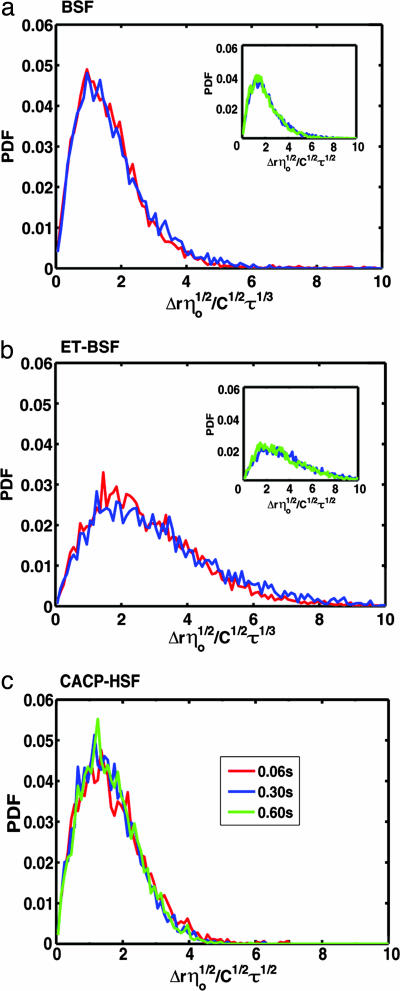
The probability density functions (PDFs) of the measured displacements, normalized with respect to the lag time of measurement and zero-shear viscosity and a constant C = 4kBT/6πa, for the individual particles of radius a embedded in the HA solutions, exhibited the shape of a Poisson distribution (Fig. 3), as expected for a random walk measured in radial coordinates. The normalized Einstein–Stokes relation, which describes each fluid, is illustrated on the abscissa of each plotted PDF. The reference lag times of 60 (red), 300 (blue), and 600 (green) ms were used to plot the PDF of the displacement for each sample. The square of the mean for each curve in a displacement PDF (not shown) is the MSD for the specific lag time; its change with respect to the different lag times is shown in Fig. 2. The root MSD (RMSD), which is a measure of the spread of the tracers, scales with the square root of the lag time for Newtonian fluids (9), where D is the diffusion coefficient (D = kBT/6πηa). Fig. 3 a and b show that the RMSD of both BSF and ET-BSF, respectively, scale with the cube root of shorter (τ ≤ 300 ms) lag times [〈Δr2(τ)〉1/2 ≈ τ1/3] and with the square root of longer (τ > 300 ms) lag times (Insets). It may also be seen that the tracers in BSF exhibited greater spreading after digestion with trypsin (in ET-BSF). Both the RMSD of glycerol (not shown) and CACP-hSF (Fig. 3c) solutions scaled with the square root of the lag times [〈Δr2(τ)〉1/2 ≈ τ1/2] for the whole range of lag times.

Fig. 3.

Fig. 3.

Open in a new tab

Normalized displacement PDFs of particle tracers embedded in the synovial fluid samples measured after 60 (red), 300 (blue), and 600 (green) ms. The RMSD of the tracers in both BSF (a) and ET-BSF (b) solutions exhibit a scaling with the cubic root of lag times <300 ms and with the square root of lag times >300 ms (Insets). (c) Similar to a purely viscous fluid, CACP-hSF scales to the square root of all lag times.

Shear-Rate Dependence of the Dynamic Viscosity.

At lower shear rates, the dynamic viscosity of the synovial fluid solutions exhibited a nearly constant value close to the zero-shear-rate viscosity (η0) (Fig. 4). The zero-shear-rate viscosity of BSF increased after enzyme digestion. Conversely, when lubricin, at a physiologic concentration of 300 μg/ml, was added to human umbilical cord HA (UHA), the zero-shear-rate viscosity decreased, which suggests that lubricin can provide structure to HA polymers and influence their shear flow (5). Consistent with this observation, we found the zero-shear-rate viscosity value for CACP-hSF (≈1.5 Pa·s) is an order of magnitude higher than that of the normal BSF (0.4 Pa·s). At higher shear rates, both fluids exhibited shear-thinning viscosity, characterized by the power-law region of the curves. The transition to power-law region in the viscosity with respect to the shear rate reveals differences between the fluids, namely the distribution of molecular weights of the polymeric molecule responsible for the bulk behavior. For CACP-hSF, the transition range of shear rates was ≈0.2–20 s−1 (Fig. 4), which may indicate that the distribution of HA molecular weights is broader than that of normal HA present in BSF with a transition range of shear rates of 0.1–2 s−1 (17). There was no significant difference in the value of shear rate (0.1–0.2 s−1) at which the onset of shear thinning occurs for both fluids.

Fig. 4.

Fig. 4.

Open in a new tab

Shear-rate-dependent viscosity of the CACP-hSF, BSF, ET-BSF, UHA, and UHA with added lubricin measured in the rheometer. After addition of lubricin, the zero-shear viscosity of UHA decreased considerably. An increase in zero-shear viscosity was also noted in BSF after digestion with trypsin. The onset of power-law behavior (between arrows) at greater shear rates in the CACP-hSF sample may be attributable to a wider range in the molecular weight distributions of HA.

The values of the intrinsic viscosity exhibited by Healon, CACP-hSF, and BSF were 18.8, 18.4, and 13.6 centistokes, respectively. Healon was chosen for these experiments because it is a pure HA preparation with a molecular weight similar to that of synovial HA. The main polymer in BSF (HA) possessed a significantly lower intrinsic viscosity than that of both CACP-hSF and Healon, which is consistent with the decrease in viscosity after the addition of lubricin to UHA and the increased viscosity after the digestion of BSF with trypsin, because intrinsic viscosity is a measure of the capacity of a polymer to enhance the viscosity of a solvent.

Unsteady Shear-Flow Behavior.

The complex linear viscoelastic modulus (G*) for BSF was obtained from the time-dependent MSD (Eq. 1), decomposed into the shear storage modulus (G′) and the shear loss modulus (G″), and compared with the rheological data obtained with bulk rheometry (Fig. 5). The rheometer data allowed the assessment of the behavior of synovial fluid at higher frequencies and also served as validation of the MPTM technique for the study of these samples. The agreement between the MSD and the bulk rheometry data, for BSF, is because of the use of probes with a mean diameter greater than the characteristic mesh size of the network in the semidilute solution. This agreement did not exist for ET-BSF, providing evidence for an increase in characteristic mesh size after enzymatic digestion (data not shown). The decomposition of the complex modulus into the shear storage and shear loss moduli showed that at low angular frequencies, G″ dominates the behavior of BSF, ET-BSF, CACP, and UHA, initially rising with a slope near unity and subsequently approaching a plateau (data not shown). At higher angular frequencies, G′ dominates G*, crossing over to higher values. This intersection is the longest relaxation time, which is the time required for induced stresses to relax. The longest relaxation time exhibited by BSF is an order of magnitude higher than that of CACP-hSF and UHA (Table 1). Both the CACP-hSF and UHA solutions exhibited the expected shear moduli profile of an unentangled polyelectrolyte solution (17). The CACP-hSF shear moduli resemble those of a stiff polymer solution. The longest relaxation time for BSF did not change significantly after proteolytic enzyme digestion (Table 1).

Fig. 5.

Fig. 5.

Open in a new tab

Comparison of MPTM technique and rheometry in measurement of shear storage modulus (G′) and shear loss modulus (G″) for BSF. The MPTM technique recapitulates the observations made by rheometry for G″ and more closely for G′.

Table 1.

Relaxation times for different samples of synovial fluid and HA

Sample Relaxation time(s), s
BSF 0.100–0.125
ET-BSF 0.08–0.10
CACP-hSF 0.014–0.016
UHA 0.010–0.016
Open in a new tab

Discussion

Apgar et al. (8) used MPTM techniques to describe the effects of regulatory proteins on the assembly of actin structures and subsequently on the heterogeneity and viscoelasticity of semidilute actin solutions. We have used MPTM to provide evidence of an interaction between lubricin and HA in synovial fluid. Our results suggest that HA alone does not account for synovial fluid's biophysical properties; rather, these properties result from the interaction between HA and other synovial fluid constituents, with lubricin seeming to be a major participant in this interaction.

Xu et al. (18) used MPTM to demonstrate the relationship of concentration and viscoelasticity in wheat gliadin suspensions. We used MPTM to demonstrate subdiffusive and elastic behavior of BSF, as evidenced by the particle entrapment of 200-nm probes at lag times <300 ms (Fig. 2). The purely diffusive behavior, throughout the range of lag times (Fig. 2), and the increase in spread (RMSD) of the tracers (Fig. 3b) while having increased its bulk viscosity (Fig. 4) after enzymatic treatment of BSF point to an increase in the characteristic mesh size of the HA molecular network, whereby the probes move with greater ease through the network. These data show that the thermodynamics of the HA network in the synovial fluid environment were not changed significantly, because the digestion of all of the proteins present in the fluid will lead to a suspension of peptides and amino acids, maintaining the flexibility of HA filaments and therefore bulk elasticity.

We found the same result by using patient-derived CACP-hSF (i.e., the absence of subdiffusive behavior despite increased viscosity) (Figs. 2 and 4). Assuming that lubricin is the only missing component in the synovial fluid of patients with CACP (12), this result strongly supports a direct role for lubricin in organizing HA molecules within synovial fluid. In the absence of lubricin, HA adopts a more rigid conformation and is unable to layer and demonstrate shear thinning. The linear viscoelastic moduli G′ and G″ of CACP-hSF were very similar to UHA (data not shown), suggesting that in the absence of lubricin the biophysical properties of synovial fluid are no different from that of purified HA.

The mammalian diarthrodial joint is a complex mechanism that uses weeping lubrication by articular cartilage (19, 20), interstitial fluid pressurization (21, 22), and boundary lubrication of flattened asperities. Lubricin and HA interact on a bearing surface providing boundary lubrication and do so under high load (5). What might be the advantages of also having lubricin and HA interact within synovial fluid? We postulate that lubricin–HA complexed within synovial fluid is in equilibrium with similar complexes located within the lamina splendens. Normally, when load is applied to opposing cartilage surfaces, synovial fluid and the lamina splendens need to be able to reversibly deform in an elastic manner. The time it takes for synovial fluid to release this energy and come to complete relaxation (i.e., the longest relaxation time) was shorter for CACP-hSF than it was for BSF. In fact, CACP-hSF behaved like pure UHA in this regard. Therefore, we conclude that lubricin enables the synovial fluid network to absorb energy, deform, and slowly dissipate strain energy. This component of chondroprotection is distinct from the component provided by boundary lubrication. Moreover, the observed small-particle subdiffusive behavior by the HA network in the presence of lubricin (Fig. 2) also suggests that lubricin could possibly play a role in creating an osmotic barrier to small biomolecules, which help maintain chondrocyte metabolism and joint health.

We have shown that the MPTM technique can be used to characterize physiologic suspensions of clinical importance. This technique allows probing of the local environment of complex fluids and facilitates the study of scarce fluids, because the amount needed is <100 μl. Analysis of data with this technique, using Eq. 1, yielded results for biophysical properties that are comparable to those obtained by bulk viscometry methods (Fig. 5), which require larger quantities of fluid and physical deformation.

In the diarthrodial joint, the synovial fluid/lamina splendens transitions from a state of stress to a relaxed state, where the strain energy is dissipated. Thus, entanglements, mediated by lubricin or its fragments, lengthened relaxation times because of the elastic contributions of this biomolecule (Table 1). The lengthened relaxation time is within a physiologic range. It is possible that the thermodynamics of the HA network in the synovial fluid environment were not changed significantly, because the digestion of all of the proteins present in the fluid will lead to a suspension of peptides, maintaining the flexibility of HA filaments and, therefore, bulk elasticity. The concentration of HA, among the samples studied, was normalized and consistent with normal synovial fluid. In this manner the network-forming molecule was maintained at a controlled concentration, and any changes in network formation were caused by the regulatory molecules. CACP-hSF genetically lacks lubricin, thereby serving as a control to study the function of lubricin molecules attached to the HA copolymer. The subdiffusive behavior exhibited by BSF after dilution, and the diffusive behavior along with the absence of elasticity in CACP-hSF at physiological shear rates (Fig. 2), is evidence for an interaction of lubricin–HA in which lubricin increases the degree of entropy of an otherwise stiffer HA molecule. This interaction would lead to a more flexible HA molecule, as seen by the reduced intrinsic viscosity of normal synovial fluid. Lubricin allows the HA polymer to align in the direction of the flow, thus reducing the dynamic viscosity of the HA solutions, which plays a role in the characteristic stringy behavior of synovial fluid. Although CACP-hSF proved to be more viscous than the rest of the fluid samples with similar HA concentration, it nevertheless lost its subdiffusive behavior. Adding lubricin to the CACP-hSF in the MSD experiments was not performed, because the HA concentration was abnormally high and its dilution would have affected the concentration of other protein components. Synovial and serum proteins interact with HA and may also play a role in regulating mesh size.

The implication of these results to our understanding of chondroprotection is significant. Lubricin, with its amphipathic nature (23), makes the attachment of HA to cartilage possible. Together, HA and lubricin, or the related PRG4 protein product superficial zone protein (24), comprise the chondroprotective features of synovial fluid, conferred by lubricating and nanoelastic activities.

In summary, we have used MPTM techniques to characterize physiologic suspensions of clinical importance. Using BSF and synovial fluid from a patient with CACP, we have shown that lubricin affects the diffusive behavior of synovial fluid. In the macromechanical realm, we also found that lubricin contributed to the elastic absorption and energy dissipation of synovial fluid at physiological shear frequencies. In the absence of lubricin, HA molecules adopted an extended and more rigid conformation, and synovial fluid would be less able to dissipate the energy of impact that occurs during mammalian locomotion. Therefore, lubricin provides a chondroprotective feature to synovial fluid that is distinct from the role lubricin plays at the cartilage surface as a boundary lubricant. Additional MPTM experiments, which involve reintroducing lubricin to HA in the presence of the synovial protein milieu, are needed.

Methods

Sample Preparations.

Each fluid was tested at least 3 times to ensure reproducibility. Solutions studied for the characterization and application of the MPTM system are listed below.

Glycerol.

ACS reagent 99.5+ vol% (G789-3, Sigma–Aldrich) was used for the control solution because of its Newtonian behavior and its viscosity of 1 P (1 P = 0.1 Pa·s), which approximates the low shear-rate viscosity of BSF. Glycerol was diluted to 80% (wt/vol) with distilled deionized water.

BSF.

Undiluted BSF (57099-0, Pel-Freez Biologicals). BSF was also diluted with 80% glycerol (wt/vol).

ET-BSF.

BSF was digested with 1-tosylamide-2-phenylethyl chloromethyl ketone-treated trypsin (Sigma–Aldrich). The amount of 25 μl of a 2 mg/ml solution of trypsin in calcium-free PBS was added to 1 ml of BSF and incubated for no less than 2 h in a shaker at 750 rpm and 37°C. The loss of boundary-lubrication ability was confirmed in a tribometer by using a latex-glass bearing (7).

CACP-hSF.

Synovial fluid was obtained from a patient with CACP syndrome resulting from a loss-of-function mutation in PRG4. Collection of the synovial fluid by joint aspiration was approved by the local institutional review board.

UHA.

UHA (Sigma–Aldrich did not contain lubricin and was used in bulk rheology experiments.

Healon.

The sodium HA solution had a molecular mass of 4 MDa (Advanced Medical Optics, Santa Ana, CA).

In all preparations containing HA, the HA concentration was adjusted to 3.5 mg/ml.

HA Concentration Determination.

Synovial fluid aspirates were assayed by the manual carbazole reaction for uronic acid (25). HA concentration was reported in units of milligrams per milliliter after factoring in a 10-fold dilution.

MPTM.

Fluorescent microspheres (Duke Scientific, Palo Alto, CA) of 200 nm mean diameter were added to the solutions being tested (0.3% volume fraction). An aliquot (≈2–5 μl) of the sample was deposited onto a hydrophobic multiwell slide (Erie Scientific, Portsmouth, NH) to prevent flow. This static condition of the fluid was confirmed by observing the relative motion of probes over an extended amount of time (t > 20 s). The slide was covered to prevent evaporation and placed on the stage of an inverted light microscope (Nikon Eclipse TE200) with a 100-W mercury-lamp light source (Chiu Technical, Kings Park, NY). A thermistor (TS67 series probes, Oven Industries, Mechanicsburg, PA) embedded next to the slide was used in conjunction with a Thermoelectric Cooler chip (Melcor, Trenton, NJ) and temperature controller (Oven Industries) to maintain the system at constant temperature (295 K). An objective with 100× optical amplification and a 1.4 numerical aperture (Nikon) was used for magnification. The fluorescent beads were tracked with a 1500-EX charged-coupled device camera (IDT, Tallahassee, FL) of 6.45 × 6.45 μm/pixel resolution and 12-bit dynamic range with 1 × 1 binning, for an effective 64.5 × 64.5 nm/pixel resolution for the optical system.

Particles at different locations in a region of interest in the middle plane of the sample were tracked separately by using algorithms developed in MATLAB. Images were acquired at 16 Hz. In each image, the bright spots of tracer particles were identified and their centers computed by fitting a Gaussian distribution to the Airy disk formed by the light emitted from the fluorophores in each particle. This computation yielded the location of the particle center to within ≈1/10th of a pixel (6.45 nm). A region of interest of ≈8 × 8 μm was used to confirm that the same particle was being tracked frame after frame. Approximately 100 particles were individually tracked over 12 s, yielding >3,000 steps per lag time.

To avoid particle–particle interaction artifacts, only particle probes separated from other probes by a distance of 2 μm (10 times the probe diameter) were tracked. The structural and mechanical heterogeneity of the network in the dilute solutions were probed by observing the time-dependent MSD of the probes (16, 18). The time-dependent complex modulus ∣G*(ω)∣ along with its components, the shear storage G′(ω) and shear loss G″(ω) moduli, for the samples was calculated (26) and compared with the values obtained from bulk rheology. The time-dependent complex modulus is given by

graphic file with name zpq01507-5931-m01.jpg

where 〈Δr2(1/ω)〉 is the MSD with respect to the angular frequency (ω) of interest, Γ is the gamma function, and dln〈Δr2(τ)〉/dlnτ∣τ=1/ω is the slope of the MSD, 〈Δr2(τ)〉, with respect to the lag time (τ) between measurements. It is assumed that the fluid being probed is isotropic and incompressible around the sphere, which is acceptable at these low Reynolds numbers. The characteristic mesh size of the network in the complex fluid is much smaller than the diameter of the particle, if there is agreement in the shear storage modulus calculated from Eq. 1 and from bulk rheometry, which ensures particle entanglement in the molecular network. This premise is essential for the correlation of bulk rheology with the MSD measurements.

Bulk Rheology of Synovial Fluid.

The rheological studies of the synovial fluid samples (BSF, ET-BSF, and CACP-hSF) were performed in the AR 2000 (TA Instruments, New Castle, DE) rheometer at 21°C with a steel head of cone angle of 0°, 30 min, and 14 s, 40-mm diameter, and 19-μm truncation. Measurements on each sample were performed in steps, with 2 s between steps, to allow for relaxation of the fluid. The experiments were performed within 10 min of setup and repeated by using new samples of each solution to avoid the artifacts from evaporation and degradation of the sample after each test. Shear-flow tests were performed on each fluid sample to measure the shear-rate-dependent dynamic viscosity at a shear-rate range of 10−1 to 2 × 102 s−1 and 5% strain. Unsteady or oscillatory shear-flow measurements were obtained at an angular frequency range of 100 to 103 rad/s.

The intrinsic viscosity (ηr) of BSF, CACP-hSF, and Healon, a commercially available solution of pure HA, was measured by progressively diluting the solutions with 0.9% NaCl and reintroducing it into an Ubbelohde-type viscometer (Cannon Instruments, State College, PA). Measurements were conducted at 37°C. Calculation of the intrinsic viscosity was performed in accordance with American Standard for Testing of Materials D2857-95.

Acknowledgments

We thank Drs. Anubhav Tripathi and Donna M. Meyer for guidance and suggestions for this manuscript. We also gratefully acknowledge the financial support provided by the National Institute of Arthritis and Musculoskeletal Diseases (NIAMS Grant RO1 AR05018001) of the National Institutes of Health, Department of Health and Human Services. M.L.W. is an Investigator with the Howard Hughes Medical Institute and a recipient of a Clinical Scientist Award in Translational Research from the Burroughs Wellcome fund.

Abbreviations

HA

hyaluronate

BSF

bovine synovial fluid

MPTM

multiple-particle-tracking microrheology

CACP

camptodactyly-arthropathy-coxa vara-pericarditis

hSF

human synovial fluid

MSD

ensemble-averaged mean-squared displacement

RMSD

root MSD

ET-BSF

enzyme-treated BSF

PDF

probability density function

UHA

human umbilical cord HA.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

‖

Jay, G. D., Carpten, J. D., Rhee, D. K., Torres, J. R., Marcelino, J., Warman, M. L., Transactions of the Annual Meeting of the Orthopedic Research Society, Feb. 3, 2003, New Orleans, LA, p. 134 (abstr.).

References

  • 1.Schurz J, Ribitsch V. Biorheology. 1987;24:385–399. doi: 10.3233/bir-1987-24404. [DOI] [PubMed] [Google Scholar]
  • 2.Mow VC, Sugalski MT. In: Physiological Basis of Rehabilitation Medicine. Gonzalez EG, Myers SJ, Edelstein JE, Downey JA, Darling RC, Edelstein J, editors. New York: Butterworth-Heinemann; 2001. p. 138. [Google Scholar]
  • 3.Tadmor R, Chen N, Israelachvilli J. Macromolecules. 2003;36:9519–9526. [Google Scholar]
  • 4.McCutchen CW. New Sci. 1962;15:412–415. [Google Scholar]
  • 5.Jay GD, Lane BP, Sokoloff L. Connect Tissue Res. 1992;28:245–255. doi: 10.3109/03008209209016818. [DOI] [PubMed] [Google Scholar]
  • 6.Jay GD, Harris DA, Cha CJ. Glycoconj J. 2001;18:807–815. doi: 10.1023/a:1021159619373. [DOI] [PubMed] [Google Scholar]
  • 7.Elsaid KA, Jay GD, Warman ML, Rhee DK, Chichester CO. Arthritis Rheum. 2005;52:1746–1755. doi: 10.1002/art.21038. [DOI] [PubMed] [Google Scholar]
  • 8.Apgar J, Tseng Y, Fedorov E, Herwig MB, Almo SC, Wirtz D. Biophys J. 2000;79:1095–1106. doi: 10.1016/S0006-3495(00)76363-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Berg HC. Random Walks in Biology. Princeton: Princeton Univ Press; 1993. pp. 5–12. [Google Scholar]
  • 10.Marcelino J, Carpten JD, Suwairi WM, Gutierrez OM, Schwartz S, Robbins C, Sood R, Makalowaska I, Baxevanis A, Johnstone B, et al. Nat Genet. 1999;23:319–322. doi: 10.1038/15496. [DOI] [PubMed] [Google Scholar]
  • 11.Rhee DK, Marcelino J, Baker M, Gong Y, Smits P, Lefebvre V, Jay GD, Stewart M, Wang H, Warman ML. J Clin Invest. 2005;115:622–631. doi: 10.1172/JCI200522263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Rhee DK, Marcelino J, Al-Mayouf S, Schelling DK, Bartels CF, Cui Y, Laxer R, Goldbach-Mansky R, Warman ML. J Biol Chem. 2005;280:31325–31332. doi: 10.1074/jbc.M505401200. [DOI] [PubMed] [Google Scholar]
  • 13.Boal D. Mechanics of the Cell. Cambridge, UK: Cambridge Univ Press; 2002. p. 100. [Google Scholar]
  • 14.Gribbon P, Heng BC, Hardingham TE. Biochem J. 2000;350:329–335. [PMC free article] [PubMed] [Google Scholar]
  • 15.Krause WE, Bellomo EG, Colby RH. Biomacromolecules. 2001;2:65–69. doi: 10.1021/bm0055798. [DOI] [PubMed] [Google Scholar]
  • 16.Barbi M, Place C, Popkov V, Salerno M. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Top. 2004;70:41901–41906. [Google Scholar]
  • 17.Rubinstein M, Colby RH. Polymer Physics. New York: Oxford Univ Press; 2003. [Google Scholar]
  • 18.Xu J, Tseng Y, Carriere CJ, Wirtz D. Biomacromolecules. 2002;3:92–99. doi: 10.1021/bm015586b. [DOI] [PubMed] [Google Scholar]
  • 19.McCutchen CW. Nature. 1959;184:1284–1285. doi: 10.1038/1841284a0. [DOI] [PubMed] [Google Scholar]
  • 20.Morrell KC, Hodge WA, Krebs DE, Mann RW. Proc Natl Acad Sci USA. 2005;102:14819–14824. doi: 10.1073/pnas.0507117102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Krishnan R, Kopacz M, Ateshian GA. J Orthop Res. 2004;22:565–570. doi: 10.1016/j.orthres.2003.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Olsen S, Oloyede A, Adam C. Comput Meth Biomech Biomed Eng. 2004;7:111–120. doi: 10.1080/10255840410001672185. [DOI] [PubMed] [Google Scholar]
  • 23.Jay GD. Connect Tissue Res. 1992;28:71–88. doi: 10.3109/03008209209014228. [DOI] [PubMed] [Google Scholar]
  • 24.Flannery CR, Hughes CR, Schumacher BL, Tudor D, Aydelotte MB, Kuettner KE, Caterson B. Biochem Biophys Res Commun. 1999;254:535–541. doi: 10.1006/bbrc.1998.0104. [DOI] [PubMed] [Google Scholar]
  • 25.Bitter T, Muir HM. Anal Biochem. 1962;4:330–334. doi: 10.1016/0003-2697(62)90095-7. [DOI] [PubMed] [Google Scholar]
  • 26.Mason TG, Ganesan K, van Zanten JH, Wirtz D, Kuo SC. Phys Rev Lett. 1997;79:3282–3285. [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES