Evidence for proton transfer in the rate-limiting step of a fast-cleaving Varkud satellite ribozyme

Abstract

A fast-cleaving version of the Varkud satellite ribozyme, called RG, shows an apparent cis-cleavage rate constant of 5 sec⁻¹, similar to the rates of protein enzymes that catalyze similar reactions. Here, we describe mutational, pH-rate, and kinetic solvent isotope experiments that investigate the identity and rate constant of the rate-limiting step in this reaction. Self-cleavage of RG exhibits a bell-shaped rate vs. pH profile with apparent pK_as of 5.8 and 8.3, consistent with the protonation state of two nucleotides being important for the rate of cleavage. Cleavage experiments in heavy water (D₂O) revealed a kinetic solvent isotope effect consistent with proton transfer in the rate-limiting step. A mutant RNA that disrupts a peripheral loop–loop interaction involved in RNA folding exhibits pH- and D₂O-independent cleavage ≈10³-fold slower than wild type, suggesting that this mutant is limited by a different step than wild type. Substitution of adenosine 756 in the putative active-site loop with cytosine also decreases the cleavage rate ≈10³-fold, but the A756C mutant retains pH- and D₂O-sensitivity similar to wild type, consistent with this mutant and wild type being limited by the chemical step of the reaction. These results suggest that the RG ribozyme provides a good experimental system to investigate the nature of fast, rate-limiting steps in a ribozyme cleavage reaction.

Since the discovery of RNA catalysis, several natural RNAs and many more RNA and DNA sequences obtained by in vitro selection have been shown to catalyze the cleavage and/or ligation of phosphodiester bonds, as well as other chemical activities. Recent work has begun to investigate the range of catalytic mechanisms used by ribozymes and to understand the similarities and differences with protein enzymes (1–3). The local environment of a folded RNA can shift the pK_a of certain nucleobases by two or more pH units into the range where they could function as proton donors or acceptors in general acid–base catalysis, similar to histidines in their protein counterparts (4). Charged nucleobases could also participate in electrostatic stabilization in the transition state. Indeed, the bell-shaped rate vs. pH curves typical of protein enzymes that use general acid–base catalysis have been observed for certain hepatitis delta virus (HDV) ribozymes (5, 6) and Varkud satellite (VS) ribozyme (this study).

Most previously characterized versions of the Neurospora VS ribozyme showed rather slow cis- or trans-cleavage apparent rate constants (k_obs) in the range of 1 min⁻¹ or less and were only slightly affected by pH between pH 5.5 and 9.0 (7); however, a trans-ligating construct did exhibit pH dependence below pH 7.0 (8). Other observations have also raised the possibility that a protonated group could be involved in the rate-limiting step of a VS ribozyme reaction pathway. For example, Strobel and colleagues (9) observed pH-dependent rescue of a ligation reaction by using nucleotide analog substitutions at position 756 in the putative active-site loop of the ribozyme but not at other positions. Also, Lilley and coworkers (10) showed that substitution of A756 with imidazole supported cleavage and ligation, although it was not reported whether this effect was unique to position 756 or whether the reaction was affected by pH.

Recently, VS (11) and hammerhead (12, 13) ribozymes have been described that exhibit cleavage and/or ligation rate constants two to three orders of magnitude faster than observed with previous constructs, and in the range of those of protein enzymes that catalyze similar reactions. These RNAs appear to have overcome whatever slow step was limiting the observed rate of previous versions of the ribozyme and they may provide experimental systems to investigate faster steps in the kinetic pathway of site-specific phosphodiester bond cleavage. In the current work, we provide evidence consistent with proton transfer and general acid–base catalysis in the rate-limiting chemical step of the VS cleavage reaction.

Results and Discussion

The Fast-Cleaving VS Ribozyme, RG, Exhibits pH- and Heavy Water (D₂O)-Sensitive Cleavage.

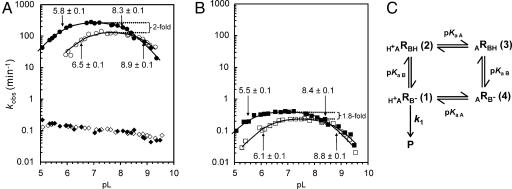
If one or more protonated species are involved in the rate-limiting step of cleavage, the observed rate of the cleavage reaction would be expected to vary with pH. Fig. 1A (filled circles) shows that this is indeed the case, with the reaction exhibiting a bell-shaped curve very similar to that of certain HDV ribozymes (5, 6) and some protein enzymes that employ general acid–base catalysis (15–17). We fit these data to the model in Fig. 1C, which describes the expected rate vs. pH behavior of a hypothetical enzyme in which one functional group must be protonated, and another deprotonated to obtain the maximal cleavage rate (18, 19). The experimental data fit very well to this model, which provides estimates of 270 min⁻¹ for the maximal cleavage rate, and 5.8 and 8.3 for the apparent pK_a values of the two hypothetical functional groups. These data show that the rate-limiting step of RG cleavage is pH-dependent and provide circumstantial evidence for the involvement of two titratable functional groups.

Fig. 1.

The effect of pH and D₂O on cleavage rate. (A) Rate vs. pL (pH or pD) profiles of RG in H₂O (filled circles), RG in D₂O (open circles), RGkV in H₂O (filled diamonds), and RGkV in D₂O (open diamonds). (B) pL (pH or pD) profiles of 756C in H₂O (filled squares) and in D₂O (open squares). See Materials and Methods and Fig. 5 for a description of RNAs and mutants. The apparent first-order rate constant for cleavage (k_obs) is plotted as a function of pL at 37°C (see Materials and Methods). (C) Kinetic model for self-cleavage of an RNA, R, which contains a single general acid of the functional form HA⁺ and single general base of the functional form B⁻. The extent of protonation of the acid and base is determined by their pK_a values: pK_aA and pK_aB, respectively (from ref. 18). This model assumes the protonation states of the acid and base do not influence each other and that products (P) are only formed from RNA molecules in which both the general acid and base are in their active forms, _H+AR_B− (1); the proportion of RNA in this active form is abbreviated as f_R(1). k₁ is the intrinsic cleavage rate constant of the bond breaking step. Apparent pK_a values for RG and 756C RNAs were estimated by fitting data to the equation k_obs = f_R(1) × k₁ = k₁/[1 + 10^(pKaB−pH) + 10^{(pKaB−pKaA)} + 10^(pH−pKaA)] (18).

Herschlag and coworkers (20) have pointed out that an apparent pK_a can result from deprotonation of multiple functional groups each with a pK_a significantly greater than the apparent pK_a. We attempted to fit the RG data in Fig. 1A to a model in which one of the apparent pK_a values resulted from such a phenomenon by using a range of hypothetical pK_a values (from 8.3 to 9.8) and titratable groups (from n = 1 to 20). The shapes of these curves are qualitatively different from the bell-shaped curve [except in the case of pK_a = 8.3 and n = 1, which reduces to the same model as in Fig. 1C; also see supporting information (SI) Fig. 6] so we conclude that this is not a likely explanation for the apparent pK_a values estimated from our data. Whether the apparent pK_a values represent titrations of individual functional groups or kinetic pK_a values due to a change from a pH-dependent to a pH-independent rate-limiting step (21) is considered below.

In principle, the functional groups responsible for the rate vs. pH profile observed in Fig. 1A could be involved in RNA structure and/or chemistry, and it may not be possible to completely separate these roles. In a simple example of the former case, a particular base may need to be in a protonated or deprotonated state for the RNA structure to fold correctly (22). In the latter case, one or more protons actually transfer to or from RNA functional group(s) in the rate-limiting step. Because we initiate the cleavage reaction by addition of MgCl₂, it is also possible that Mg²⁺ ions induce a conformational change in which a protonation or deprotonation event required for correct folding occurs; alternatively, as has been proposed for other ribozymes, the apparent titratable functional groups may be the general acid, general base, or electrostatic stabilizer in the chemical step of the reaction (6, 19, 23–27).

For some enzymes, insights into reaction mechanisms involving transfer of protons in the rate-limiting step can be gained from site-specific hydrogen isotope substitution of nonexchangeable protons (28). However, the two protons that transfer in the chemical step of the cleavage by VS RNA and the other small ribozymes, i.e., deprotonation of the 2′-OH of the nucleophile and protonation of the 5′ oxygen of the leaving group, are in rapid exchange with protons in the solvent water, making site-specific isotope substitution impossible. Instead, these reactions can be investigated by using kinetic solvent isotope experiments in which the reaction rate is measured by using RNA and reaction solutions that have been reconstituted with D₂O replacing H₂O (29). If transfer of one or more protons occurs in the rate-limiting step, the cleavage rate in D₂O would be expected to be slower than in H₂O (29, 30); if only a particular state of protonation is required, the cleavage rate would not be expected to change in D₂O.

The data in Fig. 1A (open circles) show that, like the reaction in H₂O, the cleavage rate of RG RNA in D₂O exhibited a bell-shaped dependence on pD (−log₁₀[deuterium ion]) and also fit well to the model in Fig. 1C. Two apparent pK_a values were also observed for the cleavage reactions in D₂O: the apparent pK_a values of 6.5 and 8.9 are ≈0.6–0.7 units higher than those observed in H₂O (Fig. 1A); a shift in pK_a of this magnitude and direction is typical of those observed for deuterium vs. protium ionization in a variety of weak acids, including ammonium ions (ΔpK_a = +0.6) (29, 31) and free cytosine base (ΔpK_a = +0.53) (32), as well as several protein and RNA enzymes (ΔpK_a = +0.4 to +0.8) (25, 27, 33, 34). These observations are consistent with the apparent pK_a values observed in D₂O having the same origin as those in H₂O.

If the apparent pK_a values were kinetic pK_a values resulting from a change from a pH-dependent to a pH-independent rate-limiting step, we would expect the maximal rate of reaction, occurring at the peak or on the plateau of the rate vs. pH curve, to be the same in D₂O and H₂O because in this pH range the observed rate would not represent the chemical (proton-transferring) step of the reaction. Instead, we found that the cleavage reaction in D₂O was 2-fold slower than in H₂O at the optimum pL (pH or pD) for each reaction. If the pH-sensitive and isotope-sensitive steps represent the same step in the reaction mechanism (35), our kinetic solvent isotope data support the interpretation that the apparent pK_a values represent titration of functional groups involved in proton transfer in the rate-limiting step of the VS ribozyme cleavage reaction.

The magnitude of D₂O inhibition decreases at higher pL values, even becoming slightly positive above approximately pL 8.5. The apparent loss of D₂O effect at high pL values has also been observed with several protein enzymes, e.g., refs. 33, 34, and 36. Kinetic simulations based on the model we used to fit our rate vs. pH data show that these curves are exactly what is expected for a shift in both apparent pK_a values of approximately +0.6 units and a 2-fold decrease in rate constant (k₁) in D₂O; the simulations also show that the increased magnitude of inhibition in D₂O below the lower pK_a is also predicted by this model (SI Fig. 7). The agreement between the observed and simulated data suggests that a more complex model is not required to interpret the data. However, because of the uncertainties involved in interpreting pH and kinetic solvent isotope experiments of biological macromolecules (37), our data cannot rule out more complex models. If the solvent isotope effect measured for RG indeed represents a primary isotope effect, our data are consistent with pK_a values of two specific functional groups, participating in one or more proton transfers in a single rate-determining step.

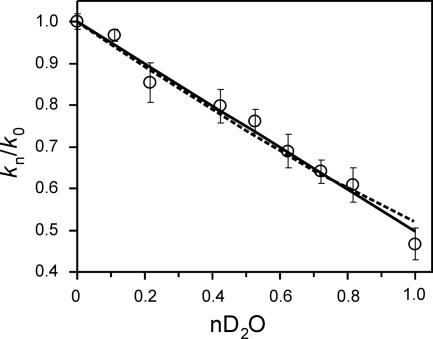
In an attempt to determine the number of protons transferred in the rate-limiting step, we performed proton inventory experiments (29) by measuring the relative cleavage rate over the range of D₂O fractions (n) (from 0 to 1). We fit our data to equations for one-proton [k_n/k₀ = (1 − n + nΦ^T); Fig. 2, solid line] and two-proton [k_n/k₀ = (1 − n + nΦ^T)²; Fig. 2, dashed line] inventories (30). Transition state fractionation factors (Φ^T) were calculated to be 0.50 ± 0.01 and 0.52 ± 0.01 for the one-proton and two-proton inventory models, respectively. The fractionation factor for the two-proton inventory assumes both transfers contribute equally to the isotope effect in the transition state. Both estimates of transition state fractionation factors are within the range observed for proton transfers involving oxygen or nitrogen atoms in other enzymes (38). The small magnitude of the isotope effect, confirmed in these experiments to be 2-fold, and the limited precision of our rate estimates (±5%) made it impossible to convincingly distinguish between models involving transfer of one proton or two protons (Fig. 2); nonetheless, these experiments provide evidence that at least one proton is transferred in the transition state.

Fig. 2.

Proton inventory for RG cleavage. The relative k_obs (normalized to 1 in 100% H₂O) was measured in different mole fractions of D₂O (nD₂O), ranging from 0 (100% H₂O) to 1 (99.9% D₂O). Each point is the average of two to nine independent trials. Data were fit to equations for a one-proton [k_n/k₀ = (1 − n + nΦ^T)] or two-proton [k_n/k₀ = (1 − n + nΦ^T)²] inventory (solid and dashed lines, respectively) and assume equal transition state contributions for the two transfers. n is the fraction of D₂O in the reaction, and Φ^T is the transition state fractionation factor (30). Data fitting was done with SigmaPlot (Systat Software, Point Richmond, CA) by using nonlinear least squares and were weighted more toward trials with greater numbers of repeats.

Disrupting the Kissing Interaction Changes the Rate-Limiting Step.

To investigate which step in the cleavage process might be rate-limiting, we examined the effect of mutations at positions previously shown or suspected to affect different steps. Previous work has shown that a kissing interaction between loops I and V is required for efficient folding of stem-loop I, which contains the cleavage site, into the core of the ribozyme (39–41). The kissing interaction is also required for a conformational change in stem-loop I in which several bases change pairing partners to adopt a conformation, termed “shifted,” that is required for cleavage (42). Mutants that constitutively adopt the shifted conformation can cleave in the absence of the kissing interaction, but at a much reduced rate compared with wild type (39), at least in part due to a weakened interaction of stem-loop I with the rest of the ribozyme (41).

We hypothesized that mutants lacking the kissing interaction are rate-limited by interaction of stem-loop I with the rest of the ribozyme, a step that occurs before the chemical step. This step might be expected to exhibit a different dependence, or lack of dependence, on pH. We have examined such a mutant, RGkV, and found that its observed cleavage rate constant is nearly independent of pH and is 2,700-fold slower than wild type at pH 7 (Fig. 1A, filled diamonds). Also, the kinetic solvent isotope effect seen in wild type is absent in the RGkV mutant, with cleavage occurring at the same rate in D₂O as in H₂O at any given pL (Fig. 1A, open diamonds). These results show that disrupting the kissing interaction changes the rate-limiting step in the reaction to one that does not involve proton transfer.

Substituting a Putative Active-Site Base, A756, with Cytosine Retains pH- and D₂O-Sensitive Cleavage.

A variety of circumstantial evidence has implicated A756, especially the ionization of this base, as contributing to the active site of the ribozyme (8–10, 43–46). Substitution of A756 with guanosine or uridine decreases the observed cleavage rate by 140,000- and 270,000-fold, respectively (SI Fig. 8). However, substitution with cytosine decreases the rate by only 700-fold at pH 7.0 (Fig. 1B, filled squares). By using a trans-cleaving VS ribozyme, Lilley and coworkers (46) also found that mutations at 756 were deleterious; however, under their conditions (subsaturating concentrations of ribozyme and Mg²⁺), the rates of the three mutants were similar. In other ribozymes, cytosine and adenosine can substitute for each other to some extent (25, 47) possibly because the pK_a of cytosine N3 and adenosine N1 can be shifted toward the neutral range by local tertiary structure and may be able to perform the same role as each other in the reaction.

Fig. 1B shows that the 756C mutant retains a bell-shaped rate vs. pH curve with apparent pK_a values of 5.5 and 8.4 and has a maximal cleavage rate of 0.4 min⁻¹, ≈700-fold slower than wild type at the optimal pH. The estimated value of the higher apparent pK_a is the same as that of wild type, and the lower apparent pK_a may be slightly less. The substitution of this adenosine by cytosine might be expected to change the local environment in the catalytic site, which could affect the pK_a of the catalytic functional groups, or the altered apparent pK_a could be that of the cytosine itself, perhaps performing the same role as A756, although less effectively. Cleavage of 756C in D₂O also exhibits a bell-shaped curve with apparent pK_a values shifted upward by 0.4–0.6 units (Fig. 1B, open squares), similar to the shifts observed for wild type (compare to Fig. 1A), and a 1.8-fold decrease in the maximal cleavage rate compared with H₂O, similar to the 2-fold effect seen for wild type. The similarities in the effect of D₂O on wild type and the 756C mutant are consistent with this substitution mutant being limited by the same proton transfer step as wild type, with the observed rate of this step being decreased ≈700-fold because of a decrease in the intrinsic rate constant of the chemical step and/or a decrease in the fraction of RNA in the catalytically competent state (see below).

An Unexpected Effect of Microviscogens.

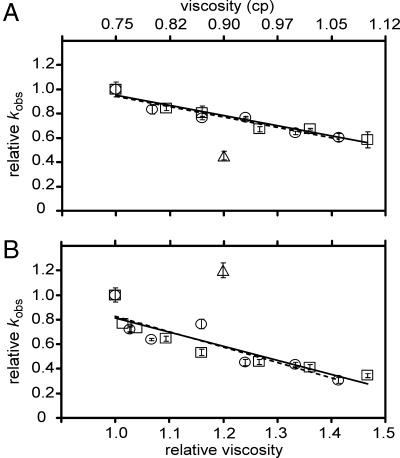
Although D₂O is among the most subtle “analog substitution” reagents available to probe a chemical reaction, even it has other properties that can affect the kinetics of an enzyme-catalyzed reaction. For example, the viscosity of D₂O is greater than that of H₂O (1.2-fold at 37°C) (29). Solvent viscosity can affect diffusion-limited reactions (48) and may affect the rate of reactions limited by movement of protein or RNA domains during folding. Control experiments using a range of concentrations of glycerol or sucrose in H₂O as a microviscogen are typically used in protein enzymology to determine whether the rate decrease observed in D₂O is actually an isotope effect rather than a viscosity effect (48). Such control experiments have not been reported in the ribozyme literature.

Because cleavage of RG is affected by pH and D₂O, suggesting that the rate was limited by the chemical step of the reaction, we did not expect an effect of viscosity on the rate. Indeed, the macroviscogen polyethylene glycol 8000 did not affect the rate of RG cleavage, even at high concentrations (10%, equivalent to a viscosity of ≈68% glycerol at 40°C; data not shown). Surprisingly, the commonly used microviscogens glycerol and sucrose each showed a small but convincing concentration-dependent decrease in cleavage rate (Fig. 3A). Inhibition was observed to an even greater extent with the RGkV mutant (Fig. 3B), which did not show any inhibition by D₂O, making it unlikely that the inhibition by glycerol or sucrose is due to increased viscosity (barring the remote possibility of a positive D₂O solvent isotope effect on the RGkV mutant that compensates for the hypothetical decrease caused by viscosity). The simplest interpretation of these observations is that glycerol and sucrose inhibit cleavage by a mechanism unrelated or in addition to their effects on viscosity, possibly by interacting directly with the RNA. The addition of viscogens, in the quantities used for our study, does not alter the pH or the dielectric constant of the solution.

Fig. 3.

Effect of microviscogen concentration on cleavage rate. Cleavage rate constants were measured in 1× SCB (Hepes pH 7.0) containing 200 mM MgCl₂ and a range of concentrations of glycerol or sucrose from 0% to 12.5%, and in the same solution lacking viscogen but containing D₂O instead of H₂O (see Materials and Methods and SI Materials and Methods). Relative k_obs (k_obs in n% viscogen per k_obs in 0% viscogen) of RG in glycerol (open squares), sucrose (open circles), or D₂O (open triangle) (A), and RGkV in glycerol (open squares), sucrose (open circles), or D₂O (open triangle) (B), plotted against the relative viscosity (x axis in B) or absolute viscosity (x axis in A). Each data point represents the mean of 2–14 individual reactions performed on multiple days with more than one RNA preparation. Standard deviations on the mean are indicated by error bars. Solid and dashed lines represent linear best fits to glycerol and sucrose data, respectively.

Irrespective of the mechanism responsible for the effect of glycerol and sucrose, the 2-fold decrease in cleavage rate of RG observed in 99.9% D₂O is substantially greater than the 1.3-fold decrease seen in the presence of glycerol or sucrose at the same viscosity, equivalent to ≈6.5% wt/vol glycerol or sucrose. So, even if the cleavage reaction was influenced by viscosity, for which there is no evidence, the D₂O effect is still greater, providing additional evidence that the D₂O effect reflects proton transfer in the rate-limiting step of RG cleavage.

Kinetic solvent isotope effects have been reported for cleavage reactions of several ribozymes in the past few years (25–27). Proton inventories of one or two have been observed, although in some cases the data do not convincingly distinguish between these values. Walter and coworkers (49) have also reported the surprising observation of an apparent kinetic solvent isotope effect on the changes in FRET signals that reflect the binding or dissociation of a trans substrate from an HDV ribozyme, even though these events were unaffected by pH. These authors cautioned that kinetic solvent isotope effects are not necessarily proof that a measured pK_a reflects a single ionization event. However, in none of these cleavage or binding experiments were viscosity control experiments performed to investigate whether rate decreases are directly due to the isotope effect (deuterium vs. protium) or to increased solvent viscosity. Even if the viscosity control experiments are performed, interpretation is not necessarily straightforward: we were surprised to find that the commonly used microviscogens glycerol and sucrose inhibit the VS ribozyme cleavage reaction by a mechanism (currently unknown) that is not due to viscosity. Glycerol has been observed to bind in the minor groove of an RNA racemate in an x-ray crystal structure (50), but its effects on the activity of catalytic RNAs do not appear to have been addressed previously. These observations should raise a caution flag in the interpretations of apparent kinetic solvent isotope effects on cleavage, ligation, folding, and binding experiments using RNA, and maybe even proteins, without considering possible effects of viscosity.

Implications for Investigating Ribozyme Function.

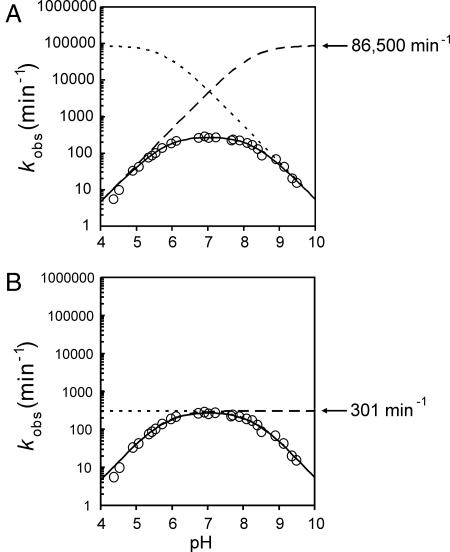
How close are current experimental approaches to being able to measure, or credibly estimate, the value of k₁, the intrinsic rate constant of the chemical step, of VS or any other ribozyme? Because k_obs= f_R(1) × k₁, where k_obsis the experimentally measured apparent rate constant and f_R(1) is the fraction of the RNA population that is in the catalytically competent state [designated _H+AR_B− (1) in Fig. 1C], we need to be able to estimate f_R(1). If the apparent pK_a values estimated for the VS ribozyme (Fig. 1A) represent ionization of two functional groups that contribute equally to general acid–base catalysis, then a maximum estimate for f_R(1) at a given pH can be obtained from the model described by Bevilacqua (18) (Fig. 1C): at the optimal pH, midway between the two pK_a values, the value of f_R(1) will be at its maximum. Because of kinetic ambiguity (16), either of two kinetic models fit such data, differing by whether the lower apparent pK_a represents the general base (the nonoverlapping titration model) or the general acid (the overlapping titration model) (Fig. 4). In the former case, when the values of the pK_a values are separated by a few pH units, f_R(1) approaches 1 and, therefore, k_obsapproaches k₁ (Fig. 4B). In the latter case, even at the optimum pH and if both pK_a values were equal to each other, only half of the general acid and half of the general base would be in the functional protonated state, leading to a theoretical maximum of one-quarter of the RNA population being in the functional state. As the pK_a values diverge from each other, f_R(1), and therefore k_obs, decreases substantially (Fig. 4A). Using the apparent pK_a and k_obsvalues in Fig. 1A with each of these two models yields estimates of 301 min⁻¹ or ≈86,500 min⁻¹ for k₁ of the RG ribozyme.

Fig. 4.

Two equivalent models of general acid–base catalysis for the VS ribozyme RG. Values for k₁ and both apparent pK_a values were estimated by fitting RG cleavage data to the model in Fig. 1C (18). Dotted and dashed lines, respectively, represent titrations of the general and base individually. Solid lines are the product of both individual titrations and k₁. Data are open circles. (A) Overlapping model where the pK_a of the acid is 5.8, the pK_a of the general base is 8.3, and k₁ is 86,500 min⁻¹. (B) Nonoverlapping model where the pK_a of the acid is 8.3, the pK_a of the general base is 5.8, and k₁ is 301 min⁻¹.

Estimates for k₁ for the other small ribozymes were derived from the nonoverlapping and overlapping titration models (SI Table 1). Some HDV ribozymes exhibit bell-shaped pH-rate curves and give estimates for k₁ as high as 17,000 min⁻¹. In other HDV ribozymes, no higher apparent pK_a was experimentally observed, and it has been speculated that a hydrated Mg²⁺ ion (pK_a = 11.4) might be the general base, leading to estimates of k₁ > 10⁶ min⁻¹ (25). For hairpin and hammerhead ribozymes, bell-shaped pH–rate curves are not experimentally observed. Apparent pK_a values of ≈6 and ≈10 have been inferred for the hairpin ribozyme (23, 26, 51), and their involvement in general acid–base catalysis (26, 51) or electrostatic stabilization (23) would provide estimates for k₁ of 10⁴ to 10⁵ min⁻¹. For the hammerhead ribozyme, two guanosine residues with pK_a values of >9 have been proposed as candidates for the general acid and base (52, 53): assuming pK_a values of 9.6 (the unshifted pK_a of free guanosine) and extrapolating k_obsfrom the log-linear portion of the pH–rate curve provides estimates for k₁ of 10³ to 10⁵ min⁻¹. By comparison, for protein enzymes such as RNase A that cleave phosphodiester bonds using particular histidine residues as the general acid and general base, k_cat values as high as 10⁴ to 10⁵ min⁻¹ have been measured; because the pK_a values of the two catalytic histidines are similar to each other, the estimated value of k₁ would be only a fewfold higher than the observed k_cat. By these estimations, the intrinsic rate constants of catalysis by ribozymes could be in the same range as those of protein enzymes.

In addition to the protonation state of the general acid and base, there are other factors affecting the fraction of the RNA population in the catalytically competent state, and therefore affecting k_obs. For example, in any ribozyme, it is reasonable to expect that there are folding and possibly protonation–deprotonation events that precede the chemical step, and that the rates and equilibria of these events can affect the k_obsby decreasing the fraction of the RNA that is in the catalytically competent state. Thus, the values of f_R(1) described in the preceding paragraph are maximal estimates under the given model and therefore, the estimates of k₁ are minimal estimates. There are also conceptual challenges in defining where folding ends and the chemical step begins. For HDV and hammerhead ribozymes, there are examples of mutations distant from the active site contributing to changes in k_obsin constructs that are thought to be limited by the rate of the chemical step (54–56). Do such mutants cleave slowly simply because f_R(1) is low? Or can the rigidity of an RNA helix transmit structural alterations from peripheral regions of mutant ribozymes into the active site and change k₁? In the VS ribozyme, the RGkV mutation, which disrupts a peripheral loop–loop interaction that may be analogous to the loop I–II interaction in extended hammerheads, decreases k_obsby 10³-fold and loses pH- and D₂O-sensitivity. We interpret this to mean that the cleavage of this mutant is limited by a slow folding step, rather than a decrease in the rate of the chemical step. In contrast, the A756C mutation in the active-site loop, which also cleaves ≈10³-fold slower than wild type, retains pH- and D₂O-sensitivity, consistent with the chemical step being rate-limiting. Because the two apparent pK_a values in the A756C mutant are essentially the same as those of the wild type, f_R(1) due to protonation equilibria should also be similar in wild type and A756C. Thus, the decrease in k_obsof the A756C mutant ribozyme may represent a decrease in intrinsic k₁. Alternatively, the A756C mutation could have a subtle structural effect that decreases the proportion of RNA in the catalytically competent state; in this situation, the putative inactive conformation would be in rapid equilibrium with the competent state, relative to the rate of the chemical step. The data presented here suggest that the VS ribozyme is a good model system for the study of rapid steps in RNA-catalyzed reactions.

Materials and Methods

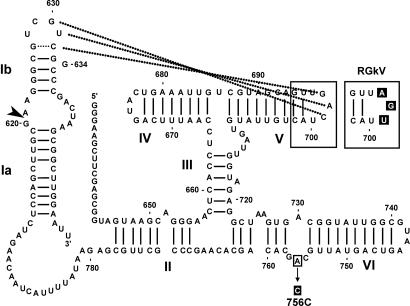
VS RNA clones, as described in ref. 42, are derivatives of RS19 (42) in which stem-loop I adopts the constitutively shifted conformation due to the presence of either a 634G substitution (mutant RG) or 624C + 636G substitutions (mutant CG; Fig. 5) (11, 39, 41, 45); the two mutational routes to shifting stem-loop I are thought to be functionally equivalent. Mutant RGkV disrupts the kissing interaction with three substitutions in loop V and was made in the context of the RG stem-loop I (11, 39). Mutant A756C changes the putative active-site base A756 to C and is in the context of the CG stem-loop I (45).

Fig. 5.

Secondary structure of RG and mutant derivatives. Nucleotides and helices are numbered as in ref. 14. Nucleotides involved in the peripheral loop–loop kissing interaction are connected with dotted lines. The cleavage site is indicated with an arrowhead. Regions that have been mutated in other constructs are enclosed in boxes, and the mutation(s) is highlighted in black (see Materials and Methods).

RNAs were synthesized in the presence of [α-³²P]GTP by in vitro transcription from plasmid templates linearized with EcoRI and purified by gel electrophoresis as described in refs. 7 and 57. Precursor RNAs were divided in half; one half was dissolved in water and the other in 99.9% deuterium oxide (Sigma, St. Louis, MO). Each batch was subsequently dried down and redissolved in their respective solvents.

Cleavage reactions were performed at 37°C, as described in ref. 11, by using self-cleavage buffers (SCBs) at various pH levels in the presence of 200 mM MgCl₂ (chosen to be high enough that Mg²⁺ binding would not limit the cleavage reaction). 1× SCB contained 40 mM buffer (sodium acetate, pH 4.2–4.8; Mes, pH 4.6–5.8; sodium cacodylate, pH 6.0–6.8; sodium Hepes, pH 7.0–7.8; Tris·HCl, pH 8.0–8.8; and CAPSO, pH 9.0–9.6), 50 mM KCl, and 2 mM spermidine. The pH values used in data analysis were those of the final reaction conditions (1× SCB, 200 mM MgCl₂, but not including RNA) measured at 37°C by using a SympHony pH calomel microelectrode (VWR Scientific Products, West Chester, PA). For reactions in D₂O, RNA, SCBs, and MgCl₂ were evaporated to dryness and reconstituted in 99.9% deuterium oxide twice (due to evaporation of acetic acid, acetate buffers were not used for experiments with D₂O). The pD of 1× SCB solutions containing 200 mM MgCl₂ was determined by measuring, as described above, at 37°C and adding 0.4 units (29). Reactions were initiated by mixing 1 vol of 2× RNA (≈20 nM) in 1× SCB with 1 vol of 2× MgCl₂ (400 mM) in 1× SCB. For proton inventory experiments, appropriate ratios of RNA, SCB, and MgCl₂ solutions in H₂O or 99.9% D₂O were mixed to obtain the desired mole fraction of D₂O. The difference in density of H₂O and D₂O was taken into account (29). By choosing SCB containing Hepes buffer (pH 6.9 in H₂O; pD 7.5 in D₂O), these experiments were conducted on the plateau of the rate vs. pL curve (see Fig. 1A). Cleavage reactions of RG (Fig. 1A) were performed by using a Kintek RQF-3 rapid quench flow instrument (Kintek, Clarence, PA) at 37°C, according to the manufacturer's instructions. For slower cleaving RNA, reactions were initiated by manual mixing. Aliquots from appropriate time points were quenched by addition of 10 vol of RNA loading dye (80% formamide, 200 mM EDTA, and 0.01% each xylene cyanol and bromophenol blue), separated by denaturing gel electrophoresis, and exposed to a PhosphorImager screen. Band intensities were quantified by using ImageQuant software (Molecular Dynamics/Amersham Biosciences).

Observed cleavage rate constants (k_obs) were determined by fitting the fraction of product formed vs. time to a first-order equation as described in ref. 11. All reactions fit well to this analysis (R² ≥ 0.99, and observed maximal extents of cleavage typically were 80–95%). Values of k_obsare the mean of typically two to five determinations. For clarity, error bars are not shown: typical day-to-day variation in k_obswas approximately ±15%. Plots of k_obsvs. pH were fit to the model in Fig. 1C (18) to obtain estimates for apparent pK_a values. Errors on apparent pK_a values from nonlinear least squares fits, weighted more toward trials with greater number of repeats, were smaller (±0.03–0.06 units) than errors on pH measurements of the same SCB solutions on different days (±0.1 units); therefore, the larger of the two error values were used in our apparent pK_a estimates.

Abbreviations

D₂O

heavy water

VS

Varkud satellite

HDV

hepatitis delta virus

pD

−log₁₀[deuterium ion]

pL

pH or pD

SCB

self-cleavage buffer.