Abstract
Postcolumn derivatization reactions can enhance detector sensitivity and selectivity, but their successful combination with capillary liquid chromatography has been limited because of the small peak volumes in capillary chromatography. A capillary Taylor reactor (CTR), developed in our laboratory, provides simple and effective mixing and reaction in a 25-μm-radius postcolumn capillary. Homogenization of reactant streams occurs by radial diffusion, and a chemical reaction follows. Three characteristic times for a given reaction process can be predicted using simple physical and chemical parameters. Two of these times are the homogenization time, which governs how long it takes the molecules in the analyte and reagent streams to mix, and the reaction time, which governs how long the molecules in a homogeneous solution take to react. The third characteristic time is an adjustment to the reaction time called the start time, which represents an estimate of the average time the analyte stream spends without exposure to reagent. In this study, laser-induced fluorescence monitored the extent of the postcolumn reaction (reduction of Os(bpy)33+ by analyte to the photoluminescent Os(bpy)32+) in a CTR. The reaction time depends on the reaction rates. Analysis of product versus time data yielded second-order reaction rate constants between the PFET reagent, tris(2,2′-bipyridine)osmium, and standards ((ferrocenylmethyl)trimethylammonium cation and p-hydroquinone) or catechols (dopamine, epinephrine, norepinephrine, 3, 4-dihydroxyphenylacetic acid. The extent of the reactions in a CTR were then predicted from initial reaction conditions and compared to experimental results. Both the theory and experimental results suggested the reactions of catechols were generally kinetically controlled, while those of the standards were controlled by mixing time (1–2 s). Thus, the extent of homogenization can be monitored in a CTR using the relatively fast reaction of the reagent and p-hydroquinone. Kinetically controlled reactions of catechols, however, could be also completed in a reasonable time at increased reagent concentration. A satisfactory reactor, operating at 1.7 cm/s (2 μL/min) velocity with solutes having diffusion coefficients in the 5 × 10−6 cm2/s range, can be constructed from 8.0 cm of 25-μm-radius capillary. Slower reactions require longer reaction times, but theoretical calculations expect that a CTR does not broaden a chromatographic peak (N = 14 000) from a 100-μm-capillary chromatography column by 10% if the pseudo-first-order rate constant is larger than 0.1 s−1.
Among various quantitative detection methods used in capillary HPLC,1,2 electrochemical (EC)1 and laser-induced fluorescence (LIF)3 approaches are two frequently used techniques due to the ease of miniaturization. LIF has lower mass detection limits than EC, detecting down to a single molecule. The challenge associated with LIF detection, however, is that not all analytes are fluorescent in a specific optical range: few combinations of analytes can be detected simultaneously with a single-source excitation and a set of detection optics.
Because of this major limitation, derivatization of analytes is often necessary. The derivatization step is either before the separation (precolumn) or after (postcolumn). Precolumn derivatization is often preferred to avoid problems associated with reaction kinetics and band spreading. However, derivatization changes the chemical properties of analytes and the sample matrix; thus, optimal separation conditions are often different before and after derivatization. The problem of multiple peaks due to multiple reactive sites in peptides or proteins is another concern.4,5 Postcolumn derivatization methods do not have such problems. A successful postcolumn derivatization method, however, should satisfy following criteria: (1) The reagent itself must not be detected. (2) The reagent and the reaction product must be stable during the experiment. (3) The reaction yield should be high and unrelated to the analyte concentration. (4) The reaction must be fast so that no significant band broadening occurs during the derivatization.6
The photoluminescence-following-electron-transfer (PFET) technique, developed in our laboratory, is a useful postcolumn derivatization scheme that satisfies the above criteria and is useful in chromatography.7,8 The PFET reagent used in this study is tris-(2,2′-bipyridine)osmium (1), which changes its spectroscopic properties according to the oxidation state:9 when excited at 483 nm, 12+ luminesces at 723 nm while 13+ is not photoluminescent. The molar absorptivity (ε) of 12+ is 11 900 cm−1·M−1 in a 50:50 water/acetonitrile mixture, and the quantum yield (φ) in acetonitrile is 0.005.9 The redox potential of 13+/12+ couple is 0.84 V versus NHE,10 ~0.4 V less positive than that of the similar but more widely studied complex, tris(2,2′-bipyridine)ruthenium. Many studies used 1 as a mediator10–14 because of its fast electron-transfer rate11,15 and stability in both oxidation states. With all these properties, 1 is a good electron-transfer postcolumn derivatization reagent: 13+ oxidizes analytes in column effluents, creating 12+, which is optically detected.
Having a good reagent is only one requirement for success. The column eluent and derivatization reagent must mix before a reaction can occur. There have been many ingenious approaches to achieve efficient fluid mixing and reaction in micrometer-sized devices (micromixers), for example, coaxial reactors,16,17 gap-junction reactors,18,19 and sheath flow reactors.20–22 Most studies, however, focus mainly on the workability of devices but not much on their efficiency of reaction. Excessive dilution of analytes during reaction often occurs,17 or not all analytes react with a derivatizing reagent.18 Low reproducibility is another problem. For example, a coaxial reactor does not function well if the two tubes are slightly off-axis.23
Increasing interest in micromixers is not solely from analytical chemists. Increasing demands on microfluidic devices initiated rigorous theoretical studies by chemical and mechanical engineers.23–25 Their main focus is, however, on fast mixing of fluids, which often includes turbulent mixing.26 Another interesting application of micromixers utilizes fast convective flow to prevent fluid mixing, allowing only small molecules in the fluids to diffuse across the interface.27,28 These approaches are, in any case, not preferable for a postcolumn reactor coupled with a capillary HPLC. A publication from the Whitesides group showed a mixer made by soft lithography.29 Its imprinted patterns on the wall create radial chaotic flow to enhance radial mixing while minimizing axial broadening at a wide range of flow conditions. Despite its good performance, fabricating such devices is still not trivial; thus, a simple device with a comparable performance is desirable.
A particularly simple postcolumn reactor is the capillary Taylor reactor (CTR).30 Previous studies of postcolumn copper complexation with enkephalins showed successful mixing of two fluid streams by radial diffusion alone. Convective dispersion in a fluoropolymer mixer followed by a simple open tube capillary reactor is experimentally indistinguishable from a simple capillary.31,32 In this study, we show that a simple fluoropolymer/silica CTR creates effective radial mixing of two fluid streams. PFET can be achieved with 1 as a postcolumn reagent. The extent of reaction generally depends on the reaction kinetics, and the limitation of low signal intensity due to slow reaction kinetics can be avoided by careful selection of postcolumn derivatization reagent conditions.
EXPERIMENTAL SECTION
Reagents. All commercial chemicals were used as received without further purification except where noted. Reagents and sources were as follows: trifluoroacetic acid (TFA) from Acros (Geel, Belgium); acetonitrile, 2-propanol, and sodium acetate from EMD (Gibbstown, NJ); 1-propanol, lead dioxide, glacial acetic acid, and disodium EDTA from J.T. Baker (Phillipsburgh, NJ); (ferrocenylmethyl)trimethylammonium iodide from Lancaster Synthesis (Windham, NH); p-hydroquinone, 1-heptanesulfonic acid sodium salt monohydrate, anhydrous sodium iodide, and sodium perchlorate from Aldrich (Milwaukee, WI); dopamine, 3, 4-dihydroxyphenylacetic acid (DOPAC), epinephrine, and norepinephrine from Sigma (St. Louis, MO). Sodium perchlorate was recrystallized in methanol once to remove chloride. All aqueous solutions were prepared with deionized water (18.2 MΩ·cm resistivity) from a Millipore Milli-Q Synthesis A10 system (Billerica, MA).
Os(bpy)3(PF6)2 (1) was synthesized in our laboratory according to a previously reported procedure.33 Crystals of the osmium complex were dissolved in acetonitrile to make a 1.0 mM stock solution. Aliquots of the stock solution were diluted in an acidic electrolyte solution (0.2% TFA and 0.1 M NaClO4 in acetonitrile) to prepare the postcolumn derivatization reagent. The resulting postcolumn derivatization reagent was introduced into the system after passing a 0.45-μm PTFE/PP syringe filter (Chrom Tech, Apple Valley, MN). Stock solutions of 1.0 mM catechols and standards were prepared in 0.1 M acetic acid and stored frozen. The frozen stock solutions were thawed before each use and were diluted to desired concentrations in degassed flow injection solutions.
Optical Setup
A laser beam from a 30-mW variable-power blue-line argon ion laser (model 2201-30BL, Cyonics/Uniphase, San Jose, CA) passed through a 488-nm band-pass filter and was focused onto an optically transparent capillary. Photoluminescence from 12+ was measured using an epifluorescence optical setup: a microscopic objective lens (Plan Neofluar 20x, NA 0.5, Carl Zeiss, Thornwood, NY) focused the optical emission from the capillary and a combination of a dichroic mirror (cutoff at 500 nm) and optical filters (a 600-nm long-pass filter and a 750-nm band-pass filter, angle tuned) allowed the photoluminescence into an IR-sensitive photomultiplier tube (R374, Hamamatsu, Bridgewater, NJ).
General Flow Injection Apparatus
Two HPLC pumps (models 590 and 600/626S, Waters, Milford, MA) with simple tees as flow splits or a dual syringe pump (model 11VPF, Harvard Apparatus, Holliston, MA) delivered solutions at ~1 μL/min. The flow rate from each source was frequently checked by measuring the volume of solutions delivered in a specific time, to ensure the correct flow rate is maintained during experiments.
Capillary Taylor Reactor Construction
Reactors were prepared according to the previously reported procedure.30 The ends of two 18-μm tungsten wires (Goodfellow, Devon, PA) were each threaded into two 50-μm fused-silica capillaries (Polymicro Technologies, Phoenix, AZ). The other ends were both threaded into another 50-μm fused-silica capillary to form a Y-shaped device. The third capillary was either polyimide-coated (normal CTR) or transparent (transparent CTR). When the third capillary was a polyimide-coated one, an optical window of 1-cm width was made by burning off the coating. The junction between three capillaries was placed in a piece of dual shrink/melt tubing (Small Parts, Miami Lakes, FL). After sufficient heat was applied and the device was allowed to cool, the tungsten wires were removed to create fluid conduits of 18-μm diameter between 50-μm capillaries.
Determination of Reaction Rate Constant of 13+ with Analytes
13+ was prepared before each use as follows: electrolyte solutions containing 12+ were mixed with a solid oxidant, PbO2, and stirred. The resulting slurry was passed through a disposable syringe filter with a pore size of 0.45 μm. The clear filtrate was quickly mixed with analyte solutions of the same volume in a quartz fluorometer cell seated in a fluorometer (Jobin-Yvon, Edison, NJ) at room temperature. The analyte solutions were pH 4.0 acetate buffers containing analyte. Typical concentrations of reactants were as follows: 2.0–20 μM 13+ with 3.0–40.0 μM (ferrocenylmethyl) trimethylammonium cation (2), where 2 was always in excess; 2.0 μM 13+ with 1.5 μM p-hydroquinone and 20.0 μM 13+ with 20.0 μM catechols. The mixture was optically excited at 470 nm, and the photoluminescence was monitored at 722 nm for 60 s with an integration time of 0.01 s. Traces of signal intensity versus time were converted to product–time traces and fit into a second-order reaction kinetics model with the reaction rate constant as a variable. The SOLVER function in the Microsoft Excel spreadsheet found the optimum value of the variable, which gave the minimum sum of squared deviations.
Flow Injection System with Continuous Analyte Flow
A 2.0 μM solution of 12+ was divided into two aliquots. An excess of PbO2 oxidant particles was added into one, producing a 2.0 μM solution of 13+. A dual-syringe pump delivered a 10.0 μM p-hydroquinone in aqueous 0.1% TFA solution and either 12+ or 13+ at a flow rate of 1 μL/min into a transparent CTR. The photoluminescence was monitored at various detection points along the length of transparent capillary. Random selection of detection points helped minimize the possible time-dependent signal changes. Focusing on the capillary was carefully checked to achieve a maximum signal after each move of the detection point.
Flow Injection System with Analyte Bands
A packed bed of PbO2 converted 12+ into 13+. The online conversion of 1 is efficient; up to 99.8% of 12+ was converted. Typically, the conversion is ~98%. A Rheodyne 7125 injector (Rohnert Park, CA) connected the PbO2-packed column into the system for fast and easy start/stop control of 13+ generation. An HPLC pump with a split delivered this reagent at 1 μL/min to one arm of a CTR.
Each analyte was prepared in the flow injection buffer at various concentrations ranging from 0.25 to 2.5 μM. The flow injection buffer, which represents the HPLC effluent, was made as follows: aqueous buffer containing 50 mM sodium acetate, 0.15 mM disodium EDTA, and 0.4 mM sodium salt of 1-heptanesulfonic acid (pH was adjusted to 4.0 with glacial acetic acid) was mixed with acetonitrile (95:5, v/v) and passed through a Nylon filter with 0.45-μm pores (Osmonics, Minnetonka, MN). This solution was pumped by another HPLC pump with a split and delivered to the other arm of the CTR. An Upchurch loop microinjector (Oak Harbor, WA) introduced 4 μL of each analyte into the system. Resulting photoluminescence was detected in a CTR either 3.0 or 8.0 cm from the confluence.
Data Collection
A Keithley 6485 picoammeter (Cleveland, OH) converted photocurrent from the photomultiplier tube to a dc voltage signal. An IBM-compatible computer with a PeakSimple Chromatographic Data System (SRI Instruments, Torrance, CA) collected the dc signal after a 0.4-Hz eight-pole low-pass filter (Wavetek 852 Dual filter, San Diego, CA).
RESULTS AND DISCUSSION
Determination of Reaction Rate Constants
To make quantitative estimates of the required length of a postcolumn reaction, knowledge of rate constants is necessary. The reaction rate constant of a reaction between 13+ and 2, a 1-electron-transfer standard,10 was calculated from the Marcus outer-sphere electron-transfer theory34 with known parameters.11,15,35 The calculated rate constant of 1.7 × 109 M−1·s−1 suggests the reaction is fast. The reaction time for such a 1-electron oxidation reaction can be predicted from a simple second-order reaction kinetics model,
| (1a) |
| (1b) |
where k1 is a second-order reaction rate constant (M−1·s−1). Solving the above differential equation for the time variable, t, gives,
| (2) |
where [C]i is the initial concentration of a solute C and x is the concentration of the product ([P]) at time t. A value of the reaction time can be determined in any particular case with knowledge of the starting concentrations, the rate constant, and an assumption about the necessary extent of reaction (e.g., 50, 80, and 95%).
Hydroquinone analogues such as p-hydroquinone and catechols generally undergo a 2-election oxidation. The oxidation reaction follows the “scheme of squares”,36–38 and application of the Marcus theory is not straightforward. It is also known that the actual mechanism varies according to reaction conditions.39 Earlier work showed that the oxidation of p-hydroquinone or catechols on a platinum and a carbon paste electrode36,38 follows an eHHe mechanism at pH 4.0, where the first electron-transfer reaction is the rate-determining step. Thus, the reaction can be approximated as second order. The reaction rate laws shown in eqs 1 and 2 need small modifications,
| (3a) |
| (3b) |
where H2Q/Q denotes the redox pair of hydroquinone analogues and k2 is a second-order reaction rate constant (M−1·s−1).
| (4) |
| (5) |
where F = exp[k2t([13+]i − 2[H2Q]i)].
Direct measurement of the photoluminescence in a spectro-fluorometer as a function of time following mixing of reagent and analytes can reveal the reaction rate constants of 13+ with p-hydroquinone and catechols. Figure 1 is a typical trace of such measurements, where the photoluminescence was converted to the concentration of product. The typical rise time of the photoluminescence signal varied from 1 to 4 s, according to the reaction rate. A reaction of a blank pH 4.0 buffer with 20.0 μM 13+ as a control experiment showed the signal increased by less than 1% in the initial 5 s. Another control experiment of mixing 2 with 12+, the photoluminescent form of the reagent, revealed the mixing time in a fluorometer cell to be ~0.5 s.
Figure 1.
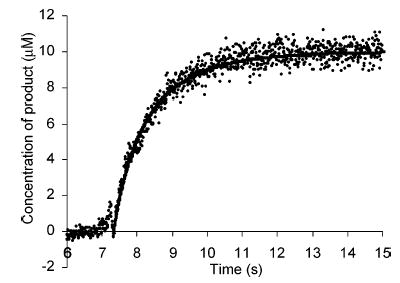
Measurement of the photoluminescence in a spectro-fluorometer as a function of time following mixing of 20.0 μM 13+ and 20.0 μM dopamine. The rise time of the signal here is ~4 s, which varied from 1 to 4 s depending on the analytes. The resulting photoluminescence intensity was converted to the amount of 12+ produced (points). Nonlinear fitting of data (solid line) revealed the reaction rate constants summarized in Table 1.
Experiments of 13+ with 2 at various reactant concentrations showed the rise time of ~0.5 s, almost same as in the control mixing experiment. Reproducible fitting was thus not possible, and this suggests that the reaction of 13+ and 2 is indeed fast. Table 1 is the summary of measured reaction rate constants and corresponding standard errors of the mean (SEMs).
Table 1.
Rate Constants of Analytes for Second-Order Reactions with 13+a
| analyte | k (M−1·s−1) | error (n) | relative error (%) |
|---|---|---|---|
| 2 | 1.7 × 109b | ||
| p-hydroquinone | 8.04 × 105 | 3.4 × 104 (5) | 4.3 |
| dopamine | 6.88 × 104 | 3.3 × 103 (6) | 4.8 |
| DOPAC | 1.93 × 105 | 5.4 × 103 (3) | 2.8 |
| norepinephrine | 7.97 × 104 | 3.5 × 103 (4) | 4.4 |
Experimental errors in SEM with numbers of replicates in parentheses.
Calculated using the Marcus theory.
Nonlinear fit of the reaction between 13+ and epinephrine was not successful using the simple second-order reaction kinetics model because in this case the absorbance increased linearly and reached a plateau (data not shown). The oxidation of epinephrine is complex because adrenalinequinone, the 2-electron oxidation product of epinephrine, regenerates epinephrine after a series of reactions including cyclization.40
Theoretical Considerations on Mixing
The column effluent and derivatization reagent must mix before a reaction can occur. There is a range of specific experimental conditions known as the Taylor dispersion regime, in which the radial concentration gradient of a solute due to the parabolic velocity profile of a laminar flow in a tube is relaxed to form a radially homogeneous Gaussian band. The resulting concentration dispersion relative to a plane moving with a mean linear velocity, v, resembles the concentration distribution resulting from molecular diffusion with the Taylor dispersion coefficient, 𝒟, replacing the molecular diffusion coefficient, D.
![]()
where a is the radius of the tube.
Although the idea of Taylor dispersion was originally developed using a narrow band of a single component in laminar flow, it is evident that two parallel fluid streams created by the confluence of a reagent stream and an analyte stream in a single tube will be completely homogenized when the flow is in the Taylor dispersion regime.
The Taylor regime has two criteria; (1) the axial molecular diffusion is negligible compared with the dispersion effect, and (2) the cylindrical tube is long enough for a solute to have enough time to relax the radial concentration gradient established by the flow profile. Writing the first criterion in a mathematical form gives
![]()
which can be rearranged using the Peclet number, Pe, a ratio of mass transported by linear convection and by radial diffusion,
| (8a) |
| (8b) |
Rephrasing the second criterion states that the time it takes a solute to diffuse in the radial direction is shorter than or equal to the residence time of a solute. The radial diffusion time of a solute in a tube with a radius a, is tD = a2/4D, and the residence time for a tube of length L, is tL = L/v. The mathematical expression of the second criterion is thus,41
| (9a) |
| (9b) |
If we use, somewhat arbitrarily, a factor of 10 to be “much greater than”, then we arrive at the criteria in eq 10.
| (10a) |
| (10b) |
Figure 2 shows the resultant inequalities in a plane of log Pe versus log L/a.41 The arrow on the diagram indicates where on the graph capillaries (a = 25 μm, v = 1.7 cm/s, and D(1) = 3.5 × 10−6 cm2/s,42 which is Pe ~ 1200) of increasing length are. Note the wide range of the transition region, which satisfies 0.4L/a < Pe < 10L/a. Precise theoretical prediction of minimum mixing length is not possible. The flow in a CTR is expected to be in the Taylor dispersion regime after ~8 cm (Pe < 0.4L/a), but a shorter length might work as well. Some authors define the Taylor regime based on the less tight criterion of Pe < L/a,29,43 which in our case would be L > 3.0 cm.
Figure 2.
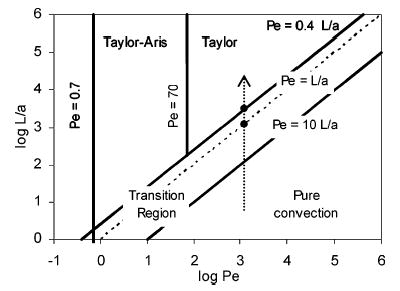
Diagrammatic representation of various solution dispersion regimes. The arrow indicates the positions for the mixed flow in our experiments, traveling at 1.7 cm/s along a 50-μm capillary (Pe ~ 1200). Two dots are at lengths of 3.0 and 8.0 cm, respectively. Adapted and modified from Figure 4.6.5.41
Determination of the Mixing Length
As seen from the previous section, theoretical calculations give estimates of the mixing length in a capillary tube. Precise estimation of the mixing length, however, is not possible by theoretical calculations only, because the boundaries in Figure 2 are somewhat arbitrary. A simple experiment was devised to monitor the mixing in our system. Photoluminescence intensity was measured from combined equal flow rate solutions of 2.0 μM 12+, the photoluminescent form of the reagent, and 10.0 μM p-hydroquinone at various detection lengths. Measured values can be referred to the photoluminescence from pure 1.0 μM 12+, its expected final concentration after complete homogenization. The result is in Figure 3. There is a decrease in the signal as detection length increases to reach a steady state after ~3 cm (~1.8 s).
Figure 3.
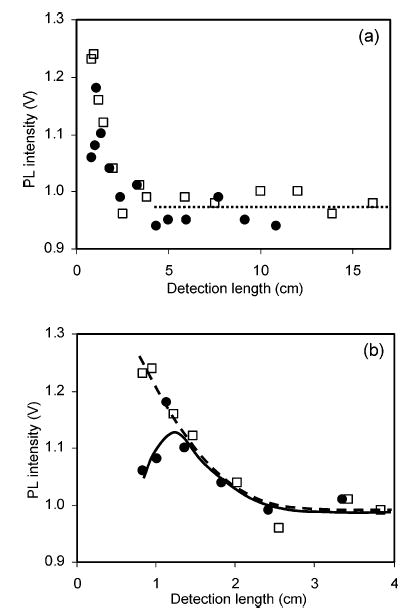
Photoluminescence (PL) signal intensity at different detection lengths when 10.0 μM p-hydroquinone was mixed with 2.0 μM 12+ (□, dashed line) and 13+ (•, solid line) in a flow system, (a) overall and (b) blow-up. Both 12+/13+ show PL decreasing to the same steady-state value (dotted line in panel a).
A comparison with a similar experiment using 13+ instead of 12+ can assess the extent of reaction. An excess of analyte rather than reagent was used to make the reaction fast and to remove ambiguity about the extent of the reaction. The experimental photoluminescence signal along the reaction length is overlaid in Figure 3. The signal reached a maximum at ~1.5 cm (~0.9 s) and stabilized also at a steady state after ~3 cm (~1.8 s). The experiments with 13+ and 12+ gave the same steady-state signal, confirming that the extent of the chemical reaction of 13+ approached 100%.
Determining the Extent of Derivatization at Low Reactant Concentration
The reaction of 2 μM 13+ with 10 μM p-hydroquinone in the fluoropolymer/silica CTR was completed in ~3 cm (~1.8 s), but it should be noted that the analyte was in excess. The reaction of analytes at low concentration, however, is different and is important in the context of improving detection limits in chromatography. Figure 4 shows the signals from bands of four catechols and two standards, at two reaction lengths at a single concentration of reagent. The use of analyte bands instead of a continuous flow was for the experimental convenience. 2 is expected to react very fast with 13+ with 1:1 stoichiometry. From the experiment, however, 2 μM 2 showed only 81% of the maximum signal at 3.0-cm reaction length. The extent of the reaction at 8.0 cm was close to 100%.
Figure 4.
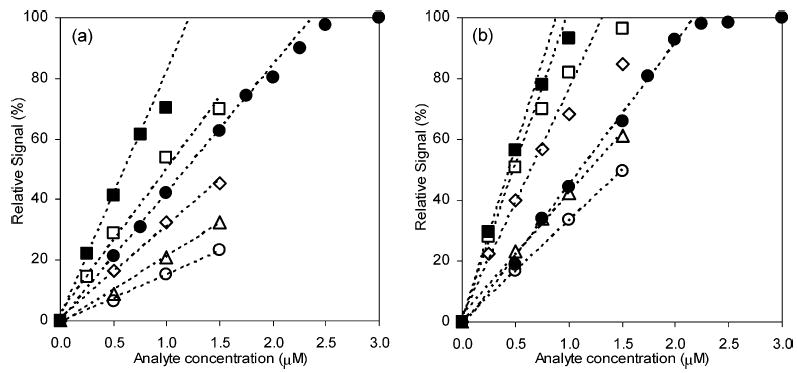
Relative signal intensity for slow reactions. 2.0 μM 12+ was combined with standards and catechols: 2 (•), p-hydroquinone (▪), dopamine (○), DOPAC (□), epinephrine (⋄), and norepinephrine (▵). Straight lines are least-squares fittings on the linear ranges. Detection lengths were (a) 3.0 and (b) 8.0 cm, respectively.
A rate law predicts that the reaction rate will slow as a reagent depletes. The slope of signal intensity versus each analyte concentration on the graphs is linear at low analyte concentrations with typical R2 values higher than 0.995 and slowly decreases to zero at higher concentrations. The slopes of the linear range, when compared with that of a standard, are the observed number of electrons transferred (nobs). Table 2 shows nobs values for the reaction with 13+. It is clear that p-hydroquinone undergoes a 2-electron oxidation. The nobs values of catechols, however, are in general less than or equal to p-hydroquinone. Values of nobs increase as the reaction length increases. It is clear that nobs increases as k: slow kinetics results in small apparent nobs and, consequently, decreased photoluminescence signal.
Table 2.
(nobs) for Solutes as a Function of 13+ Concentration and Detection Length
| detection length, cm | 3.0 | 8.0 | 8.0 | 8.0 |
| 13+ concn, μM | 2.0 | 2.0 | 6.0 | 10.0 |
| 2 | 1.0 | 1.0 | 1.0 | 1.0 |
| p-hydroquinone | 1.9 | 1.8 | 1.9 | 1.9 |
| dopamine | 0.4 | 0.6 | 1.2 | 1.4 |
| DOPAC | 1.3 | 1.6 | 2.2 | 2.1 |
| epinephrine | 0.7 | 1.3 | 2.9 | 3.3 |
| norepinephrine | 0.5 | 0.8 | 1.6 | 1.9 |
Since the reactions of 13+ and catechols follow second-order reaction kinetics, increasing 13+ concentration makes the reactions faster. The reaction kinetics can be approximated as pseudo first order at high 13+ concentration. Using a high concentration of 13+ has also the advantage of a larger linear dynamic range in chromatographic applications. Figure 5 shows data for a single reaction length and three concentrations of reagent. Corresponding nobs are summarized in Table 2. As expected, nobs approaches 2 for all catechols except epinephrine, which approaches 3.3. This larger value of nobs is again due to the regeneration of epinephrine. Regeneration of catechols includes a cyclization of the corresponding oxidation product as the rate-determining step. The first-order reaction rate of this step for epinephrine at pH 4.0 is much higher than those of other catechols.40
Figure 5.
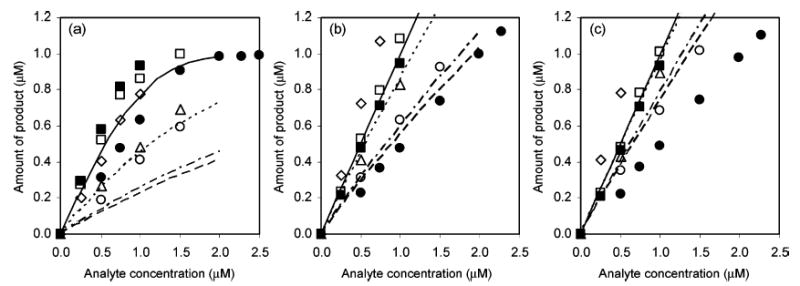
Amounts of products when (a) 2.0, (b) 6.0, and (c) 10.0 μM 13+ were reacted with various analytes. Detection length was 8.0 cm. Points denote experimental data and lines denote theoretical calculations with a 4.4-s reaction time. 2 (•), p-hydroquinone (▪, solid line), dopamine (○, broken line), DOPAC (□, dashed line), epinephrine (⋄), and norepinephrine (▵, broken/dotted line).
We note as an aside that 2 in our experiments has iodide as a counterion. The redox potential of iodide falls in the oxidizable range by 13+. (E° = 0.5355 V vs NHE for I2 + 2e = 2I−, E° = 0.536 V for I3− + 2e = 3I−) However, injection of sodium iodide at micromolar concentrations did not yield any photoluminescence, while millimolar concentrations produced a small photo-luminescence. This inactivity of iodide in the flow injection system is due to the slow kinetics of the reaction. Previous studies showed that 13+ undergoes a series of reactions with iodide as follows,44
| (11a) |
| (11b) |
| (11c) |
| (11d) |
where the forward direction rate constants for reactions are 1.7 × 101, 9.2 × 103, 7.6 × 109, and 2.9 × 1010 M−2·s−1, respectively.44 Because the equilibrium constants for first two steps are far less than unity (7.7 × 10−10 and 9.2 × 10−5 M−1, respectively), fast reactions (11c), (11d), or both do not occur significantly. Thus, the effect of iodide in the experiments was ignored.
Bridging Theoretical Calculations and the Experimental Results
The mixing length was evaluated from calculations and experiments in the previous sections. Theoretical calculation predicted the mixing length will be shorter than 8 cm from eq 10b (Pe < 0.4L/a), but precise prediction was not possible due to the uncertainties in boundaries. The experimentally found mixing length is ~3 cm in a 50-μm capillary. The length corresponds to the minimum length for a flow in the Taylor regime when the criterion Pe < L/a was applied, and we define this as LH, the length of homogenization.
Homogenization of two fluid streams, however, does not mean that all the reactants are converted to products. The characteristic length at which the signal-producing species has been formed from the analyte and the reagent we define as LR. LR is thus greater than or equal to LH. The difference of two lengths is related to the reaction time, tK.
The time at which the streams first meet cannot be taken as t = 0 because the reagents are not completely mixed as soon as the two separate streams come into contact. On the other hand, the homogenization length specifies the time at which mixing is fairly complete. Certainly the “starting time” for the reaction is between these two values. We have developed a very approximate method to specify an average start time for the reaction. We consider the solutes in a plane perpendicular to the flow direction and moving with the average velocity. At short times, the solutes are distributed radially from r = 0 to r = a/ (Figure 6) (reagent occupies half of this circle from θ = 0 to π, while the analyte occupies the other “D-shaped” half of the circle for θ = π to 2π). To determine an average time for mixing, we use the simple, one-dimensional Einstein equation, t ~ l2/2D. However, we must average the squared distances (l1, l2, ...) diffused to arrive at the average time at which analyte, A, and reagent, R, are mixed to a significant degree in this plane.
Figure 6.
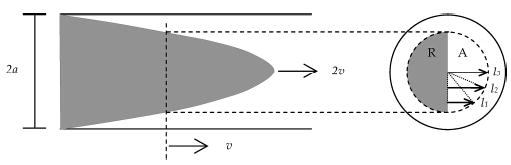
Parabolic shape of an analyte in a laminar flow inside a tube. The flow travels at an average linear velocity of v, with maximum velocity of 2v in the center. There is a plane that travels at v, and this plane is taken as a representative plane of analytes moving as a parabola (denoted as a dashed circle). The radius of the dashed circle is a/ where the reagent, R, occupies half of this circle, and the analyte, A, occupies the other half. The average diffusional relaxation time in the disk is calculated using eq 13, where r is the radial distance from the center of the tube.
From simple geometry, the lengths (l1, l2, ... see Figure 6) are dependent on the distance from the center line.
| (12) |
The mean start time is
| (13) |
For example, the calculated 〈ts〉 is 0.3 s in a tube with 25-μm radius, which corresponds to 0.5 cm for a velocity of 1.7 cm/s. Qualitatively and approximately (i.e., recognizing that the velocity is most easily described in a cylindrical coordinate system, but the diffusion field is Cartesian), this is the time at which the two reactant “halves” of the flow stream have intermingled to a modest degree over a fraction of the capillary radius. The two halves have intermingled to a greater degree in lamina moving faster than the average velocity and have intermingled virtually not at all for lamina near the wall.
The length required for the reaction, LR, is the product of the sum of the chemical reaction time and the average start time and the mean fluid velocity unless this product is smaller than the homogenization length, LH (i.e., the reaction is fast). In the latter case, the chemical reaction length is taken to be LH.
| (14) |
Figure 7 shows a plot of LR as a function of rate constants for [A] = 1 μM and [B] = 0.5 μM reacting with 1:1 stoichiometry. The dotted line in Figure 7 shows the expected LR with 2:1 stoichiometry for [A] = 1 μM and [B] = 5 μM. It predicts that the expected reaction length of 5 μM p-hydroquinone with 1 μM 13+ (k2 of 8.04 × 105 M−1·s−1 and 95% completion) occurs at around LH (3.0 cm). This value corresponds to the experimentally determined reaction length.
Figure 7.
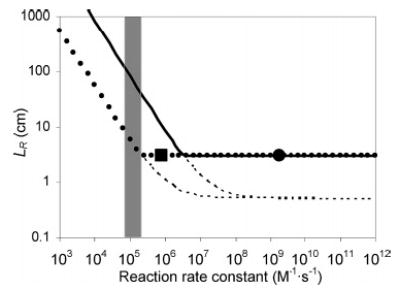
Plot of LR as a function of second-order reaction rate constant, k. For a reaction of A + B → P at [A] = 1 μM and [B] = 0.5 μM (solid line), and 2A + B → 2P at [A] = 1 μM and [B] = 5 μM (dotted line), where [C] denotes concentration of C in the mixed flow. The extent of reaction defining 〈tR〉 (from eq 2 or 4) is 95%. The dashed lines denote (〈ts〉 + 〈tK〉)v for each reaction condition (refer to eq 14). The reaction rate constants of 2 (1.7 × 109 M−1·s−1, calculated) is represented as a dot and that of p-hydroquinone (8.04 × 105 M−1·s−1, measured) as a square. Rate constants of catechols lie in the shaded area.
Comparing the reaction length and the mixing length, the presence of a signal maximum in Figure 3b indicates that the reaction is complete much earlier than predicted. One possible reason for the short reaction length comes from the flow paths. The fluid streams from the postcolumn reagent and from the column eluent travel through 18-μm cylindrical channels. The Reynolds number is very near unity, so it is not possible to be sure that the flow is either intertial or viscous. It is possible that the two adjacent streams are constrained for a short time before they diffuse radially to fill a 50-μm diameter capillary. The homogenization could be completed in a shorter length than predicted because the diffusion distances are shorter than the 50-μm diameter of the reaction capillary. The signal decay with 12+, along with the presence of the signal maximum with 13+, suggests the radial relaxation of fluids occurs in a CTR. When 13+ is used, the reaction increases the concentration of the product, while the radial relaxation process dilutes the product. If two processes have the same time scales, signal maximum would occur. A similar phenomenon was reported in a theoretical study of a coaxial mixer.23 Another uncertainty comes from the laser focal point onto the capillary in association with the radially confined flow. The beam was focused to give a maximum signal during the experiment, but we do not know exactly where in the capillary we are measuring.
Overlaying the measured reaction rate constants of catechols with 13+ onto the theoretical calculation in Figure 7 shows that the corresponding reactions are relatively slow and thus kinetically controlled. The corresponding photoluminescence signal intensity indeed depended on the rate constants at an intermediate reaction length as seen from the experimental results.
From the reaction rate constant, one can calculate the theoretical yields of the product, 12+. Lines in Figure 5 show the expected concentrations of products at different analyte concentrations at L = 8.0 cm. This length corresponds to 4.4-s reaction time plus 0.3-s start time. The experimentally measured concentrations of products are generally more than the calculated amounts when 2.0 μM 13+ was used. As the reagent concentration increases to 6.0 and 10.0 μM, the amounts of products match the calculated amounts.
Comparison of a CTR with a Chaotic Mixer.29
The chaotic mixer (staggered herringbone mixer, SHM) reported by the Whitesides group can mix fluids in a very short length, without adding significant axial dispersion compared to an open rectangular channel of similar dimensions. It is thus worthwhile to compare the axial dispersion in a CTR with that of an SHM, as a measure of mixer efficiency.
From basic chromatographic relations, the time equivalent of the plate height, Ht, is the ratio of the peak variance, σt, to the peak elution time, tr (second central moment/first moment), as in eq 15. By measuring the peak widths (4σt at the baseline) and the retention time from Figure 4c,29 Ht of the SHM was found to be 1 s.
| (15) |
The linear velocity of the flow was 0.1 cm/s with given parameters (Pe, 1 × 104; D, 1 × 10−7 cm2/s). The SHM mixes 90% of the fluids as it travels 1 cm. This takes 10 s and results in a band spreading, σt, of 3.2 s, sweeping a volume of 0.17 μL.
Let us compare this to a simple CTR. When a flow in a tube of radius a is in the Taylor dispersion regime, Ht is a function of a and D (eq 16).
| (16) |
From this relation, a CTR with 16-μm radius has Ht = 1 s for a solute with D = 1 × 10−7 cm2/s. A flow in the CTR with the same Pe (1 × 104, v = 0.65 cm/s), is expected to be in the Taylor regime after it travels 16 cm (Pe < L/a). The corresponding residence time is 24 s, with expected σt of 4.9 s. The longer CTR has a smaller physical volume (0.12 μL) than the SHM, due to a small cross-sectional area of a capillary tube. However, this small area along with the long tube length does require back pressure. The Hagen–Poiseuille equation predicts an aqueous fluid traveling in a CTR will develop a back pressure of only 5 psi, which can be easily managed with conventional systems.
σt in a chromatographic sense is a measure of axial dispersion, and each dispersion contributes to a total peak broadening as follows,
| (17) |
Although σt from a CTR is ~1.5 times larger than that from an SHM, the actual contribution to total peak broadening in capillary HPLC is still comparable. Taking the actual chromatographic data from a similar study using a CTR (σcolumn = 3.4 s, σpostcolumn(CTR) = 0.88 s)31 and assuming that σt value from a CTR is 1.5 times larger than that of an SHM in capillary HPLC conditions (σpostcolumn-(SHM) = 0.58 s), the extra peak broadening from the SHM is 1.5% of the capillary column band broadening, compared to that of the CTR being 3.2%. A similar calculation with a CTR of 50-μm diameter, however, predicts the travel time to be 60–160 s with an expected σt of 13–20 s. Clearly, a 33-μm-diameter CTR is comparable to the SHM, whereas the 50-μm-diameter reactor is not. The sensitive efficiency change of a CTR to a small change in a diameter is explainable, considering that the major mixing process occurs by radial diffusion.
The above comparison was based on a slow-diffusing analyte with D ~ 10−7 cm2/s, and the diffusion coefficients of common analytes in HPLC are in the 10−5–10−6 cm2/s range. Direct comparison of the SHM and the CTR using the conditions in the Whitesides work shows that the efficiency of an SHM is certainly a little better than that of a CTR. However, the CTR’s figures of merit are much better when values of the diffusion coefficient are in the small solute range. Because the fabrication of a CTR does not need lithographic techniques and sophisticated facilities, a simple CTR with appropriate selection of flow conditions is thus very useful and effective for postcolumn reaction.
General Considerations for Applications to Chromatographic Systems
As a simple reactor, a CTR can mix fluid streams by radial diffusion without significant band broadening. However, certain analytes react more slowly than others, making the total time for the reaction longer. Since the extra time in a reactor causes extra band broadening, which is a major challenge for a postcolumn derivatization methods in chromatography, it is worthwhile to figure out how fast a reaction should be to maintain the separation efficiency.
Taking the actual chromatographic data again from the previous study (number of theoretical plates (N) = 14 000, σcolumn = 3.4 s, D = 4.1 × 10−6 cm2/s, and a = 25 μm)31 and eqs 16 and 17, we can find out the residence time of a fluid in a CTR that adds 10% extra band broadening (i.e., when σTOTAL is 3.7 s). The calculated residence time is on the order of 40 s.
In a PFET postcolumn chromatographic system, analyte concentrations are usually far less than the reagent concentration. The kinetics of such reactions follows a pseudo-first-order rate law, as in eqs 18,
| (18a) |
| (18b) |
where k3 is a pseudo-first-order reaction rate (= k1[13+]) (with units s−1). Evaluating the solution of the differential equation with 95% extent of reaction at 40-s reaction time gives a k3 value of 0.1 s−1. Reactions with smaller pseudo-first-order rate constants thus are expected to suffer either more than 10% of extra column band broadening with full signal or acceptable band spreading with less than full signal. When 10 μM 13+ is used as the reagent, the corresponding minimum second-order reaction rate constant, kmin, is ~2 × 104 M−1·s−1. A similar calculation assuming 5% extra band broadening yields the residence time of ~20 s and kmin of 3 × 104 M−1·s−1. However, it is always possible to make the derivatization reaction faster (i.e., to decrease the extra column band broadening) by increasing the concentration of 13+. For example, using 1 mM 13+ as the reagent decreases kmin to 2 × 102 M−1·s−1 for 10% band broadening. Generally kmin is inversely proportional to the concentration of 13+ at a given reaction time; thus. increased reagent concentrations enable the reactions with small rate constants to be eligible for postcolumn reaction. Although these estimates are based on a specific chromatographic peak with σcolumn of 3.4 s, in general, such estimate gives a simple method to optimize the reaction conditions and to predict the extent of band broadening based on basic kinetics laws.
CONCLUSION
A capillary Taylor reactor serves as a simple and effective postcolumn reactor for various analytes with different reaction rates. Two processes, homogenization and chemical kinetics, in the capillary reactor govern the reaction length. There is a minimum pseudo-first-order reaction rate constant of ~0.1 s−1 necessary to avoid significant band broadening in capillary HPLC when using a 50-μm-i.d. CTR.
Acknowledgments
We thank to the NIH for financial support through Grant 2R01GM044842-12. We acknowledge Dr. Eskil Sahlin for synthesis of Os(bpy)3(PF6)2.
References
- 1.Kennedy RT, Jorgenson JW. Anal Chem. 1989;61:1128–1135. doi: 10.1021/ac00180a012. [DOI] [PubMed] [Google Scholar]
- 2.Tsuda T, Novotny M. Anal Chem. 1978;50:271–275. [Google Scholar]
- 3.Folestad S, Johnson L, Josefsson B, Galle B. Anal Chem. 1982;54:925–929. [Google Scholar]
- 4.Nickerson B, Jorgenson JW. J Chromatogr. 1989;480:157–168. doi: 10.1016/s0021-9673(01)84285-0. [DOI] [PubMed] [Google Scholar]
- 5.Jorgenson JW, Lukacs KD. Science (Washington, DC) 1983;222:266–272. doi: 10.1126/science.6623076. [DOI] [PubMed] [Google Scholar]
- 6.Huber JFK, Jonker KM, Poppe H. Anal Chem. 1980;52:2–9. [Google Scholar]
- 7.Woltman SJ, Even WR, Sahlin E, Weber SG. Anal Chem. 2000;72:4928–4933. doi: 10.1021/ac000170u. [DOI] [PubMed] [Google Scholar]
- 8.Woltman SJ, Even WR, Weber SG. Anal Chem. 1999;71:1504–1512. doi: 10.1021/ac981181e. [DOI] [PubMed] [Google Scholar]
- 9.Kalyanasundaram, K. Photochemistry of polypyridine and porphyrin complexes; Academic Press Inc.: San Diego, CA, 1992.
- 10.Fultz ML, Durst RA. Anal Chim Acta. 1982;140:1–18. [Google Scholar]
- 11.Nakabayashi Y, Nakamura K, Kawachi M, Motoyama T, Yamauchi O. J Biol Inorg Chem. 2003;8:45–52. doi: 10.1007/s00775-002-0385-8. [DOI] [PubMed] [Google Scholar]
- 12.Weaver MJ. J Phys Chem. 1990;94:8608–8613. [Google Scholar]
- 13.Zakeeruddin SM, Fraser DM, Nazeeruddin MK, Graetzel M. J Electroanal Chem. 1992;337:253–283. [Google Scholar]
- 14.Zhang C, Haruyama T, Kobatake E, Aizawa M. Anal Chim Acta. 2000;408:225–232. [Google Scholar]
- 15.Hupp JT, Weaver MJ. Inorg Chem. 1983;22:2557–2564. [Google Scholar]
- 16.Zhang L, Yeung ES. J Chromatogr, A. 1996;734:331–337. [Google Scholar]
- 17.Emmer A, Roeraade J. J Chromatogr, A. 1994;662:375–381. [Google Scholar]
- 18.Kostel KL, Lunte SM. J Chromatogr, B. 1997;695:27–38. doi: 10.1016/s0378-4347(97)00173-4. [DOI] [PubMed] [Google Scholar]
- 19.Zhu R, Kok WT. J Chromatogr, A. 1995;716:123–133. [Google Scholar]
- 20.Oldenburg KE, Sweedler JV. Analyst (Cambridge, UK) 1997;122:1581–1585. doi: 10.1039/a705394k. [DOI] [PubMed] [Google Scholar]
- 21.Coble PG, Timperman AT. J Chromatogr, A. 1998;829:309–315. doi: 10.1016/s0021-9673(98)00799-7. [DOI] [PubMed] [Google Scholar]
- 22.Ye M, Hu S, Quigley WWC, Dovichi NJ. J Chromatogr, A. 2004;1022:201–206. doi: 10.1016/j.chroma.2003.09.037. [DOI] [PubMed] [Google Scholar]
- 23.Andreev VP, Koleshko SB, Holman DA, Scampavia LD, Christian GD. Anal Chem. 1999;71:2199–2204. doi: 10.1021/ac981037t. [DOI] [PubMed] [Google Scholar]
- 24.Scampavia LD, Blankenstein G, Ruzicka J, Christian GD. Anal Chem. 1995;67:2743–2749. doi: 10.1021/ac00113a004. [DOI] [PubMed] [Google Scholar]
- 25.Oak J, Pence DV, Liburdy JA. Microscale Thermophys Eng. 2001;5:233–246. [Google Scholar]
- 26.Bessoth FG, deMello AJ, Manz A. Anal Commun. 1999;36:213–215. [Google Scholar]
- 27.Weigl BH, Bardell RL, Kesler N, Morris CJ. Fresenius' J Anal Chem. 2001;371:97–105. doi: 10.1007/s002160100997. [DOI] [PubMed] [Google Scholar]
- 28.Choban ER, Markoski LJ, Wieckowski A, Kenis PJA. J Power Sources. 2004;128:54–60. [Google Scholar]
- 29.Stroock AD, Dertinger SKW, Ajdari A, Mezit I, Stone HA, Whitesides GM. Science (Washington, DC) 2002;295:647–651. doi: 10.1126/science.1066238. [DOI] [PubMed] [Google Scholar]
- 30.Sahlin E, Beisler AT, Woltman SJ, Weber SG. Anal Chem. 2002;74:4566–4569. doi: 10.1021/ac025622c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Beisler AT, Sahlin E, Schaefer KE, Weber SG. Anal Chem. 2004;76:639–645. doi: 10.1021/ac034785d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Beisler AT, Schaefer KE, Weber SG. J Chromatogr, A. 2003;986:247–251. doi: 10.1016/s0021-9673(02)02018-6. [DOI] [PubMed] [Google Scholar]
- 33.Gaudiello JG, Bradley PG, Norton KA, Woodruff WH, Bard AJ. Inorg Chem. 1984;23:3–10. [Google Scholar]
- 34.Marcus RA, Sutin N. Biochim Biophys Acta. 1985;811:265–322. [Google Scholar]
- 35.Yang ES, Chan MS, Wahl AC. J Phys Chem. 1980;84:3094–3099. [Google Scholar]
- 36.Laviron E. J Electroanal Chem. 1984;164:213–227. [Google Scholar]
- 37.Laviron E. J Electroanal Chem. 1983;146:15–36. [Google Scholar]
- 38.Deakin MR, Wightman RM. J Electroanal Chem. 1986;206:167–177. [Google Scholar]
- 39.DuVall SH, McCreery RL. J Am Chem Soc. 2000;122:6759–6764. [Google Scholar]
- 40.Hawley MD, Tatwawadi SV, Piekarski S, Adams RN. J Am Chem Soc. 1967;89:447–450. doi: 10.1021/ja00978a051. [DOI] [PubMed] [Google Scholar]
- 41.Probstein RF. Physicochemical Hydrodynamics. John Wiley & Sons; New York: 1994. [Google Scholar]
- 42.Rodriguez M, Bard AJ. Anal Chem. 1990;62:2658–2662. doi: 10.1021/ac00223a002. [DOI] [PubMed] [Google Scholar]
- 43.Shankar A, Lenhoff AM. J Chromatogr. 1991;556:235–248. [Google Scholar]
- 44.Nord G, Pedersen B, Farver O. Inorg Chem. 1978;17:2233–2238. [Google Scholar]


