Abstract
Repeat proteins are constructed from a linear array of modular units, giving rise to an overall topology lacking long-range interactions. This suggests that stabilizing repeat modules based on consensus information might be added to a repeat protein domain, allowing it to be extended without altering its overall topology. Here we add consensus modules the ankyrin repeat domain from the Drosophila Notch receptor to investigate the structural tolerance to these modules, the relative thermodynamic stability of these hybrid proteins, and how alterations in the energy landscape influence folding kinetics. Insertions of consensus modules between repeats five and six of the Notch ankyrin domain have little effect on the far- and near-UV CD spectra, indicating that neither secondary nor tertiary structure is dramatically altered. Furthermore, stable structure is maintained at increased denaturant concentrations in the polypeptides containing the consensus repeats, indicating that the consensus modules are capable of stabilizing much of the domain. However, insertion of the consensus repeats appears to disrupt cooperativity, producing a two-stage (three-state) unfolding transition in which the C-terminal repeats unfold at moderate urea concentrations. Removing the C-terminal repeats (Notch ankyrin repeats six and seven) restores equilibrium two-state folding and demonstrates that the high stability of the consensus repeats is propagated into the N-terminal, naturally-occurring Notch ankyrin repeats. This stability increase greatly increases the folding rate, and suggests that the transition state ensemble may be repositioned in the chimeric consensus-stabilized proteins in response to local stability.
Keywords: Ankyrin repeats, protein folding, stabilization, consensus, insertion
Introduction
Repeat proteins are structurally modular domains comprised of tandem arrays of repeated structural elements ranging in length from approximately 20 to 50 residues. These short modules are attractive targets for protein design compared with globular domains, because a relatively small set of interactions defines each repeat module, whereas globular domains are comprised of complex network of interactions. Because of structural redundancy and high gene frequencies, there are many repeat sequence of each type in the sequence databases. Thus, although sequence variation is high, consensus sequences are well determined. Recently, ankyrin repeat, tetratricopeptide repeat (TPR), and leucine-rich repeat (LRR) domains have been successfully designed using this consensus information.1–4
In general, the consensus-based repeat domains have higher thermostability than their naturally-occurring counterparts. For example, Mosavi et. al. used consensus information together with simple physical principles to design ankyrin repeat domains that contain one to four identical repeats. The constructs that contain three and four ankyrin repeats are stable at temperatures 20 ºC and 30 ºC higher than naturally-occurring ankyrin domains.1,5 Consensus information also has been used to design ankyrin repeat and LRR domains that include some sequence variability, with the aim of creating novel binding domains.2,4,6,7 As was observed with the consensus ankyrin repeat domains that contain identical repeats, these highly sequence-similar consensus ankyrin domains appear to fold cooperatively and have both large unfolding free energies and high thermostability.7 In contrast, the designed LRR domains appear to have very broad unfolding transitions and do not fold cooperatively.4 This may arise from the fact that the designed LRR domains are quite large and contain between 250 and 461 residues. Main et. al. have used consensus information to design TPR domains,3 which also appear to have relatively high thermostability. These examples demonstrate that for repeat proteins, consensus information alone can be used to design domains ranging in size from 100 to 500 residues that are more stable than their naturally-occurring counterparts, suggesting that naturally-occurring proteins have made compromises in stability under functional pressure.
The seven-repeat ankyrin domain of the Notch transmembrane receptor has been extensively characterized in terms of equilibrium thermodynamics and kinetics of folding.8–10 The Notch ankyrin domain folds cooperatively via an equilibrium two-state mechanism,8,9 although destabilizing point substitutions result in multistate equilibrium unfolding.9 Kinetic studies indicate that an on-pathway intermediate is populated in folding, and that structure in this intermediate, along with the preceding rate-limiting transition state ensemble, is restricted to the central repeats.10,11 Thermodynamic studies of the Notch ankyrin domain have utilized the modular nature of repeat proteins to successfully alter protein length through the deletion and insertion of individual repeats.12,13 Using an array of polypeptides of varying repeat number constructed through terminal deletions, the average free energy associated with the individual repeats of the Notch ankyrin domain has been determined to be approximately 2.2 kcal·mol−1.12
Our focus here is to determine whether designed consensus repeats can be added to naturally-occurring repeat domains to increase the stability of the domain, and to determine the extent to which stabilizing effects can be propagated throughout the domain. In addition, we wish to apply an analysis similar to that used for the terminal deletion series12 to quantitatively compare the free energy associated with individual consensus repeats directly with the value determined for naturally-occurring repeats (2.2 kcal·mol−1·repeat−1), and to examine the effects of consensus repeats on the folding free energy landscape. Finally, by perturbing the stability distribution within the domain, we seek to determine how changes in the equilibrium energy landscape correlate to changes in the regions that are structured in the rate limiting step in folding.
Results
Our method for consensus-driven design is similar to those successfully implemented by several other groups.1–5,7,14 Our initial sequence was determined from a sequence alignment from Bork that contained over 650 ankyrin repeats.15 From this alignment, we calculated the frequency of each residue at each of the 33 positions within the alignment. Twenty-seven positions were determined from consensus alone. Although pairwise covariation was also considered, it was only detected at positions already specified by strong conservation bias. Residues at the remaining six positions were selected to impart net positive charge at neutral pH, as is seen for the parent construct. The final consensus sequence generated by our method (Figure 1A) has high sequence identity (70–95%) to those of other groups.1,2,4,7
Figure 1. Consensus repeat sequence and insertion into the Notch ankyrin domain.

(A) Sequences of the C-terminal repeats (five through seven) of the Notch ankyrin domain (top) and the consensus sequence used in the current study. Sequence matches in the Notch ankyrin repeats to the consensus are shaded green. Regions of expected α-helix formation are shaded yellow. (B) The structure of the Notch ankyrin domain (1ot8)37, with individual repeats (numbered) in alternating shades of blue (repeats 1–5) and red (repeats 6, 7), using the insertion site (blue-red junction between repeats 5 and 6) to define boundaries.
We chose the long loop connecting adjacent repeats as the site for insertion/extension (Figure 1B) for several reasons. First, this loop is a common site for insertion within ankyrin repeat domains. Second, this loop has relatively low sequence conservation and relatively high solvent exposure (and therefore low packing density), suggesting that it may be tolerant to minor perturbations. Third, use of this site avoids insertions within either of the two helices that define the repeat structure. Fourth, most introns in ankyrin repeat genes cluster to this loop, indicating this loop to be a site of elaboration through repeat duplication in naturally occurring ankyrin repeat proteins.6 We selected the loop between the fifth and sixth repeats of the Notch ankyrin domain for insertion because the interface between these repeats is the most similar to the interface expected to generated from the consensus repeat sequence.
Although the consensus sequence studied here is based on ankyrin repeat sequences, the sequence differs substantially from the ankyrin repeats of Notch (and of most other naturally occurring ankyrin repeat sequences) as a result of the high sequence variation among ankyrin sequences. There are between 20 and 29 sequence differences (out of 33 positions) between our consensus sequence and Notch ankyrin repeat sequences flanking the site of insertion (repeats five, six, and seven; Figure 1A).
Structural and thermodynamic consequences of internal insertion of consensus repeats
To determine the structural consequences of insertion of designed ankyrin repeats between the fifth and sixth repeat of the Notch ankyrin domain, far- and near-UV CD spectra were collected. The far-UV CD spectra of constructs that contain one (Nank1-5C16-7) and two (Nank1-5C26-7) copies of the consensus ankyrin repeat are nearly identical to the parent construct (Nank1-7*; Figure 2A), suggesting that the constructs that contain internal consensus repeats adopt a native fold with similar α-helical content to the parent construct (Nank1-7*). The near-UV CD spectra of Nank1-5C16-7 and Nank1-5C26-7 are nearly identical to each other, and are similar in shape to the spectrum of Nank1-7*, although the overall intensities are somewhat larger (Figure 2B). Although the origin of this intensity difference is not clear, the shape similarities of all three spectra indicate that the constructs with the consensus repeats have similar tertiary structure to the parent construct.
Figure 2. Circular dichroism spectroscopy of constructs containing consensus ankyrin repeats.
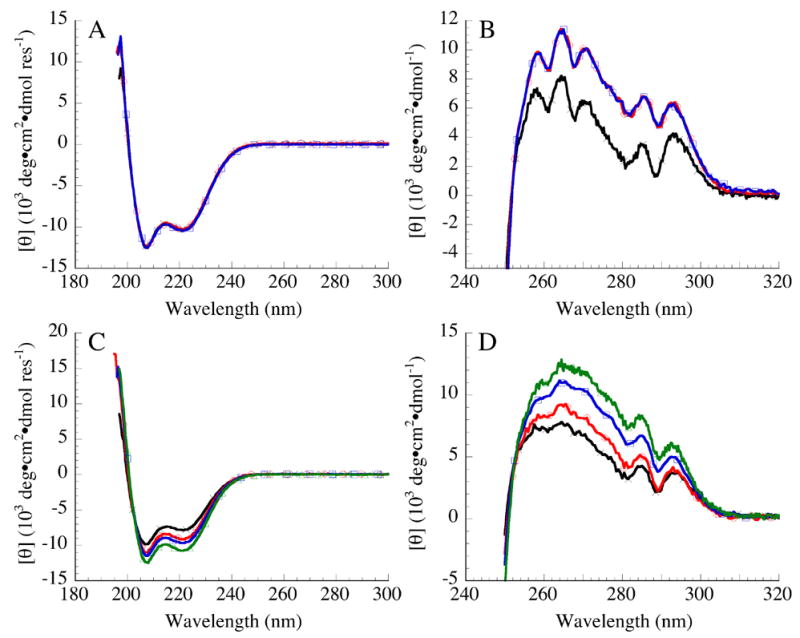
(A) Far- and (B) near-UV CD spectra of Nank1-7* (black, ×), Nank1-5C16-7 (red, ○), and Nank1-5C26-7 (blue, □). (C) Far- and (D) near-UV CD spectra of Nank1-5 (black, ×), Nank1-5C1 (red, ○), Nank1-5C2 (blue, □), and Nank1-5C3 (green, ▵). Conditions: 25 mM Tris·HCl, 150 mM NaCl, pH 8, 20 °C.
To determine the thermodynamic consequences of insertion of consensus repeats, urea-induced unfolding was monitored by both CD and fluorescence spectroscopy. When monitored by tryptophan fluorescence (which probes a single tryptophan in the fifth repeat), the unfolding transitions of Nank1-5C16-7 and Nank1-5C26-7 show a single cooperative step, as is observed for Nank1-7* (Figure 3A). The midpoints of the unfolding transitions of Nank1-5C16-7 and Nank1-5C26-7 are shifted to higher urea concentrations than Nank1-7* (Table 1). In contrast to the fluorescence-monitored unfolding transitions (and to the CD-monitored transition of Nank1-7*, which is identical to the fluorescence-monitored transition; Table 2), the CD-monitored unfolding transitions for Nank1-5C16-7 and Nank1-5C26-7 (a measure of α–helical structure) occur in two distinct steps that bracket an unfolding intermediate at moderate urea concentrations (Figure 3B).
Figure 3. Urea-induced unfolding of constructs containing consensus ankyrin repeats.
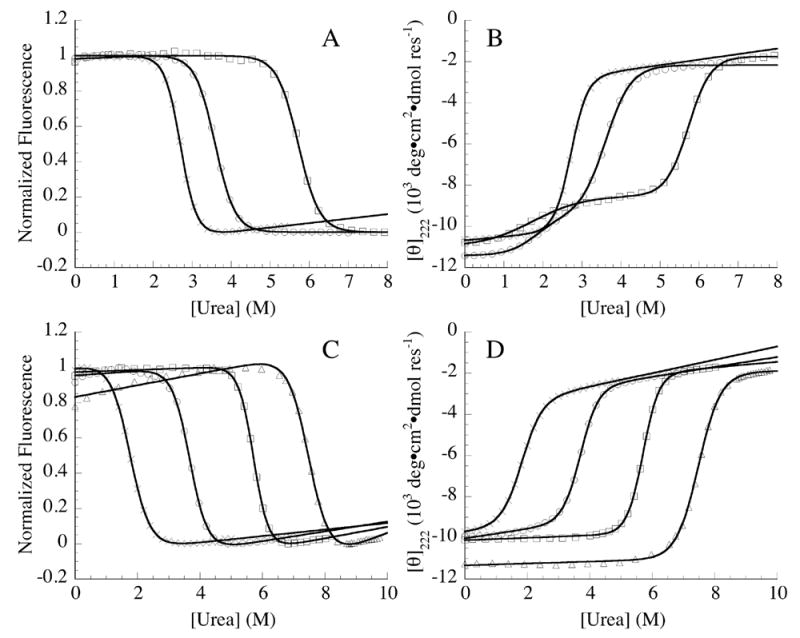
(A) fluorescence- and (B) far-UV CD-monitored unfolding transitions of Nank1-7* (×), Nank1-5C16-7 (○), and Nank1-5C26-7 (□). (C) Fluorescence- and (D) far-UV CD-monitored unfolding transitions of Nank1-5 (×),Nank1-5C1 (○), Nank1-5C2 (□), and Nank1-5C3 (▵). Solid lines represent fits of the data by two- (A, C, and D) and three-state models (B). Conditions: 25 mM Tris·HCl, 150 mM NaCl, pH 8, 20 °C.
Table 1.
Parameters for urea-induced unfolding for variants of the Notch ankyrin domain containing consensus ankyrin repeats inserted internally
| CDa |
Fluorescenceb |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| ΔGºNI, H2O | mNI-value | Cm,NI | ΔGºID H2O | mIU-value | Cm,IU | ΔGºu H2O | m-value | Cm | |
| Nank1-7* | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 7.64 ± 0.08 | 2.86 ± 0.02 | 2.67 ± 0.01 |
| Nank1-5C167 | 2.66 ± 0.24 | 1.50 ± 0.06 | 1.77 ± 0.18 | 7.13 ± 0.17 | 1.96 ± 0.05 | 3.61 ± 0.01 | 8.39 ± 0.09 | 2.33 ± 0.03 | 3.60 ± 0.01 |
| Nank1-5C267 | 1.38 ± 0.12 | 0.83 ± 0.02 | 1.66 ± 0.15 | 12.07 ± 0.11 | 2.10 ± 0.02 | 5.74 ± 0.01 | 13.57 ± 0.78 | 2.36 ± 0.13 | 5.75 ±0.02 |
Unfolding free energies, m-values, and unfolding midpoints (Cm) are reported in kcal·mol−1, kcal·mol−1·M−1, and M, respectively. Uncertainties are standard errors on the mean of at least three independent measurements. Conditions: 25 mM Tris·HCl, 150 mM NaCl, pH 8.0, 20ºC.
CD data for Nank1-5C1,67 and Nank1-5C267 were fitted using a three-state model.
Fluorescence data were fitted using a two-state model.
Table 2.
Parameters for urea-induced unfolding of variants of the Notch ankyrin domain containing consensus ankyrin repeats at the C-terminus
| ΔGºu H2O |
m-value
|
Cm |
||||
|---|---|---|---|---|---|---|
| CD | Fluorescence | CD | Fluorescence | CD | Fluorescence | |
| Nank1-7* | 7.74 ± 0.07a | 7.64 ± 0.08 | 2.89 ± 0.04a | 2.86± 0.02 | 2.68 ± 0.01a | 2.67 ± 0.01 |
| Nank1-5 | 3.21 ± 0.09 | 3.29 ± 0.03 | 1.78 ± 0.03 | 1.84 ± 0.01 | 1.80 ± 0.09 | 1.78 ± 0.02 |
| Nank1-5C1 | 7.31 ± 0.17 | 7.50 ± 0.09 | 1.98 ± 0.10 | 2.05 ± 0.03 | 3.67 ± 0.04 | 3.65 ± 0.02 |
| Nank1-5C2 | 13.02 ± 0.03 | 13.25 ± 0.4 | 2.28 ± 0.01 | 2.30 ± 0.07 | 5.70 ± 0.01 | 5.70 ± 0.01 |
| Nank1-5C3 | 12.60 ± 0.12 | 13.66 ± 0.58 | 1.67 ± 0.03 | 1.83 ± 0.08 | 7.57 ± 0.14 | 7.48 ± 0.04 |
Unfolding free energies, m-values, and unfolding midpoints (Cm) are reported in kcal·mol−1, kcal·mol−1·M−1, and M, respectively. Uncertainties are standard errors on the mean of at least three independent measurements. Conditions: 25 mM Tris·HCl, 150 mM NaCl, pH 8.0, 20ºC.
Data for Nank1-7* are from reference 13.
Although a two-state model can be adequately fitted to the fluorescence-monitored unfolding transitions of Nank1-5C16-7 and Nank1-5C26-7, a three-state model that includes an intermediate state (I) is required for the CD-monitored unfolding transitions (Table 1). For both of these two constructs, the fitted midpoints of the second (I to denatured state, D) CD transition (Cm,ID) and the single fluorescence transitions occur at same urea concentrations, as are values of ΔG°ID,H2O (Table 1). Moreover, the Cm,ID values of Nank1-5C16-7 and Nank1-5C26-7 are increased by one and three molar over the Cm of Nank1-7*, consistent with a large stabilizing effect from the designed repeats on part of the Notch ankyrin domain (Table 1). This stabilizing effect is reflected in the fitted free energy changes associated with this transition (ΔG°ID,H2O Table 1). The minor conformational transition seen by CD at low denaturant concentration is not seen by fluorescence, indicating that the fifth repeat and its interface with the fourth repeat (the site of the single tryptophan) are intact. Thus, the minor CD transition is likely to be limited to the C-terminal side of the consensus repeats (repeats six and seven). The unfolding free energies associated with this minor unfolding transition (ΔGºNI, ,H2O) in Nank1-5C16-7 and Nank1-5C26-7 are similar and small, 1.3 and 2.7 kcal·mol−1 (Table 1).
The m-values obtained from fits of the CD-monitored unfolding transitions for both Nank1-5C167 and Nank1-5C267 are larger for the I to D transition (mID-value) than for the native (N) to I transition (mNI-value). Because m-values have been shown to be correlated to changes in the solvent accessible surface area on folding 16, these data suggest that the transition between the I and D states exposes more surface area than the transition between the N and I states. This is consistent with a model where unfolding in the I state is limited to the sixth and seventh repeats Furthermore, as is seen with the unfolding free energies, the m-values obtained for Nank1-5C167 and Nank1-5C267 from the fluorescence-monitored unfolding transitions are similar to the m-values associated with the transition from I to D determined by CD (Table 1).
Structural and thermodynamic consequences of terminal extension with consensus repeats
To determine if the intermediate observed by CD for Nank1-5C167 and Nank1-5C267 arises from the uncoupling of the two C-terminal repeats (six and seven) from repeats one through five and the consensus repeats, we deleted the sixth and seventh repeats from our consensus constructs. The far-UV CD spectra of Nank1-5C1, Nank1-5C2, and Nank1-5C3 (which contain one, two, and three consensus repeats, respectively) are similar in shape to the parent construct (in this case Nank1-5, Figure 2C), but show slight increases in the intensity of the minima at 208 nm and 222 nm, suggesting that there is an increase in the α-helical content on a per residue basis with each insertion of a designed ankyrin repeat. The near-UV spectra of the terminal addition series have similar fine structure to the parent construct (Figure 2D), indicating a well-defined tertiary structure similar to that of the parent construct, but also show increased intensity (Figure 2D). The increase in the magnitude of the near-UV spectra may result from a slight alteration in the environment of the single tryptophan in the fifth repeat, or to quenching of fluctuations surrounding this tryptophan.
To determine the thermodynamic consequences of the terminal extension with consensus repeats, urea-induced unfolding was monitored by CD and fluorescence spectroscopy. Both spectroscopic probes reveal single sigmoidal transitions for all three terminally extended constructs (Figure 3D), consistent with the assignment of the first CD-detected unfolding transition in Nank1-5C167 and Nank1-5C267 (Figure 3B) to unfolding of repeats six and seven. For the terminal extension series, the midpoint of the transitions increases by approximately 2 M urea with each added consensus repeat (Figure 3C & D, Table 2).
Comparison of thermodynamic unfolding parameters obtained from urea-induced unfolding transitions monitored by tryptophan fluorescence and CD can be used as a test for cooperative folding. As with the parent construct (Nank1-5) and the full-length Notch ankyrin domain (Nank1-7*), the unfolding free energies of Nank1-5C1 and Nank1-5C2 obtained from fluorescence and CD are the same within error. In contrast, free energies of unfolding of Nank1-5C3 obtained from fluorescence and CD differ significantly (Table 2). This is consistent with Nank1-5C1 and Nank1-5C2 populating only native and denatured species despite the substantial increase in stability resulting from the addition of consensus repeats. In contrast, although the midpoint of Nank1-5C3 unfolding is shifted to over seven molar urea indicating a further increase in stability, the difference in free energy estimates from CD versus fluorescence (Table 2) indicate a breakdown of two-state unfolding in the transition, such that additional partly folded species are populated (and thus Gºu, H2O estimates for this construct are not valid).
Folding kinetics of terminally extended Notch ankyrin constructs
To determine how the addition of the consensus repeats affect the kinetics of refolding and unfolding, we performed stopped-flow tryptophan fluorescence refolding and unfolding experiments on Nank1-5C1 and Nank1-5C2, both of which appear to conform to a equilibrium two-state unfolding mechanism. Refolding traces of both constructs are multi-exponential: a single exponential model fits the refolding traces of both constructs poorly (blue curves, Figures 3A & C), producing large nonrandom residuals (Figure 4A & C, top panel). In contrast, a double-exponential model fits the refolding traces of Nank1-5C1 and Nank1-5C2 adequately (red curves, 3A & C), producing small, randomly distributed residuals. The improved fit using the double-exponential model is indicated by a substantial decrease in the χ2r compared to the single exponential model (Table 3).
Figure 4. Refolding and unfolding kinetics of constructs containing terminal extensions of consensus ankyrin repeats monitored by stopped-flow fluorescence.
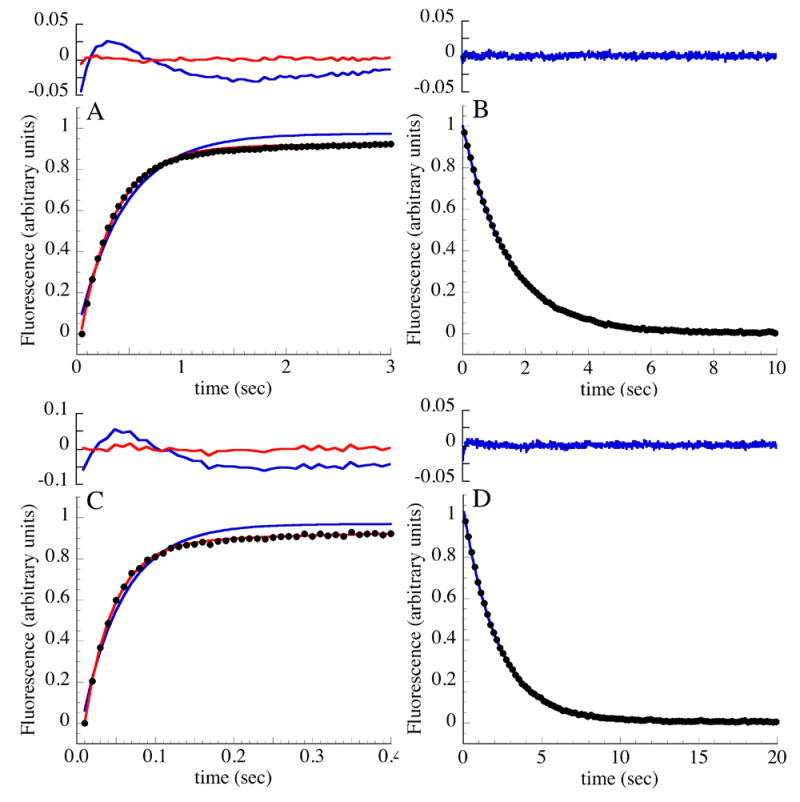
(A) Refolding of Nank1-5C1 following rapid dilution from 5.0 to 0.83 M urea. (B) Unfolding of Nank1-5C1 following rapid addition of urea from 2.0 to 7.0 M urea. (C) Refolding of Nank1-5C2 following rapid dilution from 7.0 to 0.64 M urea. (D) Unfolding of Nank1-5C2 following rapid addition of urea from 4.05 to 8.18 M urea. Fluorescence transitions are normalized to range from zero to one. Results from fits to single and double exponential functions are shown in blue and red, respectively; residuals from each fit are shown above. Conditions: 25 mM Tris·HCl, 150 mM NaCl, pH 8, 20 °C.
Table 3.
Fluorescence-detected refolding and unfolding rate constants for constructs containing consensus ankyrin repeats.a
| refolding
|
unfolding
|
|||
|---|---|---|---|---|
| Single Exponential
|
Double Exponential
|
Single Exponential
|
||
| Nank1-5 | k1 | 0.13 ± 0.001 | 0.20 ± 0.001 | 4.41 ± 0.01 |
| k2 | 0.03 ± 0.001 | |||
| χ2r | 0.04 | 0.0002 | 0.001 | |
| Nank1-5C1 | k1 | 2.26 ± 0.06 | 3.14 ± 0.05 | 0.65 ± 0.0001 |
| k2 | 0.07 ± 0.004 | |||
| χ2r | 0.03 | 0.001 | 0.001 | |
| Nank1-5C2 | k1 | 12.32 ± 0.78 | 23.32 ± 0.69 | 0.31 ± 0.0006 |
| k2 | 0.58 ± 0.09 | |||
| χ2r | 0.02 | 0.001 | 0.002 | |
| Nank1-7* | k1 | 0.17 | 0.22 | 0.23 |
| k2 | 0.03 | |||
Refolding was at final urea concentrations of 0.85 M. Unfolding was at final urea concentrations of 6.85 M. Rate constants are reported in sec−1. Uncertainties on rate constants are standard errors on the mean of four to six independent fitted progress curves; for Nank1-7*, uncertainties are less than one percent of the mean.11 χ2r is the reduced chi squared for typical fits; see Mello et al11 for χ2r for Nank1-7*.
Of the two phases obtained from the double exponential fits of refolding traces, the fast phase has the largest amplitude, comprising 80% of the total fluorescence change. The rate constants for the fast (dominant) phases of Nank1-5C1 and Nank1-5C2 increase by 15 and 115-fold, respectively, compared with Nank1-5 (Table 3), consistent with the increase in equilibrium stability that results from adding consensus repeats. A similar enhancement in rate constant is seen relative to the full-length Notch ankyrin domain (Nank1-7*),11 which has approximately the same rate as Nank1-5 (Table 3). The rate constant for folding of Nank1-5C2 is accelerated to a value close to that measured for an ankyrin domain composed of three consensus repeats.17 The rate constants of the slower (minor) phases of Nank1-5C1 and of Nank1-5C2 are also larger than that of Nank1-5 and Nank1-7*, but the increase is not as dramatic as for the dominant refolding phase.
The unfolding traces of Nank1-5C1 and Nank1-5C2 are well-described by a single exponential model (Figure 4B & D), as is that of Nank1-5. The quality of the fit does not improve substantially when a second exponential is added (not shown). Compared to Nank1-5, the fitted unfolding rate constant decreases as stabilizing consensus repeats are added (although the effect is smaller than the increase seen for refolding), dropping by around seven and fifteen fold with the addition of two consensus repeats (Table 3). The decreased unfolding rate for Nank1-5C2 matches the rate constant for the major unfolding phase of the full-length Notch ankyrin domain (Figure 5C).
Figure 5. Urea dependence of refolding and unfolding rate constants constructs containing terminal extensions of consensus ankyrin repeats.
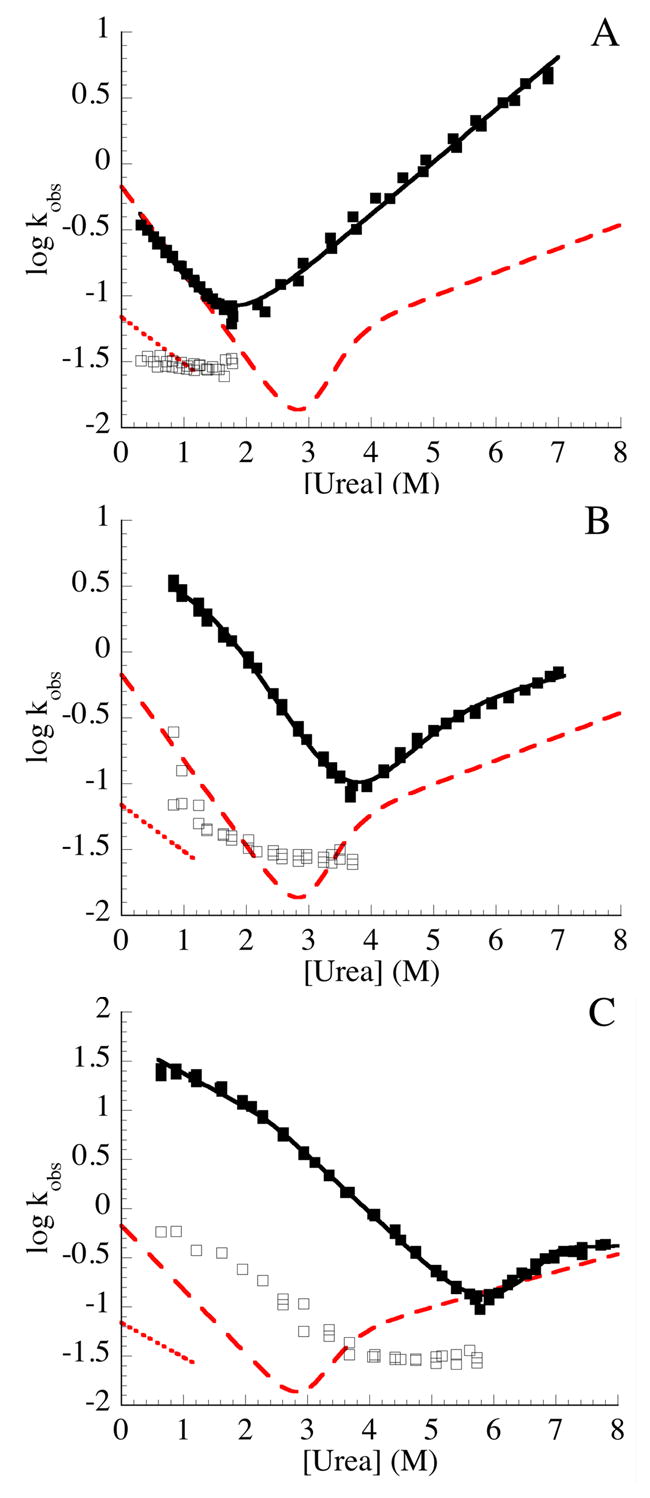
The urea dependence of the refolding and unfolding kinetics of Nank1-5 (A), Nank1-5C1 (B), and Nank1-5C2 (C) were measured by stopped-flow fluorescence. The major fast refolding phase and the single unfolding phase are shown with solid symbols; the slow refolding phase is shown with open symbols. The solid lines are obtained from fitting kinetic two-state (A) and three-state models (B, C; see materials and methods) to the major refolding and unfolding phases. Red lines show corresponding kinetic phases (long dashed line shows the major refolding and unfolding phase, dotted line shows the slow proline-limited refolding phase) for the full-length Notch ankyrin domain (Nank1-7*)11 Conditions: 25 mM Tris·HCl, 150 mM NaCl, pH 8, 20 °C.
Urea dependence of folding kinetics of terminally extended Notch ankyrin constructs
To gain detailed mechanistic insight into the kinetic effects of consensus stabilization on folding, the urea dependence of the refolding and unfolding reactions were determined. For the full-length Notch ankyrin domain, the non-proline-limited rate constants for refolding and for unfolding show a nonlinear logarithmic variation with urea concentration.11 Like the full-length construct, the major refolding and unfolding rate constants of Nank1-5C1 and Nank1-5C2 are nonlinear with urea when depicted as Chevron plots (the log of measured rate constants with urea concentration), with the greatest curvature for the longer construct (Figure 5).
For the full-length Notch ankyrin domain, the nonlinear urea dependence of the major refolding and the two unfolding rate constants and their amplitudes strongly supports a kinetic three-state mechanism with a kinetic on-pathway intermediate:
| (1) |
and allowed the four underlying rate constants to be quantified (the prime is adopted to distinguish the kinetic intermediate from the equilibrium intermediate described above).11 The nonlinear urea dependence of refolding and unfolding rate constants for Nank1-5C1 and Nank1-5C2 can also be fitted by an on-pathway three-state model (solid lines, Figure 5B, C), consistent with a kinetic multistate mechanism. However, in the absence of a second unfolding, the parameters of the kinetic three-state model are not uniquely determined without additional constraints (see Materials and Methods).
Although for Nank1-5 there may be a very slight deviation from linearity at low urea concentrations (Figure 5A), the Chevron plot of Nank1-5 is approximately linear, and can adequately fitted by a kinetic two-state model. (solid line, Figure 5A). Given that repeats six and seven are disordered in the Nank1-7* kinetic folding intermediate, Nank1-5 may be considered to be a model for this kinetic intermediate, and thus may be expected to lack much of the kinetic complexity seen in the kinetics of refolding of the full-length Notch ankyrin domain.
Effect of prolyl isomerization on refolding kinetics
Refolding kinetics are often limited by the isomerization between the cis and trans isomers of x-pro peptide bonds, because these bonds can populate both cis and trans configurations in the denatured state, but are usually restricted to one configuration in the native state.18 Ankyrin repeat sequences have a conserved proline residue near the N-terminus of the first helix.15 The full length Notch ankyrin domain (Nank1-7*) contains seven proline residues. Of these, the four proline residues visible in the crystal structure are trans (the other three are in disordered N and C-terminal regions). Collectively, these prolines have been shown to be responsible for the minor refolding phase, with the largest contribution resulting a combination of prolines in repeats one, three, and four.11,19 Although Nank1-5 contains only three proline residues, each consensus repeat adds another proline residue.
For Nank1-5, the rate constant for the slow kinetic phase is similar that of the full-length Notch ankyrin domain and shows a similarly modest denaturant dependence,11 consistent with prolylisomerization (Table 3, Figure 5A). However, for the consensus-stabilized Nank1-5C1 and Nank1-5C2 constructs, the slow phase is faster than that of the full length Notch ankyrin domain, and shows a steeper urea dependence (Figure 5B, C). To determine if the minor refolding phases of Nank1-5C1 and Nank1-5C2 are also limited by prolyl isomerization, we performed refolding in the presence of cyclophilin, a peptidyl-prolyl isomerase. At low concentrations, addition of cyclophilin to the refolding of Nank1-5C1 increased the rate of the minor slow phase, whereas it had no effect on the dominant fast phase (Figure 6A), demonstrating that like the full-length Notch ankyrin domain, the slow phase is limited by prolyl isomerization but the fast phase is not. At approximately 2 μM cyclophilin, the rate constant for the slow phase plateaus at around 0.6 sec−1. In contrast to Nank1-5C1, cyclophilin had no effect on either refolding phase of Nank1-5C2 (Figure 6A). Although it is possible that neither refolding phase is limited by prolyl isomerization, we note that the rate constant of the minor refolding phase of Nank1-5C2 is larger than the maximum rate constant for the minor phase of Nank1-5C1 at high cyclophilin concentration. It is possible the minor phase of Nank1-5C2 remains limited by prolyl isomerization, but that the increased stability compared to Nank1-5C1 accelerates the rate of prolyl isomerization through partial structure formation, making these proline residues inaccessible to prolyl isomerase.
Figure 6. The effect of prolyl isomerization on the kinetics of refolding.

(A) The effect of cyclophilin, a peptidyl-prolyl isomerase, on the refolding rate constants of the terminal extensions series. Rate constants for the fast (filled symbols) and slow (open symbols) phases of Nank1-5C1 (red, circles) and Nank1-5C2 (blue, squares) in the presence of a range of cyclophilin concentrations. Refolding was initiated by the dilution of urea to final concentrations of 0.83 and 1.17 M urea, respectively. (B) Interrupted unfolding double-jump assay to test for heterogeneity in the unfolded state. Nank1-5C1 (red, ^) and Nank1-5C2 (blue, ▪) were rapidly unfolded by the addition of urea to final concentrations of 5 and 7 M urea, respectively. Following a variable delay time, refolding was initiated by the rapid dilution of urea to a final concentration of 0.83 M and 1.16 M urea, respectively. Amplitudes were obtained by fitting the resulting fluorescence-monitored refolding traces with a double-exponential function. The relative amplitude is the fitted amplitude of the slow phase to the total amplitude change. Solid lines represent single exponential fits. Conditions: 25 mM Tris·HCl, 150 mM NaCl, pH 8, 20 °C.
To further test the role of prolyl isomerization in refolding, particularly for Nank1-5C2, we performed double-jump interrupted unfolding,18,20,21 where protein is unfolded for a fixed delay time and then refolded. If refolding heterogeneity results from proline isomerization-related heterogeneity in the denatured state, such heterogeneity should be reduced or absent at short unfolding delay times, but should build with a rate constant characteristic of proline isomerization. Indeed, for both Nank1-5C1 and Nank1-5C2, at early delay times only the dominant kinetic phase is seen (Figure 6B). As the delay time is increased, the second (slow) kinetic phase emerges. These results suggest that the biphasic refolding kinetics of both Nank1-5C1 and Nank1-5C2 arise from heterogeneity in the denatured state. A single exponential fit of the relative amplitude of the slow phase as a function of delay time gives the rate that the slow phase builds in of approximately 0.02 and 0.04 sec−1 for Nank1-5C1 and Nank1-5C2, respectively (solid lines, Figure 6B), well within the range determined for trans to cis proline isomerization in unstructured peptides under these conditions (0.01 and 0.05 sec−1).18 Together with the effects of cyclophilin on Nank1-5C1, these results strongly suggest that the slow refolding phases of the consensus-stabilized constructs result from prolyl isomerization.
Discussion
Consensus ankyrin repeats stabilize a major potion of the Notch ankyrin domain
The modular nature of repeat proteins allows the insertion and deletion of individual repeats without major structural consequences.12,13 Here we take advantage of this modularity, combining naturally-occurring sequences from the Notch ankyrin domain with designed consensus sequences through insertion and extension. This approach allows us to use a stable, cooperative monomeric protein as a host to examine the stability of consensus repeats, and to determine whether and over what distance the stability of consensus repeats be propagated into the naturally-occurring host. Our method to design a consensus ankyrin repeat is similar to those of others.1–3,14,15 Our consensus sequence differs by approximately 15% from the sequences of other consensus ankyrin repeats,1,7 with differences at positions that are either not conserved, or have equal preferences for more than one residue of the same type. We inserted one and two copies of the consensus ankyrin repeat into the Notch ankyrin domain, increasing the length of the protein from seven to a total of nine repeats.
CD spectroscopy confirms that the chimeric proteins adopt well-defined native structures, with similar overall secondary structure and tertiary structure in the vicinity of the aromatic residues. Urea-induced unfolding indicates that the consensus repeats stabilize the N-terminal repeats (one through five). The midpoints of the fluorescence-monitored unfolding transitions of Nank1–5C167 and Nank1-5C267 are increased from 3 M urea for the parent construct to 4 M and 6 M urea, respectively. While the CD-monitored unfolding transitions are more complex, there is a major unfolding transition for both Nank1-5C167 and Nank1-5C267 that occurs at urea concentrations where the parent construct is unfolded. Thus, although cooperativity throughout the domain is lost, the consensus ankyrin repeats greatly stabilize a large part of the Notch ankyrin domain. Conversely, the lower midpoint of the minor conformational transition detected by CD indicate that a smaller region of the Notch ankyrin domain (repeats six and seven) is destabilized, presumably because of packing defects between repeat six and the neighboring consensus repeat. These results, together with the observations of others,1-3,14 demonstrate that repeat modules designed from consensus information are of greater stability than those from naturally occurring ankyrin repeat genes. Furthermore, these results suggest that depending on context, consensus repeats can be used to stabilize naturally-occurring repeat domains.
Insertion of consensus ankyrin repeats disrupts cooperativity in the Notch ankyrin domain
Although the insertion of consensus ankyrin repeats stabilizes a large part of the Notch ankyrin domain, cooperativity is disrupted, revealing a highly populated equilibrium unfolding intermediate. This intermediate is formed via a minor unfolding transition at urea concentrations slightly lower than the unfolding transition of Nank1-7*. The intermediate is observed by CD-monitored unfolding, whereas fluorescence-monitored unfolding shows a single transition that matches the major transition seen by CD at high urea concentration. The fluorescence arises primarily from a single tryptophan in the fifth repeat, whereas CD at 222 nm monitors the overall α-helical structure and is thus a global probe of structure (Figure 1). This suggests that the consensus repeats pack against the fifth repeat, where the single tryptophan is located, stabilizing the N-terminal repeats, while uncoupling the two C-terminal repeats. Thus, in the equilibrium intermediate, the N-terminal repeats through repeat five are folded and packed against the consensus ankyrin sequences, whereas the C-terminal repeats (six and seven) are unfolded. This structural model is also consistent with the amplitudes and slopes of the two CD-monitored unfolding transitions, which are both smaller for the first transition (repeats 6 and 7) than the second transition (N-terminal and consensus repeats).
Previous studies have shown that the interfaces between neighboring repeats are important both for stability and cooperativity,12,13 indicating that perhaps the consensus repeats form a strong interface with repeat five, whereas the interface between the consensus repeats and repeat six is weak. Our model for uncoupling suggests that a favorable interface is formed between the fifth repeat and the consensus repeat, while the interface between sixth repeat and the consensus repeat is more readily uncoupled.
Removal of the two C-terminal repeats restores cooperativity
If the equilibrium unfolding intermediate seen for Nank1-5C167 and Nank1-5C267 consists of a folded region including the N-terminal and consensus repeats, with repeats six and seven unfolded, then removal of the sixth and seventh repeats (Nank1-5C1–3) should mimic this intermediate, producing only a single transition that matches the I to D transition seen with the internal consensus repeat insertions. Indeed, only a single unfolding transition is observed in Nank1-5C1 and the larger terminal addition constructs. Furthermore, the unfolding parameters obtained from CD-monitored unfolding transitions of Nank1-5C1 and Nank1-5C2 match those from fluorescence, suggesting that these constructs unfold via a two-state mechanism. Because the entire domain unfolds in a concerted reaction in these terminal consensus constructs, the stabilizing effects of these consensus sequences enhance the stability of the entire domain.
In contrast, the addition of a third consensus repeat appears to diminish cooperativity, resulting in a shallower unfolding transition. The thermodynamic parameters obtained from CD- versus fluorescence-monitored unfolding transitions differ for Nank1-5C3, indicating that a limit has been reached beyond which cooperative interactions are not propagated. Moreover, the fitted ΔGº u,H2O values for Nank1-5C3 are lower than expected based on the increased urea midpoint, owing to the decreased slope and long extrapolation involved in calculating this parameter. Nonetheless, structure persists to higher denaturant concentrations for Nank1-5C3, with an increase in the Cm by approximately 2 M urea compared to Nank1-5C2. It appears that despite the highly stabilizing C-terminal repeats in Nank1-5C3, the domain is uncoupled and partial unfolding is observed.
Because Nank1-5C1 and Nank1-5C2 fold via a two-state mechanism, we can determine the unfolding free energy associated with each consensus repeat and compare our results to free energies determined for the naturally-occurring repeats of the Notch ankyrin domain (2.2 kcal·mol-1 on average).12 The terminal consensus repeats increase unfolding free energy by approximately 4.4 kcal·mol-1, nearly twice the average free energy of the naturally-occurring Notch ankyrin repeats. Because the sixth repeat of the Notch ankyrin domain is relatively unstable, the stabilization associated with replacement of repeats six and seven with consensus repeats corresponds to a free energy increment of 5.4 kcal·mol−1. This stability enhancement is consistent with studies of other consensus helical repeat proteins: the consensus repeats are significantly more stable than naturally occurring repeat proteins of the same length.1–5,7,17,22
Consensus ankyrin repeats greatly increase the rate of folding
Much of the increased stability imparted by consensus repeats kinetically partitions into increased folding rates. Compared to Nank1-5, adding consensus repeats on the C-terminus increases the rate of folding by one order of magnitude per repeat. Because Nank1-5 has the same refolding rate as the major rate-limiting step in folding as the full-length Notch ankyrin domain, a similar rate enhancement is obtained in comparing Nank1-5C2 with Nank1-7*, which can be regarded as a substitution of two naturally occurring C-terminal repeats with consensus repeats. Compared to Nank1-5, adding consensus repeats decreases the rate of unfolding, although the effect is more modest than in the refolding direction, taking two consensus repeats to lower the rate constant of refolding by a order of magnitude.
The urea dependence of the refolding and unfolding rate constants of the consensus stabilized repeats are nonlinear, and can be fitted to the same kinetic three-state model that describes unfolding of the full-length Notch ankyrin domain. Because we were unable to detect a second unfolding phase for the consensus-stabilized repeats, the fitted parameters for the three state model are not as well determined as for the full-length Notch ankyrin domain. Thus, to evaluate the kinetic effects of consensus repeats within the three-state framework without depending on subjective fitting constraints, we compare directly measured rate constants for the consensus-stabilized constructs with analogous rate constants for the full-length Notch ankyrin domain at urea concentrations where the full-length rate constants match individual stepwise reactions.
At 0.8 M urea concentration, the observed folding rate constant for the Notch closely approximates that for formation of the kinetic intermediate (I’) from the denatured state (D, see scheme 1 above).11 Thus, the large increase in the folding rate at low denaturant concentration for Nank1-5C2 suggests a substantial increase in the rate of formation of I’ from D. At 6.8 M urea concentration, the rate constant for the major unfolding phase closely approximates that of the unfolding of I’ to D.11 Thus, the similarity of the unfolding rate constants of Nank1-5C2 to the full-length construct suggests that the effect of consensus stabilization has an early influence on this reaction, and that the kinetic intermediate and transition-state ensemble for this step are stabilized to the same degree.
Alteration of the Energy landscape
Site-directed mutagenesis studies of the full-length Notch ankyrin domain indicate that the folding of the denatured state to the on-pathway intermediate involves structure formation in the central repeats (three through five), whereas the two C-terminal repeats remain unstructured until the intermediate converts to the native state.10 The observation that Nank1-5, which contains the three central repeats that initiate folding, folds at the same rate as the full-length construct at low denaturant concentration supports this structural model for folding. Thus, the large rate enhancement seen in the folding of the C-terminal consensus-stabilized constructs suggests a change in the folding pathway. Specifically, C-terminal consensus stabilization may shift the order in which repeats become structured such that the C-terminal repeats fold first, and the N-terminal and perhaps the central repeats follow at a later stage.
Further insight into the potential for a change in the folding pathway can be obtained from evaluation of the change in the energy landscape resulting from C-terminal consensus stabilization. The energy landscape of Nank1-7* has been determined experimentally using a series of constructs where terminal repeats were progressively removed.12 A linear heterogeneous model was used to determine the stability associated with each repeat and neighboring interfaces, quantitatively mapping the landscape. In this model, the free energy of folding is described as a linear sum of energy increments from individual repeats. These single-repeat energy increments have both interfacial (nearest-neighbor) and intrinsic contributions. For Nank1-7*, the interfacial contributions are strongly stabilizing, offsetting the destabilizing intrinsic terms and resulting in high cooperativity.
To determine the energy landscape for Nank1-5C2, which conforms to an equilibrium two-state mechanism, we have combined coefficients determined previously for the first five repeats with free energy increments determined here for the consensus repeats of from Nank1-5C1 and Nank1-5C2. The folding energy landscape of Nank1-5C2 is tipped down in the C-terminal portion compared to that of Nank1-7*, reflecting increased local stability (Figure 7), and shows a new low energy folding pathway. The introduction of a new low energy pathway between the denatured and native states may be expected to accelerate folding, consistent with the large enhancement in overall folding rate of Nank1-5C1 and Nank1-5C2 (Figures 4, 5; Table 3). In addition, this new low energy route should shift the folding pathway from one in which the central repeats fold first10 to one in which the C-terminal consensus repeats initiate folding. The large increase in the rate constant for the first step in refolding (from D to I’) supports such a pathway shift. The extent of this shift away from the central repeats will be explored by examining the effects of point substitutions on folding rates in the consensus stabilized background.
Figure 7. Energy landscapes of the naturally-occurring Notch ankyrin domain and the C-terminally stabilized construct.
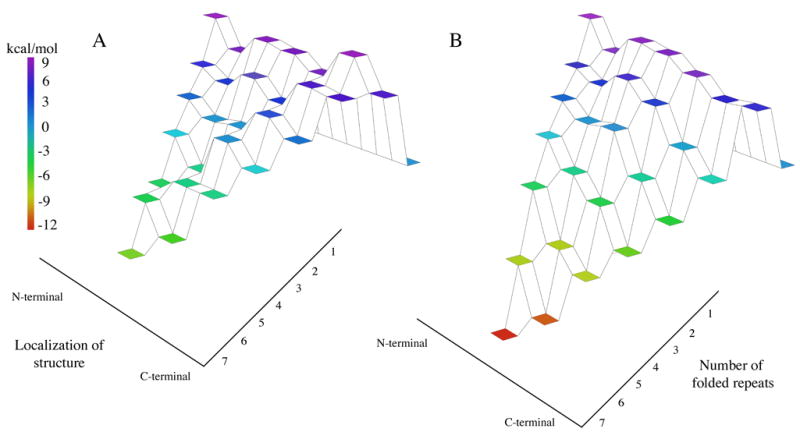
Nank1-7* (A)12 and Nank1-5C2 (B). The vertical axis indicates free energy relative to the denatured state (represented as a flat tier set to zero free energy), and is indicated by coloring. The right axis indicates the number of folded repeats, and the left axis indicates structure localization going from the N-terminus (left) to the C-terminus (right).
Although there theoretical studies relating energy landscapes to protein folding have gained popularity in recent years,23-27 there has been little direct experimental correlation demonstrated between energy landscapes and kinetic mechanism for folding. Here we have exploited the modular nature and local topological uniformity of repeat proteins to rationally alter the equilibrium energy landscape of a protein (Figure 7). We find that providing a new low-energy route connecting the native and denatured states greatly enhances the rate of folding and appears to shift the transition state ensemble. This shift is consistent with a significant thermodynamic component to folding pathway selection wherein the regions of greatest local stability initiate folding.28–31
Materials and Methods
Subcloning, Protein expression, and purification
Constructs encoding copies of consensus ankyrin repeats inserted into the Notch ankyrin domain were derived from a pET15b expression vector (Novagen, Madison, WI) that contains the Notch ankyrin domain.8 An NheI restriction site was incorporated into the region of the DNA sequence that corresponds to the loop between the fifth and sixth repeats (Figure 1) using site-directed mutagenesis (QuickChange Kit; Stratagene, La Jolla, CA). Duplex-forming DNA oligonucleotides (Integrated DNA Technologies, Coralville, IA) encoding consensus ankyrin repeats flanked with the appropriate Nhe1-compatible cohesive ends were treated T4 Polynucleotide Kinase (NEB, Beverley, MA), heated to 70 ºC, and cooled slowly to room temperature prior to ligation with the NheI digested vector.
Constructs encoding Nank1-5C16-7 and Nank1-5C26-7 were used as templates in PCR to generate constructs that encode Nank1-5C1 and Nank1-5C2. Primers were complementary to the N-terminal sequence of the Notch ankyrin domain and the C-terminal sequence of the consensus ankyrin repeat. PCR products were subcloned into the pET15b vector. The construct encoding Nank1-5C3 was constructed from Nank1-5C2, which contained a restriction site (NheI) at the C-terminus, ligating the consensus oligonucleotides described above.
All polypeptides were expressed in E. coli (BL21 [DE3]) and purified using Ni-NTA affinity chromatography followed by gel-filtration chromatography (Sephacryl S200; Amersham Pharmacia Biotech, Piscataway, NJ) as described previously. 8,9 Purified polypeptides were dialyzed against 25 mM Tris·HCl, 150mM NaCl, pH 8.0, flash frozen and stored at −80 ºC.
Circular dichroism spectroscopy
CD measurements were made using an Aviv 62DS Spectropolarimeter. Far-UV measurements were collected in an 0.1 cm cuvette at 20ºC, with protein concentrations ranging from 8 to 20 μM. Near-UV measurements were collected in a 1 cm cuvette at 20ºC, with protein concentrations ranging from 50 to 90 μM.
Equilibrium unfolding
Urea-induced unfolding transitions were monitored using the CD signal at 222nm and tryptophan fluorescence. Fluorescence emission stimulated using a 280 nm excitation, and was detected using a perpendicular 320 nm cutoff filter. Equilibrium unfolding measurements were made using a computer-controlled Hamilton Microlab syringe titrator (Hamilton, Reno, NV). Urea, purchased from Amresco (Solon, OH), was treated with mixed-bed resin (Bio-Rad; Hercules, CA) prior to use. Urea concentrations were determined by refractometry.32 Samples contained 2-4 μM protein, 25 mM Tris·HCl, 150 mM NaCl, pH 8.0, and were maintained at 20ºC.
Unfolding free energies in the absence of denaturant were estimated assuming a linear dependence of the unfolding free energy on urea concentration 32,33:
| (2) |
The unfolding transitions were fitted by a two-state model, where the observed signal (Yobs ) is a population-weighted average of signals from the native (YN) and denatured proteins (YD):
| (3) |
This can be related to the unfolding free energy, ΔGº, by its substitution with -RTlnKU, where KU represents the unfolding equilibrium constant, [D]/[N] to yield:
| (4) |
An analogous three-state model was obtained by adding a third term into equation (4) that accounts for an intermediate species. Writing the equation in terms of the equilibrium constants yields the following:
| (5) |
where KND and KID are equilibrium constant representing the transition between native and to denatured species, respectively.34
Kinetic measurements
Refolding and unfolding kinetics were measured on an Applied Photophysics SX.18MV–R stopped-flow rapid mixing device (Leatherhead, UK). Final protein concentrations, after dilution, were between 1.5 and 3.0 μM. Fluorescence measurements were detected perpendicular to a 280nm excitation using a 320 nm cutoff filter.
Rate constants and amplitudes of unfolding and refolding were obtained from fits to the individual progress curves using the following equation:
| (6) |
where Yobsis the observed signal, Y∞ represents the fluorescence at long times, Yi represents the amplitude change associate with the ith phase, and ki represents the rate constant for the ith phase. Versions of equation (6) with different numbers of phases (i = 1, 2, or 3) were fitted, those having the minimum number of phases that produced random residuals and low reduced χ2 values were used for kinetic analysis.
Microscopic rate constants and their urea dependences were fitted to either a 2-state or a 3-state model. For Nank1-5 the urea dependences of the fast refolding phase and the single unfolding phase were adequately fit using the following equation, which assumes two-state kinetics:
| (7) |
In contrast, for Nank1-5C1 and Nank1-5C2 the urea dependence of the fast refolding phase and the single unfolding phase required a model with an on-pathway intermediate to describe the observed rate constants. This model has been used to describe the folding kinetics of Nank1-7*, the parent construct.11 For Nank1-7*, a second unfolding phase facilitated determination of the four rate constants in scheme (1) and their log-linear urea dependencies. Since this second unfolding phase is not observed for the consensus-stabilized constructs, we applied an additional constraint, meq=(mNI’+mI’D-mDI’−mI’N), to uniquely determine these parameters. Fitting was done using the program ProFit 6.0.0 (Quantum Soft, Switzerland)35.
Human cyclophilin was expressed in the E. coli strain XA90 from a construct provided from the laboratory of Dr. Chris Walsh. Purification of cyclophilin was achieved according to the protocol described in Liu et al.36, with an additional purification step using a gel filtration column. Interrupted unfolding double-jump experiments were performed on an Applied Photophysics SX.18MV–R stopped flow fluorometer, using a sequential mixing attachment.10
Acknowledgments
We thank Dr. Chris Walsh and C. Gary Marshal for providing the human cyclophilin expression construct. We thank Drs. Mark Zweifel and David E. Wildes for critical reading of the manuscript. We thank Drs. Thomas Kiefhaber and Andreas Moglich for kindly providing the fitting functions for an on-pathway intermediate. This work was funded by a Young Investigator Award from the Arnold and Mabel Beckman Foundation, and by the National Institutes of Health (GM68462).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Mosavi LK, Minor DL, Peng ZY. Consensus-Derived Structural Determinants of the Ankyrin Repeat Motif. Proc Natl Acad Sci USA. 2002;99:16029–16034. doi: 10.1073/pnas.252537899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kohl A, Binz HK, Forrer P, Stumpp MT, Pluckthun A, Grutter MG. Designed to Be Stable: Crystal Structure of a Consensus Ankyrin Repeat Protein. Proc Natl Acad Sci USA. 2003;100:1700–1705. doi: 10.1073/pnas.0337680100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Main ER, Xiong Y, Cocco MJ, D'Andrea L, Regan L. Design of Stable Alpha-Helical Arrays from an Idealized Tpr Motif. Structure (Camb) 2003;11:497–508. doi: 10.1016/s0969-2126(03)00076-5. [DOI] [PubMed] [Google Scholar]
- 4.Stumpp MT, Forrer P, Binz HK, Pluckthun A. Designing Repeat Proteins: Modular Leucine-Rich Repeat Protein Libraries Based on the Mammalian Ribonuclease Inhibitor Family. J Mol Biol. 2003;332:471–87. doi: 10.1016/s0022-2836(03)00897-0. [DOI] [PubMed] [Google Scholar]
- 5.Tripp KW, Barrick D. Folding by Consensus. Structure (Camb) 2003;11:486–7. doi: 10.1016/s0969-2126(03)00078-9. [DOI] [PubMed] [Google Scholar]
- 6.Street TO, Rose GD, Barrick D. The Role of Introns in Repeat Protein Gene Formation. J Mol Biol. 2006;360:258–66. doi: 10.1016/j.jmb.2006.05.024. [DOI] [PubMed] [Google Scholar]
- 7.Binz HK, Stumpp MT, Forrer P, Amstutz P, Pluckthun A. Designing Repeat Proteins: Well-Expressed, Soluble and Stable Proteins from Combinatorial Libraries of Consensus Ankyrin Repeat Proteins. J Mol Biol. 2003;332:489–503. doi: 10.1016/s0022-2836(03)00896-9. [DOI] [PubMed] [Google Scholar]
- 8.Zweifel ME, Barrick D. Studies of the Ankyrin Repeats of the Drosophila Melanogaster Notch Receptor. 1. Solution Conformational and Hydrodynamic Properties. Biochemistry. 2001;40:14344–14356. doi: 10.1021/bi011435h. [DOI] [PubMed] [Google Scholar]
- 9.Bradley CM, Barrick D. Limits of Cooperativity in a Structurally Modular Protein: Response of the Notch Ankyrin Domain to Analogous Alanine Substitutions in Each Repeat. J Mol Biol. 2002;324:373–386. doi: 10.1016/s0022-2836(02)00945-2. [DOI] [PubMed] [Google Scholar]
- 10.Bradley CM, Barrick D. The Notch Ankyrin Domain Folds Via a Discrete, Centralized Pathway. Structure (London, England) 2006;14:1303–12. doi: 10.1016/j.str.2006.06.013. [DOI] [PubMed] [Google Scholar]
- 11.Mello CC, Bradley CM, Tripp KW, Barrick D. Experimental Characterization of the Folding Kinetics of the Notch Ankyrin Domain. J Mol Biol. 2005;352:266–81. doi: 10.1016/j.jmb.2005.07.026. [DOI] [PubMed] [Google Scholar]
- 12.Mello CC, Barrick D. An Experimentally Determined Protein Folding Energy Landscape. Proc Natl Acad Sci USA. 2004;101:14102–7. doi: 10.1073/pnas.0403386101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tripp KW, Barrick D. The Tolerance of a Modular Protein to Duplication and Deletion of Internal Repeats. J Mol Biol. 2004;344:169–78. doi: 10.1016/j.jmb.2004.09.038. [DOI] [PubMed] [Google Scholar]
- 14.Main ERG, Jackson SE, Regan L. The Folding and Design of Repeat Proteins: Reaching a Consensus. Curr Opin Struct Biol. 2003;13:482–489. doi: 10.1016/s0959-440x(03)00105-2. [DOI] [PubMed] [Google Scholar]
- 15.Bork P. Hundreds of Ankyrin-Like Repeats in Functionally Diverse Proteins: Mobile Modules That Cross Phyla Horizontally? Proteins. 1993;17:363–74. doi: 10.1002/prot.340170405. [DOI] [PubMed] [Google Scholar]
- 16.Myers JK, Pace CN, Scholtz JM. Denaturant M Values and Heat Capacity Changes: Relation to Changes in Accessible Surface Areas of Protein Unfolding. Protein Sci. 1995;4:2138–48. doi: 10.1002/pro.5560041020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Devi VS, Binz HK, Stumpp MT, Pluckthun A, Bosshard HR, Jelesarov I. Folding of a Designed Simple Ankyrin Repeat Protein. Protein Sci. 2004;13:2864–70. doi: 10.1110/ps.04935704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Brandts JF, Halvorson HR, Brennan M. Consideration of the Possibility That the Slow Step in Protein Denaturation Reactions Is Due to the Cis-Trans Isomerization of Proline Residues. Biochemistry. 1975;14:4953–4963. doi: 10.1021/bi00693a026. [DOI] [PubMed] [Google Scholar]
- 19.Bradley CM, Barrick D. Effect of Multiple Prolyl Isomerization Reactions on the Stability and Folding Kinetics of the Notch Ankyrin Domain: Experiment and Theory. J Mol Biol. 2005;352:253–65. doi: 10.1016/j.jmb.2005.06.041. [DOI] [PubMed] [Google Scholar]
- 20.Schmid FX, Grafl R, Wrba A, Beintema JJ. Role of Proline Peptide Bond Isomerization in Unfolding and Refolding of Ribonuclease. Proc Natl Acad Sci USA. 1986;83:872–876. doi: 10.1073/pnas.83.4.872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schmid FX, Baldwin RL. Acid Catalysis of the Formation of the Slow-Folding Species of Rnase A: Evidence That the Reaction Is Proline Isomerization. Proc Natl Acad Sci USA. 1978;75:4764–4768. doi: 10.1073/pnas.75.10.4764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Binz HK, Kohl A, Pluckthun A, Grutter MG. Crystal Structure of a Consensus-Designed Ankyrin Repeat Protein: Implications for Stability. Proteins: Struct Funct Bio. 2006 doi: 10.1002/prot.20930. [DOI] [PubMed] [Google Scholar]
- 23.Veitshans T, Klimov D, Thirumalai D. Protein Folding Kinetics: Timescales, Pathways and Energy Landscapes in Terms of Sequence-Dependent Properties. Fold Des. 1997;2:1–22. doi: 10.1016/S1359-0278(97)00002-3. [DOI] [PubMed] [Google Scholar]
- 24.Dill KA, Chan HS. From Levinthal to Pathways to Funnels. Nature Struct Biol. 1997;4:10–9. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- 25.Socci ND, Onuchic JN, Wolynes PG. Protein Folding Mechanisms and the Multidimensional Folding Funnel. Proteins. 1998;32:136–58. [PubMed] [Google Scholar]
- 26.Nymeyer H, Socci ND, Onuchic JN. Landscape Approaches for Determining the Ensemble of Folding Transition States: Success and Failure Hinge on the Degree of Frustration. Proc Natl Acad Sci USA. 2000;97:634–9. doi: 10.1073/pnas.97.2.634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Onuchic JN, Nymeyer H, Garcia AE, Chahine J, Socci ND. The Energy Landscape Theory of Protein Folding: Insights into Folding Mechanisms and Scenarios. Adv Pro Chem. 2000;53:87–152. doi: 10.1016/s0065-3233(00)53003-4. [DOI] [PubMed] [Google Scholar]
- 28.Dinner AR, Karplus M. The Roles of Stability and Contact Order in Determining Protein Folding Rates. Nature Struct Biol. 2001;8:21–2. doi: 10.1038/83003. [DOI] [PubMed] [Google Scholar]
- 29.Englander SW, Mayne L, Rumbley JN. Submolecular Cooperativity Produces Multi-State Protein Unfolding and Refolding. Biophys Chem. 2002;101–102:57–65. doi: 10.1016/s0301-4622(02)00190-4. [DOI] [PubMed] [Google Scholar]
- 30.Li R, Woodward C. The Hydrogen Exchange Core and Protein Folding. Protein Sci. 1999;8:1571–90. doi: 10.1110/ps.8.8.1571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hilser VJ, Garcia-Moreno EB, Oas TG, Kapp G, Whitten ST. A Statistical Thermodynamic Model of the Protein Ensemble. Chem Rev. 2006;106:1545–1558. doi: 10.1021/cr040423+. [DOI] [PubMed] [Google Scholar]
- 32.Pace CN. Determination and Analysis of Urea and Guanidine Hydrochloride Denaturation Curves. Methods Enzymol. 1986;131:266–80. doi: 10.1016/0076-6879(86)31045-0. [DOI] [PubMed] [Google Scholar]
- 33.Santoro MM, Bolen DW. Unfolding Free Energy Changes Determined by the Linear Extrapolation Method. 1. Unfolding of Phenylmethanesulfonyl Alpha-Chymotrypsin Using Different Denaturants. Biochemistry. 1988;27:8063–8. doi: 10.1021/bi00421a014. [DOI] [PubMed] [Google Scholar]
- 34.Barrick D, Baldwin RL. Three-State Analysis of Sperm Whale Apomyoglobin Folding. Biochemistry. 1993;32:3790–6. doi: 10.1021/bi00065a035. [DOI] [PubMed] [Google Scholar]
- 35.Sanchez IE, Kiefhaber T. Evidence for Sequential Barriers and Obligatory Intermediates in Apparent Two-State Protein Folding. J Mol Biol. 2003;325:367–76. doi: 10.1016/s0022-2836(02)01230-5. [DOI] [PubMed] [Google Scholar]
- 36.Liu J, Albers MW, Chen C, Schreiber L, Walsh CT. Cloning, Expression, and Purification of Human Cyclophilin in Escherichia Coli and Assessment of the Catalytic Role of Cysteines by Site-Directed Mutagenesis. Proc Natl Acad Sci USA. 1990;87:2304–2308. doi: 10.1073/pnas.87.6.2304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zweifel ME, Leahy DJ, Hughson FM, Barrick D. Structure and Stability of the Ankyrin Domain of the Drosophila Notch Receptor. Protein Sci. 2003;12:2622–2632. doi: 10.1110/ps.03279003. [DOI] [PMC free article] [PubMed] [Google Scholar]


