Abstract
We introduce a new approach to frequency-selective homonuclear dipolar recoupling in solid state nuclear magnetic resonance (NMR) with magic-angle spinning (MAS). This approach, to which we give the acronym SEASHORE, employs alternating periods of double-quantum recoupling and chemical shift evolution to produce phase modulations of the recoupled dipole-dipole interactions that average out undesired couplings, leaving only dipole-dipole couplings between nuclear spins with a selected pair of NMR frequencies. In principle, SEASHORE is applicable to systems with arbitrary coupling strengths and arbitrary sets of NMR frequencies. Arbitrary MAS frequencies are also possible, subject only to restrictions imposed by the pulse sequence chosen for double-quantum recoupling. We demonstrate the efficacy of SEASHORE in experimental 13C NMR measurements of frequency-selective polarization transfer in uniformly 15N,13C-labeled L-valine powder and frequency-selective intermolecular polarization transfer in amyloid fibrils formed by a synthetic decapeptide containing uniformly 15N,13C-labeled residues.
Introduction
Recoupling techniques are radio-frequency (rf) pulse sequences applied in synchrony with sample rotation that restore nuclear spin interactions that are otherwise averaged out by magic-angle spinning (MAS). The development of recoupling techniques for chemical shift anisotropy1–4, homonuclear dipole-dipole couplings5–14, heteronuclear dipole-dipole couplings15,16, and scalar couplings17,18 has revolutionized the application of solid state nuclear magnetic resonance (NMR) to chemically and structurally complex materials, where MAS is generally required to permit spectroscopic resolution of NMR signals from inequivalent sites and to enhance sensitivity. Recoupling techniques allow anisotropic interactions to be measured in the evolution periods of a multidimensional NMR measurement, while preserving the high resolution and high sensitivity afforded by MAS in the signal detection period. Recoupling techniques also permit polarization transfers through dipole-dipole or scalar couplings in mixing periods between evolution and/or detection periods.
In solid state 15N and 13C NMR, dipolar recoupling techniques were originally developed for structural measurements on samples that are isotopically labeled at selected sites, typically a 13C-13C or 15N-13C spin pair. Lately, experiments on samples with numerous isotopic labels have become more common, motivated by the goal of obtaining maximal information from a single sample and by the relative ease of preparing uniformly labeled proteins by expression in bacteria. Measurement of dipolar couplings (and hence inter-nuclear distances) between selected spin pairs in the in the presence of couplings to other spins requires frequency-selective recoupling techniques.
In the case of heteronuclear dipolar recoupling, Jaroniec et al. have introduced frequency-selective versions of the rotational echo double resonance (REDOR)19,20 and transferred echo double resonance (TEDOR) techniques21 that are effective as long as at least one spin in the pair of interest has a sufficiently well resolved signal under MAS that it can be selectively inverted by a weak π pulse.
In the case of homonuclear dipolar recoupling, frequency-selective techniques have also been proposed22–25. These techniques depend on the ability to match the sum or difference of effective fields in the rotating frame for the spin pair of interest to the MAS frequency or a multiple thereof. For good selectivity, the spins to be recoupled must have effective fields in the rotating frame , where ν1 is the rf field strength and Δν is the resonance offset) that are significantly different from those of other spins. In particular, the differences in effective fields must be greater than the dipole-dipole coupling strengths for the undesired spin pairs. These considerations make it difficult to achieve good selectivity unless there are large differences in the resonance offsets, i.e., large chemical shift differences. For aliphatic 13C sites, experimentally relevant chemical shift differences may be in the 5–20 ppm range, corresponding to resonance offset differences in the 0.7–3.0 kHz range in a 14.1 T field, while dipole-dipole coupling constants (dIS = γ2 Ħ/2πRIS3 where RIS is the distance between spins I and S) are as large as 2.3 kHz. A further complication is that large differences in effective fields can only be achieved when ν1 ≤ |Δν|, which in turn means that low MAS frequencies must be used if selective recoupling is to be achieved for spins with small chemical shift differences.
Previously proposed frequency-selective homonuclear dipolar recoupling techniques22–25 are extensions of the rotational resonance (RR) effect, in which recoupling occurs in the absence of applied rf fields when the resonance offset difference matches a multiple of the MAS frequency6,26. RR itself has been shown to be useful in uniformly labeled samples27–29, but obviously does not apply when the chemical shift differences are small. The RR matching condition can be broadened in a controlled manner by the application of appropriate amplitude-modulated or phase-modulated rf pulse sequences30, but this does not eliminate the requirements for large chemical shift differences, weak rf fields, and relatively low MAS frequencies.
In this paper, we describe and demonstrate a new approach to selective homonuclear dipolar recoupling that overcomes the limitations described above. This approach employs pulse sequences in which blocks of nonselective recoupling alternate with blocks of free precession under isotropic chemical shifts. Separation of the recoupling and chemical shift evolution periods eliminates the need for weak rf fields. By adjusting the lengths of the chemical shift evolution periods, selective recoupling can be achieved in principle for arbitrary sets of chemical shift differences. The MAS frequency can also be arbitrarily high, subject only to limitations imposed by the nonselective recoupling technique employed in the recoupling blocks. We refer to this approach to selective homonuclear dipolar recoupling by the acronym SEASHORE (Shift-Evolution-Assisted Selective HOmonuclear REcoupling). In the following sections, we describe the theoretical basis for SEASHORE, present initial demonstrations of selective 13C-13C polarization transfer under SEASHORE in experiments on uniformly 15N,13C-labeled L-valine powder and on an amyloid fibril sample containing uniformly labeled amino acid residues, and discuss likely applications and extensions of SEASHORE.
Theory
As shown in Fig. 1a, the SEASHORE pulse sequence consists of alternating blocks of dipolar recoupling, for time period mτR, and chemical shift evolution, for time period nτR, where τR is the rotor period and m and n are integers. During the recoupling blocks, the effective Hamiltonian is assumed to include only dipole-dipole coupling terms. In the experiments described below, a double-quantum recoupling technique is used, so the effective Hamiltonian for a pair of spins has the form
Figure 1.
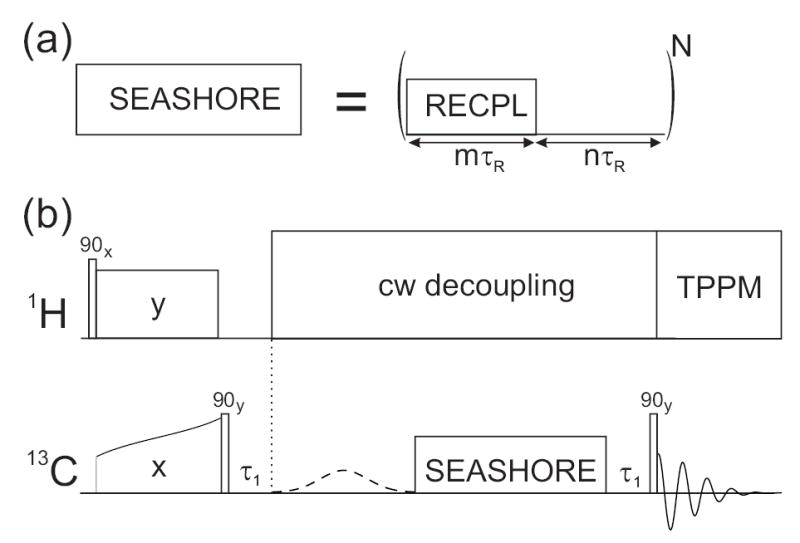
Pulse sequences for frequency-selective homonuclear dipolar recoupling. (a) The SEASHORE sequence consists of N alternating blocks of dipolar recoupling (RECPL) and chemical shift evolution for multiples of the MAS period τR. (b) For demonstrations of frequency-selective spin polarization transfer in solid state 13C NMR in Figs. 2–5, 13C polarization was generated by cross polarization from 1H spins. After storage as longitudinal magnetization for τ1, the polarization of a single 13C site was selected by a Gaussian-shaped pulse present every second scan, and transferred under the SEASHORE sequence. 13C NMR signals were detected with TPPM 1H decoupling, with receiver phase alternation corresponding to the presence or absence of the Gaussian-shaped pulse.
| (1) |
where ωd is a complex coupling constant with orientation dependence and scaling factor determined by the details of the recoupling technique. During the chemical shift evolution blocks, the effective Hamiltonian has the form
| (2) |
where ωI and ωS are the resonance offsets for spins I and S. Eq. (2) assumes that the dipole-dipole couplings and chemical shift anisotropy are averaged to zero by MAS during the chemical shift evolution blocks, i.e., that the MAS frequency is large compared with the couplings and that RR conditions are avoided. After N repetitions of double-quantum recoupling and chemical shift evolution blocks, the total evolution operator UT(N) is
| (3b) |
| (3c) |
where
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
UDQ and UCS are evolution operators for the double-quantum recoupling and chemical shift evolution blocks, respectively. is the evolution operator for the Mth repetition in an interaction representation with respect to the chemical shifts, with effective Hamiltonian . Phase modulation of , with constant phase increments φIS, is due to the chemical shift evolution periods and follows from the relation eiIzθI+e−iIzθ = eiθI+. In the limit Γd ≡ |mωdτR| << 1, the approximation
| (9) |
is valid. Then, since
| (10) |
phase modulation of will tend to cancel out evolution under the double-quantum recoupling blocks, leading to UT(N) ≈ UCSN, unless φIS is zero or a multiple of 2π. For a sample with any set of chemical shifts, it is generally possible to find combinations of n, τR, and rf carrier frequency such that recoupling occurs for one pair of NMR lines (most simply by setting the carrier frequency to the average of the two NMR frequencies, so that ωI + ωS = 0) and is suppressed for all other pairs of lines. Exact cancellation over N repetitions occurs when φIS = 2π k/N, for integer k satisfying 0 < k < N, but exact cancellation is not necessarily required for experiments to be successful.
The above arguments are valid for nuclei with arbitrary spin quantum numbers. In the special case of spin-1/2 nuclei, we can use the direct product basis
| (11) |
and the fictitious spin-1/2 operators31 defined by
| (12a) |
| (12b) |
| (12c) |
to represent HDQ as
| (13a) |
| (13b) |
where
| (14a) |
| (14b) |
| (14c) |
Thus, evolution under HDQ is a nutation of the initial sum magnetization (represented by a density operator term proportional to Iz(1,4)) at frequency about the x’ axis, which is a vector in the xy plane,. When restricted to the {|1〉,|4〉} subspace, HCS can be written as
| (15) |
According to Eqs. 14 and 15, evolution under SEASHORE can be viewed as an alternating series of rotations about x’ by Γd and about z by φIS. When Γd ≪ 1 and φIS is not close to a multiple of 2π, the rotations about ′ have no net effect, as in the DANTE technique commonly used for frequency selective excitation in NMR32.
Experimental results
Pulse sequence
Experiments were performed at 9.39 T and room temperature, using a Varian InfinityPlus NMR spectrometer and a Varian 3.2 mm MAS probe. Fig. 1b shows the full pulse sequence used in our initial demonstrations of SEASHORE. 13C spin polarization was first generated by cross polarization (CP) from protons33 and placed onto the rotating frame z axis by a hard 13C π/2 pulse. After a short delay τ1 (100 μs in our experiments), a frequency-selective Gaussian-shaped π pulse (1.2 ms long and applied every second scan with corresponding alternation of the receiver phase) selected signals derived from nuclear magnetization originating at a single 13C site. The subsequent SEASHORE period allowed polarization transfers to proximate 13C sites. After another τ1 delay, a final hard 13C π/2 pulse allowed measurement of NMR signals. Continuous wave (cw) proton decoupling was applied during the Gaussian-shaped pulse and SEASHORE periods. Two-pulse phase modulated (TPPM) decoupling34 was applied during signal detection. Polarization transfer efficiencies consistently improved with increased proton decoupling fields during SEASHORE recoupling blocks, up to the maximum field possible for our NMR probe (150 kHz). For long total recoupling times, it was also advantageous to trigger the beginning of each double-quantum recoupling block with a square wave from the MAS tachometer, to ensure synchronization of the SEASHORE pulse sequence with the sample rotation even in the presence of small instabilities (< 0.05%) in the MAS frequency.
Double-quantum recoupling was achieved with the POST-C7 technique of Hohwy et al.8, with m = 2 (i.e., one full POST-C7 cycle per recoupling block). MAS frequencies of between 6.32 and 9.76 kHz were used, implying 13C rf fields between 44.24 and 68.32 kHz. During the POST-C7 and chemical shift evolution blocks, the 13C rf carrier frequency was set to the average of the NMR frequencies of the two sites to be recoupled, except as described below for Fig. 3. Values of n and τR were chosen to suppress the recoupling of dipole-dipole interactions involving other sites, according to the principles described above.
Figure 3.
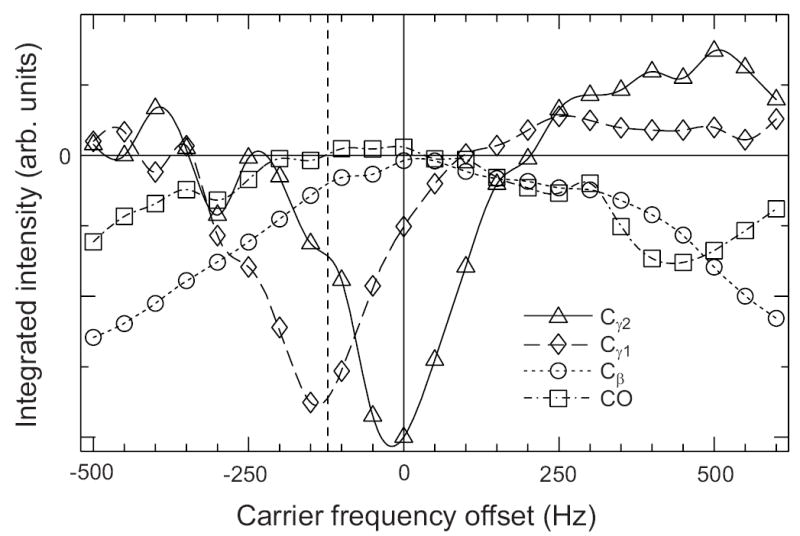
Dependence of polarization transfers under SEASHORE on the rf carrier frequency. Data are for uniformly 15N,13C-labeled L-valine powder. Experimental parameters other than the carrier frequency are as in Fig. 2c. Carrier frequency offset of zero corresponds to the midpoint of the Cα and Cγ2 NMR frequencies, where conditions were optimized for selective recoupling of Cα and γ2. Vertical dashed line marks the midpoint of the Cα and Cγ1 NMR frequencies. Lines through the data points are guides to the eye.
Selective polarization transfers within uniformly 13C-labeled valine
Fig. 2 demonstrates the efficacy of SEASHORE in experiments on uniformly 15N,13C-labeled L-valine powder. The conventional 13C MAS NMR spectrum is shown in Fig. 2a. The remaining spectra were obtained with the pulse sequence in Fig. 1b. Fig. 2b shows the spectrum obtained with initial selection of Cα spin polarization and subsequent recoupling for 2.286 ms without chemical shift evolution blocks (i.e., n = 0). These conditions lead to recoupling of dipole-dipole interactions between all 13C spins, and therefore to transfer from Cα to all other carbon sites. The double-quantum nature of POST-C7 recoupling leads to alternating signs for NMR lines of spins that are polarized primarily by a series of single-bond transfers. In particular, the Cγ2 NMR line is positive in Fig. 2b because it results primarily from two single-bond polarization transfers from Cα. Fig. 2c shows the spectrum obtained with initial selection of the Cα spin polarization and subsequent SEASHORE recoupling of the Cα-Cγ2 interaction, with n = 3 and N = 14 (3.841 ms of POST-C7, 9.605 ms total recoupling time). The Cγ2 NMR line is negative in Fig. 2c, indicating that this line results from direct polarization transfer between 13C sites that are separated by two bonds. All other transfers are suppressed, except for a weak transfer to Cγ1 due to the small chemical shift difference between Cγ1 and Cγ2 NMR lines, even though Cα-Cβ and Cα-CO dipole-dipole couplings are approximately 4.4 times stronger than Cα-Cγ1 and Cα-Cγ2 couplings. Fig. 2d shows the spectrum obtained with initial selection of the CO spin polarization and subsequent SEASHORE recoupling of the CO-Cγ2 interaction, with n = 4 and N = 26 (7.560 ms of POST-C7, 22.601 ms total recoupling time). Again, the Cγ2 NMR line is negative in Fig. 2d and all other transfers are strongly suppressed, indicating selective recoupling of the CO-Cγ2 interaction and direct polarization transfer from CO to Cγ2, separated by three bonds.
Figure 2.
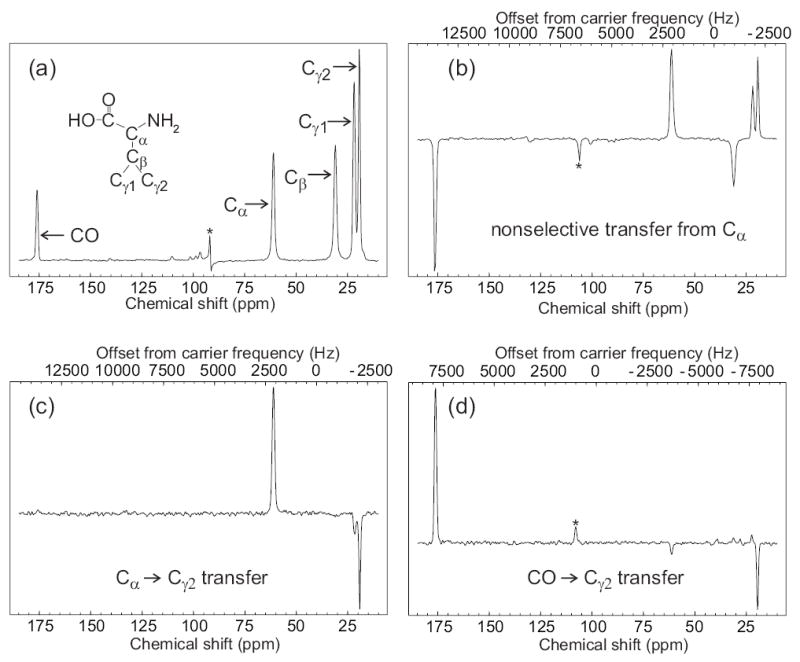
Demonstration of frequency-selective polarization transfer in uniformly 15N,13C-labeled L-valine powder under SEASHORE, using the POST-C7 recoupling technique. (a) Conventional 13C NMR spectrum with peak assignments, obtained at 100.4 MHz 13C NMR frequency with 8.000 kHz MAS. (b) Spectrum obtained with the pulse sequence in Fig. 1, with selective excitation of the Cα peak, N = 8, m = 2, n = 0, and 7.000 kHz MAS. (c) Spectrum obtained with selective excitation of the Cα peak, N = 14, m = 2, n = 3, and 7.288 kHz MAS. (d) Spectrum obtained with selective excitation of the CO peak, N = 26, m = 2, n = 4, and 6.878 kHz MAS. All spectra were obtained with 16 scans at 100.4 MHz 13C NMR frequency, using a 10 mg sample, and 110 kHz proton decoupling throughout the Gaussian-shaped pulse, SEASHORE recoupling, and signal acquisition. For parts c and d, rf carrier frequencies during the SEASHORE period were set to the midpoint of the 13C NMR frequencies of the spin pair of interest. Values of n and the MAS frequency were chosen to optimize the selectivity of dipolar recoupling. Asterisks indicate an artifact at the carrier frequency in part a and MAS sideband lines in parts b and c.
Fig. 3 shows the effects of varying the 13C rf carrier frequency away from its optimal value for Cα-Cγ2 recoupling, which is the average of the Cα and Cγ2 NMR frequencies. Plotted are the integrated intensities of the CO, Cβ, Cγ1, and Cγ2 NMR lines as functions of the offset from the optimal carrier frequency. Pulse sequence parameters were optimized for suppression of all undesired transfers at the optimal carrier frequency. Deviation from the optimal carrier frequency results in loss of the desired transfer and growth of undesired transfers. The strongest undesired transfer is from Cα to Cγ1, which is maximized as expected when the carrier frequency equals the average of the Cα and Cγ1 NMR frequencies, marked by the vertical dashed line in Fig. 3.
Time dependence of selective polarization transfers
Fig. 4 demonstrates the selective measurement of internuclear distances in uniformly 15N,13C-labeled L-valine powder, through the dependence of frequency-selective polarization transfers on the total recoupling time in the SEASHORE sequence. We quantify polarization transfer by the value of (Fi + Fj)/(Fi − Fj), where Fi and Fj are peak integrals proportional to longitudinal spin angular momenta of spins i and j, respectively, immediately after the SEASHORE recoupling period. The normalizing factor (Fi − Fj) is included to account partially for loss of signal due to transverse nuclear relaxation during the SEASHORE period, and would be time-independent in the limit of pure double-quantum evolution without relaxation.
Figure 4.
The dependences of selective double-quantum polarization transfers on the total time of POST-C7 recoupling. Data in parts a, b, and c are for selective Cβ-Cγ2 (filled and hollow triangles), Cα-Cγ2 (filled squares), and CO-Cγ2 (filled diamonds) transfers in uniformly 15N,13C-labeled L-valine powder. MAS frequencies were 8.45 kHz, 6.32 kHz, and 9.76 kHz, respectively. Polarization transfers are quantified by (Fi + Fj)/(Fi − Fj), as explained in the text. Peak integrals Fi and Fj were extracted from NMR spectra obtained in 100 scans. Proton decoupling field amplitudes during POST-C7 blocks were 150 kHz (all filled symbols) or 110 kHz (hollow triangles). POST-C7 blocks were actively synchronized with an MAS tachometer signal. Decoupling fields were 110 kHz during the Gaussian-shaped pulse, chemical shift evolution periods, and signal acquisition. Simulated curves are for two-spin systems with the indicated internuclear distances, under ideal pulse sequence conditions. Exponential damping with a 5 ms time constant is applied to all simulated curves.
As shown in Fig. 4a, frequency-selective polarization transfer from Cβ to Cγ2 exhibits a damped oscillatory time dependence, with stronger damping at lower proton decoupling fields. Comparison with the oscillations in simulated curves, calculated for a two-spin system under ideal POST-C7 pulse sequence conditions, indicates a distance of 1.50 ± 0.05 Å. The true Cβ-Cγ2 distance is 1.53 Å, according to the crystal structure of L-valine35, which contains two inequivalent L-valine molecules in the unit cell. As shown in Fig. 4b, frequency-selective polarization transfer from Cα to Cγ2 also exhibits a damped oscillatory time dependence. Comparison with simulated curves indicates a distance of 2.50 ± 0.05 Å. Distances from Cα sites to Cγ sites in the crystal structure range from 2.53 Å to 2.56 Å.
As shown in Fig. 4c, frequency-selective polarization transfer from CO to Cγ2 is weakly oscillatory. The normalized polarization transfer does not decay to zero. We attribute this observation to the fact that the CO and Cγ2 NMR lines are actually superpositions of lines with small, unresolved chemical shift differences, arising from the two inequivalent molecules in the L-valine crystal structure. Given the relatively long internuclear distances and weak dipole-dipole couplings for CO-Cγ2 pairs, complete polarization transfer may then be prevented by small offsets from the exact condition ωI + ωS = 0 (see below). Simulated curves in Fig. 4c are for the four distinct intramolecular distances between CO and Cγ sites in crystalline L-valine. The assignment of Cγ1 and Cγ2 lines to specific Cγ sites is not known. Two-dimensional solid state NMR spectra of uniformly 15N,13C-labeled L-valine powder (data not shown) indicate that both inequivalent L-valine molecules contribute to the Cγ2 line, implying four pairs of internuclear distances that may be assigned to CO-Cγ2 distances35: 2.90 Å and 2.98 Å; 2.98 Å and 3.29 Å; 2.90 Å and 3.90 Å; 3.29 Å and 3.90 Å. The experimental data in Fig. 4c appear more consistent with the first two possible assignments.
All simulated curves in Fig. 4 include artificial damping with a 5 ms time constant to produce approximate agreement with the experimental data. One important source of damping in experimental data is imperfect proton decoupling, as the oscillations in Fig. 4 increase in amplitude when the proton decoupling fields during POST-C7 blocks are increased from 110 kHz to 150 kHz. Inhomogeneity of rf fields may also contribute to the damping of oscillatory polarization transfers. To address this issue, simulations were performed for a two-spin system with a 1.50 Å internuclear distance, τR = 100 μs, m = 2, n = 1, and rf field amplitudes ranging from 0.85 to 1.15 times the ideal value for POST-C7 recoupling, in increments of 0.01. Summation of the simulated curves, with equal weighting, produced a curve with an apparent damping time constant of approximately 5 ms.
Application to amyloid fibrils
Fig. 5 shows an initial application of the SEASHORE technique to a system of genuine biochemical complexity, namely a 6 mg sample of lyophilized amyloid fibrils formed by residues 14–23 of the full-length β-amyloid peptide associated with Alzheimer's disease (Aβ14–23, amino acid sequence HQKLFVVAED), synthesized with uniform 15N and 13C labeling of Val18 and Ala2136. Determination of the molecular structures of amyloid fibrils formed by various peptides and proteins is an area of current activity in several solid state NMR groups37–46. Earlier measurements on Aβ14–23 fibrils, using proton-mediated two-dimensional 13C NMR exchange spectroscopy45,47, had shown that these fibrils contain highly ordered antiparallel β-sheets in which intermolecular hydrogen bonds connect residue 16+j of each Aβ14–23 molecule with residue 23-j of a neighboring molecule (data not shown). Thus, Val18 and Ala21 are aligned in the antiparallel β-sheets, producing nearest-neighbor intermolecular distances of approximately 4.2 ± 0.3 Å between Cα of Val18 and Cα of Ala21. The corresponding intramolecular distance is greater than 10 Å, so that any observed polarization transfers must be primarily intermolecular in nature.
Figure 5.
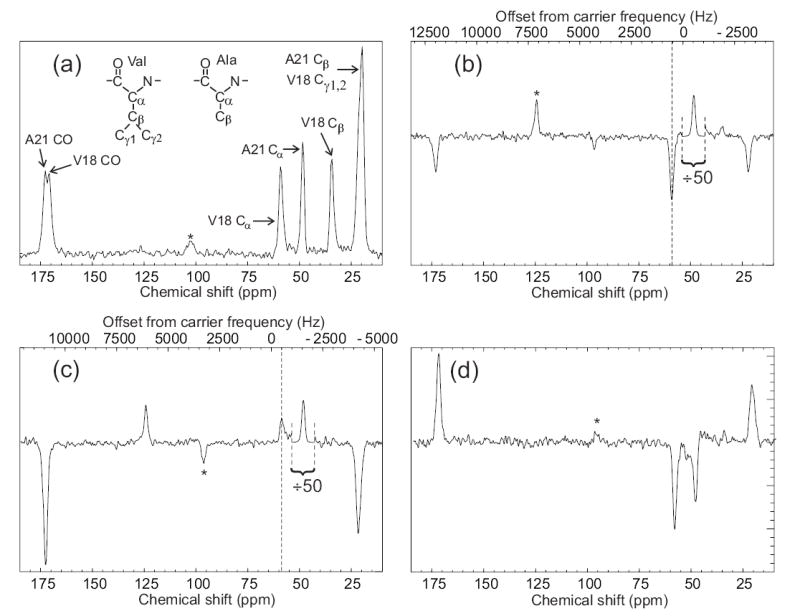
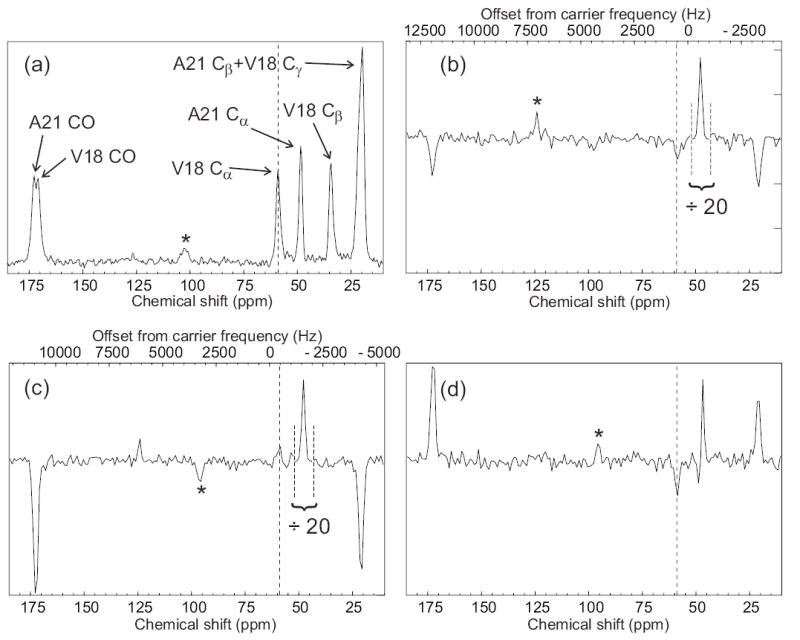
Observation of an intermolecular polarization transfer between Aβ14–23 peptide molecules within amyloid fibrils using SEASHORE. Aβ14–23 molecules were uniformly 15N,13C-labeled at Val18 and Ala21. (a) Conventional 13C NMR spectrum with peak assignments, obtained at 100.4 MHz 13C NMR frequency in 16 scans with 7.00 kHz MAS. (b) Spectrum obtained with the pulse sequence in Fig. 1, with selective excitation of the Ala21 Cα peak, N = 32, m = 2, n = 1, and 7.626 kHz MAS. The rf carrier frequency was set to the midpoint of the Ala21 Cα and Val18 Cα NMR frequencies. This spectrum is the result of 50,000 scans. The Ala21 Cα peak is scaled down by a factor of 50 relative to the rest of the spectrum. Vertical dashed line marks the Val18 Cα NMR frequency. (c) Spectrum obtained as in part b, but with a 1000 Hz shift of the carrier frequency during the SEASHORE period to prevent Ala21-Val18 recoupling. (d) The difference of spectra in parts b and c. Asterisks indicate MAS sideband lines.
Fig. 5a shows the conventional 13C MAS NMR spectrum of the Aβ14–23 fibril sample. Fig. 5b shows a spectrum obtained with initial selection of the Ala21 Cα spin polarization and subsequent polarization transfer with SEASHORE under conditions chosen to recouple the intermolecular, inter-residue Cα-Cα dipole-dipole interactions while suppressing all other couplings involving the Cα sites (N = 32, n = 1, 8.392 ms of POST-C7, 12.589 ms total recoupling time, 13C rf carrier at the average of the Ala21 Cα and Val18 Cα NMR frequencies). Although intra-residue Cα-CO and Cα-Cβ polarization transfers are not completely eliminated, they are strongly attenuated. Moreover, the desired intermolecular Cα-Cα polarization transfer in Fig. 5b is stronger than the intra-residue transfers, despite the fact that the intermolecular Cα-Cα dipole-dipole coupling is roughly 20 times weaker than the intra-residue couplings. Fig. 5c shows a spectrum obtained under identical conditions, except that the 13C rf carrier frequency during the SEASHORE period is shifted by 1000 Hz. Undesired transfers increase at the expense of the desired intermolecular polarization transfer. The small positive signal at the Val18 Cα chemical shift in Fig. 5c is attributable to weak off-resonance excitation by the Gaussian-shaped pulse. Fig. 5d shows the difference between spectra in Figs. 5b and 5c. The negative sign of the signal at the Val18 Cα NMR frequency in Fig. 5d, together with the absence of Val18 CO and Cβ signals, shows that this signal is not an artifact of spectrometer instability, spin relaxation, imperfect phase cycling, or other effects. The integrated Val18 Cα signal camplitude in Fig. 5b is 1.4% and 3.6% of the A21 Cα signal amplitudes in Figs. 5a and 5b, respectively. Assuming a 4.2 Å internuclear distance, the ideal polarization transfer efficiency under the conditions in Fig. 5b would be 21%. For comparison, proton-mediated Cα-Cα polarization transfers have efficiencies of roughly 5–10% in antiparallel β-sheet structures under experimental conditions used for structural measurements45,47.
Discussion
We envision many applications of SEASHORE in structural studies of solids, including organic, inorganic, and biochemical materials. Of immediate interest to us are structural studies of amyloid fibrils37–46, integral membrane proteins48–54, and peptides bound to antibodies or receptor proteins29,55. In systems such as these, samples with multiple uniformly 15N,13C-labeled residues are prepared to enable efficient measurements of 13C NMR chemical shifts, from which secondary structure elements are identified. Rough estimates of 13C-13C distances in these samples, which are needed for the development of full structural models, can be obtained from two-dimensional 13C-13C NMR exchange spectroscopy with long exchange periods56 or from proton-mediated two-dimensional 13C-13C NMR exchange spectroscopy57, but more quantitative measurements of pairwise 13C-13C distances with SEASHORE would permit structures to be determined with greater detail and precision.
At present, the maximum distances measurable with good precision by SEASHORE are limited by damping of oscillations in the time-dependent polarization transfer curves. When these oscillations are overdamped, internuclear distances can not be measured precisely without a detailed analysis of spin relaxation processes. As demonstrated in Fig. 4a, oscillations were less strongly damped when the proton decoupling field amplitudes during SEASHORE recoupling periods were increased from 110 kHz to 150 kHz. It is likely that proton decoupling fields above 150 kHz would further improve the polarization transfer data. Inhomogeneity of the 13C rf field amplitude across the sample volume is also a contributing factor, as oscillations were less strongly damped when the 10 mg sample used in Fig. 4 was replaced with a 2 mg sample (data not shown).
The SEASHORE technique is also sensitive to inhomogeneous broadening of the 13C MAS NMR lines in a manner similar to other frequency-selective techniques, such as RR6,26–30. If the dipole-dipole couplings for the spin pairs of interest are small compared with the inhomogeneous linewidths in the MAS spectrum, as will be the case for measurements of relatively large internuclear distances in noncrystalline samples, then recoupling under SEASHORE will tend to be suppressed. This is true because a weak coupling necessitates a long recoupling period, which in turn implies a narrow recoupling bandwidth. Some of the spin pairs of interest will then be outside the recoupling bandwidth. This effect reduces the Val18 Cα signal amplitude in the experiments on Aβ14–23 fibrils in Fig. 5b. In these experiments, the relevant coupling strength is approximately 100 Hz and the inhomogeneous 13C NMR linewidths are approximately 200 Hz. In Fig. 4c, the experimental polarization transfer is also limited by a narrow recoupling bandwidth.
In principle, the recoupling bandwidth under SEASHORE can be increased by the insertion of hard 13C π pulses into the SEASHORE pulse sequence, with a spacing comparable to the inverse of the inhomogeneous linewidths58. We are currently exploring this possibility.
Recoupling sequences other than POST-C7 can be incorporated into SEASHORE, including pulse sequences that produce zero-quantum effective dipole-dipole couplings12–14,17,18. For example, if the effective couplings have the zero-quantum form
| (16) |
then chemical shift differences will average the couplings to the form
| (17) |
unless n(ωI – ωS)τR is an integer multiple of 2π. With the form in Eq. (17), all homonuclear dipole-dipole couplings commute with one another and with resonance offsets. Among other reasons, this property is useful because it allows homonuclear dipole-dipole couplings to be refocused by frequency-selective π pulses.
Independently, Chan and coworkers have shown that the introduction of chemical shift evolution periods into the R-TOBSY recoupling sequence leads to frequency-selective polarization transfers59. R-TOBSY produces a scalar, zero-quantum effective coupling Hamiltonian18. Chemical shift precession produces a phase modulation that truncates the effective Hamiltonian to the form in Eq. (17) unless n(ωI – ωS)τR is an integer multiple of 2π.
Acknowledgments
This work was supported by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health, and by a grant to R.T. from the NIH Intramural AIDS Targeted Antiviral Program. We thank Dr. David J. E. Callaway for providing the Aβ14–23 sample used in this work. The analogy between SEASHORE and DANTE was suggested to us by Dr. G. Bodenhausen.
References
- 1.Alla MA, Kundla EI, Lippmaa ET. Jetp Lett. 1978;27:194. [Google Scholar]
- 2.Tycko R, Dabbagh G, Mirau PA. J Magn Reson. 1989;85:265. [Google Scholar]
- 3.Chan JCC, Tycko R. J Chem Phys. 2003;118:8378. [Google Scholar]
- 4.Liu SF, Mao JD, Schmidt-Rohr K. J Magn Reson. 2002;155:15. doi: 10.1006/jmre.2002.2503. [DOI] [PubMed] [Google Scholar]
- 5.Meier BH, Earl WL. J Chem Phys. 1986;85:4905. [Google Scholar]
- 6.Meier BH, Earl WL. J Am Chem Soc. 1987;109:7937. [Google Scholar]
- 7.Tycko R, Dabbagh G. Chem Phys Lett. 1990;173:461. [Google Scholar]
- 8.Hohwy M, Jakobsen HJ, Eden M, Levitt MH, Nielsen NC. J Chem Phys. 1998;108:2686. [Google Scholar]
- 9.Brinkmann A, Eden M, Levitt MH. J Chem Phys. 2000;112:8539. [Google Scholar]
- 10.Carravetta M, Eden M, Zhao X, Brinkmann A, Levitt MH. Chem Phys Lett. 2000;321:205. [Google Scholar]
- 11.Gregory DM, Mitchell DJ, Stringer JA, Kiihne S, Shiels JC, Callahan J, Mehta MA, Drobny GP. Chem Phys Lett. 1995;246:654. [Google Scholar]
- 12.Gullion T, Vega S. Chem Phys Lett. 1992;194:423. [Google Scholar]
- 13.Bennett AE, Ok JH, Griffin RG, Vega S. J Chem Phys. 1992;96:8624. [Google Scholar]
- 14.Ishii Y. J Chem Phys. 2001;114:8473. [Google Scholar]
- 15.Oas TG, Griffin RG, Levitt MH. J Chem Phys. 1988;89:692. [Google Scholar]
- 16.Gullion T, Schaefer J. J Magn Reson. 1989;81:196. doi: 10.1016/j.jmr.2011.09.003. [DOI] [PubMed] [Google Scholar]
- 17.Baldus M, Meier BH. J Magn Reson Ser A. 1996;121:65. [Google Scholar]
- 18.Chan JCC, Brunklaus G. Chem Phys Lett. 2001;349:104. [Google Scholar]
- 19.Bennett AE, Becerra LR, Griffin RG. J Chem Phys. 1994;100:812. [Google Scholar]
- 20.Jaroniec CP, Tounge BA, Herzfeld J, Griffin RG. J Am Chem Soc. 2001;123:3507. doi: 10.1021/ja003266e. [DOI] [PubMed] [Google Scholar]
- 21.Jaroniec CP, Filip C, Griffin RG. J Am Chem Soc. 2002;124:10728. doi: 10.1021/ja026385y. [DOI] [PubMed] [Google Scholar]
- 22.Takegoshi K, Nomura K, Terao T. Chem Phys Lett. 1995;232:424. [Google Scholar]
- 23.Takegoshi K, Nomura K, Terao T. J Magn Reson. 1997;127:206. doi: 10.1006/jmre.1997.1191. [DOI] [PubMed] [Google Scholar]
- 24.Costa PR, Sun BQ, Griffin RG. J Am Chem Soc. 1997;119:10821. [Google Scholar]
- 25.Ladizhansky V, Griffin RG. J Am Chem Soc. 2004;126:948. doi: 10.1021/ja037138c. [DOI] [PubMed] [Google Scholar]
- 26.Raleigh DP, Levitt MH, Griffin RG. Chem Phys Lett. 1988;146:71. [Google Scholar]
- 27.Williamson PTF, Verhoeven A, Ernst M, Meier BH. J Am Chem Soc. 2003;125:2718. doi: 10.1021/ja028210u. [DOI] [PubMed] [Google Scholar]
- 28.Petkova AT, Tycko R. J Magn Reson. 2004;168:137. doi: 10.1016/j.jmr.2004.02.007. [DOI] [PubMed] [Google Scholar]
- 29.Sharpe S, Kessler N, Anglister JA, Yau WM, Tycko R. J Am Chem Soc. 2004;126:4979. doi: 10.1021/ja0392162. [DOI] [PubMed] [Google Scholar]
- 30.Chan JCC, Tycko R. J Chem Phys. 2004;120:8349. doi: 10.1063/1.1737369. [DOI] [PubMed] [Google Scholar]
- 31.Vega S. J Chem Phys. 1978;68:5518. [Google Scholar]
- 32.Morris GA, Freeman R. J Magn Reson. 1969;29:433. [Google Scholar]
- 33.Pines A, Gibby MG, Waugh JS. J Chem Phys. 1973;59:569. [Google Scholar]
- 34.Bennett AE, Rienstra CM, Auger M, Lakshmi KV, Griffin RG. J Chem Phys. 1995;103:6951. [Google Scholar]
- 35.Torii K, Iitaka Y. Acta Crystallographica Section B-Structural Crystallography and Crystal Chemistry. 1970;B 26:1317. doi: 10.1107/s0567740870004065. [DOI] [PubMed] [Google Scholar]
- 36.Tjernberg LO, Tjernberg A, Bark N, Shi Y, Ruzsicska BP, Bu ZM, Thyberg J, Callaway DJE. Biochem J. 2002;366:343. doi: 10.1042/BJ20020229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lansbury PT, Costa PR, Griffiths JM, Simon EJ, Auger M, Halverson KJ, Kocisko DA, Hendsch ZS, Ashburn TT, Spencer RGS, Tidor B, Griffin RG. Nat Struct Biol. 1995;2:990. doi: 10.1038/nsb1195-990. [DOI] [PubMed] [Google Scholar]
- 38.Benzinger TLS, Gregory DM, Burkoth TS, Miller-Auer H, Lynn DG, Botto RE, Meredith SC. Proc Natl Acad Sci U S A. 1998;95:13407. doi: 10.1073/pnas.95.23.13407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jaroniec CP, MacPhee CE, Bajaj VS, McMahon MT, Dobson CM, Griffin RG. Proc Natl Acad Sci U S A. 2004;101:711. doi: 10.1073/pnas.0304849101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kammerer RA, Kostrewa D, Zurdo J, Detken A, Garcia-Echeverria C, Green JD, Muller SA, Meier BH, Winkler FK, Dobson CM, Steinmetz MO. Proc Natl Acad Sci U S A. 2004;101:4435. doi: 10.1073/pnas.0306786101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Siemer AB, Ritter C, Ernst M, Riek R, Meier BH. Angew Chem-Int Edit. 2005;44:2441. doi: 10.1002/anie.200462952. [DOI] [PubMed] [Google Scholar]
- 42.Antzutkin ON, Balbach JJ, Leapman RD, Rizzo NW, Reed J, Tycko R. Proc Natl Acad Sci U S A. 2000;97:13045. doi: 10.1073/pnas.230315097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Balbach JJ, Ishii Y, Antzutkin ON, Leapman RD, Rizzo NW, Dyda F, Reed J, Tycko R. Biochemistry. 2000;39:13748. doi: 10.1021/bi0011330. [DOI] [PubMed] [Google Scholar]
- 44.Petkova AT, Ishii Y, Balbach JJ, Antzutkin ON, Leapman RD, Delaglio F, Tycko R. Proc Natl Acad Sci U S A. 2002;99:16742. doi: 10.1073/pnas.262663499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Petkova AT, Buntkowsky G, Dyda F, Leapman RD, Yau WM, Tycko R. J Mol Biol. 2004;335:247. doi: 10.1016/j.jmb.2003.10.044. [DOI] [PubMed] [Google Scholar]
- 46.Chan JCC, Oyler NA, Yau WM, Tycko R. Biochemistry. 2005;44:10669. doi: 10.1021/bi050724t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tycko R, Ishii Y. J Am Chem Soc. 2003;125:6606. doi: 10.1021/ja0342042. [DOI] [PubMed] [Google Scholar]
- 48.Hiller M, Krabben L, Vinothkumar KR, Castellani F, van Rossum BJ, Kuhlbrandt W, Oschkinat H. Chembiochem. 2005;6:1679. doi: 10.1002/cbic.200500132. [DOI] [PubMed] [Google Scholar]
- 49.van Gammeren AJ, Hulsbergen FB, Hollander JG, de Groot HJM. J Biomol NMR. 2005;31:279. doi: 10.1007/s10858-005-1604-8. [DOI] [PubMed] [Google Scholar]
- 50.Patel AB, Crocker E, Reeves PJ, Getmanova EV, Eilers M, Khorana HG, Smith SO. J Mol Biol. 2005;347:803. doi: 10.1016/j.jmb.2005.01.069. [DOI] [PubMed] [Google Scholar]
- 51.Tian CL, Gao PF, Pinto LH, Lamb RA, Cross TA. Protein Sci. 2003;12:2597. doi: 10.1110/ps.03168503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Isaac B, Gallagher GJ, Balazs YS, Thompson LK. Biochemistry. 2002;41:3025. doi: 10.1021/bi015759h. [DOI] [PubMed] [Google Scholar]
- 53.Ma C, Marassi FM, Jones DH, Straus SK, Bour S, Strebel K, Schubert U, Oblatt-Montal M, Montal M, Opella SJ. Protein Sci. 2002;11:546. doi: 10.1110/ps.37302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zysmilich MG, McDermott A. Proc Natl Acad Sci U S A. 1996;93:6857. doi: 10.1073/pnas.93.14.6857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Luca S, White JF, Sohal AK, Filippov DV, van Boom JH, Grisshammer R, Baldus M. Proc Natl Acad Sci U S A. 2003;100:10706. doi: 10.1073/pnas.1834523100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Castellani F, van Rossum BJ, Diehl A, Rehbein K, Oschkinat H. Biochemistry. 2003;42:11476. doi: 10.1021/bi034903r. [DOI] [PubMed] [Google Scholar]
- 57.Lange A, Becker S, Seidel K, Giller K, Pongs O, Baldus M. Angew Chem-Int Edit. 2005;44:2089. doi: 10.1002/anie.200462516. [DOI] [PubMed] [Google Scholar]
- 58.Goobes G, Boender GJ, Vega S. J Magn Reson. 2000;146:204. doi: 10.1006/jmre.2000.2126. [DOI] [PubMed] [Google Scholar]
- 59.Mou Y, Chan JCC. Chem Phys Lett. 2006;419:144. [Google Scholar]


