Screened Nonbonded Interactions in Native Proteins Manipulate Optimal Paths for Robust Residue Communication

Abstract

A protein structure is represented as a network of residues whereby edges are determined by intramolecular contacts. We introduce inhomogeneity into these networks by assigning each edge a weight that is determined by amino acid pair potentials. Two methodologies are utilized to calculate the average path lengths (APLs) between pairs: to minimize i), the maximum weight in the strong APL, and ii), the total weight in the weak APL. We systematically screen edges that have higher than a cutoff potential and calculate the shortest APLs in these reduced networks, while keeping chain connectivity. Therefore, perturbations introduced at a selected region of the residue network propagate to remote regions only along the nonscreened edges that retain their ability to disseminate the perturbation. The shortest APLs computed from the reduced homogeneous networks with only the strongest few nonbonded pairs closely reproduce the strong APLs from the weighted networks. The rate of change in the APL in the reduced residue network as compared to its randomly connected counterpart remains constant until a lower bound. Upon further link removal, this property shows an abrupt increase toward a random coil behavior. Under different perturbation scenarios, diverse optimal paths emerge for robust residue communication.

INTRODUCTION

Interactions, delay, and feedback are the three key characteristics of complex fluids. Using these features, entities at different time and length scales communicate with great accuracy, efficiency, and speed (1). Self-assembling molecular systems are complex fluids with robust and adaptable architectures that incorporate nanoscopic and mesoscopic length scales decisive on their emergent properties over different timescales; proteins, whose internal motions are decisive on their folding, stability, and function, are exquisite examples of these (2–4). Proteins regularly experience perturbations in their environment—e.g., in the cell where other small and large molecules are densely and heterogeneously distributed—or in the test tube with only water around, displaying ceaseless fluctuations around their folded structure. Since proteins function efficiently, accurately, and rapidly in the crowded environment of the cell, they are expected to be effective information transmitters by design. Whether the protein is functional or not depends on the size and location of these fluctuations, making use of the concerted action of residues positioned at different regions of the protein (5–8). It is, therefore, of utmost interest to investigate how proteins respond to changes in the environment under physiological or extreme conditions.

The response of any structure to perturbations depends on its general architecture. For proteins, local, regular packing geometries (9) cannot provide short distances between highly separated residues for fast information transmission. In fact, it has been shown that random packing of hard spheres similar to soft condensed matter is observed in a set of representative proteins (10). Consistent with the concurrent requirement of order and randomness in the protein structure, we (11) and others (12–14) have recently shown that proteins are organized within the small-world network topology. A network is referred to as “small-world” if the average shortest path between any two vertices scales logarithmically with the total number of vertices, provided that a high local clustering is observed (15). Such properties are common in many real-world complex networks (16,17), and there are examples from a diverse pool of applications such as the world wide web (18), the internet (19), math coauthorship (20), power grid (15), and residue networks (11).

In recent years, we treated proteins as networks of interacting amino acid pairs to determine their network structure and to identify the adaptive mechanisms in response to perturbations (11,21,22). In fact, similar network treatments of proteins predict collective domain motions, hot spots, and conserved sites (5,23–26). For these networks we used the term “residue networks” (11) to distinguish them from “protein networks”, which are used to describe systems of interacting proteins (27). We carried out a statistical analysis to show that proteins may be treated within the small-world network topology. We analyzed the local and global properties of these networks with their spatial location in the three-dimensional structure of the protein. We also showed that the shortest path lengths in the residue networks and residue fluctuations are highly correlated. In the past few years, the network treatment of residues in proteins has been adopted to study their various features such as conserved long-range interactions (28), functional residues (29,30), protein-protein association (31), and detection of structural elements (32).

In all these treatments, which have been successful in describing many important properties of proteins and provide insight as to how they function, the identities of individual amino acids are omitted in the calculations. In other words, specificity is taken into account in an indirect manner by assuming that the locations of the different amino acid types along the contour of the polymeric chain have been operational in determining the particular average three-dimensional structure. In this viewpoint, the interactions between different pairs, triplets, etc. of amino acids are assumed to be smeared out, and the observed behavior once the protein is folded is driven by the overall structure. In fact, it has been noted that the residue nonspecific interactions (i.e., those depending on the relative placement of residue pairs, irrespective of their identity) contribute more to the overall stability of proteins by a factor of about five, compared to distinct residue-residue interactions (33). The question remains, however, as to the extent to which such a coarsened description of the folded protein may be used to determine other crucial properties, especially those pertaining to dynamics.

In this study, we further elaborate on the paths between residue pairs, which we term “information pathways”, to understand how they relate to dynamic phenomena in proteins. In particular, it is of interest to understand allosteric interactions mediated through the changes in the dynamic fluctuations around the average structure, both in the presence and absence of conformational changes, the latter having very recently been shown to exist in proteins through a series of NMR experiments (34). To this end, we attribute weights to the links between residue pairs using knowledge-based potentials (35,36) and discuss the relationship between dynamic phenomena occurring in proteins and the optimal path lengths obtained from these weighted networks. We show that it is possible to extract minimal subgraphs from the fully connected networks of residues, where a few designed interactions overlaying the backbone are sufficient to display communication path lengths similar to that of the full residue network. We also demonstrate an application of these ideas using a nonredundant data set of interacting proteins and extract residue pairs on the interface of the receptor/ligand that frequently appear along information pathways.

METHODS

Spatial residue networks

For the single protein calculations, we utilize 595 single-chain proteins with sequence homology <25% (37) and sizes spanning 54–1021 residues. This protein set is identical to that used in our previous study of residue networks (11). Forty-five of the proteins in the set have fewer than 100 residues, the number of proteins in the ranges (101–200), (201–300), (301–400), and more than 400 residues are 234, 122, 108, and 86, respectively. A list of all the proteins used, their sizes, and the distribution of the sizes in counting bins of size 20 are provided as Supplementary Material. For the receptor-ligand complexes, on the other hand, we use the nonredundant benchmark set of Weng and collaborators developed for testing docking algorithms that contains overall 59 pairs of proteins with 22 enzyme-inhibitor complexes, 19 antibody-antigen complexes, 11 other complexes, and 7 difficult test cases (38). We form spatial residue networks from each of these proteins using their Cartesian coordinates reported in the Protein Data Bank (PDB) (39). In these networks, each residue is represented as a single point centered on the C_β atoms; the C_α atoms are used for glycine residues. Given the C_β coordinates of a protein with N residues, a contact map can be formed for a selected cutoff radius, r_c, an upper limit for the separation between two residues in contact. This contact map also describes a network that is generated such that if two residues are in contact, then there is a connection (edge) between these two residues (nodes) (11). Thus, the elements of the so-called adjacency matrix, A, are given by

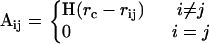(1)

Here, r_ij is the distance between the ith and jth nodes and H(x) is the Heaviside step function given by H(x) = 1 for x > 0 and H(x) = 0 for x ≤ 0. We adopt the value for the cutoff distance r_c = 6.7 Å, which includes all neighbors within the first coordination shell around a central residue. For the set of 595 proteins here, the C_β-C_β radial distribution function was calculated and was displayed as an inset to Fig. 6 of Atilgan et al. (11), where the first, second, third, and fourth coordination shells were shown to be located at 6.7, 8.5, 10.5, and 12.0 Å, respectively. The former two show distinct locations, whereas the latter two are interwoven, in agreement with the liquid-like free-volume distributions in proteins (40).

FIGURE 6.

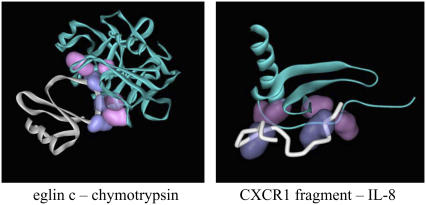
Example systems for bridging residues between interacting proteins; pairs that are on the largest number of pathways between the smaller and the larger polypeptide chains are shown in purple and pink, respectively: (left) Eglin c (white) in complex with α-chymotrypsin (cyan); PDB code: 1acb. The interacting pairs are (inhibitor-enzyme): LEU-45-VAL-213, LEU-45-TRP-215, TRP-215-PHE-41, TYR-49-PHE-39; note that LEU-45 on eglin c interacts with two residues and is on 54% of the strong paths. TRP-215-PHE-41 occurring in only 3% of the pathways is shown in a slightly lighter shade. (Right) CXCR1 fragment (white) in complex with the chemokine il8 (cyan); PDB code: 1ilq. The interacting pairs are (fragment-chemokine): MET-8-PHE-17, TYR-15-ILE-10, TYR-15-CYS-50.

In the case of the weighted residue networks, we assign weights to the edges according to the interresidue interaction “potentials” of Miyazawa and Jernigan (35) and Thomas and Dill (36). These are statistical potentials extracted from a protein database. Both potentials have been extensively tested in threading algorithms (41,42), protein stability, and designability studies (43), folding and binding energetics, as well as amino acid classification (44). The Miyazawa-Jernigan (MJ) potential is based on a set of protein subunit structures exceeding 1600 in number (35). In their treatment of the problem, the system is taken as an equilibrium mixture of unconnected residues and effective solvent atoms. The quasichemical (Bethe) approximation is employed to estimate the contact energies from the numbers of contacts that arise in the sample (45,46). Excluded volume is taken into account by the inclusion of a hard-core repulsion between the residues and a repulsive packing-density-dependent term. The Thomas-Dill (TD) potential, on the other hand, utilizes a much smaller data set of 37 proteins (36). The authors use the folded chain conformation as the reference state, instead of a collection of randomly mixed particles of residues and solvent molecules (in treatments using the Bethe approximation, the problem of reference states has been addressed and corrections have been proposed (47)). Thomas and Dill employ an iterative method that extracts pair potentials that incrementally drive the system toward a lowest energy structure that corresponds to the native structure. The main discrepancies in the statistical potentials that result from the approximate treatment or neglect of excluded volume, chain connectivity, and interdependence of pairing frequencies are therefore intrinsically taken care of.

In this study, we have repeated all the calculations using both the MJ and the TD knowledge-based potentials. Despite differences in details, the main results and conclusions reached do not change with the choice of potential. In what follows, we therefore report only results from the TD potentials. We assign e_ij, the value of the connection between the ith and jth residue, according to the interresidue interaction potential between the ith and jth residue types. Thus, the links connecting the residue pairs with the least favorable interaction energy have the lowest weight, i.e., the highest value.

Network descriptors

The networks are classified by local and global parameters, all of which can be derived from the adjacency matrix (Eq. 1). In the absence of edge weights, the most general descriptors of the network structure are average connectivity of a node and the average shortest path length through the network. The connectivity k_i of residue i is the number of neighbors of that residue, 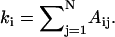The average connectivity of the network is thus K = 〈k_i〉, where the brackets denote the average over all nodes. The connectivity distribution of the residue networks follows the Gaussian distribution (11).

The shortest path length, 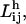of a homogeneous network, where the links have no weights, is the average over the minimum number of connections that must be traversed to connect residue pair i and j. In computing the shortest path between a pair of nodes, we make use of the fact that the number of different paths connecting a pair of nodes i and j in n steps is given by (Aⁿ)_ij. Thus, the shortest path between nodes i and j is given by the minimum power, m, of A for which (A^m)_ij is nonzero.

In the presence of weights, it is possible to redefine the path lengths to take into account the skewing effects of the weights. Weights may be factored into the path lengths using different optimality criteria. We define two criteria for paths between two residues (48–50): weak disorder and strong disorder. In the former, the optimal path connecting residues i and j is the length of the path, 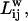that minimizes the sum of the weights along the path. We employ the Dijkstra algorithm to compute the optimal paths in the weak disorder case. In the latter (strong disorder) case, 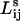is the length of the shortest path that minimizes the maximum weight along the path. To obtain 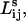we sort the links in descending order and sequentially remove the links beginning with the highest weight (lowest energy). We continue to remove the links until we find the bottleneck link that will cause the connectivity between vertices i and j to be lost. We then compute the length of this remaining path in terms of the number of intervening links. Note that once the optimal path connecting residues i and j is determined, the path length is simply the sum of the connections along the path; i.e., the step lengths themselves are not weighted.

The characteristic path length of the network is the average,

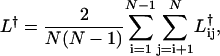(2)

where the dagger symbol, †, represents the homogeneous, weak, or strong paths, L^h, L^w, and L^s, respectively. Note that L^† is a measure of the global properties, reflecting the overall efficiency of the network, under the imposed constraints; i.e., the lower L^† is, the faster information is communicated through the network.

RESULTS

Random coils as a basis for comparison

Proteins may be modeled as networks where a special set of interactions are imposed on chain connectivity, and the extent to which such interactions are specially designed is of interest here. In this study, we generate a variety of networks based on selected proteins. A firm basis for comparing the various networks that may be formed from a given chain with a known contact number is a chain of the same length and the same number of connections for each of its nodes but a randomized set of links between the nodes. To generate such networks, we rewire every residue (node) randomly to another residue chosen from a uniform distribution such that each residue has the same number of neighbors (contact number, k_i) while the contact order changes; chain connectivity is preserved by keeping the (i, i + 1) contacts intact. For this purpose, we manipulate the adjacency matrix (Eq. 1) so that the block diagonal of three elements remains unchanged, whereas the rest of the off-diagonal terms are randomly reassigned while maintaining the symmetry of the matrix. Such a network corresponds to the random coil conformation of a polymer chain at an arbitrary point in time. In our previous study, it was established that the proteins have a Poisson distribution of contacts (11). It is also known from network theory that a completely random, Poisson distributed network has the shortest path length (51),

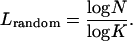(3)

As shown in Fig. 1 (bottom curve) it is verified that the randomized chains behave exactly as expected from a completely random collection of nodes. Average path lengths on the residue networks, L^h, on the other hand, are significantly higher than the randomized networks while still preserving the approximately logarithmic dependence on number of residues, as shown with the filled circles in Fig. 1. The loss of high optimality (i.e., a twofold increase in the shortest path lengths compared to a random network) must be compensated for by the emergence of functionality in the self-organized structure. This exchange is achieved along the scaffold of the nonrandom networks formed by the residues of the proteins.

FIGURE 1.

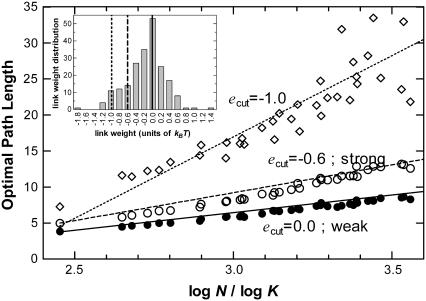
Optimal path lengths, L^h (•), L^w (○), L^s (Δ), of the protein networks in comparison to those of the theoretical value of Poisson distributed random networks of the same size and number of neighbors (L_random, Eq. 3). Results are presented for the nonredundant set of 595 proteins whereby values for proteins of size (m ± 1) × 10; m = 3,5, … are averaged. Protein path lengths computed with the weak disorder limit are almost indistinguishable from those of shortest paths on homogeneous networks; both may be best-fitted by a line of slope 5.2. Optimization with the strong criterion results in networks with significantly longer path lengths (best-fitting line through the data has slope of 9.0). For comparison, random coils have also been generated by random rewiring of the residue networks while preserving connectivity (see text). These networks provide the same result as a totally randomized network (no chain connectivity) of the same size (slope is 1.0). At the other extreme, randomized weights have been imposed on the original residue networks (dotted line). L^s for these are longer by a factor of ∼1.3, indicating that the weights in a protein are specifically distributed.

Optimal paths in the presence of weights

In the absence of weight information of the links (i.e., for a homogeneous network), L^h is the only parameter we can use as a measure of the distance between nodes in the network with N vertices. In the presence of weights, the heterogeneity of the medium is taken into account; hence different types of optimality criteria can be defined. In the case of weak disorder, the sum of the potentials along the optimal path is minimized to obtain L^w. This can be interpreted as the path that causes the minimum possible total disturbance to the residues along the path. The links with lower potentials are more likely to tolerate the disturbances. In Fig. 1 we display a comparison of shortest paths of homogeneous and weak disordered networks, L^h (shown by a solid circle), and L^w (shown by an open circle), respectively, with that of the random coil. The correlation between the two data sets is excellent, showing that the weighted network in the weak disorder limit behaves similar to the homogeneous network. The optimal path in the strong disorder, on the other hand, is the path that minimizes the maximum of the potentials along the path, which can be interpreted as the shortest path that causes minimal maximum disturbance along the path. As exhibited in Fig. 1 for the strong disorder case (see the data shown by a triangle), L^s is significantly larger than L^w by an average factor of 1.3.

Are weights imposed on the links significant for the protein?

To answer this question, we randomly reassign the potentials attributed to pairs of residues. This is achieved by redistributing the 210 different types of pair potentials in the TD potential matrix; e.g., the original Ala-Thr value may now be assigned to the Val-Glu pairs. As such, the underlying network structure remains unchanged, whereas the optimal paths that are preferred will be affected. The results based on these networks are obtained from five realizations of this randomization.

Two major observations are made for such networks: In the weak disorder limit, the optimal path lengths increase (data not shown), signifying that the residue pairs are specially distributed in the protein network to have similar allotments of weights around a given node, although the values themselves have a large span [−1.8 … 1.5]. Moreover, the strong paths in the weight-randomized networks are longer (shown by the dashed line in Fig. 1), further corroborating this finding with the more stringent constraint that key links minimizing the maximum weight along given paths exist in the folded protein.

Identifying redundancies in the protein communication pathways by extracting subnetworks

We deduce subnetworks from the original residue networks of each of the 595 proteins utilized in this work by systematically removing links that have values higher than a given cutoff value, e_cut. Chain connectivity is preserved regardless of the residue types flanking a given bond. We rely on the fact that a protein under external disturbance will have a higher tendency to lose communication through high-energy contacts, whereas the low energy ones will be more cohesive. Thus, although the protein loses the ability to use some paths, it is intrinsically assumed that additional and/or alternate paths do not arise from such disturbances. The shortest path lengths of each of the remaining networks are subsequently computed. Several important cases are presented in Fig. 2 as a function of the random coil of the same size, N, and the same original number of neighbors, K (Eq. 3). The distribution of the links is shown in the inset to this figure, and the chosen cutoff values are marked on the distribution.

FIGURE 2.

Optimal path lengths of the protein networks constructed with various schemes as a function of the randomized counterparts of the original networks (Eq. 4). Subnetworks from the original residue networks are deduced using the edge values, whose distribution for the 210 possible residue pair interactions are shown in the inset. Edges with values higher than a given cutoff, e_cut, are removed and the new shortest path lengths of these subnetworks are computed; connectivity is preserved. The redundancy in the proteins is such that, when approximately half of the long-range contacts are removed (e_cut = −0.0 k_BT, shown by the symbol •), the system still has the same path length (L^w, solid line). Upon further removal of contacts, the paths get longer and they overlap with L^s (dashed line) at e_cut = −0.6 k_BT, shown by the symbol ○ (only ∼20% of the long-range contacts remaining). Further removal of contacts results in a sudden increase in the shortest path lengths, exemplified by the case of e_cut = −1.0 k_BT shown by ◊ symbol (best-fitting line is shown dotted; slope = 22.6).

The redundancy in the proteins is such that when approximately half of the nonbonded contacts are disregarded, e_cut = 0, the system still has the same shortest path length as the full protein that preserves all of its contacts. Upon further removal of links, the paths get longer, and they overlap with L^s at e_cut = −0.6 k_BT. At this point, only ∼20% of the long-range contacts remain in the subnetworks. Further removal of contacts results in a sudden increase in the shortest path lengths, exemplified by the case of e_cut = −1.0 k_BT. In Fig. 2, this data set is shown, along with the best-fitting line (slope = 22.6, in comparison to the random networks where the slope is 1). Note also that the scatter in the data is extreme, signifying that the logarithmic dependence of path lengths on number of residues is lost.

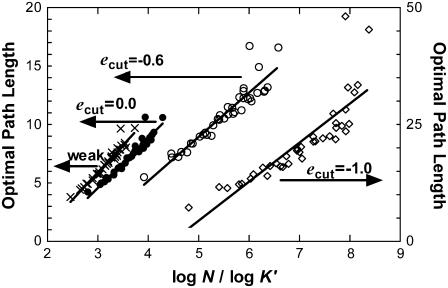
Another way to observe these data is by plotting the shortest path lengths of the subnetworks as a function of the random coil of the same size, N, and the modified (reduced) number of neighbors, K′ (Fig. 3). Although the path length increases as networks with fewer contacts are formed, as expected, the slope of the best-fitting line remains constant until e_cut = −0.6 k_BT, i.e., coincides with the original, fully connected network that utilizes the strong paths as was shown in Fig. 2. Further removal of links results in a dramatic increase in the shortest paths, as exemplified by the e_cut = −1.0 k_BT case (shown by the ◊ symbol; values on the right y axis). Again, it is observed that the scatter in the data increases as the subnetworks approach a linear chain (e_cut = −1.8 k_BT, i.e., only connectivity remains).

FIGURE 3.

Optimal path lengths of the protein networks constructed with various schemes as a function of the randomized counterparts of the newly constructed networks, L′_random = log N/log K′. Subnetworks are formed as described in the caption to Fig. 2. Although the path length increases as networks with fewer contacts are formed, the slope of the best-fitting line remains constant until e_cut = −0.6 k_BT, i.e., coincides with the original, fully connected network that utilizes the strong paths. Further removal of links results in a dramatic increase in the shortest paths, as exemplified by the e_cut = −1.0 k_BT case (shown by ◊; values on the right y axis). Also notice that the scatter in the data increases as the subnetworks approach a linear chain (e_cut = −1.8 k_BT, i.e., only connectivity remains).

DISCUSSION

A folded protein needs to perform its function under the constraints that the overall shape is suitable for the task it undertakes while it is not energetically penalized. As a molecular machine, it needs to optimize the time it takes to communicate the incoming information, which, to a first approximation, may be assumed to be linearly dependent on the shortest path length in its residue network. Excluded volume imposes another limit on the size of the molecule. As incoming information, we refer to perturbations that are imparted on one or several of the residues. Changes in the environmental conditions that are reflected on thermodynamic parameters, such as the temperature, will affect the whole system. The latter are not of concern in this study, since these may potentially change the overall network structure.

In the previous section we displayed results that introduce several different perspectives to evaluate how folded proteins are organized to manage their redundancies under suboptimal conditions. Our basis for comparison is the random coil, whereby a Poisson distributed arrangement of residues will always lead to the most optimal path length, given by the analytical relationship of Eq. 3. The random networks constructed for Fig. 1 have the same average number of neighbors as their folded network counterparts (K = 6.9, as shown in Atilgan et al. (11)). They may be thought of as compact chains that constantly change their partners at different points in time. They, therefore, represent an average over many significantly different configurations, in direct opposition to the case of a folded protein, where residues always keep the same neighbors while they fluctuate in space. For a given amount of excluded volume, decided upon by chain connectivity and the number of long-range contacts, the random coils give a limiting value for how fast information may be spread through the system.

On the other hand, information spreading will take on different forms in a protein depending on the type of local perturbation that is received. Two limiting situations may be distinguished: i), Proteins experience constant random fluctuations from the environment under the usual conditions in which they function; e.g. random collisions with solvent molecules, formation of local hot spots, etc. We classify these perturbations, extensive in number but small in the size of fluctuation they invoke, as “everyday events”. ii), At other times, there will be large perturbations that will be targeted on specific regions, such as those occurring during binding, or approach of a large cellular body to unspecified regions of the protein. We classify these perturbations as “extreme events”. The modes of response from the protein are expected to be different for the two types of events. In other biological systems, such modified reactions to different types of input (global versus pathway-specific noise) were also observed and quantified, e.g., for the variation in the behavior of genetically identical cells (52,53).

In folded proteins, the network structure, equivalent to a coarse graining obtained from the average conformation of the folded structure, is expected to remain nearly the same under both conditions. However, the way the energy will be transmitted throughout the network will differ according to the type of perturbation. Noting that the network is mostly made up of residues held together by nonbonded interactions, the proximity of pairs of residues will not differ; e.g., in many cases, the structure of the bound and unbound forms of a ligand protein to its receptor is less than the experimental uncertainty, as in the case of chymotrypsin inhibitor II (5). However, the transfer of information (energy) along the residue network will only occur if the fluctuations in neighboring residues are correlated along any chosen pathway (as conformational variability increases, the communication of a signal in a molecule, e.g., conductance, occurs with less strength and over a broader range of values, as was recently demonstrated through unique experiments in a series of diphenyl-containing small molecule systems (54)). For small perturbations caused by random fluctuations, the correlations between neighboring residues are expected not to be affected, and the most probable pathway for information transmission is the lowest energy one — i.e., L^w. For large impacts (extreme events), although the overall network structure will be preserved due to the pressure exerted by the compact structure of the molecule, the correlations between pairs of residues that are weakly connected to each other will be lost. For the purpose of information propagation, those pathways may be assumed to be nonexistent; i.e., those network connections will be lost.

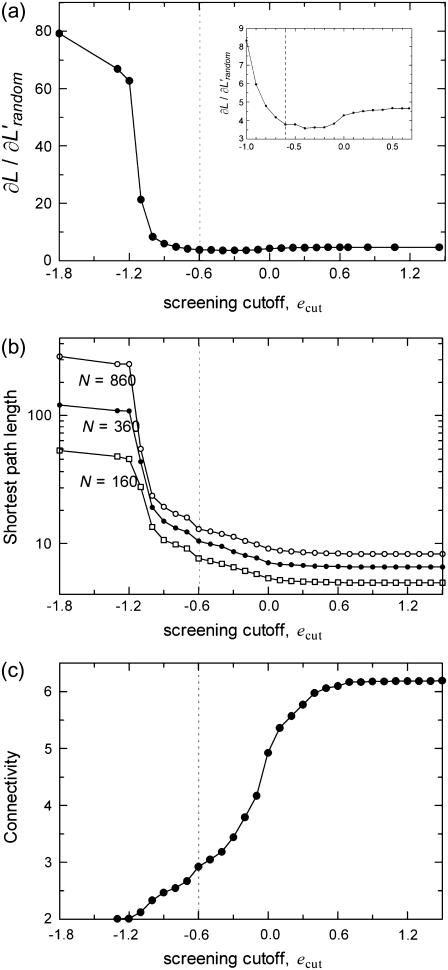
Usually, the impacts imparted on the protein in its usual environment will be intermediate between the two extremes of small perturbations and large impacts. Our analysis in Fig. 3 shows the operational limits of these molecular machines: We may classify those perturbations that delete nearly half the nonbonded contacts from being functional (i.e., e_cut = 0.0 k_BT) as everyday events. The change in the average path length of the protein relative to the change in that of the randomly rewired counterpart (∂L′/∂L′_random, where L′ refers to path length on the subnetworks with the lower average connectivity, K′) remains fixed for that range (Fig. 3). The latter quantity is shown for the whole range of values of e_cut in Fig. 4 a. In the same range of values, the average shortest path length, a size-dependent quantity, is also constant (Fig. 4 b). The change in the average number of neighbors of a node is also relatively small, decreasing from 6.2 to 5 (Fig. 4 c). Noting that two of these neighbors are located along the chain, at e_cut = 0.0 k_BT an average node has lost one of its four nonbonded neighbors.

FIGURE 4.

Change in network parameters of the subnetworks formed as described in the caption to Fig. 2, with cutoff imposed on the link values, e_cut, to include the screening effect: (a) For a wide range of e_cut, the slopes of the curves of Fig. 3, ∂L′/∂L′_random, remain nearly constant. Once ∼85% of the nonbonded contacts are removed, there is a sudden increase in the slopes. A close-up look at this range in the inset shows that there is a dip in the slopes before this departure from protein-like behavior. (b) Change in subnetwork shortest path lengths with e_cut for different protein sizes. The differences between the logarithms of the path lengths for different network sizes remain constant until the transition region of e_cut. (c) Dependence of chain connectivity on e_cut, which is commensurate with the distribution of the link values (inset to Fig. 2).

Further removal of the links signifies even larger perturbations to the protein. Up to ∼e_cut = −0.6 k_BT, where the shortest path lengths on the subnetworks coincide with the strong paths of the original weighted residue networks (marked by the dashed lines in Fig. 4, a–c), the quantity ∂L′/∂L′_random shows a decreasing trend (inset to Fig. 4 a). In the range of e_cut = −0.6–0.0 k_BT, the increase in L is less than a factor of two for all sizes of proteins, whereas its value increases logarithmically beyond that cutoff (e_cut < −0.7 k_BT; see Fig. 4 b). The logarithmic dependence of the path length on chain size is also preserved in this range (see Figs. 2 and 3). Note that at this critical value of the cutoff, only about one nonbonded contact per average node remains (Fig. 4 c).

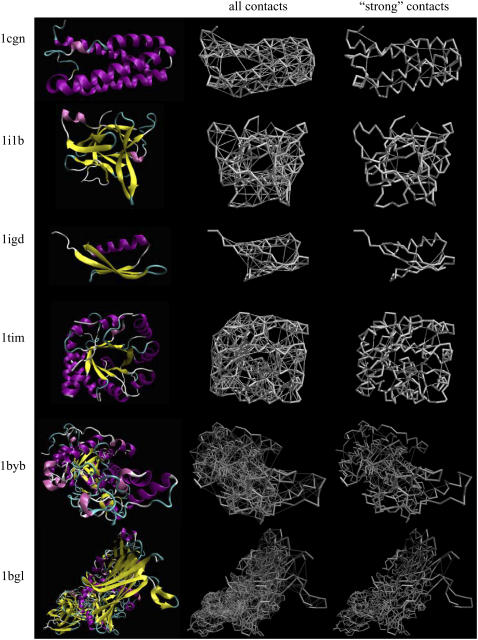
Representative proteins of α, β, and α/β types are shown in Fig. 5; ribbon diagrams of the structures deposited in the PDB are shown in the first column. All nonbonded contacts (thin lines) superimposed on the backbone (thick lines) are shown in the second column. The strongest links that form the underlying structure and that give the polymeric chain its protein-like path lengths are shown in the third column. Any other interactions added to these create redundancies that contribute to the robustness of the structure so that the protein is able to function under the harsh conditions of the cell. In reality, depending on the size and direction of the impact, some of the weaker links that are located far from that site may be preserved; i.e., we do not expect the links to be lost hierarchically. Nevertheless, the protein's reaction to the perturbation, as measured by the average path lengths of the effectively remaining contacts, is relatively insensitive to size and direction, as long as the most cohesive of the interactions remains intact.

FIGURE 5.

Example networks from proteins with common folds. The respective columns represent the ribbon structure, total networks, and “strong” networks. In the network representations, the backbone traces are shown by the thicker lines, and the nonbonded contacts are shown by the thin gray lines. 14%, 21%, 13%, 18%, 23%, and 17% of the nonbonded contacts remain in these proteins, PDB codes 1cgn, 1i1b, 1igd, 1tim, 1byb, and 1bgl, respectively.

Illustrative examples supplementıng biophysical knowledge

Comparison with evolutionarily conserved networks of residues that regulate allostery

To understand allosteric communication in proteins and how signals that originate in one part of the protein propagate to remote regions, a sequence-based statistical approach was proposed (55,56) and further developed (57). Based on the assumption that residues that are functionally and/or structurally coupled to each other should coevolve, these authors predicted a set of residues that communicate signals through the protein core in a chain-like manner for several protein families. They showed that the predictions were confirmed by mutagenesis studies.

We have studied one of the poxvirus and zinc finger domain representatives (PDB code 1a68) with our structural methodology. We find that the residues that were identified in the sterically connected path as (77→118→149→148) in the statistical study (55) lie on one of the two alternative shortest paths connecting residues 77 and 148 (these are PHE-77→LEU-122→ILE-121→THR-149→PHE-148 and PHE-77→PHE-118→ILE-121→THR-149→PHE-148). The former is slightly more favorable in the weak path due to the lower contact potential between LEU-ILE compared to that of PHE-ILE; the two paths are equivalent in terms of strong path length since the bottleneck contact is brought about by the THR-PHE pair in the last step. Similarly, for the PDZ domain representative, we find that all the optimal paths connecting HIS-76 and ALA-51 go through ILE-31 and PHE-29, where the latter was found to be strongly coupled to perturbations at position 76 (our calculations are based on the structure with PDB code 1bfe, but we use the numbering scheme in Lockless and Ranganathan (55)).

In the case of the GPCR family, we study the paths between LYS-296, which was perturbed in the statistical analyses (56,57), and TYR-136, which participates in one of the regions that undergoes a structural change upon light activation in rhodopsin. An allosteric communication exists between them since the two residues are located ∼30 Å apart from each other. The weak path connecting the two is five-steps long (LYS-296→SER-298→ALA-124→LEU-128→ALA-132→TYR-136) and mainly utilizes a direct passage from helix 7 to helix 3 that leads to residue 136 on its edge, as a highway. The strong path, on the other hand, is nine-steps long (LYS-296→PHE-293→PHE-294→THR-297→TYR-301→ILE-305→TYR-136→LEU-128→ALA-132→TYR-136) and initially utilizes helix 7, containing the epicenter as a highway, including residue 294, which was identified as functionally important by Suel et al. (56). It then passes on to helix 3 through the single residue MET-257 in helix 6. This residue is known to participate in constitutive activity of the molecule, possibly through interactions with the conserved motif involving residues 302–306 on helix 7 (58). As this latter example clearly shows, strong pathways are more descriptive of locating the important residues that participate in allosteric communication.

Optimal paths identify key interactions that moderate binding affinity

We postulate that residues, frequently found along the paths connecting a receptor-ligand pair, control the communication between the two proteins. Since binding is an event that requires exchange of large amounts of energy, in this treatment, we use the optimal paths with strong disorder, which emphasize the largest barriers to be crossed along the way. Using the benchmark set of 59 receptor-ligand complexes (38) described in the Methods, we seek the pairs of residues that are most significant in determining key interactions. In the data set, there are ∼2 × 10⁶ such pathways, giving a statistically significant number for our analysis.

We first record the pairs that form bridges between receptor and ligand for every path that originates in the receptor and ends in the ligand; i.e., residue i is located on the receptor and residue j is located on the ligand and they are connected within the network formed by the protein-protein complex. We then take into account the fact that the propensity of a selected amino acid type being located along the interaction surface significantly varies, as reported by Ma et al. (59); e.g., TRP, ARG, and GLN are the residues that are found most frequently on the interface. Therefore, we normalize the probability of finding a residue pair along the strong pathways, p_i↔j. Thus, the conditional probability, p(i↔j|i, j), can be computed by relating the probability that the pair actually appears along the selected paths to the probability of each of the residues in the pair being located on the interface, q_i and q_j:

(4)

where p_i↔j is assumed to be proportional to the frequencies that these pairs are observed in the interface along the strong paths determined in this study. q_i and q_j are taken to be proportional to the propensity of the residue to be found in the interface of either the ligand or the receptor, as reported in the literature (59). The resulting conditional probabilities of the most significant pairs are listed in Table 1, along with the value of the TD contact potential.

TABLE 1.

Residue pairs that appear in the interface with significantly enhanced probabilities

Residue pair (receptor → ligand)	Propensity-normalized probability, p(i↔j|i, j)	Contact potential (units of kBT)
ILE-VAL	0.13	−0.98
ALA-ILE	0.041	−0.64
ILE-ILE	0.039	−0.71
ILE-LEU	0.036	−1.04
GLU-LYS	0.032	−0.09
LEU-ILE	0.030	−1.04
VAL-VAL	0.027	−1.15

Note that the pairs that are used in the paths consist mostly of the hydrophobic-hydrophobic interaction types, though not necessarily appearing in the order of cohesive energy. In fact, if all amino acids are grouped in the broadest sense of hydrophobic, polar, charged, and GLY, over 42% of all pairs that appear along the interface and that are on the strong paths make hydrophobic-hydrophobic contacts. Furthermore, the interactions need not be symmetric; in fact, the most significant pairs have ILE on the receptor and VAL on the ligand (normalized probability is 0.13). The reverse arrangement does not appear to be significant. A similar observation is also made for the ALA-ILE pair. In contrast, ILE and LEU pairs appear to be involved in specific interactions, though not with a significant preference for the ligand or the receptor.

Although tens of residues appear on the protein-protein interfaces, in general, only a small set of mainly hydrophobic contacts dominate the affinity, as verified by mutagenesis studies (see Atwell et al. (60), and references sited therein). One example ligand-receptor system of α-chymotrypsin in complex with eglin c is shown in Fig. 6. Residue pairs that are on the largest number of pathways between the smaller and the larger polypeptide chains are shown in purple and pink (out of the total of 14,868), respectively. Note that in the large interaction surface of the protein pairs, it is possible to identify four key interactions utilizing three residues on the ligand and four on the substrate. Of these, those involving LEU-45 on eglin c is on two of the most frequently utilized paths connecting the two proteins, participating in 54% of the strong paths connecting the two proteins. This residue is the primary specificity residue of eglin c, whose nature greatly affects the strength and specificity of the association between the inhibitor and the enzyme, as shown by the equilibrium constants determined for the interaction between chymotrypsin and the inhibitors expressed with variants of LEU-45 (61). TYR-49, on the other hand, participates in 43% of the strong paths. In fact, in another innovative study, libraries of randomly constructed variants of eglin c at positions 33, 35, 37, 39, 40, 47, 49, 50, 65, and 68 were constructed and screened for activity (62). Therein, position 49 solely emerged as having a significant effect on the binding affinity of eglin c to various substrates.

Another example presented in Fig. 6 is between the chemokine, interleukin 8 (IL-8), and a fragment from its receptor CXCR1 whose structure was determined by NMR (63) and on which we previously conducted an analysis of the structure/function relationships (64). The generally accepted scheme for the binding mode between CXC chemokines that contain an ELR motif and their receptors is that the N-loop residues of the chemokine interact with the N-terminal domain residues of the receptor (site I), and the N-terminal residues of the chemokine interact with the receptor exoloops and transmembrane residues (site II) (65). The structure we study here corresponds to site I, and therein, interactions between the fragment-chemokine residues MET-8-PHE-17, TYR-15-ILE-10, TYR-15-CYS-50 emerge as key bridging pairs on the strong pathways. MET-8 and TYR-15 residues are utilized nearly equally between the two proteins. On the other hand, since TYR-15 is toward the C-terminus of the peptide that leads to the seven transmembrane helices, it is expected that if this study were to be conducted on the full CXCR1, there would be a predominant shift of the distribution toward the contacts made by this residue. In fact, TYR-15 is known from studies on alanine analogs of the fragment to be important for affinity, whereas truncation of residues up to and including MET-8 does not affect binding affinity (63). Thus, this analysis, which emphasizes the strong paths in the case of large perturbations (i.e., binding) experienced by a protein, is successful in identifying the key interactions on the binding surface.

CONCLUSION

In this study, we have taken a network perspective of analyzing proteins and have shown that residue specificity plays an important role in protein functioning. A statistical analysis on nearly 600 nonhomolog proteins has led us to define key quantities for discriminating the underlying structure that make the protein robust in the environment where it is functional. In particular, the quantity ∂L′/∂L′_random (Figs. 3 and 4 a) has been uniquely defined for finding a critical threshold value to determine the key interactions in the protein, if it is to survive extreme events and to continue carrying out its function. Our results also support the finding that optimized protein sequences can tolerate relatively large random errors in pair potentials obtained using a variety of methodologies (47,66). In fact, none of our conclusions change when the work here is repeated with the pair potentials of Miyazawa and Jernigan (35), rather than that of Thomas and Dill (36), although there are differences in the details of, e.g., Fig. 4.

In this work, we propose that in events involving small perturbations, the total energy to traverse that path will be important and information will flow through the optimal paths with weak disorder, similar to that in the homogeneous network. On the other hand, when large perturbations are involved, such events require surpassing the largest energy barriers along the paths. In this approach, the same pair potentials are used as thermodynamic measures in the former case and as kinetic measures in the latter. If a pair of residues has high contact energy, it may be assumed that the energy that must be used to separate them will be commensurate with its value to a first approximation. Due to other effects such as the size and the shape of the residues, slight modifications may be included. We feel that the network approach used here—involving many approximations as well as a large amount of coarse graining overlaying the atomic structure—has firm grounds. The strong paths, therefore, set a limit on the protein whereby the robust structure resists large amounts of external perturbations and preserves its protein-like communication pathways. Furthermore, using this approach, we have been able to define key contacts that form bridges between interacting proteins (Table 1). Note that nearly half the surface area of the total protein, and therefore an overwhelming number of residue pairs, is involved in protein-protein interactions. As a possible practical application of this approach, the few key contact pairs identified may be used as primary links in recognizing the interaction geometry, overlaid by the energy lowering contributions from the rest of the pairs in solving protein-protein interaction problems.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.