Evidence for Outer Hair Cell Driven Oscillatory Fluid Flow in the Tunnel of Corti

Abstract

Outer hair cell (OHC) somatic motility plays a key role in mammalian cochlear frequency selectivity and hearing sensitivity, but the mechanism of cochlear amplification is not well understood and remains a matter of controversy. We have visualized and quantified the effects of electrically evoked OHC somatic motility within the gerbil organ of Corti using an excised cochlear preparation. We found that OHC motility induces oscillatory motion of the medial olivocochlear fibers where they cross the tunnel of Corti (ToC) in their course to innervate the OHCs. We show that this motion is present at physiologically relevant frequencies and remains at locations distal to the OHC excitation point. We interpret this fiber motion to be the result of oscillatory fluid flow in the ToC. We show, using a simple one-dimensional hydromechanical model of the ToC, that a fluid wave within the tunnel can travel without significant attenuation for distances larger than the wavelength of the cochlear traveling wave at its peak. This ToC fluid wave could interact with the cochlear traveling wave to amplify the motion of the basilar membrane. The ToC wave could also provide longitudinal coupling between adjacent sections of the basilar membrane, and such coupling may be critical for cochlear amplification.

INTRODUCTION

External sounds are transformed into traveling waves on the cochlear basilar membrane (BM), and these waves peak at different places along the cochlea depending on the frequency of stimulation. Experimental evidence for the existence of such traveling waves was first provided by von Békésy's work on cadaver cochleae (1). More recent measurements on live animals confirm the existence of traveling waves and also reveal that in the peak region the wave is amplified and more localized (or sharply tuned) than that observed by von Békésy (for a review, see Patuzzi (2) and Robles and Ruggero (3)). Experimental evidence suggests that outer hair cells (OHCs) are essential for this enhanced response to occur.

OHCs change length in response to changes in their membrane potential (4,5) and appear to actively amplify BM vibration, a process that is often referred to as cochlear amplification (6). OHC electromotility is driven by prestin, a voltage-sensitive motor protein located in the cell's membrane (7). Prestin mutant mice have a 40–60 dB hearing loss and lack OHC motility in vitro (8), further supporting OHCs as key players in cochlear amplification. Another mechanism that might, in part or in whole, contribute to mammalian cochlear amplification is stereocilia motility (as opposed to somatic motility) (9). To date, the mechanism of cochlear amplification is poorly understood and remains an area of active research (for a review, see Patuzzi (2) and Robles and Ruggero (3)).

To understand the role of OHC somatic electromotility in cochlear amplification, we developed a technique to measure the micromechanical responses within the organ of Corti (OC) due to OHC forces. We used an excised cochlea preparation because it allowed us to gain good visual access to the cochlear turn of interest while keeping the anatomical architecture of the OC in that turn intact. A detailed presentation of this preparation is given in Karavitaki (10) and in Karavitaki and Mountain (11). The tissue was stimulated electrically using sinusoidal current, and the resulting motion was captured at specific phases within the stimulus period using stroboscopic video microscopy. Animations of these motions were created by playing the frozen images from each phase in succession. We then calculated the amplitude and phase of motion for each structure using a two-dimensional cross correlation technique.

During electrical stimulation, in addition to the expected OHC movements (10,12), we were surprised to find a prominent displacement of the medial olivocochlear (MOC) fibers where they cross the tunnel of Corti (ToC) (representative animations of the OHCs and the MOC fibers motion are shown in Movies 1 and 2, respectively, in the Supplementary Material). We hypothesize that when the OHCs contract, the cross sectional area of the OC decreases and fluid is pushed into the ToC where it displaces the MOC fibers. To quantify the influence of the OHC motility on oscillatory fluid flow in the ToC, we have measured the displacements of the MOC fibers and the OHCs. Data were collected from 15 middle-turn experiments and 1 apical-turn experiment where we were able to visualize MOC fibers. The characteristic frequency (CF) of the measurement locations was estimated using the frequency place map of the gerbil cochlea (13) and ranged between 0.4–4 kHz.

MATERIALS AND METHODS

The surgical preparation of gerbil cochleae, the video microscopy system, electrical stimulation, data analysis, and control experiments have been described in detail (10,11). Here, we briefly mention the key aspects of our methodology and highlight additions or differences.

Surgical preparation of gerbil cochleae

Young female Mongolian gerbils were decapitated after being anesthetized (no paw-withdrawal reflex and no corneal reflex) with an intraperitoneal injection of sodium pentobarbital (60 mg/Kg, Steris Laboratories, Phoenix, AZ) or using a mixture of ketamine (0.16 mg/g, Fort Dodge Animal Health, Fort Dodge, IA) and xylazine (0.008 mg/g, Bayer Corporation, Shawnee Mission, KS). The procedures followed an institutionally approved protocol and guidelines provided by the Laboratory Animal Care Facility at Boston University. All chemicals were purchased from Sigma Chemicals (St. Louis, MO) unless noted otherwise. After decapitation both temporal bones were excised and the bullae opened. The temporal bones were immersed in oxygenated culture medium (Leibovitz L-15) supplemented with 5 mM D-glucose (pH 7.3 adjusted using NaHCO₃, J. T. Baker Chemical Company, Phillipsburg, NJ). In later experiments, the medium was a Cl⁻-modified perilymph-like solution composed of 140 mM D-gluconic acid, 6.6 mM NaCl, 100 μM CaCl₂, 3 mM KCl, 5 mM NaH₂PO₄, 100 μM MgCl₂, 5 mM D-glucose, 5 mM HEPES (298 mOsm, pH 7.3 adjusted using 1M NaOH). Both solutions were at room temperature (∼18°C) during the experiment. The later solution was formulated to improve the condition of the preparation and the viability of the cells. Using this solution we were able to collect data for a maximum of 9 h after decapitation.

The next step in the surgical procedure was to transfer the immersed bone under a dissecting microscope (AO570, American Optical, Buffalo, NY) where the tympanic membrane, the malleus, incus, and parts of the semicircular canals were removed. Enough temporal bone was left intact to provide a stable means of holding the cochlea. The turn of interest was then exposed with care not to damage Reissner's membrane. The bone surrounding the scala vestibuli of the lower turn was subsequently removed to improve the optical path to the structures of interest. Surgical procedures were usually completed within 20 min after decapitation.

Video microscopy system

After dissection, the preparation was mounted in a custom-made chamber and placed on the stage of an upright microscope (BX50WI, Olympus, Melville, NY) sitting on a vibration-isolation table. A 20× 0.5 NA (Olympus) or a 60× 0.9 NA (Olympus) water immersion lens with an additional 2× magnification was used for detailed observation of the OC in the regions of interest. A CCD camera (C2400-77, Hamamatsu, Bridgewater, NJ) was mounted on the phototube of the microscope. Analog contrast enhancement and brightness enhancement was accomplished by using an image processor (Argus-20, Hamamatsu). The output of the image processor was connected to an externally triggered frame grabber (AG-5, Scion Corporation, Frederick, MD) for real time frame capture and averaging.

Electrical stimulation set-up: hardware and software

Alternating current (AC) was delivered with glass pipettes filled with 3M NaCl. The pipettes were sealed with agar (Agarose, Type III: High EEO, Sigma Chemicals) at their tip to prevent NaCl leakage and were connected to an optically isolated constant current source (BSI-1, BAK Electronics, Mount Airy, MD). The input current electrode was placed near the scala vestibuli of the turn of interest, and the return current electrode was placed near the former location of the scala vestibuli in the next more basal turn. During electrical stimulation, current levels were limited to 4 mA or less to prevent tissue damage. Our current stimulus is expected to cause a 0.8–4 mV/mA OHC transmembrane voltage drop, which is comparable to that used to study somatic motility in isolated OHC preparations (for an extensive discussion, see Karavitaki (10) and Karavitaki and Mountain (11). The injected current was monitored by measuring the voltage across a 100-Ω resistor in the current return path. A computer-controlled analog interface (System II, Tucker-Davis Technologies, Alachua, FL) was used to generate the input to the current source and to store the stimulating current.

The stimuli were sine waves with frequencies from 30 Hz to 9 kHz. The frequencies were approximately logarithmically spaced and were randomly presented in two groups to monitor repeatability. The first group covered the entire frequency range of interest, and the second group also covered the entire frequency range and filled in additional frequencies. Movements synchronized to the stimulus frequency were captured using stroboscopic illumination. A custom-made current source was used to deliver current pulses of 200 mA peak to a light emitting diode (AND190AYP, Purdy Electronics Corporation, Sunnyvale, CA). The light emitting diode was mounted on a holder designed to replace the light source of the microscope. The input pulses to the strobe system were generated using the Tucker-Davis Technologies system. The pulses occurred at fixed phases within the period of the stimulus with duration equal to 10% of the stimulus period.

Data were collected for five or eight equally spaced phases and for two conditions: 1), with the stimulating current present; and 2), with the stimulating current turned off, referred to as the “no-stimulus condition”. The no-stimulus condition gave us an estimate of the magnitude of the minimum resolvable motion of our system and also verified that the motions observed were due to the applied current. For most of the experiments, stimulus phases were randomized. For each sample time window, strobe pulses occurred only at one particular phase. Thus, to collect data from eight phases the same frequency was played eight times. For each frequency/phase combination the sample window was repeated to provide enough images for subsequent averaging. Typically we used a 16-frame average. The video frames of interest were subsequently digitized, and animations of the observed motion were created for each frequency by playing the images from each phase in succession.

Image processing and motion estimation

Cross correlation was used to estimate the displacement of different structures. Cross correlation between two images was performed by first extracting a region from one image containing a feature of interest like the edge of a hair cell or a portion of an MOC fiber. The same region was then extracted from a second image taken at a subsequent stimulus phase or from the corresponding no-stimulus condition. Because the motion of interest was generally less than our 432-nm pixel size, the extracted images were interpolated in the frequency domain by zero padding their two-dimensional fast Fourier transform. Using interpolation we were able to increase the resolution to 27 nm per pixel. Once the extracted images were interpolated, the two-dimensional cross correlation was computed in the frequency domain and the peak of the cross correlation function in the spatial domain was used to estimate the magnitude and direction of motion between the original images. This procedure was repeated for all the stimulus phases to derive the time waveform of the motion.

Fourier analysis was then performed on the displacement time series to estimate the peak amplitude and the phase of motion for each frequency. Phase data were referenced to our sine phase stimuli. From this two-dimensional analysis we were able to estimate motion in two directions. The first was the radial direction (referring to the axis running from spiral lamina to spiral ligament), and the second was the longitudinal direction (referring to the axis running along the OC, from base to apex).

The noise level in our data depended on the mechanical stability of the preparation and the contrast of the structures of interest in the images. Depending on the experiment and the structure imaged, the noise level varied between 10 and 100 nm.

RESULTS

Data organization

The cartoon in Fig. 1 A is a partial view of our preparation and is designed to aid in the identification of key structures of the OC and the presentation of our results. Structures that have been omitted in this cartoon but were present in our preparation include the Reissner's membrane, the tectorial membrane, the BM, and some of the supporting cells in the OC. Fig. 1 B is a surface view of the OC at a focal level near the basal end of the OHC (the level and angle of view are shown in Fig. 1 A with a gray plane) taken using our stroboscopic video microscopy system. In this view we have indicated the location of the inner hair cells (IHCs), the pillar cells, and the three rows of OHCs. Fig. 1 D shows a magnified view of the OHCs region. Similarly, Fig. 1 C is a surface view of the OC at a focal level near the MOC fibers (the level and angle of view are shown in Fig. 1 A with a gray plane). In this view we have indicated several MOC fibers, which are further magnified in Fig. 1 E.

FIGURE 1.

Anatomical cross sections of the OC. (A) A cartoon of the OC emphasizing some of the major structures: the three rows of OHCs (OHC1, OHC2, OHC3), the IHCs, the inner pillar cells (IPC), the outer pillar cells (OPC), the arcuate zone (AZ) of the BM, the MOC fibers, and the ToC. The ToC has a triangular cross sectional area and is filled with fluid. The anatomical structures that form the three sides of the tunnel are the IPC, the OPC, and the AZ of the BM. The tunnel communicates with the spaces of Nuel (the fluid space that surrounds the basolateral membrane of the OHCs) via the space between the OPCs. Three axes of optical coordinates are shown: 1) the vertical axis, which is parallel to the optical axis of the microscope objective; 2) the radial axis, extending from the spiral lamina (LAM) to the spiral ligament (LIG); and 3) the longitudinal axis, extending from base to apex. Both the radial and the longitudinal axis are parallel to the surface of the objective. (B and C) Optical cross sections at the levels close to the basal end of the OHCs and the MOC fibers, respectively. Depending on the preparation, the bottom of the image leads toward either the apex or the base of the cochlea. For the experiment illustrated in this figure the bottom of the image leads toward the base. (D and E) The boxed regions of B and C are shown magnified in D and E, respectively. Scale bar for B, 44 μm and for D, 22 μm.

Because the OHCs are situated at an oblique angle with respect to the optical axis, their contraction can be resolved into vertical, longitudinal, and radial components (Fig. 1 A). These components refer to optical coordinates as opposed to anatomical coordinates. Here, we present data for the longitudinal and radial components because these are the only components that can be computed directly from our surface views of the OC (Fig. 1, B–E). Radial and longitudinal displacements were measured for OHCs in all three rows (OHC1, OHC2, and OHC3) and for the MOC fibers. The OHC measurements were taken close to their basal end (Fig. 1 B).

Middle-turn experiments

For all experiments, the OHCs moved in both the radial and the longitudinal direction (10,11) and the MOC fibers moved mostly (∼90% of the total magnitude) in the longitudinal direction. This is illustrated in Fig. 2 where we show the image of OHC and MOC fibers taken at three different time points during one cycle of the stimulus. In Fig. 2 A the OHCs are shown in their relaxed state when no current is applied. In Fig. 2, B and C, the same OHCs are shown in response to a 30-Hz electrical stimulus at phase 90° and 270°, respectively. Fig. 2, D–F, shows the MOC fibers for the same conditions as the OHCs. In this magnified view, we see that during electrical stimulation the shape of the MOC fibers did not show any major changes compared to that in their relaxed state. The longitudinal displacement was much larger than the radial displacement, and therefore only this major component of MOC displacement is presented here. The magnitude responses of all three rows of OHCs had displacements in both the radial and longitudinal directions that were qualitatively similar. For simplicity of presentation we show only the radial component.

FIGURE 2.

Images of OHCs and MOC fibers taken at different times within one stimulus period. (A and D) No stimulus condition. (B and E) Phase 90°. (C and F) Phase 270°. The dotted line in each of the images is added as a reference to emphasize the observation that during the stimulus period the OHCs are displaced in the radial direction (also longitudinal in most of the experiments), and the MOC fibers are displaced in the longitudinal direction. Also note that the MOC fibers are displaced without significant shape changes. In this figure the bottom of the images leads toward the base of the cochlea.

In the majority of our experiments MOC fiber displacements were oscillatory (i.e., only had an AC component; the direct current (DC) component, if present, was in the noise level). In 3 of our 15 experiments the ratio of the DC component to the AC component (DC/AC) was 33%. The DC/AC ratio was largest for the experiment with the largest MOC fiber displacements and smallest for the experiment with the smallest MOC fiber displacements. In two out of these three experiments the OHC DC/AC ratio was comparable to the MOC fiber DC/AC ratio. We hypothesize that for these experiments the DC component observed in the MOC fiber displacements reflects the DC component of the OHC displacement. The latter may reflect an asymmetry in the OHC length change in response to the applied transmembrane potential.

In Fig. 3 we present the results from 2 of our 15 middle-turn preparations. Fig. 3, A and D, shows the average magnitude of displacement for OHC1 and MOC fibers (from experiment 131R and 213R, respectively). For all experiments the magnitude responses of OHC2 and OHC3 were qualitatively similar to OHC1 and are therefore not shown in the figure. The longitudinal displacement of the MOC fibers was similar in magnitude to (Fig. 3 D) or larger than (Fig. 3 A) the radial displacement of the OHCs. The magnitude responses shown in Fig. 3, A and D, have a low-pass shape with a cutoff frequency below the estimated CF of our measurement location. We believe that the low-pass shape of the OHC response is due to the shunting effect of the capacitance in the stria vascularis (14). The low-pass shape of the MOC fibers response mirrors that of the OHC response, suggesting that the two responses are tightly coupled.

FIGURE 3.

Frequency response of OHC1 (solid symbols) and MOC fibers (open symbols) for experiment 131R (A–C) and 213R (D–F). Each data point represents the average of several cells of the corresponding structures. Specifically, the data in panels A and B are the average of eight OHC1 (solid symbols) and eight MOC fibers (open symbols) and the data in panels D and F are the average of eight OHC1 (solid symbols) and two MOC fibers (open symbols). The error bars indicate the standard deviation. For OHC1 the displacement shown is in the radial direction, whereas for the MOC fibers the displacement is in the longitudinal direction. For both experiments, zero phase for the OHCs corresponds to motion toward the spiral ligament and for the MOC fibers corresponds to motion toward the base. The noise floor in these experiments is ∼60 nm peak-to-peak (PP).

At low frequencies, the OHC1 displacement was ∼180° out of phase and the MOC fiber displacement was nearly in phase with the stimulus (Fig. 3, B and E). While keeping in mind the oscillatory nature of the responses, we found it helpful to reference phase to a specific direction of motion relative to the positive phase of the stimulus. Specifically, for a structure of interest, positive phase difference with respect to the stimulus corresponds to motion toward the spiral ligament in the radial direction or toward the base in the longitudinal direction. Therefore, for the data shown in Fig. 3, B and E, at low frequencies during the positive phase of the stimulus period, the OHC1 moved toward the spiral lamina and the MOC fibers moved toward the base of the cochlea. The direction of motion reversed during the negative phase of the stimulus. We will keep this convention for the rest of the work and continue to remind the reader of the oscillatory nature of the response by referring to an “oscillatory direction” of motion.

For three of our experiments MOC fiber displacement was in phase and for eight of our experiments MOC fiber displacement was 180° out of phase at frequencies < 1 kHz (i.e., as shown in Fig. 3, E and F) relative to OHC1 displacement. At higher frequencies their phase difference was more complex. In 4 of our 15 experiments the phase difference rotated ∼70° and this phase difference occurred fairly linearly from ∼30 Hz to 1 kHz (i.e., as shown in Fig. 3, B and C). Above 1 kHz this phase difference was more complex.

The magnitude and phase of the OHC and MOC fiber displacements differed between experiments. The relative magnitude of the OHC and MOC fiber displacements depended on the distance between the electrode location and the imaging site (for details, see Karavitaki (10) and Karavitaki and Mountain (11). The direction of MOC fiber displacement during the positive phase of the stimulus was sometimes toward the apex and other times toward the base of the cochlea. To investigate the relative magnitude and phase of OHC and MOC fiber displacements, we performed measurements at multiple longitudinal locations in the same cochlea while keeping the location of the electrode fixed. Shown in Fig. 4 are the results of these measurements for two out of three experiments where multiple locations were imaged. Here we show results from OHC3 (instead of OHC1) because we were able to image them simultaneously with MOC fibers (in the same focal plane), thus enabling us to directly compare OHC and MOC fiber displacements.

FIGURE 4.

OHC3 total displacement and resulting ToC flow as a function of longitudinal position for experiments 1011R (A and B) and 1026R (C and D). The stimulus frequency is 60 Hz. Each point in the graph represents the average displacement/flow along a 200-μm cochlea length. Different locations were measured in random order, and their time sequence is indicated by the number next to the data point, i.e., data point 1 was collected first, data point 2 was collected second, etc. The arrows indicate the location of the basal cut (B), the electrode (E), and the apical cut (A). The noise level for experiment 1011R is ∼40 nm and for experiment 1026R it is ∼30 nm.

In Fig. 4, A and C, we generally see that as we moved far away from the electrode the magnitude of OHC3 displacements decreased. One exception is data point 5 in Fig. 4 A, which although located closer to the electrode shows a smaller OHC3 displacement compared to data points 4 and 1, which show responses from locations farther away from the electrode. To explain this we note two things: 1) data point 5 was collected last and the condition of the OHCs had probably deteriorated so that OHC contractions were smaller; 2) at locations very close to the electrode, cells usually deteriorate faster because the electrical field there is the strongest. Finally, for experiment 1011R (Fig. 4 A) OHC3 displacements were in the noise level at locations farthest from the electrode.

In Fig. 4, B and D, we present the MOC fiber displacements resulting from the OHC contractions described above. Note that to compare MOC fiber displacements with our modeling results (see Discussion) we converted them into fluid flow. The conversion was done by first calculating MOC fiber velocity for a given frequency and then multiplying the velocity with the ToC area. To estimate the ToC area we approximated the ToC as a triangle with base equal to the width of the AZ of the BM and height equal to the height of the IPC. The values of these structures at the location of our measurements were estimated from Edge et al. (15) and resulted in an area of 1.6 × 10³ μm². This value is representative of the 4-kHz region where most of our data were collected.

In Fig. 4, B and D, positive values indicate fluid flow toward the apex and negative values indicate fluid flow toward the base of the cochlea during the positive phase of the stimulus. The direction of flow at each location reversed during the negative phase of the stimulus. In these figures we see a shift in the direction of flow going from base to apex at a location apical to the electrode. In addition, the absolute flow magnitude increased as we moved away from the zero flow location.

Apical-turn experiment

It was very difficult to find MOC fibers in the apical turn of the gerbil cochlea. In general, we observed that the number of MOC fibers crossing the ToC decreases toward the apex of the cochlea. Studies in the guinea pig cochlea have also shown that the MOC fiber innervation decreases toward the apex (16). In one of our apical-turn experiments where we could clearly identify MOC fibers, the results were similar to the middle-turn experiments. The displacement of the MOC fibers was similar in magnitude to that of the OHCs; and at low frequencies, during the positive half of the stimulus period, the MOC fibers moved toward the base of the cochlea. In this experiment the helicotrema, the most apical cochlear location, was intact.

DISCUSSION

What is the link between OHC contractions and MOC fiber displacement?

Several observations provide strong evidence that the displacements of the MOC fibers are closely associated with OHC contractions. MOC fibers show no displacement in experiments where the OHCs show no response to electrical stimulation. The large MOC fiber displacements (up to ∼2 μm peak-to-peak) observed in this study in response to relatively small electrical fields (<50 mV in SM; see Karavitaki et al. (10) and Karavitaki and Mountain (11)) argue against the possibility that the MOC fibers are displaced due to the applied electrical field. Previous studies (17) have shown that the main effect of the electrical field on nerve fibers is swelling and the resulting displacement is usually <10 nm. In experiments with multiple longitudinal imaging locations (Fig. 4, A and B), we observed no OHC contractions at locations distal to the stimulating electrode, whereas MOC fiber displacements persisted even at these locations. Clearly at these distal locations the electrical field was too weak to evoke OHC contractions yet MOC fiber displacements occurred (presumably due to oscillatory fluid flow generated from OHC contractions near the stimulating electrode—see below). For the same set of experiments the phase of MOC fiber displacements changed depending on the location of the stimulus electrode relative to the imaging location. If the MOC fiber displacement were due to the applied electrical field, then we would have expected to see similar changes in the phase of the OHC displacements; this was not the case. Finally, we reported that in some of our experiments the MOC fiber DC/AC displacement ratio was comparable to the OHC DC/AC ratio, suggesting that the two displacements are linked. The above observations strongly associate the displacements of MOC fibers to OHC contractions.

To understand the link between OHC contractions and MOC fibers displacement, we have considered two hypotheses: 1) the longitudinal displacements of the MOC fibers could be due to the OHC contractions increasing and decreasing tension in the fibers, and 2) the MOC fibers move due to oscillatory fluid flow in the ToC induced by OHC contractions. If hypothesis 1 were correct, we would have expected to see the shape of the MOC fibers change as the length of the OHCs changed. In addition, we would have expected the MOC fibers to exhibit significant displacement in the radial direction and very little displacement in the longitudinal direction. Neither of these predictions was observed in our preparations (see Fig. 2). Even if the contractions of the OHCs were the cause of the longitudinal MOC fiber displacement, we would have expected the direction of this displacement to vary randomly from one fiber to the next. This is because the orientation of the MOC fibers is different from one OHC to the next. In contrast, our experimental data show that, within a single field of view, all the MOC fibers show similar motion (both magnitude and phase). A representative animation of the MOC fiber motion is shown in Movie 2 in the Supplementary Material.

The large longitudinal displacements of the MOC fibers provide strong evidence for hypothesis 2. Hypothesis 2 is also consistent with the anatomy of the OC. When OHCs contract, the reticular lamina will be pulled closer to the BM, which will decrease the volume of the spaces of Nuel. This will force some of the fluid in this space into the ToC, leading to longitudinal oscillatory fluid flow.

Further support for hypothesis 2 comes from experiments in which we imaged multiple regions of the cochlea along the longitudinal dimension (Fig. 4, A and B). In regions close to the stimulating electrode, we observed OHC contractions and MOC fiber longitudinal displacements (points 1, 4, and 5). In regions away from the stimulating electrode, we observed MOC fiber displacements but the OHC contractions were in the noise level (points 2 and 3). This observation supports the idea that oscillatory fluid flow generated at one location can propagate at a more distal location.

Direct measurements of oscillatory fluid flow in the ToC were not performed in our experiments. Instead oscillatory fluid flow in the ToC was estimated by first calculating the MOC fiber velocity. For the experiments shown in Fig. 3 the velocity range was 130–1800 μm/s. The velocity range across all of our experiments was 30–1800 μm/s. The oscillatory fluid flow in the ToC was then estimated by multiplying the velocity with the ToC area (as described in the Results section). The resulting flow for the experiments shown in Fig. 3 ranged between 208 and 2880 pl/s, and for all of our experiments the range was between 48 and 2880 pl/s. In our excised cochlea preparation the distance from the electrode location where the current amplitude was ∼37% of that at the electrode was ∼1.5 mm. This distance represents ∼25% of the total excised cochlear length and was estimated using experiments such as the one shown in Fig. 4. Therefore, the MOC fiber displacements and flow estimates presented in this work reflect the contribution of a large number of OHCs.

Magnitude and direction of ToC oscillatory fluid flow

To understand the magnitude and the direction of oscillatory fluid flow we used a simple one-dimensional hydromechanical model of the ToC (Fig. 5). We solved the model analytically for low stimulus frequencies (<120 Hz) because at those frequencies our experimental signal/noise ratio is high and the impedance of the volume compliance of the AZ, compared to the combined impedance of the fluid mass and the tube resistance, at the 4 kHz region is large (∼7 orders of magnitude) and can be ignored. Please note that the modeling results represent an AC calculation; and therefore when we talk about direction of flow we reference it to the positive phase of the stimulus (as previously mentioned in the Results).

FIGURE 5.

One-dimensional hydromechanical model of the ToC. The fluid mass in the ToC per unit length is represented by an inductor (L_ToC), the tube resistance per unit length is represented by a resistor (R_ToC), and the volume compliance of the AZ per unit length is represented by a capacitor (C_AZ). Parameter values were calculated as follows: L_ToC = ρ/A_ToC from Benade (35), 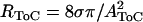from Benade (35), C_AZ from Naidu and Mountain (18), where the density of water ρ = 10⁻¹² g/μm³, the coefficient of shear viscosity in water σ = 10 ⁻⁶ g/(μm s), the cross sectional area of the ToC A_ToC = H_ToC W_ToC/2, H_ToC is the ToC height estimated as the height of IPC from Edge et al. (15), W_ToC is the ToC width estimated as the width of AZ from Edge et al. (15). H_ToC varied from 55 μm to 76 μm and W_ToC varied from 42 μm to 52 μm from base to apex. The resulting values for R_ToC varied from 19 × 10⁻¹² g/(μm⁵ s) at the base to 6.5 × 10⁻¹² g/(μm⁵ s) at the apex. The values for L_ToC varied from 8.7 × 10⁻¹⁶ g/(μm⁵ s) at the base to 5.1 × 10⁻¹⁶ g/(μm⁵ s) at the apex. The input to the model is the oscillatory fluid flow generated per section from the contractions of the OHCs (U_OHC(y)). The output of the model is the oscillatory ToC flow (U_ToC(y)) which by convention is positive if directed toward the apex.

The ToC is treated as an elastic tube with a cross sectional area equal to the cross sectional area of the ToC. Parameter descriptions are given in Fig. 6, and their values were based on anatomical and experimental measurements from gerbil cochlea and varied from base to apex. In our preparation the basal and apical ends of the cochlea are open; therefore the pressure difference at these points is zero. We represent these points in our model as short circuits. The input to the model is the oscillatory fluid flow generated per section from the contractions of the OHCs (U_OHC(y)). Our hypothesis is that when OHCs contract, they decrease the volume in the surrounding spaces of Nuel and force the fluid from these spaces into the ToC. The size of the OHC contractions depends on the stimulating current, which decreases as we move away from the electrode; therefore the contractions of the OHC and the resulting oscillatory fluid flow that they generate will decrease as we move away from the stimulating electrode (Fig. 4, A and C). We model the decrease of flow generated by the OHCs as a Gaussian function whose mean is at the location of the electrode and whose standard deviation is ∼1.5 mm (our estimate of the current spread in our preparation). The output of the model is the ToC flow (U_ToC(y)), which by convention is positive if directed toward the apex.

FIGURE 6.

Model input (“OHC flow”) and output (“ToC flow”) for two electrode positions (indicated by the arrows in panel A): 2 mm from the base (E1, gray line) and 8 mm from the base (E2, black line). “OHC flow” represents the flow generated from the OHCs per section and is the input to our model. “ToC flow” represents the flow in the ToC that results from the “OHC flow”. The location where the “ToC flow” shifts direction depends on both the electrode location and the impedance of the tunnel on each side of the electrode.

As shown in Fig. 5 the flow generated from the OHCs in one section is distributed toward the apical and basal end of the tunnel. The percentage of flow going toward each end depends on the relative impedance looking into the tunnel in either direction. For more apical sections more of the OHC flow will become ToC flow toward the apex than toward the base. The resulting ToC flow is the sum of all these flows in either direction (shown by the arrows in Fig. 5).

Shown in Fig. 6 is the input flow generated from the OHCs (Fig. 6 A) and the predicted ToC flow (Fig. 6 B) for two electrode locations. The predicted ToC flow is sigmoidal and saturates at distances away from the electrode location. This is because at locations progressively farther from the electrode the magnitude of flow generated from the OHCs decreases and therefore less flow is distributed on each side of the tunnel. The model predicts that there will be locations along the length of the cochlea where there will be large ToC flow with little flow generated from adjacent OHCs. In addition, for both locations we see a reversal in the flow direction at a location close to the electrode. When the electrode is located close to the basal end (Fig. 6, gray line) the point of zero flow is located apical to the electrode, whereas when the electrode is located close to the apical end (Fig. 6, black line) the point of zero flow is located basal to the electrode. In addition, the model predicts that the location of zero flow will be biased toward the location of the closest cut.

Our experimental results shown in Fig. 4 agree qualitatively with both model predictions. In our data we do not see saturation in the ToC flow with increasing distance from the electrode, presumably because we could not image fibers at such distal locations. An observation that is not predicted by the model is the decrease in the OHC3 displacement at locations close to the electrode (i.e., point 5 in Fig. 4 A). Note that this was the last data point to be collected and probably the condition of OHCs had deteriorated. In our preparation, the OHC contractions decreased when cell condition had deteriorated.

Our experimental results from the apical turn showed that fluid flow was directed toward the base. In this experiment the scalae were not open at the apex (i.e., the helicotrema was intact) and, according to our model, flow was directed toward the base due to the lower impedance of the basal termination.

Relation to the intact cochlea

Low-level acoustic stimulation excites only a small section of the cochlea at any given frequency. To understand how far and how fast a fluid wave launched by a small group of OHCs can propagate in the ToC, we used the ToC model described above and assumed that the values of the chosen elements were constant. The numerical values were computed for a section of tube that was 200 μm in length and were specific for the 4-kHz region, where most of the physiological data were collected. The space constant, λ, defined as the distance over which the fluid wave in the ToC will be attenuated by 37%, was calculated from Eq. 1 and the velocity of propagation of the fluid wave, ν, in the ToC was calculated from Eq. 2.

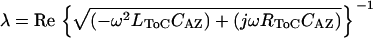(1)

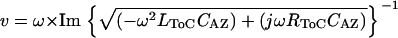(2)

The resulting values used for this region are L_ToC = 6.25 × 10⁻¹⁶ g/μm⁵, R_ToC = 9.8 × 10⁻¹² g/(s μm⁵), C_AZ = 18 μm³ s²/g from Naidu and Mountain (18), H_ToC = 64 μm, W_ToC = 50 μm, A_ToC = 1.6 × 10³ μm², ω = 2πf, where the stimulus frequency f = 30–9000 Hz.

Using Eq. 1 we have estimated that around the 4 kHz cochlear region at CF, a ToC fluid wave can propagate for ∼1.3 mm (i.e., ∼11% of the cochlear length) before it gets attenuated to 37% of its original amplitude. This distance is larger than the wavelength of the BM traveling wave at its peak, which is ∼0.5 mm for the 4-kHz region (19). In addition, using Eq. 2 we have estimated that around the 4-kHz cochlear region at CF, the velocity of propagation of the ToC fluid wave is ∼9 m/s. This value is similar to the guinea pig BM traveling wave velocity calculated (3) to be 5–6 m/s at the 5–9 kHz CF region using the data of Kohllöffel (20).

Significance of oscillatory fluid flow to cochlear micromechanics

Our experimental results using an electrically stimulated semiintact cochlear preparation support the in vitro existence of oscillatory fluid flow in the ToC. Such a flow, if present in vivo, could be very important to cochlear function. Our results together with our calculations argue that the observed flow is tightly linked with OHC contractions and is not an artifact of our preparation. In experiments where the anatomy of the scala media was compromised (holes in the BM), MOC fiber displacements were not observed although OHC motion was present. How could ToC oscillatory fluid flow influence cochlear mechanics? We hypothesize that at the peak of the traveling wave OHC contractions would pump fluid into the ToC, augmenting the original motion of the BM and stimulating the IHC hair bundles, as recently hypothesized (21). Our model calculations show that the space constant and velocity of propagation of the ToC fluid wave is similar to that of the BM traveling wave; the two can therefore work together in amplifying the BM motion. Our hypothesis implies that when OHCs are contracting, the PZ of the BM would move toward the scala vestibuli, whereas the AZ of the BM (due to the pumping of fluid) would move toward the scala tympani. Such significant phase changes across the BM have been seen using electrical stimulation (22,23) and acoustic stimulation in vivo (24). The possible stimulation of IHC hair bundles via the OHC-pumped fluid (21) could also support the in vivo observed MOC-induced inhibition of the first peak of the auditory nerve fiber response, which cannot be explained using the traditional traveling-wave-induced BM motion (25).

Oscillatory fluid flow in the ToC could also have significant implications for cochlear modeling efforts. In most of the current cochlear models the only means of longitudinal coupling is through the cochlear fluids. These models are referred to as “classical models” and although they have been successful in replicating some experimental data, they still fail to replicate all the unique features of cochlear responses (for a review, see de Boer (26)). A number of nonclassical models have been proposed, each requiring a different source of longitudinal coupling to successfully replicate experimental measurements of BM motion. For example, Geisler and Sang (27) as well as Steele et al. (28) assume that longitudinal coupling exists because the apical end of the OHCs is tilted toward the basal end of the cochlea. Therefore, as the BM traveling wave propagates toward the apex, the OHC's forces from one location would be applied to a more apical location (often referred to as feed-forward coupling). Such longitudinal OHC tilt might be a species-specific characteristic. Our own measurements (10,11) do not show this tilt in the gerbil cochlea. Therefore, this type of feed-forward coupling would not be applicable to the gerbil cochlea.

De Boer and Nuttall (29) have extended the feed-forward models by proposing that the “input to the ‘amplifying elements’ (OHCs) is a weighted average of the BM velocity, averaged over space”. The weighting function does not include any time delay and is assumed to be frequency independent. From the analysis of their experimental data, they concluded that the input to the OHCs results from a combination of feed-forward and feed-backward components possibly shaped by the longitudinal mechanical interaction within the OC.

A very different approach to longitudinal coupling is incorporated in Hubbard's (30) traveling-wave amplifier model, which includes two modes of wave propagation. The first mode is hypothesized to correspond to the traditional BM displacement wave. Hypotheses for possible physical correlates of the second mode include oscillatory fluid flow in the ToC (31). Such flow was first considered in de Boer's (32) formulation of the sandwich model, but this model did not address the functional role of ToC flow in cochlear amplification.

Hubbard et al. (33) explicitly incorporated the ToC in a multicompartmental hydromechanical model of the cochlea, which successfully replicated BM motion. In this model, in addition to the BM traveling wave, there is also a fluid wave in the ToC (ToC wave) which is driven by the OHC motility. At a location basal to the best place, energy of the BM wave is transferred to the ToC wave subsequently amplified by the OHCs. The fact (34) that the time course of maturation of the ToC parallels the maturation of cochlear sensitivity provides additional evidence for the involvement of the ToC in cochlear amplification. These nonclassical models (30,33) posed a challenge because, to our knowledge, until now there was no experimental evidence to confirm oscillatory fluid flow in the ToC.

Our experimental data demonstrate that the ToC can support oscillatory fluid flow along the length of the cochlea. The fact that OHC contractions lead to oscillatory fluid flow is not surprising. The novel aspect of our findings is that the fluid does not merely flow back and forth in the radial direction but also appears to have a significant component in the longitudinal direction through the ToC. Using a simple hydromechanical model of the ToC we have shown that a fluid wave in the ToC can travel without significant attenuation for distances larger than the wavelength of the BM traveling wave at its peak. Our findings suggest that OHC somatic motility produces oscillatory fluid flow in the ToC, which results in the long-range longitudinal coupling needed by nonclassical cochlear models. If these (30,33) nonclassical models are correct, then ToC oscillatory fluid flow is critical for cochlear amplification.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.