A Milestoning Study of the Kinetics of an Allosteric Transition: Atomically Detailed Simulations of Deoxy Scapharca Hemoglobin

Abstract

Atomically detailed simulations are used to compute the kinetics of the R-to-T transition in deoxy Scapharca hemoglobin. A computational approach called milestoning is utilized that combines 1), an efficient reaction path algorithm; and 2), a “fragment and glue” approach for classical trajectories. Milestoning computes the R-to-T transition kinetics on the microsecond timescale based on atomically detailed trajectories that rarely exceed a nanosecond. Eleven reference hypersurfaces (milestones) are constructed along the reaction coordinate, which is computed with a global path optimization algorithm. Two-hundred classical trajectories are calculated for each of the milestones to collect local distributions of first passage times. These local distributions are used in a non-Markovian theory to compute the overall timescale. Exponential enrichment of reactive trajectories, an important component of the milestoning approach, makes these calculations possible. The overall timescale of the reaction is estimated as 10 ± 9 μs, in accord with available experimental data. The barrier is not sharp and is spread over four milestones. Even after the most significant structural changes are completed (phenylalanine F4 ring flips), highly collective and activated motions continue. The calculations suggest an additional late free energy barrier.

One of the important mechanisms of response to environmental changes in biology is that of allostery. Adjustments in protein packing and assembly affect basic protein activity in reaction to changes of ligand concentration, products, pH, and other effectors. Naturally these processes have attracted considerable experimental and theoretical interest. Most investigations focus on human (tetrameric) hemoglobin HbA for which we now have vast data, models, and some remaining questions due to the complexity of the system (1). Interestingly, a dimeric hemoglobin (Scapharca hemoglobin (HbI)) (2) shows a profoundly different allosteric mechanism than HbA while maintaining a tertiary fold typical of a globin. The allosteric transition in HbI is significantly simpler than the transition in HbA and more accessible to calculation and experiment. The most apparent structural changes observed in the allosteric transition of HbI are flips of two amino-acid rings and adjustments of water molecules at the interface of the homodimer. No large changes in subunit orientation are observed (in contrast to HbA), allowing for a recent study of the transition using time-dependent x-ray diffraction (3).

The time-resolved experiments provide a detailed picture of the progress of the reaction. However, the connection of the structural images to energetic, kinetic, and thermodynamic properties of the system is not obvious. Atomically detailed computer simulations hold the promise to bridge the gap. Unfortunately, computer simulations are difficult to perform in this case because: 1), the experimentally measured timescale is long (microseconds); and 2), there is no clear and narrow transition state or barrier domain. The first observation excludes the application of straightforward molecular dynamics simulations. Even if a few microsecond trajectories could be computed, they would not be sufficient to estimate the kinetics. The last observation makes it difficult to apply approaches appropriate for activated processes (4,5). These approaches require the actual transition time to be short (the short-time trajectories can be rare, leading to long timescale).

For the study of long time kinetics in complex systems with potentially broad spatial barriers and intermediates (experiment suggests a nanosecond intermediate in HbI (3)), the method of milestoning (6,7) seems appropriate. There are three steps to a milestoning calculation:

• Step 1. Sampling from local-equilibrium ensembles in cross-sections (milestones) between the reactant and product (Fig. 1);

• Step 2. Computing trajectories between nearby milestones and estimating local first-passage time distributions (LFPTD) between them; and

• Step 3. Computing the overall time dependence of the process using all the LFPTD-s in a stochastic model.

FIGURE 1.

A schematic two-dimensional energy landscape illustrating the milestoning approach. A reaction coordinate, q, is computed between the two minima (R and P). A milestone i is a hyperplane perpendicular to the reaction coordinate at q_i. Also shown is a sampled trajectory, which starts at milestone i and terminates at milestone i+1.

The two end structures (the structures of the R and T states of HbI) were prepared from 1HBI (8) and 4SDH (9) of the protein databank (10) by building missing hydrogens, and minimizing the energy for 50 steps. A discrete reaction coordinate with nine intermediates was computed with the self-penalty walk method (11) of the program MOIL (12). A milestone (hyperplane) is defined by its normal and a position in the plane, X_i. The calculation of the reaction coordinate includes only the protein and crystal waters. A movie of the computed reaction coordinate is included in the Supplementary Material.

Each configuration along the reaction coordinate was then solvated and equilibrated in a periodic box of water. The total number of atoms in the system was ∼17,100 (the number of water molecules varies slightly for different water boxes along the reaction coordinate). In the next step we sample configurations at 300 K in each milestone by calculating a trajectory constrained to the hyperplane. Coordinates are saved every picosecond of a 200-ps trajectory, providing a total of 200 initial conditions for Step 2. Straightforward molecular dynamics trajectories were initiated at each milestone using the previously described sampling. Each trajectory, initiated at milestone i was examined during the calculation to determine the termination time at milestone i+1 or i−1. The termination times were binned to generate the LFPTD (or K_ij(t)—the probability that a trajectory initiated at milestone i will terminate at milestone j after time t). In Fig. 2 we show K₇₆(t) and K₇₈(t).

FIGURE 2.

The local first passage time distribution (LFPTD) of milestone 7. The times of trajectories initiated at milestone 7 and terminated at the previous or the next milestone are binned. The times from milestone 7 to 6 are black and from 7 to 8 are red. Moving forward (from 7 to 8) is significantly less likely, suggesting a free energy barrier (only nine trajectories made it to milestone 8).

Once all the LFPTD (or K_ij(t)) are computed, we calculate the time evolution of the system. In Faradjian and Elber (6) and West, Elber, and Shalloway (7), an integral equation was introduced for P_i(t), the probability of finding the system at milestone i at time t. We also introduced Q_i(t), the probability of making a transition to milestone i exactly at time t. The outer integrals below are from zero to t and the inner integral from zero to t−t′,

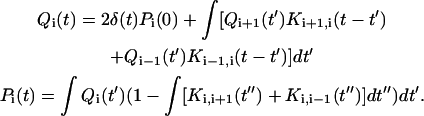The first equation provides the probability of transition to i exactly at time t. The right-hand side is a sum of the probabilities of past transitions to milestones i ± 1 and a transition at the right time into i. The second equation is for the probability of being at i at time t. The right-hand side is the probability of making a transition to i some time in the past and remaining there until t. These integral equations can be solved directly with the initial condition P_i(0) and setting the last milestone to be absorbing. They can also be solved in terms of moments as has been shown in Rousseau et al. (13). Of special interest is the first moment, the so-called mean first passage time 〈〈τ〉〉 that is widely used to assess timescales of stochastic processes: 〈〈τ〉〉 = ∫τ · dP_f/dτ · dτ, where f denotes the last absorbing boundary. The first passage time was estimated as 10 ± 9 μs. Although the error bars are large, the results are within experimental values (14,15).

With an agreement with experiment on the overall timescale at hand, the atomically detailed simulations allow us to investigate mechanistic questions. For example, are the phenylalanine flips the cause of the free energy barrier, or are other processes contributing significantly to the free energy profile? In Fig. 3 we show the distribution of the distances between the two phenylalanine rings that are useful indicators of their R (or T) states.

FIGURE 3.

The distributions of the Cz–Cz distances of the two Phenylalanines Phe-97 for milestones 3 (black), 5 (red), 7 (green), and 9 (blue). This distance is a useful measure for the R (or T) transition. Most of the side-chain transitions are performed in the neighborhood of milestone 5. The distribution of milestone 7 is similar to milestone 9, suggesting that the side-chain transitions are complete at milestone 7.

Fig. 3 demonstrates the interplay between different steps of the calculations. The calculation of the reaction coordinate (or the determination of the positions of the milestones) suggests that the final rearrangement of the protein structure are of a global nature and not associated with the side-chain transition since the side-chain transition is essentially complete in milestone 7 (see also Fig. 4). This observation was confirmed by the thermal sampling in the milestone plane. But how relevant is the last phase, which does not include the phenylalanines? The first passage calculations at milestone 7 indicate that the free energy barrier for the last phase is significant and impacts the kinetics (in addition to an earlier barrier associated with the rotation of the side chains). Structural differences between milestone 7 and the deoxy state are shown in Fig. 4.

FIGURE 4.

The difference in the packing of Phe-97 (white) against the heme (red) in milestone 7 (top) and the deoxy state (bottom). While the phenylalanine packing is essentially complete, there remain numerous adjustments. The lysine and the water molecules should come higher and Phe-97 requires a slight rotation. The carboxyl groups of the heme also change orientation.

What are the factors that allowed milestoning to complete a calculation not accessible to straightforward molecular dynamics? There are three factors:

1. The existence of milestones allows bootstrapping of rare trajectories. If we place a milestone halfway to the top of the barrier, then climbing to the top will be easier when initiating trajectories half the way.

2. Since the trajectories are diffusive and keep moving forward and backward, placing milestones reduces the number of backward and forward cycles we need to compute explicitly with the trajectories (the cycles are considered in the integral equations).

3. The large number of short trajectories is easy to distribute on a cluster of computers, a common facility in computationally oriented laboratories.

In conclusion, we illustrated the capacity of milestoning to study the kinetics in a complex system and point out a late activated phase in the allosteric transition of HbI, a step of nonlocal structural rearrangements.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.