Abstract
We present the results of molecular dynamics simulations of small peptide nucleic acid (PNA) molecules, synthetic analogs of DNA, at a lipid bilayer in water. At neutral pH, without any salt, and in the NPnγT ensemble, two similar PNA molecules (6-mers) with the same nucleic base sequence and different terminal groups are investigated at the interface between water and a 1-palmitoyl-2-oleoylphosphatidylcholine lipid bilayer. The results of our simulations suggest that at low ionic strength of the solution, both PNA molecules adsorb at the lipid-water interface. In the case where the PNA molecule has charged terminal groups, the main driving force of adsorption is the electrostatic attraction between the charged groups of PNA and the lipid heads. The main driving force of adsorption of the PNA molecule with neutral terminal groups is the hydrophobic interaction of the nonpolar groups. Our simulations suggest that the system free energy change associated with PNA adsorption at the lipid-water interface is on the order of several tens of kT per PNA molecule in both cases.
INTRODUCTION
Peptide nucleic acids (PNA) are lab-created analogs of DNA, in which the nucleic bases (adenine, guanine, thymine, and cytosine) are attached to a pseudopeptide backbone. PNA can hybridize to its complementary DNA target in a sequence-dependent manner (1). Unlike most oligonucleotide analogs, PNA binds very tightly to double-stranded DNA as well. Because of this property, PNA molecules are intensively exploited in gene chemistry. They provide a novel, straightforward, and versatile approach for permanently attaching proteins, peptides, fluorophores, and other molecules to plasmid DNA without interfering with transcriptional activity (2).
Recently, due to PNA's neutral backbone, a new potential application emerged. PNA or backbone modified lipophilic PNA can act as the genetic material in a minimal self-replicating nanomachine or protocell design proposed by Rasmussen and Chen (3,4). According to this design, a minimal protocell able to utilize resources, grow, self-replicate, and evolve could be as simple as a small lipid aggregate (micelle) acting as a container by anchoring a PNA molecule to its exterior and a photosensitizer to its interior. In such a protocell, light-driven metabolic processes from the lipid aggregate interior could synthesize lipids and PNA, from appropriate precursor molecules with PNA acting as both an information carrier and as a catalyst, leading to a spontaneous growth of the protocell. Micellar lipid clusters in water are thermodynamically stable below some critical size only; therefore the growing containers would divide as soon as they become large enough, providing the next generation of the protocells.
To verify this scenario we need to answer a number of important questions. Unlike DNA or RNA, our knowledge of PNA is still relatively limited and a number of important issues have not been addressed so far. One of them is whether PNA molecules at high local concentrations are going to spontaneously gather at a lipid-water interface, and if not, how hydrophobic the PNA backbone has to be before such an attachment occurs. The PNA-lipid attachment is a sine qua non condition for the protocell replication process. Molecular dynamics (MD) computer simulation is a suitable method for addressing this problem. This technique has been exploited with a significant success in many areas of bioscience and bioengineering, including some recent PNA-related phenomena (5,6). MD simulation is also one of the main tools used in theoretical studies of membranes and lipid bilayers (7). In this article we present results of our MD simulations on the affinity of a small PNA molecule to a lipid-water interface.
METHODS
General
All the MD simulations were conducted with NAMD, version 2.6b1 (8) using CHARMM27 topology and parameter files (9). We used VMD, version 1.8.3 (10), to prepare input files and to analyze the MD trajectories, as well as for visualization. All the calculations were performed on Mauve, the SGI Altix supercomputer of the Los Alamos National Laboratory (LANL) and on the Linux cluster of the Center for Nonlinear Studies at LANL.
Topology and parameterization
Unfortunately, the topology and parameters for PNA residues are not directly available in the standard molecular dynamics packages such as CHARMM (11) because PNA molecules are not natural or common. To the best of our knowledge, only two sets of parameters for PNA have been published in the literature (12–14). Both parameter sets, however, seem to be a little inconsistent with each other. More importantly, some of the parameters in these sets are different than parameters found in CHARMM27 parameter file for similar chemical structures (compare, e.g., partial atomic charges for the peptide bond). Therefore, to be consistent with the other parameters used in our simulations, we have obtained the parameters in PNA residues by comparison with similar chemical groups found in the CHARMM27 parameter file (15–21). We have also assigned the atom types of the atoms involved in PNA residues as reported in Sen and Nilsson (13), to follow CHARMM atom type definitions (see Fig. 1). This effort makes most of the bond, angle, and dihedral and all of the nonbonded parameters directly available from the combined CHARMM all-hydrogen parameter set for nucleic acids, lipids, and proteins. These, which are not available directly, are listed in the Supplementary Material. Corresponding topology and parameters files for NAMD calculations are also available upon request. Our force-field parameters have been tested in ongoing simulations of PNA partition in water-octanol system and the experimentally verified results will be published elsewhere.
FIGURE 1.
Schematic representation of the chemical structure of the monomeric unit of PNA.
Construction and equilibration of the starting structures
We extracted all the atoms' coordinates of one palmitoyl-oleoyl-phosphatidyl-choline (POPC) molecule from the file fluid-H.pdb.Z that we downloaded from Dr. H. Heller's web page (22,23). The molecule was aligned with z axis and replicated 6 × 6 times in the directions of the axes x and y every 0.75 nm. This procedure produced a monolayer of 36 lipid molecules in the xy plane. The second compartment of the bilayer was produced by reflection of the monolayer in this plane. The two monolayers were separated with a gap of 4.5 nm. We used the SOLVATE facility of VMD to fill the gap with 2895 TIPS3P water molecules. The resulting system of the size 4.5 × 4.5 × 10.6 nm was then energy-minimized for 500 time steps to avoid overlapping of atoms. After that, a short (4500 time steps) simulation was run at constant temperature, pressure, and constant shape of the simulation box in directions x and y (x/y ratio) to allow shape relaxation of the unit cell. Next we conducted an ∼4-ns-long simulation at constant temperature, constant pressure component normal to xy plane, and constant area of the unit cell in this plane. At this stage of the simulation, the dimensions of the unit cell in the directions x and y were fixed at 4.743 nm that allowed the bilayer to expand to this size, which corresponds to the molecular area 0.625 nm2 per lipid found in experiments (24). At the same time the size of the unit cell in the direction z decreased to the value of 7.75 nm. Finally, we ran several 40-ns simulations of the system at constant temperature, normal pressure, shape of the simulation box in directions x and y, and a few values of the surface tension. We found that at the surface tension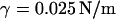 
the molecular area was 
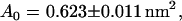which fitted best the experimental result. Therefore, all the further simulations involving the lipid bilayer were conducted at this specific value of the surface tension.
The coordinates of the atoms in the single-stranded 6-mer PNA with the base sequence C1G1TAC2G2 were extracted from the crystal structure of the corresponding PNA duplex (Protein Data Bank identifier 1PUP (25)). The coordinates of the missing H-atoms of the PNA molecule were generated by the GUESSCOORD facility of VMD. We created two PNA molecules with the same base sequence and different terminal groups. One of them, hereafter referred to as s-PNA, has standard C- and N-terminus, i.e., the charged groups −COO− and 
respectively. The second molecule that we will call a-PNA has two neutral termini: amidated C-terminus −NH2 and acetylated N-terminus −CO−CH3 (see Fig. 2). Each of the molecules was solvated in water and equilibrated for 40 ns at constant temperature, pressure, and cross-section area. The size of the simulation boxes in the directions x and y was fixed at the value corresponding to the size of the lipid bilayer, i.e., at 4.743 × 4.743 nm. The z dimension of the box fluctuated around 3.9 nm.
FIGURE 2.
Schematic representation of the terminal groups used in our MD simulations (from left to right): standard C-terminus of the s-PNA molecule, standard N-terminus of the s-PNA molecule, amidated C-terminus of the a-PNA molecule, and acetylated N-terminus of the a-PNA molecule. Both PNA molecules contain the same base sequence (C1G1TAC2G2).
After the equilibration, each of the two PNA molecules was inserted into the equilibrated lipid bilayer in the following way. First, the equilibrated lipid bilayer system was moved along z axis in such a way that the layer of water was located in the center of the simulation box. Next, the PNA molecule was centered in its simulation box. Then, we removed a volume of water from the center of the lipid bilayer system; the volume was 0.2 nm thicker in z direction than the size of the corresponding PNA molecule. Finally, the empty space was replaced with the PNA molecule together with its surrounding water molecules. The resulting system was then energy-minimized for 400 time steps to avoid overlapping of atoms and then used for the subsequent MD simulations.
It should be noted that our systems are different than experimental systems that have been studied so far, e.g., in the PNA vesicle encapsulation experiments (26). First of all, there is no salt or electrolyte in our systems and the lipid-water interface in our simulations is electrostatically neutral. In contrary, the experimental systems have usually been studied at the buffer concentration on the order of at least several millimolar and the measured surface potential of the lipid-water interface is on the order of 102mV (26). This large value of the interface surface potential suggests that strong ion adsorption or desorption can take place at the interface, which in turn can produce a compact hydration layer and influence the PNA molecule behavior at the interface. Indeed, preliminary results of our simulations of the lipid bilayer at ionic strength on the order of fraction of mol/dm3 suggest that this is the case. It should also be noted that because of the MD length-scale limitation the PNA and lipid concentrations in our systems are equal to ∼10−2 M and 0.7 M, respectively, and so they are very high compared to the experimental conditions.
Molecular dynamics protocols
We employed NAMD (version 2.6b1) with its standard empirical potential energy function (8). We used periodic boundary conditions and the particle mesh Ewald (PME) approach (27,28) for evaluating long-range electrostatic effects. The distance between subsequent grid points on the mesh was ∼0.1 nm. A time step of 2 fs was used for the integration of Newton's equations, since all the bond lengths between each hydrogen atom and the atom to which it was covalently bonded were constrained to their equilibrium values using the SHAKE algorithm (29). A cutoff at 1.2 nm was used for the Lennard-Jones interactions and for electrostatics with smoothing functions activated at a switching distance 1.0 nm. The nonbonded pair list was updated every 10 steps and the maximum distance between atoms for inclusion in the list was 1.35 nm. The long-range Coulombic forces were updated every two steps. For electrostatic calculations a relative dielectric constant of 1.0 was used; 1-2 and 1-3 nonbonded interactions were excluded; 1-4 electrostatic interactions were taken into account without any modification and 1-4 van der Waals parameters were modified according to the CHARMM27 parameter file.
Simulations were carried out in the ensemble NPnγT at the constant pressure component normal to the lipid-water interface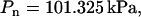 
surface tension 
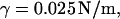and temperature 
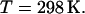Constant temperature was maintained by using the Langevin dynamics method (30). We applied the Langevin damping coefficient to nonhydrogen atoms only. Its value was setup to 5/ps for the first 4000 time steps, when our systems were far from equilibrium. Then the coefficient was fixed at 1/ps. A combination of the Nose-Hoover constant pressure method (31) with piston fluctuation control implemented using Langevin dynamics (32) was used to control the pressure along the z axis and the surface tension in the xy plane. The Langevin piston oscillation period and the oscillation decay time were equal to 100 fs and 50 fs, respectively. The constant ratio of the unit cell dimensions in the xy plane was kept during the simulations while allowing cell shape fluctuations along all axes. The pressure was calculated using the hydrogen-group-based pseudomolecular virial and kinetic energy (useGroupPressure option of NAMD) in conjunction with the SHAKE algorithm.
Calculation of the free energy
We calculated the free energy change in our systems using several different methods. The first method was based on the adaptive biasing force (ABF) approach (33). This method, implemented as a suite of Tcl routines directly available from the main configuration file used to run molecular dynamics simulations with NAMD, efficiently calculates the potential of mean force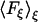 
acting between two groups of atoms along a reaction coordinate ξ, and applies ABFs that are needed to overcome free energy barriers and provide uniform sampling. This potential of the mean force is a measure of the system's free-energy change ΔG corresponding to the change in the reaction coordinate of a system from ξ1 to ξ2:
 |
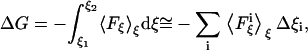(1) |
where Δξi is the width of the bin over which the force is averaged.
As discussed in the section “Mean force and the free energy profile”, however, results of our simulations suggest that any biasing force acting on a flexible molecule like PNA or molecular structure such as the lipid bilayer can disturb its conformation and thus cause additional change of the free energy of the system. Therefore, to avoid the effect of the biasing force on the free energy calculation, we conducted our simulations monitoring the system's free energy without introducing any bias (applyBias option of NAMD).
The second method is strictly applicable to a system at equilibrium. Using the simulation data we can calculate the time evolution of the reaction coordinate and find the density of the distribution of this coordinate:
 |
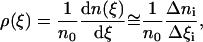(2) |
where n0 is the total number of the saved microstates of the system, n(ξ) is the number of the microstates of the system in which the value of the reaction coordinate is smaller than ξ, and Δni is the number of the force measurements in the bin Δξi. The last equality is correct for large numbers Δni and small width of the bins Δξi. If the system is near equilibrium we can use the distribution density of the reaction coordinate ξ to calculate the change of the system free energy associated with the change of this coordinate. According to the Boltzmann relationship
 |
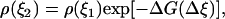(3) |
where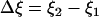 
is the change of the reaction coordinate and the free energy is expressed in kT units. The change of the system free energy ΔG corresponding to the change in the reaction coordinate of the system from ξ1 to ξ2 can be calculated from Eq. 3 as
 |
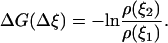(4) |
If the width of the bin Δξi is constant, the change of the system free energy can be calculated from the formula
 |
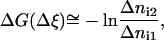(5) |
where Δni1 and Δni2 are the numbers of force measurements collected in the bins corresponding to the reaction coordinates ξ1 and ξ2, respectively. Equation 5 is convenient because the numbers Δni are directly available in ABF calculations with NAMD. Note that if the free energy changes by more then few kT units in the whole reaction-coordinate interval of interest then the ABF simulation with no biasing force applied will take a very long time. To avoid this inconvenience the whole interval of reaction coordinate should be divided into smaller pieces, in which the free energy varies little, with a harmonic bias enforced at their borders (forceConst parameter of NAMD).
As the reaction coordinate we chose the distance along the axis z between a PNA molecule and one of the lipid-water interfaces. Specifically, we calculated the z coordinate of the PNA molecule by averaging the z coordinates of its selected 14 atoms. These were six atoms of the nucleic bases (O4, N4, N6, and O6 in the residues thymine, cytosine, adenine, and guanine, respectively), six atoms N2′ of the backbone, and two atoms of the terminal groups: N1′ and C1′ of the s-PNA molecule, and NT and CAY of the a-PNA molecule. The z coordinate of the lipid-water interface was calculated by averaging the z coordinates of the 36 N atoms and the 36 P1 atoms in this interface. The mean force was calculated between the 14 atoms of the PNA molecule and the 72 atoms of the lipid bilayer. The width of the bins in which the forces are accumulated has to be small enough to ascertain that the free energy profile varies regularly in the ξ-interval. On the other hand, it should be large enough to ensure sufficient sampling and avoid large fluctuations in the average force. In our system we used the bin width equal to 10 pm, which allowed us to collect the number of force samples in most of the bins on the order of 105–106. To decrease the force fluctuation we averaged the mean force over 20 pm (dSmooth parameter of NAMD).
As discussed in the next section, the molecule s-PNA adsorbs rapidly and forms hydrogen bonds with the charged groups of the lipid molecules that can be easily identified. In this system we can use yet another approach to estimate the PNA adsorption free energy. We can estimate the change of the system free energy by summing up the free energy of these bonds. When the s-PNA molecule adsorbs at the interface during the first nanosecond of the simulation and its distance from the interface does not evolve in a systematic way, we can assume that the system is at equilibrium after the first several nanoseconds and use Eq. 4 to calculate the free energy of each of the bonds. In these calculations we can assume that the lengths of the formed hydrogen bonds are uncorrelated and use the distance between the atoms forming a specific hydrogen bond as the reaction coordinate.
SIMULATION RESULTS AND DISCUSSION
In the following sections we present and discuss the results of the MD simulations of the s-PNA and a-PNA molecules in the lipid-water system: i), the variation of the distance between the molecules and the lipid-water interface; ii), the variation of the lipid molecular area; and iii), the molecule-interface free energy profile.
PNA distance from the lipid interface
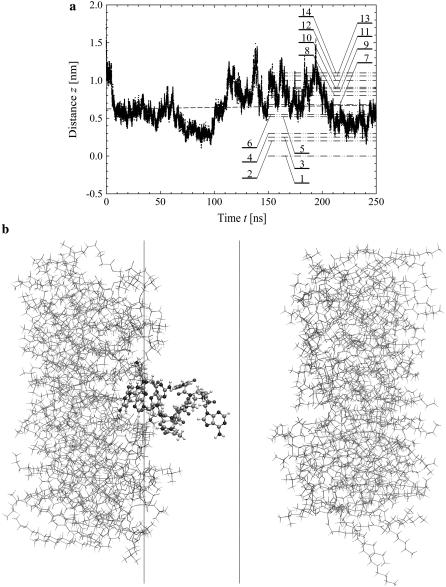
The time evolution of the mean distance of the s-PNA molecule from the interface is presented in Fig. 3 a and in Fig. 3 b the final configuration is shown at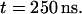 
The distance fluctuates around the mean value 
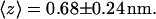No systematic drift of the distance can be observed in the timescale of the conducted simulation. From the simple linear regression analysis conducted over the entire time of the simulation we find that the slope of the dashed regression line is very small and equal to 0.20 ± 0.02 mm/s. The molecule approaches the interface quickly (in the first nanosecond of the simulation) and does not leave its position at the interface. Dash-dot-dot lines denote the mean distances of the 14 individual atoms of the molecule from the interface. The values of the mean distance and its standard deviation are listed in Table 1. Based on these data we can conclude that the molecule s-PNA is attached to the interface with its positively charged N-terminus, whereas the negatively charged C-terminus is pushed away from the interface.
FIGURE 3.
(a) Variation of the distance z between the lipid-water interface and the molecule s-PNA. Dots represent the distance between the molecule and the interface. The dashed lines represent the least square fitting of a straight line to the simulation results over the total time of the simulation. Dash-dot-dot lines represent the mean values of the distance z between the interface and the PNA molecule as well as between the interface and the 14 individual atoms of the molecule calculated during the last 100 ns of the simulations. Numbers correspond to the individual atoms of the molecule listed in the order of growing distance from the interface: 1 – N1′ (C1), 2 – N4 (C1), 3 – N2′ (C1), 4 – O6 (G1), 5 – N2′ (G1), 6 – N4 (C2), 7 – center of the molecule, 8 – N2′ (T), 9 – O6 (G2), 10 – N2′ (C2), 11 – N2′ (A), 12 – O4 (T), 13 – N6 (A), 14 – C1′ (G2) and N2′ (G2). (b) The final configuration of the system. The left and right vertical lines depict the coordinate 
and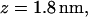 
respectively.
TABLE 1.
Mean distance from the interface and its standard deviation calculated for individual atoms and the geometrical center of the molecule s-PNA
| Atom name and residue | Mean distance from interface | Standard deviation | Position from interface |
|---|---|---|---|
| N1′ (C1) | 0.0 | 0.4 | 1 |
| N2′ (C1) | 0.25 | 0.36 | 3 |
| N4 (C1) | 0.2 | 0.4 | 2 |
| N2′ (G1) | 0.52 | 0.33 | 5 |
| O6 (G1) | 0.3 | 0.6 | 4 |
| N2′ (T) | 0.80 | 0.27 | 8 |
| O4 (T) | 1.0 | 0.4 | 12 |
| N2′ (A) | 0.91 | 0.26 | 11 |
| N6 (A) | 1.06 | 0.43 | 13 |
| N2′ (C2) | 0.89 | 0.31 | 10 |
| N4 (C2) | 0.55 | 0.45 | 6 |
| N2′ (G2) | 1.1 | 0.4 | 14 |
| O6 (G2) | 0.85 | 0.73 | 9 |
| C1′ (G2) | 1.1 | 0.4 | 14 |
| Center of molecule | 0.68 | 0.24 | 7 |
The distance was averaged over the final stage of the simulation (100 ns). The numbers in the last column represent the position of the atoms in the order of growing distance from the interface.
Such an orientation of the molecule suggests that the attraction between the phosphate group of the POPC molecule and the N-terminus is stronger than that between the saturated amine group of the lipid molecule and the C-terminus of the s-PNA molecule. This difference in the attractive interaction results from the difference in the partial atomic charges of the attracting atoms, which are: 0.25e for each of the hydrogen atoms H11 through H43 of the saturated amine group, −0.67e for each of the oxygen atoms OT1 and OT2 of the PNA C-terminus, 0.33e for each of the hydrogen atoms HT1 through HT3 of the PNA N-terminus, and −0.78e for each of the oxygen atoms O3 and O4 of the lipid phosphate group, where e is the elementary proton charge. Note that the product of the oxygen-hydrogen partial atomic charges for the atoms of the N-terminus and the phosphate group is equal to −0.2574e2, whereas for the atoms of the amine group and the C-terminus this product is equal to −0.1675e2, which is 65% of the former value. This large difference between the products of the partial atomic charges suggests that the dipole-dipole interaction between the amine group and the C-terminus is weaker than that between the phosphate group and the N-terminus. Therefore, the hydrogen bonds between the lipid phosphate group and the N-terminus of the PNA molecule are energetically more favorable than those between the lipid amine group and the C-terminus of the PNA.
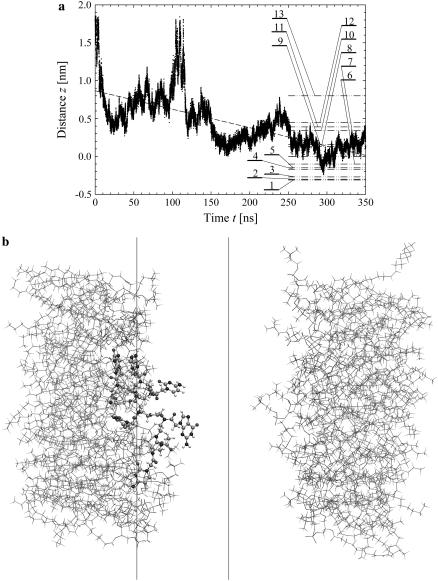
The time evolution of the mean distance of the a-PNA molecule from the interface is presented in Fig. 4 a and the final configuration is shown in Fig. 4 b at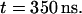 
Unlike the s-PNA molecule, the a-PNA molecule approaches the interface relatively slowly. Between 100 and 120 ns the molecule is even detached from the interface. We note a systematic drift of the mean distance of the a-PNA molecule from the interface toward smaller values. Slope of the dashed regression line calculated from the linear regression analysis of the simulation results is equal to −2.433 ± 0.012 mm/s. This large and negative value of the slope suggests that the molecule slowly sinks into the interface. Therefore, to achieve the equilibrium conformation of the system, we continued this simulation for a longer time until we saw that the free energy profile did not change any more, as discussed below. The mean distance of the a-PNA molecule from the interface, calculated in the time interval between 250 and 350 ns, fluctuates around the value 
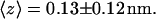Thus, the distance is smaller by ∼0.5 nm than that of the s-PNA molecule. Dash-dot-dot lines denote the mean values of the distance between the 14 individual atoms of the a-PNA molecule and the interface. The distances and their standard deviations are listed in Table 2. Based on these data we can conclude that the a-PNA molecule is attached to the interface with its hydrophobic groups, namely the acetylated N-terminus and amidated C-terminus. The smallest value of the z coordinate is that of the atom O4 of thymine. The collected frames of the simulation suggest that this is because there is a hydrogen bond between this atom and the N-terminus of the a-PNA molecule. Thus, the terminal groups of the molecule as well as the thymine base in the central part of the molecule sink into the interface. Therefore we can conclude that the main driving force of a-PNA adsorption is the hydrophobic interaction. Note that all values of the standard deviation listed in Table 2 are smaller than those in Table 1, which suggests that although the a-PNA adsorption process is slower than that of s-PNA, it eventually results in a stronger attachment of the molecule to the interface.
FIGURE 4.
Same as Fig. 3 but for the molecule a-PNA. 1 – O4 (T), 2 – NT (G2), 3 – N2′ (G2), 4 – N4 (C1), 5 – O6 (G2), 6 – CAY (C1), 7 – N2′ (C1), 8 – center of the molecule, 9 – N2′ (T) and N6 (A), 10 – N2′ (C2), 11 – N2′ (A), 12 – N2′ (G1), 13 – O6 (G1) and N4 (C2). Note the systematic drift of the distance z toward the smaller values indicating that the hydrophobic parts of the a-PNA molecule slowly sink into the interface.
TABLE 2.
Mean distance from the interface and its standard deviation calculated for individual atoms and the geometrical center of the molecule a-PNA
| Atom name and residue | Mean distance from interface | Standard deviation | Position from interface |
|---|---|---|---|
| CAY (C1) | −0.1 | 0.3 | 6 |
| N2′ (C1) | 0.0 | 0.2 | 7 |
| N4 (C1) | −0.17 | 0.32 | 4 |
| N2′ (G1) | 0.45 | 0.14 | 12 |
| O6 (G1) | 0.8 | 0.3 | 13 |
| N2′ (T) | 0.16 | 0.16 | 9 |
| O4 (T) | −0.31 | 0.24 | 1 |
| N2′ (A) | 0.39 | 0.15 | 11 |
| N6 (A) | 0.16 | 0.16 | 9 |
| N2′ (C2) | 0.34 | 0.17 | 10 |
| N4 (C2) | 0.8 | 0.3 | 13 |
| N2′ (G2) | −0.27 | 0.15 | 3 |
| O6 (G2) | −0.15 | 0.21 | 5 |
| NT (G2) | −0.3 | 0.2 | 2 |
| Center of molecule | 0.13 | 0.12 | 8 |
The distance was averaged over the final stage of the simulation (100 ns). The numbers in the last column represent the position of the atoms in the order of growing distance from the interface.
Molecular area per lipid
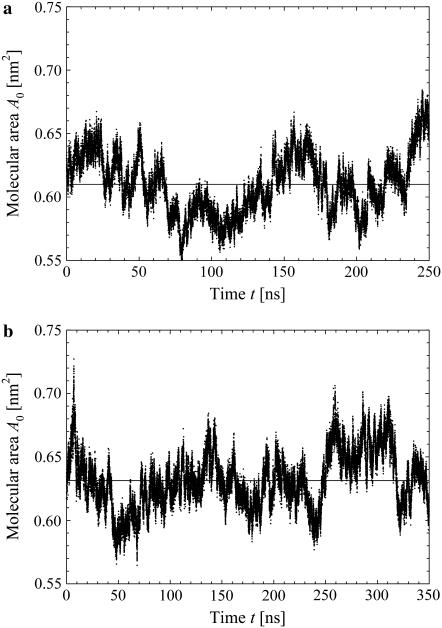
The time evolutions of the molecular area per lipid molecule, calculated for the systems with s-PNA and a-PNA, are presented in Fig. 5, a and b, respectively. The mean values of the molecular area are equal to 0.610 ± 0.025nm2 and 0.631 ± 0.023nm2, respectively. The calculated mean values of the molecular area deviate only slightly from the experimentally found value 0.625 nm2 as well as from the value 0.623 found in our simulations without the PNA molecules. This means that introducing the PNA molecules does not change the surface tension of the lipid bilayer. Note that the mean value of the molecular area per lipid molecule is larger in the system with the a-PNA molecule by ∼3% than that for the system with s-PNA. This may result from sinking of the hydrophobic parts of the a-PNA molecule into the internal part of the bilayer, as discussed in the previous section. The difference between both molecular areas, however, is below the calculated standard deviation. Therefore longer simulations would be necessary to verify this hypothesis.
FIGURE 5.
Time evolution of the molecular area per lipid calculated for the system containing the molecule s-PNA (a) and a-PNA (b). Solid lines denote the average values of the molecular area.
Mean force and free energy profile
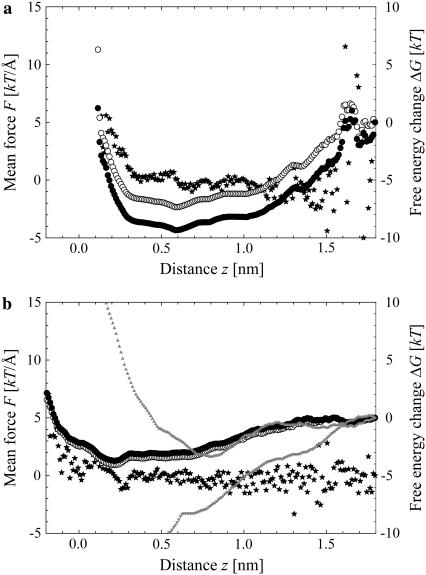
The mean force and free energy profiles of our systems at the end of the simulations for the s-PNA and a-PNA molecules are presented in Fig. 6, a and b, respectively. Stars depict the calculated values of the mean force, whereas open and solid circles denote the values of the free energy calculated using Eqs. 1 and 4, respectively. The reference value of the free energy in all the profiles was set at the value corresponding to the distance 1.8 nm. Results obtained with both methods are very similar, especially in the case of a-PNA. Because of the rapid adsorption of the s-PNA molecule the sampling at the distance >1.5 nm is not sufficient. That is why at this range of the distance the fluctuations of the mean force are large and the free energy profile is inaccurate. Consequently, the free energy profiles in Fig. 6 a calculated with Eqs. 1 and 4 are shifted away from each other by ∼2 kT units. Therefore, it is difficult to predict an exact depth of the free energy minimum based on the results obtained in our simulations.
FIGURE 6.
Free energy profile and mean force between the lipid-water interface and the molecule s-PNA (a) and a-PNA (b). Stars denote the mean force, open circles the free energy change calculated using Eq. 1, and solid circles depict the free energy change calculated using Eq. 5. Note large fluctuations of the force and free energy in the plot (a) above the distance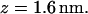 
Gray triangles in panel b denote the free energy profiles calculated with Eq. 1 when ABF is applied. These two profiles correspond to adsorption (
) and desorption (
) of a-PNA molecule.
The profile calculated for a-PNA is smoother. However, the configurations of our systems saved during the simulations suggest that once the PNA molecule adsorbs to the interface, the force measured between the molecule and the interface corresponds rather to a stretching of the molecule and the lipid bilayer than to detachment of the molecule from the interface, as the latter process is very rare. Therefore, we cannot estimate the value of the free energy change associated with adsorption of the a-PNA molecule from the data presented in Fig. 6 b.
For a comparison, two free energy profiles calculated with Eq. 1 and nonzero biasing force are presented in Fig. 6 b as well. The profiles correspond to adsorption and desorption of a-PNA molecule. Both profiles are quite different from the profiles obtained with no biasing force applied. The adsorption free energy profile calculated with the biasing force is shifted toward the larger distance z by ∼0.5 nm. This shift is a direct consequence of pushing a-PNA molecule toward the interface, which does not allow a sufficient equilibration of the lipid bilayer. Therefore, the rapid increase of the adsorption free energy below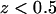 
represents mainly the change of the system free energy corresponding to the deformation of the lipid bilayer under nonequilibrium conditions. The desorption free energy, on the other hand, increases monotonically with the distance z. This change of the system free energy results from a stretching of a-PNA molecule mainly and is not a good estimate of the PNA adsorption free energy as well.
The results obtained with the applied biasing force suggest therefore that the ABF method is not well suitable for calculating the system free energy change in the case of flexible molecules or molecular structures in general. In its classical formulation, the method can offer an accurate estimation of desorption energy only if there is a single, well-defined bond between the molecule and the interface, which can be chosen as the reaction coordinate. If there are a number of bonds between the molecule and the interface, however, calculating the free energy of a single bond will inevitably result in a deformation of the molecule and in an additional change of the system free energy. The applicability of the method can be improved through additional harmonic constraints applied to the flexible parts of the simulated system (P. Weroński and Y. Jiang, unpublished data).
As discussed above, the results presented in Fig. 3 a suggest that the main driving force of s-PNA adsorption at the lipid-water interface is the electrostatic attraction between these atoms of the POPC molecules and s-PNA molecule, which bear high partial atomic charges and form hydrogen bonds. Therefore, to estimate the s-PNA adsorption free energy more accurately, we used the approach based on the summation of the free energy of the hydrogen bonds formed between the PNA molecule and the interface. We used this method to calculate the depth of the free energy primary minima for selected 14 atoms of the first two residues, C1 and G1, which approach the lipid-water interface the most. We chose the atoms identified as hydrogen bond donors or acceptors: N1′ that is the N-terminus nitrogen atom, O1′, O2, N3, N4, and O3′ of the cytosine; and N2, O3′, N3, O6, N7, O1′, H1′, and H1 of the guanine.
Note that in case of the atoms N4 of the cytosine and N2 of the guanine, which are covalently bonded to more than one hydrogen atom, we calculated the distribution density of the distances between the nitrogen atoms and the nearest oxygen atom of the phosphate groups. In case of atoms N1 and N1′ of guanine, which are covalently bonded to single hydrogen atoms, we calculated the distribution density of the distances between these hydrogen atoms, H1 and H1′, and the nearest oxygen atom O3 or O4 instead. The other nine of the chosen 14 atoms, namely O2, N3, O1′, and O3′ of the cytosine; and N3, O6, N7, O1′, and O3′ of the guanine; formed hydrogen bonds with the hydrogen atoms of the lipid amine groups. For these atoms, the distribution density of the distance between them and the nearest hydrogen atom of the POPC amine groups was calculated.
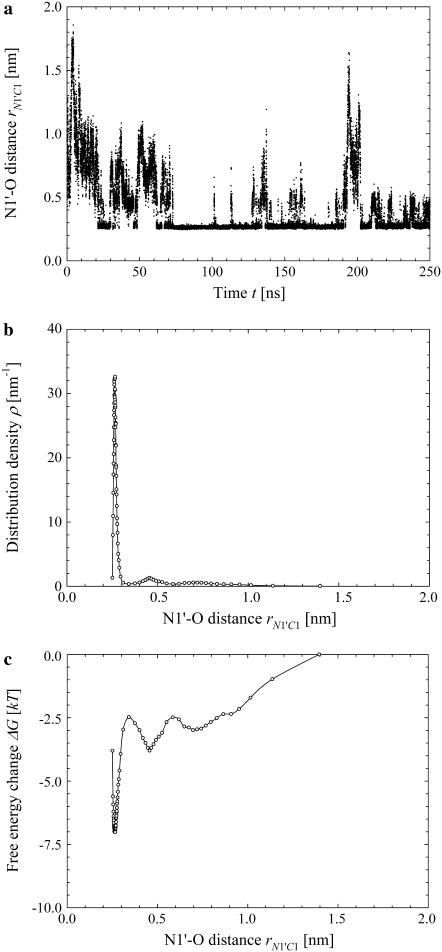
The time evolution of the distance rN1′C1 between the nitrogen atom N1′ of the cytosine C1, to which the terminal hydrogen atoms HT1 through HT3 are bonded, and the nearest of the oxygen atoms O3 and O4 of the POPC molecules is presented in Fig. 7 a. The distribution density ρ(rN1′C1) calculated with Eq. 2 for our system at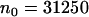 
is presented in Fig. 7 b. We chose the intervals of the distance rN1′C1 in such a way to keep the number of the microstates constant and equal to 
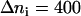except the last interval, where 
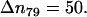The values of the distance rN1′C1 reported in Fig. 7 b represent the average values calculated for each of the intervals.
FIGURE 7.
Simulation results for the hydrogen bond between the hydrogen atoms of the standard N-terminus and the oxygen atoms of the lipid phosphate groups. (a) Time evolution of the distance rN1′C1 between the terminal nitrogen atom N1′ of the molecule s-PNA and the nearest oxygen atom O3 or O4 of the lipid phosphate groups; 250 ns of the time evolution is represented by 31,250 measurements of the distance rN1′C1 at each 8 ps. The intervals ΔrN1′C1 are chosen in such a way to keep the number of the rN1′C1 measurements per interval constant and equal to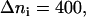 
except the last interval where 
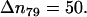The reported values of the distance rN1′C1 represent the average values calculated for each of the intervals. (b) Distribution density ρ of the distance rN1′C1 between the terminal nitrogen atom N1′ of the molecule s-PNA and the nearest oxygen atom O3 or O4 of the lipid phosphate groups. The distribution density was calculated using Eq. 2. (c) Change of the system free energy ΔG as a function of the distance rN1′C1 between the terminal nitrogen atom N1′ of the molecule s-PNA and the nearest oxygen atom O3 or O4 of the lipid phosphate groups. The free energy change was calculated with Eq. 4 and the distribution density at the largest distance 
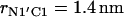was used as the reference value. Note the deep primary minimum at the distance 
when the N-terminus nitrogen atom is separated from the nearest oxygen atom with a single hydrogen atom, as well as the three successive minima of decreasing values, located at the distance rN1′C1 equal to 0.46, 0.70, and 0.91 nm, corresponding to the system configurations in which the N-terminus is separated from the lipid-water interface with one, two, and three water molecules.
The change of the system free energy calculated with Eq. 4 is presented in Fig. 7 c. We used the distribution density at the largest distance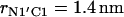 
as the reference value. Fig. 7 c shows that the depth of the primary minimum at the distance 
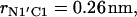when the N-terminus nitrogen atom is separated from the nearest oxygen atom with a single hydrogen atom of the N-terminus, is equal to about −7 kT. Fig. 7 c also shows that, in addition to the primary well, the free energy profile exhibits three successive minima of decreasing values, located at the distance rN1′C1 equal to 0.46 nm, 0.70 nm, and 0.91 nm. These minima correspond to the system configurations in which the N-terminus is separated from the lipid-water interface with one, two, and three water molecules.
The results of our calculations are listed in Table 3. The deepest energy minimum of the value −7 kT is related to the hydrogen bonds formed by the terminal hydrogen atoms HT1 through HT3, bonded to the atom N1′ of the residue C1. The adsorption energy of the s-PNA molecule estimated as a sum of the contributions originating from the individual atoms is equal to about −64 kT units, which is one order of magnitude larger than the values calculated from the free energy profiles in Fig. 6 a. We believe that this value is a better approximation of the actual PNA adsorption energy.
TABLE 3.
Partial atomic charge and hydrogen bond free energy calculated for six atoms of the residue C1 and eight atoms of the residue G1 of the molecule s-PNA
| Mother atom name and residue | Hydrogen atoms names | Partial atomic charges (e) | Total bond free energy (kT) |
|---|---|---|---|
| N1′ (C1) | HT1 | 0.33 | −7.0 |
| HT2 | 0.33 | ||
| HT3 | 0.33 | ||
| O1′ (C1) | – | −0.51 | −5.1 |
| O2 (C1) | – | −0.49 | −4.8 |
| N3 (C1) | – | −0.66 | −4.4 |
| N4 (C1) | H41 | 0.37 | −3.5 |
| H42 | 0.33 | ||
| O3′ (C1) | – | −0.51 | −3.1 |
| N2 (G1) | H21 | 0.32 | −5.1 |
| H22 | 0.35 | ||
| O3′ (G1) | – | −0.51 | −4.9 |
| N3 (G1) | – | −0.74 | −4.8 |
| O6 (G1) | – | −0.51 | −4.6 |
| N7 (G1) | – | −0.60 | −4.5 |
| O1′ (G1) | – | −0.51 | −4.1 |
| N1′ (G1) | H1′ | 0.31 | −4.1 |
| N1 (G1) | H1 | 0.26 | −3.8 |
| Total ΔG | −63.8 |
The values of the free energy change were calculated using Eq. 4 and the interatomic distance distribution density found in the MD simulation that lasted 250 ns.
The PNA-bilayer interaction is very short ranged. The mean radii of the PNA molecules, calculated in the systems without a bilayer during equilibration of the PNA molecules in water, were equal to 0.7 ± 0.3 nm and 0.78 ± 0.34 nm for the molecule with charged and neutral termini, respectively. The smaller mean radius of the s-PNA molecule could result from the attractive interaction between its charged termini, which can make the molecule more compact. The data presented in Fig. 6, a and b, suggest that the interaction range of the PNA molecules and the lipid-water interface is comparable to the mean size of the molecules. It seems to be a little larger in the case of the molecule with charged termini, which is consistent with the fact that the electrostatic or molecular dipole interaction is longer ranged than the hydrophobic interaction.
The mean force and energy profiles changed during the simulations. In the case of the a-PNA molecule the change was caused by slow sinking of the molecule into the bilayer, as discussed above. Therefore, one can see that the free energy profile calculated for the a-PNA molecule extends to smaller values of the molecule-interface distance.
CONCLUSIONS
We use all-atom MD simulations to investigate adsorption of small PNA molecules at a lipid bilayer. Our results suggest that in a lipid-water system at low ionic strength PNA molecules spontaneously accumulate at the lipid-water interface. Considering that standard PNA molecules are typically soluble in water but not in organic solvents, it is interesting to find the PNA association with the lipid bilayer. We conclude that the change of the system free energy associated with adsorption of the small PNA molecules at the lipid-water interface is on the order of several tens of kT per PNA molecule consisting of six monomers. In the case of s-PNA molecules with charged terminal groups the main driving force of adsorption is the electrostatic attraction between the charged groups of the molecules and the charged heads of lipids. The absolute values of the partial atomic charges of the oxygen atoms of the POPC phosphate group, as well as the hydrogen atoms of the PNA N-terminal, are higher than the absolute values of the partial charges of the oxygen atoms of the PNA C-terminal and the hydrogen atoms of the lipid amine group, respectively. Therefore, preferentially the positively charged terminus of the s-PNA molecule is bonded to the phosphate group of the POPC molecule, whereas the negatively charged C-terminus is pushed away from the interface. In the case of a-PNA molecules with neutral termini the main driving force of adsorption is the hydrophobic interaction of the nonpolar PNA groups. The hydrophobic parts of the a-PNA molecule sink into the organic interior of the bilayer, and therefore the mean distance of the molecule from the interface is smaller by a few angstroms compared to that of the s-PNA.
The PNA membrane association for low ionic strength and high concentration of the lipid and PNA is an interesting and perhaps even an unexpected prediction because PNA is known to solvate easily in water. Preliminary results of our simulations of the lipid bilayer at ionic strength and pH corresponding to the physiological conditions, however, suggest that strong adsorption of ions at the lipid-water interface takes place. Therefore, we conjecture that at higher ionic strength a compact hydration layer associated with the interface can effectively prohibit PNA adsorption, in agreement with the experimental results. At these conditions, due to the only weak adsorption of the standard PNA, we conjecture a backbone modified PNA could be more suited as a simple gene for the proposed protocell. Exactly how the backbone modifications need to be done has to be calculated and ultimately tested experimentally, where the presented results can be used as benchmarks. It should also be noted that the predicted PNA-lipid adsorption could play a role for the investigations based on PNA for gene therapy utilizing liposome delivery systems.
SUPPLEMENTARY MATERIAL
A supplement to this article can be found by visiting BJ Online at http://www.biophysj.org. The partial atomic charges for the atoms of the PNA backbone as well as the additional PNA parameters used in our simulations that are not provided in the standard CHARMM27 parameter files are available in the Supplementary Material.
Supplementary Material
Acknowledgments
We thank Prof. Lennart Nilsson for providing us with his topology and parameters files for PNA, Profs. Peter Nielsen and Ole Mouritsen for their comments and discussions of the simulation results, and all co-workers of the Protocell Assembly team at the Los Alamos National Laboratory for the many stimulating discussions and valuable suggestions.
This work was carried out under the auspices of the National Nuclear Security Administration of the U.S. Department of Energy at Los Alamos National Laboratory under contract No. DE-AC52-06NA25396.
References
- 1.Nielsen, P. E., and M. Egholm. 1999. An introduction to peptide nucleic acid. Curr. Issues Mol. Biol. 1:89–104. [PubMed] [Google Scholar]
- 2.Zhilina, Z. V., A. J. Ziemba, and S. W. Ebbinghaus. 2005. Peptide nucleic acid conjugates: synthesis, properties and applications. Curr. Top. Med. Chem. 5:1119–1131. [DOI] [PubMed] [Google Scholar]
- 3.Rasmussen, S., L. Chen, M. Nilsson, and S. Abe. 2003. Bridging nonliving and living matter. Artif. Life. 9:269–316. [DOI] [PubMed] [Google Scholar]
- 4.Rasmussen, S., L. Chen, D. Deamer, D. C. Krakauer, N. H. Packard, P. F. Stadler, and M. A. Bedau. 2004. Transitions from nonliving to living matter. Science. 303:963–965. [DOI] [PubMed] [Google Scholar]
- 5.Leach, A. R. 2001. Molecular Modelling: Principles and Applications, 2nd Ed. Prentice Hall, Harlow, UK.
- 6.Norberg, J., and L. Nilsson. 2002. Molecular dynamics applied to nucleic acids. Acc. Chem. Res. 35:465–472. [DOI] [PubMed] [Google Scholar]
- 7.Gumbart, J., Y. Wang, A. Aksimentiev, E. Tajkhorshid, and K. Schulten. 2005. Molecular dynamics simulations of proteins in lipid bilayers. Curr. Opin. Struct. Biol. 15:423–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kale, L., R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan, and K. Schulten. 1999. NAMD2: greater scalability for parallel molecular dynamics. J. Comp. Phys. 151:283–312. [Google Scholar]
- 9.CHARMM web site. http://www.charmm.org/document/Charmm/c31b1/index.html. Accessed February 10, 2005.
- 10.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- 11.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karpus. 1983. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 12.Shields, G. C., C. A. Laughton, and M. Orozco. 1998. Molecular dynamics simulation of a PNA·DNA·PNA triple helix in aqueous solution. J. Am. Chem. Soc. 120:5895–5904. [Google Scholar]
- 13.Sen, S., and L. Nilsson. 1998. Molecular dynamics of duplex systems involving PNA: structural and dynamical consequences of the nucleic acid backbone. J. Am. Chem. Soc. 120:619–631. [Google Scholar]
- 14.Sen, S., and L. Nilsson. 2001. MD Simulations of Homomorphous PNA, DNA, and RNA single strands: characterization and comparison of conformations and dynamics. J. Am. Chem. Soc. 123:7414–7422. [DOI] [PubMed] [Google Scholar]
- 15.Schlenkrich, M., J. Brickmann, A. D. MacKerell, and M. Karplus. 1996. Empirical potential energy function for phospholipids: criteria for parameter optimization and applications. In Biological Membranes: A Molecular Perspective from Computation and Experiment. K. M. Merz and B. Roux, editors. Birkhauser, Boston, MA. 31–81.
- 16.MacKerell, A. D., D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, et al. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- 17.Feller, S. E., and A. D. MacKerell. 2000. Improved empirical potential energy function for molecular simulations of phospholipids. J. Phys. Chem. B. 104:7510–7515. [Google Scholar]
- 18.Foloppe, N., and A. D. MacKerell. 2000. All-atom empirical force field for nucleic acids. I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comput. Chem. 21:86–104. [Google Scholar]
- 19.MacKerell, A. D., and N. K. Banavali. 2000. All-atom empirical force field for nucleic acids. II. Application to molecular dynamics simulations of DNA and RNA in solution. J. Comput. Chem. 21:105–120. [Google Scholar]
- 20.Feller, S. E., K. Gawrisch, and A. D. MacKerell. 2002. Polyunsaturated fatty acids in lipid bilayers: intrinsic and environmental contributions to their unique physical properties. J. Am. Chem. Soc. 124:318–326. [DOI] [PubMed] [Google Scholar]
- 21.Mackerell, A. D., M. Feig, and C. L. Brooks. 2004. Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 25:1400–1415. [DOI] [PubMed] [Google Scholar]
- 22.Heller H. http://www.lrz-muenchen.de/∼heller/membrane/fluid-H.pdb.Z. Accessed May 20, 2005.
- 23.Heller, H., M. Schaefer, and K. Schulten. 1993. Molecular dynamics simulation of a bilayer of 200 lipids in the gel and in the liquid-crystal phases. J. Phys. Chem. 97:8343–8360. [Google Scholar]
- 24.Vacklin, H. P., F. Tiberg, G. Fragneto, and R. K. Thomas. 2005. Phospholipase A2 hydrolysis of supported phospholipid bilayers: a neutron reflectivity and ellipsometry study. Biochemistry. 44:2811–2821. [DOI] [PubMed] [Google Scholar]
- 25.Rasmussen, H., J. S. Kastrup, J. N. Nielsen, J. M. Nielsen, and P. E. Nielsen. 1997. Crystal structure of a peptide nucleic acid (PNA) duplex at 1.7 A resolution. Nat. Struct. Biol. 4:98–101. [DOI] [PubMed] [Google Scholar]
- 26.Wittung, P., J. Kajanus, K. Edwards, G. Haaima, P. E. Nielsen, B. Norden, and B. G. Malmstrom. 1995. Phospholipid membrane permeability of peptide nucleic acid. FEBS Lett. 375:27–29. [PubMed] [Google Scholar]
- 27.Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald: an N.log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 28.Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
- 29.Ryckaert, J. P., G. Ciccote, and J. C. Berendsen. 1977. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
- 30.van Gunsteren, W. F., and H. J. C. Berendsen. 1982. Algorithms for Brownian dynamics. Mol. Phys. 45:637–647. [Google Scholar]
- 31.Martyna, G. J., D. J. Tobias, and M. L. Klein. 1994. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 101:4177–4189. [Google Scholar]
- 32.Feller, S. E., Y. H. Zhang, R. W. Pastor, and B. R. Brooks. 1995. Constant pressure molecular dynamics simulation: the Langevin piston method. J. Chem. Phys. 103:4613–4621. [Google Scholar]
- 33.Henin, J., and C. Chipot. 2004. Overcoming free energy barriers using unconstrained molecular dynamics simulations. J. Chem. Phys. 121:2904–2914. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.